Abstract
We study models of two sequential enzyme-catalyzed reactions as a basic functional building block for coupled biochemical networks. We investigate the influence of enzyme distributions and long-range molecular interactions on reaction kinetics, which have been exploited in biological systems to maximize metabolic efficiency and signaling effects. Specifically, we examine how the maximal rate of product generation in a series of sequential reactions is dependent on the enzyme distribution and the electrostatic composition of its participant enzymes and substrates. We find that close proximity between enzymes does not guarantee optimal reaction rates, as the benefit of decreasing enzyme separation is countered by the volume excluded by adjacent enzymes. We further quantify the extent to which the electrostatic potential increases the efficiency of transferring substrate between enzymes, which supports the existence of electrostatic channeling in nature. Here, a major finding is that the role of attractive electrostatic interactions in confining intermediate substrates in the vicinity of the enzymes can contribute more to net reactive throughput than the directional properties of the electrostatic fields. These findings shed light on the interplay of long-range interactions and enzyme distributions in coupled enzyme-catalyzed reactions, and their influence on signaling in biological systems.
INTRODUCTION
Biochemical reactions in cells are well-orchestrated by sequential coupling and tight regulation, and as a result, they form complex reaction networks, as is observed in signal transduction,1 gene expression regulation,2, 3 and sequential metabolic enzymatic reactions.4 Approaches for characterizing, analyzing, and modeling the networks5, 6, 7, 8, 9, 10 have included, for example, the modeling of biochemical reactions based on coupled chemical kinetic equations,9 the construction of topology models of metabolic networks,6 the identification of functional motifs,10 and modularization7 in biochemical reaction networks. All of these system-level or network-level approaches have provided useful insights and conceptual frameworks for better understanding the reaction networks, but a molecular-level understanding of how biochemical reactions influence each other is still lacking, even in the relatively simple two-enzyme coupled reaction cases, which represent minimal functional units of reaction networks.
In two-enzyme coupled reactions, the transfer of intermediate substrates between enzymes is one key factor in determining the strength of coupling. In many cases, the intermediates are transported via diffusion in solution and thus it is natural to implement diffusion-reaction equations as a basis of the system's physical description. However, the modeling of realistic biological systems still requires many other considerations such as the molecular crowding effect11 and the influence of neighboring reactive molecules,12 in addition to the primary considerations of chemical reactions themselves such as identifying reaction sites and determining their reactivities. Because of all these important considerations, it is very challenging to create models that take into account all the molecular details in a system. However, consideration of some molecular factors may be crucial in characterizing the biological function of the coupled chemical reactions as well as in determining their reaction efficiencies.
To understand how molecular factors affect two-enzyme coupled reactions in detail, we focus on the simplest cases of coupled biochemical reactions where the product of the first enzymatic reaction is transferred to the second enzyme to serve as the substrate for the second enzyme-catalyzed reaction. In this case, the reaction events occur sequentially, and so we can consider that the signal or information flows in a one-directional way. Thus, sequential enzyme-catalyzed reactions can be modeled as a transducer in functional motifs of the network-level approach.10 Furthermore, the functional utility of this module may be evaluated as the transfer efficiency of intermediate substrate between two enzymes, and again this transfer efficiency may be dependent on several molecular factors including the separation between the two enzymes, the molecular geometry of the involved enzymes, the existence of a “crowded” cellular environment, the electrostatic interactions between enzymes and substrates, as well as other considerations. Therefore, a central concern is to determine how the transfer efficiency depends on these molecular parameters. In fact, this transfer efficiency has been previously discussed in the context of substrate channeling,13, 14, 15 and particularly it was suggested that electrostatic interactions play an important role in sequential enzymatic reactions by creating electrostatic channels between the two enzymes that serve to guide the product of the first reaction toward the active site of the second enzyme.16, 17, 18
Electrostatic channeling is a mechanism of substrate transport which was first proposed as a possible explanation for unusually fast reaction kinetics involving coupled two-enzyme reactions that do not contain any intermolecular tunnels capable of shielding the substrate from diffusing into the bulk solution.13, 14, 15, 17 As in a typical instance of substrate channeling, the role of an electrostatic channel is also to restrict the diffusive motion of the substrate to paths between the two enzymes.18 However, in contrast to substrate channeling by molecular tunnels, this type of “channel” is established only by electrostatic potential, not by geometric confinement of the substrate, and thus, there is always a nonzero probability for the substrate to escape to the bulk solution, resulting in a reduced transfer efficiency. With this in mind, it is critical that the charge distribution responsible for the electrostatic potential favors transport of the substrate to the second enzyme's active site. For example, the bifunctional enzyme Dihydrofolate Reductase-Thymidylate Synthase (DHFR-TS) from the protozoan Leishmanina major reveals that an electrostatic potential favorable for substrate transport is formed between two active sites (or two enzymes in our context) from the x-ray crystal structure.16 A computer simulation18 as well as experimental kinetic19, 20 studies also support the existence of electrostatic channeling in L. major DHFR-TS. Later, other instances of electrostatic channeling were observed in sulfate-activating complex,21Toxoplasma gondii DHFR-TS,22 and a fusion protein of malate dehydrogenase and citrate synthase.23
The goal of this work is to systematically study two-enzyme sequential reactions with a few molecular parameters as a minimal model for biochemical reaction networks and also to provide a basic understanding of the role of electrostatic interactions in sequential enzyme-catalyzed reactions with an emphasis on the formation of electrostatic channeling. For this purpose, we employ simple sphere models that are similar to the ones in our previous research,12 which retain key molecular parameters such as separation distance between the two enzymes and electric charges. We numerically solve the coupled differential equations describing the model systems and based on the numerical solutions, we investigate the basic principles behind sequential enzyme-catalyzed reactions. Note that the set of coupled equations in our microscopic model is different from a similar set of coupled ordinary differential equations in the macroscopic models that are traditionally implemented in models of enzyme kinetics; the former has spatial dependence based on diffusion while the latter does not have spatial dependence but only time-dependence.
This paper is organized as follows: In Sec. 2, we describe our sequential enzyme reaction model and explain its mathematical and physical background. Next, we discuss the effect of electrostatic interaction in general terms by implementing a single enzyme reaction model. In Sec. 3, we initially study the sequential enzyme reactions in non-electrostatic cases by numerically solving the coupled diffusion-reaction equations. From these solutions, we investigate the coupling effect by examining the reaction rates as a function of separation between enzymes. Next, we consider the effect of electrostatic interactions on the concentrations as well as the reaction rates (note that in this system, the enzymes and the intermediate are electrically charged). Finally, we study the cases where a strong electrostatic potential exists in between two coupled enzymes and discuss how the inclusion of the electrostatic potential accelerates the reaction kinetics and causes electrostatic channelling. In Sec. 4, we summarize our findings and discuss some of the implications of our work.
MODEL AND THEORY
Sequential enzyme reaction model
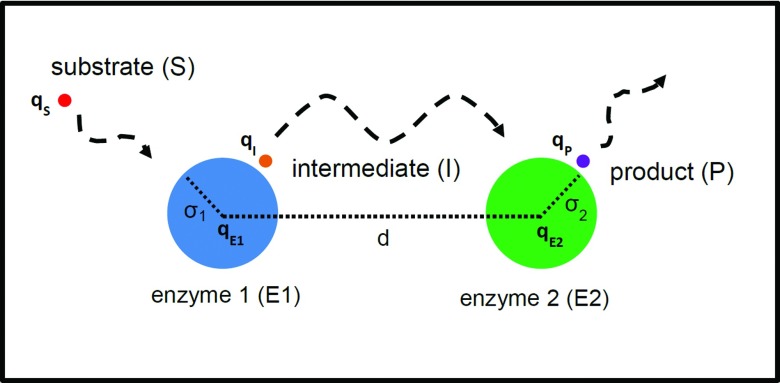
To study sequential enzymatic reactions with electrostatic interactions, we introduce a simple reaction model based on the spherical representation of molecules shown in Figure 1. For simplicity, we assume the active site of each enzyme is uniformly distributed over the sphere surface and the electric charge is located at the center of sphere. We further simplify the model by assuming that the system has reached steady-state and the reactions are diffusion-limited; reactions in this model occur immediately once two reactants encounter each other. Moreover, we assume the enzymes have a finite size, while other chemical species such as substrate are treated as point particles (but with finite diffusion constants) so that the reaction encounter distances are the radii of the enzymes. Since this system represents sequential enzymatic reactions, the product of the first reaction at Enzyme 1 (E1) is used as the substrate for the second reaction at Enzyme (E2). We name this common reactant that participates in both reactions as the intermediate, thus giving the following reaction scheme:
Since one main concern is how the separation between the two enzymes influences the reactions, we consider various cases with different separation distances between E1 and E2. Specifically, we fix the positions of the enzymes in our coordinate system, and in that given separation, we allow other chemical species to freely diffuse under the influence of electrostatic potentials, with the same diffusion constant. Reaction events are taken into account by the absorbing boundary conditions such that the concentrations of substrate at E1 and intermediate at E2 are zero (see Table 1).24 Additionally, as a result of a reaction, we assume that all substrates at E1 are chemically transformed into the intermediates via enzyme-catalyzed reactions so that the reaction rate of substrate at E1 is equal to the production rate for intermediate, which is used for the boundary condition of the intermediate at E1 (see Table 1). We use an analogous boundary condition for the product in reaction 2, when the intermediate reacts with E2 to form product. In the actual numerical calculation, there is slight numerical disagreement between the given flux from the boundary condition (input) and the calculated flux from the solution (output). To correct this, we apply a modest scaling factor for the estimated flux in the boundary condition to ensure that the calculated intermediate (or product) flux is exactly the same with the substrate (or intermediate) flux. The scaling factor (less than 1.25 in most cases) is necessary for computing correct magnitudes of concentrations as well as production rates, as is demonstrated in Sec. 2B.
Figure 1.
Schematic of two sequential enzyme-catalyzed reactions in our model.
Table 1.
Boundary conditions in our sequential enzyme reaction model. ci and ki (i = S, I, P) are the concentration and the reaction/production rate, respectively.
| Boundary condition (BC) | At E1 | At E2 | At outer boundary |
|---|---|---|---|
| Substrate (S) | Absorbing BC | Reflecting BC | cS = 1 |
| Intermediate (I) | kI = kS | Absorbing BC | cI = 0 |
| Product (P) | Reflecting BC | kP = kI | cP = 0 |
In addition to defining the chemical reactions using boundary conditions, other boundary conditions are also introduced to make the model mathematically well-posed. Since the substrate does not react with E2, we use a reflecting boundary condition for the substrate at E2, which means that E2 only impacts the substrate reaction rate indirectly via its excluded volume. Similarly, the same reflecting boundary condition is applied to the product at E1 because the product and E1 do not react. Furthermore, since our model is in steady-state, we assume the substrate is continuously supplied from the bulk solution, and so at large distances, the concentration of the substrate is constant and equal to its bulk concentration.24 On the contrary, at large distances, we assume that the concentrations of the intermediate and the product are zero, supposing that other scavenger molecules consume these chemical species or that they are escaping from the system. All the boundary conditions mentioned above are summarized in Table 1.
For electrostatic interaction, we employ a simple Coulombic model for which the steady-state solutions24 and the time-transient solutions (Green's functions)25, 26, 27 are available. In the model, the concentration of one reactant (A) around the other stationary reactant (B) is simply governed by the following diffusion equation:
| (1) |
where c, D, kB, T, and U are the concentration of A, the relative diffusion constant, the Boltzmann constant, the absolute temperature, and the external potential, respectively. In this case, U is given by the Coulombic interaction between A and B, and as in Eq. 2, it can be simply expressed with the Bjerrum length (or Onsager length), λB = e2/4πε0εkBT, where e, ε0, and ε are the elementary charge, the vacuum permittivity, and the relative permittivity of the solution, respectively,
| (2) |
Here, q1 and q2 are the electric charges of A and B in units of the elementary charge, respectively, and r is the distance between A and B.
We extend this model to study sequential enzyme reactions by modifying the electrostatic interaction and coupling the equations with the boundary conditions given in Table 1. In the model, the diffusion equations are formulated in the following way:
| (3) |
with
| (4) |
where ci, qi, rE1 − i, rE2 − i, qE1, and qE2 are the concentration and the charge of i, the distances of i from E1 and E2, and the charges of E1 and E2, respectively. Here, the index i could be S (substrate), I (intermediate), or P (product). In principle, by solving these three coupled equations, we obtain the spatial distributions of concentration and from them, we calculate other physical quantities such as reaction rate ki, as is shown below,
| (5) |
which is the surface integral of the flux of i over the enzyme surface of E. We use this quantity to set up the boundary conditions for the intermediate and the product in Table 1, but actually we use a stronger condition where the integrands, or the fluxes, satisfy the same relations with the integrated ones, or the rates (e.g., kI = kS), since the chemical reactions can be position-dependent over the reactive surface. For example, we use the following boundary condition for the intermediate at E1:
| (6) |
Note that the incoming and the outgoing fluxes have opposite signs and are spatially-dependent over the E1 surface. It is worth noting that for diffusion-limited reactions, the reaction rate is determined by the transport (flux) of reactant to the reaction site as in Eq. 5. However, when the subsequent reaction at the enzyme surface occurs at a significantly slower rate compared to the diffusion process, as is characteristic of reaction-limited cases, the observed acceleration of reaction-diffusion kinetics could have contributions both from an increased intrinsic rate constant at the surface or higher transfer efficiency (e.g., electrostatic channeling).28
Ideally, it would be desirable to analytically solve the coupled diffusion-reaction equations to get the exact solutions. However, it is very challenging because of the absence of a good coordinate system for representing the boundary conditions given in Table 1. We already discussed some details of this difficulty in our previous work.12 To avoid this issue and to extend our study to non-spherical systems, we use a numerical method to solve the equations.
The numerical method we employ essentially consists of two parts: (1) generating molecular meshes and (2) based on these meshes, solving the equations numerically. Specifically, we represent our model systems using the meshes in Cartesian coordinates, and in the discrete space constructed by the meshes, we numerically solve the differential equations using the numerical technique called the finite element method (FEM). The basic idea of the FEM is to reformulate partial differential equations in a weak form, and then use variational methods to obtain stable solutions.29 In detail, for creating molecular meshes, we use the GAMER toolkit.30 We use higher resolution finite element tetrahedra to numerically estimate the strong concentration gradients arising at the enzymes, where substrate is generated or depleted, while far from the reactive centers lower resolution meshes are employed. For the FEM, we extend the python-based program Smolfin31 to apply to our model systems. Smolfin is the software designed for solving Smoluchowski-type equations based on the FEniCS solver (http://fenicsproject.org).32 Finally, by solving the coupled equations numerically, we obtain the concentrations of substrate, intermediate, and product, and from these concentrations, we calculate the reaction rates using Eq. 5.
Additionally in our model, we use the normalized concentration, which is the concentration divided by the bulk concentration of substrate. Thus, a concentration of 1 means that it has the same concentration as the bulk substrate concentration. For the diffusion constant, we use D = 780 μm2s−1 of Ca2+ in solution.31 For other parameters, λB is 7 Å (for water at room temperature) and the radius of enzymes is 10 Å unless otherwise mentioned. The radius of the sphere used to define the outer boundary condition is 500 Å.
Accuracy test of our numerical method with a single enzymatic reaction
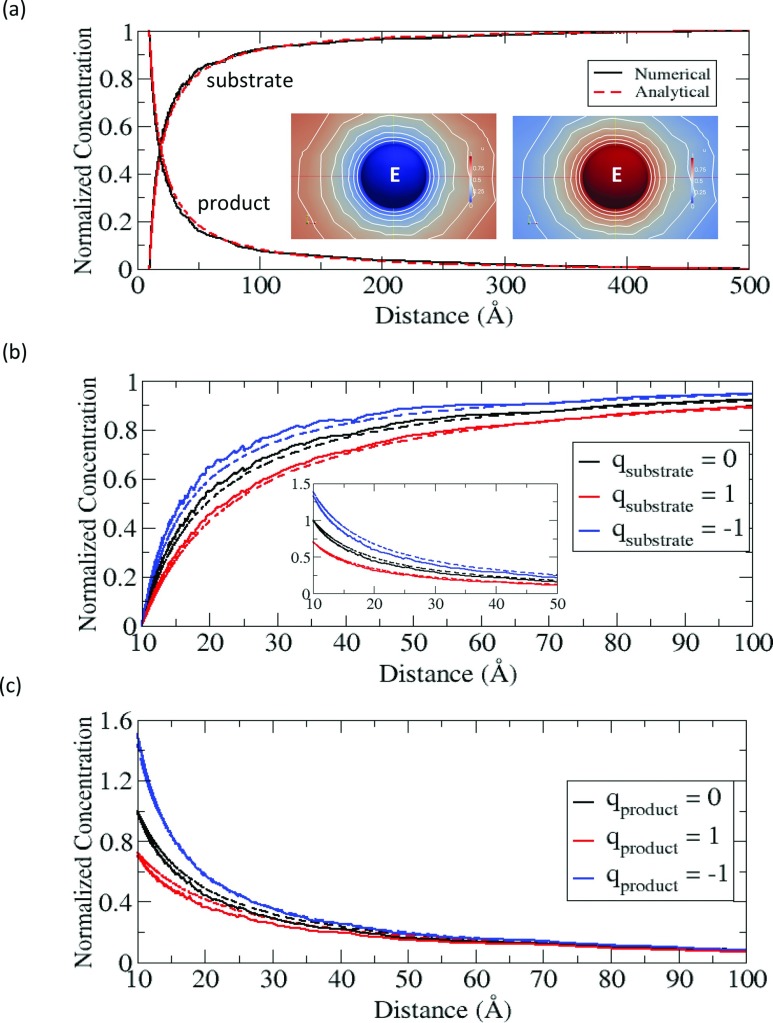
Before we apply the numerical method to our sequential enzyme reaction system, we first test this method using the simple Coulombic model of a single enzymatic reaction to evaluate the accuracy of our numerical calculation. Compared to the sequential reaction model, the reaction scheme is basically the same, but we ignore the E2-dependent part. In the single enzyme case, the diffusion-reaction equations can be solved analytically and the exact solutions are given in Appendix A. Fig. 2 shows the solutions (concentrations) obtained from our numerical calculation in the electrically neutral case (Fig. 2a) and in the charged cases with an enzyme charge of +1 (Figs. 2b, 2c). To compare the numerical results with the exact solutions, we calculate the normalized concentration profiles of the substrate and the product. The comparison (solid vs. dotted lines) shows close agreement both in the non-electrostatic and in the electrostatic cases. The deviations from the exact solutions, especially in the intermediate region (d = 20–40 Å), are probably caused by the large variation of solutions in the volumetric meshes with relatively low spatial resolution.
Figure 2.
(a) Normalized concentration profiles of substrate and product in a single enzyme reaction model as a function of the distance from the enzyme in a non-electrostatic case. The left and right insets are the concentrations of substrate and product, respectively, represented in the color maps (pure red = 1, pure blue = 0). (b) Normalized concentration profiles of substrates with qsubstrate, when qE = +1 and qproduct = 0. The inset is the profiles of products corresponding to the same colored substrates. (c) Normalized concentration profiles of products with qproduct, when qE = +1 and qsubstrate = 0.
Besides examining the concentrations, we also evaluate the accuracy of the reaction rates for the three cases in Fig. 2b. The numerical error is less than 5%, as is shown in Table 2.
Table 2.
Reaction rates for the single enzymatic reaction in the three cases of Fig. 2b. The enzyme has +1 charge.
| Case | Numerical calculation (109M−1 s−1) | Analytical calculation (109M−1 s−1) | Relative error (%) |
|---|---|---|---|
| qsubstrate = +1 | 4.39 | 4.19 | 4.8 |
| qsubstrate = +0 | 6.15 | 6.02 | 2.1 |
| qsubstrate = –1 | 8.28 | 8.32 | 0.6 |
Electrostatic effects in a single enzymatic reaction model
In addition to evaluating the accuracy, the previously described single enzymatic reaction model can reveal how the electrostatic interaction influences the reaction in terms of the reaction rate of the substrate and the concentration profiles. For the attractive case with a substrate charge of −1, the reaction rate increases compared to the neutral case (see Table 2), and the concentration of substrate is higher than is calculated for the neutral case (see Fig. 2b). Clearly, the attraction between the substrate and the enzyme bring them closer and as a result the substrate concentration increases near the enzyme, and this also leads to an increase of incoming flux of substrate toward the enzyme. In contrast to this, the electrostatic repulsion experienced with a substrate charge of +1 exhibits the opposite effect, and thus, the concentration in Fig. 2b is shifted away from the enzyme and the reaction rate in Table 2 decreases compared to the other cases. Not only does the electrostatic interaction between the substrate and the enzyme affect the substrate itself, but it also affects the product, despite the product not being charged. This is because the generating rate for product at the enzyme is directly proportional to the reaction rate of substrate. Consequently, for the attractive case, the concentration of product increases, as shown in the inset of Fig. 2b. But for the repulsive case, it shows the opposite trend. Irrespective of this influence, when the product itself is electrically charged after the reaction, the electrostatic interaction between the enzyme and the product also influences the concentration profile of the product near the enzyme, as is shown in Fig. 2c. Consistent with Fig. 2b, the attraction with the product charge of –1 increases the local concentration of product around the enzyme, and the repulsion with the product of charge +1 decreases the product concentration around the enzyme.
RESULTS AND DISCUSSION
Sequential enzyme reaction in non-electrostatic cases
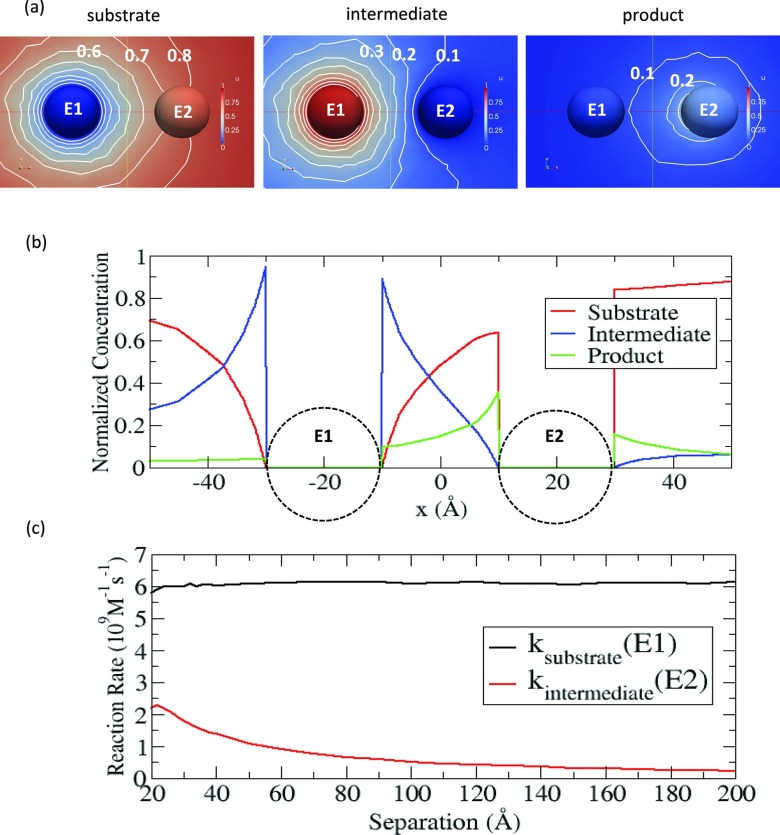
First, we numerically solve the coupled diffusion-reaction equations for the sequential enzyme reactions in non-electrostatic cases, to understand the pure coupling effect itself before adding the electrostatic features to our model. Since the coupling effect is dependent on the separation distance (d), we consider each of the cases with various separation distances. Fig. 3a shows one example with d = 40 Å, in which the numerical solutions for the substrate, the intermediate, and the product are represented in the color maps. In the sequential enzyme reactions, the spherical symmetry of the substrate concentration observed in a single enzyme case is broken due to the presence of the second enzyme. In fact, Fig. 3b demonstrates that the normalized concentration profile is asymmetric around E1 (as revealed by comparing the concentrations at x = –40 Å and x = 0 Å). In this case, the degree of asymmetry is relatively small, but as the size of E2 increases or if E2 is reactive with the substrate, the neighbouring effect by E2 on the substrate becomes significant12 and the substrate profile would be more asymmetric. For the concentrations of the intermediate and the product, they also have asymmetry around E1 and E2. Note that because of leakage of the intermediate to the bulk during the transport of intermediate from E1 to E2, the amount of product generated at E2 is less than the amount of intermediate generated at E1, and thus the concentration of product is also lower than the concentration of intermediate.
Figure 3.
(a) Normalized concentrations of substrate (left), intermediate (middle), and product (right) in the color maps (pure red = 1, pure blue = 0), when the separation distance is 40 Å. The white lines are the contours of concentrations in an interval of 0.1 (0.1, 0.2, …) (b) Normalized concentration profiles of substrate (red), intermediate (blue), and product (green) along the line connecting E1 at –20 Å and E2 at 20 Å (c) Reaction rates of the substrate at E1 and the intermediate at E2 are shown as a function of separation.
To study the dependence of the reactions on the separation between two enzymes, we calculate the reaction rates of substrate at E1 and of the intermediate at E2 as a function of the separation distance between E1 and E2. As revealed in Fig. 3c, the reaction rate for the substrate at E1 is fairly stable except at the very short separation distances (d < ∼25 Å). As mentioned previously, when E2 is non-reactive and its size is relatively small compared to E1, the neighbouring effect is insignificant so that the rate is very close to the rate as predicted in the absence of E2. However, the reaction rate for the intermediate at E2 decreases significantly with the separation. This is because as the separation increases, the intermediate has more chances to escape to the bulk solution without reacting with E2. This decrease is consistent with observations made in similar systems.33, 34
Interestingly, as shown in Fig. 3c, we observe a small peak (d = ∼22 Å) in the calculated reaction rate of intermediate. This is a result of the coupling between the two reactions. As we discussed in previous work,12 the reaction rate is lower in the presence of other particles in the proximity of a reactant. Thus, to increase the reaction rate of substrate, it is advantageous to separate the two enzymes as far apart as possible. However, this increasing of separation is a disadvantage for the second reaction because it increases the loss of intermediate during transport between the two enzymes, and consequently, the reaction rate of intermediate at the second enzyme decreases. Therefore, since these two opposite effects are competing with each other, there could exist an optimal distance, at which the reaction rate for the second reaction is maximized. But when E2 is small and non-reactive, the neighboring effect by E2 does not significantly affect the reaction at E1 and the challenge of transporting intermediate with increasing separation becomes more important. In this case, the maximum reaction rate always appears at the closest separation distances (or the contact distances).
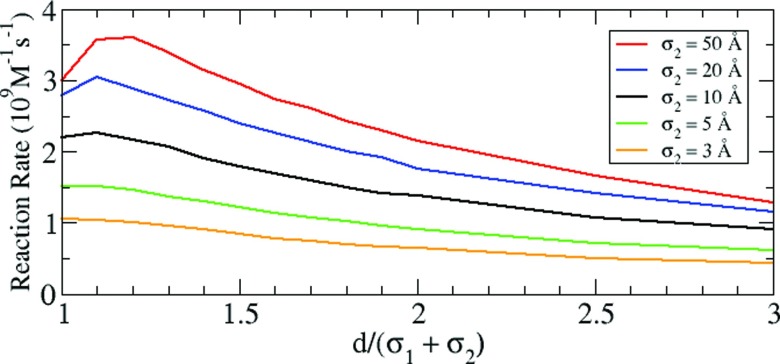
To clearly see this coupling effect, we further consider other cases, specifically where E2 is larger than E1 so that the first reaction is significantly influenced by E2. Fig. 4 shows that as the size of E2 is increased, the optimal distance for the maximum reaction rate is shifted from the short contact distance to larger separation distances. This suggests that when E2 is much larger than E1, the contact distance is not necessarily the optimal distance for maximizing the reaction rate.
Figure 4.
Reaction rate of the intermediate at E2 with σ2 = 3, 5, 10, 20, and 50 Å. σ1 ( = 10 Å) and σ2 are the radii of E1 and E2, respectively.
Sequential enzyme reaction in electrostatic cases
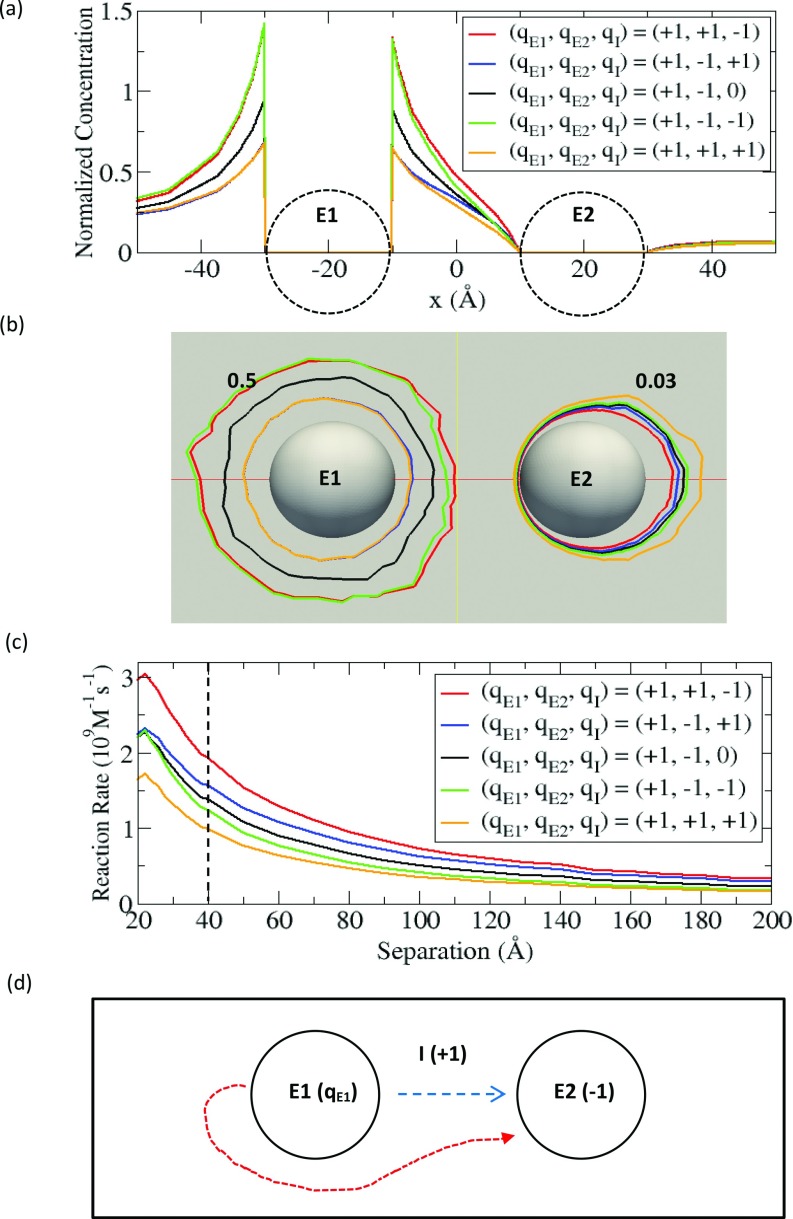
Next, we study the effect of electrostatic interaction on sequential enzyme reactions. Since our primary interest is in the transport of intermediate between the two enzymes, we restrict ourselves to the cases where the substrate and the product are electrically neutral but the intermediate is electrically charged. To systematically investigate this subject, we consider all possible charge combinations of E1, E2, and the intermediate (I) with charges of +1 and –1. For the sake of convenience, we introduce a simple notation (qE1, qE2, qI) to describe the charge on each state variable. The first, second and third component in the above parenthesis represent the electric charges of E1, E2, and the intermediate. Since the Coulomb potential has symmetry with respect to exchanging charges between particles and inverting all the charges to the opposite cases, we exclude these duplicate cases in our study; for example, (+1, +1, –1) and (–1, –1, +1) are equivalent, and (+1, +1, +1) and (–1, –1, –1) are also equivalent. Thus, with a fixed charge of +1 on E1, we examine the four cases of (+1, +1, +1), (+1, +1, –1), (+1, –1, +1), and (+1, –1, –1). Additionally, we include one neutral case of (+1, –1, 0) as a reference, which is identical to the non-electrostatic case in Sec. 3A. As demonstrated in Sec. 3A, for each case, we solve the coupled equations for a given separation. All these results are summarized in Fig. 5.
Figure 5.
(a) Normalized concentration profile of intermediate along the line connecting E1 at –20 Å and E2 at 20 Å. (b) Contours of the intermediate concentrations of 0.5 (near E1) and 0.03 (near E2). (c) Reaction rates of the intermediate at E2 with the fixed qE1 and various qE2 and qI expressed as a function of separation distance. (d) Schematic of diffusion processes from E1 and E2 in the system of (qE1, –1, +1).
Since the electrostatic interaction can influence both the concentration and the reaction rate as demonstrated for the single enzyme case in Sec. 2C, we first investigate how the electrostatic interaction modifies the intermediate concentration compared to the non-electrostatic case in Sec. 3A. In order to accomplish this, we calculate the normalized concentration profiles at d = 40 Å, as was previously performed in Fig. 3b. As expected, Fig. 5a shows the local concentration of intermediate around E1 increases or decreases depending on the nature of the electrostatic interaction. For the cases of (+1, ±1, –1) (red and green), where the interaction between E1 and the intermediate is attractive, the concentration increases compared to the neutral case (black), while the concentration decreases for the repulsive cases of (+1, ±1, +1) (blue and orange). Although we expect a similar effect near E2, it is hard to distinguish the lines in Fig. 5a because of the low concentrations. Instead, we calculate the contours of concentration of 0.03 for each case in Fig. 5b. The contour lines are closer to E2 for the attractive cases of (+1, +1, –1) (red) and (+1, –1, +1) (blue), while the contour lines for the repulsive cases of (+1, +1, +1) (orange) and (+1, –1, –1) (green) are further away from E2, compared to the neutral case of (+1, –1, 0) (black). Similarly, we also calculate the contours of 0.5, which appear near E1 (the source). Because of attractive electrostatic interaction in the cases of (+1, ±1, –1) (red and green), the concentration is relatively high near E1 and thus, the contour lines appear at larger distances from E1 compared to the neutral case. However, the same contour lines for the repulsive cases of (+1, ±1, +1) (orange and blue) appear at smaller distances from E1.
In fact, the contours (0.03) around E2 in Fig. 5b are directly related to the predicted reaction rates of intermediate. The observation of higher concentration around E2 implies that the incoming flux of intermediate toward E2 is greater, which means the reaction rate is higher. As shown in Fig. 5b, we can expect that (+1, +1, –1) (red) has the highest rate and (+1, +1, +1) (orange) has the smallest rate. Indeed, the reaction rates as a function of separation distance in Fig. 5c clearly reveal that this trend (see the dotted line in Fig. 5c).
Fig. 5c shows a general trend that attractive interactions increase the reaction rate but repulsive interactions decrease the reaction rate. This result is also consistent with the single enzyme case in Sec. 2C. Thus, the case of (+1, +1, –1) (red), where both enzymes are attractive with the intermediate, has the largest rate, and the case of (+1, +1, +1) (orange), where both enzymes are repulsive, has the lowest reaction rate. In Fig. 5c, it is also interesting to compare the case of (+1, –1, +1) (blue) with the case of (+1, –1, –1) (green), where the interaction with one enzyme is attractive but the interaction with the other enzyme is repulsive. In this case, a central question is which side between E1 and E2 contributes the most in determining the reaction rate at E2. Fig. 5c shows that the electrostatic interaction at the E2 side is more influential than the interaction at the E1 side. For example, in the case of (+1, –1, +1) (blue), the influence from the attraction between E2 and the intermediate is dominant over the influence from the repulsion between E1 and the intermediate, so that the reaction rate is larger than that observed in the neutral case. Another interesting observation from Fig. 5c is that near the contact distance (d < ∼22 Å), the reaction rates in the cases of (+1, –1, +1) (blue) and (+1, –1, –1) (green) are approximately the same as the reaction rates calculated for the neutral case (black). This can be simply explained by the case of two oppositely charged enzymes in close proximity, where the attraction and the repulsion cancel each other, which results in electrostatic interactions not playing a large role.
If we only consider the electrostatic potential generated by E1 and E2, one might predict that the reaction rate in the case of (+1, –1, +1) (blue) would be higher than the reaction rate in the case of (+1, +1, –1) (red) because of the directional potential gradient from E1 to E2. However, this prediction is not true when we consider both the electrostatic potential and the probability density (or concentration) of the intermediate together. For this discussion, we consider the model with (qE1, –1, +1), as is shown in Fig. 5d. With the electrostatic potential, we can imagine the diffusion process of the intermediate from E1 to E2. Since the potential is position-dependent, we consider two extreme cases of the diffusion process. The first case is where the intermediate is generated at the closest point to E2 on the E1 surface and it diffuses along the path connecting the centers of E1 and E2 (see the blue dashed line in Fig. 5d). This is the case where the intermediate feels the potential gradient maximally; particularly, for the cases with qE1 > 0, the potential is monotonically decreasing with the greatest slope along the direction from E1 to E2. Since this is essentially a one-dimensional problem, we can solve the corresponding diffusion-reaction equation, and the solution is given in Appendix B. In a steady state with a given production rate at E1, the solution indicates that the reaction rate does not depend on the electrostatic potential, or qE1. This is because in this one-dimensional case, the production rate at E1 should be the same with the reaction rate at E2 to maintain the steady state, irrespective of the electrostatic potential. Physically, this can be interpreted as the result of the cancelation between two opposing effects of electrostatic potential. For example, in the flux from E1 to E2 for qE1 > 0, the kinetic gain directly from the potential gradient (∇Ui in Eq. 5) is exactly balanced by the loss in the probability density of the intermediate due to the repulsion (the decrease of the concentration ci in Eq. 5), while for qE1 < 0, the kinetic loss is compensated by the gain in the probability density due to attraction. Therefore in this case, there is no advantage to considering the directional electrostatic potential (qE1 > 0). The second case is where the intermediate is generated at the farthest point from E2 on the E1 surface and it subsequently diffuses to E2 (see the red dotted line in Fig. 5d). In this second case, the balance we discussed in the first case cannot hold and it is advantageous to have more negative qE1 to accelerate the kinetics than to have a more positive qE1. This is because for qE1 > 0, the electrostatic repulsion pushes the intermediate away from E2 and also decreases the probability density (kinetic loss, and loss in probability density), while for qE1 < 0 the attraction brings the intermediate closer to E2 and increases the probability density (kinetic gain, and gain in probability density). Overall, (qE1 < 0, –1, +1) (or equivalently (qE1 > 0, +1, –1)) can have larger reaction rates than (qE1 > 0, –1, +1) (or equivalently (qE1 < 0, +1, –1)).
From the discussion above, we conclude that it is difficult to accelerate the reaction kinetics using the directionality only from the electrostatic potential gradient, but it is more effective to use attractive electrostatic potential for increasing the probability density (or concentration), by preventing the intermediate from diffusing away to the bulk solution. Actually, within the confined space made by attractive electrostatic potential, the directionality in diffusion naturally comes from the concentration gradient between the enzymes (source and sink). Thus, it seems that individual attractive electrostatic potentials between each enzyme and the intermediate for confining the intermediate is more important than the directional electrostatic potential between the two enzymes. Because of this, we observe that the case where all the enzymes are oppositely charged to the intermediate is the most favourable for accelerating sequential reaction kinetics (red in Fig. 5c), while the opposite case with the same charges is the most unfavourable (orange).
Electrostatic channeling in sequential enzyme reactions
Effect of the electrostatic potential formed in between two enzymes
In Sec. 3B, we systematically studied the influence of the electrostatic interaction between the charged enzymes and the charged intermediate and we discussed electrostatic conditions that can maximize the reaction rate. Here, we discuss how we can further accelerate the kinetics by further restricting the diffusive motion to the path between the two enzymes. In order to do this, we place a small non-reactive charged particle (an electrostatic mediator) with a radius of 3 Å in between the two enzymes, to create additional attractive electrostatic potential. In this case, although the added particle is not directly involved in any of the enzyme-catalyzed reactions, it can affect the sequential enzyme reactions by increasing the transfer efficiency of intermediate between two enzymes. As we discussed in our previous work,12 this mediator is so small that the excluded volume effect is negligible. Therefore, we can conclude that the role of the electrostatic mediator is only to provide electrostatic potential between two enzymes. In the diffusion-reaction equation, the non-reactivity of the mediator gives a reflecting boundary condition.
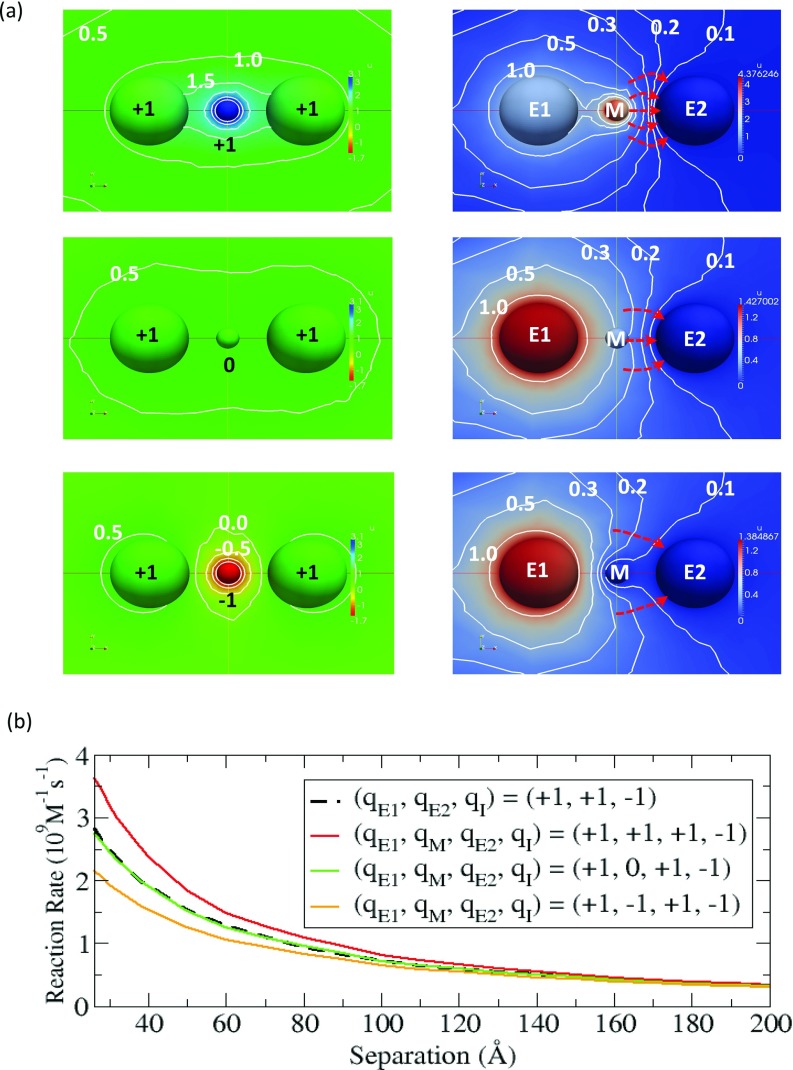
Since we are interested in maximizing the reaction rate, we use the system of (+1, +1, –1) from Sec. 3B. This system has the largest reaction rate and we put the mediator in the middle between the two enzymes. We examine the three cases where the mediator can have a charge of +1, 0, or –1. For each case, we solve the coupled equations and obtain the concentration of intermediate as the solution of the equations. At d = 40 Å, the electrostatic potential generated by the two enzymes and the mediator is shown in the left panel of Fig. 6a and the concentration of intermediate is also displayed in the right panel of Fig. 6a. When the mediator is positively charged (top in Fig. 6a), the potential is higher than in the neutral case (middle). This increases the concentration of the negatively charged intermediate located in between E1 and E2 and consequently, the reaction rate increases. However, when the intermediate is negatively charged (bottom), the trend is opposite to the positively charged case (top). Note that for all the cases, the electrostatic potential is symmetric. As a result, there is no directionality between E1 and E2, as has been previously observed in Brownian dynamics simulations of bifunctional DHFR-TS.18 However, as we mentioned before, the diffusive motion of the intermediate has a natural directionality due to the concentration gradient developed between the source (E1) and the sink (E2). By combining the electrostatic effect and the concentration gradient together, the flux toward E2 is the largest in the positive potential case (top). In fact, the stream lines perpendicular to the contours in the right panel of Fig. 7a (red dashed lines) clearly support this mechanism because more lines lead to E2 compared to the other cases that are examined.
Figure 6.
(a) Electrostatic potential created by E1, E2, and the mediator (left panel) and the normalized concentration of intermediate (right panel) in the color maps. In the left panel, units are kBT/e, and pure blue and pure red represents 3.1 kBT/e and –1.7 kBT/e, respectively. In the right panel, pure red represents the maximum value in each case, and pure blue corresponds to zero. The red-dashed arrow lines indicate the flow lines perpendicular to the contours. (b) Reaction rate of the intermediate at E2 with and without a charged or uncharged mediator.
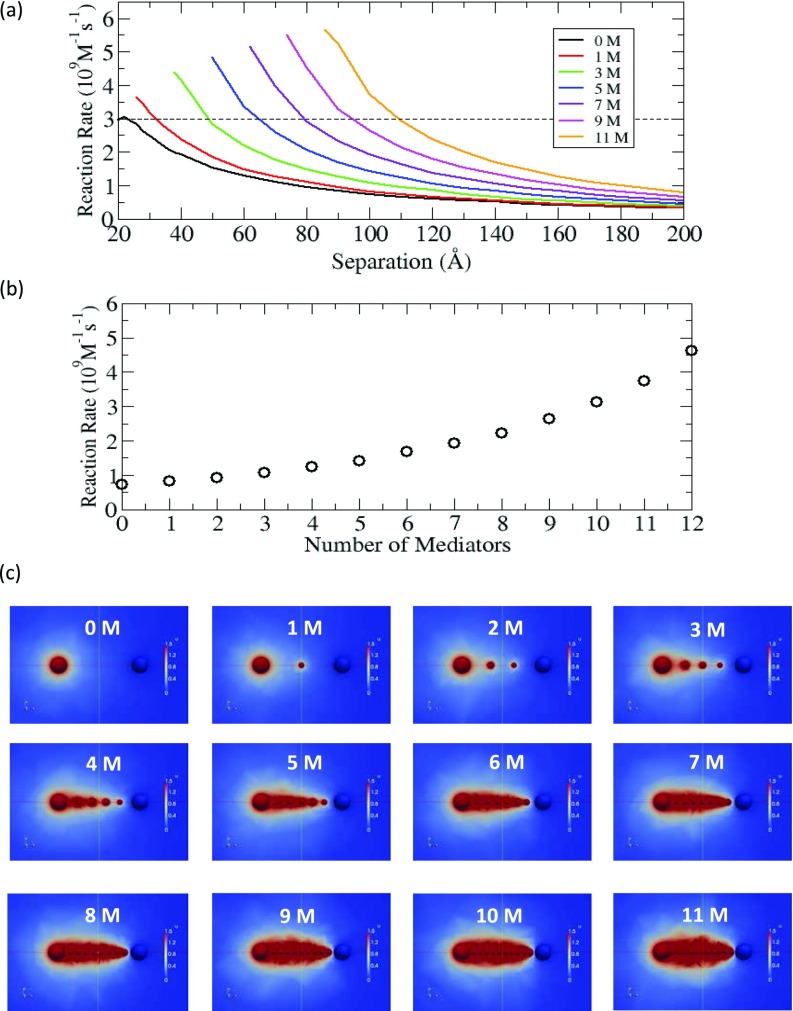
Figure 7.
(a) Reaction rate of the intermediate at E2 in the system of (+1, +1, –1) with positively charged mediators (M), as a function of the separation between E1 and E2. For each curve, the smallest distance in the plot corresponds to the distance where E1, E2, and mediators are touching each other. (b) At d = 100 Å, the reaction rate of the intermediate at E2, as a function of the number of mediators. (c) Color maps of the concentration of intermediate with different numbers of mediators, up to eleven. Pure red indicates high concentration region (≥1.5).
To better understand how this electrostatic mediator effect is dependent on the separation between the two enzymes, we calculate the reaction rate as a function of the separation distance. The result is presented in Fig. 6b. As the separation distance increases, the mediator effect decreases because the electrostatic potential gets weaker between the enzymes. At each separation distance, the case of a mediator with +1 charge has the largest reaction rate while the case with –1 charge has the lowest reaction rate. As expected, we see that the reaction rate in the uncharged mediator (green) is very similar to the one in the case without the mediator (dotted line). Based on the results from this study, we find that the reaction rate can vary significantly for a system depending on the nature of the electrostatic potential formed in between the two enzymes.
Formation of an electrostatic channel
From Sec. 3C1, we know that an electrostatic potential that restricts the diffusive motion of the intermediate to the inter-enzyme space can significantly increase the reaction rate. Now the question is how much the reaction kinetics can be enhanced by strengthening the attractive electrostatic potential, and also if we can observe any supporting evidence for the existence of electrostatic channelling. To investigate this question, we extend the method above to include additional positively charged mediators between the two enzymes in the system of (+1, +1, –1) with equal spacing of the inserted mediators in the inter-enzyme space. Again, we solve the coupled differential equations with the given numbers of mediators and determine the reaction rates as a function of separation between the two enzymes. Fig. 7a shows that the reaction rate remarkably increases with additional mediators when compared to the case without any electrostatic mediator. For example, at d = 90 Å, the reaction rate in the case with eleven mediators (orange) is five times larger than the one in the case without any mediator (black). Also, this strong electrostatic potential maintains high reaction rate even at large distances. For example, along the dotted line in Fig. 7a, the case of eleven mediators (orange) still can have a similar magnitude of the maximum reaction rate in the absence of mediator (black), even at distances greater than 100 Å.
Next, in order to investigate the relationship between the number of mediators and the reaction rate, we plot the reaction rate as a function of the number of mediators at d = 100 Å. Note that this separation distance may be comparable to the separation distances reported in examples of substrate channeling in real metabolic pathways; for example, ∼25 Å in tryptophan synthase (molecular tunnel),35 ∼40 Å in bifunctional DHFR-TS (electrostatic channeling),16 and ∼100 Å in carbamoyl phosphate synthetase (molecular tunnel).36 Fig. 7b shows that the reaction rate increases in a nonlinear manner, and with the number of mediators it approaches the production rate for the intermediate at E1 (∼6 × 109M−1s−1, see Fig. 2b). In fact, when there is a strong electrostatic field with twelve mediators, the reaction rate at E2 reaches approximately 80% of the production rate, which reveals very high transfer efficiency of the intermediate between E1 and E2.
In addition to the change in the reaction rate, we also study the influence of electrostatic potential on the concentration of intermediate. For this study, we represent the concentration of the intermediate using the color maps in Fig. 7c. In these maps, we use pure red color to represent high concentration regions (concentration ≥ 1.5) to more clearly visualize the concentration change. As revealed by these maps, as the number of mediators increases, the high concentration is extended from E1 to E2 and the concentration directionality from E1 and E2 is developed. For example, when the number of mediators is low, we see isolated red regions, but when the number of mediator is larger than six, we see one dominant red region. Note that once the large red region is formed, the high concentration region is maintained without expanding but is still localized. Therefore, the strong electrostatic potential generated by the mediators induces a high concentration region between the two enzymes, which essentially creates a channel which is functionally similar to the substrate channels formed by molecular tunnels. This study strongly suggests that when a strong attractive electrostatic potential exists between the enzymes, there can be a high probability of having electrostatic channeling in sequential reactions.
CONCLUSIONS
In this work, we have studied two aspects of sequential enzyme reactions using simple diffusion-limited reaction models, coupling and electrostatic effects. For the coupling effect, it may be a common belief that the overall reaction rate for sequential enzyme reactions is maximized when the two reaction sites are at the closest distance. However, we showed that this is not always true. In the cases where the second enzyme is large enough, we observed that the maximal reaction rate is displaced from the point of minimal separation. Therefore, although the reaction events take place sequentially from the first enzyme to the second enzyme, the second enzyme conversely affects the reaction at the first enzyme, which indicates that the two reactions are mutually influenced by the interaction between the two enzymes.
For the electrostatic effect, we systematically studied how electrostatic interactions influence the transportation of the intermediate between two enzymes with a focus on understanding the role of electrostatic interactions accelerating the reaction kinetics. In this study, we found that when the interaction between each enzyme and the intermediate is attractive, the reaction rate is maximized. We also considered other cases in which non-reactive particles participate in the sequential reactions by changing electrostatic potential in between the two enzymes. In these cases, we showed that when the generated potential from the mediators is strongly attractive for the intermediate, the reaction rate is remarkably increased, as is the concentration of the intermediate between the enzymes. This is similar to what would be expected in situations where the substrate is channelled via molecular tunnels. This result strongly supports the existence of electrostatic channeling as proposed in the previous studies.16, 17, 18 A key finding here is that the effect of electrostatic attraction in keeping the intermediate “in play” may be more important than the directional properties of the electrostatic field.
An important question raised from this study is which systems in nature can possibly have such electrostatic channeling besides the known systems such as DHFR-TS. Our study suggests that as long as strong attractive electric potential is formed in between the two sequential enzymes, the possibility of an electrostatic channel exists. One possible way to establish such a strong potential is that two consecutive enzymes form a complex, and the intermediate diffuses along an electrostatic channel formed on the molecular surface with charged residues, as in the bifunctional DHFR-TS enzyme.16, 17 Additionally, this electrostatic channeling may have some potential applications; for example, it may be used to design enzyme complexes in modulating the reaction rates, or to design drugs capable of breaking or weakening the transfer efficiency of electrostatic channels.
In this study, we investigated the steady-state reaction kinetics at fixed separation distances between two enzymes, but in real biological systems, the enzymes can also diffuse under the influence of interactions with other biomolecules. Considering this effect, the separation distances could vary as a function of time. Further examination of how reaction kinetics is modulated for mobile enzymes could be performed in future studies, which we expect will give considerable insight into the kinetics of complex reaction networks in cells.
ACKNOWLEDGMENTS
This work was supported in part by the Howard Hughes Medical Institute, the National Institutes of Health, the National Science Foundation, the National Biomedical Computational Resource (Award No. P41 GM103426), the American Heart Association and the Center for Theoretical Biological Physics. P.M.K.-H. was supported by AHA award 13POST14510036 and NIH award 1F32HL114365-01A1.
APPENDIX A: STEADY-STATE SOLUTION OF THE DIFFUSION-REACTION EQUATION IN A SINGLE ENZYME REACTION MODEL
In a steady-state single enzymatic reaction (S + E → P + E), the diffusion-reaction process is governed by the following differential equation with a Coulomb potential U,
| (A1) |
with
| (A2) |
where ci, qi, rE−i, qE, and λB are the concentration and the electric charge of i, the distance of i from the enzyme (E), the charge of the enzyme and the Bjerrum length (or Onsager length), respectively. Here, the index i indicates the substrate (S) or the product (P).
In this model, since we use the spherical representation of molecules, it is natural to employ the spherical coordinates. Using these coordinates, Eq. A1 can be rewritten in the following way:
| (A3) |
After some further manipulation, this equation is simply reduced to the following second-order ordinary differential equation:
| (A4) |
where
For the substrate (S), the boundary conditions are given by cS(R1) = 0 (reaction) and cS(R2) = 1 (bulk concentration). Here, R1 and R2 are the radii for the inner and outer boundary conditions. For the product (P), the boundary conditions are kP(R1) = kS(R1) (production rate = reaction rate) and cP(R2) = 0 (escape from the system).
By solving the coupled equations with the given boundary conditions, we can obtain the solutions for the substrate and the product. From the solutions, the normalized concentration of substrate is given by
| (A5) |
and the reaction rate kS is
| (A6) |
Note that as R2 approaches infinity, we can get the familiar expressions.24 Furthermore, as QS goes to zero, cS(r) and kS approach the Smoluchowski concentration, cS(r) = 1 − R1/r, and the Smoluchowski rate, kS = 4πR1D, respectively.
For the product, the normalized concentration cP(r) is given by
| (A7) |
In the non-electrostatic limit with R2 = ∞, cP(r) is simply reduced to R1/r and in this case cS(r) + cP(r) = 1, independent of r.
We use these analytical solutions to compare with our numerical solutions.
APPENDIX B: STEADY-STATE SOLUTION OF THE DIFFUSION-REACTION EQUATION FOR THE INTERMEDIATE IN A ONE-DIMENSIONAL SEQUENTIAL ENZYME REACTION MODEL
Let us assume that one enzyme (E1) with a radius of σ1 and a electric charge of qE1 is located at –d/2, and the other enzyme (E2) with σ2 and qE2 = −1 is at d/2 in a coordinate system, and the intermediate (I) with qI = +1 is generated at the E1 surface and diffuses to the E2 surface with a diffusion constant D, along the shortest pathway between E1 and E2. Since this is essentially a one-dimensional problem, we can introduce an equivalent one-dimensional coordinate system, where E1 is at the origin and E2 is at d, as shown in Fig. 8.
Figure 8.

Schematic of simplified one-dimensional diffusion of the intermediate between E1 and E2 under the electrostatic potential generated by both E1 and E2.
In a steady-state with a given production rate for the intermediate at E1 (kS), the diffusion-reaction equation is
| (B1) |
where
The boundary conditions are given by and cI(d − σ2) = 0. Note that in the first boundary condition, the negative sign denotes an outgoing flux.
In fact, because of the boundary condition at σ1 and the steady-state condition in Eq. B1, the flux is always −kS, irrespective of UI. Thus, the reaction rate at E2, or the negative flux at x = d − σ2, is kS. Physically, this makes sense because in order to maintain a steady-state in the one-dimensional case, the flux should be preserved, so that the production rate at E1 must be the same with the reaction rate at E2, independent of UI.
However, UI influences the concentration of intermediate between the two enzymes. To show this without loss of generality, we can consider a case with qE2 = 0, where the analytical solution is available,
| (B2) |
where Ei is the exponential integral.
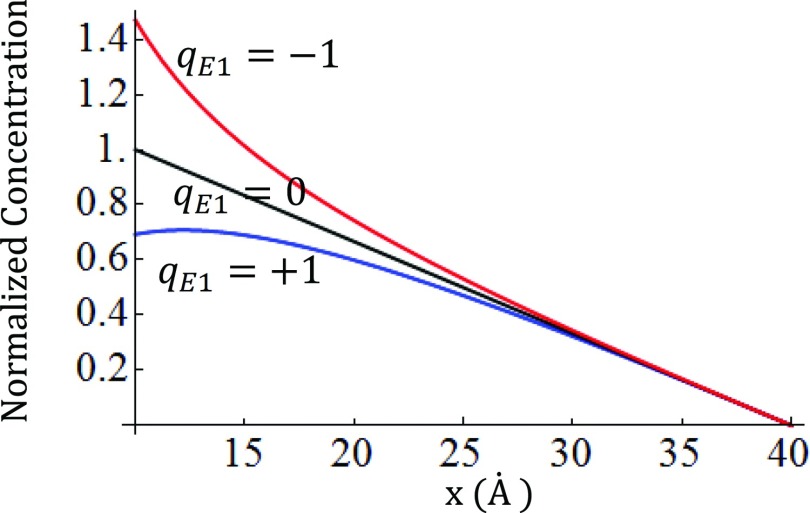
The solutions for , , , and kS = 1 with various qE1 are given in Fig. 9. Again, the flux is always constant (−kS) which is independent of qE1 and x. Thus, the potential gradient between E1 and E2 is not important for the kinetics, but the potential between E1 and I influences the concentration of intermediate, as is shown in Fig. 9. Even though the concentration is different in each case, the reaction rate is always the same because of the cancellation between two opposing effects. For example, for repulsive cases (qE1 > 0), the loss of concentration due to the repulsion (blue in Fig. 9) is compensated by the kinetic gain from the same repulsion ( in the flux), while for the attractive cases (qE1 < 0), the kinetic loss from the attraction ( in the flux) is compensated by the gain in the concentration (red in Fig. 9). This balance physically explains why the flux is always constant.
Figure 9.
Concentration profiles of intermediate along the x axis in the one-dimensional system of (qE1, 0, +1).
References
- Somlyo A. P. and Somlyo A. V., Nature 372, 231 (1994). 10.1038/372231a0 [DOI] [PubMed] [Google Scholar]
- Shen-Orr S. S., Milo R., Mangan S., and Alon U., Nat. Gen. 31, 64 (2002). 10.1038/ng881 [DOI] [PubMed] [Google Scholar]
- Davidson E. H., Rast J. P., Oliveri P., Ransick A., Calestani C., Yuh C.-H., Minokawa T., Amore G., Hinman V., and Arenas-Mena C., Science 295, 1669 (2002). 10.1126/science.1069883 [DOI] [PubMed] [Google Scholar]
- Srere P. A., Annu. Rev. Biochem. 56, 89 (1987). 10.1146/annurev.bi.56.070187.000513 [DOI] [PubMed] [Google Scholar]
- Arkin A. and Ross J., Biophys. J. 67, 560 (1994). 10.1016/S0006-3495(94)80516-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H., Tombor B., Albert R., Oltvai Z. N., and Barabási A.-L., Nature (London) 407, 651 (2000). 10.1038/35036627 [DOI] [PubMed] [Google Scholar]
- Papin J. A., Reed J. L., and Palsson B. O., Trends Biochem. Sci. 29, 641 (2004). 10.1016/j.tibs.2004.10.001 [DOI] [PubMed] [Google Scholar]
- Shinar G. and Feinberg M., Science 327, 1389 (2010). 10.1126/science.1183372 [DOI] [PubMed] [Google Scholar]
- Chen W. W., Niepel M., and Sorger P. K., Genes Dev. 24, 1861 (2010). 10.1101/gad.1945410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson J. J. and Novák B., Annu. Rev. Phys. Chem. 61, 219 (2010). 10.1146/annurev.physchem.012809.103457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H.-X., Q. Rev. Biophys. 43, 219 (2010). 10.1017/S0033583510000120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eun C., Kekenes-Huskey P. M., and McCammon J. A., J. Chem. Phys. 139, 044117 (2013). 10.1063/1.4816522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles E. W., Rhee S., and Davies D. R., J. Biol. Chem. 274, 12193 (1999). 10.1074/jbc.274.18.12193 [DOI] [PubMed] [Google Scholar]
- Huang X., Holden H. M., and Raushel F. M., Annu. Rev. Biochem. 70, 149 (2001). 10.1146/annurev.biochem.70.1.149 [DOI] [PubMed] [Google Scholar]
- Zhang Y.-H. P., Biotechnol. Adv. 29, 715 (2011). 10.1016/j.biotechadv.2011.05.020 [DOI] [PubMed] [Google Scholar]
- Knighton D. R., Kan C.-C., Howland E., Janson C. A., Hostomska Z., Welsh K. M., and Matthews D. A., Nat. Struct. Mol. Biol. 1, 186 (1994). 10.1038/nsb0394-186 [DOI] [PubMed] [Google Scholar]
- Stroud R. M., Nat. Struct. Biol. 1, 131 (1994). 10.1038/nsb0394-131 [DOI] [PubMed] [Google Scholar]
- Elcock A. H., Potter M. J., Matthews D. A., Knighton D. R., and McCammon J. A., J. Mol. Biol. 262, 370 (1996). 10.1006/jmbi.1996.0520 [DOI] [PubMed] [Google Scholar]
- Meek T. D., Garvey E. P., and Santi D. V., Biochemistry 24, 678 (1985). 10.1021/bi00324a021 [DOI] [PubMed] [Google Scholar]
- Liang P.-H. and Anderson K. S., Biochemistry 37, 12195 (1998). 10.1021/bi9803168 [DOI] [PubMed] [Google Scholar]
- Cheng Y., Chang C.-E. A., Yu Z., Zhang Y., Sun M., Leyh T. S., Holst M. J., and McCammon J. A., Biophys. J. 95, 4659 (2008). 10.1529/biophysj.108.140038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trujillo M., Donald R. G., Roos D. S., Greene P. J., and Santi D. V., Biochemistry 35, 6366 (1996). 10.1021/bi952923q [DOI] [PubMed] [Google Scholar]
- Elcock A. H. and McCammon J. A., Biochemistry 35, 12652 (1996). 10.1021/bi9614747 [DOI] [PubMed] [Google Scholar]
- Rice S. A., Comprehensive Chemical Kinetics. Diffusion-Limited Reactions, Vol. 25 (Elsevier, Amsterdam, 1985). [Google Scholar]
- Hong K. M. and Noolandi J., J. Chem. Phys. 68, 5163 (1978). 10.1063/1.435636 [DOI] [Google Scholar]
- Hong K. M. and Noolandi J., J. Chem. Phys. 68, 5172 (1978). 10.1063/1.435581 [DOI] [Google Scholar]
- Rice S. A., Butler P. R., Pilling M. J., and Baird J. K., J. Chem. Phys. 70, 4001 (1979). 10.1063/1.438020 [DOI] [Google Scholar]
- Zhou H.-X., Phys. Biol. 2, R1–R25 (2005). 10.1088/1478-3975/2/3/R01 [DOI] [PubMed] [Google Scholar]
- Brenner S. C. and Scott R., The Mathematical Theory of Finite Element Methods (Springer Verlag, New York, 2008). [Google Scholar]
- Hake J., Edwards A. G., Yu Z., Kekenes-Huskey P. M., Michailova A. P., McCammon J. A., Holst M. J., Hoshijima M., and McCulloch A. D., J. Physiol. 590, 4403 (2012). 10.1113/jphysiol.2012.227926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kekenes-Huskey P. M., Gillette A., Hake J., and McCammon J. A., Comput. Sci. Discovery 5, 014015 (2012). 10.1088/1749-4699/5/1/014015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logg A., Mardal K.-A., and Wells G., Automated Solution of Differential Equations by the Finite Element Method (Springer, Heidelberg, 2012). [Google Scholar]
- McDonald N. and Strieder W., J. Chem. Phys. 118, 4598 (2003). 10.1063/1.1543937 [DOI] [Google Scholar]
- Bauler P., Huber G., Leyh T., and McCammon J. A., J. Phys. Chem. Lett. 1, 1332 (2010). 10.1021/jz1002007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyde C. C., Ahmed S. A., Padlan E. A., Miles E. W., and Davies D. R., J. Biol. Chem. 263, 17857 (1988). [PubMed] [Google Scholar]
- Thoden J. B., Holden H. M., Wesenberg G., Raushel F. M., and Rayment I., Biochemistry 36, 6305 (1997). 10.1021/bi970503q [DOI] [PubMed] [Google Scholar]