Skip to main content
PMC home page
Biomicrofluidics logoLink to Biomicrofluidics
. 2014 Jan 29;8(1):014104. doi: 10.1063/1.4863723

Red blood cell dynamics in polymer brush-coated microcapillaries: A model of endothelial glycocalyx in vitro

Luca Lanotte 1,2, Giovanna Tomaiuolo 1,3,a), Chaouqi Misbah 2, Lionel Bureau 2, Stefano Guido 1,3
PMCID: PMC3977877  PMID: 24753725

Abstract

The confined flow of red blood cells (RBCs) in microvasculature is essential for oxygen delivery to body tissues and has been extensively investigated in the literature, both in vivo and in vitro. One of the main problems still open in microcirculation is that flow resistance in microcapillaries in vivo is higher than that in vitro. This discrepancy has been attributed to the glycocalyx, a macromolecular layer lining the inner walls of vessels in vivo, but no direct experimental evidence of this hypothesis has been provided so far. Here, we investigate the flow behavior of RBCs in glass microcapillaries coated with a polymer brush (referred to as “hairy” microcapillaries as opposed to “bare” ones with no coating), an experimental model system of the glycocalyx. By high-speed microscopy imaging and image analysis, a velocity reduction of RBCs flowing in hairy microcapillaries as compared to bare ones is indeed found at the same pressure drop. Interestingly, such slowing down is larger than expected from lumen reduction due to the polymer brush and displays an on-off trend with a threshold around 70 nm of polymer brush dry thickness. Above this threshold, the presence of the polymer brush is associated with an increased RBC deformation, and RBC velocity is independent on polymer brush thickness (at the same pressure drop). In conclusion, this work provides direct support to the hypothesis that the glycocalyx is the main factor responsible of the higher flow resistance found in microcapillaries in vivo.

INTRODUCTION

Blood flow in microcirculation is essential for delivery of nutrients and removal of metabolic waste products to/from tissues.1, 2 These functions are ensured by proper regulation of blood flow down to the capillary level. One of the main factors controlling capillary blood flow is microvascular resistance. The latter, in spite of extensive investigation, is still to be fully elucidated, and some fundamental issues remain open. In particular, when comparing experimental data of red blood cell (RBC) flow behavior under confined conditions in vitro and in vivo, some significant discrepancies are found, which are still unexplained. As recently reviewed,3, 4, 5 the flow of RBCs has been characterized in vivo by high-speed and high resolution imaging6 and in vitro either in silica microcapillaries or in PDMS microchannels7, 8, 9 with dimension comparable to cell size (inner diameter up to 10 μm) by high speed imaging, both in steady-state10, 11, 12, 13 and in transient14 conditions. When they are not subjected to external stresses or constraints, RBCs show a biconcave disk shape with diameter of 7–8 μm and thickness of 1–2 μm, while in confined conditions they are able to flow due to their high deformability,15 whose essential features can be modeled by lipid vesicles16, 17 and capsules.16, 18, 19 One of the main questions arises from observation of RBC velocity in capillaries: why is RBCs velocity in small vessels in vivo strongly reduced with respect to glass capillaries of the same apparent size in vitro? Several explanations, based on peculiar features of microcirculation in vivo, which are not found in vitro, have been proposed in the literature, such as: (i) the irregularity of vessel diameters;20, 21 (ii) the effects of capillaries with relatively short length21 and vascular bifurcations;22, 23 (iii) the presence of white blood cells;24, 25 and (iv) the role played by a macromolecular layer lining vessel walls, known as endothelial glycocalyx, acting to reduce the effective capillary lumen. It has been shown that the first three effects, by themselves, cannot quantitatively justify the observed RBC slowing down in vivo.26 On the other hand, the endothelial glycocalyx has been advocated to be the predominant reason of flow reduction in microvessels in vivo.27

The glycocalyx layer, located on the inner surface of the vascular endothelium, is a network of proteoglycans and glycoproteins with a thickness ranging from 100 to 1000 nm.28 It plays a number of functions such as determining vascular permeability, mediating blood cell-vessel wall interactions and shear stress sensing (mechanotransduction28, 29, 30), regulating clotting and immune response through the complement cascade, controlling the interaction between leukocytes and endothelial cells, fulfilling a vasculo-protective action and influencing the microvascular hematocrit.28, 31, 32, 33 Several vascular diseases, such as diabetes, ischemia, and atherosclerosis are associated to alterations of the glycocalyx.28, 33 Moreover, as previously stated, the glycocalyx is considered to affect blood flow in microcirculation since lower flow resistance and increased hematocrit are found in glass microcapillaries (where the glycocalyx is not present) as compared to microvessels in vivo.34

Given the physiopathological role of the glycocalyx layer on blood flow, various experimental techniques have been employed to assess its effect on microcirculation,35, 36 but these measurements are typically limited to relatively large microvessels. In the case of capillaries in the micron range, the glycocalyx layer and its interaction with blood cells were modeled by both theoretical and numerical studies.37, 38, 39, 40, 41, 42 To our knowledge, however, a quantitative experimental study of the effect of glycocalyx on RBC fluid dynamic behavior under microconfined shear flow is not currently available.

Here, polymer brush coated capillaries are applied as a model of glycocalyx-lined microvessels. Polymer brushes can be described as an assembly of flexible linear macromolecules which are tethered by one end to a surface, forming a compact layer of polymer chains which are stretched perpendicularly to the surface.43 Polymer brushes have recently attracted considerable attention, due to numerous applications in a broad range of fields,44 such as enhancement of lubrication properties of surfaces,45, 46 tailoring of adhesion and wetting properties,47 improvement of drugs biocompatibility,48 creation of protective coatings to prevent protein adsorption in biological environments,49 biomolecules analysis in microfluidic devices,50 and design of thermosensitive surfaces or interfaces.51 Polymer brushes have been used in combination with soft-lithography techniques to create complex three-dimensional pattern to allow the capture and release of medicine and nanoparticles.52

The aim of the present study is to provide a quantitative analysis of RBC dynamics, in terms of velocity and deformability, in microcapillaries lined with polymer brushes53 to simulate in vitro the effect of the glycocalyx layer. The effects of pressure drop and polymer brush thickness have been investigated as well.

METHODOLOGY

Experimental apparatus

10 μm internal diameter fused silica capillaries (Polymicro Technologies, USA) have been lined with polymer brushes, using surface-initiated atom transfer radical polymerization as described in details elsewhere.53 The polymer that has been chosen to coat the microcapillaries with is pHEMA (poly-Hydroxy Ethyl Methacrylate), for its hydrophilic character which allows the brush to swell in the presence of aqueous media flowing inside the tubing. The dry thickness of the elaborated polymer brushes, tdry, ranges from 25 to 190 nm, with a standard deviation of 7 nm. All the brushes used in the present study have the same nominal grafting density σ, which is fixed by the ATRP initiator density, and have various chain lengths N, the latter being controlled by the polymerization time. The ratio between the swollen and dry thickness of such brushes has been determined in a recent study of our groups, using surface forces apparatus measurements, to be tswell/tdry ≈ 2. The polymer coatings lining the inner walls of the microcapillaries therefore have swollen thicknesses which are comparable to the one of the endothelial glycocalyx in human microvessels.28 From the measured swollen ratio α = tswell/tdry, one can further make a crude estimate of the molecular parameters σ and N, as described in details in a previous paper:53 the brush grafting density can be first estimated as σ ≈ a2α3/2, where a is the monomer size (a ≈ 0.5 nm), and N is then deduced from the relationship tdry/ σ = Na3. This yields a grafting density σ ≈ 0.7 chain/nm2, and N ranging from 280 to 2200 monomers/chain for tdry between 25 and 190 nm. From what is known from previous studies on the endothelial glycocalyx,54 this layer has a brush-like structure made of fibers of diameter around 10 nm, with an average separation of 20 nm (hence a surface density of 2.5.10-3 fiber/nm2). From the structural point of view, the polymer brushes used in the present study are therefore a highly simplistic model of a true glycocalyx, in that they are made of flexible molecules and not fibers, grafted at a much larger density. Moreover, pHEMA is a neutral polymer, while the glycocalyx exhibit surface charges.55 However, it has been shown in a previous work53 that the flow reduction of water in capillaries coated with pHEMA brushes of swollen thickness 400 nm was consistent with that observed in vivo.34 This motivated a further investigation of the flow of RBCs in such channels, considering pHEMA brushes as a first step towards more refined bioinspired polymer layers. The brush-coated capillaries were placed on a coverslip at the bottom of a flow cell which has been already described in the literature.10, 11, 12, 14 The flow cell was connected by two flexible tubings to two glass reservoirs, one for the feed and the other for the outlet stream. By adjusting the distance between the liquid menisci in the two reservoirs, it was possible to regulate the pressure drop across the silica microcapillaries (other contributions to the pressure drop, such as the ones in the flexible tubings and the flow cell, being negligible).

The flow cell was placed on a motorized stage of an inverted microscope (Zeiss Axiovert 100) and the images of the flowing RBC were acquired by using a high speed camera (Phantom 4.3) that can operate up to 1000 frames per second. The large number of recorded images were processed off-line by custom macros based on the library of a commercial software package (Image Pro Plus) to measure the velocity and the deformation index (defined as the ratio between of the long side and the short side of a box enclosing the cell) of single RBCs.

Blood samples

Fresh venous blood samples were drawn from healthy consenting donors, collected into EDTA test-tubes and used within 4 h from collection. The samples were diluted with anticoagulant ACD (0.6% citric acid, 1.1% anhydrous dextrose, 2.3% sodium citrate, 96% water) supplemented with BSA (Bovine serum Albumin), to obtain a 0.1% RBC concentration by volume. RBC viability was checked before each experiment by observing cell morphology under static conditions at high magnification (100x objective).

RESULTS AND DISCUSSION

RBC deformation

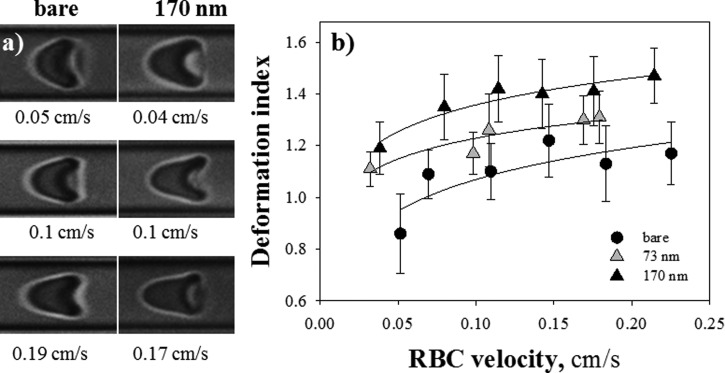
In order to evaluate and quantify the effect of pHEMA brushes on RBC flow, the attention was focused on the morphology of axisymmetric cells. In Figure 1 (left), RBCs shapes at similar values of cell velocity are shown for both bare and polymer coated capillaries (tdry = 170 nm). In both cases, RBCs assume the typical parachute-like shape, tending to an asymptotic configuration at increasing cell velocity. It is evident that cells flowing in bare capillaries are less deformed than those in polymer brush coated capillary. A quantitative analysis of RBC shape is presented on the right panel of Figure 1, where the cell deformation index DI (measured as the aspect ratio of a bounding box enclosing the cell body) is plotted as a function of RBC velocity for bare and pHEMA coated capillaries with a brush dry thickness of 73 and 170 nm. The continuous lines are just a guide to the eye.

Figure 1.

Figure 1

Open in a new tab

(a) Images of RBCs flowing in microcapillaries at similar values of cell velocity for both bare and polymer coated capillaries (tdry = 170 nm); plot of RBC deformation index (DI) as a function of cell velocity for bare and pHEMA coated capillaries with tdry = 73 and 170 nm.

Error bars give the dispersion of the measurements over an average number of RBCs of about 30 for each velocity and it is mainly due to the image analysis process and to the RBC size distribution, the distribution width (RDW) being equal to ∼14% in normal subjects. They are plotted in order to represent a confidence interval of 50% for each data set. For all the samples, increasing values of DI are observed, with a leveling-off at higher RBC velocities. The trend obtained for the bare capillary is in agreement with previous data on RBC deformation in microchannels.10 The experimental measurements indicate that RBCs morphology is closely affected by the presence of a polymer brush: the deformation index in 170 nm brush-coated capillaries is seen to be systematically higher than the one in bare tubes, confirming the qualitative difference in the observed shapes shown on the left side of Figure 1. A t-test has also been performed to confirm a statistically significant difference (P = <0.001) between the two extreme data sets (i.e., bare and 170 nm polymer brush coated capillaries). On the other hand, no significant differences were found between the average DI values for bare and 25 nm polymer brush capillaries within the experimental accuracy (data not shown).

RBC velocity

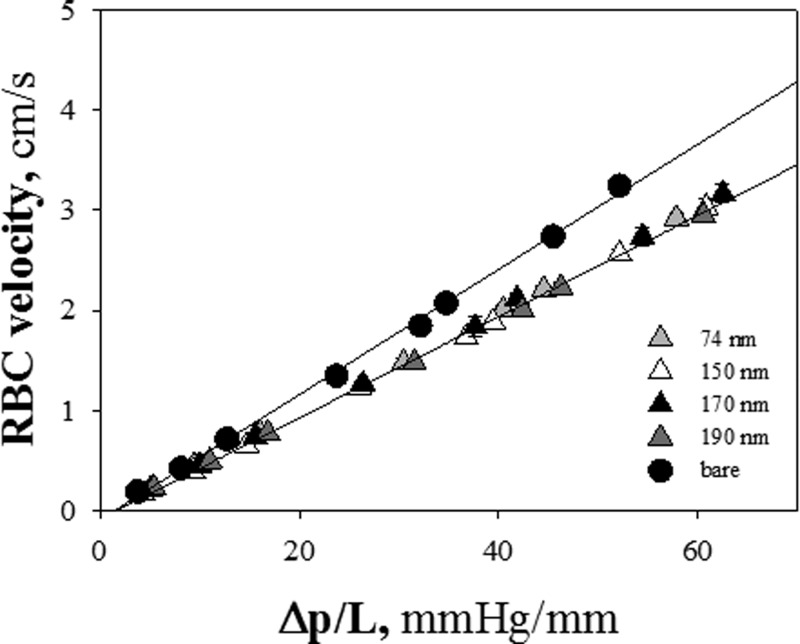
As known from the literature,10 at any given pressure drop, RBC velocity increases with microcapillary diameter. Furthermore, in a recent work53 on fluid dynamic characterization of microcapillaries lined with polymer brushes, flow resistance of a microchannel was found to increase monotonously with polymer layer thickness. Therefore, a slowing down of RBC velocity in hairy capillaries is expected in comparison with bare tubes, due to the double effect of the decrease of the available lumen and the dissipation enhancement in the presence of a polymer brush. This hypothesis is consistent with the experimental results presented in Figure 2, where RBC velocity is plotted as a function of pressure drop (ΔP/L) for bare and hairy capillaries of different brush thickness. Error bars (such as in the following figures) represent the standard deviation of the measurements (the average number of RBCs for each velocity is ≈ 30), which is mainly correlated to the size distribution of RBCs and to image analysis process. A decrease of RBCs velocity of about 20% is found in 170 nm hairy capillaries as compared to bare ones. This value is in agreement with the measured velocity reduction of pure water flowing in microcapillaries coated with pHEMA brushes of comparable thickness.53 Being the ratio between RBC velocity and average suspending fluid velocity a constant function of the applied pressure drop,10, 56 the reduction of RBC velocity is comparable with the one of water, at the same experimental conditions.

Figure 2.

Figure 2

Open in a new tab

RBC velocity vs pressure drop per unit length for bare and polymer coated capillaries (tdry = 74, 150, 170, and 190 nm) (circles and triangles, respectively).

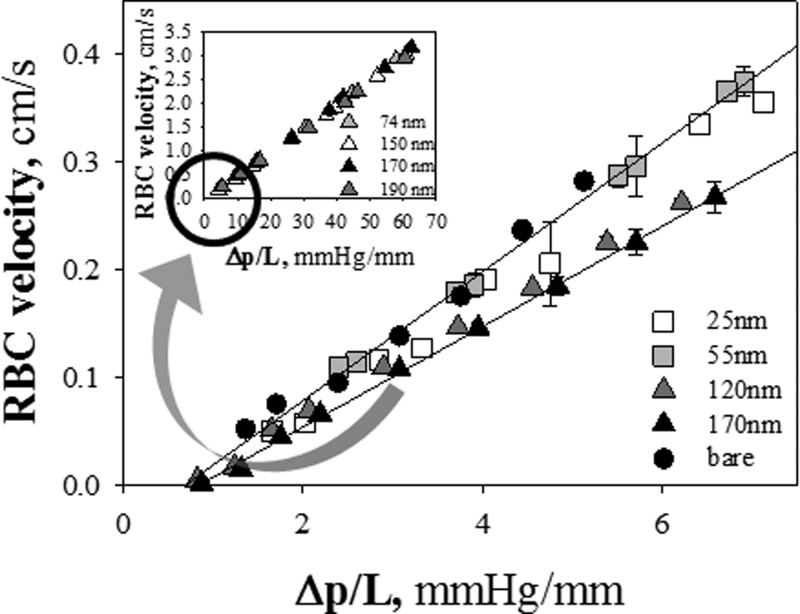
Strikingly enough, in the range of pressure drops explored here, RBC velocities for tdry = 74, 150, 170 and 190 nm are found to be identical, irrespective of the polymer brush thickness. Thus, although it would have been plausible to expect an inverse proportionality between the velocity of red blood cells and tdry (such as for the velocity of pure fluid53), it is evident that the slowing down of RBCs does not depend on the pHEMA brush thickness in the range we have explored (tdry ≈ 70–190 nm). A possible explanation of these results lies in the fact that pressure drops used in our experiments are high and tend to reduce cell-wall interactions.57 Indeed, the results shown in Figure 2 have been obtained at ΔP/L about one order of magnitude larger than the ones used in the previous study on pure water flow in brush-coated microcapillaries. Therefore, RBC velocity was monitored at lower values of pressure drops (10–35 mmHg (Ref. 58)). In fact, such low values of ΔP are usually observed in microvessels in vivo,58 where RBCs are less deformed and have a deeper interaction with the endothelial glycocalyx, since the fluid layer separating cell membrane and walls is very thin. In Figure 3, RBC velocity in brush-coated microcapillaries in the low ΔP range is plotted for values of tdry spanning a larger range of thickness (between 25 and 170 nm). The lines fitting with experimental outcomes do not perfectly converge to the origin of the axes, probably because of the contribution of minor ΔPs. A non-monotonic dependence of RBC velocity on brush thickness is now apparent. The data of RBC velocity for tdry < 60 nm superimpose to each other and to the data of bare capillaries, and lie above the results for tdry > 100 nm (the same trend observed in Figure 2 and in the inset of Figure 3). Thus, the effect of tdry on RBC velocity seems to be on-off (as opposed to a gradual dependence of RBC deformation on brush thickness).

Figure 3.

Figure 3

Open in a new tab

Plot of RBC velocity as a function of pressure drop per unit length for values of tdry spanning a larger range of thickness (between 25 and 170 nm) (Figure 2 is shown in the inset).

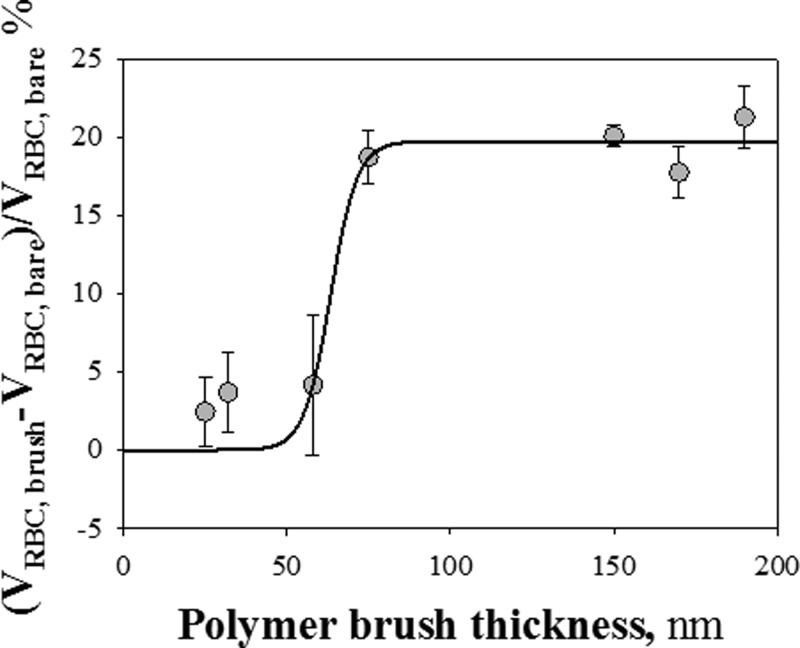
This finding is better illustrated by plotting the normalized difference of velocity (ΔVRBC)/VRBC, bare, where ΔVRBC = VRBC, brush-VRBC, bare, as a function of tdry, as shown in Figure 4. A strong reduction of RBC velocity (ΔVRBC/VRBC, bare ≈ 20–23%) in capillaries lined by pHEMA brushes with tdry > 70 nm can be noticed. On the contrary, thinner polymer brush layers do not affect RBC flow, as described above. The ΔV jump in a narrow range of tdry, as shown by the sigmoid fitting the data, further confirms this on-off behavior.

Figure 4.

Figure 4

Open in a new tab

Plot of the normalized difference of velocity (ΔVRBC)/VRBC, bare, where ΔVRBC = VRBC, brush − VRBC, bare, as a function of tdry.

In Figure 5, the plot of the ratio between RBC velocity (VRBC) and average suspending fluid velocity (⟨vflow⟩) as a function of Δp/L for different values of tdry is shown. ⟨vflow⟩ has been computed from the average velocity of tracers, i.e., spherical particles with diameter of 200 nm, flowing in the microtubes.53 This velocity ratio is equal to 2 for a particle moving along the centerline and so small as to not perturb the flow field (i.e., travelling with the maximum velocity of Poiseuille flow).

Figure 5.

Figure 5

Open in a new tab

VRBC/⟨vflow⟩ as a function of ΔP/L for different values of tdry.

For each value of tdry, VRBC/⟨vflow⟩ is found to be constant with the applied pressure drop. For RBCs flowing in a bare capillary, this ratio is around 1.5, in fair agreement with previous results obtained in the same confinement conditions.10 For tdry = 190 nm, the velocity ratio lies slightly above 1.6. As tdry decreases in the range 74–190 nm, VRBC/⟨vflow⟩ undergoes a decrease too. This is due to the fact that the average suspending fluid velocity is inversely proportional to tdry, as reported in the literature,53 while RBC velocity stays constant with brush thickness in this range. Whatever the brush thickness, RBCs are observed to travel at a velocity in between the maximum and the average velocities of Poiseuille flow. The results obtained for tdry = 190 and 150 nm, which show values of VRBC/⟨vflow⟩ lying close above that measured for a bare channel, are consistent with the fact that, as shown on Figure 1, RBCs are more deformed in the presence of thick brushes: the flow perturbation induced by a cell is indeed expected to be reduced for a more elongated and a narrower RBC, leading to a larger ratio VRBC/⟨vflow⟩. Within such a picture, one would therefore expect the “bare capillary” situation to yield a lower bound for the value of VRBC/⟨vflow⟩. However, the data set obtained for tdry = 74 nm is difficult to reconcile with this rationale, as we observe a value of the velocity ratio for this thickness that clearly lies below that measured in the bare channel. We do not have at present a plausible explanation for this puzzling observation.

To summarize, it has been shown that the presence of a polymer brush lining the walls of a microcapillary affects both deformation and speed of flowing red blood cells. Such an experimental study is, to the best of our knowledge, the first report on the effect of a synthetic macromolecular layer mimicking the role of the endothelial glycocalyx on RBC flow behavior. However, since pHEMA is a neutral polymer, electrostatic interactions between flowing RBCs and charged polymer chains have been neglected in this work and the attention was mainly focused on hydrodynamics. An increase of RBC deformation is observed in the presence of a brush, with a trend suggesting that RBC deformation is larger for thicker brushes. On the other hand, RBC velocity is found to be reduced by about 20% in microcapillaries bearing brushes of dry thickness larger than 70 nm. The magnitude of such a velocity reduction is compatible with early in vivo observations by Pries et al.,26 who reported a change in blood flow resistance of 20–30% in 20 μm microvessels after enzymatic degradation of the endothelial glycocalyx.

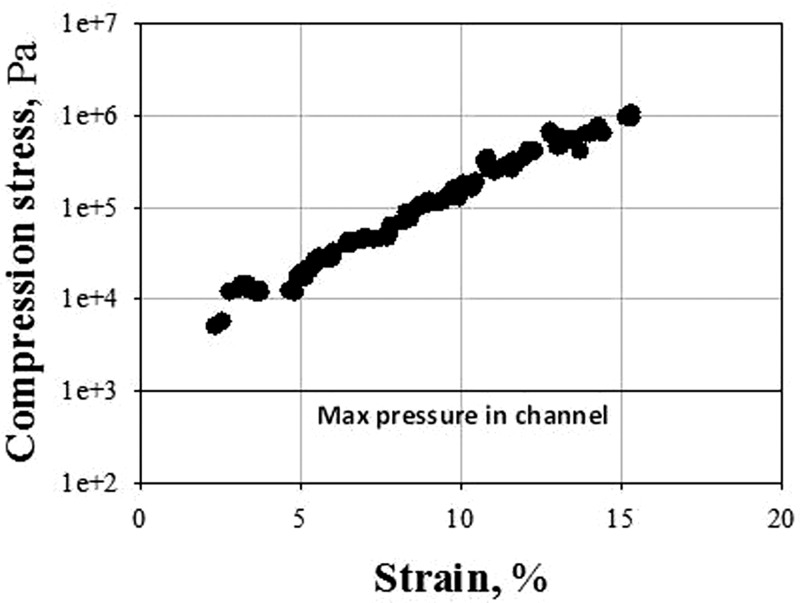
Our results further suggest that, for a given pressure drop and for polymer brushes of tdry > 70 nm, RBCs tend to adapt their deformation in order to maintain a constant velocity. A possible explanation to such a “velocity selection” phenomenon is to consider that, in capillaries of internal dimension comparable with the size of RBCs, the rim of the RBC body bulges outwards in the trailing edge with a corresponding decrease of the fluid gap (which can be considered as a lubrication layer) between the cell membrane and the capillary wall. The outward bulge at the trailing edge generates a pressure overshoot (above the externally imposed pressure) in the lubrication layer, as shown by Secomb et al. in their seminal theoretical work on RBC flow inside bare microcapillaries.57 In principle, such an overpressure could also cause the compression of the polymer brush. Within such a qualitative picture, one can expect that the thicker the brush (hence the smaller the available fluid gap in the lubrication layer), the larger the overpressure, resulting in RBCs being more deformed and brushes being more compressed. The latter effect could account for our observations only if it is hypothesized that, above some overpressure threshold, all the polymer brushes adopt the same “effective” hydrodynamic thickness, thus yielding comparable RBC velocity reductions, irrespective of the brush unperturbed thickness. Here, this scenario is tested quantitatively and a crude estimate of such an overpressure is made by using the numerical results of Secomb et al.57 In their paper, these authors show that for a model RBC suspended in a fluid having the viscosity of water and flowing at 100 μm/s in a tube of 8 μm inner diameter, the maximum value of the extra pressure existing in the lubrication gap between the cell and the wall pgap is 1.5P0 (see Fig. 5(c) of Ref. 46), where P0 is the overall driving pressure drop. The total pressure acting on the brush upon the passage of an RBC is therefore P0 + 1.5P0, which is at most of the order of 1 kPa to reach velocities of a few hundreds μm/s as in our study. This number has moreover to be taken as an upper bound, since in our experiments the RBC confinement is lower, and the cell velocity is larger than what has been simulated in Ref. 46, two effects which tend to further reduce the gap pressure. This estimate of the total pressure has to be compared with the pressure required to compress by a significant amount the polymer brushes. The pressure vs compression strain behavior of the synthesized brushes can be computed from our previous Surface Forces Apparatus (SFA) measurements on PHEMA layers,53 in which the thickness (h) of water-immersed brushes has been monitored as they are subjected to an increasing compression force (F). As described in a recent work by Richter,59 the pressure (P) vs strain (ε) curves are computed from the measured F(h) curves using: P = 1/(2 π R)dF/dh and ε = 1 − h/hswell, where R is the radius of curvature of the substrates used in our SFA experiments and hswell is the unperturbed brush swollen thickness. Using the F(h) data obtained on a brush of 110 nm dry thickness (see Fig. 4 of Ref. 45), the corresponding P(ε) curve is plotted on Figure 6. It can clearly be seen that a total pressure of 1 kPa corresponds to a negligible brush compression, since stresses of several kPa induce only a 2% deformation of the brush. Therefore, the possibility of brush compression caused by RBC flow cannot quantitatively explain our results. The reliability of this estimate is reinforced by a very good agreement with a recent study,60 where numerical simulations have been carried out on RBC flow in microcapillaries (the diameter being equal to 10 μm) lined with glycocalyx. This paper clearly shows that in such channels the passage of RBCs does not influence the brush height due to the presence of a thick cell-free fluid layer.

Figure 6.

Figure 6

Open in a new tab

Stress vs strain curve obtained from a Surface Forces Apparatus experiment during the compression of a brush of dry thickness 110 nm.

Thus, there are two plausible qualitative arguments left in order to try to rationalize our results. One is that RBC shape, controlled by the viscoelastic properties of cell membrane, is more sensitive to the brush presence than RBC velocity, the latter being primarily affected by the brush roughness rather than by its absolute thickness. Another possible mechanism at play in the situation that has been studied in this work is associated to normal stresses at the brush/fluid interface. Such stresses, due to polymer chain stretching under flow, may affect non-trivially RBC shape and velocity. Numerical simulations are currently under way in our group in order to assess the relevance of such normal stresses on RBC microconfined flows.

CONCLUSIONS

In this work, the flow behavior of RBCs in hairy microcapillaries is investigated as a function of the polymer brush thickness and the applied pressure drop. One of the main results is that, above a given threshold of polymer brush thickness, RBCs travel with a velocity significantly lower than that in bare capillaries at the same pressure drop. In fact, such velocity reduction is more pronounced than how much would be expected just based on the lumen reduction due to the presence of the polymer brush. These results are consistent with the hypothesis that the increased flow resistance found in microcapillaries in vivo is due to a macromolecular layer (the glycocalyx) lining endothelial cells on vessel walls. While in the literature this hypothesis is based on hemodynamic simulations with a capillary diameter dependent glycocalyx thickness as a fitting parameter,27 to our knowledge our work provides the first direct experimental determination of the RBC slowing down induced by a polymer layer in the same thickness range of the glycocalyx. Furthermore, the dependence of the RBC velocity reduction on polymer brush thickness is in line with the experimental results reported for the glycocalyx, whose disruption has been shown to have a significant effect on the velocity profile and the RBC shape in microcapillaries in vivo.61, 62 This work is also relevant as a model system to investigate the glycocalyx modulation of local blood viscosity and hematocrit, and the role of glycocalyx as a mechanotransducer.28 In this respect, it should be noticed that a well-controlled model system of the glycocalyx in vitro is especially valuable since the hydrodynamically relevant endothelial cell glycocalyx observed in vivo has been reported to be absent in vitro.62

ACKNOWLEDGMENTS

This study is related to the activity of the European network action COST MP1106 “Smart and green interfaces—from single bubbles and drops to industrial, environmental and biomedical applications.” Funding from the Italian Ministry of University and Research (PRIN program 2010-2011, prot. 20109PLMH2), from the French-Italian University for providing a PhD scholarship to Luca Lanotte under the 2009 Vinci program, and from the Regione Campania (MICROEMA project, 220 APQ-RT02 2008) is acknowledged.

References

  1. Hoffman R. and Benz E. J., Hematology: Basic Principles and Practice (Philadelphia, 2000).
  2. Popel A. S. and Johnson P. C., Annu. Rev. Fluid Mech. 37, 43–69 (2005). 10.1146/annurev.fluid.37.042604.133933 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Guido S. and Tomaiuolo G., C. R. Phys. 10, 751–763 (2009). 10.1016/j.crhy.2009.10.002 [DOI] [Google Scholar]
  4. McHedlishvili G. and Maeda N., Jpn. J. Physiol. 51, 19–30 (2001). 10.2170/jjphysiol.51.19 [DOI] [PubMed] [Google Scholar]
  5. Li X., Vlahovska P. M., and Karniadakis G. E., Soft Matter 9, 28–37 (2013). 10.1039/c2sm26891d [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Zharov V., Galanzha E., Menyaev Y., and Tuchin V., J. Biomed. Opt. 11, 054034 (2006). 10.1117/1.2355666 [DOI] [PubMed] [Google Scholar]
  7. Tomaiuolo G., Barra M., Preziosi V., Cassinese A., Rotoli B., and Guido S., Lab Chip 11, 449–454 (2011). 10.1039/c0lc00348d [DOI] [PubMed] [Google Scholar]
  8. D'Angelo P., Barra M., Cassinese A., Guido S., and Tomaiuolo G., Macromolecular Symposia (2007), p. 247.
  9. Yaginuma T., Oliveira M. S. N., Lima R., Ishikawa T., and Yamaguchi T., Biomicrofluidics 7, 054110 (2013) 10.1063/1.4820414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Tomaiuolo G., Simeone M., Martinelli V., Rotoli B., and Guido S., Soft Matter 5, 3736–3740 (2009). 10.1039/b904584h [DOI] [Google Scholar]
  11. Tomaiuolo G., Lanotte L., Ghigliotti G., Misbah C., and Guido S., Phys. Fluids 24, 051903–051908 (2012). 10.1063/1.4721811 [DOI] [Google Scholar]
  12. Tomaiuolo G., Rossi D., Caserta S., Cesarelli M., and Guido S., Cytometry. Part A 81, 1040–1047 (2012) 10.1002/cyto.a.22215. [DOI] [PubMed] [Google Scholar]
  13. Tomaiuolo G., Preziosi V., Simeone M., Guido S., Ciancia R., Martinelli V., Rinaldi C., and Rotoli B., Ann Ist Super Sanita 43, 186–192 (2007). [PubMed] [Google Scholar]
  14. Tomaiuolo G. and Guido S., Microvas. Res. 82, 35–41 (2011). 10.1016/j.mvr.2011.03.004 [DOI] [PubMed] [Google Scholar]
  15. Hou H. W., Gan H. Y., Bhagat A. A. S., Li L. D., Lim C. T., and Han J., Biomicrofluidics 6, 024115 (2012) 10.1063/1.4710992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Misbah C., J. Phys.: Conf. Ser. 392, 012005 (2012) 10.1088/1742-6596/392/1/012005. [DOI] [Google Scholar]
  17. Pommella A., Caserta S., and Guido S., Soft Matter 9, 7545–7552 (2013). 10.1039/c3sm50617g [DOI] [PubMed] [Google Scholar]
  18. Bagchi P. and Kalluri R. M., Phys. Rev. E 80, 016307 (2009) 10.1103/PhysRevE.80.016307. [DOI] [PubMed] [Google Scholar]
  19. Walter J., Salsac A. V., and Barthes-Biesel D., J. Fluid Mech. 676, 318–347 (2011). 10.1017/S0022112011000486 [DOI] [Google Scholar]
  20. Pries A. R., Schonfeld D., Gaehtgens P., Kiani M. F., and Cokelet G. R., Am. J. Physiol. 272, H2716–2725 (1997). [DOI] [PubMed] [Google Scholar]
  21. Secomb T. W. and Hsu R., Microcirculation 4, 421–427 (1997). 10.3109/10739689709146806 [DOI] [PubMed] [Google Scholar]
  22. Secomb T. W. and Hsu R., J. Biomech. Eng. 118, 538–544 (1996). 10.1115/1.2796041 [DOI] [PubMed] [Google Scholar]
  23. Sherwood J. M., Dusting J., Kaliviotis E., and Balabani S., Biomicrofluidics 6, 024119 (2012) 10.1063/1.4717755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fenton B. M., Wilson D. W., and Cokelet G. R., Pflugers Arch 403, 396–401 (1985). 10.1007/BF00589252 [DOI] [PubMed] [Google Scholar]
  25. Sutton D. W. and Schmid-Schonbein G. W., Am. J. Physiol. 262, H1646–1650 (1992). [DOI] [PubMed] [Google Scholar]
  26. Pries A., Secomb T., Jacobs H., Sperandio M., Osterloh K., and Gaehtgens P., Am. J. Physiol. 273, H2272–2279 (1997). [DOI] [PubMed] [Google Scholar]
  27. Pries A. R. and Secomb T. W., Am. J. Physiol. Heart Circ. Physiol. 289, H2657–2664 (2005) 10.1152/ajpheart.00297.2005. [DOI] [PubMed] [Google Scholar]
  28. Reitsma S., Slaaf D. W., Vink H., van Zandvoort M. A. M. J., and o. Egbrink M. G. A., Pflugers Arch. 454, 345–359 (2007). 10.1007/s00424-007-0212-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Han Y. F., Weinbaum S., Spaan J. A. E., and Vink H., J. Fluid Mech. 554, 217–235 (2006). 10.1017/S0022112005007779 [DOI] [Google Scholar]
  30. Weinbaum S., Zhang X. B., Han Y. F., Vink H., and Cowin S. C., Proc. Natl. Acad. Sci. U.S.A 100, 7988–7995 (2003). 10.1073/pnas.1332808100 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Xiong W. and Zhang J., Annu. Biomed. Eng. 38, 2649–2659 (2010). 10.1007/s10439-010-0017-3 [DOI] [PubMed] [Google Scholar]
  32. Damiano E., Microvasc. Res. 55, 77–91 (1998). 10.1006/mvre.1997.2052 [DOI] [PubMed] [Google Scholar]
  33. Salmon A. H. and Satchell S. C., J. Pathol. 226, 562–574 (2012). 10.1002/path.3964 [DOI] [PubMed] [Google Scholar]
  34. Pries A., Secomb T., Gessner T., Sperandio M., Gross J., and Gaehtgens P., Circ. Res. 75, 904–915 (1994). 10.1161/01.RES.75.5.904 [DOI] [PubMed] [Google Scholar]
  35. Kim M. B. and Sarelius I. H., Microcirculation 10, 167–178 (2003) 10.1038/sj.mn.7800182. [DOI] [PubMed] [Google Scholar]
  36. Lipowsky H. H., Kovalcheck S., and Zweifach B. W., Circ. Res. 43, 738–749 (1978). 10.1161/01.RES.43.5.738 [DOI] [PubMed] [Google Scholar]
  37. Secomb T., Hsu R., and Pries A., Am. J. Physiol. 74, H1016–1022 (1998). [DOI] [PubMed] [Google Scholar]
  38. Secomb T., Hsu R., and Pries A., Biorheology 38, 143–150 (2001). [PubMed] [Google Scholar]
  39. Secomb T., Hsu R., and Pries A., Microcirculation 9, 189–196 (2002) 10.1038/sj.mn.7800132. [DOI] [PubMed] [Google Scholar]
  40. Zhang J., Johnson P. C., and Popel A. S., Microvas. Res. 77, 265–272 (2009). 10.1016/j.mvr.2009.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Liu M. and Yang J., Microvas. Res. 78, 14–19 (2009). 10.1016/j.mvr.2009.04.002 [DOI] [PubMed] [Google Scholar]
  42. Wu T. and Feng J. J., Biomicrofluidics 7, 044115 (2013) 10.1063/1.4817959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Milner S. T., Science 251, 905–914 (1991). 10.1126/science.251.4996.905 [DOI] [PubMed] [Google Scholar]
  44. Binder K., Kreer T., and Milchev A., Soft Matter 7, 7159–7172 (2011). 10.1039/c1sm05212h [DOI] [Google Scholar]
  45. Klein J., Ann. Rev. Mater. Sci. 26, 581–612 (1996). 10.1146/annurev.ms.26.080196.003053 [DOI] [Google Scholar]
  46. Klein J., Science 323, 47–48 (2009). 10.1126/science.1166753 [DOI] [PubMed] [Google Scholar]
  47. Mansky P., Liu Y., Huang E., Russell T. P., and Hawker C., Science 275, 1458–1460 (1997). 10.1126/science.275.5305.1458 [DOI] [Google Scholar]
  48. Storm G., Belliot S. O., Daemen T., and Lasic D. D., Adv. Drug Deliv. Rev. 17, 31–48 (1995). 10.1016/0169-409X(95)00039-A [DOI] [Google Scholar]
  49. Hucknall A., Simnick A. J., Hill R. T., Chilkoti A., Garcia A., Johannes M. S., Clark R. L., Zauscher S., and Ratner B. D., Biointerphases 4, FA50–FA57 (2009). 10.1116/1.3151968 [DOI] [PubMed] [Google Scholar]
  50. Wang A.-J., Xu J.-J., and Chen H.-Y., J. Chromatogr. A 1147, 120–126 (2007). 10.1016/j.chroma.2007.02.030 [DOI] [PubMed] [Google Scholar]
  51. Malham I. B. and Bureau L., Langmuir 26, 4762–4768 (2010). 10.1021/la9035387 [DOI] [PubMed] [Google Scholar]
  52. Yom J., Lane S. M., and Vaia R. A., Soft Matter 8, 12009–12016 (2012). 10.1039/c2sm26277k [DOI] [Google Scholar]
  53. Lanotte L., Guido S., Misbah C., Peyla P., and Bureau L., Langmuir 28, 13758–13764 (2012). 10.1021/la302171a [DOI] [PubMed] [Google Scholar]
  54. Arkill K. P., Knupp C., Michel C. C., Neal C. R., Qvortrup K., Rostgaard J., and Squire J. M., Biophys. J. 101, 1046–1056 (2011). 10.1016/j.bpj.2011.07.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Vink H. and Duling B., Am. J. Physiol. Heart Circ. Physiol. 278, H285–289 (2000). [DOI] [PubMed] [Google Scholar]
  56. Albrecht K., Gaehtgens P., Pries A., and Heuser M., Microvasc. Res. 18, 33–47 (1979). 10.1016/0026-2862(79)90016-5 [DOI] [PubMed] [Google Scholar]
  57. Secomb T. W., Skalak R., Özkaya N., and Gross J. F., J. Fluid Mech. 163, 405–423 (1986). 10.1017/S0022112086002355 [DOI] [Google Scholar]
  58. Cortinovis A., Crippa A., Cavalli R., Corti M., and Cattaneo L., Clin. Hemorheol. Microcirc. 35, 183–192 (2006). [PubMed] [Google Scholar]
  59. Attili S. and Richter R. P., Langmuir 28, 3206–3216 (2012). 10.1021/la204602n [DOI] [PubMed] [Google Scholar]
  60. Deng M., Li X., Liang H., Caswell B., and Karniadakis G. E., J. Fluid Mech. 711, 192–211 (2012). 10.1017/jfm.2012.387 [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Vink H. and Duling B. R., Circ. Res. 79, 581–589 (1996). 10.1161/01.RES.79.3.581 [DOI] [PubMed] [Google Scholar]
  62. Potter D. R. and Damiano E. R., Circ. Res. 102, 770–776 (2008) 10.1161/CIRCRESAHA.107.160226. [DOI] [PubMed] [Google Scholar]

Articles from Biomicrofluidics are provided here courtesy of American Institute of Physics

RESOURCES