Quantitative modeling of the accuracy in registering preoperative patient-specific anatomic models into left atrial cardiac ablation procedures

Abstract

Purpose: In cardiac ablation therapy, accurate anatomic guidance is necessary to create effective tissue lesions for elimination of left atrial fibrillation. While fluoroscopy, ultrasound, and electroanatomic maps are important guidance tools, they lack information regarding detailed patient anatomy which can be obtained from high resolution imaging techniques. For this reason, there has been significant effort in incorporating detailed, patient-specific models generated from preoperative imaging datasets into the procedure. Both clinical and animal studies have investigated registration and targeting accuracy when using preoperative models; however, the effect of various error sources on registration accuracy has not been quantitatively evaluated.

Methods: Data from phantom, canine, and patient studies are used to model and evaluate registration accuracy. In the phantom studies, data are collected using a magnetically tracked catheter on a static phantom model. Monte Carlo simulation studies were run to evaluate both baseline errors as well as the effect of different sources of error that would be present in a dynamic in vivo setting. Error is simulated by varying the variance parameters on the landmark fiducial, physical target, and surface point locations in the phantom simulation studies. In vivo validation studies were undertaken in six canines in which metal clips were placed in the left atrium to serve as ground truth points. A small clinical evaluation was completed in three patients. Landmark-based and combined landmark and surface-based registration algorithms were evaluated in all studies. In the phantom and canine studies, both target registration error and point-to-surface error are used to assess accuracy. In the patient studies, no ground truth is available and registration accuracy is quantified using point-to-surface error only.

Results: The phantom simulation studies demonstrated that combined landmark and surface-based registration improved landmark-only registration provided the noise in the surface points is not excessively high. Increased variability on the landmark fiducials resulted in increased registration errors; however, refinement of the initial landmark registration by the surface-based algorithm can compensate for small initial misalignments. The surface-based registration algorithm is quite robust to noise on the surface points and continues to improve landmark registration even at high levels of noise on the surface points. Both the canine and patient studies also demonstrate that combined landmark and surface registration has lower errors than landmark registration alone.

Conclusions: In this work, we describe a model for evaluating the impact of noise variability on the input parameters of a registration algorithm in the context of cardiac ablation therapy. The model can be used to predict both registration error as well as assess which inputs have the largest effect on registration accuracy.

INTRODUCTION

Catheter ablation therapy is a minimally invasive procedure for treating atrial fibrillation, a condition in which the atria of the heart beat rapidly and irregularly. In this procedure, a catheter is guided into the left atrium and radiofrequency energy is delivered into the endocardial wall to interrupt aberrant electrical pathways. While the exact etiology of the disease is unknown, it is believed that the ectopic foci often originate in the pulmonary veins.¹ For this reason, a typical treatment strategy is to ablate circumferential patterns around each pair of pulmonary veins in order to achieve electrical isolation within the left atrium.² Accurate anatomic guidance is necessary to create effective tissue lesions in order to eliminate fibrillation.

Guidance of the catheter relies on real-time imaging technologies such as fluoroscopy and intracardiac ultrasound as well as generation of a three-dimensional electroanatomic map of the left atrium and pulmonary veins. This map is constructed by sampling points on the left atrial endocardial surface with a tracked catheter and reconstructing a surface to produce a rough estimate of 3D patient anatomy. While fluoroscopy, ultrasound, and electroanatomic maps are important guidance tools, they lack sufficient information regarding detailed patient anatomy which can be obtained from high resolution imaging techniques such as computed tomography (CT) and magnetic resonance imaging. For this reason, there has been significant effort in incorporating detailed, patient-specific models into the ablation procedure.^{3, 4, 5, 6, 7, 8, 9}

Incorporating a preoperative patient model into a cardiac ablation procedure requires several steps. Prior to the procedure, a patient-specific model is constructed by segmenting the left atrium and pulmonary veins from a high-resolution imaging scan and tessellating the binary segmentation to create a surface model. During the procedure, the tip of the catheter is magnetically tracked in three-dimensional space. The transformation between real-world patient space and preoperative image space is computed using a combination of paired landmark and surface-based alignment techniques. The computed transformation is applied to the tracked catheter to provide real-time guidance in reference to the patient-specific model.

Both clinical^{10, 11, 12, 13, 14, 15, 16} and animal^{3, 4, 7, 17, 18} studies have investigated registration and targeting accuracy when using preoperative models; however, the effect of various error sources on registration accuracy has not been quantitatively evaluated. In this work, we propose a model for evaluating the impact of noise variability on the input parameters of a standard registration approach in the context of cardiac ablation therapy. The model can be used to predict registration error as well as assess which inputs have the largest effect on registration accuracy. First, we characterize the inherent errors in computing a registration transformation between real-world patient space and image-space using a magnetically tracked catheter and a static left atrial patient model. Next, we evaluate how different sources of error in a dynamic in vivo setting affect the registration accuracy by varying the noise on the input parameters in a series of Monte Carlo simulations. The results from the Monte Carlo simulations are then compared with those found in in vivo canine and patient studies. The main contribution of this work is the quantitative assessment of the effect of various error sources on registration accuracy in the context of cardiac ablation therapy.

METHODS

Registration algorithm and error metrics

In this section, we define the types of points collected for use in the registration algorithm along with details of the algorithm itself. We also define each of the error metrics used throughout the paper to evaluate the registration results. The goal of the registration algorithm is to compute a transformation between the real-world patient space and preoperative image-space. Inputs to the algorithm are a preoperative, patient-specific surface model, a collection of anatomic landmark fiducial pairs, and a set of surface points. In this work, all preoperative models are generated from high-resolution CT scans. First, the left atrium and pulmonary veins are segmented from a CT dataset using a previously validated, semiautomatic segmentation algorithm.¹⁹ Next, a surface model is generated from the segmented binary volume using a modified marching cubes method with an adaptive polygonal reduction step.²⁰ Anatomic landmark fiducials are defined in image-space by clicking with a mouse on the surface model. The location of these image landmark fiducial locations are defined as ${\mathit{P}}_{\text{ILF}}$. Anatomic landmark fiducials are defined in physical space by positioning the tracked catheter at the corresponding anatomical location and sampling a point. The location of these physical landmark fiducial locations are defined as ${\mathit{P}}_{\text{PLF}}$. Physical surface points, defined as ${\mathit{P}}_S$, are also collected with the tracked catheter by sequentially positioning the catheter on the left atrial endocardial surface and sampling a point.

The registration algorithm consists of two steps. In the first step, a point-based, rigid registration,²¹T_LF, is found to minimize the distance between the anatomical landmark fiducial in image-space and physical space as follows:

$$C\left(T_{\text{LF}}\right)=\sum _{i=1}^N{|T_{\text{LF}}\left({\mathit{P}}_{{\text{PLF}}_i}\right)-{\mathit{P}}_{{\text{ILF}}_i}|}^2,$$ (1)

where C(T_LF) is the cost associated with the landmark-based registration transformation T_LF and N is the number of landmark fiducial pairs. In the second step, the initial landmark registration is refined using a point-to-surface distance minimization between the transformed surface points, $\widehat{{\mathit{P}}_S}=T_{\text{LF}}\left({\mathit{P}}_S\right)$, and the preoperative surface model. A downhill simplex optimization is used to minimize

$$C\left(T_S\right)=\sum _{i=1}^{N}d\left(T_S\left(\widehat{{\mathit{P}}_{s_i}}\right)\right),$$ (2)

where C(T_S) is the cost associated with the surface-based registration transformation T_S, d() is the distance from a transformed surface point to the preoperative surface model, and N is the total number of surface points. d() is the distance transform from the model surface boundary, with value zero at the boundary and increasing positively in both directions away from the boundary. Registration results are evaluated using fiducial registration error (FRE),²¹ target registration error (TRE),²¹ and point-to-surface (PTS) distances defined as follows.

Fiducial registration error:

$${\text{FRE}}^2=\frac{1}{N}\sum _{i=1}^N{|T_{\text{LF}}\left({\mathit{P}}_{{\text{PLF}}_i}\right)-{\mathit{P}}_{{\text{ILF}}_i}|}^2,$$ (3)

where N is the number of anatomical landmark fiducial pairs. FRE quantifies the residual error between fiducial point pairs following landmark registration.

Target registration error following landmark registration:

$${\text{TRE}}_{\text{LF}}^2=\frac{1}{N}\sum _{i=1}^N{|T_{\text{LF}}\left({\mathit{P}}_{{\text{PT}}_i}\right)-{\mathit{P}}_{{\text{IT}}_i}|}^2,$$ (4)

where N is the number of targets, ${\mathit{P}}_{\text{PT}}$ are the physical target locations, and ${\mathit{P}}_{\text{IT}}$ are the image target locations. TRE_LF quantifies the error between transformed physical target locations and image target locations using landmark registration only. Targets are known locations, separate from the landmark fiducial points, used to measure registration accuracy.

Target registration error following landmark and surface registration:

$${\text{TRE}}_{\text{LF}+\text{S}}^2=\frac{1}{N}\sum _{i=1}^N{|T_S\left(\widehat{{\mathit{P}}_{{\text{PT}}_i}}\right)-{\mathit{P}}_{{\text{IT}}_i}|}^2,$$ (5)

where $\widehat{{\mathit{P}}_{\text{PT}}}=T_{\text{LF}}\left({\mathit{P}}_{\text{PT}}\right)$ are the physical targets transformed by the landmark registration and N is the number of targets. TRE_{LF + S} quantifies the error between the transformed physical target locations and the image target locations using landmark registration refined by surface-based registration.

Point-to-surface registration error following landmark registration:

$${\text{PTS}}_{\text{LF}}=\frac{1}{N}\sum _{i=1}^{N}d\left(T_{\text{LF}}\left({\mathit{P}}_{{\text{TS}}_i}\right)\right),$$ (6)

where N is the number of test surface points, ${\mathit{P}}_{\text{TS}}$, which is a separate set of surface points that are not used to compute the transformation T_S in Eq. 2.

Point-to-surface registration error following landmark and surface registration:

$${\text{PTS}}_{\text{LF}+\text{S}}=\frac{1}{N}\sum _{i=1}^{N}d\left(T_S\left(\widehat{{\mathit{P}}_{{\text{TS}}_i}}\right)\right).$$ (7)

where $\widehat{{\mathit{P}}_{\text{TS}}}=T_{\text{LF}}\left({\mathit{P}}_{\text{TS}}\right)$ is a set of N test surface points transformed by the landmark registration.

Phantom studies

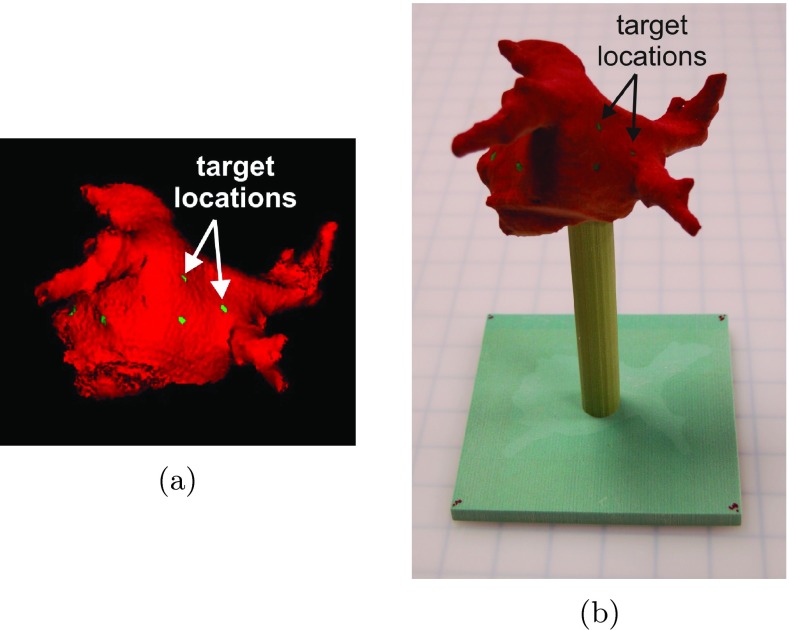
A physical phantom was constructed from a patient dataset using the following steps. First, the left atrium and pulmonary veins were segmented from the CT scan of a patient dataset. Next, image target points, ${\mathit{P}}_{\text{IT}}$, were marked in six locations across the left atrium and these locations were recorded. A surface model was generated and subsequently printed using a Z Corporation Spectrum Z510 rapid prototyping printer. A volume rendering of the computer model and the corresponding physical model are shown in Fig. 1. The physical target locations, ${\mathit{P}}_{\text{PT}}$, have a direct one-to-one correspondence with the known image target locations, ${\mathit{P}}_{\text{IT}}$, and are used for registration validation.

Figure 1.

(a) Surface model with target locations. (b) Printed physical model.

Data were collected on the physical phantom with a 7 F (2.3 mm tip), magnetically tracked catheter interfaced to a Biosense CARTO XP system (Diamond Bar, CA) using a research API for direct access to catheter locations. These locations were read into our inhouse prototype research system²² which we used for all registration and visualization tasks. Point locations were collected at the six target locations, four anatomical fiducial locations, and across the surface of the left atrium and pulmonary veins. The four anatomical locations are: the carina between the left atrial appendage and left superior pulmonary vein, the inferior point of the left inferior pulmonary vein ostium, the inferior point of the right inferior pulmonary vein ostium, and the superior point of the right superior pulmonary vein. Data were collected as follows:

• 1.The catheter tip was positioned on each of the six marked physical targets, ${\mathit{P}}_{\text{PT}}$, and one sample of the catheter location was recorded. This was repeated 20 times.
• 2.The catheter tip was positioned on each of the four physical landmark fiducials, ${\mathit{P}}_{\text{PLF}}$, and one sample of the catheter location was recorded. This was repeated 20 times.
• 3.The catheter tip was positioned across the left atrium, left atrial appendage, and pulmonary veins and a total of 400 surface points, ${\mathit{P}}_S$, were sampled and recorded.
• 4.On the image-derived surface model, the mouse was positioned at each of the four image landmark fiducial, ${\mathit{P}}_{\text{ILF}}$, and the location was recorded. This was repeated 20 times.

Monte Carlo simulations were run to quantify registration error in both the static phantom set-up as well as simulated in vivo procedures. For the static phantom, the x, y, and z locations for each of the ${\mathit{P}}_{\text{PT}}$, ${\mathit{P}}_{\text{PLF}}$, and ${\mathit{P}}_{\text{ILF}}$ are modeled as Gaussian distributions,

$$f(p;\mu ,\sigma )=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-{\left(p-\mu \right)}^2/2{\sigma }^2}$$ (8)

with μ and σ estimated from data collected on the phantom and image-derived surface model. The mean of the physical targets, ${\mu }_{{\text{PT}}_{ij}}$, and standard deviation of the physical targets, ${\sigma }_{{\text{PT}}_{ij}}$, for i = 1...6 and j = 1, 2, 3 where i is each of the physical targets and j is each of the x, y, and z dimensions, are estimated as the mean and variance of the 20 sampled locations recorded in Step 1. The mean of the physical landmark fiducials, ${\mu }_{{\text{PLF}}_{ij}}$, and the standard deviation of the physical landmark fiducials, ${\sigma }_{{\text{PLF}}_{ij}}$, for i = 1...4 and j = 1, 2, 3 where i is each of the physical landmark fiducials and j is each of the x, y, and z dimensions, are estimated as the mean and variance of the 20 sampled locations recorded in Step 2. The mean of the image landmark fiducials, ${\mu }_{{\text{ILF}}_{ij}}$, and standard deviation of the image landmark fiducials, ${\sigma }_{{\text{ILF}}_{ij}}$, for i = 1...4 and j = 1, 2, 3 where i is each of the image landmark fiducials and j is each of the x, y, and z dimensions, are estimated from the locations recorded in Step 4.

Surface points are modeled as ${\mathit{P}}_S+\mathit{\eta }$ where ${\mathit{P}}_S$ are points collected in Step 3 and each of the x, y, and z components of η is modeled as zero mean, σ_η Gaussian random noise. Image target locations, ${\mathit{P}}_{\text{IT}}$, are known, deterministic locations recorded during construction of the phantom. For all simulated inputs, a standard Box-Muller method²³ is used to generated random deviates with a Gaussian distribution.

A block diagram of the Monte Carlo simulation is shown in Fig. 2 with each step detailed below.

• 1.Generate random samples of the locations for each of the ${\mathit{P}}_{\text{PLF}}$ from $f(p;{\mu }_{{\text{PLF}}_{ij}},{\sigma }_{{\text{PLF}}_{ij}})$.
• 2.Generate random samples of the locations for each of the ${\mathit{P}}_{\text{ILF}}$ from $f(p;{\mu }_{{\text{ILF}}_{ij}},{\sigma }_{{\text{ILF}}_{ij}})$.
• 3.Compute T_LF as described in Sec. 2A.
• 4.Randomly sample 100 of the 400 surface points, ${\mathit{P}}_S$, for use in the surface-based registration algorithm and model as ${\mathit{P}}_S+\mathit{\eta }$.
• 5.Compute T_S as described in Sec. 2A.
• 6.Generate random samples of the locations for each of the ${\mathit{P}}_{\text{PT}}$ from $f(p;{\mu }_{{\text{PT}}_{ij}},{\sigma }_{{\text{PT}}_{ij}}$).
• 7.Randomly sample 50 of the 300 surface points which were not used in Step 4 for use as surface test points, ${\mathit{P}}_{\text{TS}}$, and model as ${\mathit{P}}_{\text{TS}}+\mathit{\eta }$.
• 8.Compute each of the error metrics, FRE, TRE_LF, TRE_{LF + S}, PTS_LF, and PTS_{LF + S} as described in Sec. 2A.

Figure 2.

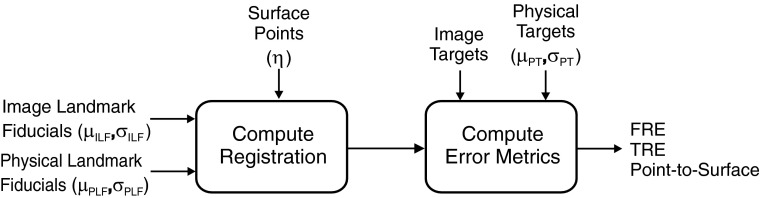
Block diagram for Monte Carlo simulation studies.

The proposed model is used to evaluate registration errors in the static phantom set-up as well as characterize the registration algorithm under different levels of variability in the input parameters. Errors from the static phantom set-up provide minimum expected errors given the inherent variabilities in the inputs such as magnetic tracking error and localization of image fiducial points, physical fiducial points, and physical target points.

In an in vivo procedure, registration algorithm inputs from physical space will have increased variability due to cardiac and respiratory motion, as well as increased difficulty in localizing the physical fiducial and target points. Commercial mapping systems can compensate for much of the cardiac motion by gating sampled catheter points to match the cardiac phase of the preoperative imaging scan, however, respiratory motion potentially contributes a large amount of variability. The ability of a physician to position the catheter at specific anatomic or target locations under fluoroscopic and ultrasound guidance will depend on a wide variety of factors including physician experience, geometry of the patient's anatomy, and quality of the real-time images. In this work, we consider five Monte Carlo simulations to quantify how variability in sampling physical landmark fiducials, physical targets, and surface points affects the registration algorithm. In each simulation, all values of μ are set using estimates from the phantom set-up and values of σ are varied as described.

• Simulation 1:

  All values of σ were set using the estimates from the phantom set-up. This simulation provides baseline error estimates for the registration algorithm in a static, physical setting.

• Simulation 2:

  σ_PLF is varied from 2.0 to 10.0 mm to model different levels of variability in sampling physical landmark fiducial locations with a catheter in vivo. All other values of σ are set using estimates from the static phantom set-up. This simulation demonstrates how errors in localization of the physical landmark fiducials affect registration accuracy.

• Simulation 3:

  σ_PT is varied from 1.0 to 5.0 mm to model different levels of variability in sampling physical target locations with a catheter in vivo. σ_PLF is set to a constant value of 6.0 mm and all other values of σ are set using estimates from the static phantom set-up. In an in vivo study, even the target points which are used to evaluate the accuracy of the registration algorithm, will have some inherent error in identifying their location. This simulation demonstrates how the computed registration errors will be affected by measurement error in the target locations.

• Simulation 4:

  σ_η is varied from 3.0 to 15.0 mm to generate ${\mathit{P}}_S+\mathit{\eta }$ for modeling different levels of variability in sampling surface points. In this simulation, noise is not added to the test points, ${\mathit{P}}_{\text{TS}}$. σ_PLF is set to a constant value of 6.0 mm and all other values of σ are set using estimates from the static phantom set-up. This simulation demonstrates how noise in the surface points affects registration accuracy.

• Simulation 5:

  σ_η is varied from 2.0 to 10.0 mm to generate ${\mathit{P}}_S+\mathit{\eta }$ and ${\mathit{P}}_{\text{TS}}+\mathit{\eta }$ to model different levels of variability in sampling surface points used in the registration algorithm as well as the test points. σ_PLF is set to a constant value of 6.0 mm and all other values of σ are set using estimates from the static phantom set-up. This is a more realistic simulation of measured registration accuracy in an in vivo setting since points used in both the registration algorithm as well as the test surface points will have inherent error associated with the procedure.

For each simulation study, 1000 iterations were run and means (std) were computed for each of the previously described registration error metrics.

Canine studies

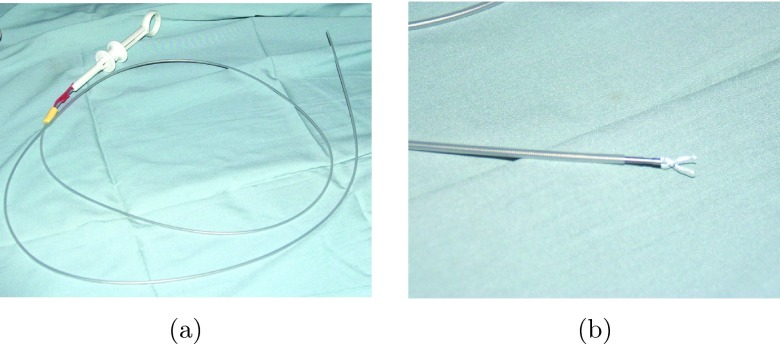
Six canine studies were conducted according to a protocol approved by the Mayo Foundation Institutional Animal Care and Use Committee. After establishing deep anesthesia, positive-pressure ventilation was started, and vascular access was obtained percutaneosly. Surface ECG and blood pressure were continuously monitored throughout the procedure. After obtaining access to the left atrium through transseptal catheterization, cardiac catheters were used to place metal clips in the left atrium and pulmonary veins of the canine under fluoroscopic and ultrasound guidance. The metal clips are visible under CT, ultrasound, and fluoroscopy, and serve as physical target locations in the experiments. A photograph of the catheter is shown in Fig. 3a with a close-up of the clip at the end of the catheter in Fig. 3b. In each dog, an attempt was made to place a total of five clips. Since the endocardial surface of the left atrium is smooth, a subset of the clips either did not attach, or detached between the initial and follow-up procedure. In cases where clips did not initially attach, an attempt was made to insert an additional clip, however, no more than one or two additional clips were attempted per dog since each clip will appear in the CT data and multiple extraneous clips could potentially confound proper identification of the attached clips.

Figure 3.

(a) A photograph of the catheter used to deliver the metal clip and (b) a close-up of the tip of the catheter with the clip open.

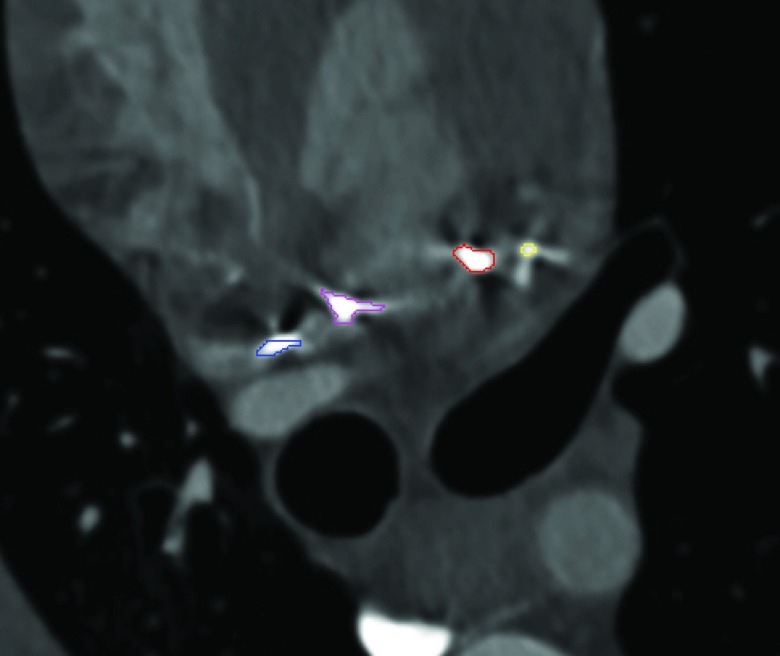
Next, a contrast-enhanced, 64-slice multidetector CT scan was collected with the clips in place. Helical CT scanning was performed 10–20 s after intravenos injection of 40 ml of contrast media at a rate of 4 ml/s. The CT scan was cardiac-gated and collected at end expiration. The dataset constructed at 80% of the R-R interval was utilized for analysis. In these experiments, the target location was the insertion point of the clip into the endocardial surface; however, as seen in Fig. 4, the clips create star shaped artifacts in the CT scan making it difficult to precisely localize this point. For this reason, we instead segmented each clip near its insertion point into the endocardium, attempting to exclude the star-shaped artifacts, as shown in Fig. 4. A distance transform is then computed from the segmented clip and used to compute TRE. In addition, the left atrium and pulmonary veins were segmented to generate a triangulated surface model.

Figure 4.

Segmented clips shown in CT scan.

During a follow-up procedure, our prototype research system was used to collect the following data:

• 1.The physical target locations, ${\mathit{P}}_{\text{PT}}$, are determined by navigating the catheter to point where the metal clip inserts into the endocardium using ultrasound and biplane fluoroscopy for guidance. This was done for each clip and the entire procedure was repeated three times in order to obtain three samples for each clip location.
• 2.Anatomic landmark pairs were collected in image space and physical space. The catheter was guided to anatomical locations in the left atrium under ultrasound and fluoroscopic guidance and the point location, ${\mathit{P}}_{\text{PLF}}$, was sampled. The corresponding landmark was located on the preoperative surface model and the point location in image space ${\mathit{P}}_{\text{ILF}}$ was recorded.
• 3.Points along the endocardial surface, ${\mathit{P}}_S$, were sampled with the catheter under ultrasound and fluoroscopic guidance.

Across the six studies, a total of 20 clips were placed with a range of 1–5 clips per canine (mean 3.3 ± 1.6). A range of 4–8 landmark pairs were collected (mean 6.0 ± 1.7), and 46–113 surface points were sampled (mean 81.8 ± 23.4). The landmark fiducial point pairs were used to compute T_LF and the surface points were used to compute T_S. Error metrics FRE, TRE_LF, TRE_{LF + S}, PTS_LF, and PTS_{LF + S} were computed as described in Sec. 2A. A leave-one-out technique was used for computation of the PTS_{LF + S} errors. Error metrics involving target locations, ${\mathit{P}}_{\text{PT}}$, were computed three times, once for each time the catheter was navigated to the clip location.

Clinical evaluation

A small clinical evaluation was conducted with our prototype research system in which the registration algorithm was evaluated in three patients. Preoperative CT scans were collected on each patient and a left atrial model was constructed. During the procedure, data were collected using our prototype research system. Landmark fiducial pairs, endocardial surface points, and point locations during ablation burns were collected and recorded. Points collected during the ablation burns were not used for calculation of the registration, but were instead used as independent surface test points. Across the three patients, the number of landmark pairs ranged from 5 to 7 (mean 6.0 ± 1.0), the number of surface points ranged from 216 to 236 (mean 227.7 ± 10.4), and the number of ablation points ranged from 223 to 276 (mean 245.3 ± 27.5). Error metrics FRE, PTS_LF, and PTS_{LF + S} were computed as described in Sec. 2A.

RESULTS

Phantom studies

The following variance values were found for data collected during the phantom experiments: the median (min,max) ${\sigma }_{{\text{PT}}_{ij}}$ across all i, j was found to be 0.56 (0.24, 1.00) mm, the median (min, max) ${\sigma }_{{\text{PLF}}_{ij}}$ across all i, j was found to be 0.74 (0.40, 1.76) mm, and the median (min, max) ${\sigma }_{{\text{ILF}}_{ij}}$ across all i, j was found to be 1.03 (0.41, 2.19) mm. The variability in sampled catheter points was higher when sampling physical landmark fiducial locations than physical target locations. This is expected as the targets are marked locations on the phantom, while the landmark fiducials are defined by anatomic location only. Locating image landmark fiducials had an even higher variability. The user-selected landmark location can vary depending on the rotation of the model, which is likely to be slightly different each time the user selects the point, potentially leading to this higher variability.

Results from Simulation 1, which quantifies errors in the static phantom set-up, are given in the top row of Table 1. The baseline variations for localization of the physical targets, physical landmark fiducials, and image landmark fiducials in the inputs to the registration algorithm lead to errors of 2.6 mm for FRE and 2.9 and 2.6 mm for TRE_LF and TRE_{LF + S}, respectively. Static point-to-surface errors are 1.5 mm for PTS_LF and 1.3 mm for PTS_{LF + S}. The surface-based registration only marginally improves the landmark-based registration as measured by the mean TRE or PTS in the static case since there is already good registration alignment with landmark registration alone. For both registration types, PTS error is lower than the TRE. This is because PTS measures the distance from a sampled point to the nearest point on the preoperative surface model, where TRE measures distance between two specific target points.

Table 1.

Mean (std) error metrics for Simulation 1, the static phantom set-up (top row). Results from Simulation 2 where σ_PLF is varied from 2.0 to 10.0 are given in subsequent rows. All values are given in mm.

σPLF	FRE	TRELF	TRELF + S	PTSLF	PTSLF + S
Static	2.6 (0.6)	2.9 (0.5)	2.6 (0.3)	1.5 (0.2)	1.3 (0.1)
2.0	3.4 (1.0)	3.7 (0.9)	2.7 (0.4)	1.9 (0.4)	1.3 (0.2)
4.0	5.3 (1.6)	5.7 (3.6)	3.3 (3.0)	2.7 (1.1)	1.4 (0.7)
6.0	7.4 (2.1)	9.7 (7.6)	5.5 (7.2)	4.0 (2.0)	2.0 (1.7)
8.0	9.6 (2.8)	13.5 (9.3)	7.8 (9.5)	5.2 (2.5)	2.6 (2.1)
10.0	11.7 (3.6)	16.9 (10.4)	10.1 (10.9)	6.2 (2.7)	3.1 (2.5)

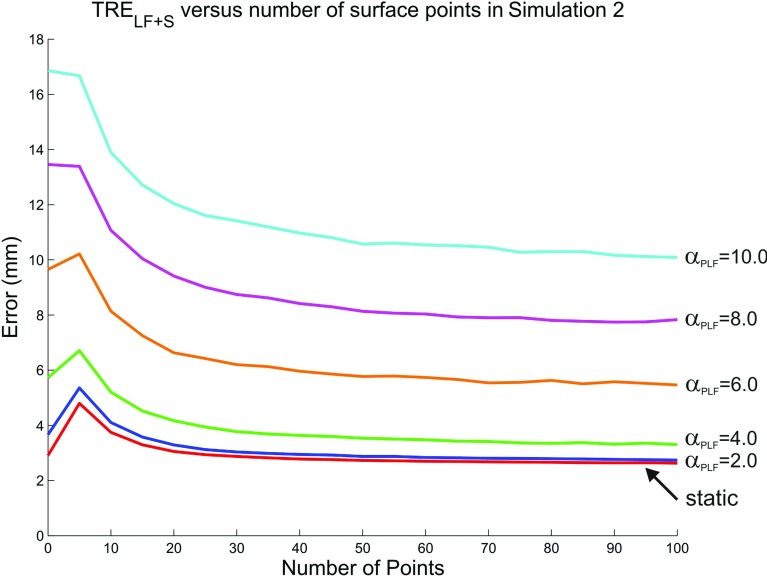
In Simulation 2, σ_PLF is varied from 2.0 to 10.0 mm and results of this simulation are given in the subsequent rows of Table 1. As expected, increasing values of σ_PLF, lead to larger values of FRE and TRE_LF. Note, however, that FRE and TRE have been shown to be uncorrelated,²⁴ and therefore FRE cannot be used to predict TRE_LF. Of particular interest, is the relationship between TRE_LF and TRE_{LF + S}. As σ_PLF increases, TRE_LF increases, but TRE_{LF + S} holds relatively stable until σ_PLF reaches 6.0 mm. Thus, at these lower levels of variance, the surface-based registration can compensate for errors in localization of the physical landmark fiducials. The surface-based registration continues to improve the initial fiducial landmark registration for all values of σ_PLF, however, as values rise above 6.0 mm, the surface-based registration is not always able to correct the initial misalignment as demonstrated by a larger overall mean and standard deviations of the errors. A similar pattern is observed with the PTS errors. In order to demonstrate the effect of the surface registration on the initial landmark registration, a plot of TRE_{LF + S} versus number of surface points (at increments of five) is shown for each value of σ_PLF in Fig. 5. At each increment of five surface points, the initial landmark registration is refined by the surface registration. For lower values of σ_PLF, TRE_{LF + S} initially increases before decreasing. This occurs since the initial landmark-based registration is reasonably accurate and the surface based registration can cause a misalignment when only a few points are utilized. In general, the plots demonstrate that when approximately 20 points or more are sampled, the surface based registration consistently improves the landmark based registration. In addition, the surface based registration provides a larger decrease in registration error for higher values of variability in landmark localization.

Figure 5.

TRE_{LF + S} versus number of surface points (at increments of five) for static case (lowest line) and incremental values of σ_PLF in Simulation 2.

Results of Simulation 3 are given in Table 2. As σ_PT increases, both TRE_LF and TRE_{LF + S} increase, demonstrating the effect of target localization on measured registration accuracy. That is, even if the variability on the inputs to the registration algorithm are held constant, the measured error will vary based on localization of the validation targets. This demonstrates realistic measurable errors in an in vivo catheter-based experiment since there will be inherent error in localization of the targets used for validation. This simulation demonstrates that if the variability of localizing the target is too high, the registration results can be obscured in the noise of target localization.

Table 2.

Results from Simulation 3 where σ_PT is varied and σ_PLF is set to 6.0 mm. All values are given in mm.

σPT	TRELF	TRELF + S
Static	9.5 (7.3)	5.3 (6.8)
1.0	9.9 (7.6)	5.7 (6.9)
2.0	10.3 (7.3)	6.6 (6.5)
3.0	10.9 (6.7)	7.7 (5.7)
4.0	11.8 (6.6)	9.1 (6.0)
5.0	13.3 (6.8)	10.8 (6.0)

Results of Simulation 4 are shown in Table 3. As σ_η is increased in ${\mathit{P}}_s+\mathit{\eta }$, both TRE_{LF + S} and PTS_{LF + S} increase. For lower values of σ_η, the surface algorithm can compensate for the noise on the surface points and continues to improve the landmark fiducial registration. As the noise on the surface points increases, the surface algorithm provides minimal, if any, improvement to the initial registration result. These results characterize the behavior of the surface-based registration in response to increasing amounts of noise on the points used in the registration. This simulation does not, however, give realistic values of PTS errors that would be measured in an in vivo experiment, since the test surface points would also be subject to the same levels on noise as the registration surface points. This is addressed in Simulation 5 with the results shown in Table 4. In this simulation, measured errors for PTS_LF and PTS_{LF + S} are higher since noise is also added to the test surface points. Again, as σ_η increases, the surface registration is less able to improve the initial fiducial landmark registration results.

Table 3.

Results from Simulation 4 where σ_η is varied in ${\mathit{P}}_s+\mathit{\eta }$ and σ_PLF is set to 6.0 mm. All values are given in mm.

ση	TRELF	TRELF + S	PTSLF	PTSLF + S
Static	9.0 (6.6)	4.9 (6.1)	3.8 (1.8)	1.9 (1.4)
3.0	10.1 (7.9)	6.3 (7.2)	4.0 (2.1)	2.3 (1.7)
6.0	9.7 (7.5)	7.1 (6.7)	4.0 (2.0)	2.7 (1.6)
9.0	9.3 (7.3)	7.8 (6.4)	3.9 (1.9)	3.1 (1.6)
12.0	9.6 (7.5)	8.9 (6.6)	3.9 (2.0)	3.6 (1.7)
15.0	9.6 (7.4)	9.8 (6.5)	4.0 (2.0)	4.0 (1.7)

Table 4.

Results from Simulation 5 where σ_η is varied in ${\mathit{P}}_S+\mathit{\eta }$ and ${\mathit{P}}_{\text{TS}}+\mathit{\eta }$ and σ_PLF is set to 6.0 mm. All values are given in mm.

ση	PTSLF	PTSLF + S
Static	3.9 (2.0)	1.9 (1.5)
2.0	4.1 (1.8)	2.5 (1.3)
4.0	4.8 (1.7)	3.7 (1.2)
6.0	5.7 (1.5)	5.0 (1.1)
8.0	6.8 (1.4)	6.3 (1.1)
10.0	7.8 (1.3)	7.5 (1.1)

Canine studies

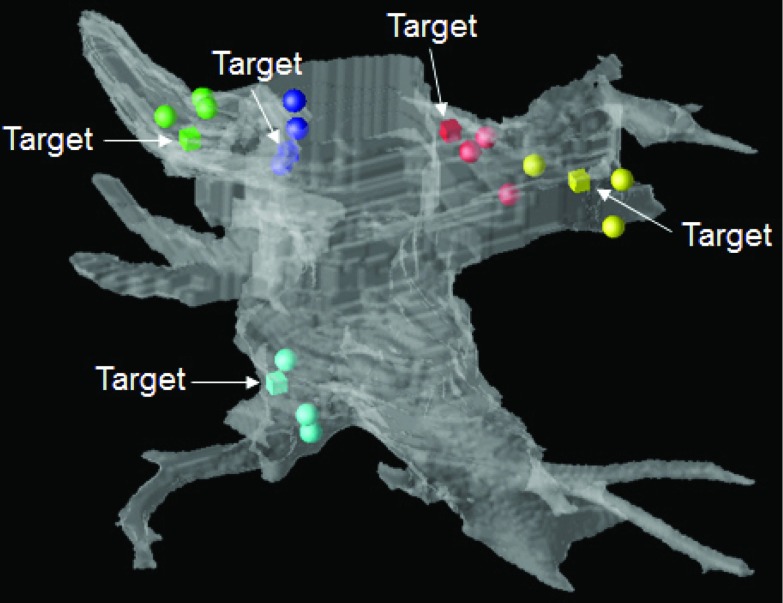
An image of the result from one canine study is given in Fig. 6. In this image, the location of the target clip as determined by the CT images is shown as a cube. The spheres represent locations of the three sampled catheter locations following landmark and surface-based registration. These images provide a visual assessment of both the in vivo variability in sampling a target clip location with a catheter as well as the accuracy of the registration algorithm. Errors for all six canine studies are given in Table 5. For each study, measurements of TRE are made three times, once for each time the target clip location was navigated to and sampled with the catheter. These results demonstrate that the surface-based registration improves registration accuracy as measured by both TRE and PTS which is consistent with the results from the Monte Carlo simulation studies. The FREs for all but one of the six studies range from 7.6 to 11.1 mm which most closely match results when σ_PLF ranges from 6.0 to 10.0 mm in Simulation 2. The mean TRE_{LF + S} of 5.8 mm most closely aligns with results from Simulation 3 where σ_PLF is set to 6.0 mm and σ_PT is set to 1.0 mm and results from Simulation 4 where σ_PLF is set to 6.0 mm and σ_η is 3.0 mm. The overall mean PTS_LF and PTS_{LF + S} errors are 4.1 and 3.2 mm which most closely align with results from Simulation 5 where σ_PLF is set to 6.0 mm and σ_η is 2.0–4.0 mm.

Figure 6.

Canine study registration results from posterior view. Left atrial surface model is semitransparent in white, locations of target clips are displayed as cubes (and indicated with arrows), and the registered, sampled points are displayed as spheres. The cardiologist navigated to each target clip three separate times.

Table 5.

Errors for canine studies. All results are given in mm.

Canine	FRE	TRELF	TRELF + S	PTSLF	PTSLF + S
1	12.9	14.7 (2.9)	7.0 (3.2)	6.9	5.6
2	9.4	9.7 (1.6)	3.9 (1.9)	3.2	1.8
3	10.8	7.1 (0.5)	4.7 (0.7)	4.1	2.3
4	11.1	6.7 (2.3)	4.9 (2.2)	2.6	2.8
5	8.8	9.7 (1.4)	8.3 (0.7)	5.2	3.7
6	7.6	6.6 (1.4)	5.7 (1.5)	2.7	2.7
Mean	10.1 (1.9)	9.1 (3.3)	5.8 (2.2)	4.1 (1.7)	3.2 (1.4)

Patient evaluation

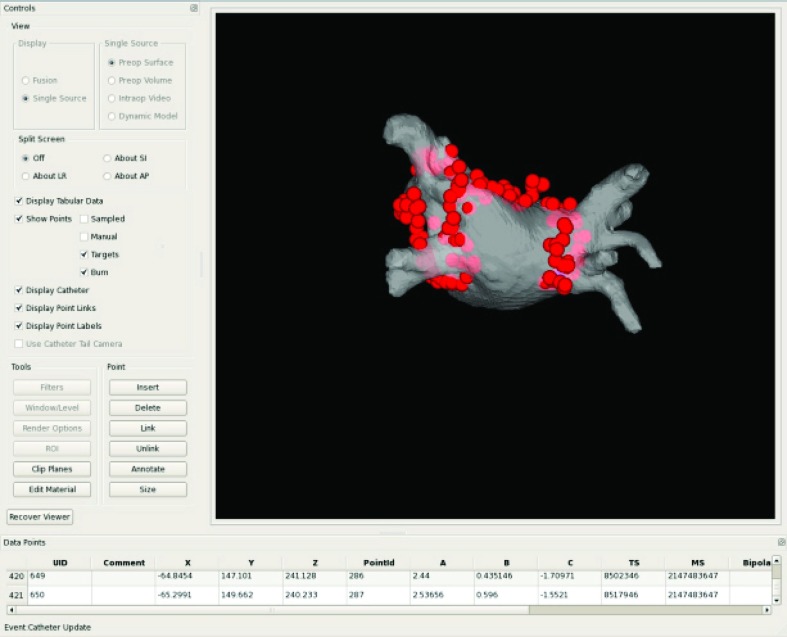
A snapshot from the user interface of our prototype system is shown for one of the registered patient cases in Fig. 7. Quantitative results from the patient evaluation study are as follows: FRE = 8.6 ± 1.3 mm, PTS_LF = 5.0 ± 2.5 mm, and PTS_{LF + S} = 3.5 ± 0.8 mm. Overall, these errors are similar to those found in the canine studies. In Simulation 2, a FRE of this magnitude is predicted with when σ_PLF is between 6.0 and 8.0 mm. PTS errors of this magnitude are predicted when σ_PLF = 6.0 mm and σ_η is set to 4.0 mm for ${\mathit{P}}_S+\mathit{\eta }$ and ${\mathit{P}}_{\text{TS}}+\mathit{\eta }$ in Simulation 5.

Figure 7.

Snapshot of user interface during one of the patient studies. Spheres are the registered ablation points encircling the pulmonary veins, displayed on the preoperative surface model from a posterior view.

DISCUSSION

In this work, we evaluated the effect that various error sources have on registration accuracy in the application of image-guided cardiac ablation therapy. We considered the variability of inputs to the registration algorithm including localization of physical landmark fiducials, physical target fiducials, and noise on the surface points. In an in vivo experiment, there will be error in localizing targets and the effect of this variability was demonstrated. A simulation was also performed to evaluate the effect of noise on sampled surface points in both the registration algorithm as well as the point-to-surface error metric. Simulation results were then compared with results from in vivo canine and patient studies.

Registration accuracy of preoperative models into a cardiac ablation procedure is currently of great interest in the clinical community as evidenced by a large number of studies on this topic. Evaluation of registration accuracy has been investigated using a variety of techniques including animal, clinical, simulation, and phantom studies; however, the effect of various error sources on registration accuracy has not been quantitatively evaluated. In prior clinical studies,^{10, 11, 12, 13, 14, 15, 16} a standard error metric for registration accuracy is point-to-surface distance between either the mapping or ablation points and the surface model. This error provides an overall measure of fit, however, point-to-surface distances can be small even when there are large errors in the registration alignment. Another technique for quantifying registration error is to compute target registration error using anatomic points which are independently identified with intracardiac ultrasound.¹⁴ Another approach compared the location of pulmonary vein points mapped with the tracked catheter to that of the preoperative model.¹¹ These studies provide valuable information regarding registration accuracy in a clinical setting, however, they do not provide a complete quantitative assessment that can be evaluated against a true gold standard.

Prior simulation studies evaluating registration accuracy have considered surface-based only²⁵ as well as a combined landmark and surface-based approach where the landmarks were located in the right atrium.¹⁷ While providing insight into the behavior of registration algorithms, these studies do not emulate the current clinical approach of combined landmark and surface-based registration using left atrial landmark locations. In a prior phantom study,⁶ a model of the left atrium, pulmonary veins, and aorta was constructed and a surface-based approach (without landmark pairs) was evaluated. This study demonstrated that the surface-based approach using points from the left atrium alone or the left atrium and pulmonary veins often resulted in a local minimum and that the aorta points were necessary to avoid this problem. In the present study, we initialize the registration algorithm with a landmark pair alignment to provide a reasonably close initialization and thereby avoid local minimum solutions that are far from the correct registration result. A prior in vivo porcine study⁴ which assessed point-to-surface registration accuracy, found a final mean distance of approximately 3.5 mm which is consistent with our canine mean point-to-surface errors of 3.2 mm. Another in vivo canine study¹⁷ which assessed registration accuracy for different registration strategies in the left atrium, found a mean TRE of approximately 7 mm when using landmarks combined with left atrial surface points which is similar in magnitude to the mean TRE of 5.8 mm in our canine study. In the study of Ref. 17, however, the targets were located on the epicardial surface so their reported distances also include the thickness of the left atrial wall.

The current study is unique in that it systematically assesses the effects of variability in the different inputs to the registration algorithm. There were several important conclusions drawn from this work. First, using a series of simulation studies with our phantom data, we demonstrated that surface-based registration improves landmark-based registration provided the variability in the surface-based points is not excessively high. The improvement of landmark-based registration by surface-based registration was also demonstrated in our canine and patient studies as well as other published studies.^{11, 12} Second, we demonstrated that increased variability on the landmark fiducials resulted in increased registration errors; however, refinement of the initial landmark registration by the surface-based algorithm can compensate for small initial misalignments. In a prior study,¹⁷ the authors empirically observed the important effect that errors in localization of landmark fiducials can have on registration accuracy. In the current study, the Monte Carlo simulation studies directly quantify the effects of landmark selection variability on registration accuracy. Finally, we demonstrated that the surface-based registration algorithm is quite robust to noise on the surface points and continues to improve landmark registration even at high levels of noise on the surface points.

There were several limitations to the current study. First, several sources of error were modeled by each variability parameter. For example, the parameter representing variation in physical landmark selection, σ_PLF, represents errors in magnetic tracking, cardiac and respiratory motion, and the ability to navigate to a specific anatomic location with the catheter. The parameter representing variation in physical target selection, σ_PT, represents errors in magnetic tracking, cardiac and respiratory motion, and the ability to navigate to a specific visible target location with the catheter. The parameter representing variation on the surface points, σ_η, represents magnetic tracking errors, cardiac and respiratory motion, and the ability to position the catheter on the endocardial surface. Finally, the parameter representing variation on the image landmark selection, σ_ILF, represents the ability of a user to repeatedly identify the same anatomical landmark as well as the variability of clicking on the same point using a 3D rendering. A more extensive simulation could directly model each error source and use these to determine the variability in each input parameter. Characterizing the interrelationship of these various error sources and how they impact inputs into the registration algorithm is a challenging problem, but could provide important additional insight into registration accuracy. A second limitation is that only one magnetic tracking system was considered in this study. Other tracking systems could, however, be similarly evaluated and compared using the proposed techniques. A third limitation is that only a single, rigid-based surface registration algorithm was evaluated. Other registrations, including nonrigid^{18, 26} algorithms where the preoperative surface is morphed to the intraoperative data, or other rigid-based approaches²⁵ could also be studied.

A limitation in the in vivo canine study involved the ability to precisely localize the insertion point of the metal clip into the endocardial surface in both the CT scan and with the catheter in physical space. The clip created star shaped artifacts in the CT scan which we attempted to exclude during the segmentation procedure; however, this will still be a source of error. Since the final TRE is computed using a distance transform to the segmented clip as opposed to a single localized point, this could potentially bias our results to overall lower values than the true TRE at the insertion point. In addition, precisely locating the insertion point of the clip with the catheter in the in vivo studies is challenging as evidenced by the variability in location of the sampled points in Fig. 6. We attempted to average out this error by navigating the catheter to these locations three separate times; however, this also contributes to the final error as modeled by σ_PT in the simulation studies.

In cardiac ablation therapy, accurate guidance is necessary for appropriate placement of lesion lines. Typically, circumferential lines around the pulmonary veins are combined with other anatomically guided, linear lesion lines in order to remove triggers of atrial fibrillation or modify the arrhythmogenic substrate.² In addition, lesions are typically placed approximately 5 mm apart in order to avoid gaps in the ablation line.²⁷ Ablation locations are visualized in commercial electroanatomic mapping systems as red spheres on the preoperative model which are used as both an anatomic guide as well as an indication of the spacing between lesions. Thus, errors in the registration process could result in either improperly placed ablation lines or gaps between lesions, eventually leading to reconduction across the ablation line²⁸ and subsequent recurrence of atrial fibrillation.²⁹ This underscores the importance of the quantitative modeling and evaluation of registration accuracy for this procedure. In future work, we will use the developed model to not only evaluate other tracking systems and registration algorithms but also to determine the optimal set of landmark locations and surface points necessary to obtain the most efficient and accurate registration results. While clinical studies often use anatomical landmarks near the junctions of the pulmonary veins,^{12, 13} there is still a need to define the optimal set of landmarks for this application.^{30, 31} These analyses are important intermediary steps toward our overall goal of improving intraprocedural guidance and targeting for improved outcomes in ablative treatment of cardiac arrhythmias.