Human radiation dosimetry of 6-[¹⁸F]FDG predicted from preclinical studies

Abstract

Purpose: The authors are developing 6-[¹⁸F]fluoro-6-deoxy-D-glucose (6-[¹⁸F]FDG) as an in vivo tracer of glucose transport. While 6-[¹⁸F]FDG has the same radionuclide half-life as 2-[¹⁸F]fluoro-2-deoxy-D-glucose (2-[¹⁸F]FDG) which is ubiquitously used for PET imaging, 6-[¹⁸F]FDG has special biologic properties and different biodistributions that make it preferable to 2-[¹⁸F]FDG for assessing glucose transport. In preparation for 6-[¹⁸F]FDG use in human PET scanning, the authors would like to determine the amount of 6-[¹⁸F]FDG to inject while maintaining radiation doses in a safe range.

Methods: Rats were injected with 6-[¹⁸F]FDG, euthanized at specified times, and tissues were collected and assayed for activity content. For each tissue sample, the percent of injected dose per gram was calculated and extrapolated to that for humans in order to construct predicted time-courses. Residence times were calculated as areas under the curves and were used as inputs to OLINDA/EXM in order to calculate the radiation doses.

Results: Unlike with 2-[¹⁸F]FDG for which the urinary bladder wall receives the highest absorbed dose due to urinary excretion, with 6-[¹⁸F]FDG there is little urinary excretion and osteogenic cells and the liver are predicted to receive the highest absorbed doses: 0.027 mGy/MBq (0.100 rad/mCi) and 0.018 mGy/MBq (0.066 rad/mCi), respectively. Also, the effective dose from 6-[¹⁸F]FDG, i.e., 0.013 mSv/MBq (0.046 rem/mCi), is predicted to be approximately 30% lower than that from 2-[¹⁸F]FDG.

Conclusions: 6-[¹⁸F]FDG will be safe for use in the PET scanning of humans.

INTRODUCTION

We have been developing 6-[¹⁸F]fluoro-6-deoxy-D-glucose (6-[¹⁸F]FDG) as a novel tracer of glucose transport in vivo.^{1, 2, 3, 4, 5} 2-[¹⁸F]fluoro-2-deoxy-D-glucose (2-[¹⁸F]FDG, also known as ¹⁸FDG), which is used ubiquitously in clinical positron emission tomography (PET), is transported into cells, phosphorylated, and trapped intracellularly. In contrast, 6-[¹⁸F]FDG is not phosphorylated as it lacks the hydroxyl group on carbon 6.^{3, 6} In particular, the lack of phosphorylation of 6-[¹⁸F]FDG suggests that it may be more successful than 2-[¹⁸F]FDG for resolving the transport step of glucose metabolism. Therefore, we evaluated the various attributes of 6-[¹⁸F]FDG in a series of studies and have shown that it is transported similarly to glucose by both facilitative glucose transporters (GLUTs) and sodium-dependent cotransporters (SGLTs),³ its uptake in skeletal muscle is sensitive to insulin stimulation,¹ its uptake in skeletal muscle is competitively inhibited by hyperglycemia,⁵ there are few radioactive metabolites appearing over the time-scale of PET imaging,² 6FDG distributes in body water,³ and urinary excretion of ¹⁸F is slow [6% in 6 h (Ref. ²)] except in the case of hyperglycemia or when a drug that inhibits SGLTs has been administered.^{1, 2, 3, 5} We also developed a new model for the quantitative analysis of 6-[¹⁸F]FDG concentration time-courses measured using PET imaging and confirmed that the model predicts that insulin and hyperglycemia lead to increased glucose transport with insulin causing an increase and hyperglycemia causing a decrease in intracellular concentrations of the tracer.⁴ Taken together, these studies demonstrate the potential for using 6-[¹⁸F]FDG to measure in vivo glucose transport at the tissue level and in a minimally invasive way.

Encouraged by these findings, we plan to extend our work to human studies. Specifically, we expect to be able to estimate the glucose delivery rate, transport into cells, interstitial concentration, intracellular concentration, and maximum transport rate (V_max). All of these terms are parameters or fluxes which can be uniquely determined using our model⁴ which accounts for the competition between glucose and 6-[¹⁸F]FDG, the radiolabeled glucose analog. The major advantage of using 6-[¹⁸F]FDG rather than 2-[¹⁸F]FDG is that the former tracer specifically allows the measurement of transmembrane glucose transport, whereas the tissue accumulation of 2-[¹⁸F]FDG-6-phosphate reflects the composite of both the transport and phosphorylation steps. The unique ability to measure only the transport step will be of value in various conditions including: studies intended to increase the understanding of the mechanism of action of specific blood-glucose-lowering pharmacological agents; the role of alterations of glucose transport in obesity, type 2 diabetes, and exercise physiology; and in the mapping of the glucose transport rate in various brain regions in patients with Alzheimer's disease.

To demonstrate that 6-[¹⁸F]FDG administration for PET scanning would be safe to use in humans, we considered the radiation dose that various organs could potentially receive. We then conducted a dosimetry study in rats and extrapolated the results in order to predict the appropriate amount of 6-[¹⁸F]FDG activity to administer for the PET scanning of humans. Data presented herein will be key components for approval of an Investigational New Drug application by the FDA.

METHODS

6-[¹⁸F]FDG preparation

6-[¹⁸F]FDG was synthesized from the 3,5-O-benzylidene-6-deoxy-1,2-O-isopropylidene-6-(4^′-methylbenzene)sulfonyloxy-alpha-D-glucofuranose precursor using modification of a previously described method^{1, 6} and using a GE Healthcare TRACERlab FX_F-N automated synthesis module. The resulting product was purified using combined C-18 and neutral Alumina Sep-Paks (Waters Corporation) and was formulated in sterile water for intravenous injection. The product was analyzed using radio-thin-layer chromatography (acetonitrile:water, 8:2, v/v, Rf = 0.45–0.7) and verified by cospotting with a 6-FDG nonradiolabeled standard (Carbosynth Limited). Produced by us in this way, radiochemical purity is greater than 99%.¹

Dosimetry studies

Adult male Sprague–Dawley rats were purchased from Harlan Sprague–Dawley, Inc. and were housed in the Animal Resource Center of Case Western Reserve University. The rats had free access to food and water. There was light from 08:00 to 20:00 and it was turned off from 20:00 to 08:00. Tissue radioactivity concentrations were measured at 5, 15, 60, 240, and 900 min following injection. Rats, three per time-point, were anesthetized using 2% isoflurane in oxygen, weighed, injected with 6-[¹⁸F]FDG in the tail vein, and euthanized under 5% or greater isoflurane in oxygen. The net activity administered, calibrated to the time of injection, was determined using a dose calibrator (CRC-7, Capintec Inc.) to assay the syringe before and after injection and while noting the assay times.

Euthanized rats were dissected and the kidney, heart, brain, spleen, small intestine, adrenals, testes, bone, skeletal muscle, liver, and blood of each rat were collected and weighed. At times that were recorded, tissues were assayed in a gamma-counter (Compugamma-1282; LKB-Wallac). Tissue activity was decay-corrected to the euthanasia time and was divided by the injected activity in order to determine the percent of injected dose (%ID). This was, in turn, divided by the tissue mass to determine the activity expressed as the percent of the injected dose per gram of tissue (%ID/g).

In order to maximize the accuracy and precision of the tissue activity measurements and have the portion of the area under the curve that is extrapolated beyond the last time point be small relative to the rest of the area, the target amounts of activity to inject into rats were determined taking into account radioactive decay. Specifically, the target amounts of activity were determined so that at the time the tissues were counted, the injected activity would be decayed to approximately 1.85 MBq (50 μCi). Our rationale was that this amount, distributed uniformly throughout a 200 g rat, would yield 4.81 kBq (0.13 μCi) in a typical 0.5 g tissue sample which would provide good counting statistics while avoiding dead time. The exception was animals used for the 900-min or last time point. In these we capped the target to 18.5 MBq (500 μCi) at the time of injection, in the interest of the safety of the research personnel.

The accuracy of the dose calibrator was confirmed using NIST-traceable calibration standard sources to be within 2.9% of the standard for ⁶⁰Co and within 0.1% for ¹³⁷Cs. The dose-calibrator and gamma-counter were cross-calibrated by measuring the activity in an aliquot in the dose-calibrator and, after a suitable amount of time for decay to achieve an appropriate activity level, also measuring it in the gamma-counter. Although we did not use a NIST-traceable, positron-emitting standard such as ⁶⁸Ge/⁶⁸Ga and there is the potential for small, systematic errors in absolute measures of activity, values calculated as the ratio of gamma-counter to dose-calibrator values such as %ID would be correct.

The experimental procedures were reviewed and approved by the Institutional Animal Care and Use Committee of Case Western Reserve University. Animal care was supervised by veterinarians and the IACUC and adheres to the NIH Guidelines for Lab Animal Care and the Animal Welfare Act.

Data analysis

The human dosimetry of 6-[¹⁸F]FDG was determined by extrapolating data obtained in rats in a manner analogous to that used by Waterhouse et al. for [¹⁸F]FPS.⁷ Briefly, the %ID/g tissue concentrations in rats were multiplied by the ratio of the total body masses of rat-to-human with the masses of rats being measured and with a 70-kg nominal model human assumed. The results were multiplied by tissue masses obtained from a model of the adult human male (Table B-3 of Ref. 8) in order to determine the %ID in human tissue:

$$\begin{array}{ccc}& & \%\mathrm{ID}\left(\mathrm{in}\mathrm{human}\mathrm{tissue}T\right)\hfill \\ & & =\%\frac{\mathrm{ID}}{\mathrm{g}}\left(\mathrm{rat}\right)\times \frac{\mathrm{rat}\mathrm{body}\mathrm{mass}}{\mathrm{human}\mathrm{body}\mathrm{mass}}\hfill \\ & & \times \mathrm{human}\mathrm{tissue}T\mathrm{mass}.\hfill \end{array}$$

The means and standard deviations of these calculated human %ID values were plotted vs time. A dual-exponential model was fit to these data and was used to calculate the area under the curve (AUC) out to infinite time, thus representing complete decay of the radionuclide. The AUC for the injected dose was also calculated and from it was subtracted the sum of the AUCs of the 11 types of tissues, except for blood, in order to determine the AUC for the remainder of the body; blood activity was included in the remainder. No excretion of the radioactivity was assumed to occur; and the radioactivity was assumed to be uniformly distributed throughout the remainder-of-the body and to be removed only by physical decay.

For calculations of tissue absorbed doses and the effective dose using OLINDA/EXM,⁹ residence times were calculated as %ID AUCs divided by 100. Small intestine had minimal contents so we assigned it zero activity as an OLINDA/EXM source organ and included intestine wall activity in the remainder. Bone AUC was split into two components, 62% trabecular and 38% cortical.¹⁰ With OLINDA/EXM effective dose is calculated using ICRP 60 tissue weighting factors¹¹ modified by omitting esophagus and dividing the other weights by 0.95 so they sum to one. The resultant residence times used as OLINDA/EXM inputs are listed in Table 1. As the activity for the remainder of the body was calculated assuming no excretion, the calculated radiation dose estimates would be expected to be the upper limits of the actual doses.

Table 1.

OLINDA/EXM input residence times.

Tissue	Residence time (h)
Adrenals	0.000470
Brain	0.0512
Heart wall	0.0145
Kidneys	0.0153
Liver	0.104
Muscle	0.460
Cortical bone	0.069
Trabecular bone	0.113
Spleen	0.00675
Remainder	1.80

RESULTS AND DISCUSSION

Rat total body masses were 212.9 ± 6.7 g with a range of 199.5 to 221.3 g. The net injected activities were 2.00 ± 0.29, 2.11 ± 0.27, 3.91 ± 0.16, 7.82 ± 0.52, and 21.00 ± 1.72 MBq (53.9 ± 8.0, 57.1 ± 7.2, 105.6 ± 4.4, 211.4 ± 13.9, and 567.6 ± 46.4 μCi), respectively, in rats used for the 5, 15, 60, 240, and 900 min time points. The biodistribution, expressed as %ID/g, is summarized in Table 2. At 5 min, the earliest time point of the data, activity in three tissue types, i.e., kidney, liver, and blood, achieved values greater than 1% ID/g. Values in all tissue types declined over time, and there was no tissue with particularly high activity. For all time points and all tissue types except adrenals which had a mass of less than a tenth of a gram, the measured count rates were significantly above background count rates. Even the count rates from tissues at the 900-min time point exceeded the background count rate by, at minimum, a factor of 9.8.

Table 2.

Rat %ID/g (mean ± SD) for each time and tissue. There were n = 3 for each value and the data were corrected for the radioactive decay that occurred from the time of euthanasia to the time of counting. Over time, the data tend to zero activity representing no further radiation dose to the tissue.

Tissue	5 min	15 min	60 min	240 min	900 min
Kidneys	1.17 ± 0.15	0.84 ± 0.02	0.39 ± 0.08	0.11 ± 0.00	0.0004 ± 0.0000
Heart	0.91 ± 0.17	0.78 ± 0.02	0.37 ± 0.08	0.10 ± 0.01	0.0004 ± 0.0001
Brain	0.78 ± 0.08	0.57 ± 0.03	0.28 ± 0.07	0.08 ± 0.00	0.0004 ± 0.0000
Spleen	0.54 ± 0.05	0.53 ± 0.06	0.34 ± 0.09	0.09 ± 0.00	0.0003 ± 0.0000
Small intestine	0.85 ± 0.14	0.62 ± 0.11	0.35 ± 0.07	0.09 ± 0.01	0.0005 ± 0.0001
Adrenals	0.43 ± 0.06	0.32 ± 0.23	0.28 ± 0.07	0.05 ± 0.03	0.0004 ± 0.0001
Testes	0.27 ± 0.07	0.32 ± 0.04	0.25 ± 0.06	0.10 ± 0.00	0.0008 ± 0.0000
Bone	0.37 ± 0.07	0.35 ± 0.02	0.27 ± 0.07	0.19 ± 0.02	0.0072 ± 0.0009
Skeletal muscle	0.15 ± 0.00	0.18 ± 0.01	0.22 ± 0.04	0.09 ± 0.00	0.0005 ± 0.0001
Liver	1.18 ± 0.16	0.94 ± 0.01	0.45 ± 0.10	0.11 ± 0.00	0.0005 ± 0.0001
Blood	1.15 ± 0.13	0.96 ± 0.01	0.44 ± 0.10	0.11 ± 0.00	0.0004 ± 0.0000

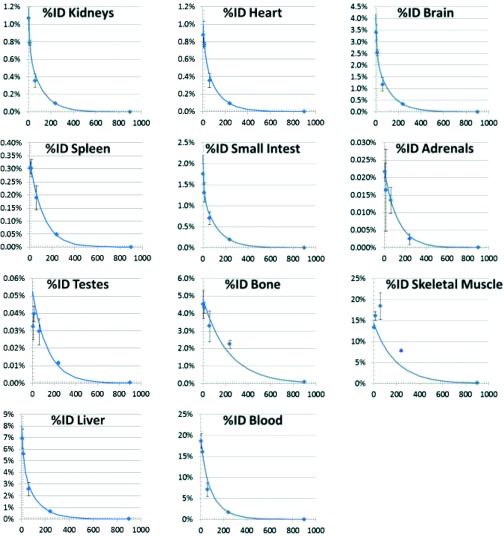
Figure 1 shows the %ID time-courses estimated for each human tissue based on rat data and the nominal model human, and with the tissue masses given in Table 3. Superimposed on the data which are indicated by diamonds are the exponential model fit curves. Decay correction over time was not applied as the number of disintegrations must account for both the biodistribution and the radioactive decay. Indeed, the residence times, presented in Table 3, are a measure of the number of disintegrations occurring in source tissues. Human dose estimates using OLINDA/EXM (Ref. ⁹) are listed in Table 4. As shown therein, predicted human radiation absorbed dose is relatively uniform across tissues with approximately a factor of three difference in doses in the tissues receiving the highest and lowest doses. Specifically, the absorbed dose is predicted to be highest in osteogenic cells, 0.027 mGy/MBq (0.100 rad/mCi), and the liver, 0.018 mGy/MBq (0.066 rad/mCi), and lowest in muscle, 0.009 mGy/MBq (0.035 rad/mCi), and skin, 0.008 mGy/MBq (0.031 rad/mCi).

Figure 1.

Plots show time-courses of human %ID, predicted from rat tissue. The diamonds indicate means and the error bars denote ±1 standard deviation. The curves show the double exponential fit to the data. The y axes denote %ID and the x axes denote the time in minutes from the time of injection.

Table 3.

Residence times and tissue masses for the nominal human model (Table B-3 of Ref. 8).

Tissue	Residence time (h)	Mass (g)
Remainder	1.47
Skeletal muscle	0.460	28 000
Blood	0.303	5300
Bone	0.182	4000
Liver	0.104	1910
Brain	0.0512	1420
Small intestine	0.0281	677
Kidneys	0.0153	299
Heart	0.0145	316
Spleen	0.00675	183
Testes	0.00125	39.1
Adrenals	0.000470	16.3

Table 4.

Predicted human radiation doses.

Target organ	mGy/MBq	rad/mCi
Osteogenic cells	0.027	0.100
Liver	0.018	0.066
Kidneys	0.016	0.061
Heart wall	0.016	0.060
Red marrow	0.014	0.053
Gallbladder wall	0.014	0.053
Small intestine	0.014	0.053
Pancreas	0.014	0.052
Uterus	0.014	0.052
ULI wall	0.014	0.052
Ovaries	0.014	0.051
Spleen	0.014	0.051
LLI wall	0.013	0.049
Adrenals	0.013	0.050
Stomach wall	0.013	0.048
Urinary bladder wall	0.013	0.048
Testes	0.011	0.042
Thymus	0.011	0.042
Brain	0.011	0.042
Lungs	0.011	0.041
Thyroid	0.011	0.041
Breasts	0.010	0.036
Muscle	0.009	0.035
Skin	0.008	0.031
	mSv/MBq	rem/mCi
Effective dose	0.013	0.046

Our estimated effective dose from 6-[¹⁸F]FDG of 0.013 mSv/MBq (0.046 rem/mCi) is approximately 30% lower than that from 2-[¹⁸F]FDG 0.019 mSv/MBq (0.070 rem/mCi).¹² This was the case despite our assumption that there is no excretion of 6-[¹⁸F]FDG which would tend to make our dose estimates on the high side. Nevertheless, we made this assumption because it would lead us to err on the low side regarding the amount of activity that would be allowable to inject into a person which is a conservative approach. For example, using our tabulation we predict that a 185 MBq (5 mCi) injection of 6-[¹⁸F]FDG would achieve an effective dose of no more than 2.3 mSv (0.23 rem) and with the highest absorbed dose being 5.0 mGy (0.50 rad) to osteogenic cells and the next highest absorbed dose, 3.3 mGy (0.33 rad), to the liver. In light of the uncertainties of estimating human radiation doses by extrapolating preclinical data, we expect that a 185 MBq (5 mCi) injection of 6-[¹⁸F] is an appropriately conservative approach noting that our estimated doses are approximately an order of magnitude lower than the limits specified in United States Federal Regulations for Radioactive Drugs for Certain Research Uses (21CFR361.1).

Whereas with 2-[¹⁸F]FDG, the urinary bladder wall receives the highest radiation dose, i.e., 0.073 (Ref. ¹³) to 0.13 (Ref. ¹²) mGy/MBq, the dose delivered to the bladder wall with 6-[¹⁸F]FDG was much smaller. This is to be expected given that there is negligible concentration of 6-[¹⁸F]FDG in urine.^{2, 3} Indeed, 6-[¹⁸F]FDG is reabsorbed well by SGLTs in the proximal tubules of the kidney unless a blocker, such as phlorizin, is given or the subject is hyperglycemic, in which case the 6-[¹⁸F]FDG excretion reflects the specific activity of glucose in the blood.^{1, 2, 3, 5}

If a study were designed to include diabetic subjects, hyperglycemia is possible and would be predicted to lead to urinary excretion of activity if the glomerular filtration of glucose exceeds the renal threshold for glucose absorption. In this case we could use the urinary bladder wall dose from 2-[¹⁸F]FDG as the upper limit of the radiation dose from 6-[¹⁸F]FDG.³

The last time point was selected to be particularly late as we expected minimal urinary excretion and wanted to avoid imprecision that results from vagaries of extrapolating a curve to infinite time. In fact, the area under an exponential curve from time T to infinite time relative to the area under the entire curve equals exp(−λT), where λ is the decay constant. As we anticipated little urinary clearance, we set λ to reflect the radioactive decay and determined that T = 724 min (approximately 12 h) would have 1% of the area after T. Given the practicalities of long experimental days, we decided to use a 900 min (15 h) time point implemented by injecting the animal during the day and euthanizing it the next morning.

Our experimental design determined target values of activity to inject with the goal of achieving adequate count statistics. That all tissue samples, save that of the very small adrenals, achieved count rates that exceeded that of background by approximately tenfold or higher (even in the 900-min data), suggests that we achieved our goal and that the error bars primarily reflect biologic variation. Furthermore, because of the sensitivity, dynamic range, and absence of the partial volume effect when dose estimates are based on activity in excised tissues measured with a gamma counter, we were able to detect activity and its clearance in kidneys, heart, brain, and liver despite our prior PET imaging studies suggesting less clearance.³ Also, in comparing results of that work to the present results it must be taken into account that the time–activity curves generated previously were decay-corrected which is not the case in the present work.

Besides radiation dosimetry, another safety consideration is possible toxicity of 6-FDG as a chemical. The literature contains two studies^{14, 15} and one review¹⁶ regarding 6-FDG toxicity. The lowest dose in rats and mice that caused an observed effect was 120 mg/kg administered orally with the effect being temporary inhibition of spermatogenesis.¹⁵ In mice doses up to 960 mg/kg did not impact male fertility.¹⁵ In rats, doses of 500 mg/kg caused some necrosis of centrilobular hepatocytes with recovery in six days.¹⁴ The LD50 in mice and rats is 200 mg/kg IP.¹⁴ In summary, the lowest dose to have an effect in rats or mice was 120 mg/kg (660 μmol/kg), so we consider it in assessing the human dose. In our experience, when 6-[¹⁸F]FDG is prepared as a radiopharmaceutical for PET imaging, its specific activity is in the range 7.4–74 TBq/mmol (200–2000 Ci/mmol), which is typical of ¹⁸F-labeled radiopharmaceuticals. Injection of even a large activity dose of this tracer (740 MBq or 20 mCi) into a 70 kg human would result in a mass-normalized dose of 26–260 ng/kg (0.14–1.4 nmol/kg). This is of the order of a millionth of the lowest dose (120 mg/kg) which produced an observable effect in rodents. Thus, we expect 6-[¹⁸F]FDG PET scanning could be done safely in humans. As a point of reference, 2-[¹⁸F]FDG is used routinely in clinical scans with no reports of toxicities and the threefold greater toxicity of 6-FDG than 2-FDG—LD50 of 200 vs 600 mg/kg in mice and rats¹⁴—is dwarfed by the 6 orders of magnitude safety margin. Hence, use of 6-[¹⁸F]FDG for PET should result in no toxicity or complications.

CONCLUSION

It is expected that 6-[¹⁸F]FDG will be safe for use in the PET scanning of humans.