Rapid Monte Carlo simulation of detector DQE(f)

Abstract

Purpose: Performance optimization of indirect x-ray detectors requires proper characterization of both ionizing (gamma) and optical photon transport in a heterogeneous medium. As the tool of choice for modeling detector physics, Monte Carlo methods have failed to gain traction as a design utility, due mostly to excessive simulation times and a lack of convenient simulation packages. The most important figure-of-merit in assessing detector performance is the detective quantum efficiency (DQE), for which most of the computational burden has traditionally been associated with the determination of the noise power spectrum (NPS) from an ensemble of flood images, each conventionally having 10⁷ − 10⁹ detected gamma photons. In this work, the authors show that the idealized conditions inherent in a numerical simulation allow for a dramatic reduction in the number of gamma and optical photons required to accurately predict the NPS.

Methods: The authors derived an expression for the mean squared error (MSE) of a simulated NPS when computed using the International Electrotechnical Commission-recommended technique based on taking the 2D Fourier transform of flood images. It is shown that the MSE is inversely proportional to the number of flood images, and is independent of the input fluence provided that the input fluence is above a minimal value that avoids biasing the estimate. The authors then propose to further lower the input fluence so that each event creates a point-spread function rather than a flood field. The authors use this finding as the foundation for a novel algorithm in which the characteristic MTF(f), NPS(f), and DQE(f) curves are simultaneously generated from the results of a single run. The authors also investigate lowering the number of optical photons used in a scintillator simulation to further increase efficiency. Simulation results are compared with measurements performed on a Varian AS1000 portal imager, and with a previously published simulation performed using clinical fluence levels.

Results: On the order of only 10–100 gamma photons per flood image were required to be detected to avoid biasing the NPS estimate. This allowed for a factor of 10⁷ reduction in fluence compared to clinical levels with no loss of accuracy. An optimal signal-to-noise ratio (SNR) was achieved by increasing the number of flood images from a typical value of 100 up to 500, thereby illustrating the importance of flood image quantity over the number of gammas per flood. For the point-spread ensemble technique, an additional 2× reduction in the number of incident gammas was realized. As a result, when modeling gamma transport in a thick pixelated array, the simulation time was reduced from 2.5 × 10⁶ CPU min if using clinical fluence levels to 3.1 CPU min if using optimized fluence levels while also producing a higher SNR. The AS1000 DQE(f) simulation entailing both optical and radiative transport matched experimental results to within 11%, and required 14.5 min to complete on a single CPU.

Conclusions: The authors demonstrate the feasibility of accurately modeling x-ray detector DQE(f) with completion times on the order of several minutes using a single CPU. Convenience of simulation can be achieved using GEANT4 which offers both gamma and optical photon transport capabilities.

INTRODUCTION

Since its introduction over a decade ago, the digital x-ray flat panel detector has matured to a point where it has replaced film in most medical applications. As the limits of both detection efficiency and spatial resolution are pushed, the task of making improvements in these areas is becoming increasingly difficult. The current state-of-the art is the indirect detector in which x rays interact with a scintillating material, resulting in a burst of light which is then detected by an array of photosensitive detectors. Optimization of these types of imagers requires characterization of the underlying interactions and particle transport mechanisms for both x rays and optical photons, with the goal of yielding the best image quality using minimal dose. Since flat panel imagers are expensive and time-consuming to build, large-scale multivariable experimental studies for design optimization are impractical. Analytical approaches quickly lead to intractable expressions, thereby necessitating a numerical approach. Hence, Monte Carlo modeling is the current tool of choice.

Spatial resolution, as characterized by the modulation transfer function (MTF), is an important detector metric; and the literature is rich with published Monte Carlo detector optimizations which focus primarily on MTF.^{1, 2, 3, 4, 5, 6, 7} However, optimization of the MTF fails to account for the contribution of noise to imaging performance. A better figure-of-merit is the frequency-dependent detective quantum efficiency [DQE(f)], which is the spectral representation in Fourier domain of the signal-to-noise characteristics of a given detector configuration.

Experimental determination of detector DQE is well established and practiced regularly to evaluate performance. The DQE can be written

$$\text{DQE}\left(f\right)=\frac{\text{MTF}{\left(f\right)}^2}{q·\text{NNPS}\left(f\right)},$$ (1)

where q is the x-ray photon (gamma) fluence in units of gammas/mm², and NNPS is the normalized noise power spectrum. Using an angled line source and the analysis procedure outlined by Fujita et al.,⁸ Monte Carlo modeling of the MTF is straightforward, and requires relatively few incident gammas. The computational burden, and therefore the opportunity for time savings, lies in the determination of NPS(f). In this work, we demonstrate methods to reduce the number of gammas required to accurately generate the NPS, resulting in simulation times of minutes on a single CPU with no loss of accuracy.

Table 1 describes the variables used in this study.

Table 1.

Symbol definitions.

Symbol	Description	Symbol	Description
Nx	Number of detector pixels (1D geometry)	χ2	Mean squared error of the qNNPS estimate
n	Pixel index: n = 1, 2, …, Nx	$\tilde{R}\left(t\right)$	Estimate of noise autocorrelation function
I(n)	Total detected signal intensity: I(n) = S(n) + Q(n)	t	Noise autocorrelation index: t = −Nx/2, Nx/2 + 1, …, Nx/2
S(n)	Detected nonstochastic signal intensity	Qph	Zero-frequency quantum noise of detected signal
Q(n)	Detected stochastic noise	Nγ	Number of gammas launched per flood image
f	Frequency index: f = −Nx/2, −Nx/2 + 1, …, Nx/2	Nfl	Number of flood images per experiment
NNPS(f)	Normalized noise power spectrum	g	Flood field index: g = 1, 2, …, Nfl
Iin(n)	Input flux intensity (photons/pixel)	Δx	Pixel spacing (mm)
q	Input fluence at detector (photons/mm2)	Nl	Number of layers in Lubberts model
$\tilde{q}\text{NNPS}\left(f\right)$	Estimate of q · NNPS	l	Layer number: l = 1, 2, …, Nl
qNNPSact(f)	Actual q · NNPS	h(l, n)	Line-spread function associated with layer l
η	Quantum efficiency	H2( f )	NPS shape normalized so H2(0) = 1
$\tilde{\eta }$	Estimated quantum efficiency	Hint	Integral of H4( f )/Nx from f = −Nx/2 to Nx/2

METHODS

Monte Carlo modeling environment

The bulk of the simulations in this study were performed using the open-source C⁺⁺ package, GEANT4,⁹ version 9.4, patch release 3. GEANT4 is unique in that it offers both radiative and optical photon transport capabilities, thus providing a convenient tool for modeling indirect x-ray detectors in a self-contained fashion.¹⁰ To maximize flexibility, different configurations of interaction and transport models are bundled into “physics lists” which can be called into the user code. Each physics list represents a trade-off between simulation speed and accuracy. The simulations in this work were performed using “Penelope Low Energy” physics in order to maximize accuracy. Another user-definable parameter is the so-called “range-cut,” or “production threshold,” which is in place to increase computational efficiency. Before a secondary particle (e.g., a Compton electron) with a given energy is created, its projected transport distance is calculated. If the projected distance is less than the specified range-cut value, the particle will not be transported and instead its energy will be deposited immediately at the site of its creation. For our simulations, the range cut was set to 0.5 μm for all particles.

The x-ray beam spectrum that was used was also generated with GEANT4 following the methodology of Constantin et al.¹¹ for the Varian TrueBeam system (Varian Medical Systems, Palo Alto, CA). The model included a 6 MV electron beam impinging on a tungsten target producing x rays through a brehmmstrahlung process. The forward-directed x rays were attenuated by a tungsten flattening filter and interacted with relevant hardware including the “jaw” collimators which were set to produce a 10 × 10 cm field at a distance of 100 cm from the source.

NPS from a flood image ensemble

The standard procedure to determine the NPS of an x-ray detector is documented by the International Electrotechnical Commission (IEC).¹² In this method, the NPS is measured by capturing a series of flood images satisfying a number of detailed criteria, with the system configured similarly to its intended use. Following the IEC nomenclature, the 2D NPS for a discrete detector is defined as

$$\begin{array}{ccc}& & \text{NPS}(f_x,f_y)\hfill \\ & & =\frac{\Delta x\Delta y}{N_x{N}_y{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}{\left|\sum _{n=1}^{N_x}\sum _{m=1}^{N_y}[I_g(n,m)-S_g(n,m)]e^{\frac{-i2\pi (n{f}_x+m{f}_y)}{N_x{N}_y}}\right|}^2,\hfill \end{array}$$ (2)

where I_g(n, m) is the detected signal for flood image number, g, and pixel index, (n, m); Δx, Δy are the pixel dimensions; S(n, m) is the nonstochastic signal; f_x, f_y are integers labeling discrete points on the 2D frequency plane. The subtraction of the nonstochastic signal S from I removes any systematic trends, leaving only stochastic noise.

From Eq. 2, the number of photons in a NPS simulation is governed by three parameters

• 1.The signal intensity, I(n, m).
• 2.The number of pixels in the region of interest (ROI), N_x, N_y.
• 3.The number of flood images in the statistical ensemble, N_fl.

The IEC procedure provides a minimum 4 × 10⁴ pixel guideline for the product of N_fl, N_x, and N_y. For instance, a ROI having 200×200 pixels would require an ensemble of no less than N_fl = 100. Much of the theoretical basis for this can be found in the works of Dobbins et al.,^{13, 14} in which it is shown that the ROI dimensions should be much larger than the longest spatial correlations.

The final variable most directly affecting the number of simulated gammas is the desired signal intensity, I(n, m). For this, the IEC procedure stipulates that the flood fields be measured at 0.3, 1, and 3 times the manufacturer-specified usage dose.¹² This is important for investigating the magnitude and influence of electronic noise sources resulting from nonidealities in the detector. However, since a simulation is free of such nonidealities, we can consider whether the number of launched gamma photons in a flood field can be lowered from the experimental requirements, which are typically on the order of 10³ photons/pixel, or 10⁸ photons/flood field.

To determine a minimum signal intensity required for an accurate simulation, we calculate the dependence of the denominator in the DQE formula [Eq. 1], denoted in this work as qNNPS, on the number of launched gammas, N_γ, and flood images, N_fl. qNNPS is defined as the NPS in Eq. 2 multiplied by the input fluence q and divided by square of the average signal, ${\overline{I}}^2$

$$\begin{array}{ccc}& & q\text{NNPS}(f_x,f_y)\hfill \\ & & =\frac{q\Delta x\Delta y}{N_x{N}_y{\overline{I}}^2{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}{\left|\sum _{n=1}^{N_x}\sum _{m=1}^{N_y}[I_g(n,m)-S_g(n,m)]e^{\frac{-i2\pi (n{f}_x+m{f}_y)}{N_x{N}_y}}\right|}^2.\hfill \end{array}$$ (3)

$\overline{I}$, which is sometimes referred to as the “large area signal,” can be determined in several ways. In the case of a simulation, we have the luxury being able to ensure a spatially uniform flux profile with no temporal drift. Hence, $\overline{I}$ is just the mean of the detected signal

$$\overline{I}=\frac{1}{N_{\text{fl}}{N}_x{N}_y}\sum _{g=1}^{N_{\text{fl}}}\sum _{n=1}^{Nx}\sum _{m=1}^{Ny}{I}_g(n,m).$$ (4)

For purposes of simplicity, we perform the ensuing analysis in one dimension (x) with the understanding that the results can readily be generalized to 2D.¹⁴ Following the formalism of Dobbins et al.,^{13, 14} the pixel intensity, I(n), is represented in terms of its nonstochastic signal, S(n), and an additive zero-mean noise component, Q(n)

$$I\left(n\right)=S\left(n\right)+Q\left(n\right).$$ (5)

For a given input intensity, I_in = N_γ/N_x, the expected value, E, of the detected signal is

$$\begin{array}{ccc}\hfill E\left[I\right]& & =E[S+Q]\hfill \end{array}$$ (6)

$$\begin{array}{c}\hfill =E\left[S\right]+E\left[Q\right]\end{array}$$ (7)

$$\begin{array}{c}\hfill =\eta I_{\text{in}},\end{array}$$ (8)

where η is the quantum detective efficiency, an intrinsic property of the detector defined as the fraction of incoming gamma photons that interact with the detector to produce a signal. For this initial analysis, we assume use of a “photon counting” detector whose produced signal is independent of an incoming photon's energy. We note that the results derived here are also applicable to energy-integrating detectors by taking into account the Swank factor.¹⁵

In practice, η is not known and must be estimated from the average signal, $\overline{I}$, as part of the process of determining the qNNPS. The estimated value, $\tilde{\eta }$, is the ratio of the averaged detected signal to the input signal

$$\tilde{\eta }=\frac{\overline{I}}{I_{\text{in}}}=\frac{{\sum }_{g=1}^{N_{\text{fl}}}{\sum }_{n=1}^{N_x}{I}_g\left(n\right)}{I_{\text{in}}{N}_{\text{fl}}{N}_x},$$ (9)

where we have substituted in Eq. 4 (in 1D) for $\overline{I}$.

The 1D qNNPS estimate, denoted as $\tilde{q}\text{NNPS}$, is obtained by substituting I_in = qΔx into the 1D representation of Eq. 3

$$\tilde{q}\text{NNPS}\left(f\right)=\frac{1}{I_{\text{in}}{\tilde{\eta }}^2{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}{\left|\sum _{n=1}^{N_x}{Q}_g\left(n\right)e^{\frac{-i2\pi f_{x}n}{N_x}}\right|}^2.$$ (10)

To evaluate the impact of different simulation parameters on the accuracy of the qNNPS estimate, it is first necessary to characterize the noise processes relevant to an x-ray detector. A key metric is the noise autocorrelation function, R(t), which has the following estimate, $\tilde{R}\left(t\right)$:

$$\tilde{R}\left(t\right)=\frac{1}{N_x}\sum _{n=1}^{N_x+t}Q\left(n\right)Q(n+t),\text{for}t\ge 0.$$ (11)

As the noise processes are assumed to be wide-sense stationary, $\tilde{R}\left(t\right)=\tilde{R}(-t)$.

We start with the idealized case of a “perfectly” pixelated detector with no additional blurring. Since the incoming photons are uncorrelated with a Poisson distribution yielding a signal variance equal to the signal mean ($\tilde{\eta }{I}_{in}$), the expectation of this detector's noise autocorrelation function, denoted as $E\left[{\tilde{R}}_{\text{ph}}\right]$, is a delta function scaled by the signal mean

$$\begin{array}{ccc}\hfill E\left[{\tilde{R}}_{\text{ph}}\left(t\right)\right]& & =\underset{N_x\to \infty }{\lim }\left(\frac{1}{N_x}\sum _{n=1}^{N_x+t}{Q}_{\text{ph}}\left(n\right)Q_{\text{ph}}(n+t)\right)\hfill \\ & & =E\left[Q_{\text{ph}}\left(n\right)Q_{\text{ph}}(n+t)\right]\hfill \\ & & =E\left[\tilde{\eta }\right]I_{\text{in}}\delta \left(t\right).\hfill \end{array}$$ (12)

For almost all physical detectors, the detected noise, Q, is colored by detector-specific blurring mechanisms including light sharing and x-ray photon scattering (we ignore electronic noise for this analysis). As discussed by Lubberts,¹⁶ this noise coloring filter, h, differs from the cumulative blurring filter which operates on the signal, S, and which determines the MTF. The discrepancy between the signal blurring and noise coloring filters is the cause of a nonideal DQE(f) shape that decreases as f increases. Lubberts¹⁶ demonstrated that the NPS can be computed by summing the square magnitudes of the Fourier transforms of the optical line-spread functions (LSFs) associated with all layers of a phosphor screen, while the MTF is computed by averaging the LSFs from each layer before the Fourier transform is taken. Thus, for a given layer, l, the noise coloring operation can be represented by the convolution of the deposited signal, Q_ph(l), with a wide-sense stationary filter having a layer-dependent impulse response, h(s, l),

$$Q(n,l)=\sum _s{Q}_{\text{ph}}(n-s,l)h(s,l).$$ (13)

The amplitudes of h(l) will vary as a function of layer number to reflect that layer's contribution to the overall signal. For this (more idealized) detector, we conserve the received signal, Q_ph, by normalizing the LSFs so that ∑_{n, l}h(n, l) = 1.

After substitution of Eq. 13 into Eq. 11, the estimated noise autocorrelation function, $\tilde{R}(t,l)$, for layer l is

$$\begin{array}{ccc}\hfill \tilde{R}(t,l))& =& \frac{1}{N_x}\sum _{n=1}^{N_x+t}\sum _s{Q}_{\text{ph}}(n-s,l)h(s,l)\hfill \\ & & \times \sum _r{Q}_{\text{ph}}(n-r+t,l)h(r,l).\hfill \end{array}$$ (14)

The total noise autocorrelation estimate, $\tilde{R}\left(t\right)$, is then the sum of the noise autocorrelation functions from each layer.

Expectation of qNNPS

In order to determine the impact of key simulation parameters on accuracy and execution time, we first solve for the expectation of the qNNPS [Eq. 10]. The Wiener-Khintchine relations can be used to write the expression for the qNNPS estimate, $\tilde{q}\text{NNPS}$, as a function of the noise autocorrelation function estimate, $\tilde{R}$

$$\begin{array}{c}\hfill \tilde{q}\text{NNPS}\left(f\right)=\frac{1}{I_{\text{in}}{\tilde{\eta }}^2{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\sum _{l=1}^{N_l}\left|\sum _{t=-N_x/2}^{N_x/2}\tilde{R}(t,g,l)e^{\frac{-i2\pi f_{x}t}{N_x}}\right|,\end{array}$$ (15)

and, from this equation, a solution for $E\left[\tilde{q}\text{NNPS}\right]$ is found in Appendix A

$$E\left[\tilde{q}\text{NNPS}\left(f\right)\right]=H^2\left(f\right)E\left[\frac{1}{\tilde{\eta }}\right].$$ (16)

H²( f ) is the sum of the Fourier transforms of the noise autocorrelation functions of each layer, and is normalized so that H(0) = 1. An estimate of $E[1/\tilde{\eta }]$ can be generated by averaging the measurements of $1/\tilde{\eta }$, obtained using Eq. 9, over many experiments as shown in Eq. A7. However, this estimate may be biased unless a sufficient number of photons are launched due to the characteristic of the random variable $\tilde{\eta }$ that

$$E\left[\frac{1}{\tilde{\eta }}\right]\ne \frac{1}{E\left[\tilde{\eta }\right]}.$$ (17)

This, in turn, will incorrectly scale the qNNPS (and DQE) estimates since

$$E\left[\tilde{q}\text{NNPS}\left(0\right)\right]=E\left[\frac{1}{\text{DQE}\left(0\right)}\right]=E\left[\frac{1}{\tilde{\eta }}\right].$$ (18)

Remarkably, as shown in Sec. 3, very few photons are required per flood field to eliminate the bias.

Simulation error, χ²

We next solve for the mean squared error, χ², of the qNNPS estimate, defined as the average squared difference between $\tilde{q}\text{NNPS}$ and its actual value, qNNPS_act = H²(f)/η

$$\begin{array}{c}\hfill {\chi }^2=\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{\left[\frac{1}{N_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)-\frac{1}{\eta }{H}^2\left(f\right)\right]}^2,\end{array}$$ (19)

where f = N_x/2 is the Nyquist frequency. The expectation of the estimation error is also solved for in Appendix A

$$\begin{array}{ccc}\hfill E\left[{\chi }^2\right]& \approx & H_{\text{int}}·\left(\left\{\frac{1}{N_{\text{fl}}}E\left[\frac{2}{{\tilde{\eta }}^2}\right]-\frac{1}{N_{\text{fl}}}{E}^2\left[\frac{1}{\tilde{\eta }}\right]\right\}\right.\hfill \\ & & \left.+\left\{E^2\left[\frac{1}{\tilde{\eta }}\right]-\frac{2}{\eta }E\left[\frac{1}{\tilde{\eta }}\right]+\frac{1}{{\eta }^2}\right\}\right),\hfill \end{array}$$ (20)

where

$$H_{\text{int}}=\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{H}^4\left(f\right).$$ (21)

The first two terms in Eq. 20 are proportional to the reciprocal of the number of flood fields (1/N_fl) thus indicating a reduction in error as N_fl is increased. The last three terms describe a flood-independent error due to the estimation bias only. For cases when there is a sufficient fluence rate such that the estimation bias is effectively eliminated (i.e., $E[1/\tilde{\eta }]\approx 1/\eta$), then

$${\chi }^2\approx \frac{H_{\text{int}}}{{\eta }^2{N}_{\text{fl}}}.$$ (22)

Equation 20 shows the important result that there is little benefit to launching more photons per flood field beyond the minimum required to avoid biasing the estimate. At that point, for a given detector characterized by fixed values of η and H_int, the mean squared error of the qNNPS estimate decreases in proportion to the number of simulated flood fields as shown by Eq. 22.

MTF and NPS from a point-spread function (PSF) ensemble: Fujita-Lubberts-Swank (FLS) method

The above results imply that the number of detected gammas for a flood-based Monte Carlo simulation can be dramatically reduced from experimental levels, which are typically on the order of N_γ = 10⁸ photons per flood image. In Sec. 3, it is shown that only 10–100 photons per flood image need to be detected to avoid biasing the estimate. In this section, we propose a method to lower the input flux even further to the limit that each instance becomes a single-gamma event producing a PSF rather than a flood field. The method, which also allows for simultaneous computation of the MTF, is illustrated in Fig. 1 and described below.

Figure 1.

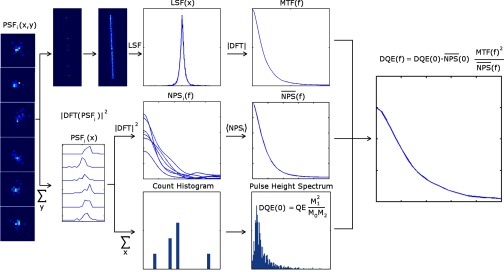
Schematic flow chart for the proposed FLS simulation method (optical transport may or may not be included). Each gamma photon that interacts with the imager produces a typically unique 2D point-spread function. To compute the NPS, each PSF is summed along one dimension to yield a PSF projection which is Fourier transformed and squared to generate a NPS (Ref. ¹⁶). The NPS' from all events are summed and normalized to compute the NPS shape (middle row). Each PSF is also individually summed to give the total received counts for that event, which is then tallied into a pulse height spectrum from which the DQE(0) is calculated using the Swank formalism (Ref. ¹⁵) (bottom row). By directing the gammas along an angled line, the MTF can be determined following the Fujita procedure (Ref. ⁸) (top row). The results of these calculations are then combined to yield the final DQE(f) (right).

For the ensuing analysis, we return to the more general 2D geometry. To compute the shape of the 1D NPS along the x axis, the 2D PSF produced by each detected gamma photon, p, is summed in the y-direction and its corresponding NPS is calculated

$${\text{NPS}}_p\left(f\right)={\left|{\text{DFT}}_i\left(\sum _j{\text{PSF}}_p(i,j)\right)\right|}^2,$$ (23)

where i, j label detector pixels along the x, y directions, respectively, and DFT_i is the 1D discrete Fourier transform in the i direction. The shape of the final 1D NPS curve, up to a scale factor, is then obtained by averaging NPS_p(f) in Eq. 23 over all detected events, N_p

$$\overline{\text{NPS}\left(f\right)}\equiv \frac{1}{N_p}\sum _{p=1}^{N_p}{\text{NPS}}_p\left(f\right).$$ (24)

To determine the proper NPS scaling factor, we propose using the Swank equation¹⁵ which applies to both photon-counting and energy-integrating detectors by accounting for the effects on signal-to-noise ratio of x-ray beam quality and the energy-specific detector response. For each detected event, p, the total signal, T(p), is computed. A histogram composed of all the values of T is then generated to create a pulse height spectrum (PHS). $\tilde{q}\text{NNPS}\left(0\right)$ is subsequently computed from the estimated quantum efficiency ($\tilde{\eta }=N_p/N_{\gamma }$) and the PHS using the Swank formula

$$\tilde{q}\text{NNPS}\left(0\right)=\frac{M_2{M}_0}{\tilde{\eta }{M}_1^2},$$ (25)

where M_i label the ith moment of the pulse height spectrum.

Combining this result with Eq. 24 and normalizing the NPS to 1 by dividing by its zero-frequency value, $\overline{NPS\left(0\right)}$, yields an expression for the denominator of the DQE(f) in Eq. 1

$$\tilde{q}\text{NNPS}\left(f\right)=\tilde{q}\text{NNPS}\left(0\right)·\frac{\overline{\text{NPS}\left(f\right)}}{\overline{\text{NPS}\left(0\right)}}.$$ (26)

With the assumption of shift invariance, the PSFs can be placed anywhere on the detector face. If the incident gammas are directed along an angled line, the MTF can also be readily calculated from an oversampled LSF following the analysis of Fujita et al.⁸ This MTF estimate can be combined with Eq. 26 to calculate DQE(f) using Eq. 1. Angling the input gammas also ensures adequate sampling for the NPS estimate particularly for pixelated arrays. Because this approach combines the established methods of Fujita,⁸ Lubberts,¹⁶ and Swank,¹⁵ we have appropriately named it the “FLS” method.

Modeling optical transport

The simulation of scintillators, whether using a flood image ensemble or a point-spread function ensemble, requires the generation and tracking of optical photons, which in turn introduces additional parameters to optimize in order to minimize simulation times. One of the more obvious of these is the number of optical photons generated per scintillation event. In a Monte Carlo simulation, the number of optical photons created is determined from a Poisson distribution with mean μ_opt, given by

$${\mu }_{\text{opt}}=\beta E_{\text{dep}},$$ (27)

where E_dep is the energy deposited just before a scintillation event and β is a constant with units Energy⁻¹, known as the scintillation yield.

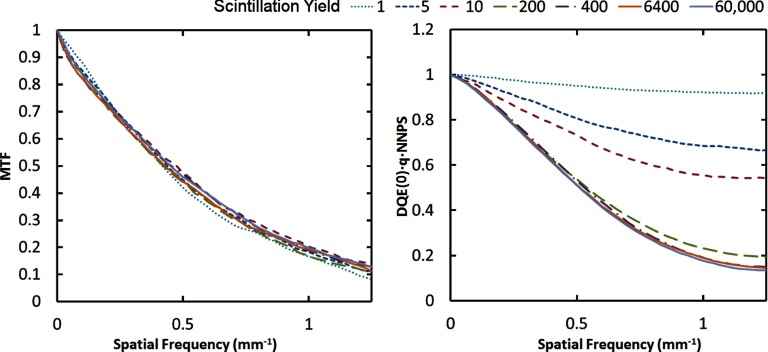
In a physical scintillator, β depends on the details of the material chemistry and electronic band structure. In most cases, it is desired that this value be as high as possible in order to ensure that quantum noise is larger than electronic noise. However, for a simulation that is devoid of electronic noise, the scintillation yield can be minimized to reduce execution time once its effect on the MTF(f) and NPS(f) estimates is understood. To explore this question, the FLS technique was applied to the AS1000 electronic portal imager (EPID) (Varian Medical Systems, Palo Alto, CA) utilizing a GOS screen as detailed in Sec. 2E4. β was varied from the true physical yield of 60 000 opticals/MeV (Ref. ¹⁷) down to 1 optical/MeV, while the number of incident gammas was held constant at 200 000. The resulting MTF and NPS curves, shown in Fig. 2, indicate that there is a much more profound effect on the NPS than the MTF. The NPS changes from a nearly flat shape when β = 1 to the more accurate sloped shape as β is increased. Using a 6 MV spectrum, a yield of 400 opticals/MeV resulted in an average detection rate of 57 opticals/gamma event and the resulting NPS curve differed by an average of only 4% from the maximum yield (β = 60 000) curve. In general, the optimal yield for a given simulation experiment will depend on the desired accuracy, the incident beam energy, and relevant optical properties such as scatter and attenuation. In our experience, at least 50 optical photons/scintillation event should be detected to achieve good accuracy, a requirement which can be programmed into the simulator if desired.¹⁸

Figure 2.

Varian AS1000 MTF and NPS shapes (see Sec. 2E4) simulated using the FLS technique with varying scintillation yield ranging from 1 to 64 000 optical photons/MeV. The $\tilde{q}\text{NNPS}$ has been multiplied by DQE(0) so that it is normalized to a value of 1 at zero frequency. While the MTF remains relatively unaffected by the choice of optical yield, an insufficient number of optical photons results in an artificial increase in the high frequency NPS values. As the scintillation yield is increased, the simulated NPS asymptotically converges to its true shape.

Validation studies

We first validated the formulas for the expectations of the qNNPS and χ² estimates [Eqs. 18, 20] using a 1D multilayer model to show that the number of launched gammas required for a simulation is greatly reduced compared to experimental levels. We then compared our simulations of a thick pixelated scintillator to full-exposure simulations previously published by Wang et al.¹⁹ Finally, we compared a simulation of a Varian AS1000 EPID, including gamma and optical transport, with measurements made at 6 MV on a TrueBeam radiation therapy system (Varian Medical Systems, Palo Alto, CA).

1D multilayer model

A 1D multilayer Lubberts model of light dispersion in a scintillator was built using Matlab (Mathworks, Natick, MA). Each layer of the scintillator had associated with it a LSF modeled as the sum of two Gaussian functions, one of which was relatively narrow and one relatively wide. The standard deviations, σ, of the Gaussians changed linearly as a function of layer number to simulate increased broadening for events originating in layers further from the photodiode array. The contribution from each layer to the overall signal intensity was also set to be a function of layer number to model light attenuation in the scintillator. Taking the above considerations into account, the LSF, h(n,l), was computed as a function of layer l and pixel index n as follows:

$$\begin{array}{ccc}\hfill h(n,l)& =& \frac{A\left(l\right)}{A_{\text{int}}}\left[\frac{{\sigma }_a\left(l\right)}{\sqrt{\pi }}\exp \left(\frac{-n^2}{2{\sigma }_a^2\left(l\right)}\right)\right.\hfill \\ & & \left.+B\frac{{\sigma }_b\left(l\right)}{\sqrt{\pi }}\exp \left(\frac{-n^2}{2{\sigma }_b^2\left(l\right)}\right)\right].\hfill \end{array}$$ (28)

The coefficients for the above equation are explained in further detail in Table 2.

Table 2.

Parameters for the 20-layer scintillator model described by Eq. 28 comprising the sum of two Gaussians. Layer l = 1 has the sharpest LSF while Layer l = 20 has the broadest. The standard deviation, σ_a, of the narrow Gaussian ranges from 0.5 to 1.5 while the standard deviation, σ_b of the broad Gaussian ranges from 1.5 to 5. The narrow Gaussian is weighted ten times as much as the wide Gaussian (B = 0.1), and Layer 1 contributes twice as much to the overall signal as does layer 20 [A(1) = 1, A(20) = 0.5].

Parameter	Formula	Description
σa(l)	$0.5+\frac{l-1}{N_l-1}$	Narrow Gaussian sigma
σb(l)	$5+5\frac{l-1}{N_l-1}$	Wide Gaussian sigma
B	0.1	Wide-to-narrow Gaussian weighting ratio
A(l)	$1-0.5\frac{l-1}{N_l-1}$	Layer weighting factor
Nl	20	Number of layers
Aint	${\sum }_{l=1}^{N_l}A\left(l\right)(1+B)$	Normalization factor

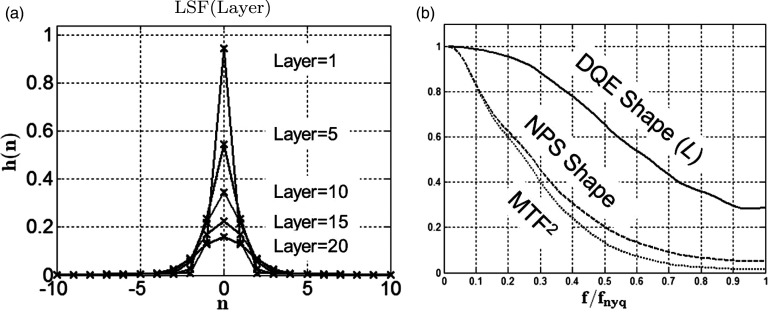
Figure 3a shows the LSFs from five different layers for the model described above. Figure 3b shows the resulting theoretical MTF²(f), qNNPS(f) shape, and DQE(f) shape, also known as the Lubberts' fraction, L( f )

$$L\left(f\right)=\frac{{\text{MTF}}^2\left(f\right)q\text{NNPS}\left(0\right)}{q\text{NNPS}\left(f\right)}.$$ (29)

A sensitivity analysis was performed to evaluate the dependence of the qNNPS estimate on the number of launched gammas, N_γ, and the number of flood images, N_fl. For a given “experiment” comprising N_fl 1D flood images, the number of received photons for each flood image was determined from a Poisson distribution with mean and variance equal to ηN_γ (η was set to be 0.5 for all cases, and the number of received photons was capped at N_γ). In each flood image, each received photon was randomly assigned to a layer l, following which the appropriate LSF was computed using Eq. 28 and 10% speckle noise was added. This noisy LSF was dropped into the (1D) received signal buffer at a random position (n = 1, 2, …, N). After all photons for a given flood buffer were received and all floods for a given experiment simulated, the qNNPS for that experiment was estimated using Eq. 10, where $\tilde{\eta }$ was computed according to Eq. 9. For the sensitivity analysis, N_γ was varied over 6 orders of magnitude from 2 to 2 × 10⁶ gammas/flood image, and N_fl was varied from 50 to 800. For each combination of N_γ and N_fl, 20 experiments were performed.

Figure 3.

Lubberts model described in Table 2. (a) Representative LSFs from 5 (of 20) layers. (b) Resulting theoretical MTF² curve, NPS shape given by the ratio of qNNPS/qNNPS(0), and DQE shape given by the Lubberts' fraction [Eq. 29].

Pixelated scintillator simulation

Wang et al.¹⁹ used Monte Carlo simulations to investigate several scintillator array designs for portal imaging. All the arrays had a 1.106 mm pitch but comprised different materials of varying thicknesses. We chose to analyze the 40 mm thick cesium iodide (CsI) configuration since it has the highest DQE of the structures that were studied and involves the most particle interactions. In their work, EGSnrc was used to launch a total of 3.6 × 10⁸ gamma photons per flood image, sampled from a 6 MV linac spectrum. The launched photons were distributed uniformly across a 60 × 60 cm field that was incident on a 600×600 pixel array. Energy deposition events resulting from gamma interactions within the scintillators were scored (optical transport was not modeled) to create a total of 50 energy deposition flood images. To process the data, the central 500×500 pixels from each flood image were extracted and divided into smaller images of size 250 × 100. These smaller images were then averaged over the shorter dimension resulting in a total of 500 “slit” images for calculating the qNNPS. This technique, known as the “synthesized slit,” differs somewhat from the IEC method but has been validated in numerous publications.^{20, 21, 22}

Applying GEANT4 to an identical simulation geometry, we generated several flood data sets for comparison. Following the IEC approach to processing flood data, the 2D qNNPS was first computed from the central 500×500 pixels of each flood image (no tiling) using Eq. 3. This was then transformed into a 1D qNNPS by averaging the first ten rows on either side of, but not including, the zero-frequency axis. To study the impact of different fluence levels on simulation accuracy, the average number of detected photons, ηN_γ, was varied from one photon per flood image up to the experimental level of 1 × 10⁸ photons per flood image (note, since the quantum efficiency of this detector is approximately 0.5 and only the central 500 pixels were used for processing, the actual number of launched photons ranged from 3 to 2.5 × 10⁸). The number of flood images was varied from 50 to 500.

For the FLS simulation, a total of 20 000 gamma photons were sampled from the TrueBeam spectrum and distributed along a line of length 80 mm that was angled at 1.875° with respect to the array edge. The use of a line source rather than a flood source allowed us to reduce the readout array to 150×150 pixels. The qNNPS was calculated using the method outlined in Fig. 1.

Simulation accuracy was evaluated using a mean squared error metric. A baseline qNNPS curve was first generated using our best possible reproduction of the Wang simulation parameters, namely, N_fl = 50 and N_γ = 3.8 × 10⁸ gammas/pixel/flood. This baseline estimate was fitted to a sixth order polynomial using least-squares regression to generate a reference curve, Polyfit. The residual mean squared error, χ², for each simulated qNNPS curve was then calculated

$${\chi }^2=\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{\left[\tilde{q}\text{NNPS}\left(f\right)-PolyFit\left(f\right)\right]}^2.$$ (30)

We note that the 6 MV TrueBeam spectrum used for our simulations may have differed slightly from the 6 MeV Linac spectrum that Wang et al.¹⁹ used.

AS1000 EPID measurements

Measurements of AS1000 MTF, NPS, and DQE were made on a TrueBeam system operating at 6 MeV with the flattening filter in place. The AS1000 EPID comprises a 1 mm thick copper buildup plate attached to a Gd₂O₂S (GOS) screen which is coupled to an amorphous silicon photodiode array having a pitch of 0.392 mm. The readout array size is 1024×768 pixels.

The MTF was measured by illuminating the panel through a 300 μm slit formed by two parallel tungsten blocks, each 15 cm thick, positioned next to each other.²³ The detector was located 140 cm from the source, and the exit side of the slit assembly was situated 4 mm from the face of the detector. The slit was tilted 2.3° with respect to the vertical axis to allow for spatial oversampling, and the beam was collimated down to a field size of 70 × 20 mm² centered on the blocks. Twenty-five frames of data, each collected with 1.5 machine monitor units (MU) (calibrated at 100 cm) were averaged together resulting in a total detector exposure of 16.7 MU. For processing, the Fujita method was used to generate an oversampled LSF from the dark field- and gain-corrected slit image. To ensure that the tails of the LSF approached zero, a sloping linear baseline was subtracted prior to the MTF calculation.

Two data sets were used to determine the qNNPS. One set comprised 100 images acquired with the radiation beam turned off (dark field). For the other set, 512 images were acquired with a 15 × 15 cm² illumination field at the detector (flood field). The dose was 1.5 MU/image at isocenter (100 cm from the source) and 0.67 MU/image at the detector (150 cm from the source), and the frame rate was 10 frames/s. We irradiated across a 15 × 15 cm² field rather than the entire detector for two reasons: First, we desired to reduce the amount of scattered radiation from the detector housing and support structures. Second, since the flattening filter changes the spectrum in a spatially dependent manner which will result in a spatially nonuniform NPS, we irradiated with a sufficiently small field over which the spectrum is approximately uniform.

To process the qNNPS data, the dark field images were averaged, and the resulting mean dark field image was subtracted from each of the flood field images to correct for panel offset. Further detrending was achieved by normalizing to an average flood image constructed from the flood field sequence. The qNNPS was then estimated from the central 256×256 pixels of the flattened flood field sequence using Eq. 3. Corrections were also made for the effects of dark field noise and lag on the NPS, which were less than 5% in total.

Determination of the qNNPS requires knowledge of the input fluence, q. This entails a conversion from a reported MU value to a fluence value (gamma photons per unit area). For the TrueBeam system on which the measurements were made, 1 MU was calibrated to deliver a 1 cGy dose at a depth of 16 mm in water at the machine isocenter for a 10 × 10 cm² field. The corresponding quantity of gamma photons was estimated by summing the product of the beam spectrum and the kinetic energy released in matter (KERMA) determined from the values published by Rogers.²⁴ The results of our analysis yielded a KERMA dose equivalent factor of 1.42 × 10⁷ photons/(cGy mm²).

AS1000 EPID simulations

Detector model

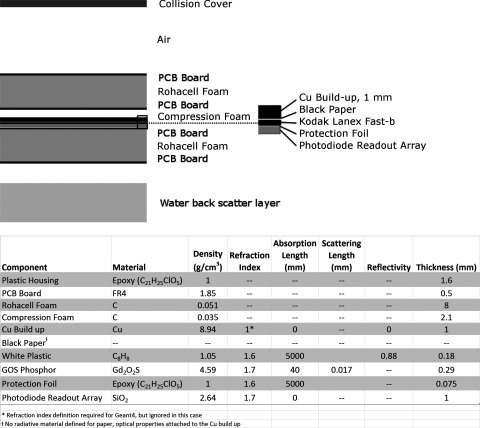
The physical layout of the AS1000 imager is shown in Fig. 4 and is similar to the model of the AS500 described by Kirkby and Sloboda.²⁵ The conversion layer is a FastBack (Fast-b) GOS screen (Carestream Health, Rochester, NY), and there are several key optical parameters, including scattering and attenuation lengths, that are relevant to the simulation. We used an isotropic scattering model with a scattering length of 17 μm as described by Kirkby and Sloboda.²⁵ In Appendix B, we show that this gives functionally the same result as the Mie scattering model of Liaparinos,³ but runs three times faster. The attenuation length was 40 mm (Ref. ²⁶) which corresponds to an imaginary component of the index of refraction of 10⁻⁶.³ The composite refraction index of the GOS screen was 1.7.³ The top reflective support layer was modeled having a specular reflectivity of 0.88.²⁷ The protection foil was modeled as clear plastic with an index of refraction of 1.5. The photodiode layer had an index of refraction of 1.7 and was assumed to be perfectly absorptive.²⁸ For all of our simulations, the wavelength dependence of the optical parameters was neglected. Siebers et al.²⁹ showed the necessity of placing a 10 mm water layer behind the AS1000 to account for backscatter. Of note is that the backscattering sources, which include the support arm and cables, are not uniformly distributed, hence the 10 mm thickness represents an overall average across the entire detector.

Figure 4.

Schematic cross-section of AS1000 model geometry.

Simulation parameters

For the flood field simulation, the irradiated area was 15 × 15 cm² to match the experimental conditions. Radiative transport throughout the entire detector of size 40 × 30 cm² was calculated in order to capture all backscatter effects. To match the measurement, the qNNPS was computed from the central 256×256 pixels using the IEC processing method. In total, 400 flood images were simulated, each with 6000 incident gamma photons sampled from the 6 MeV TrueBeam spectrum. At 6 MeV, the AS1000 has a quantum efficiency of approximately 0.02, which translates to an average of 120 detected photons per flood field thus ensuring a unbiased qNNPS estimate. The scintillation yield was 400 opticals/MeV, based on the sensitivity study shown in Fig. 2.

For the FLS simulation, 400 000 gamma photons were launched and distributed evenly over a rectangle of dimensions 70 × 0.3 mm², angled at 2.3° to match the MTF measurement conditions. The detector area was 15 × 15 cm². The number of gammas was chosen to achieve a sufficiently “smooth” MTF curve. If we were just interested in qNNPS accuracy, then a factor of 10 fewer photons could have been launched.

RESULTS

1D multilayer Lubberts model

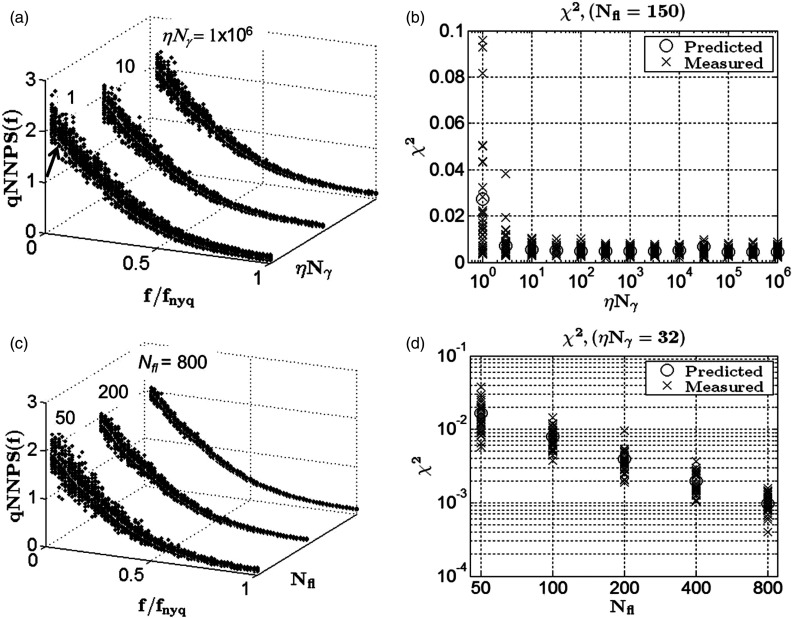
Figure 5 shows NPS simulation results using the multilayer Lubberts model detailed in Table 2. The top two subfigures (a) and (b) show behavior as a function of the number of detected photons, ηN_γ, with the number of flood images, N_fl, fixed at 150. Figure 5a displays $\tilde{q}\text{NNPS}$ distributions for three different flux levels (ηN_γ = 1, 10, 1 × 10⁶ detected photons/flood). For each flux level, 20 simulation experiments were initiated with different random seeds. Hence, the vertical distribution of the dots is indicative of the amount of random simulation noise. The lightly colored solid curve in each plot in Fig. 5a is the theoretical qNNPS given by Eq. A9.

Figure 5.

Simulation results using the layered model described in Table 2. (a) Stacked plot of $\tilde{q}\text{NNPS}\left(f\right)$ for three different signal intensities, ηN_γ. Each plot shows the superimposed qNNPS estimates from 20 simulations started with different random seeds. A bias is seen for ηN_γ = 1 (arrow) while the distributions of the plots for ηN_γ = 10 and ηN_γ = 10⁶ are nearly identical and show no bias. (b) Distribution of χ² vs ηN_γ. The circles show expected values from Eq. 20 while the x's show a measured value for each experiment. (c) $\tilde{q}\text{NNPS}$ distribution as a function of the number of flood fields, N_fl, with ηN_γ set to 32. (d) Measured (x) and predicted (o) χ² distributions. Combined, these plots show there is no further value to increasing the number of launched photons per flood image beyond that required to eliminate the bias in the $\tilde{\eta }$ estimate. However, there is significant value to increasing the total number of flood images to reduce noise.

A bias in the $\tilde{\eta }$ estimate occurs for the very low fluence simulation (ηN_γ = 1) as indicated by an arrow in Fig. 5a. This bias, which is manifest as a scaling error, is eliminated once ηN_γ > 10. That only ten gamma photons require detection to obtain an accurate simulation using this model is confirmed in Fig. 5b which shows the χ² error as a function of the number of launched photons plotted over a 6-order of magnitude range. As predicted by Eq. 20, the simulation error is independent of the signal intensity once the flux is sufficient to eliminate the bias.

The bottom row shows behavior as a function of the number of flood images with the number of detected photons held fixed at 32. As seen qualitatively in the qNNPS distributions in Fig. 5c, the noise decreases as N_fl is increased. Quantitatively, as predicted by Eq. 22, the variance is inversely proportional to the number of flood images [Fig. 5d].

Wang pixelated detector: Flood image ensemble

Figure 6 shows the simulation results from the flood-based technique superimposed on the qNNPS curve published by Wang et al.¹⁹ In all cases, only radiative transport was modeled. Good agreement is obtained between our results and those of Wang¹⁹ although there is a small (5%–10%) scaling difference between the two that may result from use of slightly different spectra. Of note is that the curves generated by our procedure are less noisy. This is likely because the IEC analysis method utilizes a larger portion of information from the 2D NPS profile than does the synthesized slit technique.

Figure 6.

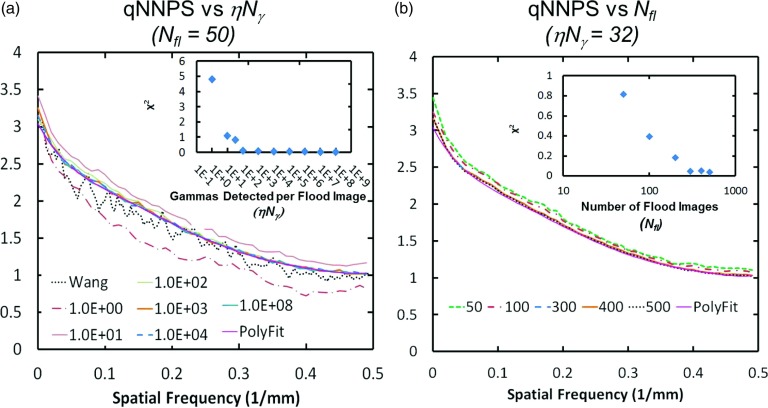
Simulation of pixelated CsI detector described by Wang et al. (Ref. ¹⁹): (a) $\tilde{q}\text{NNPS}\left(f\right)$ vs number of detected gammas/flood, ηN_γ, for a fixed number of flood fields, N_fl = 50. A scaling error, due to the $\tilde{\eta }$ estimation bias, is seen for very low numbers of detected photons/flood. This bias is eliminated once ηN_γ ⩾ 100. (b) $\tilde{q}\text{NNPS}\left(f\right)$ as a function of N_fl for an average detection level of ηN_γ = 32 gammas/flood image. The curve labeled “Wang” in (a) is directly from the publication (Ref. ¹⁹). The curve labeled Polyfit in (a) and (b) is a sixth order polynomial fit to the qNNPS curve we generated using the Wang simulation parameters, namely, N_fl = 50 and N_γ = 3.6 × 10⁸ gammas/pixel/flood. The insets in the upper right of each plot show the χ² error from Eq. 30 for each qNNPS estimate. Improved accuracy is obtained as N_fl is increased, while there is no benefit to increasing the number of detected gammas/flood beyond that required to eliminate the bias.

Similar to the results from the 1D multilayered model described above, an estimation bias (manifest as a scaling error) is also seen for low fluence rates. As shown in Fig. 6a, the bias is removed once ηN_γ reaches 100. Similarly, if the input fluence is held fixed so that ηN_γ = 32, the MSE is reduced as N_fl is increased. As shown in Fig. 6b, as N_fl is increased from 50 to 300, there is a large reduction in χ² due to the elimination of the remainder of the bias. Once N_fl reaches approximately 300, the reduction in χ² continues but becomes less pronounced. Together, Figs. 6a, 6b demonstrate that the most efficient approach is to use as low a value of ηN_γ as possible while increasing N_fl to improve accuracy and reduce noise.

Wang pixelated CSI detector: FLS simulation

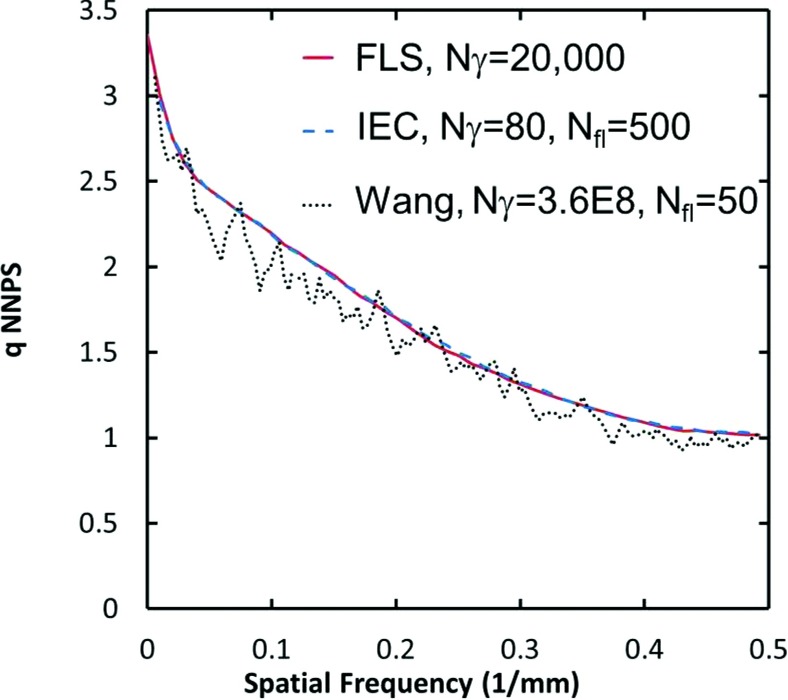
Figure 7 shows the qNNPS estimate produced by the FLS simulation of the Wang detector. Also shown is the reduced-gamma IEC flood-based estimate from Fig. 6 for N_fl = 500 and N_γ = 80 gammas/flood (32 mean detected gammas/flood). The IEC and FLS qNNPS(f) curves are in excellent agreement with each other, having a maximum and average discrepancy of 2.8%, and 1.5%, respectively. For this study, the FLS simulation required half as many input photons as the flood-based simulation to produce equivalent curve smoothness. Both the IEC and FLS results show reduced noise compared to the Wang simulation which utilized a total of 3.6 × 10⁸ incident gammas/flood image.

Figure 7.

Comparison of the simulated qNNPS(f) from Wang et al. (Ref. ¹⁹) with the simulated qNNPS(f) from both reduced gamma methods (IEC and FLS) presented in this work. The reduced gamma IEC and FLS results coincide to within 1.5% of each other and are in close agreement with the Wang curve albeit with reduced noise.

AS1000 portal imager: Simulation vs experiment

Figure 8 shows excellent agreement between measured and simulated AS1000 MTF(f), qNNPS(f), and DQE(f) curves. Since the flood method only generates a qNNPS(f) estimate, the MTF plot comes from the FLS simulation, and because the flood- and FLS-based qNNPS estimates completely overlap, only the FLS DQE(f) simulation is shown. The root mean squared (RMS) differences between the measured and simulated MTF²(f), qNNPS(f), and DQE(f) estimates are 0.015, 3.85, 0.00048, respectively, while the mean MTF²( f ), qNNPS(f), and DQE(f) estimates are 0.22, 36.0, 0.0044, respectively. Thus, the average discrepancy between measurement and simulation is 3% for the MTF²( f ), 7% for the qNNPS(f), and 11% for the DQE(f). We note that the slight “bumpiness” in the simulated DQE(f) curve is mainly due to noise in the simulated MTF(f) and not in the qNNPS(f) estimate.

Figure 8.

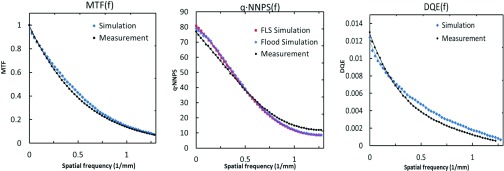
Simulated and measured MTF, qNNPS, and DQE curves for the AS1000 imager operating at 6 MeV with the flattening filter in place. Very good agreement is obtained between measurement and simulation, which included both radiative and optical transport. Sixth order polynomials were fit to each set of data points (solid lines).

Computation times

Table 3 summarizes the CPU times required to generate the curves in Figs. 78. The first entry is an estimated execution time for the synthesized slit simulation of Wang et al.¹⁹ since no timing numbers were explicitly reported. The estimate comes from a study subsequently published by the same group using a nominally identical detector geometry and simulation parameter set which quoted an execution time of 150 000 CPU h for 2560 runs.³⁰ Therefore, a nominal value of 59 CPU h (3540 CPU min) was assumed for the execution time required by Wang et al.¹⁹ to generate a single flood image. By comparison, a total of 53 000 CPU min (second row) were required per flood image to generate the baseline curve in Fig. 6 using nominally identical simulation parameters, but different transport code (GEANT4 with Penelope physics vs EGSnrc). Although the GEANT4 code is found to be significantly slower than the EGSNRC code, a 4–5-order reduction in execution time was still achieved using the optimized methods. The final entry in Table 3 contains the run time for the FLS AS1000 simulation reported in Fig. 8 with an optical yield of 400/MeV.

Table 3.

Comparison of execution times using a single 2.2 GHz CPU for different simulation runs. The reduce gamma flood and FLS simulation times are all on the order of minutes, even with the inclusion of full optical transport.

Geometry	Reference	Simulation method	Incident gammas per flood	Number of flood images	Total incident gammas	Total CPU min
Pixelated scintillator	Wang et al. (Ref. 19)	Synthesized slit (NPS only)	3.4 × 108	50	1.7 × 1010	177 000 (estimated)
Pixelated scintillator	Current work	IEC (NPS only)	3.4 × 108	50	1.7 × 1010	2 650 000
Pixelated scintillator	Current work	IEC (NPS only)	80	500	4 × 104	8.3
Pixelated scintillator	Current work	FLS (MTF, NPS, DQE)	…	…	2 × 104	3.1
AS1000 EPID with optical transport	Current work	FLS (MTF, NPS, DQE)	…	…	4 × 105	14.5

DISCUSSION

The results show that very fast simulation times of DQE(f) can be achieved without loss of accuracy by prudently reducing the number of gamma and optical particles that are launched relative to what is required for a typical experimental acquisition. Using the flood-based approach, it was possible to reduce the number of launched gamma photons per flood image by a factor of 10⁷ relative to experimental values without degrading the qNNPS estimate. The lower limit of incident gammas is dictated by the uncertainty estimating the quantum efficiency which leads to a bias that can be overcome by using information from all events to estimate DQE(0) through the Swank relation. This allows for an additional reduction in input gammas as the flood image is reduced to a single-gamma event, and forms the basis for the newly proposed FLS method that also has the advantage of generating data for MTF and NPS estimates concurrently. Ultimately, this translated to a reduction in GEANT4 execution time for simulating the Wang detector from 2 650 000 CPU min if using experimental acquisition parameters to 3.1 CPU min when using optimized simulation parameters, while yielding a significantly less noisy NPS curve. A general guideline for simulation parameter optimization is that at least 10 000 gamma photons should be detected in total and, if modeling optical transport, the yield should be set so that an average of at least 50 optical photons are detected per scintillation event.

A key observation from the study is that random simulation noise is inversely proportional to the number of flood images (or total launched photons for the FLS method) provided that the number of launched gammas per flood is sufficiently high to eliminate the bias in the quantum efficiency estimate. Thus, for a given simulation experiment, it is most efficient to “spend” those photons creating as many individual NPS estimates as possible for averaging. This, naturally, favors the use of point-spread functions over flood images. There also may be other advantages to using point-spread functions. As Dobbins¹⁴ point out, Eq. 2 is exactly valid only for a detector of infinite extent, and care must be taken in the definition of the ROI size so as not to introduce finite extent effects even for experimental dose levels. Since the FLS method relies on the PSFs produced from single gamma events for its noise correlation information, the detector extent needs only to be sufficiently large so as to contain the entire PSF along the simulated line. Another advantage of the FLS method is that it generates an explicit estimate for qNNPS(0) whereas qNNPS(0) must be extrapolated using the flood-based technique. These advantages in speed and robustness, combined with the ability to acquire NPS and MTF data simultaneously would point to a preference for using the FLS technique. Nevertheless, it should be noted that since actual experimental NPS data are (by necessity) acquired using the IEC flood field-based method, it still may be desired to employ the reduced gamma flood simulation approach for purposes of determining the magnitude of finite-extent (and other) artifacts in the experimental data.

The FLS procedure shares some features in common with previously published cascaded models, most notably those of Kausch et al.²⁶ and Badano et al.³¹ who also used point sources to determine the NPS. In both approaches, the scintillator is subdivided into many layers in the z-direction. A “library” of optical PSFs is first generated by launching a finite number of optical photons isotropically from a point-source in the middle of each layer and storing the information. A 3D radiative energy deposition profile is then simulated by directing gamma photons from the source to a single point on the detector and recording the energy deposited as a function of x, y, and z. Then, for each layer, a combined PSF (and NPS) is calculated by convolving the simulated energy deposition profile with that layer's optical PSF. Using the Lubberts formalism, the final NPS is computed by summing the NPS from each layer while the MTF is the Fourier transform of the cumulative point-spread function from all layers.³²

Kausch et al.²⁶ used the cascaded method to calculate DQE(f), but employed a formula which differs from the conventional definition [Eq. 1], and we have not been able to match their results using conventional simulation approaches (it appears that their estimate of qNNPS may be biased). In their work, Badano et al.³¹ did not determine DQE(f) but instead studied the effects of various experimental parameters on the Lubberts fraction to relate the shapes of the MTF and NPS curves to each other. A key innovation introduced by the FLS algorithm is the use of DQE(0) calculated from the Swank equation to transform the Lubberts fraction L(f) into DQE(f).

The cascaded approaches described above require execution of several separate programs including one for creating the library of optical PSFs, one for creating the 3D radiative energy deposition profile, and one for combining the results. This may increase execution times, data storage requirements, and complexities of operation compared to the proposed FLS algorithm which requires only one program to be run and takes advantage of GEANT4's capabilities to simultaneously transport optical and gamma photons. Another difference is that oversampling of the PSF using the cascaded approach was achieved by making artificially small pixels. This may lead to errors when modeling periodic, spatially inhomogeneous detectors such as a pixelated scintillator unless multiple point sources are used to adequately sample the actual (i.e., larger) scintillator pixels. Sampling must not only be adequate in the z-, but also the x- and y-directions, a feature that is “built-in” to the angled line Fujita method, provided the line angle is properly selected.

We expect the techniques presented here will help facilitate the use of in silico design methods to optimize the performance of both direct and indirect x-ray detectors with the largest benefit likely conferred upon indirect detectors which, previously, have not been well modeled due to prohibitively high computational loads. There are three main categories of such detectors: (1) Particle-in-binder screens (e.g., GOS), (2) pixelated arrays, (3) vapor-deposited columnar structures [e.g., CsI(Tl)], all three of which can be modeled using the proposed techniques. For a particle-in-binder screen, optimization of build-up layer thickness and material, screen thickness, particle material and size, and binder index of refraction may yield improved performance for a given beam energy. For a pixelated array configuration, optimization of scintillator material and thickness, pixel size, polishing parameters, reflector properties, and glue material can be explored. For a scintillator with a columnar structure, the column geometry including packing fraction, surface roughness, and column shape may warrant investigation.

Finally, we note that for both the FLS and rapid flood-field simulation methods that we propose, the reduction in launched particles is made possible by exploiting the idealized condition that no electronic noise sources (e.g., kTC noise, video amplifier noise, digitization noise) are present. When desired, however, these noise sources can still be accounted for by adjusting the qNNPS curves appropriately. Since in most cases, the electronic noise sources are white, a constant value can be added to the qNNPS after simulation of x-ray and optical transport is completed. The amount added will depend on the nature of the electronic noise sources which can be readily determined via measurement and simulation of the readout components.²⁸ This assessment need only be done once for a given set of electronics.

CONCLUSIONS

By judiciously reducing the number of gamma and optical photons that are launched as part of a simulation experiment of an indirect x-ray detector, DQE(f) can be modeled in minutes on a single CPU with no loss of accuracy. In addition to optimizing the conventional flood-field approach for measuring NPS, we demonstrated the validity of a novel simulation method using an ensemble of point-spread functions which offers even higher efficiency and robustness. Implementation of these techniques using the GEANT4 simulation package provides a powerful tool allowing for multiple design iterations to be performed in a short amount of time, which we anticipate will result in a quicker path to developing improved x-ray imaging products.

APPENDIX A: qNNPS(f) ESTIMATION ERROR

In this appendix, we derive formulas of the expectation of the error of the qNNPS(f) estimate as a function of the number of photons launched per flood field, N_γ and the number of flood fields per experiment, N_fl.

Expectation of qNNPS

Since the qNNPS(f) is proportional to the Fourier transform of the noise autocorrelation function [Eq. 15], we start by taking the expectation of the estimated noise-autocorrelation function $\tilde{R}$, which is defined in Eq. 14. The expectation of $\tilde{R}$ is a function of received signal, Q_ph, and the blurring function, h, associated with layer number l

$$\begin{array}{ccc}& & E\left[\tilde{R}(t,l)\right]\hfill \\ & & =\underset{N_x\to \infty }{\lim }\frac{1}{N_x}\sum _{n=1}^{N_x+t}\sum _s{Q}_{\text{ph}}(n-s,l)h(s,l)\hfill \\ & & \times \sum _r{Q}_{\text{ph}}(n-r+t,l)h(r,l)\hfill \\ & & =E\left[\sum _s{Q}_{\text{ph}}(n-s,l)h(s,l)\sum _r{Q}_{\text{ph}}(n-r+t,l)h(r,l)\right]\hfill \\ & & =\sum _r\sum _{s}E\left[Q_{\text{ph}}(n-s,l)Q_{\text{ph}}(n-r+t,l)\right]h(s,l)h(r,l)\hfill \\ & & =E\left[\tilde{\eta }\right]I_{\text{in}}\sum _r\sum _s\delta (t-s+r)h(s,l)h(r,l)\hfill \\ & & =E\left[\tilde{\eta }\right]I_{\text{in}}\sum _{s}h(t-s,l)h(s,l).\hfill \end{array}$$ (A1)

Equation A1 simply shows that the noise autocorrelation function of each layer is proportional to that layer's LSF convolved with itself, with the constant of proportionality given by the expectation of the mean received signal, $\tilde{\eta }{I}_{\text{in}}$.

Equation A1 can be substituted into Eq. 15 to determine the expectation of the qNNPS(f) estimate, $\tilde{q}\text{NNPS}\left(f\right)$. The qNNPS is computed by taking the Fourier transform of the noise autocorrelation function for all layers, l, averaged over all flood fields, g

$$\begin{array}{ccc}& & E\left[\tilde{q}\text{NNPS}\left(f\right)\right]\hfill \\ & & =E\left[\frac{1}{{\tilde{\eta }}^2{I}_{\text{in}}{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\sum _{l=1}^{N_l}\left|\sum _{t=-N_x/2}^{N_x/2}\tilde{R}(t,g,l)e^{\frac{-i2\pi f_{x}t}{N_x}}\right|\right]\hfill \\ & & =\frac{1}{I_{\text{in}}{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\sum _{l=1}^{N_l}\left|\sum _{t=-N_x/2}^{N_x/2}E\left[\frac{\tilde{R}(t,g,l)}{{\tilde{\eta }}^2}\right]e^{\frac{-i2\pi f_{x}t}{N_x}}\right|\hfill \end{array}$$ (A2)

$$\begin{array}{ccc}& & =\frac{1}{I_{\text{in}}{N}_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\sum _{l=1}^{N_l}\left|\sum _{t=-N_x/2}^{N_x/2}E\left[\frac{1}{\tilde{\eta }}\right]I_{\text{in}}\right.\hfill \\ & & \left.\times \sum _{s}h(t-s,l)h(s,l)e^{\frac{-i2\pi f_{x}t}{N_x}}\right|\hfill \end{array}$$ (A3)

$$\begin{array}{ccc}& & =E\left[\frac{1}{\tilde{\eta }}\right]\sum _{l=1}^{N_l}\sum _{t=-N_x/2}^{N_x/2}\sum _{s}h(t-s,l)h(s,l)e^{\frac{-i2\pi f_{x}t}{N_x}}\hfill \end{array}$$ (A4)

$$\begin{array}{ccc}& & =E\left[\frac{1}{\tilde{\eta }}\right]\sum _{l=1}^{N_l}{H}^2(f,l),\hfill \end{array}$$ (A5)

where H(f, l) in Eq. A5 is the Fourier transform of h(s, l). The substitution of Eq. A1 into Eq. 15 is made in going from step A2 to A3. In going from Eq. A3 to Eq. A4, the summation of $E\left[\tilde{R}(t,g,l)\right]/N_{\text{fl}}$ over g is replaced with $E\left[\tilde{R}(t,g,l)\right]$ since the different flood fields are statistically independent if assuming no lag from frame-to-frame. In going from Eq. A4 to Eq. A5, the Fourier convolution theorem is used to take the Fourier transform of h convolved with itself.

Equation A5 restates Lubberts' theory that the total NPS is proportional to the sum of the NPS' from each individual layer, while showing that the constant of proportionality for a simulation is $E(1/\tilde{\eta })$. The cumulative NPS shape, H( f ), is then

$$H^2\left(f\right)=\sum _{l=1}^{N_l}{H}^2(f,l).$$ (A6)

Note that H(0) = 1 since the sum of all the layer-dependent LSFs is 1 [i.e., h(l) is normalized so that ∑_{n, l}h(n, l) = 1].

Substituting Eq. A6 into Eq. A5, the expectation of the qNNPS estimate is given by

$$\begin{array}{ccc}\hfill E\left[\tilde{q}\text{NNPS}\right]& =& H^2\left(f\right)E\left[\frac{1}{\tilde{\eta }}\right],\hfill \end{array}$$

where, from Eq. 9,

$$\begin{array}{c}\hfill E\left[\frac{1}{\tilde{\eta }}\right]=\underset{N_{\text{exp}}\to \infty }{\lim }\frac{1}{N_{\text{exp}}}\sum _{I\text{exp}=1}^{N\text{exp}}\frac{N_{\text{fl}}N}{{\sum }_{g=1}^{N_{\text{fl}}}{\sum }_{n=1}^N{I}_g(n,I_{\text{exp}})}\end{array}$$ (A7)

and N_exp is defined as the number of statistically independent simulation experiments, I_exp, that are performed.

An important point to note is that $\tilde{q}\text{NNPS}$ may be biased since

$$E\left(\frac{1}{\eta }\right)\ne \frac{1}{E\left(\eta \right)}.$$ (A8)

Biasing occurs for very low fluence rates, conditions of which are explored in the main text.

As the number of launched photons becomes sufficiently large so that $E[1/\tilde{\eta }]=1/\eta$, the expectation of actual qNNPS is reached, given by

$$q{\text{NNPS}}_{\text{act}}\left(f\right)=E{\left[\tilde{q}\text{NNPS}\right]}_{E[1/\tilde{\eta }]=1/\eta }=\frac{1}{\eta }{H}^2\left(f\right).$$ (A9)

Expectation of χ²

We now compute E(χ²), the expectation of the mean squared error of the estimate by averaging the square of the error for all points f between the positive and negative Nyquist frequencies (±N_x/2)

$$\begin{array}{ccc}& & E\left[{\chi }^2\right]\hfill \\ & & =E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{\left(\frac{1}{N_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)-q{\text{NNPS}}_{\text{act}}\left(f\right)\right)}^2\right]\hfill \end{array}$$ (A10)

$$\begin{array}{c}\hfill =E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{\left(\frac{1}{N_{fl}}\sum _{g=1}^{N_{fl}}\tilde{q}{\mathit{NNPS}}_g\left(f\right)\right)}^2\right]\end{array}$$ (A11)

$$\begin{array}{c}\hfill -2E\left[\frac{1}{N_{\text{fl}}}\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)q{\text{NNPS}}_{\text{act}}\left(f\right)\right]\end{array}$$ (A12)

$$\begin{array}{c}\hfill +E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}q{\text{NNPS}}_{\text{act}}^2\left(f\right)\right].\end{array}$$ (A13)

Each of the above three terms is solved for separately. We start with the third term, Eq. A13.

Third term A13

The expectation of $q{\text{NNPS}}_{\text{act}}^2$ is straightforward as it is not affected by statistical noise

$$\begin{array}{ccc}\hfill E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}q{\text{NNPS}}_{\text{act}}^2\left(f\right)\right]& =& \frac{1}{{\eta }^2{N}_x}\sum _{f=-N_x/2}^{N_x/2}{H}^4\left(f\right),\hfill \\ & =& \frac{H_{\text{int}}}{{\eta }^2},\hfill \end{array}$$ (A14)

where H_int is defined to be the normalized integral of H⁴( f )

$$H_{\text{int}}=\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{H}^4\left(f\right).$$ (A15)

Second term A12

To compute the expectation of Eq. A12, we note that the noise associated with the estimate $\tilde{q}{\text{NNPS}}_g$ is uncorrelated with the (noiseless) curve, qNNPS_act, so that

$$\begin{array}{ccc}& & E[\tilde{q}{\text{NNPS}}_g\left(f\right)·q{\text{NNPS}}_{\text{act}}\left(f\right)]\hfill \\ & & =E\left[\tilde{q}\text{NNPS}\left(f\right)\right]·E\left[q{\text{NNPS}}_{\text{act}}\left(f\right)\right].\hfill \end{array}$$ (A16)

Hence,

$$\begin{array}{ccc}& & -2E\left[\frac{1}{N_{\text{fl}}}\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)q{\text{NNPS}}_{\text{act}}\left(f\right)\right]\hfill \\ & & =-2\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}E\left[\frac{1}{\tilde{\eta }}\right]H^2\left(f\right)\frac{1}{\eta }{H}^2\left(f\right)\hfill \\ & & =-2\frac{H_{\text{int}}}{\eta }E\left[\frac{1}{\tilde{\eta }}\right].\hfill \end{array}$$ (A17)

First term A11

To compute the expectation of Eq. A11, we divide the summation of flood images into two subterms, one of which has correlated components and the other of which has uncorrelated components

$$\begin{array}{ccc}& & E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{\left(\frac{1}{N_{\text{fl}}}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g^2\left(f\right)\right)}^2\right]\hfill \\ & & =E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g^2\left(f\right)\right]\hfill \\ & & +E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _g^{N_{\text{fl}}}\sum _{g^{\prime }\ne g}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)\tilde{q}{\text{NNPS}}_{g^{\prime }}\left(f\right)\right].\hfill \end{array}$$ (A18)

We first address the uncorrelated subterm. As previously noted, $\tilde{q}{\text{NNPS}}_g$ is statistically uncorrelated with $\tilde{q}{\text{NNPS}}_{g^{\prime }}$ (for g^′ ≠ g), and therefore the expectation of the product of these two variables is equal to the product of their expectations. Hence, the expectation of the second subterm of Eq. A18 is

$$\begin{array}{ccc}& & E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _g^{N_{\text{fl}}}\sum _{g^{\prime }\ne g}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g\left(f\right)\tilde{q}{\text{NNPS}}_{g^{\prime }}\left(f\right)\right]\hfill \\ & & =\frac{1}{N_x}\sum _{n=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _g^{N_{\text{fl}}}\sum _{g^{\prime }\ne g}^{N_{\text{fl}}}E\left[\tilde{q}{\text{NNPS}}_g\left(f\right)\right]E\left[\tilde{q}{\text{NNPS}}_{g^{\prime }}\left(f\right)\right]\hfill \\ & & =\frac{N_{\text{fl}}^2-N_{\text{fl}}}{N_{\text{fl}}^2}·\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}{E}^2\left[\frac{1}{\tilde{\eta }}\right]H^4\left(f\right)\hfill \\ & & =E^2\left[\frac{1}{\tilde{\eta }}\right]\left(1-\frac{1}{N_{\text{fl}}}\right)H_{\text{int}}.\hfill \end{array}$$ (A19)

To solve for the first (i.e., correlated) subterm of Eq. A18, Parseval's theorem can be used to relate the sum of the total (i.e., layer-independent) noise autocorrelation function squared, ${\tilde{R}}^2\left(t\right)$, in the spatial domain to the sum of $\tilde{q}{\text{NNPS}}^2\left(f\right)$ in the frequency domain

$$\begin{array}{ccc}& & E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _{g=1}^{N_{\text{fl}}}\tilde{q}{\text{NNPS}}_g^2\left(f\right)\right]\hfill \\ & & =E\left[\frac{1}{I_{\text{in}}^2{N}_{\text{fl}}^2}\sum _{g=1}^{N_{\text{fl}}}\sum _{t=-N_x/2}^{N_x/2}\frac{{\tilde{R}}_g^2\left(t\right)}{{\tilde{\eta }}^4}\right]\hfill \\ & & =\frac{1}{I_{\text{in}}^2{N}_{\text{fl}}^2}\sum _{g=1}^{N_{\text{fl}}}E\left[\sum _{t=-N_x/2}^{N_x/2}\frac{{\tilde{R}}_g^2\left(t\right)}{{\tilde{\eta }}^4}\right]\hfill \end{array}$$ (A20)

$$\begin{array}{ccc}& & =E\left[\frac{1}{I_{\text{in}}^2{N}_{\text{fl}}}\sum _{t=-N_x/2}^{N_x/2}\frac{{\tilde{R}}^2\left(t\right)}{{\tilde{\eta }}^4}\right],\hfill \end{array}$$ (A21)

where in going from Eq. A20 to Eq. A21, the summation of $E\left[{\tilde{R}}_g\right]/N_{\text{fl}}$ over g is replaced with $E\left[\tilde{R}\right]$ as described above.

Using the definition of $\tilde{R}\left(t\right)$ [Eq. 14], the summation of ${\tilde{R}}^2\left(t\right)$ can be expanded as follows:

$$\begin{array}{ccc}\hfill \sum _{t=-N_x/2}^{N_x/2}{\tilde{R}}^2\left(t\right)& =& \tilde{R}\left(0\right)+2\sum _{t=1}^{N_x/2}{\tilde{R}}^2\left(t\right)\hfill \\ & =& {\left(\frac{1}{N_x}\sum _{n=1}^{N_x}(Q\left(n\right)Q\left(n\right)\right)}^2\hfill \\ & & +2\sum _{t=1}^{N_x/2}{\left(\frac{1}{N_x}\sum _{n=1}^{N_x+t}(Q\left(n\right)Q(n+t)\right)}^2,\hfill \end{array}$$ (A22)

where the symmetry property of the noise autocorrelation function [R(t) = R( − t)] is used to allow the computation to be performed over positive values of t starting from t = 1 to t = N/2. This summation is expanded by multiplying out the terms of Eq. A22 and then regrouping using the following identity (which strictly holds for wide-sense Gaussian process but also approximately holds for a wide-sense Poisson process³³) to determine the expectation of the product of four (possibly correlated) random variables

$$\begin{array}{ccc}\hfill E\left[Q\right(1\left)Q\right(2\left)Q\right(3\left)Q\right(4\left)\right]& \approx & E\left[Q\right(1\left)Q\right(2\left)\right]E\left[Q\right(3\left)Q\right(4\left)\right]\hfill \\ & & +E\left[Q\right(1\left)Q\right(3\left)\right]E\left[Q\right(2\left)Q\right(4\left)\right]\hfill \\ & & +E\left[Q\right(1\left)Q\right(4\left)\right]E\left[Q\right(2\left)Q\right(3\left)\right].\hfill \end{array}$$ (A23)

After expansion of Eq. A22, incorporation of Eq. A23 and regrouping, the expectation of the summation of ${\tilde{R}}^2\left(t\right)$ is approximately reduced to

$$\begin{array}{ccc}& & E\left[\sum _{t=-N_x/2}^{N_x/2}{\tilde{R}}^2\left(t\right)\right]\hfill \\ & & \approx \underset{n\to \infty }{\lim }\frac{1}{N_x^2}\left(2N_x^2{E}^2\left[\tilde{R}\left(0\right)\right]+\sum _{t=1}^{N_x/2}2(N_x^2-t)E^2\left[\tilde{R}\left(t\right)\right]\right.\hfill \\ & & +\left.\left(2\sum _{k=1}^{N_x}2k\right)\sum _{t=1}^{N_x/2}{E}^2\left[R\left(t\right)\right]\right)\hfill \\ & & +\underset{n\to \infty }{\lim }\frac{1}{N_x^2}\left(O\left(N_x\right)\sum _{t^{\prime }\ne t}E\left[\tilde{R}\left(t\right)\right]E\left[\tilde{R}\left(t^{\prime }\right)\right]\right)\hfill \\ & & \approx 2E^2\left[\tilde{R}\left(0\right)\right]+4\sum _{t=1}^{N_x/2}{E}^2\left[\tilde{R}\left(t\right)\right]\hfill \\ & & \approx 2\sum _{t=-N_x/2}^{N_x/2}{E}^2\left[\tilde{R}\left(t\right)\right].\hfill \end{array}$$ (A24)

Substitution of Eq. A1 into Eq. A24 yields

$$\begin{array}{ccc}& & E\left[\sum _{t=-N_x/2}^{N_x/2}{\tilde{R}}^2\left(t\right)\right]\hfill \\ & & \approx 2E^2\left[\tilde{\eta }\right]I_{in}^2\sum _{t=-N_x/2}^{N_x/2}{\left(\sum _l\sum _{s}h(t-s,l)h(s,l)\right)}^2.\hfill \end{array}$$ (A25)

Using Parseval's theorem again, we can relate the integral of the square of the autocorrelation function to H_int

$$\begin{array}{ccc}& & \sum _{t=-N_x/2}^{N_x/2}{\left(\sum _{l=1}^{N_l}\sum _{s}h(t-s,l)h(s,l)\right)}^2\hfill \\ & & =\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\left(\sum _{l=1}^{N_l}{H}^4(f,l)\right)=H_{\text{int}}.\hfill \end{array}$$ (A26)

Now, combining Eqs. A21, A25, A26, the expectation of the first (i.e., correlated) term of Eq. A18 is

$$\begin{array}{c}\hfill E\left[\frac{1}{N_x}\sum _{f=-N_x/2}^{N_x/2}\frac{1}{N_{\text{fl}}^2}\sum _{g=1}^{N_{\text{fl}}}q{\text{NNPS}}_g^2\left(f\right)\right]\approx 2E\left[\frac{1}{{\tilde{\eta }}^2}\right]\frac{H_{\text{int}}}{N_{\text{fl}}}.\end{array}$$ (A27)

Finally, the total expression for the expectation of the mean squared error is obtained by combining Eqs. A14, A17, A19, A27

$$\begin{array}{ccc}\hfill E\left[{\chi }^2\right]& \approx & H_{\text{int}}·\left(\left\{\frac{1}{N_{\text{fl}}}E\left[\frac{2}{{\tilde{\eta }}^2}\right]-\frac{1}{N_{\text{fl}}}{E}^2\left[\frac{1}{\tilde{\eta }}\right]\right\}\right.\hfill \\ & & \left.+\left\{E^2\left[\frac{1}{\tilde{\eta }}\right]-\frac{2}{\eta }E\left[\frac{1}{\tilde{\eta }}\right]+\frac{1}{{\eta }^2}\right\}\right).\hfill \end{array}$$ (A28)

The first two terms of Eq. A28 depend on the reciprocal of the number of flood fields (1/N_fl), and show that there is a reduction in error as N_fl is increased. The last three terms describe the effects of the bias only.

APPENDIX B: EQUIVALENCE OF ISOTROPIC AND MIE SCATTERING MODELS FOR GOS

Here, we show the functional equivalence of the isotropic scattering model of Kirkby and Sloboda²⁵ and the Mie scattering model of Liaparinos et al.³ The Lanex screen consists of granules of GOS ranging in size from about 5 to 9 μm that are suspended in a polyurethane elastomer with a fill factor of 60%, resulting in a composite density of 4.6 g/cm³. This composite layer is 0.29 mm thick and is attached to an elastomer support layer containing embedded TiO₂ particles to reflect light with a probability of 0.88.²⁷, ³⁴

Liaparinos³ has shown that the transport of light in the GOS composite can be modeled using Mie scattering, which is based on solving the Maxwell equations for particles whose sizes are somewhat larger than the wavelength of light. GEANT4 has a Mie scattering class, which can be initialized through the definition of four parameters, MIEHG, MIEHG FORWARD, MIEHG BACKWARD, and MIEHG FORWARD RATIO. The parameter MIEHG is the scattering length (mm), and the remaining parameters characterize the distribution of scatter in the forward and backward direction. The underlying theory for the GEANT4 implementation is based on the Henyey-Greenstein (HG) distribution, details of which can be found in the work of Liaparinos et al.,³ and Poludniowski and Evans.²⁷

The above inputs to GEANT4 can be calculated using the HG distribution with knowledge of the particle and binder complex refractive indices, as well as the particle grain diameter. In their work on modeling of the closely related Kodak Min-R screens, Liaparinos et al.³ used a complex refractive index equal to 2.3-i 10⁶ for the GOS particles with diameter of 7 μm, and real refractive index of 1.35 for the binder. Use of these parameters results in values of 0.00367 (mm), 0.99, 0, and 0.82 for MIEHG, MIEHG FORWARD MIEHG BACKWARD, and MIEHG FORWARD RATIO, respectively.

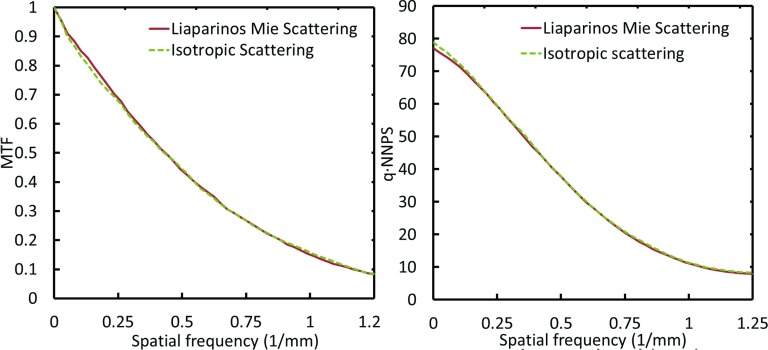
While the Mie scattering model does provide an accurate description of the scattering characteristics for GOS, there is a significant amount of calculation overhead associated with it, largely due to the short scattering lengths (in this case, 3.67 μm). Therefore, we sought to implement an isotropic scattering model yielding identical results to decrease computation time. Isotropic scattering also can be implemented using the Mie class, by using MIEHG as the isotropic scattering length, and setting MIEHG FORWARD and MIEHG BACKWARD to zero, and MIEHG FORWARD RATIO to 1. Through repeated simulations, we identified 17 μm as the optimal isotropic scattering length, consistent with the isotropic scattering model of Kirkby and Sloboda³ as is shown in Fig. 9. The isotropic model runs approximately 3× faster than the Mie model.

Figure 9.

Comparison of AS1000 simulation described in Sec. 2E4a using the Mie scattering parameters of Liaparinos et al. (Ref. ³) and the isotropic scattering model of Kirkby and Sloboda (Ref. ²⁵). The MTF and NPS curves are practically identical. To save simulation time, we opted for the isotropic scattering model of Kirkby and Sloboda (Ref. ³).