Optimal control approach to termination of re-entry waves in cardiac electrophysiology

Abstract

This work proposes an optimal control approach for the termination of re-entry waves in cardiac electrophysiology. The control enters as an extracellular current density into the bidomain equations which are well established model equations in the literature to describe the electrical behavior of the cardiac tissue. The optimal control formulation is inspired, in part, by the dynamical systems behavior of the underlying system of differential equations. Existence of optimal controls is established and the optimality system is derived formally. The numerical realization is described in detail and numerical experiments, which demonstrate the capability of influencing and terminating reentry phenomena, are presented.

1 Introduction

Owing to its importance for computational science and engineering, the field of partial differential equation (PDE) constrained optimization is a frontier problem. One such interesting application is the optimal control of the reaction-diffusion model equations in cardiac electrophysiology. The electrical behavior of the cardiac tissue is described by a system consisting of partial differential equations coupled with ordinary differential equations which model the ionic currents associated with the reaction terms. These are the so called bidomain model equations [14, 30, 39]. Mathematically, as shown in Eqs. (2-4) the bidomain equations can be cast into an elliptic partial differential equation (PDE) that links the distribution of the transmembrane voltage, v, within the tissue to the extracellular potential, u, and a parabolic PDE that describes the cellular activation and recovery processes (reaction term) and the diffusive effect onto the adjacent tissue.

The general form of a PDE-constrained optimal control problem is the following:

$$\left(P\right)\{\begin{array}{c}\min J(v,I_e)\hfill \\ e(u,v,w,I_e)=0\text{in}Q=\Omega \times [0,T]\hfill \end{array}$$ (1)

where u, v and w are the state variables, and I_e is the control variable of the optimal control problem. Here e(u, v, w, I_e) = 0 abbreviates the coupled systems of PDE and ODE constraints consisting of the bidomain equations which are given by

$$0=\nabla \cdot ({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e)\nabla u+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v+\left({\chi }_{{\Omega }_{c_1}}\right(x\left)I_e\right(t)-{\chi }_{{\Omega }_{c_2}}(x\left)I_e\right(t\left)\right)\text{in}Q$$ (2)

$$\frac{\partial v}{\partial t}=\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla u-I_{\text{ion}}(v,w)+I_{\mathit{tr}}(x,t)\text{in}Q$$ (3)

$$\frac{\partial w}{\partial t}=G(v,w)\text{in}Q$$ (4)

where u: Q → ℝ is the extracellular potential, v : Q → ℝ is the transmembrane voltage, w : Q → ℝⁿ represents the ionic current variables, ${\stackrel{‒}{\sigma }}_i:\Omega \to {ℝ}^{d\times d}$ and ${\stackrel{‒}{\sigma }}_e:\Omega \to {ℝ}^{d\times d}$ are respectively the intracellular and extracellular conductivity tensors, I_e(t) represents the time dependent extracellular current density stimulus which has a spatial support as described by the characteristic functions χΩ_c1(x) and χΩ_c2(x) in the computational domain. Further χΩ_c1(x) and χΩ_c2(x) are the characteristic functions where an anode and a cathode are placed. The term I_tr is the transmembrane current density stimulus as delivered by the intracellular electrode. The I_ion(v, w) is the current density flowing through the ionic channels and the function g(v, w) determines the evolution of the gating variables, which are determined by an electrophysiological cell model, see [1] for more description on these models. The above mentioned Eq. (2) is an elliptic type equation, Eq. (3) is a parabolic type equation and Eq. (4) is a set of ordinary differential equations which needs to be resolved in each spatial point of the computational domain. The conductivity tensors are symmetric and to satisfy for constants 0 < m < M

$$m{\mid \xi \mid }^2\le {\xi }^T{\sigma }_{i,e}\xi \le M{\mid \xi \mid }^2\text{for all}\xi \in {ℝ}^d$$ (5)

The ionic activity at the cell membrane is modeled by a ordinary differential equation. In the numerical computations, we used a modified FitzHugh-Nagumo (FHN) model, called Rogers-McCulloch model [34], which consists of only two variables and has a cubic non-linearity.

$$I_{\text{ion}}(v,w)=\mathit{gv}(1-\frac{v}{v_{\mathit{th}}})(1-\frac{v}{v_p})+{\eta }_1\mathit{vw}$$ (6)

$$G(v,w)={\eta }_2(\frac{v}{v_p}-{\eta }_{3}w)$$ (7)

where g, η₁, η₂, η₃ are positive real coeffcients, v_th > 0 is a threshold potential and v_p the peak potential.

In the absence of a conductive bath both intracellular and extracellular domains are electrically isolated along the tissue boundaries and homogeneous Neumann boundary conditions are appropriate to reflect this fact. The initial values of the transmembrane voltage and ion current variables are given by prescribed values. We set ∂Q = ∂Ω × [0, T] and specify the initial and boundary conditions by

$$\eta \cdot ({\stackrel{‒}{\sigma }}_i\nabla v+{\stackrel{‒}{\sigma }}_i\nabla u)=0\text{on}\partial Q$$ (8)

$$\eta \cdot {\stackrel{‒}{\sigma }}_e\nabla u=0\text{on}\partial Q$$ (9)

$$v(x,0)=v_0\text{and}w(x,0)=w_0\text{on}\Omega$$ (10)

where η is the outward unit normal vector to the boundary of the domain, v₀ : Ω → ℝ^d denotes the initial transmembrane potential and w₀ : Ω → ℝ^d is the initial ionic current variables at time t = 0.

Stimulated by the fact that cardiovascular diseases are among the leading causes of death in the industrialized world, the development of models which describe the bioelectric activity of the heart is an area of active research. Under healthy conditions the electrical activation of the heart takes place in a highly organized fashion in order to ensure that the heart effciently fulfills its main function, to pump blood into the circulatory systems. However, disturbances in the formation and/or propagation of electrical impulses may induce reentrant activation patterns which lead to a noticeable increase in the heart’s activation rate. Ultimately, such fast rhythms, referred to as tachycardia’s, may transition to even less organized almost chaotic activation patterns, an electrical state which is termed fibrillation. Under such conditions the heart loses its capacity to pump blood and death ensues within minutes. The only reliable therapy to restore a healthy rhythm is the delivery of a strong electrical shock. This therapy is referred to as electrical defibrillation and is nowadays reliably achieved in a large patient population via the implantation of devices, so-called implantable cardioverters defibrillators (ICD), which monitor the heart rate and, if needed, deliver a discharge to restore a normal rhythm.

Although ICD therapy has proved to be efficient and reliable in preventing sudden cardiac death [4], it is far from ideal. There are several known adverse effects secondary to the administration of electrical shocks, the most prominent are linked to electroporation [12], (i.e. the formation of pores in the cellular membrane that allow the free and indiscriminate redistribution of ions, enzymes and large molecules between intracellular and interstitial space), and its after-effects which are indirectly caused by the high field strengths required to terminate fibrillatory activity with suffciently high probability. More importantly, psychological effects on patients play a non-negligible role. Conscious patients may perceive shock delivery as extremely painful which leads to traumatization and reduction in quality of life. The link between the high shock strengths required and adverse effects provides the motivation for posing the defibrillation process as an optimization problem, as stated in Eq.(1), where one aims to achieve defibrillation with minimal energy and, consequently, with minimal detrimental side effects.

The optimal control approach to cardiac arrhythmias is to determine an applied electrical field in such a way that it optimizes a given design objective, which is, in our case, the restoration of a tissue state in which fibrillatory propagation cannot be maintained. This can be achieved by driving the whole tissue to a resting state, or equivalently, to an excited state. In both cases the main ingredients for maintaining fibrillation, namely the presence of both propagating wavefronts and a suffcient mass of excitable tissue at rest, referred to as “excitable gap”, in which these wavefronts can travel, are missing. Achieving these objectives is challenging since, on biophysical grounds, shock-induced changes in polarization of both polarities are always present during shock delivery.

The numerical results for optimal control of the monodomain model, which is a simplified version of the bidomain model, were presented by the authors in previous articles, see [22, 23]. There it was assumed that both electrodes are of the same polarity in the control regions. Here we consider a more realistic scenario based on a full bidomain model where defibrillation electrodes are modeled to be of opposite polarities. That is, one electrode induces positive polarizations (cathodal stimulus) and another electrode induces negative polarizations (anodal stimulus). By considering these different polarities the compatibility condition, which is required for the elliptic system, can be satisfied if one ensures that the total current injected at the cathodal electrode and current withdrawn at the anodal electrode match up to zero. An alternative approach can be based on using grounded electrodes. In terms of defibrillation the use of a full-blown bidomain formulation is of utmost importance to properly account for membrane responses to externally applied electric fields in the far-field distant from any stimulating electrodes. As has been shown in previous studies [36, 37], the monodomain equations predict surface polarizations only, but no polarizations of the tissue bulk since the activation function is zero in absence of unequal anisotropy ratios.

In the electrophysiological community, numerous theoretical papers have addressed the defibrillation problem [38]. These studies determine success and failure of defibrillation shocks by constructing vulnerability grids where stimuli of a given fixed pulse shape are delivered while varying the key determinants of shock success and failure, namely strength and coupling interval [2, 17, 28]. That is, an extracellular current stimulus is defined as $I_e={\widehat{I}}_e\cdot s(t-t_c)$ where magnitude ${\widehat{I}}_e$ and coupling interval t_c are varied while the pulse shape s is kept constant. Finally, for each strength a probability over all coupling intervals is computed to determine a dose-response curve. Shocks have to be chosen to cover weak strengths of low success probability up to high strength of high probability, including strengths where shocks succeed for all coupling intervals. This strength is referred to as the upper limit of vulnerability [9]. The optimal control approach to defibrillation, as presented in this study, is quite different. For a given coupling interval t_c, that is, the timing of the onset of shock delivery, both pulse shape s(t) and magnitude ${\widehat{I}}_e$ of the stimulus are the result of the optimization procedure.

The bidomain model equations themselves, which arise as constraint in Eq.(1), pose significant numerical challenge [42]. In our study, we have chosen a finite element method for the spatial discretization. A linearly implicit Runge-Kutta method, which is explained in Section 3, was used for the temporal discretization of the parabolic part. Analogous discretization methods are used for the adjoint equations. To enhance the solution process for the primal equations only, parallelization techniques have been applied successfully [29, 27, 24, 31].

Turning to the optimal control problem, we recall that the optimality system involves the primal as well as the adjoint equations. Each of these two systems has similar complexity and must be solved frequently within any iterative solution process for the optimal control problem. It is therefore most natural to employ parallelization within the solution process for the optimal control problem. In this regard, we parallelized our optimization codes based on the freely available public domain package DUNE [5].

When solving the bidomain equations the question of how to deal with the singularity of the elliptic system has to be addressed. Solvability of the elliptic equation (2) requires that the following compatibility condition holds:

$${\int }_{\Omega }\left({\chi }_{{\Omega }_{c_1}}\right(x\left)I_e\right(t)-{\chi }_{{\Omega }_{c_2}}(x\left)I_e\right(t\left)\right)\mathrm{d}x=0\forall t\in [0,T]$$ (11)

Uniqueness of the elliptic system needs to be addressed as well. In our numerical implementation, we have chosen a stabilized saddle point formulation approach adapted from Bochev and Lehoucq [7].

The organization of the remaining paper is as follows: relevant existence and uniqueness results for the bidomain model will be discussed in next section. In Section 2.2, the optimal control formulation is presented and a formal derivation of the adjoint equations and the first order optimality conditions, which are the basis for numerical solution are provided. The numerical approach to solve the optimality system is explained in Section 3. Finally, in Section 4 the numerical results with several test cases are presented to demonstrate successful defibrillation using an optimal control approach.

Notation

Throughout the paper we use standard notation and denote by Ω the bounded cardiac tissue sample domain in ℝ^d, d = 2 or 3, with Lipschitz boundary ∂Ω and outer normal η. The space-time domain and its boundary are denoted by Q = Ω × (0, T] and ∂Q = ∂Ω × (0, T], respectively. The inner product and norm in L²(Ω) are abbreviated by (·, ·) and |·| or |·|_L², and similarly the inner product and norm on H¹(Ω) are denoted by (·, ·)_H¹ and ||·|| or ||·||_H¹ respectively. Further, we denote by

$$L_0^2\left(\Omega \right)=\left\{u\in L^2\left(\Omega \right):{\int }_{\Omega }u=0\right\}$$

the L²-space of zero-mean functions, and we set H = L²(Ω), and V = H¹(Ω).

2 Analytical background

In this section we provide analytical background on the bidomain equations and the associated optimal control problem.

2.1 Weak solutions

We recall well-posedness of the bidomain equations. Throughout it is assumed that (v₀, w₀) ∈ L²(Ω) × L²(Ω), that (5) is satisfied, and that 2 ≤ p ≤ 6.

Definition 2.1. A triple (u, v, w) ∈ L² (0, T; V) × (L²(0, T; V) ⋂ C(0, T; H) ⋂ L^p(Q)) × C(0, T; H) with v_t ∈ L²(0, T; V*) + L^p′(Q) and w_t ∈ L²(0, T; V*) + L^p′(Q) is called weak solution of (2)-(4), (8)-(10), if for all (φ, ψ, χ) ∈ V × H × V/ℝ as well as for all a.e. t ∈ (0, T)

$${\int }_{\Omega }{\sigma }_i\nabla v\left(t\right)\nabla \phi \mathit{dx}+{\int }_{\Omega }({\sigma }_i+{\sigma }_e)\nabla u\left(t\right)\nabla \phi \mathit{dx}={\langle {\chi }_{{\Omega }_{c_1}}{I}_e\left(t\right)-{\chi }_{{\Omega }_{c_2}}{I}_e\left(t\right),\phi \rangle }_{V^{\ast },V}$$ (12)

$${\langle v_t\left(t\right),\psi \rangle }_{V^{\ast },V}+{\int }_{\Omega }{\sigma }_i\nabla \left(u\right(t)+v(t\left)\right)\nabla \psi \mathit{dx}+{\int }_{\Omega }{I}_{\mathit{ion}}\left(v\right(t),w(t\left)\right)\psi \mathit{dx}={\langle I_{\mathit{tr}}\left(t\right),\psi \rangle }_{V^{\ast },V}$$ (13)

$${\langle w_t\left(t\right),\chi \rangle }_{V^{\ast },V}-{\int }_{\Omega }G\left(v\right(t),w(t\left)\right)\chi \mathit{dx}=0$$ (14)

where V* denotes the dual to V with H as pivot space and $\frac{1}{p}+\frac{1}{p^{\prime }}=1$.

Theorem 2.2. (Existence, uniqueness, a-priori estimates of weak solutions) For any T > 0 there exists a weak solution to the bidomain system (2)-(4), (8)-(10) and we have the a-priori estimate​

$$\begin{gathered} {\mid (u,v,w)\mid }_X+{\mid v\mid }_{L^p\left(Q\right)}^{p∕2}+{\mid v_t\mid }_{L^{p^{\prime }}\left(V^{\ast }\right)}^{p^{\prime }∕2} \\ \le C(1+{\mid v_0\mid }_{L^2\left(\Omega \right)}+{\mid w_0\mid }_{L^2\left(\Omega \right)}+{\mid I_e\mid }_{L^2\left(ℝ\right)}+{\mid I_{\mathit{tr}}\mid }_{L^2\left(Q\right)}) \end{gathered}$$ (15)

Here |·|_X denotes the norm in $L^2\left(V\right)\times \left(L^2\right(V)\cap C(H\left)\right)\times \left(C\right(H)\cap W^{1,2}(H\left)\right)$, the dependence of the spaces on the temporal interval (0, T ) is suppressed and C is independent of (v₀, w₀, I_e, I_tr).

If (v₀, w₀) ∈ L²(Ω) × L⁴(Ω) and (I_e, I_tr) ∈ L^∞(0, T; ℝ) × L^∞(0, T; L²(Ω)), then the weak solution is unique.

For the proof we refer to [23], [18].

2.2 The optimal control problem

Here we formulate the optimal control problem. This necessitates the choice of an appropriate cost-functional which is minimized subject to the system of bidomain equations. The control variable consists of the extracellular current which must be chosen in such a manner as to facilitate defibrillation in the best possible way. More precisely we are interested to construct a cost functional which is able to terminate re-entrant arrhythmias by applying an extracellular current as a control. After substantial numerical tests with a variety of different cost functionals we propose the following procedure which is guided by the dynamical behavior of FitzHugh-Nagumo type reaction diffusion systems, see eg. [21, Chapter 7].

Let us divert for a moment and consider the nonlinear system of ordinary differential equations

$$\{\begin{array}{c}\frac{d\tilde{v}}{\mathit{dt}}=-I_{\mathit{ion}}(\tilde{v},\tilde{w})\hfill \\ \frac{d\tilde{w}}{\mathit{dt}}=G(\tilde{v},\tilde{w})\hfill \end{array}$$ (16)

To understand the qualitative behavior of this system we investigate the null isoclines $I_{ion}(\tilde{v},\tilde{w})=0$ and $G(\tilde{v},\tilde{w})=0$. It is convenient to express

$$I_{\mathit{ion}}(\tilde{v},\tilde{w})=\tilde{v}f(\tilde{v},\tilde{w}),\text{where}f(\tilde{v},\tilde{w})=g(1-\frac{\tilde{v}}{v_{\mathit{th}}})(1-\frac{\tilde{v}}{v_p})+{\eta }_1\tilde{w}$$

We find that the origin is a stable steady state of the system (16). If the system is perturbed and originates from some $({\tilde{v}}_0,{\tilde{w}}_0)$ satisfying

$${\tilde{w}}_0<-\frac{g}{{\eta }_1}(1-\frac{{\tilde{v}}_0}{v_{\mathit{th}}})(1-\frac{{\tilde{v}}_0}{v_p}),0<{\tilde{v}}_0$$

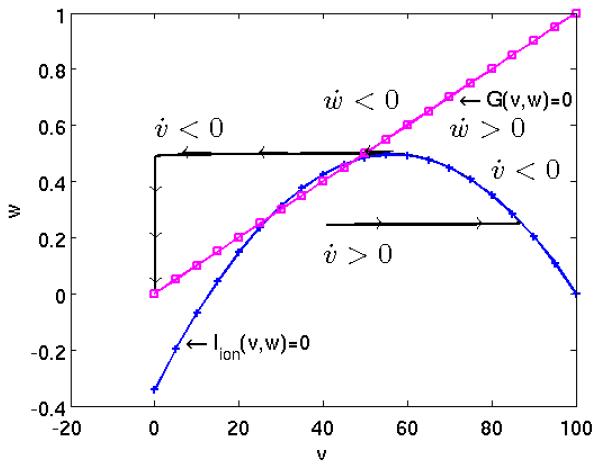
then $\frac{d\tilde{v}\left(t\right)}{dt}>0$ and $\tilde{v}\left(t\right)$ increases until $f\left(\tilde{v}\right(t),\tilde{w}(t\left)\right)=0$. Subsequently $\left(\tilde{v}\right(t),\tilde{w}(t\left)\right)$ decreases and tends to the origin as t → ∞. For typical parameters the speed in the horizontal direction is significantly faster than in the vertical direction, see Figure 1.

Figure 1.

Phase plane portrait of a modified FitzHugh-Nagumo model.

In short, if the system is perturbed above a certain threshold, the trajectory rapidly increases until a plateau is reached, from which it slowly decays and returns to the stable origin. In this consideration we ignored spatial phenomena, but we can think of this behavior taking place at every point x in the spatial domain. The trajectories (indexed by the spatial coordinates x) influence each other, leading to complex phenomena, as, for instance, the formation of virtual electrodes [36]. With this behavior in mind, the optimal control problems which we test in this study correspond to the situation where, assuming that the system was excited locally, we apply extracellular current during an optimization phase with the goal to drive the cardiac tissue in a given observation region into a pre-specified electrical state. In a successful defibrillation episode the whole tissue returns to a stable resting state during the post shock phase which follows the optimal control phase. In this scenario, in a real heart the next following naturally activation, as initiated by the sinus node, or a stimulated activation, as initiated by a cardiac pacemaker, can overtake control over the heart’s rhythm. We refer to Figure 3.

Figure 3.

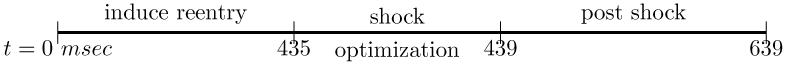
different time horizons considered in the computations.

So the optimal control problem actually refers to the optimal shock phase. During this optimization period, denoted by (0, T), the control aims at driving the transmembrane voltage v to a desired value denoted by v_d. This could be the value at the plateau, or a trajectory related to some non-optimal shock experiment. These considerations result in a term of the form ${\int }_0^T{\int }_{{\Omega }_{obs}}{\mid v-v_d\mid }^2$ in the cost functional, where domain Ω_obs ⊂ Ω denotes the observation region.

Let us next discuss the control variable I_e. We consider the case that the extracellular current I_e(t) depends only on time, with the spatial support specified and fixed by the user. In our simulations, we inject the current through the anode, supported in the subdomain Ω_c1, and withdraw current at the cathode, supported in subdomain Ω_c2. To assure conservation of current the total currents injected and width drawn at the anodal and cathodal electrode, respectively, have to sum up to zero. Since it is desirable to keep the R amount of the applied extracellular current small it is natural that a term of the form ${\int }_0^T\mid I_e\left(t\right)\mid dt$ enters the cost functional.

All together this results in the following optimal control problem:

$$\{\begin{array}{c}\min J(v,I_e)=\frac{1}{2}{\int }_0^T\left({\int }_{{\Omega }_{\mathit{obs}}}{\mid v-v_d\mid }^2\mathit{dx}+2\alpha \mid {\Omega }_{c_1}\mid {\mid I_e\left(t\right)\mid }^2\right)\mathit{dt}\hfill \\ \text{subject to}\left(2\right)-\left(4\right),\left(8\right)-\left(10\right)\text{and}{I}_e\in U\hfill \end{array}$$ (17)

Above α is the weight of the cost of the control and

$$U=\{I_e\in L^2(0,T;ℝ)\mid \mid I_e\left(t\right)\mid \le M\text{for}a.e.t\in (0,T)\}$$ (18)

for some M ∈ (0, ∞).Utilizing a pointwise norm bound on I_e is one of the possibilities to ascertain uniqueness of the solutions to the bidomain system. It can also be physiologically relevant, since it has a differently effect on the solution than the term ${\int }_0^T{\mid I_e\mid }^{2}dt$ which appears in the cost-functional. An alternative to guarantee uniqueness involves structural assumptions on the conductivity tensor, [8].

Theorem 2.3 (Existence of global minimizers). The problem of minimizing J subject to the bidomain system, i.e. problem (17), admits a global minimizer $(\tilde{u},\tilde{v},\tilde{w},{\tilde{I}}_e)$.

Proof. The proof of the theorem is given in appendix A. ∎

2.3 First order necessary optimality system

In this section we formally derive the optimality system associated to (17). We follow a Lagrangian approach and introduce the Lagrange functional

$$\begin{array}{c}\mathcal{L}(u,v,w,I_e,p,q,r)=J(v,I_e)\hfill \\ +{\int }_0^T{\int }_{\Omega }(\nabla \cdot ({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e)\nabla u+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v+({\chi }_{{\Omega }_{c_1}}\left(x\right)I_e\left(t\right)-{\chi }_{{\Omega }_{c_2}}\left(x\right)I_e\left(t\right)\left)\right)p\mathit{dx}\mathit{dt}\hfill \\ +{\int }_0^T{\int }_{\Omega }(-\frac{\partial v}{\partial t}+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla u+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v-I_{\mathit{ion}}(v,w)+I_{\mathit{tr}})q\mathit{dx}\mathit{dt}\hfill \\ +{\int }_0^T{\int }_{\Omega }(-\frac{\partial w}{\partial t}+G(v,w\left)\right)r\mathit{dx}\mathit{dt}\hfill \end{array}$$

The first order optimality system is given by the Karusch-Kuhn-Tucker (KKT) conditions. For this purpose the partial derivatives of $\mathcal{L}$ with respect to u, v and w are set equal to zero:

$$\nabla \cdot ({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e)\nabla p+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla q=0$$ (19)

$$(v-v_d)\mid {\Omega }_{\mathit{obs}}+\frac{\partial q}{\partial t}+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla p+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla q-\left(I_{\mathit{ion}}\right){}_{v}q+{\left(G\right)}_{v}r=0$$ (20)

$$-{\left(I_{\mathit{ion}}\right)}_{w}q+\frac{\partial r}{\partial t}+{\left(G\right)}_w^T(v,w)r=0$$ (21)

where p, q and r are the Lagrange multipliers associated to u, v and w respectively. The terminal conditions are

$$q\left(T\right)=0,r\left(T\right)=0,$$

and the boundary conditions for the adjoint states must satisfy

$$({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e)\nabla p\cdot \eta =0\text{on}\partial Q$$ (22)

$${\stackrel{‒}{\sigma }}_i\nabla q\cdot \eta =0\text{on}\partial Q$$ (23)

In addition the zero mean condition ${\int }_{\Omega }p\left(t\right)dx=0$ holds for all t ∈ (0, T). Finally we have the optimality condition:

$$\left(2\mid {\Omega }_{c_1}\mid \alpha I_e^{\ast }\left(t\right)+{\int }_{{\Omega }_{c_1}}p(x,t)\mathit{dx}-{\int }_{{\Omega }_{c_2}}p(x,t)\mathit{dx}\right)\left(I_e\right(t)-I_e^{\ast }(t\left)\right)\ge 0\text{for all}{I}_e\in U$$ (24)

for almost every t ∈ (0, T ), which, in case the constraints are not active becomes

$$2\mid {\Omega }_{c_1}\mid \alpha I_e^{\ast }\left(t\right)+{\int }_{{\Omega }_{c_1}}p(x,t)\mathit{dx}-{\int }_{{\Omega }_{c_2}}p(x,t)\mathit{dx}=0,\text{for}a.e.t\in (0,T)$$ (25)

3 Numerical approach

In this section we give a brief overview of the space and time discretization techniques to solve the primal and adjoint equations numerically. In spite of the fact that the solution is smooth this poses challenging numerical problems due to complicated underlying wave phenomena which put restrictions on spatial and temporal scales. In our numerical simulations we used a finite element method for the spatial discretization and linearly implicit Runge-Kutta methods for the temporal discretization.

3.1 Semi-discretization in space

In this subsection we give an overview of the spatial discretization of the primal and dual equations by a finite element method based the weak formulation which we recall for the readers convenience.

3.1.1 Space discretization of the primal problem

A weak solution triple (u, v, w) satisfies for a.e. t ∈ (0, T )

$$\langle \frac{\partial v}{\partial t},\phi \rangle =\langle \nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla u-I_{\mathit{ion}}(v,w)+I_{\mathit{tr}}(x,t),\phi \rangle$$ (26)

$$0=\langle \nabla \cdot ({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e)\nabla u+\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v+\left({\chi }_{{\Omega }_{c_1}}\right(x\left)I_e\right(t)-{\chi }_{{\Omega }_{c_2}}(x\left)I_e\right(t\left)\right),\phi \rangle$$ (27)

$$\langle \frac{\partial w}{\partial t},\phi \rangle =\langle G(v,w),\phi \rangle \text{for all}\phi \in H^1\left(\Omega \right)$$ (28)

together with initial and boundary conditions (8)-(10). Let V_h ⊂ H¹(Ω) be the finite dimensional subspace of piecewise linear basis functions with respect to the spatial grid. The approximate solutions u; v and w are expressed in the form $\mathbf{u}\left(t\right)={\Sigma }_{i=0}^N{u}_i\left(t\right){\omega }_i$, $\mathbf{v}\left(t\right)={\Sigma }_{i=0}^N{v}_i\left(t\right){\omega }_i$ and $\mathbf{w}\left(t\right)={\Sigma }_{i=0}^n{w}_i\left(t\right){\omega }_i$, respectively, where ${\left\{{\omega }_i\right\}}_{i=1}^N$ denote the basis functions. This semi-discretization in space results in the differential algebraic system:

$${\mathbf{A}}_{\mathbf{ie}}\mathbf{u}+{\mathbf{A}}_{\mathbf{i}}\mathbf{v}={\mathbf{I}}_e$$ (29)

$$\mathbf{M}\frac{\partial \mathbf{v}}{\partial t}=-{\mathbf{A}}_{\mathbf{i}}\mathbf{v}-{\mathbf{A}}_{\mathbf{i}}\mathbf{u}-{\mathbf{I}}_{\mathit{ion}}(\mathbf{v},\mathbf{w})+{\mathbf{I}}_{\mathit{tr}}$$ (30)

$$\frac{\partial \mathbf{w}}{\partial t}=\mathbf{G}(\mathbf{v},\mathbf{w})$$ (31)

together with initial conditions for v and w, where ${\mathbf{A}}_{\mathrm{ie}}={\{\langle ({\sigma }_i+{\sigma }_e)\nabla {\omega }_i,\nabla {\omega }_j\rangle \}}_{i,j=1}^N$ and ${\mathbf{A}}_i={\{\langle {\sigma }_i\nabla {\omega }_i,\nabla {\omega }_j\rangle \}}_{i,j=1}^N$ are the stiffness matrices, $\mathbf{M}={\{\langle {\omega }_i,{\omega }_j\rangle \}}_{j=1}^N$ is the mass matrix, the vectors I_e, I_itr are defined by ${\mathbf{I}}_e={\{\langle (\chi {\Omega }_{c_1}{I}_e-{{\chi }_{\Omega }}_{c_2}{I}_e),{\omega }_j\rangle \}}_{j=1}^N$ and ${\mathbf{I}}_{tr}={\{\langle I_{tr},{\omega }_j\rangle \}}_{j=1}^N$, respectively. The expression (I_ion)(v,w) is defined by

$$\left({\mathbf{I}}_{\mathit{ion}}\right)(\mathbf{v},\mathbf{w})=\left({\mathbf{I}}_{\mathit{ion}}\right)\left(\sum _{i=0}^N{v}_i{w}_i,\sum _{i=0}^N{w}_i{w}_i\right)$$

3.1.2 Space discretization of the dual problem

We use the same finite element space to discretize the dual equations. Here the approximate solutions p, q, and r can be expressed in the form $\mathbf{p}\left(t\right)={\Sigma }_{i=0}^N{p}_i\left(t\right){\omega }_i$, $\mathbf{q}\left(t\right)={\Sigma }_{i=0}^N{q}_i\left(t\right){\omega }_i$ and $\mathbf{r}\left(t\right)={\Sigma }_{i=0}^N{r}_i\left(t\right){\omega }_i$ respectively and the following semi discrete form of the dual equations is obtained:

$${\mathbf{A}}_{\mathbf{ie}}\mathbf{p}+{\mathbf{A}}_{\mathbf{i}}\mathbf{q}=0$$ (32)

$$\mathbf{M}\frac{\partial \mathbf{q}}{\partial t}={\mathbf{A}}_{\mathbf{i}}\mathbf{p}+{\mathbf{A}}_{\mathbf{i}}\mathbf{q}+{\left({\mathbf{I}}_{\mathit{ion}}\right)}_{\mathbf{v}}(\mathbf{v},\mathbf{w})-\frac{{\eta }_2}{u_p}\mathbf{Mr}-{\mathbf{M}}_{\mathit{obs}}(\mathbf{v}-{\mathbf{v}}_d)$$ (33)

$$\frac{\partial \mathbf{r}}{\partial t}={\eta }_2{\eta }_3\mathbf{r}+{\left({\mathbf{I}}_{\mathit{ion}}\right)}_{\mathbf{w}}{(\mathbf{v},\mathbf{w})}_{\mathbf{p}}$$ (34)

with terminal conditions q(T ) = 0, r(T) = 0. The locally defined mass matrix for the observation domain is ${\mathbf{M}}_{obs}={\{\langle {\omega }_i,\chi {\Omega }_{obs}{\omega }_j\rangle \}}_{i,j=1}^N$. The expressions (I_ion)_v(v, w) and (I_ion)_w(v, w) are defined by

$$\begin{gathered} {\left({\mathbf{I}}_{\mathit{ion}}\right)}_{\mathbf{v}}(\mathbf{v},\mathbf{w})=\frac{\partial \left({\mathbf{I}}_{\mathit{ion}}\right)}{\partial v}\left(\sum _{i=0}^N{v}_i{w}_i,\sum _{i=0}^N{w}_i{w}_i\right) \\ {\left({\mathbf{I}}_{\mathit{ion}}\right)}_{\mathbf{w}}(\mathbf{v},\mathbf{w})={\eta }_1\left(\sum _{i=0}^N{v}_i{w}_i\right) \end{gathered}$$

Remark 3.1. The iterative linear solver to obtain the current solution for (29) is initialized by the solution of the previous time-level. Here we make use of the fact that u₀ has zero mean. Then the compatibility condition for the singular algebraic system Eq. (29) is satisfied at each iteration level, i.e.

$${\mathbf{c}}^T(-{\mathbf{A}}_{\mathbf{i}}\mathbf{v}-{\mathbf{I}}_e)=-{\left({\mathbf{c}}^T{\mathbf{A}}_{\mathbf{i}}\right)}_{\mathbf{v}}-{\mathbf{c}}^T{\mathbf{I}}_e=0$$

where c = (1, …, 1)^T is a constant vector. Analogously, at every time-level the iterative procedure for solving (32) is initialized by a zero-mean function. Then the compatibility condition for the singular algebraic system (32) is satisfied.

3.1.3 Solving the singular linear system

The linear systems (29) and (32) are singular since the solution is only defined up to an additive constant. There are mainly two approaches to compute finite element solutions for such systems. One approach is to specify a solution datum at a particular node or in some sub region of the computational domain. The other approach is to compute a consistent singular system either by a properly modified direct procedure that recognizes zero pivots¹ or by a minimization-based iterative solvers such as the Lagrange multiplier method and a mixed formulation, see [7] for a more detailed discussion.

In our computations we adapted a stabilized saddle-point formulation from the Bochev and Lehoucq [7] to solve the elliptic system uniquely. For this purpose let ω be a smooth function satisfying (1, ω) ≥ 0 and introduce the space

$$H_w^1\left(\Omega \right)=\{u\in H^1(\Omega ):(u,\omega )=0\}$$

Also, define the orthonormal ω-mean of u by

$$u_{\omega }=\frac{(u,\omega )}{(1,\omega )}$$

Then the energy functional associated to equation (2) at any fixed t ∈ (0, T) can be expressed as: find the minimum over V of

$$\begin{gathered} F\left(u\right)=\frac{1}{2}{a}_e(u,u)-{\int }_{\Omega }\mathit{bu}\mathit{dx} \\ \text{subject to the constraint}{u}_{\omega }=0 \end{gathered}$$ (35)

where $b=\nabla \cdot {\stackrel{‒}{\sigma }}_i\nabla v(\cdot ,t)+\left({\chi }_{{\Omega }_{c_1}}{I}_e\right(t)-{\chi }_{{\Omega }_{c_2}}{I}_e(t\left)\right)$ and $a_e(u,\varphi )={\int }_{\Omega }({\stackrel{‒}{\sigma }}_i+{\stackrel{‒}{\sigma }}_e){\nabla }_u\cdot \nabla \varphi \mathrm{d}x$.

Using the stabilized saddle point approach from Bochev and Lehoucq, the unconstrained minimization of the penalized energy functional is expressed as,

$$\underset{u\in V}{\min }\left(F\left(u\right)+\frac{\rho }{2}{u}_{\omega }^2\right)$$ (36)

where ρ > 0 is a stabilizing parameter. The optimality system for (36) is given by

$$a_e(u,v)-{\int }_{\Omega }\mathit{bv}\mathrm{d}x+\rho u_{\omega }{v}_{\omega }=0\text{for all}v\in V$$ (37)

Lemma 3.2. Problem (36) or equivalently (37) has a unique solution u ∈ V for each b ∈ H.

The proof is a direct consequence from [7, Theorem 4.2, page 55]. Here the requirement b ∈ H necessitates that v is a strong, rather than a weak solution. This can be guaranteed by additional assumptions on the problem data, [18]. After the finite element discretization for (36) with basis functions {φ_i} the finite dimensional system can be expressed as follows

$${\tilde{\mathbf{A}}}_{\mathbf{ie}}\mathbf{u}=\left({\mathbf{A}}_{\mathbf{ie}}+\frac{\rho }{{\left({\Phi }^T\mathbf{c}\right)}^2}\Phi {\Phi }^T\right)\mathbf{u}=\mathbf{b}$$ (38)

where A_ie is the stiffness matrix and Φ = (φ_i, ω) is the weighted basis mean vector. Since $\frac{1}{2}{a}_e(u,u)+\frac{\rho }{2}{u}_{\omega }^2$ is positive definite on V it follows that ${\tilde{\mathbf{A}}}_{\mathrm{ie}}$ is positive definite on ℝ^N. The kernel of A_ie is spanned by the constant vector c = (1, …, 1)^T. The weighted zero mean property of elements v ∈ ℝ^N is described by Φ^Tv = 0. Moreover, A_ieu = b admits a unique solution u* with w^Tu* = 0, provided that w^Tb = 0.

We assume that $\Sigma {\varphi }_i\left(x\right)=1$, for almost every x ∈ Ω. Then

$${\mathbf{c}}^T\Phi =\sum ({\varphi }_i,w)=(1,\mathbf{w})\ge 0\text{and}{\mathbf{c}}^T\mathbf{b}=\sum (b,{\varphi }_i)=(\mathbf{b},1)=0$$

Proposition 3.3. Let $\tilde{\mathbf{u}}$ and u* be the solutions to (38) and A_ieu = b, with Φ^Tu = 0 respectively. Then ${\mathbf{\Phi }}^T\tilde{\mathbf{u}}=0$ and $\tilde{\mathbf{u}}={\mathbf{u}}^{\ast }$.

Proof. Taking the inner product of (38) with c we find that

$${\mathbf{c}}^T{\tilde{\mathbf{A}}}_{\mathit{ie}}\tilde{\mathbf{u}}={\mathbf{c}}^T{\mathbf{A}}_{\mathbf{ie}}\tilde{\mathbf{u}}+\frac{\rho }{{\left({\Phi }^T\mathbf{c}\right)}^2}{\mathbf{c}}^T\Phi {\Phi }^T\tilde{\mathbf{u}}=\frac{\rho }{{\left({\Phi }^T\mathbf{c}\right)}^2}{\mathbf{c}}^T\Phi {\Phi }^T\tilde{\mathbf{u}}=0$$

Since c^TΦ ≠ 0 this implies that ${\Phi }^T\tilde{\mathbf{u}}=0$. Moreover

$${\tilde{\mathbf{A}}}_{\mathit{ie}}\tilde{\mathbf{u}}={\mathbf{A}}_{\mathbf{ie}}\tilde{\mathbf{u}}=\mathbf{b}$$

Since the solution to A_ieu = b with Φ^Tu = 0 is unique we have $\tilde{\mathbf{u}}={\mathbf{u}}^{\ast }$, as desired. ∎

3.2 Time discretization

Now we will turn our discussion to the time discretization for the Eqs. (30) and (33). Those two equations can be expressed in the following general form,

$$\mathbf{M}\frac{\partial \mathrm{x}}{\partial t}=\mathbf{F}\left(\mathrm{x}\right),\mathbf{x}\left(t^0\right)={\mathrm{x}}^0$$ (39)

To solve (39), we introduce discrete steps:

$$0=t^0,t^1,\dots ,t^n=T$$

which are not necessarily equidistant. We further set τⁱ = tⁱ⁺¹ − tⁱ and denote by uⁱ the numerical solution at time tⁱ. For time discretization linearly-implicit Runge-Kutta methods, specifically Rosenbrock methods, are used. These belong to a large class of methods which try to avoid the nonlinear system and replace it by a sequence of linear ones. An s-stage Rosenbrock method of order p with embedding of order $\widehat{p}\ne p$ has the form

$$(\frac{1}{{\tau }^i\gamma }\mathbf{M}-\mathbf{K}){\mathbf{k}}_j=\mathbf{F}(t^i+{\tau }^i{\alpha }_j,{\mathrm{x}}^i+\sum _{l=1}^{j-1}{a}_{\mathit{jl}}{\mathbf{k}}_l)-\mathbf{M}\sum _{l=1}^{j-1}\frac{c_{\mathit{lj}}}{{\tau }^i}{\mathbf{k}}_{l}j=1,\dots ,s$$ (40)

$${\mathrm{x}}^{i+1}={\mathrm{x}}^i+\sum _{l=1}^s{m}_l{\mathbf{k}}_l$$ (41)

$${\widehat{\mathrm{x}}}^{i+1}={\mathrm{x}}^i+\sum _{l=1}^s{\widehat{m}}_l{\mathbf{k}}_l.$$ (42)

The coefficients γ, α_j, a_jl, c_jl, m_l, and ${\widehat{m}}_l$ are chosen in such a way that certain consistency order conditions are fulfilled to obtain a sufficiently high convergence order. For the construction of the Jacobian matrix K we used exact derivatives of the vector F(x). We assume that $p>\widehat{p}$ which is reasonable since one would prefer to continue the integration with the higher order solution x. In our computations the ROS3PL method, see [20], is implemented to solve the primal and adjoint equations. It has four internal stages, it is third order accurate, it satisfies the L-stability property and has no order reduction in the PDE case. After time discretization one ends up with a system of linear equations which needs to be solved by effcient iterative solvers. Here we use the BiCGSTAB [40] method with SSOR preconditioning.

During every iteration of the optimization algorithm we used uniform time steps to solve the primal and adjoint equations. For the post-shock simulations, however, adaptive time steps were used to speed up the direct simulations. These adaptive time steps were constructed by using the second solution ${\widehat{\mathrm{x}}}^{i+1}$ to compute a local temporal error between different orders of solutions. In the ROS3PL method the order of the second solution is $\widehat{p}=2$, see [20]. After the i-th integration step the value ${∊}^{i+1}=\mid \mid {\mathrm{x}}^{i+1}-{\widehat{\mathrm{x}}}^{i+1}\mid \mid$ is taken as an estimator of the local temporal error. In computations a new time step τ_new, see Gustafsson et al. [13], calculated on the basis of

$$\stackrel{‒}{\tau }≔\beta {\tau }^i{\left(\frac{TO{L}_t}{{∊}^{i+1}}\right)}^{\frac{1}{2}},{\tau }_{\text{new}}=\{\begin{array}{cc}{\beta }_{\max }{\tau }^i\hfill & \stackrel{‒}{\tau }>{\beta }_{\max }{\tau }^i\hfill \\ {\beta }_{\min }{\tau }^i\hfill & \stackrel{‒}{\tau }<{\beta }_{\min }{\tau }^i\hfill \\ \stackrel{‒}{\tau }\hfill & \text{otherwise}\hfill \end{array}$$ (43)

The parameter β > 0 is a safety factor. The factors β_min and β_max restrict the time step jumps. If εⁱ⁺¹ < TOL_t we proceed to the next time step, otherwise the time step has to be shortened and repeated. We set TOL_t = 0.001 in our computations.

3.3 Solving the complete linear system

In this subsection we give a step by step procedure to solve the full optimality system. First we describe the solution of primal system by decoupling the system as follows.

• S1: Use the solution at vⁱ, solve the ODE equation (31) for wⁱ⁺¹ by using the explicit Euler method.

• S2: Use the solution at vⁱ, solve the discretized elliptic system (29) for uⁱ⁺¹ by using the stabilized saddle point approach which is explained in subsection 3.1.3.

• S3: Finally, by utilizing the computed solutions uⁱ⁺¹ and wⁱ⁺¹, solve the discretized parabolic equation (30) for vⁱ⁺¹ by applying the linearly implicit Runge-Kutta method which is explained in subsection 3.2.

Analogously, solve the discretized adjoint system, backward in time, by decoupling the system as follows.

• D1: Using the solutions at pⁱ⁺¹ and rⁱ⁺¹, solve the discretized parabolic equation (33) for qⁱ by employing the linearly implicit Runge-Kutta method which is explained in subsection 3.2.

• D2: Using the solution at qⁱ, solve the discretized elliptic system (32) for pⁱ by adopting the stabilized saddle point approach which is explained in subsection 3.1.3.

• D3: Utilizing the solution at qⁱ, solve the ODE equation (34) for rⁱ by using the explicit Euler method.

Now we turn to the solution of the complete optimality system. To solve the discretized minimization problem, the nonlinear conjugate gradient method is used; we refer to [25] for details. The termination of the optimization algorithm is based on the following condition.

$${\Vert \nabla J\left({\mathbf{I}}_e^k\right)\Vert }_{L^2}\le {10}^{-3}\cdot \mid J\left({\mathbf{I}}_e^k\right)\mid \text{or}\mid J\left({\mathbf{I}}_e^k\right)-J\left({\mathbf{I}}_e^{k-1}\right)\mid \le {10}^{-4}$$ (44)

Next we summarize the optimization algorithm procedure that we utilize for the computational results that we present below.

• A1: Guess initial control ${\mathbf{I}}_e^k$ and set k ← 1

• A2: Solve the primal equations (2)-(4) for u^k, v^k and w^k forward in time as explained in above steps (S1)-(S3) using ${\mathbf{I}}_e^k$.

• A3: By utilizing the available solutions u^k, v^k and w^k solve the dual equations (19)-(21) backward in time as explained in steps (D1)-(D3).

• A4: Compute the gradient of the reduced cost functional $\nabla J\left({\mathbf{I}}_e^k\right)$ and update the control ${\mathbf{I}}_e^{k+1}$ using Hager-Zhang update, see [25, page no. 123, Eq.(5.50)] for more details.

• A5: If the termination criteria Eq. (44) is not satisfied, then update ${\mathbf{I}}_e^k\leftarrow {\mathbf{I}}_e^{k+1}$ and k ← k + 1 and continue with step A2.

In our optimization algorithm, the line search method is based on the Wolfe conditions, see for more details [25, page no. 33].

3.4 Parallel implementation

Recent research work on parallel tools and high performance computing for the bidomain equations is devoted to modeling techniques which can accommodate the anatomically complex geometries of the heart [32] and, at the same time, can handle such fine scale spatio-temporal simulations with suffcient effciency, see e.g. [29, 41, 26, 24, 38, 31]. In the context of optimal control of the bidomain equations the necessity of repeatedly solving the coupled forward-backwards systems of primal and adjoint equations for possibly very different inputs representing the controls, calls for using a parallel implementation, which in our case is combined with a nonlinear conjugate gradient algorithm for solving the optimal control problem.

The essence of parallel numerical simulation is to distribute the computational load evenly across all processors which is mainly achieved by domain decomposition algorithms. In our simulations we used the software package DUNE [5], which is a C++ template based programming environment for solving a general class of PDE’s. The internal parallel Yasp grid in DUNE is used for parallel grid constructions. It supports various levels of overlapping grids for parallel simulations. We used a zero level of overlapping grids, particularly non overlapping grids. For the domain decomposition technique the original domain is partitioned into subdomains and each subdomain is assigned to a single processor. On each subproblem a reduced size problem, which is coupled to adjacent problems along interface boundaries, is solved. The interface coupling can be relaxed at the expense of introducing additional communication in the solution of the algebraic system which is obtained after space and time discretization.

To solve the discretized optimality system, a variant of the non-linear conjugate gradient (NCG) method based on the Hager-Zhang update [25, page 123] is implemented. For each time step in every iteration of the linear solver we need additional communication to solve the primal and adjoint equations, which, in turn, is needed in every iteration of the optimization algorithm. Also, we need additional communication for the evaluation of the norm of the gradient of the cost functional as well as for the cost itself. Our spatial discretization routine code makes strong use of the DUNE package [5], especially the dune-pdelab discretization module.

4 Numerical Results

In this section numerical results on the basis of three different test cases are presented. In all cases the computational domain Ω = [0, 2] × [0, 2] ∈ ℝ² of size 2 * 2 cm² is fixed and a 128 × 128 uniform quadrilateral spatial grid is used. During the shock we fix the time step length Δt = 0.04 msec, while we allow adaptive time stepping criteria for the ROS3PL method during the post shock simulations to speed up the calculations.

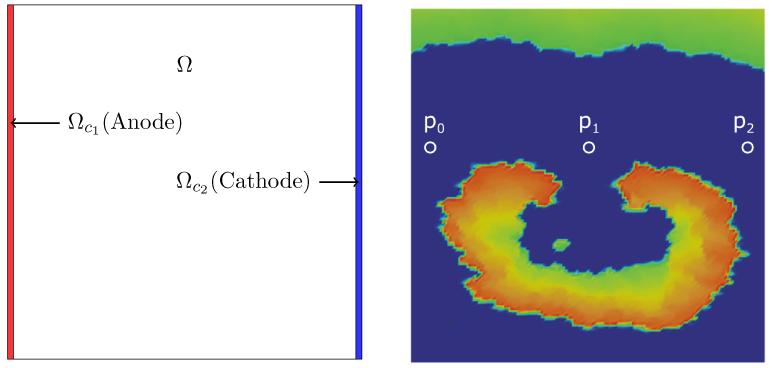
The computational domain and relevant subdomains are depicted in left Figure 2. The control domains are chosen to be Ω_c1 = [0, 0] × [0.03, 2] of size 0.03 * 2 cm² and Ω_c2 = [1.97, 0] × [2, 2] of size 0.03 * 2 cm².

Figure 2.

Computational domain with stimulation domains (left panel) and the initial state of v at the onset of the shock (right panel). Selected observation sites are located at p₀ = (0.078125, 1.20312) near near to anode, p₁ = (1.078125, 1.20312) in the middle of the domain, and p₂ = (1.92188, 1.20312) near the cathode.

To induce the reentry we a standard S₁ − S2 stimulation protocol: First, we applied an initial stimulus S1 of I_tr = 100 μA/cm² at time t = 0 msec for a duration of 5 msec along the bottom edge of the tissue sheet to induce a planar wavefront traveling towards the top edge of the sheet. At time t = 183 msec, when the critical recovery isoline arrived at the center of the sheet, a second S2 stimulus of I_tr = 100 μA/cm² was applied in a small region of 0.3 cm radius at the center of the domain for a duration of 5 msec. This S2 stimulus generated two phase singularities at the intersections between critical recovery isoline with the boundary of the S2 stimulus region, leading to a so-called Figure of Eight reentrant pattern. Direct simulation was continued until time t = 435 msec to ensure that the induced reentry is maintained for prolonged periods of time. The solution at t = 435 msec was then chosen as the initial state for our numerical study, see Figure 3 for the three temporal horizons.

Conductivities were chosen to arrive at physiological conduction velocities with the FitzHugh-Nagumo model and to keep anisotropy ratios within the range of values reported in experimental studies [35]. For the control case under healthy conditions conduction velocities of 0.65 m/s and 0.325 m/s were assumed in the longitudinal and transverse directions, respectively, with an anisotropy ratio of 4.18. These considerations led to the following choice of simulation parameters, σ_il = 2.0 · 10⁻³ S/cm, σ_it = 3.1 · 10⁻⁴ S/cm, σ_el = 2.0 × 10⁻³ S/cm, σ_et = 1.3 · 10⁻³ S/cm g = 1.5 S/cm², v_th = 13 mV, v_p = 100 mV, η₁ = 4.4 S/cm², η₂ = 0.012; η₃ = 1.

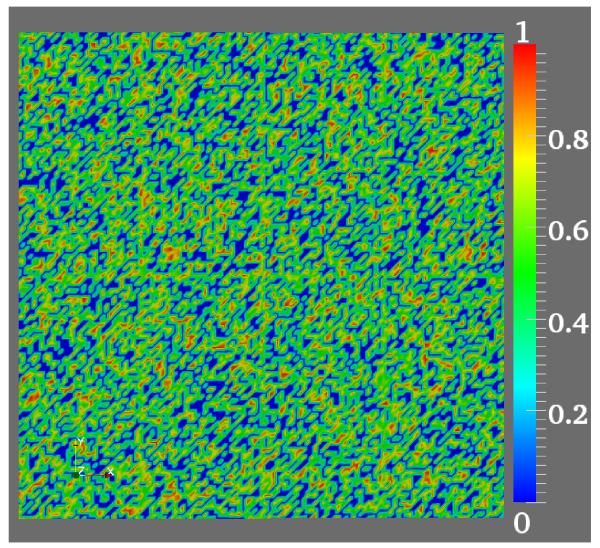
To account for structural heterogeneities, as they emerge, for instance, during fibrosis in the process of aging [11], the intracellular conductivity tensors were modified by multiplying with random numbers in the range (0, 1), see Figure 4. Further, we set those random numbers which were below a threshold of 0.34 equal to 10⁻¹². This led to regions of very low intracellular conductivity which effectively decoupled these regions and blocked any arriving wavefronts. The random distribution of these regions approximates a conductivity matrix as observed in the case of severe diffuse fibrosis where roughly 34% of the tissue is fibrotic [19]. The introduction of these heterogeneities influences upon the response of the tissue to extracellularly applied fields, leading to shock-induced changes in tissue polarization over the entire observation domain, despite the absence of heterogeneities in the electric field. Conduction velocities in this pathological scenario reduced down to 0.24m/s and 0.16m/s in the longitudinal and transverse direction, respectively. With the given parameters the action potential duration was 98 msec, resulting in a wave-length of 2.35 cm and 1.57 cm in the longitudinal and transverse direction, respectively. That is, the wavelength is at the same size scale as the dimension of the tissue of 2 cm and thus sustained reentrant activations can be induced. For all subsequent induction and defibrillation experiments these lower conductivities are used.

Figure 4.

Non-uniform distribution drawn from random number generator.

Now we turn discussion to the stopping criteria for the optimization algorithm in the computations. The optimization algorithm is terminated as soon as (44) is satisfied. If this condition is not met within the prescribed number of iterations, let us say 200 optimization iterations, then we terminated the optimization algorithm. In the line search algorithm the initial step length starts with θ = 1 for the NCG method and is reduced by a factor of 2 for subsequent rejected step sizes, see Nocedal and Wright for details [25]. We developed an optimization code based on the public domain FEM software package DUNE [5]. The parallel computations are done on Dell precision T7500 dual quad core (overall 8 cores) machine, clocked at 3 GHz and equipped with 24 GB RAM.

In the first test case the prescribed extracellular stimulus strengths is applied to the primal equations, without any optimization. This serves to understand the mechanisms by which extracellular stimuli act to terminate arrhythmogenic episodes. In the second test case we utilized these solutions, which were generated with different stimulus strengths, as desired solutions v_d for the optimization approach. The presented numerical results demonstrate that the optimal control strategies allow significant reductions of the total energies required to achieve termination of reentry. Also, as shown in the third test case, short time control can improve the reduction of total applied energy. The final test investigates whether our optimization results are robust with respect to variations of physiological parameters which appear in the ionic model.

4.1 Direct stimulus without optimization

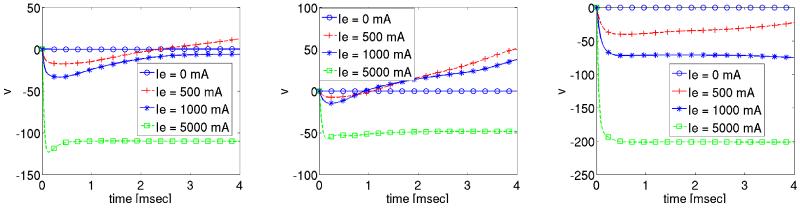
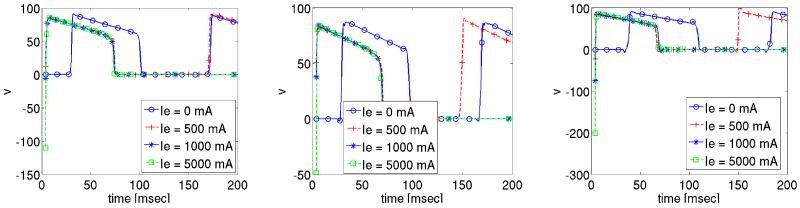
The effect of extracellular stimuli on the primal equations is presented. For this purpose a time dependent extracellular current stimulus is applied for a duration of 4 msec. During the shock we apply four different shock strengths, I_e = 0 mA/cm³, 500 mA/cm³, 1000 mA/cm³ and 5000 mA/cm³ which translated into electric field strengths ||∇u|| of 0.0067 V/cm, 5.215 V/cm, 10.268 V/cm and 49.872 V/cm. The corresponding shock and post shock numerical results for the transmembrane voltage are shown in Figures 5-6 at the three locations indicated in Fig. 2. Note that “t = 0” in the Figs. 5-6 corresponds to t = 435 in the time-horizon graph of Fig. 3.

Figure 5.

Solution of transmembrane voltage during shock administration at the observation sites p₀, p₁ and p₂.

Figure 6.

Post-shock evolution of transmembrane voltage at the observation sites p₀, p₁ and p₂.

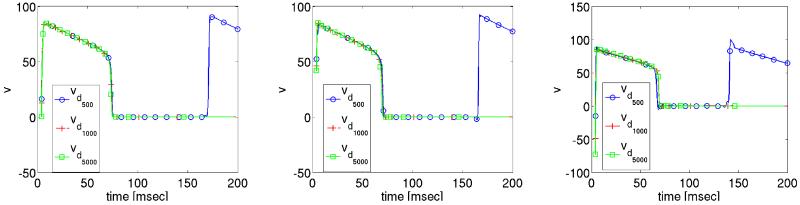
The solution of the transmembrane voltage for I_e = 0 mA/cm³ is shown in Fig. 5. At all three observation sites p_0–2 the tissue remains at rest since no wavefronts propagate there during the 4 msec shock period. For all non-zero stimulus strengths shock-induced changes in v of both polarities are induced at all three locations 5. Fig. 6, showing the post-shock evolution of v, reveals that a stimulus strengths I_e ≥ 1000 mA/cm³ is sufficient to drive the tissue to the resting level. This is not the case for the weaker stimulus I_e = 500 mA/cm³, where reentry is re-established, see Fig. 6. We further observe that with increasing strength I_e the time elapsed post-shock until all activities subsided, is reduced. For I_e = 1000 mA/cm³ this took approximately 97.8 msec, whereas it took only 84.60 msec for I_e = 5000 mA/cm³.

The solution of extracellular potential u during the shock is governed by the applied currents I_e, which establish a linear distribution of u from cathode to anode where potentials are positive at the cathode, negative at the anode and zero in the center of the tissue. That is, the electric field ∇u is constant over the entire domain.

4.2 Tracking type cost functional

Here we investigate the feasibility of applying an optimal control approach to achieve successful defibrillation. As desired states v_d we use the solution profiles of the transmembrane potentials which were obtained in the previous test case during the shock period i.e. we choose v_d in the cost functional J as

$$v_{d_{500}},v_{d_{1000}},v_{d_{5000}}$$ (45)

which are the transmembrane potentials corresponding to the stimuli strengths I_e = 500 mA/cm³, I_e = 1000 mA/cm³ and I_e = 5000 mA/cm³.

To solve the optimal control problems, we utilize the exact same setup as before, with the only difference being that I_e(t) is determined now by the optimization procedure. Again, time traces of the solution v are presented at locations p_0–2. The optimization is initialized with a starting value of (I_e)₀ = 400 mA.

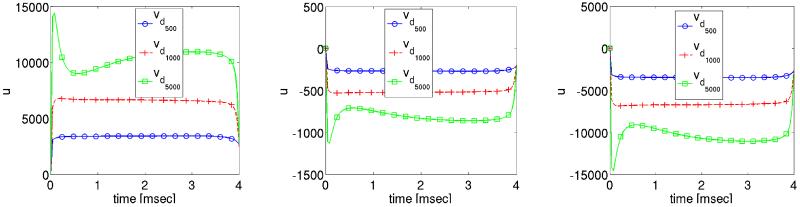
The solution profile of the extracellular potential is depicted in Figure 7. Without optimization, the extracellular potential was raised immediately to approximately 6, 840 mV (33, 436 mV ) for stimulus strength 1000 mA/cm³ (5000 mA/cm³) at p₀ and it remained there throughout the duration of the shock. In the optimization case, see left panel in Fig. 7, u is smaller. This is certainly also the case at the locations p₂ where u is a mirror image of u observed at p₀. At p₁ u is small in both cases since p₁ is located close to the center where u is zero due to symmetry reasons.

Figure 7.

Optimized extracellular potential solution profiles at three different locations during the shock period.

Figure 8.

Optimized transmembrane voltage solution profiles at three different locations during the shock period.

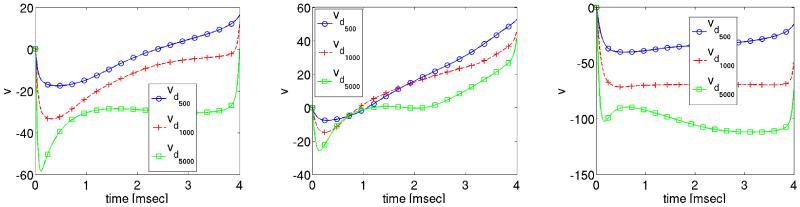
Comparing Fig. 6 and Fig. 10 reveals that the shock-induced changes in transmembrane voltage are smaller in the case where the forcing function I_e is derived on the basis of the optimization procedure.

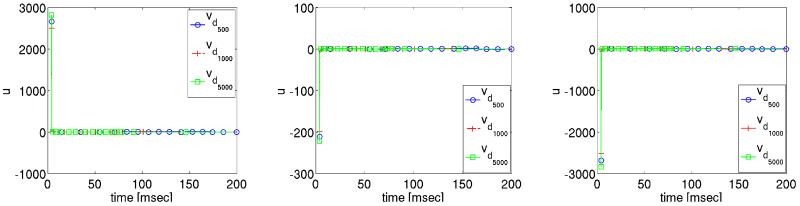
Figure 9.

Optimized extracellular potential solution profiles at three different locations during the post shock period.

Figure 10.

Optimized transmembrane voltage solution profiles at three different locations during the post shock period.

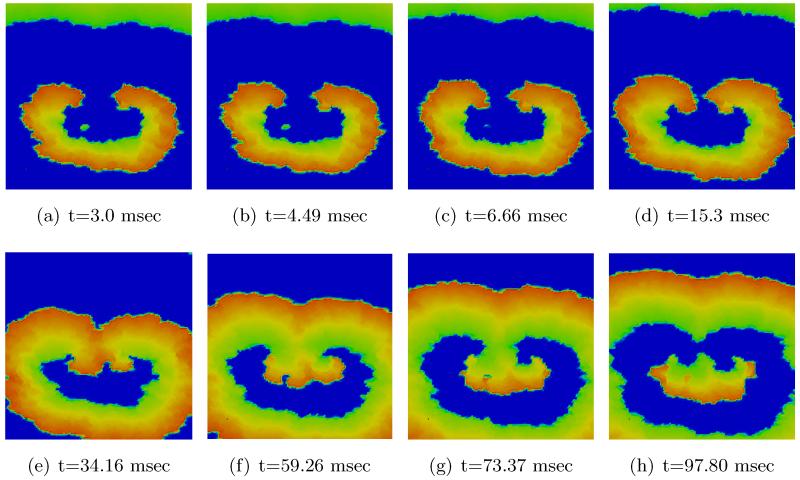
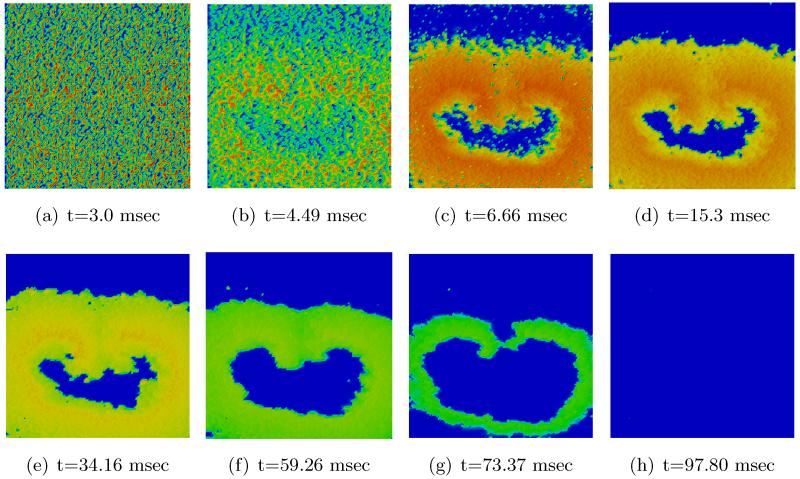
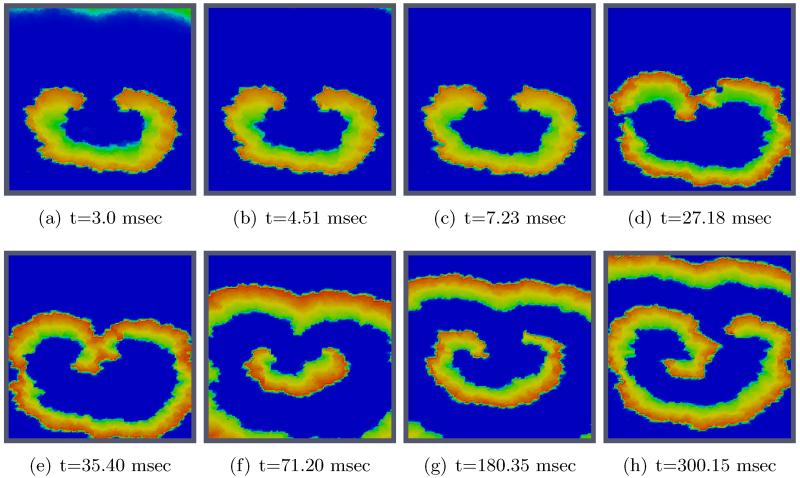
Figs. 11 and 12 show the spatio-temporal evolution of the reentrant activation for both uncontrolled and optimally controlled transmembrane voltage. Shown in Fig. 12 is the optimal control case which used v_d1000 in the cost functional J. As can be seen in the t = 3 ms panel of Fig. 11, a large number of virtual electrodes appear at the microscopic size scale. After the break of the shock, these small-scale polarizations start to diffuse out (panel t = 4.49 ms in Fig. 12). The appearance of numerous small-scale virtual electrodes all over the tissue in both excitable gap as well as in depolarized regions effectively blocked the further propagation of the spiral wave. The analysis of state variables at the end of the optimization period revealed that the values of the recovery variable w immediately ahead of the wavefront were higher as compared to the values immediately before shock onset prior to the optimization period. This increase in w was suffcient to prevent excitation of tissue ahead of the wavefront, thus driving the entire system to the resting state. Refer to Figure 1 for the phase plane portrait of the simplified FHN system.

Figure 11.

2D visualization of uncontrolled solution (v) at different times of simulation.

Figure 12.

2D visualization of optimal state solution (v) at different times of simulation.

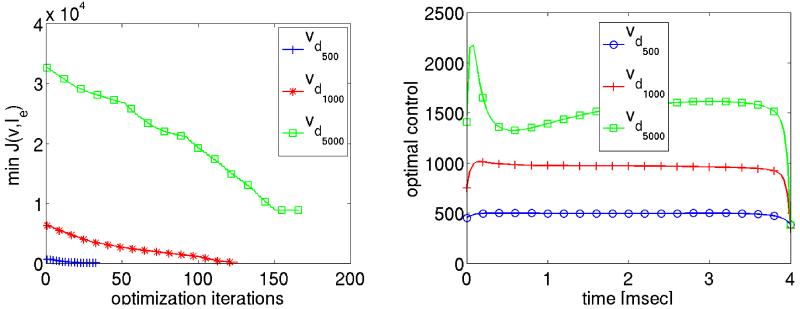
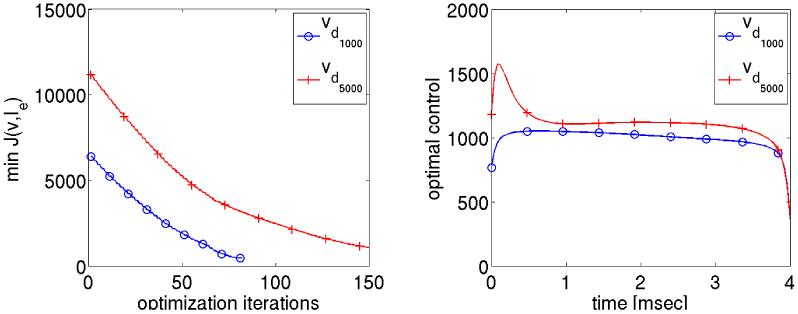
In left panel of Fig. 13, the minimum value of the cost functional is plotted as a function of the NCG iterations for different values of v_d. The final value of the cost is not small, which is consistent with our expectations: first, there is a non-eligible control cost and, secondly, we certainly do not expect v to follow v_d exactly. For v_d500 fewer optimization iterations were required than for v_d1000 and v_d500. They time course of the optimal control I_e(t) for v_di, with i = 2, 3, 4 is shown in the right panel of Fig. 13. The total energy required is clearly reduced in the optimization case as compared to case without optimization, i.e. where a constant stimulus strength was applied using the primal equations only. Although the differences are rather subtle for the weaker shock strengths v_d500 and v_d1000, for the stronger shock in the v_d5000 case there is a striking difference. It should be noted that only the cases v_d1000 and v_d5000 defibrillated successfully. In the case v_d500 which corresponds to I_e = 500 mA/cm³, this could not be achieved, independently of whether optimization was used or not.

Figure 13.

The minimum value of the cost functional and the optimal control values are shown on the left and right respectively for different desired state solutions.

4.3 Short time control

Here we present numerical results based on the following cost functional:

$$\min J(v,I_e)=\frac{1}{2}{\int }_0^{t_s}\left({\int }_{{\Omega }_{\mathit{obs}}}{\mid v-v_d\left(\gamma t\right)\mid }^2\mathrm{d}x+2\alpha \mid {\Omega }_{c_1}\mid {\mid I_e\mid }^2\right)\mathit{dt}$$ (46)

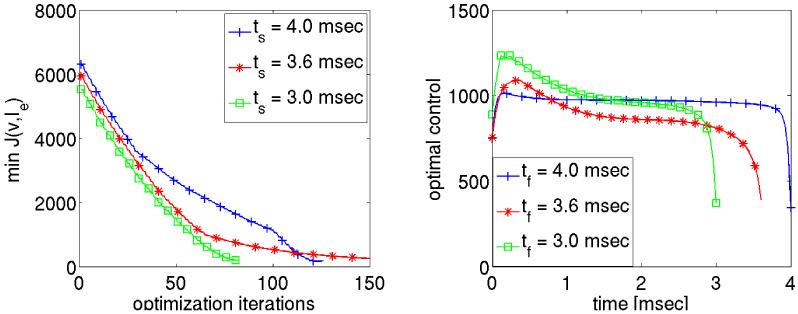
where the shock duration t_s is chosen to be shorter than in the previous case where a duration of t_s = 4 msec was used to produce the tracking functions v_d. Accordingly we set $\gamma =\frac{4}{t_s}$. The aim here is to obtain a control which requires less energy compared to the reference case t_s = 4 msec, but still drives the system to rest. Two different durations t_s = 3.6 msec and t_s = 3.0 msec were tested using v_d1000.

The optimal control values are presented in the right panel of Fig. 14. For the shock durations t_s = 3.6 msec and 3.0 msec, the optimal controls required more energy during the initial phase and less energy towards the end of the shock relative to the reference case with t_s = 4 msec. Overall, the total energy is 3.837 A s/cm for t_s = 4 msec, it is 3.157 A s/cm for t_s = 3.6 msec and 3.002 A s/cm for t_s = 3.0 msec. In all these cases the system goes to rest in the post shock period.

Figure 14.

The optimal controls for the reduced shock durations.

4.4 Robustness with respect to variations in physiological parameters

In this subsection numerical results are presented changing physiological parameters to test the robustness the approach. This can be considered as using a pre-existing trajectory solution which was computed on based on existing data and testing the successful defibrillation for different patient data. In fact, we use v_di as computed in the previous subsection. All parameters here remain the same except for

$$g=1.3S∕{\mathit{cm}}^2\text{and}{\eta }_2=0.02$$

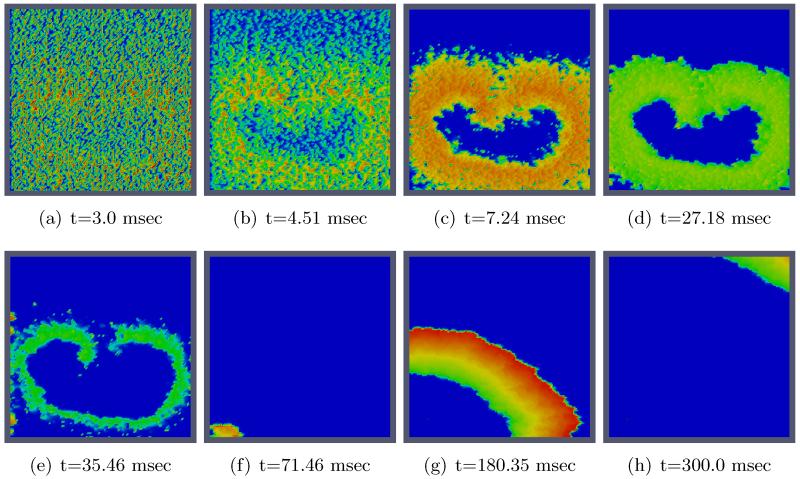
These changes result in slower conduction velocity and a shorter action potential duration, which translates into a shortened wavelength, compare Figs. 16 and 11. Specifically, the conduction velocities were 0.57 m/s and and 0.28 m/s in the longitudinal and transverse direction in the physiological control case (0.65 m/s and 0.32 m/s before). In the fibrotic case where intracellular conductivities were varied randomly, conduction velocities were reduced to 0.22 m/s and 0.14 m/s in the longitudinal and transverse direction, respectively (0.24 m/s and 0.16 m/s before). Action potential duration shortened from 98 msec down to 48 msec. Overall, this reduced the wavelength to 1.05 cm and 0.67 cm in longitudinal and transverse direction (2.35 cm and 1.57 cm before), This reduction changes the ratio between wavelength and tissue size. This provides the substrate for maintaining more complex and more sustained arrhythmias which renders achieving successful defibrillation more challenging.

Figure 16.

2D visualization of uncontrolled solution (v) at different times of simulation for changing specific simulation parameters.

The corresponding minimization value of the cost functional is depicted in the left panel of Figure 15. We can observe that the complete optimization takes less iterations to converge the algorithm comparing with the optimization considering no change parameters for the desired solution trajectory using I_e = 1000 mA/cm³ and I_e = 5000 mA/cm³, see Figure 15 and Figure 13.

Figure 15.

The minimum value of the cost functional and the optimal control are shown on the left and right respectively using modified physiological parameters.

Turning to the optimal control result we recall that before changing the parameters, the initial reentry wave disappeared completely during the post shock simulation after t = 97.80 msec. After changing the physiological parameters, the initial reentry wave front almost disappeared after time t = 66 msec (with v_d1000). But a small wave front excited from bottom left corner after the disappearance of the initial reentry wave. This introduces a single wave front in the computational domain, it passes through the domain and disappears completely from the top right corner after 320 msec, see Figure 17 for the 2D visualization of the optimally controlled transmembrane potential.

Figure 17.

2D visualization of optimal state solution (v) at different times of simulation for changing specific simulation parameters.

The optimal control for v_d1000 and v_d5000 is shown in the right panel of Fig. 15 using the modified parameters. In this case, the total energy of the controls is 3.981 A s/cm and 4.468 A s/cm, which is somewhat higher than those for before the change of the parameters.

5 Discussion

An optimal control technique for achieving successful defibrillation of reentrant activation patterns in a 2D sheet of cardiac tissue was proposed based on the bidomain equations, taking into account their dynamical systems behavior for proper choice of a cost functional. The extracellular current acting in a small strip of spatial support within the computational cardiac tissue acts as control. In the simulations, heterogeneity is modelled by allowing a non-uniform distribution of the intracellular conductivities. As a consequence a large number of virtual electrode polarizations appear within the controlled cardiac domain, inducing a change in the electrical state which prevents pre-shock wavefronts to propagate. The zero mean condition for the elliptic part of the primal and adjoint system was realized by adopting a stabilized saddle point approach, see [7]. The numerical results show that the optimal control strategies lead to successful defibrillation with lower control energy when compared to ad-hoc strategies, as they are implemented in todays defibrillation devices. Since our cost functionals use reference trajectories depending on physiological parameters we also successfully tested the efficiency of the proposed approach under perturbations of these parameters.

While we have found a promising approach for an optimal control treatment of defibrillation problems, the question of appropriate venues of applying control and optimal control strategies for such problems remains a most challenging one. Alternatives, as for instance time optimal formulations suggest themselves, but appear to be computationally very demanding.

This study demonstrates the feasibility of achieving defibrillation by applying optimal control strategies which drive fibrillating cardiac tissue into a desired state, v_d, with a minimum of energy. While this is a first important step towards using optimal control for designing optimized defibrillation protocols, the prescription of a given state v_d, in this case the post-shock state of a standard defibrillation protocol, is a drastic simplification of the problem. Optimal control applications in which v_d is not prescribed, pose a significantly more challenging problem, but the increase in overall degrees of freedom may allow to compute post-shock states which lead to defibrillation success with significantly less energy requirements. Currently, a severe limitation is still constituted by the fact that the entire tissue is used as an observation domain with v being the observed quantity. Experimentally, it is challenging to measure v accurately at the tissue and organ scale with suffcient spatio-temporal resolution. In 2D tissue preparations, as modelled in this computational study, absolute measurements of v are not feasible, only optical signals, v_opt can be recorded using optical mapping techniques which are proportional to v, i.e. v_opt ∝ v holds. This problem is further exacerbated at the organ scale in 3D, where recordings of v_opt are typically confined to a rather limited field of view at the epicardial surfaces. Panoramic imaging modalities which would allow the observation of the entire epicardial surface are still in its infancy [33], which is also true for 3D recording techniques which would allow to gather signals from the depth of the tissue [15]. Further, recorded optical signals v_opt are biased by volume scattering effects [6] which is why for determining the distribution of v_opt throughout the tissue would necessitate the solution of an inverse problem [43].

In the context of clinical applications, optical recordings of v_opt are not feasible due to i) the photo-toxicity of the dyes required for acquiring fluorescence signals, ii) the use of electro-mechanical uncouplers which suppress the vital mechanical activity of the heart, and iii) difficulties related to exposing cardiac surfaces to excitation lights. Clinically, only recordings of the extracellular potential u are feasible, a quantity which has not been considered as an observation variable in this study. Although extracellular potentials u are directly proportional to v in those cases where tissue is exposed to an insulator such as air, as it is the case in this study, this is no longer true in most in-vitro or in-vivo scenarios, where tissue is immersed in a conducting fluid. Under such conditions u is not directly proportional to v, it is rather a distance weighted sum over sources within the entire domain, requiring to solve an inverse problem first to determine v from recordings of u. Further, recordings of u are spatially sparse and limited to the epicardial surfaces, since three-dimensional recordings, as used in in-vitro experiments, rely on plunge electrodes [16] which cannot be used clinically due to damages secondary to the penetration of the myocardium with needle electrodes.

A serious limitation with regard to practical applicability are the involved costs. Even the direct problem, despite major methodological advances and the steady increase in available compute power, lags real-time by orders of magnitude [24]. Therefore, the use of optimal control in a real-time scenario is currently not feasible, however, the structure of optimal solutions computed off-line may give useful insight in practice in the mid-range future. Moreover, substantial e orts are made in the optimal control community towards computational speedup.

Finally, the model used in this study to describe cellular dynamics is simplified, capturing only the basic physiological properties of excitability and refractoriness. Other known physiological membrane properties relevant to the defibrillation process such as the asymmetry of shock-induced polarizations as a function of polarity of the virtual electrodes have not been accounted for [10].

A. Proof of theorem 2.3

Proof. Let {I_e,n} be a minimizing sequence with an associated sequence of solutions denoted by {(u_n, v_n, w_n)}. By Theorem 2.2 the sequence is bounded in

$$Y=L^2\left(V\right)\times \left(L^2\right(V)\cap L^6(Q)\cap W^{1,\frac{6}{5}}(V\left)\right)\times \left(C\right(H)\cap W^{1,2}(V^{\ast }\left)\right)$$

Hence there exists a subsequence, denoted by the same symbols, and $(u^{\ast },v^{\ast },w^{\ast },I_e^{\ast })\in Y\times L^2(0,T;ℝ)$ such that

$$(u_n,v_n,w_n,I_{e,n})\rightharpoonup (u^{\ast },v^{\ast },w^{\ast },I_e^{\ast })\text{in}Y\times L^2(0,T;ℝ)$$

where ⇀ denotes weak convergence. Moreover, since V embeds compactly into L^6–ε(Ω) for any ε > 0, we have by the Dubinskij-Aubin lemma [3],

$$v_n\to v^{\ast }\text{in}{L}^q\left(Q\right)\text{for each}q\in [2,6)$$ (47)

In passing, we note that due to the extension by Dubinskij, this convergence holds not only in L²(0, T; L^q(Ω)), but in fact in L^q(Q) as stated above.

By weak lower semi-continuity of norms we deduce that

$$J(v^{\ast },I_e^{\ast })\le J\left(v\right(I_e),I_e)\text{for all}{I}_e\in U$$

where v(I_e) denotes the v-component of a solution to the bidomain equation with control I_e. Moreover, since I_e,n ∈ U for each n, it follows that $I_e^{\ast }\in U$. It remains to argue that $(u^{\ast },v^{\ast },w^{\ast },I_e^{\ast })$ satisfies the bidomain equations. Clearly the boundary and initial conditions are satisfied. We need to pass to the limit in (12)-(14). For this purpose we choose ϕ ∈ L⁶(V) arbitrarily, integrate all equations in (12)-(14) with respect to t over (0, T) and pass to the limit with respect to n. This will conclude the proof. Passing to the limit is straightforward for all terms except for

$${\int }_0^T{\langle v_{t,n,}\varphi \rangle }_{V^{\ast },V}\mathit{dt},{\int }_0^T{\int }_{\Omega }{v}_n^3\varphi \mathit{dxdt},{\int }_0^T{\int }_{\Omega }{v}_n{w}_n\varphi \mathit{dxdt}$$ (48)

Concerning the first term in (48) we have

$$\underset{n\to \infty }{\lim }{\int }_0^T{\langle v_{t,n},\varphi \rangle }_{V^{\ast },V}\mathit{dt}={\int }_0^T{\langle v_t,\varphi \rangle }_{V^{\ast },V}\mathit{dt}$$

since $v_{t,n}\rightharpoonup v_t^{\ast }$ in L^6/5(Q) and ϕ ∈ L⁶(Q). Turning to the second term, we have $v_n^3\to v^3$ in L^3/2(Q) by (48). Since ϕ ∈ L⁶(Q) ⊂ L³(Q), this implies

$$\underset{n\to \infty }{\lim }{\int }_0^T{\int }_{\Omega }{v}_n^3\varphi \mathit{dxdt}={\int }_0^T{\int }_{\Omega }{\left(v^{\ast }\right)}^3\varphi \mathit{dxdt}$$

Finally, since w_n ⇀ w in L²(Q), v_n → v in L⁵(Q) by (47), and ϕ ∈ L⁶(Q) ⊂ L^10/3, we obtain

$$\underset{n\to \infty }{\lim }{\int }_0^T{\int }_{\Omega }{v}_n{w}_n\varphi \mathit{dxdt}={\int }_0^T{\int }_{\Omega }{\left(v^{\ast }\right)}^3{w}^{\ast }\varphi \mathit{dxdt}$$

The remaining terms in I_ion are of lower order and hence they can be treated analogously. Taking test-functions of the form ϕ(x, t) = φ(x) ψ(t) with φ ∈ V, ψ ∈ L⁶(0, T; ℝ) these facts imply that $(u^{\ast },v^{\ast },w^{\ast },I_e^{\ast })$ satisfy (12)-(14). ∎