Improving Observational Study Estimates of Treatment Effects using Joint Modeling of Selection Effects and Outcomes: The case of AAA Repair

Abstract

Background

When two treatment approaches are available, there are likely to be unmeasured confounders that influence choice of procedure, which complicates estimation of the causal effect of treatment on outcomes using observational data.

Objective

To estimate the effect of endovascular (endo) versus open surgical (open) repair, including possible modification by institutional volume, on survival following treatment for AAA, accounting for observed and unobserved confounding variables.

Research Design

Observational study of data from the Medicare program using a joint model of treatment selection and survival given treatment to estimate the effects of type of surgery and institutional volume on survival.

Subjects

We studied 61,414 eligible repairs of intact AAAs during 2001–2004.

Measures

The outcome, perioperative death, is defined as in-hospital death or death within 30 days of operation. The key predictors are use of endo, transformed endo and open volume, and endo-volume interactions.

Results

There is strong evidence of non-random selection of treatment with potential confounding variables including institutional volume and procedure date, variables not typically adjusted for in clinical trials. The best fitting model included heterogeneous transformations of endo volume for endo cases and open volume for open cases as predictors. Consistent with our hypothesis, accounting for unmeasured selection reduced the mortality benefit of endo.

Conclusion

The effect of endovascular versus open surgery varies nonlinearly with endo and open volume. Accounting for institutional experience and unmeasured selection enables better decision-making by physicians making treatment referrals, investigators evaluating treatments, and policy-makers.

Background and Introduction

Ruptured AAA is the 10^th leading cause of death in men ≥ 55 in the US with mortality exceeding 80%.^1,2 Up until recently, to prevent ruptures, elective open surgical repair (open) of AAA was typically performed with mortality of approximately 5%. Endovascular AAA repair (endo) was introduced in 1999 as a less invasive alternative to open repair with lower perioperative mortality and morbidity.^3–5 Adoption of endo repair has been rapid, comprising over 70% of elective repairs in recent years.⁶

It is generally agreed that higher volume operators and institutions generally achieve better results.^7,8 Thus, organizations such as the Leapfrog group have developed criteria for evidence based referrals for AAA repair based on institutional volume.⁹ Such guidelines, however, fail to account for potential differences in institution and operator experience with the two different approaches. The final decision on a patient’s treatment is the vascular surgeon’s, and the chosen approach will not be determined until after the surgeon assesses the patient. This decision might be influenced by several factors including institutional and operator experience, comfort with the competing approaches, and patient preferences. In some cases, anatomic considerations might require one approach instead of the other. Thus, there are likely to be unmeasured confounders that influence choice of procedure (some unknown to even the referring physician), which complicates estimation of the causal effect of treatment on outcomes of AAA repairs using observational data.

The scenario faced here is common in analysis of observational studies: treatment (endo) is suspected of interacting with other key predictors (e.g., institutional volume and unobservable variables) leading to potential selection bias. Recently, we showed that at the institutional level, the volume outcome relationships for endovascular and open repair differ, with relatively little improvements in outcomes seen for endovascular repair after a relatively low volume of approximately 10 procedures per year.¹⁰ That analysis, however, was limited by not explicitly modeling the unobserved selection effects noted above.

In this paper, we use the bivariate probit model^11–15 to account for selection bias while modeling the effects of treatment (endo versus open), institutional-volume and other observed predictors of perioperative mortality. This model is defined by a simultaneous equation system wherein an equation for treatment selection is linked to an equation for the outcome from treatment through the endogeneous treatment and a “selection parameter” that reflects the sign and magnitude of correlation between the error terms of the two equations. A priori, in a correctly specified model, we expect the selection parameter to be negative in sign, reflecting the fact that unobserved anatomical or other features that make endovascular repair inappropriate for a patient are associated with higher mortality. We use this hypothesis as an indicator of whether a specified model is appropriate in terms of representing observed confounders and, therefore, the true unmeasured selection effect. Furthermore, we embed nonlinear transformations of institutional volume as predictors, thereby only requiring that the assumption of bivariate normality hold for the transformation most supported by the data.

Methods

We used data from the Medicare program to identify all open and endovascular repairs of intact AAAs that occurred during the time period 2001–2004.⁵ We required that patients be enrolled in both Medicare Part A and Part B, have at least two years of prior Medicare experience in order to identify comorbidities that might influence the choice of approach and outcomes of AAA repair, and be eligible for either procedure based on their diagnosis. Because having a broader range of patient types is helpful for fitting selection models and estimating selection effects,¹⁵ we analyzed the full sample as opposed to using propensity scores or alternative matching method to achieve covariate balance. If we applied the bivariate probit to the matched sample, it would still need to satisfy the same assumptions as on the full sample. Therefore, if the model is correctly specified, there is no benefit to restricting the dataset. Although matching as a precursor to model fitting may make results more robust to misspecification of terms involving observed predictors, the distributions of unobserved confounders may be less well balanced following matching, rendering results more sensitive to how the model accounts for the effects of unmeasured confounders. Analyzing the full sample also has the benefit of ensuring that estimates correspond to the population of interest, in our case all aged Medicare beneficiaries with repairs of intact AAAs.

Outcomes and Covariate Assessment

Perioperative mortality was defined as death within the index hospitalization, including contiguous transfers to other acute care facilities, or within thirty days of when the procedure was performed. Mortality was assessed using the Medicare enrollment data. For each case we examined specific procedure codes to identify either endovascular or open repair. To improve the coding accuracy of repair type we also identified physician claims corresponding to the time period of the hospitalization.¹⁰ In cases where the hospital and physician codes were in conflict (<5.5% of the sample), we assigned cases based on physician claims as we thought it more likely that physicians would accurately identify and bill for the procedure they performed.

Each AAA case was assigned to a hospital using the administrative data. We computed the open and endovascular AAA repair volumes for the assigned hospital over the 365 days prior to the case. Using only past cases to define volume obviates concerns about reverse causality. We ascertained demographic information from the Medicare denominator file. From the index admission, we determined whether the patient was transferred and if the case was urgent (defined as emergency department charges of $50 or more). We also identified comorbidities from hospital and physician claims during the two-year period prior to the index admission including chronic renal insufficiency, coronary bypass surgery, coronary artery disease, congestive heart failure, COPD, vascular disease, and prior AAA diagnosis. Finally, to account for potential improvements over the time period of the study, we adjusted for date (in months since January 1, 2001) for each procedure.

Statistical Analyses

We use a bivariate probit model to jointly model treatment selection and perioperative death. Let y_i, endo_i =1 − open and x_i denote the binary indicator of perioperative mortality, the binary indicator of endo and a vector of other patient demographic and clinical characteristics respectively, for the ith case. Denote the endo and open-volume corresponding to case i by ev_i and ov_i, respectively, and let vol_i =(ev_i, ov_i). The model is then given by

$$\text{Perioperative}\text{death}\text{equation}:y_i^{\ast }=f({\text{endo}}_i,{\text{vol}}_i;{\beta }_{\mathrm{e}},{\beta }_{\mathrm{v}})+{\beta }_x^{\prime }{x}_i+{\epsilon }_i$$ (1)

$$\text{Receipt}\text{of}\text{endo}\text{equation}:{\text{endo}}_i^{\ast }=g({\text{vol}}_i;{\stackrel{\sim }{\beta }}_{\mathrm{v}})+{\stackrel{\sim }{\beta }}_x^{\prime }{x}_i+{\stackrel{\sim }{\epsilon }}_i$$ (2)

where

$$y_i=\{\begin{array}{c}1\text{if}{y}_i^{\ast }>0\\ 0\text{otherwise}\end{array}\text{and}{\text{endo}}_i=\{\begin{array}{c}1\text{if}{\text{endo}}_i^{\ast }>0\\ 0\text{otherwise}\end{array},$$

and f (endo_i, vol_i; β_e, β_v) and g(vol_i; β̃_v) are expressions involving volume (and also endo in the case of f). The role of the endo (or selection) equation is to account for unobserved endogenous factors influencing the error terms (ε_i, ε̃_i). To complete model specification we assume (ε_i, ε̃_i) has a bivariate normal distribution with means 0, variances 1, and correlation ρ (the selection effect). (The rationale for setting var(ε_i) =1 is that only the ratio β/stdev(ε_i), where β denotes a regression coefficient, is identified; an analogous justification supports setting var(ε̃_i) =1.) A negative value of the selection effect (ρ <0) indicates endo-favorable selection in that uncontrolled factors that make patients less likely to receive endo are positively associated with perioperative mortality.

Because endo is binary, the direct effect of endo on perioperative mortality conditional on endo and open volume and other covariates is given by the risk difference

$$\text{EndoEffect}({\text{vol}}_i,x_i)=\mathrm{\Phi }\left(f({\text{endo}}_i=1,{\text{vol}}_i;{\beta }_{\mathrm{e}},{\beta }_{\mathrm{v}})+{\beta }_x^{\prime }{x}_i\right)-\mathrm{\Phi }\left(f({\text{endo}}_i=0,{\text{vol}}_i;{\beta }_{\mathrm{e}},{\beta }_{\mathrm{v}})+{\beta }_x^{\prime }{x}_i\right)$$ (3)

where Φ(x) denotes the cumulative density function of the standard normal distribution evaluated at x.

Model specifications

Finding the most appropriate specifications of volume in the perioperative mortality and the selection equations was the primary goal of the model building process. However, we were also interested in the impact of the other non-clinical adjusters (procedure date, urgent admission, transfer). We restrict attention to linear specifications with the exception that the components of vol_i (or functions thereof) may undergo Box-Cox transformations (Table 2, footnote). Because there are two different approaches to repair of AAA (i.e., endo and open), there are a number of ways that volume effects can be conceptualized, the volume of the procedure being performed (within-volume), the spillover effect related to the volume of the other procedure (cross-volume), and the total of both procedures. We therefore estimated a series of bivariate probit models containing various specifications. For ease of presentation, however, we present results for four key model specifications (Table 2). Models 1 and 2 do not include volume (f (endo_i, vol_i; β_e, β_v) = β_eendo_i) and differ in the specification of the other non-clinical adjusters. The within-volume model (Model 3) confines the effects of volume to patients undergoing that procedure while the within- and cross-volume model (Model 4) also allows spillover effects of institutional experience between the procedures (as would be the case if the required skills are transferrable between procedures). That is, under Model 3

Table 2.

Parameter estimates of important terms in key models fit during the model building process

	Model 1: No non-clinical adjusters	Model 2: Add reason, source, date of admission	Model 3: Add within procedure volume	Model 4: Add cross procedure volume
Term	Estimate 95% Conf Int	Estimate 95% Conf Int	Estimate 95% Conf Int	Estimate 95% Conf Int
Bayesian Information
Criterion*	99215	97065	83706	83716
Selection parameter
Estimate	0.104 (−0.252, 0.459)	0.193 (−0.112, 0.497)	−0.123 (−0.189, −0.057)	−0.086 (−0.354, 0.181)
Standard error	0.181	0.156	0.034	0.137
Key predictors of perioperative mortality
Endovascular repair	−0.710 (−1.275, −0.144)	−0.707 (−1.186, −0.229)	−0.242 (−0.465, −0.020)	−0.315 (−1.076, 0.446)
Urgent Admission		0.293 (0.167, 0.419)	0.364 (0.290, 0.438)	0.358 (0.273, 0.443)
Transfer		0.760 (0.572, 0.949)	0.815 (0.629, 1.001)	0.805 (0.615, 0.994)
Procedure date (Endo pats)		−0.004 (−0.008, −0.001)	−0.006 (−0.009, −0.003)	−0.006 (−0.009, −0.003)
Procedure date (Open pats)		0.001 (−0.003, 0.004)	−0.003 (−0.005, −0.001)	−0.003 (−0.005, −0.001)
BC(Endo volume, Endo pats)#			−0.130 (−0.178, −0.082)	−0.112 (−0.204, −0.020)
BC(Open volume, Open pats)#			−0.066 (−0.082, −0.049)	−0.072 (−0.131, −0.012)
BC(Endo volume, Open pats)#				0.003 (−0.057, 0.064)
BC(Open volume, Endo pats)#				−0.003 (−0.018, 0.012)
λ(Endo Volume, Endo pats)&			−0.153 (−0.516, 0.209)	−0.153 (−0.516, 0.209)
λ(Open volume, Open pats)&			0.136 (−0.229, 0.501)	0.136 (−0.229, 0.501)
λ(Endo volume, Open pats)				0.647 (−3.473, 4.768)
λ(Open volume, Endo pats)				0.436 (−1.678, 2.550)
Key predictors of endo
Urgent Admission		−0.504 (−0.558, −0.451)	−0.443 (−0.502, −0.384)	−0.442 (−0.501, −0.384)
Transfer		−0.059 (−0.215, 0.096)	−0.162 (−0.326, 0.003)	−0.162 (−0.326, 0.003)
Procedure date		0.015 (0.014, 0.016)	0.002 (0.001, 0.003)	0.002 (0.001, 0.003)
Proportion Endo			3.004 (2.942, 3.065)	3.004 (2.943, 3.064)
BC(Total volume)#			1.408 (1.309, 1.507)	1.409 (1.310, 1.508)
λ(Total Volume)			−0.671 (−0.764, −0.579)	−0.671 (−0.764, −0.579)

The perioperative mortality equation of Model 1 contains only clinical adjuster variables while Model 2 includes non-clinical adjusters other than volume. Models 3 and 4 include all non-clinical adjusters with volume represented using optimal transformations. Model 4 extends Model 3 by allowing for cross-procedure spillover effects through the inclusion of the cross-volume variables as additional predictors. The Box-Cox transformation18 with parameter λ of x is given by x^(λ) = (x^λ −1) / λ if λ ≠ 0 or otherwise x^(λ) = log(x).

^*The number of observations used in each analysis is 61,414. BIC=plog(n)−2LL, where p and n are the number of estimated parameters and the sample size respectively.

^#To simplify interpretation, confidence intervals for the transformed volume predictors are conditioned on the value of the estimated transformation coefficient.

^&To help with identification of Model 4, the Box-Cox transformation parameters of the within procedure volume variables are fixed at their estimates under Model 3.

$$f({\text{endo}}_i,{\text{vol}}_i;{\beta }_{\mathrm{e}},{\beta }_{\mathrm{v}})={\beta }_{\mathrm{e}}{\text{endo}}_i+{\beta }_{\mathrm{v}1}{\text{endo}}_i{\text{ev}}_i+{\beta }_{\mathrm{v}2}{\text{open}}_i{\text{ov}}_i,$$ (4)

while Model 4 is the right-hand-side of (4) augmented with the sum of the cross-volume terms, β_v3open_i ev_i and β_v4endo_i ov_i. By embedding the Box-Cox transformations of volume predictors in the model (to simplify notation, the volume transformations are not explicitly depicted in (4)), the uncertainty in the transformation parameters is incorporated in model estimation.

In modeling the likelihood of endo we adjusted for a facility’s historical propensity to perform endo repairs by including the proportion of endo cases over the 365 days prior to individual i’s index admission, pe_i =ev_i / tv_i where the total tv_i =ev_i + ov_i is an indication of the size of the facilities vascular surgery program, in g(vol_i; β̃_v). In Table 2, pe_i and tv_i are only included in the endo equation when volume variables are included in the perioperative mortality equation (models 3 and 4).

Although we fitted models with various other combinations of the predictors (e.g., allowing volume effects to be shared across procedures), none improved upon the optimal model found herein. We confirmed using Huber-White robust standard errors¹⁶ that the effect of residual clustering of observations in hospitals had virtually no additional impact on the results.

We quantified the level of overall fit in terms of the Bayesian information criterion (BIC), originally developed as the Schwarz criterion.¹⁷ We also look for the model to cohere with our hypothesis that, due to unmeasured anatomic and other variables, the selection effect is negative.

Results

Between 2001 and 2004 there were a total of 155,402 repairs of either an intact or ruptured AAA for Medicare beneficiaries. After excluding ruptures and procedures that would not be eligible for endovascular repair (e.g., suprarenal or thoracic aneurysms), a total of 61,414 cases met the criteria for the outcomes analyses, yielding 29,518 and 31,896 patients who underwent endovascular repair and open repair respectively.

For endovascular repair, average perioperative mortality was 1.7%, whereas for open repair average mortality was 5.4% (Table 1). More recent procedure, non-urgent admission, not transferred, older age, ESRD, and prior AAA diagnosis were all predictive of endo repair. These same variables tended to be highly predictive of perioperative mortality and thus are potential confounders; prior AAA diagnosis was the lone exception.

Table 1.

Patient characteristics, Institution Volume, and Unadjusted perioperative death for Endo and Open Repair

Variable	Level	Endo Procedure		Endo volume		Open volume		Periop Death
		%	P	Mean	P	Mean	P	%	P
Endovascular repair	Yes	52.0		33.4		36.9		1.7
	No	48.0	<.0001	14.8	<.0001	36.5	0.127	5.4	<.0001
Date of procedure (months since 1/1/2001)	≤ 24			21.7		41.1		3.9
	> 24			25.7	<.0001	32.3	<.0001	3.2	0.0308
Age	67–69	41.2		22.0		36.0		1.8
	70–74	43.6		23.0		36.7		2.5
	75–79	47.4		23.8		37.0		3.5
	80 +	57.3	<.0001	25.4	<.0001	36.6	0.260	5.9	<.0001
Urgent Admission	Yes	25.9		16.7		31.9		8.7
	No	49.0	<.0001	24.0	<.0001	36.9	<.0001	3.4	<.0001
Transfer	Yes	39.5		27.7		47.1		16.7
	No	47.3	0.005	23.7	0.023	36.6	<.0001	3.5	<.0001
Gender	Male	50.7		24.2		37.1		3.2
	Female	37.8	<.0001	21.8	<.0001	35.1	<.0001	4.8	<.0001
Race	Black	46.5		22.6		32.5		4.3
	White/Other	48.0	0.218	23.7	0.114	36.8	<.0001	3.5	0.140
End stage renal disease	Yes	64.5		27.3		37.0		11.6
	No	47.8	<.0001	23.7	0.008	36.7	0.846	3.5	<.0001
Chronic renal insufficiency	Yes	51.5		26.8		37.3		7.9
	No	47.8	0.001	23.6	<.0001	36.6	0.413	3.4	<.0001
Coronary bypass surgery	Yes	39.9		22.5		38.3		2.6
	No	48.4	<.0001	23.8	0.020	36.6	0.006	3.6	0.008
Percutaneous transluminal coronary angioplasty	Yes	54.9		26.5		36.5		2.8
	No	47.6	<.0001	23.6	<.0001	36.7	0.857	3.6	0.041
Coronary artery disease without procedure	Yes	53.9		26.2		39.0		4.5
	No	46.6	<.0001	23.1	<.0001	36.1	<.0001	3.3	<.0001
Chronic heart failure	Yes	56.2		26.8		38.5		6.3
	No	46.7	<.0001	23.2	<.0001	36.4	<.0001	3.1	<.0001
Chronic obstructive pulmonry disease	Yes	49.6		24.1		36.2		4.3
	No	47.3	<.0001	23.5	0.036	36.9	0.041	3.2	<.0001
Vascular disease	Yes	47.4		25.1		37.0		4.6
	No	48.1	0.472	23.1	<.0001	36.5	0.106	3.1	<.0001
Prior AAA diagnosis	Yes	53.3		25.1		37.4		3.4
	No	36.3	<.0001	20.6	<.0001	35.2	<.0001	3.8	0.086

Chi-square tests were used for proportion endo procedure and perioperative death while F-tests were used for time, endo volume and open volume. The standard deviations of endo volume and open volume are approximately equal to their respective means.

Endo patients were treated at hospitals with higher average endo volume but similar open volume compared to institutions where open patients were treated, suggesting that endo patients tend to be treated in hospitals with high volumes of both procedures (e.g., academic medical centers and tertiary care facilities). Patients who were older, male, and with any of the comorbidities besides prior coronary bypass surgery received care at higher endo volume institutions on average while black patients were less likely to be treated at higher open volume institutions. Thus, these predictors may also be confounders with respect to volume.

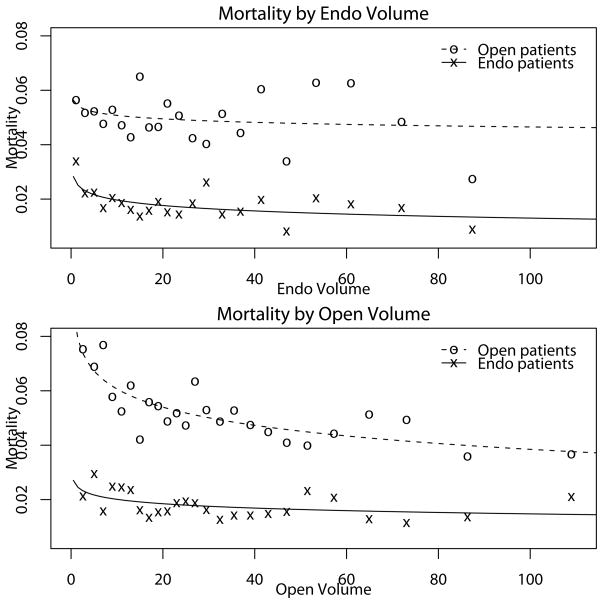
The unadjusted mortality rates for endo and open patients were plotted against the previous 12-months endo and open patient-volumes at the institution where they underwent the surgery, yielding a panel of four plots to which smooth curves were fitted (Figure 1). Comparing the plots across each row, the gradients of the within volume curves clearly exceed their cross-volume counterparts, especially over the most concentrated region of data. Despite the large groups of data contributing to each plotted point, substantial variation remains suggesting that covariate adjustment may have substantial impact.

Figure 1. Plots of Endo and Open Mortality Outcomes by Endo and Open Volume.

The raw proportions, displayed as open circles, are evaluated by binning the data with at least 1000 observations per bin. A smooth curve is superimposed on the plot to give a sense of the strength of the unadjusted relationships between volume and perioperative death.

Model Building and Determination of the Optimal Model

Model 1 included only the predictors that would typically be available in a randomized trial where adjustments for the potential confounders noted above are of less concern. The estimated selection effect (.104) has a very large standard error (.181) giving little clarity on the direction of potential bias from unmeasured selection. The addition of the non-clinical adjusters besides volume (Model 2) yields a substantial improvement in model fit, although the endo coefficient is minimally affected. The estimated selection effect (.193) is bigger than in Model 1 but still not significant (95% confidence interval (−.112,.497)).

The addition of proportion endo (pe_i) and total volume (tv_i) in the endo equation and of within procedure volume (endo_i × ev_i and open_i × ov_i) in the mortality equation (Model 3) yielded more improvement in model fit. In contrast to models 1 and 2, the selection effect was negative −.123 (−.189, −.057) and significant, providing strong evidence that this model satisfies our selection effect hypothesis. In line with the earlier descriptive results, the effects of within procedure volume were highly significant.

Extending the within-volume model through the addition of cross-volume to the outcome equation (Model 4) results in a small improvement in model fit that is outweighed by the increased BIC penalty for model complexity (Table 2). The sizable difference in the coefficients of endo and the within-volume effects between models 3 and 4 is a consequence of collinearity between the volume predictors. Therefore, the more parsimonious within-volume model (Model 3) is preferred.

Optimal Outcome Equation

In the perioperative mortality equation of Model 3, the estimated transformation parameter of within-procedure endo volume is −.153, suggesting rapid change over low volumes and smaller change thereafter, whereas the estimated transformation parameter for within-procedure open volume is .136, suggesting more gradual but consistent changes. The estimated effects, −.130 (−.178, −.082) for endo-volume on endo cases and −.066 (−.082, −.049) for open-volume effect on open cases, are highly significant.

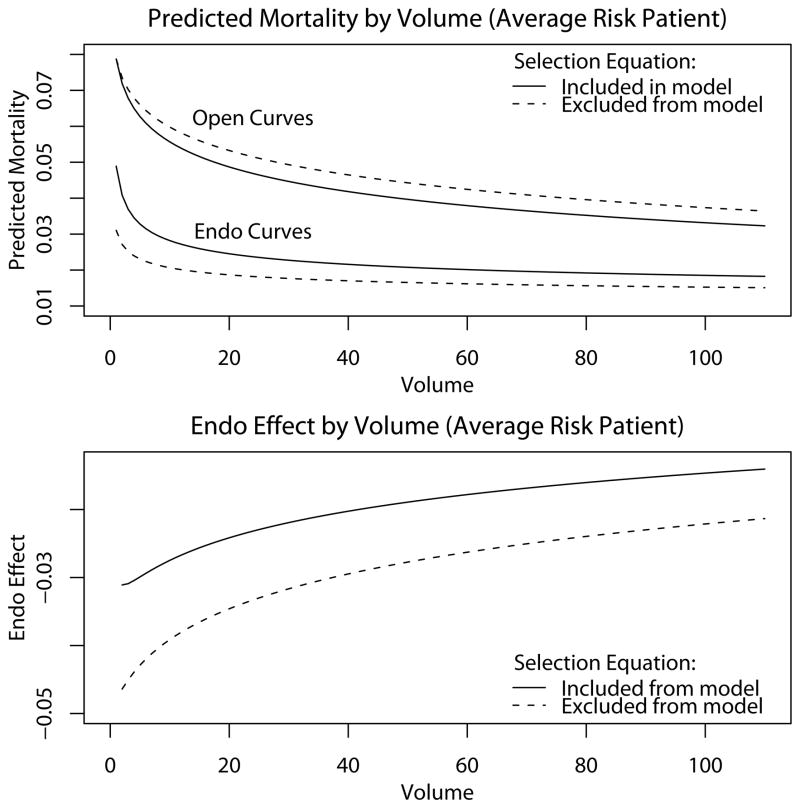
Due to the fact that different transformations have different degrees of curvature, the relative strength of endo and open volume is best seen pictorially. The predicted perioperative mortality curves (upper plot) and the risk-difference (lower plot) in Figure 2 correspond to an institution with equal endo and open volume and a hypothetical patient having the sample mean values for the other covariates. The fitted curves show that the mortality benefit of a unit increase in volume is initially greater and ultimately less for endo than for open; consequently, the endo effect decreases with volume (lower plot).

Figure 2. Plots of Predicted Probabilities of Mortality by Institutional Volume for an Average Risk Patient.

An average risk patient is a hypothetical patient having the sample average values of the covariates. The endo effect presented in the lower plot maps the curves in the upper plot onto the lines where endo and open volume are equal; a different trajectory would be obtained if (e.g.) open volume was twice endo volume or was constant. On most occasions, a patient attends a hospital where open volume exceeds endo volume and the institutional volume over the past year is less than 100 for both procedures.

To evaluate the impact of accounting for unobserved selection, the model was refit as a single equation outcome model. Comparing the resulting trajectories (dashed lines) to those for the bivariate probit (solid lines), it appears that ignoring unmeasured selection leads to under-prediction of endo mortality, over-prediction of open mortality, and thus over-estimation of the effect of endo (Figure 2). A rigorous test to determine whether unmeasured selection leads to a reduction in the effect of endo entails jointly fitting the models with and without the selection effect would require specially written code.

The significant effects of date (endo −.006 (−.009, −.003) ; open −.003 (−.005, −.001)), suggest that while outcomes from both procedures have improved over time, the rate of improvement was more rapid for endo. Urgent cases and being transferred were both risk factors. Results for the clinical predictors, of less interest here, are given in the supplementary appendix.

Optimal Selection Equation

The large positive estimated coefficient of tv_i (1.408 (1.309,1.507)) indicates that endo is more likely at higher volume institutions, while its estimated transformation parameter (−.671) shows that propensity to receive endo is more sensitive to volume in smaller institutions than in larger ones. The positive effect of date on endo (.002 (.001, .003)) is consistent with the increasing market share of endo over time. Yet, while highly significant, the effect is much smaller than under Model 2, suggesting that the increased uptake of endo is partly due to higher likelihood of endo at larger institutions.

The negative effect of transfer indicates that (net of other factors) transferred patients are less likely to receive endo, likely due to a lack of advance planning at the receiving hospital. For the receiving hospital, transfer patients may often be urgent admissions because the first hospital was not able to provide the needed care (e.g., a difficulty arose during the procedure or the case was more serious than anticipated). Urgent admissions had an independent negative effect.

Discussion

We used outcomes from endovascular and open repair of abdominal aortic aneurysms, to estimate the effect of type of AAA repair and the effect of volume while adjusting for trends over time, other non-clinical adjusters, and patient covariates. We used an innovative approach to estimating the effects that has implications for similar comparative effectiveness research using observational data. Because it has the capability to yield unbiased estimates even in the presence of unmeasured confounding, the bivariate probit model is appealing for an analysis such as this. To offset concerns about model identifiability relying on an untestable bivariate normality assumption (the primary limitation of the bivariate probit model), we used a modeling strategy that maximized the likelihood of this assumption. This included (1) using nonlinear transformations of key predictors to relax the assumption of bivariate normality to hold only for the transformation most supported by the data, and (2) careful monitoring of model fitting criteria together with an assessment of external validation based on the hypothesis that, because unobserved anatomical features that make endovascular repair less appropriate for a patient are likely to be associated with higher mortality under either procedure, the unmeasured selection effect would be negative. The second condition was strongly met for the within-volume model, implying that volume is optimally represented by an endo volume variable for endo cases and an open volume variable for open cases.

We preferred use of the Box-Cox transformation to alternative departures from linearity such as splines or other semi-parametric predictors because it supports a monotonic relationship to the outcome and its effect is easy to interpret (e.g., in relation to a linear, logarithmic, or inverse relationship). In addition, the Box-Cox transformation is supported in Proc QLIM in SAS (version 9.2) making it more accessible to potential users.

A major finding of this work is that the non-clinical adjusters, a compilation of variables not typically of concern in the analysis of randomized trials but which may have a large bearing on treatment selection in observational settings, particularly institutional volume, are highly predictive of treatment selection and subsequent outcomes. Therefore, restricting the analysis to the same variables used in a clinical trial would be problematic. Furthermore, there is evidence that ignoring unmeasured selection results in an over-estimate of the effect of endo, thereby providing policy-makers and other decision-makers suboptimal information.

Several findings hold important substantive implications for policy. First, the trajectory of endo volume for endo cases and open volume for open cases on perioperative mortality differ. Experience with endo has a large incremental benefit to around 20 cases annually (a larger number than previously estimated¹⁰) after which additional experience is much less valuable. In contrast, incremental benefits of open volume decay more slowly and extend to larger volumes. Therefore, to benefit the most from institutional experience under either procedure (as is the appropriate mindset if there is uncertainty about the treatment they will receive), a patient should seek an institution that performs at least two endo procedures per month and a larger number of open procedures. Furthermore, in support of our earlier findings based on a different approach,¹⁰ there is minimal spillover of experience across procedures.

Second, considering other non-clinical adjusters, the results for date indicate that the adoption and uptake of endo has steadily increased and operator expertise with both procedures has improved, especially with endo. Transfer and urgent cases had the opposite effect with endo less likely but mortality more likely. These findings suggest that the use of endo on riskier unplanned cases offers substantial potential for improving outcomes and that the development of improved endo training for such cases has a potentially large payoff.

Our study is subject to several limitations. First, we did not account for unobserved selection of patients to hospitals. To account for a hospital selection effect acting through volume requires adding equations with endo- and open-volume as left-hand-side variables to the system of equations. Although appealing, joint estimation of a hospital-level selection effect would require specialized software. Second, data on surgeon volume was not available for these analyses. Availability of these data would have allowed surgeon and institutional volume effects to be separated and more specific recommendations to be made about where and from whom to seek treatment. Such a study is important follow-up work.

If more detailed covariate information was available, as would be the case with a prospectively collected clinical registry, one might expect that accounting for unmeasured confounding is less necessary. However, there is no guarantee that the net effect of the unmeasured confounders would not be greater than in a less well-designed study, implying that use of the bivariate probit may be warranted in such studies.

In conclusion, observational studies are widely criticized for their inability to account for unobservable selection effects that may bias estimated treatment effects. The bivariate probit model is useful for detecting and accounting for selection bias but is reliant on an untestable assumption of bivariate normality. We sought to increase the rigor of our results by using optimal transformations of predictors and choosing a model for which the estimated selection effect cohered with external knowledge. In the process, several clinically and policy relevant findings that might have otherwise been overlooked were discovered. We recommend using methods that relax model assumptions and, where possible, using external validation to inform model choice.