Abstract
A revised density function is developed to define the molecular surface for the numerical Poisson-Boltzmann methods to achieve a better convergence and higher numerical stability. The new density function does not use any predefined functional form but is numerically optimized to reproduce the reaction field energies computed with the solvent excluded surface definition. An exhaustive search in the parameter space is utilized in the optimization using a wide-range training molecules including proteins, nucleic acids, and peptides in both folded and unfolded conformations. A cubic-spline function is introduced to guarantee good numerical behavior of the new density function. Our test results show that the average relative energy errors computed with the revised density function are uniformly lower than 1% for both training and test molecules with different sizes and conformations. Our transferability analysis shows that the performance of the new method is mostly size and conformation independent. A detailed analysis further shows that the numerical forces computed with the revised density function converge better with respect to the grid spacing and are numerically more stable in tested peptides.
Introduction
Solvation is one of the essential determinants of the structure and function of proteins and nucleic acids.1–14 To model solvation interactions in classical molecular simulations, explicit solvent models that explicitly represent every atom in a solvent molecule are natural choices. However, limitations of explicit solvent models have also been recognized. Apparently, the computational cost is a concern when explicit solvent models are used. Often overlooked are the pre-equilibration and sampling needs. Indeed the exponentially large phase space of explicit solvent degrees of freedom makes the convergence of simulations very challenging. Analyses of these limitations prompted pioneers in molecular simulations to propose implicit representations to model solvation, especially in biomolecular applications.1–14
Implicit solvent models replace explicit solvent interactions with an equivalent energetic term based on a mean field approximation. Accuracy and transferability often requires decomposing the mean field potential into electrostatic and nonelectrostatic components and modeling the two components separately. Such an approach can reduce the computation cost but has been found to provide a certain degree of accuracy in the treatment of solvation interactions.1–14 With over 20 years of developments, implicit solvent models, especially those based on the Poisson-Boltzmann (PB) theory, have been widely accepted in studies of solvation interactions. In the PB-based implicit solvent models, the electrostatic interaction or more fundamentally the electrostatic potential is assumed to obey the classical PB equation:
| (1) |
where ε is the dielectric constant, ϕ is the electrostatic potential, ρ is the charge density, i.e. all atomic charges within the solute, λ has a value of 0 wherever mobile ions cannot penetrate and a value of 1 where they can, is the number density of mobile ions of type i in the bulk solution, qi is the charge of the mobile ions of type i, and β = 1/kT. Here k is the Boltzmann constant, and T is the temperature. When the Boltzmann factor is close to zero, Eqn. (1) can be linearized as
| (2) |
Adaptation of the PB solvent models to molecular simulations requires numerical solution of the 3-D partial differential equation. However, the numerical procedure has been a bottleneck, largely limiting their application to calculations with static structures only. The difficulty lies in the numerical procedure to apply such solvent models, which involves discretization of the partial differential equation into a system of linear or nonlinear equations that tends to be rather large: it is not uncommon to have millions of unknowns in biochemical applications. In addition, the setup of the system before the numerical solution and post-processing to obtain energies and forces are both nontrivial. Three major discretization methods are widely used in biomolecular applications. The most commonly used approach is the finite-difference method.15–32 In this method, the physical properties of the solution such as atomic charges and dielectric constants are mapped onto rectangular grid points, and a discrete approximation to the governing partial differential equation is produced. The second approach is the finite-element method,33–38 which approximates the potential by a superposition of a set of basis functions. A linear or nonlinear system for the coefficients produced by the weak formulation has to be solved. The third approach is the boundary-element method.39–52 In the boundary-element method, the Poisson or PB equation is solved for either the induced surface charge39–41,43,45–46,49,52 or the normal component of the electric displacement42,44,47–48,50–51 on the dielectric boundary between the solute and the solvent.
Due to the computational expense for solving the PB equation numerically, considerable efforts have been invested in approximating the solution of the PB equation, via methods such as the semi-analytical generalized Born (GB) model,53–63 the induced multipole model,64 the dielectric screening model,65–66 and others. The pair-wise GB model, in particular, has been widely accepted as an efficient estimation of the solution of the PB equation as recently reviewed.5–6,9–11
A crucial component of all implicit solvent models within the PB framework is the dielectric model, i.e. the dielectric constant distribution of a given solution system. Typically, a solution system is divided into the low dielectric interior and the high dielectric exterior by a molecular surface. That is to say that the molecular surface is used as the dielectric interface between the two piece-wise dielectric constants. In numerical PB calculations, such as the finite-difference methods, discretization of the molecular surface is required. One possible approach is to build the molecular surface analytically and then to map it onto a grid.67–69 However, analytical procedures can be quite time consuming, and do not necessarily offer any advantages for finite difference calculations because the surface must in any case be mapped onto a grid lattice. In this study we focus on representations of molecular surface for numerical solutions of the PB equation.
In numerical solutions of the PB equation, the solvent excluded surface (SES) is the most used surface definition.24,26 Indeed, recent comparative analyses of PB-based solvent models and TIP3P solvent models show that the SES definition is reasonable in calculation of reaction field energies and electrostatic potentials of mean force of hydrogen-bonded and salt-bridged dimers with respect to the TIP3P explicit solvent.70–72 However, a previous test of the SES definition in the finite-difference solution indicates that it is numerically unstable for molecular dynamics.73 Similar numerical difficulty was also observed in the pairwise GB method when the SES definition was used.74 A major limitation of the SES definition is the reentry volume: it is found that in simulations of proteins at room temperature, large reentry volume generated by non-bonded atoms comes and goes as often as every femtosecond when the nearby atoms undergo vibrational motion.73 Thus extremely large surface derivatives with respect to atomic coordinates may occur in the SES definition. In addition, surface cusp may also exist given certain combinations of atom and probe radii and arrangements of atoms.
The van der Waals (VDW) surface, or the hard sphere surface, represents the low-dielectric molecular interior as a union of atomic van der Waals spheres. With the VDW definition, surface derivatives with respect to the atomic coordinates are much better behaved, different from the SES definition. However, surface cusp at the joint between any two spheres may still cause instability in numerical solutions and force interpretations just like the situation in the SES definition. In addition, there exist many nonphysical high (solvent) dielectric pockets inside the solute interior when the VDW definition is used, as discussed in Ref 75. These small buried “solvent pockets” result in a molecular interior too hydrophilic, which would cause proteins to unfold. In addition, the complex dielectric interface due to the buried solvent pockets also results in an unsmooth field distribution, leading to unstable dynamics simulations. Considering these limitations, the modified VDW definition was proposed. The basic idea of the modified VDW definition is to use the solvent accessible surface (SAS) definition for fully buried atoms and the VDW definition for fully exposed atoms.73 This is realized with a set of conformation-dependent modified van der Waals radii, whose calculation requires the solvent accessible surface area of all atoms to determine their solvent accessibility.73 Apparently the definition of modified VDW radii has to be smooth to be any use for dynamics simulations. The standard VDW surface can then be generated with the modified VDW radii. The harmonic dielectric smoothing is also applied to smooth the dielectric transition between solvent and solute.76 Apparently, the dielectric distribution within and around buried atoms is very smooth, i.e. it is all part of the solute low dielectric. However, the dielectric distribution around exposed atoms can still show spatial fluctuation, as in the original VDW surface. Thus, an additional step in the modified VDW definition is used to smooth the spatial fluctuation around exposed atoms,73 though it is difficult to implement and hard to be optimized to reproduce the SES.
The density approaches have recently been developed and can be used for numerical PB solutions. Either a Gaussian-like function or a smoothed step function has been explored in previous developments.77–78 In this type of approaches, a distance-dependent density/volume exclusion function is used to define each atomic volume or the dielectric constant directly. This is in contrast to the hard-sphere definition of atomic volume as in the VDW or the SES definition. Note that the use of a smooth function allows the “boundary region” or the “solute/solvent transition region” extends both inwards and outwards, i.e. the abrupt dielectric transition in the classical two-dielectric model has been replaced with a smooth dielectric transition region of finite width. Indeed extension inwards is necessary in the new definition to reproduce the results of the classical two-dielectric energetics for small training molecules.77–78 In doing so, the trailing tail outside the cavity radii can be used to smooth out the small cracks and crevices formed by neighboring atoms. Apparently, any surface cusps are removed by the use of smooth density functions. However, their agreements with the classical two-dielectric model for typical macromolecules are not very good as will be shown below even if the agreements can be excellent for the small training molecules.77–78
In this development, we have revisited the density function strategy by combining it with the modified VDW definition to balance numerical stability and model quality for numerical PB applications. Specifically, we have optimized the new density function to reproduce, as much as possible, the reaction field energies based on the SES definition due to its reasonable agreement with explicit solvent models. A large and diversified training set of biomolecules is used during the optimization. A separate test set of biomolecules is also used to validate its performance. Its benefit in improving the convergence and numerical stability of electrostatic force calculation is also discussed.
Methods
Finite-difference method
In this work, we focus on numerical solution of the linearized PB equation. However, the proposed new numerical surface procedure can certainly be applied to the full nonlinear PB equation which has been implemented in the Amber/PBSA program.25,30–32 A widely used numerical method is the finite-difference method. It requires mapping the problem domain onto a lattice of grid points. The grid points are connected with grid edges. Solute atomic charges distribution is mapped onto grid points and dielectric constant distribution is mapped onto the centers of grid edges. The linearized PB equation can then be converted into a linear system with the finite-volume scheme. Under this discretization scheme, the partial differential equation can be written as follows at each grid point
| (3) |
where h is the spacing in each dimension, i, j, and k are the grid indexes along x, y and z axes, respectively. εi(i, j, k) is the dielectric constant between grids (i, j, k) and (i+1, j, k). εj(i, j, k) and εk(i, j, k) are defined similarly. κ2 absorbs all the related coefficients in the Boltzmann term. q(i, j, k) is the total charge within the cubic volume centered at (i, j, k). We can use several methods to solve the linear system, such as Gauss-Seidel, Jacobi, successive over relaxation, conjugate gradient, and so on.79–80
Dielectric distribution model
A key issue in the solution of eqn (3) is how to map the dielectric constant distribution on all grid edges. In biomolecular calculations the dielectric constant distribution often adopts a piece-wise constant model, where the dielectric within the molecular surface is assigned to that of the solute and the dielectric outside the molecular surface is assigned to that of the solvent. Within this model, the dielectric constant on a grid edge apparently should be assigned to the dielectric constant in this region where the two neighbor grid points belong. However, when the two neighbor grid points belong to different dielectric regions, i.e. when the grid edge is a boundary grid edge, its dielectric constant is nontrivial to assign, because the dielectric constant is discontinuous across the interface. One simple treatment is the use of harmonic average (HA) of the two dielectric constants at the center of grid edges across the solute/solvent boundary.76 For example, if (i − 1, j, k) and (i, j, k) belong to solute and solvent regions, respectively, there must be an intersection point on the grid edge between (i − 1, j, k) and (i, j, k). Denote a as the distance from the intersection point to grid point (i − 1, j, k) and b as the distance from the same intersection point to grid point (i, j, k). In HA is defined as
| (4) |
This strategy has been shown to improve the convergence of reaction field energies respect to the grid spacing and reduce the grid dependence of the solvation energetics.76 The smoothed dielectric constant transition across the solute/solvent interface also makes it possible to compute dielectric boundary force via a variational approach proposed by Gilson et. al.81 Apparently, only the intersection points between the molecular surface and the boundary edges are needed to utilize eqn (4) to assign dielectric constants at boundary grid edges.
A revised density function strategy
In this study, we explored to represent the molecular surface indirectly or implicitly with a molecular density function. That is to say that the 2-D molecular surface is represented as an equi-density surface of a 3-D density function. The strategy appears to complicate the numerical problem by increasing the dimensionality of the procedure. However, the primary aim is to reduce the numerical instability arising from using hard spheres in classical molecular surface representation. In addition, the density function strategy naturally fits in the level set method that can be utilized to compute, numerically, many properties of the molecular surface in a rather straightforward manner for the finite-difference methods as will be described.
The central idea of our revised density function is the same as previous attempts to apply density functions to molecular surface or volume presentations,77–78 i.e. to use a function that smoothly maps out the interior of the SES of a molecule. However, we require here that it also reproduces the solvation energetics computed with the hard-sphere based SES definition as much as possible. Specifically atoms are described by atomic density functions and these are combined using a composite molecular density function that can be used to calculate discretized molecular surface, i.e. the intersection points between the molecular surface and boundary grid edges. As discussed above, these points are used to define the dielectric distribution of the solution system by the harmonic average method.76
Specifically, given the nth atom centered at rn, its density ρn is defined as
| (5) |
with . Here d = |r − rn| is the distance to the atomic center (rn), rc is the van der Waals radius of the atom, and rp is the solvent probe radius. The domain of the independent variable, x, is then set to be where corresponds to the atomic center and x = 1 corresponds to one probe-diameter away from the atomic van der Waals surface. Note also that x = 0 corresponds to the atomic van der Waals surface when x is so defined. Apparently the domain of the dependent variable, the density value (ρn), needs to satisfy certain constraints to be physical or reasonable and smooth for numerical PB methods. Here the density function is required to satisfy:
| (6) |
The constraints are meant to specify that (1) the density function is always positive and (2) the density value within any atomic van der Waals surface is guaranteed to be ≥ 1 within a molecule as will become clear below. A main point of this study is not to use any prescribed function form but to optimize a numerical function, i.e. a table lookup function, which satisfies the above constraints, and to achieve the best possible agreement with a given benchmark for a specific training set. The details of the benchmark, the training set, and the quality measure will be discussed below. Of course, to guarantee smoothness and good numerical behaviors the cubic-spline interpolation is used to interpolate the function value within the allowed range of x.
With the definition of atomic density functions, we can now define a molecular density function as
| (7) |
in terms of a repeated product over atomic density functions.77–78 Expanding this expression we obtain
| (8) |
where is the linear summation of all atomic terms, and the higher products, i.e. the “intersection terms”, represent corrections for over- or under-counting of atomic intersections.77–78 Use of ρmol(r) would produce a molecular volume almost the same as the “classical” VDW volume, which is not desired in numerical PB applications as reviewed in the introduction.77–78 The original density function (ρmol) was defined in such a way that ρmol > 1 corresponds the VDW volume. If only the leading term ρsum, were used, ρsum > 1 would correspond to an overestimation of the VDW volume. Corrections from the intersection terms in ρmol were used to successively correct the volume so that it eventually leads to a volume consistent with the VDW volume. That is to say that when only the leading term is used, the definition of ρsum > 1 has the potential to capture the “reentry volume” in addition to the VDW volume when properly optimized. Similar idea has been used in previous work.77–78
Combination with the modified van der Waals surface
Note that the molecular volume defined by a density function crucially depends upon the function form. A function defined to decay faster to zero would lead to a smaller molecular volume, i.e. more solvent-exposed inter-atomic crevices would exist. In contrast, a function defined to decay slower to zero would lead to a larger molecular volume, i.e. less solvent-exposed inter-atomic crevices would exist. Our initial analysis of the density function approach shows that its sensitivity to the function form makes it very difficult to reproduce the SES definition.
The limitation can be attributed to the different requirements between defining solvent-exposed surface for exposed atoms and defining solvent-excluded volume for buried atoms. Our analysis shows that the density function has to be defined to decay to zero faster to capture the solvent-exposed surface in the SES definition. However, the density function has to be defined to decay to zero slower to capture the solvent-excluded volume in the SES definition. Since more atoms on peptides are solvent-exposed, while more atoms in proteins are solvent-excluded, the density function tends to make the proteins too hydrophilic if it is optimized with respect to the peptides. In contrast, the density function tends to make the peptides too hydrophobic if it is optimized with respect to the proteins. Overall, it is too difficult to find a compromise that would work for different sized molecules.
We explored to combine the density function with the modified van der Waals (VDW) approach reviewed in the introduction to overcome its limitation. Specifically, the density function is revised as follows:
Compute solvent accessible surface (SAS) with unmodified VDW radii (rc ).
Compute modified VDW radii () based on atomic SAS (see below).
Calculate the composite density function, , with the modified VDW radii, i.e. with rc replaced by in (5).
The modified VDW radius of atom i is defined to be smoothly dependent upon atomic SAS as follows
| (9) |
where is the modified radius of atom i, rc,i is the unmodified VDW radius of atom i, η ∈ [0,1] controls how much increment to be added to the unmodified VDW radius, rp is the solvent probe radius, is the relative solvent accessibility of atom i, and Ac ∈ [0,1] is the cutoff relative solvent accessibility. Eq (9) shows that only VDW radii of buried or somewhat exposed atoms are incremented, while VDW radii of highly exposed atoms are not incremented.73
Thus, when the density function is defined with the modified VDW radii, we can achieve the goal of raising the density function value higher within the molecular interior by effectively pushing the atomic VDW surface outward while still preserving the low-density values for solvent-exposed atoms that are needed to define the solvent-exposed surface. As will be shown below, a more consistent performance can be realized among different sized molecules when the modified VDW radii are used in the density function approach. Of course, parameters η and Ac should be optimized, along with the density function, to best reproduce the reaction field energies with the SES definition.
Use of numerical function to represent the atomic density function
Up to this point, we have yet to define the atomic density function except its overall properties. As discussed, a main point of this study is not to use any prescribed function form but to optimize a numerical function for ρn(x) to achieve the best possible agreement between ρsum(r) and a given benchmark for a specific training set. Specifically five intervals in the range of [0, 1] were used to optimize the numerical function. These are then interpolated over the domain of interest with the cubic-spline interpolation to guarantee a continuous and smooth ρn(x).82 It is found that use of more intervals does not improve the quality of the agreement with the SES definition. Of course, the use of fewer intervals reduces the quality of the agreement.
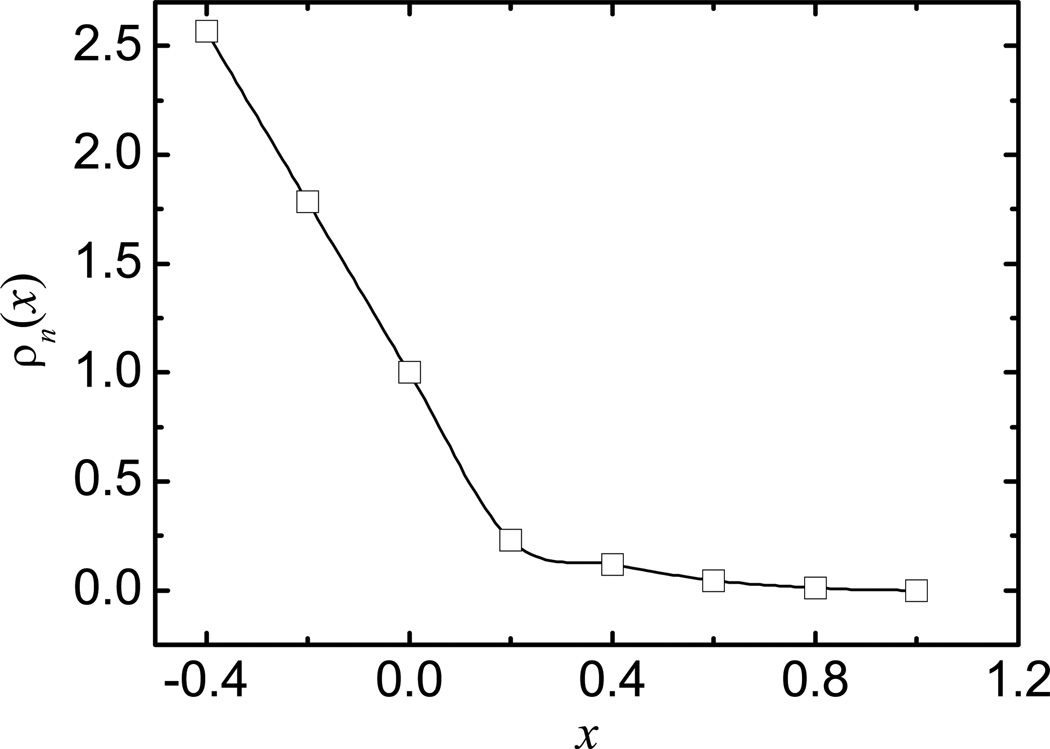
Apparently, it is perfectly reasonable to include intervals < 0 in the optimization, but these intervals are already within the atomic VDW volumes which are guaranteed to be within the molecular surface and do not contribute to the optimization quality of the function. Inclusion of these intervals only increases the difficulty of the optimization problem. Instead we extended the density function all the way to the atomic center with a linear function with the slope of the cubic-spline function at x = 0. For example, the atomic density function optimized within the range of [0, 1] is shown in Figure 1, which also plots two more intervals < 0. Note too that the numerical function within the first interval [0, 0.2] is almost linear even if the cubic-spline interpolation is used (Figure 1).
Figure 1.
Optimized atomic density function.
As described above, the numerical density function is optimized with a benchmark set. Here the PB reaction field energies in the SES definition were used in this study. Our choice of the SES definition as benchmark was based on recent comparative analyses of PB solvent models and TIP3P solvent models. These studies show that the SES definition is a reasonable surface definition in calculation of reaction field energies and electrostatic potentials of mean force of hydrogen-bonded and salt-bridged dimers with respect to the TIP3P explicit solvent.70–72 Finally to ensure transferability and universality of the density function, we used a large set of diversified biomolecules, both folded and unfolded conformations, in the optimization of the density function.
In summary, the following parameters were optimized: the four density function values at x = 0.20, 0.40, 0.60, and 0.80, respectively, to determine ρn(x); and η, and Ac to determine the optimal modified VDW radii (eqn (9)). The optimization was respect to the benchmark reaction field energies computed with the SES definition. The average error (i.e. unsigned relative deviation) between the two sets of reaction field energies was used as the optimization measure. Note that the function values at x = 0 and x = 1 have been fixed as 1.0 and 0.0, respectively, according to eqn (6). In this study, we used a three-step systematic scan of the parameter space to optimize the parameters. At step one, an initial scan in the resolution of 0.2 was used for all six parameters. At step two, a refinement scan in the resolution of 0.05 was used in the reduced search space (±0.2) centered on the best parameter set from step one. Finally at step three, a second refinement scan in the resolution of 0.01 was used in the reduced search space of (±0.05) centered on the best parameter set from step two. The optimized parameters are shown in the results and discussion.
Implicit molecular surface representation by the level-set method
Once ρsum(r) is defined on grid points, we need to know where the equi-density surface, ρsum(r) = 1, intersects all grid edges to use the harmonic average method to set up the dielectric constants of all boundary grid edges, see eqn (4). In addition, we also need the surface normal direction in the force calculation as will be shown next.
We explored to compute these numerical surface properties with the level set method.83–84 In the level set method, a scalar function, φ(r), i.e. the level set function, is used to represent the surface implicitly. For example, to describe a 2-D spherical surface with the radius of 1, we can define a level set function as φ(r) = |r|2 − 1 in the 3-D space. Thus the spherical surface consists of all the points satisfying the condition of φ(r) = 0. In addition, for any point r, we can easily determine it is within the surface if φ(r) < 0 or outside of the surface if φ(r) > 0. It should be pointed out that for a specific surface (φ(r) = 0), there may be many different level set functions because the requirement of φ(r) = 0 cannot uniquely define the 3-D function. To utilize the level set method to define the molecular surface, we need to define a level set function so that φ(r) = 0, i.e. the zero level set, corresponds to the molecular surface. In addition, positive and negative function values denote the solvent and solute sides of the surface, respectively. Thus, our revised density function can be used to define a level set function as
| (10) |
With these preparations, we proceed to compute the interaction point of a boundary grid edge and the molecular surface as follows. Without loss of generality, suppose that this is an x-edge flanked by two grid points x1 and x2. The level set function values are φ1 and φ2, respectively. Apparently, we have φ1×φ2 < 0 since the sign of the level set function defined by eqn (10) changes when crossing the molecular surface, and the intersection point is between x1 and x2. Next we choose a third grid point, x3, from the two grid points that flank the x-edge in the x-direction, i.e. it is right next to x1 or x2 and has the same y and z coordinates. Given the three grid points with their x coordinates as x1, x2, x3 and corresponding level set functions as φ1, φ2, φ3, respectively, a quadratic function φ = a2x2 + a1x + a0 can be determined to pass through three points (x1, φ1), (x2, φ2), and (x3, φ3). Thus, the intersection point is simply the root of the quadratic equation a2x2 + a1x + a0 =0 within [x1, x2]. It has been shown that the error in the calculated intersection point scales as O(h2).83–84
With the level set method, calculation of other surface properties is also straightforward. In this study, the surface normal direction is needed at every intersection point and can be computed as83–84
| (11) |
where φx is the derivative of φ with respect to x. Other symbols are defined similarly. The simplicity of the level set method makes it well suited to the finite-difference method, where these derivatives can be interpolated with accuracy of O(h2).83–84
Computation details
Electrostatic energy and force calculation
The electrostatic reaction field energy was computed via the dielectric polarization charges, which were calculated using the Gauss law and the grid potential obtained from the finite-difference solution of the PB equation.26 In the finite-difference method, the dielectric polarization charges are located on the boundary grid points, i.e. the grid points surrounded by non-uniform dielectric grid edges. To improve the convergence of reaction field energy, the polarization charges were first projected onto the molecular surface according to the procedure described by Rocchia et al26 before they were used to compute the reaction field energy as a pairwise summation of Coulombic interactions between atomic charges and polarization charges.
It is well known that the electrostatic force density can be derived through the divergence of the Maxwell stress tensor (P) as85–86
| (12) |
where ρf is the fixed charge desnity, E is the electric field, ε is the dielectric constant, and ΔΠ is the excess osmotic pressure,87 λ is the Stern layer defined so that it is 1 in regions accessible to the mobile ions and 0 elsewhere. This is consistent with the formulation of Gilson et al.81
Eqn (12) shows that there are three components in the total electrostatic forces: (1) the Coulombic and reaction field forces acting on the atomic charges, ρfE; (2) the dielectric boundary forces, or pressure acting on the dielectric boundary, ; and (3) the ionic boundary forces, or pressure on the ionic boundary. Since the Coulombic forces can be computed analytically by pairwise summation of Coulombic interactions among atomic charges, only rest of the force components were computed numerically.
Similar to the treatment of reaction field energy, dielectric polarization charges can be used to improve the convergence of reaction field forces with respect to the grid spacing. Specifically, the reaction field forces were calculated by the pairwise summation of the Coulombic interactions between polarizarion charges and atomic charges.26 The computation of dielectric boundary forces requires derivative of the dielectric constant. Thus only a smoothly varied dielectric model such as eqn (4) can be used in eqn (12),86 where the dielectric constants on grid edges across the dielectric boundary (molecular surface) were assigned as weighted harmonic averages of solvent and solute dielectric constants. The finite-difference procedure to implement given the weighted harmonic averages of dielectric boundary grid edges has been described in detail by Gilson et. al.81 Note that the dielectric boundary force element is always along the direction of the gradient of dielectric constant, which is the normal direction of the molecular surface. Thus, computation of dielectric boundary force element requires the numerical calculation of surface normal vectors, which was computed by eqn (11).
Due to the fact that the SES surface is not differentiable, the dielectric boundary force elements are distributed to nearby atoms in an ad hoc manner as follows. For the contact portion of the SES, the surface force elements are distributed to the closest atom sphere. For the reentry portion of the SES, the dielectric boundary force elements are distributed to the two nearest atom spheres proportional to the inverse of the distances to the two atom spheres. This procedure is also used to distribute the dielectric boundary force elements for the surface defined by the revised density function.
Finally the ionic boundary forces are ~O(10−2) smaller than the reaction field forces and dielectric boundary forces in water81 so that we only focus on the reaction field forces and dielectric boundary forces in the performance analysis of the revised density function below. In addition their performance is apparently more closely related to how the Stern layer is defined, which is beyond the scope of this development.
Training and test sets
To cover the highly heterogeneous molecular surface topologies, eight different structure sets were used in this study to calibrate and test the revised density function (see Table 1). Set 1 and 4 contain a large set of PDB structures ranging from small peptides to very large biomolecules (with more than 550 residues) and covering a wide variety of native protein folds.88 Set 2, 5, and 6 are unfolded protein conformations of three small global proteins from high-temperature unfolding simulations: 1PGB (alpha/beta), 1ENH (all-alpha) and 1SHG (all-beta). Set 3, 7, and 8 are from unfolding simulations of three peptides. Set 3 is a hairpin from 1PGB, set 7 is a helix from 1PGB and set 8 is a hairpin from 1SHG. These sets are used to test how well reaction field energies are reproduced for different native and nonnative conformations of the same protein. Finally, set 1 − 3 were used as training sets, and set 4 − 8 were used as test sets. All molecular structures were processed with Leap in AMBER989 and held static in all calculations. As described above, the optimization of the density function was conducted with the reaction field energies of chosen training molecules. In the surface potential analysis, the native structures of 1PGB, 1ENH, 1SHG, and the p53 DNA binding domain with and without DNA were used.
Table 1.
Training sets (1 – 3) and test sets (4 – 8) used in this study. RMSD: root-mean-squared deviation from the experimental native structure.
| Structure Set | No. Structures | No. Residues | RMSD (Å) |
|---|---|---|---|
| 1: PDB1 | 290 | 16 – 517 | 0.00 |
| 2: PGB | 314 | 56 | 0.01 – 13.80 |
| 3: HPN1 | 300 | 16 | 0.02 – 11.63 |
| 4: PDB2 | 289 | 19 – 497 | 0.00 |
| 5: ENH 6: SHG |
261 284 |
54 57 |
0.02 – 10.50 0.16 – 13.22 |
| 7: Helix 8: HPN2 |
501 451 |
19 16 |
0.02 – 8.95 0.02 – 11.28 |
Other details
In all calculations, the ion concentration was set to zero. The dielectric constant of the solvent was set to 80, i.e. for water, while the solute was set to 1. The solvent probe was set to be 0.6 Å. Our use of an unusually small probe radius was based on our previous comparative analyses of the numerical PB solvent models and TIP3P solvent models. In these analyses the reaction field energies of small molecules were found not very sensitive to the different probe sizes, but the electrostatic potentials of mean force of hydrogen-bonded or salt-bridged dimers were quite sensitive to the probe radius used and a solvent probe radius of 0.6 Å was found to best reproduce the TIP3P solvent among the tested values.72 Subsequent analysis of ion pairs on peptides and proteins also indicates that the probe radius of 0.6 Å can best reproduce the TIP3P solvent [Tan and Luo, manuscript in preparation]. The finite-difference grid spacing was set to be 0.5 Å if not mentioned otherwise. A two-level electrostatic focusing was used to speed up the assignment of electrostatic boundary condition. The coarse grid spacing was 2.0 Å. The dimension of the coarse grid was set to be twice as large as the dimension of the solute to secure the quality of the nonperiodic boundary condition in PB calculations. The finite-difference convergence criterion was set to be 10−3. All other parameters are set to be default as in the PBSA program of Amber 9.25,73,89
Results and Discussion
Optimization of the revised density function
As described in the method, the revised density function was optimized by a systematic search of the six parameters with respect to a benchmark set of reaction field energies computed with the SES definition. The optimized parameters, with the lowest average unsigned error with respect to the benchmark set, are as follows: ρn(x) = 0.21, 0.15, 0.05, and 0.01 at x = 0.2, 0.4, 0.6, and 0.8, respectively; η = 0.57; and Ac = 0.08. Once the discrete density function values are given, the cubic-spline function is utilized to interpolate the density function within the range of [0, 1] for x.82 Note that x = 0 corresponds to the atomic VDW surface and the atomic density function is defined for x < 0 as a linear function with the slope at x = 0. Figure 1 plots the cubic-spline interpolated function with the optimized discrete density function values. To fully understand the performance gain in combining the density function with the modified VDW surface, the pure density function approach, i.e. with density function defined with the unmodified VDW radii, was also optimized with respect to the same benchmark set. The optimized parameters are as follows: ρn(x) = 0.26, 0.21, 0.05, and 0.01 at x = 0.2, 0.4, 0.6, and 0.8, respectively.
It can be seen in Table 2, the revised density function with the modified VDW radii (denoted as “Revised Density” below) can achieve average errors less than 1% (PDB1: 0.47%, PGB: 0.76% and HPN1: 0.76%) for all three training sets, a respectable agreement. The corresponding values of the density function with the unmodified VDW radii (denoted as “Density” below) and modified van der Waals definition (denoted as “MVDW”) are relatively larger (PDB1: 1.26%, PGB: 0.57% and HPN1: 1.84% for Density; PDB1: 2.01%, PGB: 4.39% and HPN1: 4.37% for MVDW). The average errors of the Revised Density definition are also lower than those of the Density and the MVDW definitions in the test sets. Overall the average error of every training or test set is lower than 1% (0.45% – 0.89%) For practical purposes, it is also important, however, to minimize maximum errors and error spreads. Here the error spread is defined as the difference between the maximum positive error and the maximum negative error. It can be seen from Table 2, the unsigned maximum errors by the Revised Density definition are smaller than those of the Density and the MVDW definitions (Revised Density: 1.72% – 3.38%; Density: 2.23% – 8.44%; MVDW: 5.27% – 9.32%) and the error spreads of the Revised Density definition are narrower (Revised Density: 2.50% – 5.90%; Density: 2.90% – 10.85%; MVDW: 4.39% – 10.47%). Overall, the Revised Density definition can achieve a more consistent performance with lower average errors, maximum errors, and error spreads, than the Density and MVDW definitions in both the training and test set.
Table 2.
Average error, maximum error, and error spread (average/max/spread) for each of the training sets and test sets. Revised Density: density function definition with modified van der Waals radii. Density: density function definition with unmodified van der Waals radii. MVDW: VDW surface definition with modified van der Waals radii.
| Structure Set | Revised Density | Density | MVDW |
|---|---|---|---|
| 1: PDB1 | 0.47%/1.82%/3.11% | 1.26%/6.58%/9.40% | 2.01%/6.66%/8.07% |
| 2: PGB | 0.76%/2.38%/3.05% | 0.57%/3.50%/4.77% | 4.39%/6.75%/5.37% |
| 3: HPN1 | 0.76%/3.26%/5.90% | 1.84%/3.72%/5.36% | 4.37%/9.32%/10.47% |
| 4: PDB2 | 0.45%/2.40%/3.86% | 1.27%/8.44%/10.85% | 1.95%/5.95%/6.83% |
| 5: ENH 6: SHG |
0.58%/1.72%/2.50% 0.89%/2.47%/3.01% |
0.56%/2.23%/2.90% 0.71%/2.98%/4.32% |
3.18%/5.27%/4.39% 4.72%/7.42%/6.11% |
| 7: Helix 8: HPN2 |
0.54%/1.87%/3.66% 0.58%/3.38%/5.53% |
1.29%/2.82%/5.61% 1.24%/3.12%/5.95% |
3.88%/7.67%/7.46/% 3.89%/8.52%/9.22% |
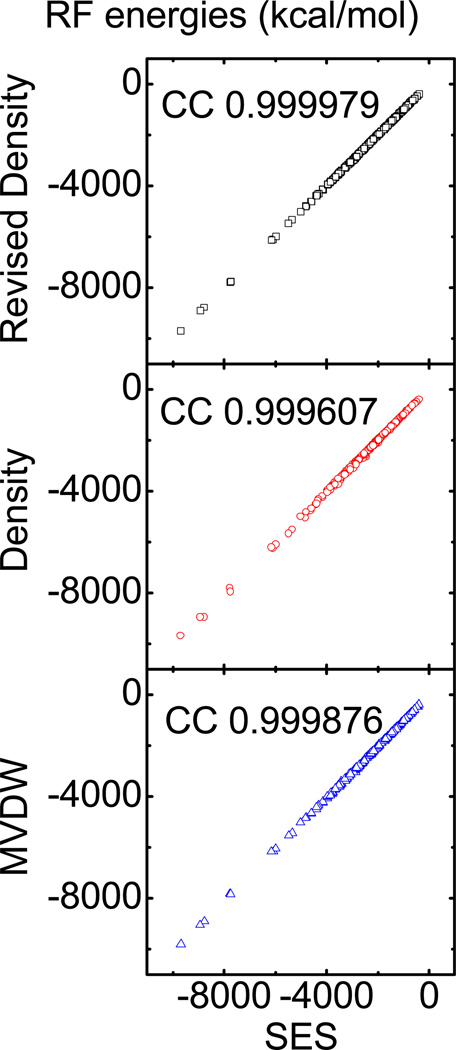
We next consider the correlation between the reaction field energies computed with the Revised Density definition and those with the SES definition for test set PDB2. As shown in Figure 2, all data fall on the diagonal line with almost no scatter. Indeed the correlation coefficient is 0.999979, slope is 0.999505, offset is 5.30848, and root-mean-square (RMS) relative deviation is 0.57%. In contrast, the correlation between the Density definition and the SES definition is 0.999607, slope is 1.01631, offset is 11.1488, and RMS relative deviation is 1.79%. The correlation between the MVDW definition and the SES definition is 0.999876, slope is 1.01112, offset is −15.306, and RMS relative deviation is 2.17%.
Figure 2.
Top: correlation between reaction field (RF) energies computed with the SES definition and those computed with the Revised Density definition (correlation: 0.999979, slope: 0.999505, offset: 5.30848, and RMS relative deviation: 0.57%). Middle: correlation between RF energies computed with the SES definition and those computed with the Density definition (correlation: 0.999607, slope: 1.01631, offset: 11.1488, and RMS relative deviation: 1.79%). Bottom: correlation between RF energies computed with the SES definition and those with the MVDW definition (correlation: 0.999876, slope: 1.01112, offset: −15.306, and RMS relative deviation: 2.17%).
Transferability considerations
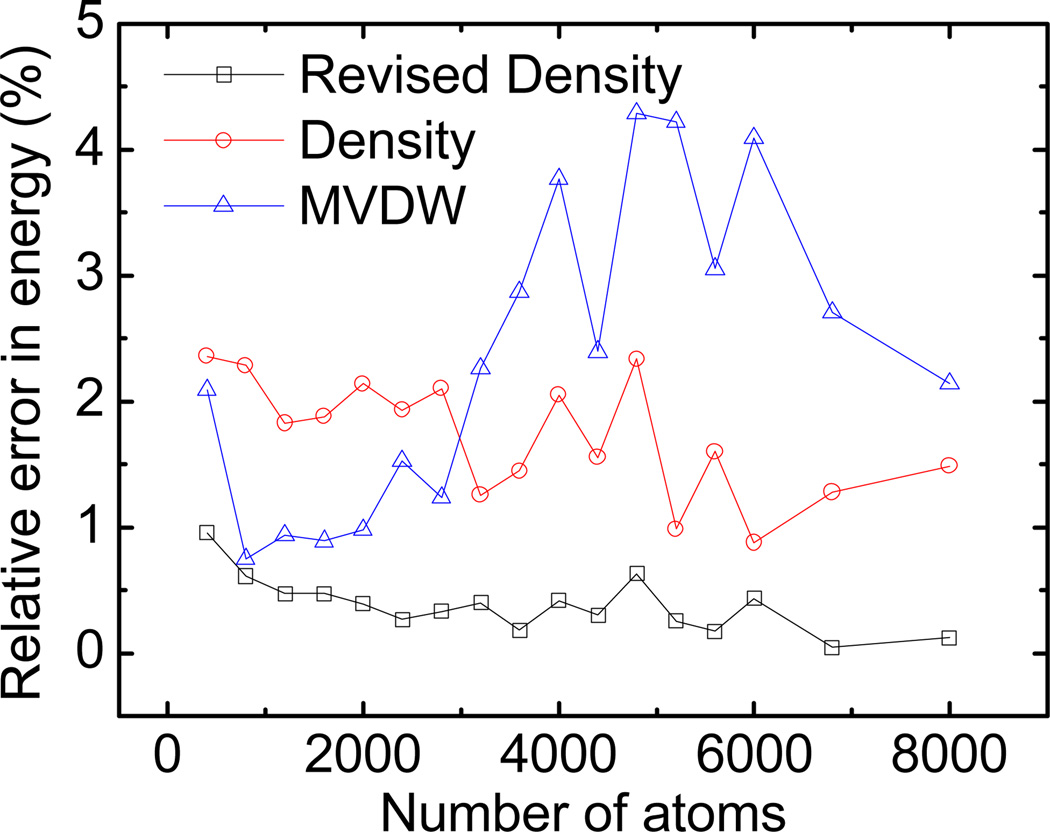
While the overall relative error in reaction field energy should be as small as possible, it is also important that the error is system and structure independent. We investigated two aspects in this regard: errors with different system sizes and different conformations (loosely packed/unfolded or folded conformations). To study the transferability of the new method, we calculated the errors versus number of atoms for the PDB2 set. Figure 3 shows that the error range of the Revised Density definition does not change much as the number of atoms increases. This confirms that the performance of the Revised Density definition and the Density definition are mostly size independent, though the Revised Density definition clearly agrees better with the SES definition. On the other hand, the size dependence effect of MVDW definition is obvious: the error increases as the number of atoms increases.
Figure 3.
Size dependence of relative errors in reaction field energies for the Revised Density definition (square), the Density definition (circle), and the MVDW definition (triangle). To improve clarity, the numbers of atoms are binned with a width of 400 and the error is averaged for each bin before plotting.
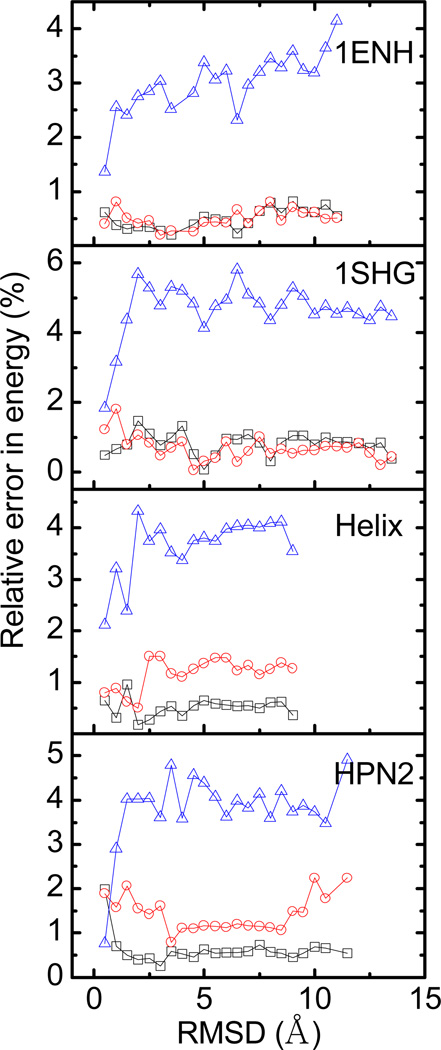
Besides the size dependence, we also studied the conformation dependence of the Revised Density definition. We unfolded two proteins (SHG/ENH) and two peptides (Helix/HPN2) with high-temperature (500 K) molecular dynamics simulations, and analyzed the correlation between energy errors and conformations for about 250 – 500 collected snapshots for each molecule. Figure 4 shows that the conformation dependence of the Revised Density definition is lower, i.e. the energy errors are uniform over the different conformations, shown as different Root Mean Squared Deviations (RMSDs). It is worth pointing out that in the SHG and ENH test sets, the reaction field energies by Revised Density definition are similar to those by the Density definition. In the Helix and HPN2 test set, however, the results by the Revised Density definition are much better than the Density and MVDW definitions. This demonstrates the more consistent performance of the Revised Density definition over different sized molecules.
Figure 4.
Conformation dependence of relative unsigned errors in reaction field energies for the Revised Density definition (square), the Density definition (circle), and the MVDW definition (triangle). To improve clarity, the RMSD’s are binned with a width of 0.5 Å and the error is averaged for each bin before plotting.
Convergence and stability of atomic electrostatic forces
Given the overall improved agreement in the computed reaction field energies between the Revised Density definition and the SES definition, we studied the convergence and the numerical stability of atomic electrostatic forces, which are important for stable dynamics simulations. The convergence quality of atomic electrostatic forces is measured by the correlation and RMSD of atomic forces at a typical coarse grid spacing (1/2 Å) with respect to those at a fine grid spacing, 1/8 Å. The numerical stability of atomic forces is measured by the average standard deviations of individual atomic forces computed with different finite-difference grid origins. Here 64 different finite-difference grid origins were used to analyze the numerical uncertainty of different methods. Two small systems, the native helix structure (from test set Helix) and the native hairpin structure (from test set HPN2), were selected in this analysis because they can be processed with the finest tested grid spacing, 1/8 Å, on our local computer servers.
Consistency of the two methods
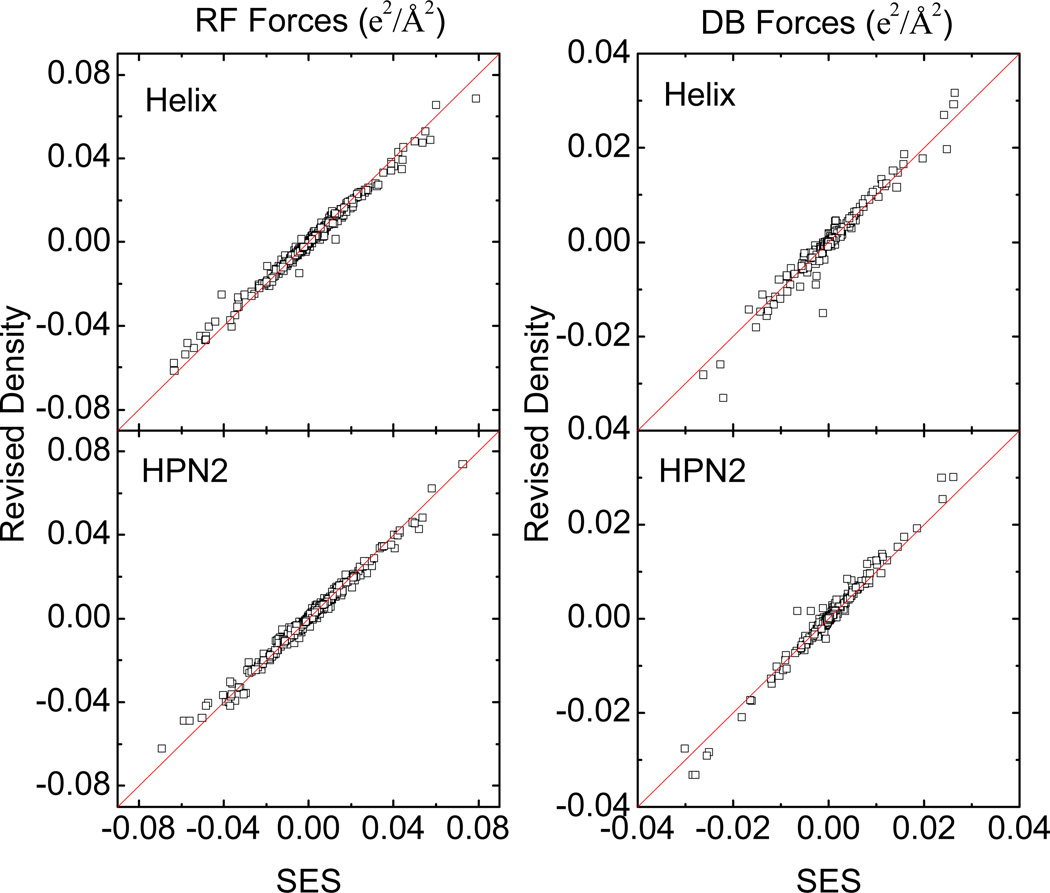
While the two surface definitions are clearly different, we have tried to optimize the Revised Density definition so that the reaction field energies computed with the two surface definitions agree as much as possible. Thus, we expect the correlation of atomic forces computed with the two surface definitions to be reasonable well, at least at the finest grid spacing tested, 1/8 Å. The correlations between the two sets of forces are shown for the two tested molecules in Figure 5. The reaction field (RF) forces are shown on the left, with the correlation coefficients of 0.98730 for the helix and 0.98912 for the hairpin, indicating that the RF forces by SES are reasonably well reproduced by the revised density function. Similarly, the right panel of Figure 5 plots the correlations of dielectric boundary (DB) forces between the two methods for the two tested molecules. The correlation coefficients are 0.95137 for the helix and 0.95848 for the hairpin. Due to the physical nature of the dielectric boundary forces, which act on the molecular surface, they are more sensitive to the exact location of molecular surface. Therefore, the correlation of DB forces is in principle lower than that of the RF forces between the two surface definitions.
Figure 5.
Left: correlation between reaction field (RF) forces computed with the Revised Density definition and those computed with the SES definition. Right: correlation between dielectric boundary (DB) forces computed with the Revised Density definition and those computed with the SES definition. All forces are computed with a grid spacing of 1/8 Å.
Convergence of forces
We next analyzed the convergence of forces at typical coarse grid spacing (1/2 Å) for biomolecular simulations for both the Revised Density and the SES definition. The convergence measures show that the Revised Density definition converges faster than the SES definition in the numerical calculation of RF forces (Table 3) and DB forces (Table 4). The correlations of RF forces for the revised density function are 0.99411 for the helix and 0.98917 for the hairpin, respectively, while the corresponding correlations for the SES definition are 0.96625 and 0.91612, respectively. The RMS deviations of RF forces computed with the revised density function are a factor about two smaller than the corresponding RMS deviations with the SES definition. The convergence comparison for the DB forces is similar. The correlations of DB forces computed with the revised density function are 0.93229 for the helix and 0.95588 for the hairpin, respectively, while the corresponding correlations computed with the SES definition are 0.90205 and 0.84782, respectively. The RMS deviations of DB forces computed with the revised density function are a factor about two smaller than the corresponding RMS deviations with the SES definition.
Table 3.
Convergence and numerical stability of reaction field forces (e2/ Å2) for the tested helix and hairpin at the coarse grid spacing of 1/2 Å. SES: solvent excluded surface definition. CC: correlation coefficient between the forces at 1/2 Å and the forces at 1/8 Å. rmsd: root-mean-squared deviation between the forces at 1/2 Å and the forces at 1/8 Å. σ: average standard deviation of individual atomic forces.
| 1/h | Revised Density | SES | |||||
|---|---|---|---|---|---|---|---|
| CC |
rmsd (×10−4) |
σ (×10−4) |
CC |
rmsd (×10−4) |
σ (×10−4) |
||
| helix | 2 8 |
.99411 NA |
12.7 NA |
3.40 .192 |
.96625 NA |
22.5 NA |
5.04 .274 |
| hairpin | 2 8 |
.98917 NA |
18.5 NA |
5.40 .238 |
.91612 NA |
39.5 NA |
7.59 .326 |
Table 4.
Convergence and numerical stability of dielectric boundary forces (e2/ Å2) for the tested helix and hairpin at the coarse grid spacing of 1/2 Å. See Table 3 for more information.
| 1/h | Revised Density | SES | |||||
|---|---|---|---|---|---|---|---|
| CC |
rmsd (×10−4) |
σ (×10−4) |
CC |
rmsd (×10−4) |
σ (×10−4) |
||
| helix | 2 8 |
.93229 NA |
16.2 NA |
7.08 1.58 |
.90205 NA |
22.4 NA |
15.9 2.27 |
| hairpin | 2 8 |
.95588 NA |
12.8 NA |
12.5 2.64 |
.84782 NA |
33.0 NA |
24.9 2.77 |
Numerical stability of forces
Finally, we analyzed the numerical stability of numerical electrostatic forces for both the Revised Density and the SES definitions. Our stability measure shows that the Revised Density definition is more stable than the SES definition in the numerical calculation of RF forces (Table 3) and DB forces (Table 4): reductions in the standard deviations by a factor about two were observed when the Revised Density definition was used for both types of forces.
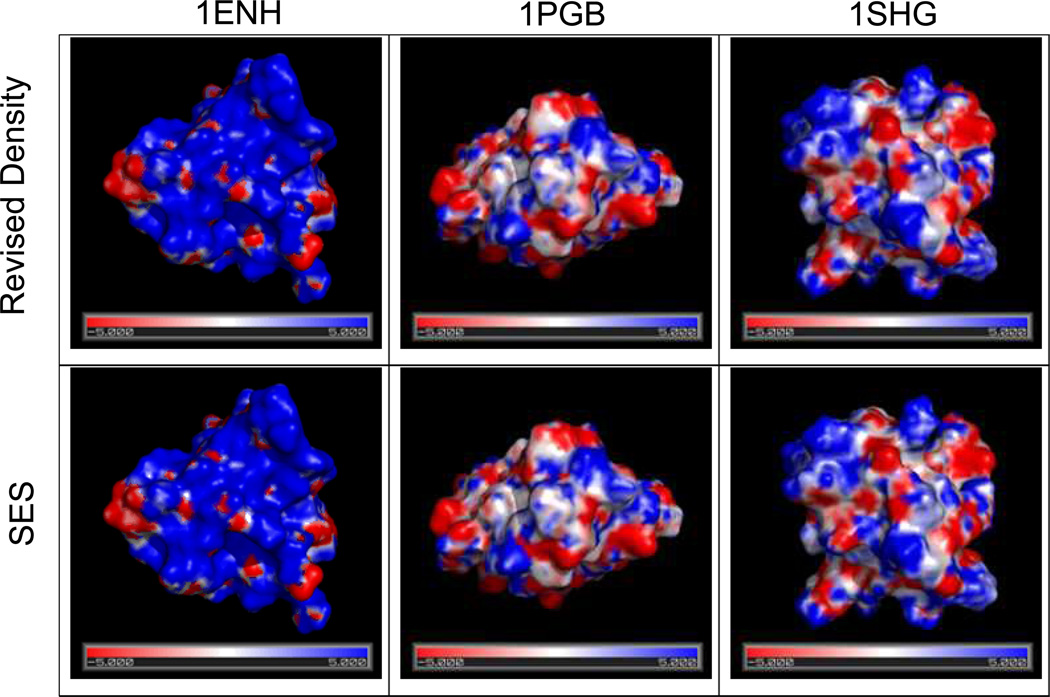
Reproduction of molecular surface
Note that we have solely relied on reaction field energies in the optimization of the Revised Density definition. This is reasonable because the measure based on reaction field energies is quite sensitive to the exact locations of molecular surface. Nevertheless, we have also studied the quality of the Revised Density definition in reproducing the molecular surfaces with the SES definition. Figure 6 shows the molecular surfaces for folded 1ENH, 1PGB and 1SHG. It can be seen that both definitions are quite consistent for these folded proteins. Figure S-1 in the Supplementary Materials shows the molecular surfaces for unfolded 1ENH, 1PGB and 1SHG with the two definitions, respectively. Here slightly more discrepancy can be observed in computed molecular surface. Overall, the molecular surface of both folded and unfolded conformations in the SES definition can be reasonably reproduced by the revised density function.
Figure 6.
Molecular surface determined by the Revised Density and SES definitions for folded conformations of 1ENH, 1PGB, and 1SHG, respectively.
Reproduction of surface electrostatic potential
We further analyzed the surface electrostatic potential of several selected proteins with the Revised Density definition. Figure 7 shows the surface potentials for PGB, ENH and SHG calculated with the revised density function and the SES definition, respectively. Clearly, the two surface potential maps agree very well for the three selected proteins. For the larger p53 tetramer with and without DNA, the agreement is also excellent, as shown in Figure S-2 in the Supplementary Materials.
Figure 7.
Surface electrostatic potential (in kT/mol-e) for protein 1ENH, 1PGB, 1SHG, respectively (from left to right). Upper panel: computed with the Revised Density definition. Lower panel: computed with the SES definition. Potential is visualized in PyMol using a continuous color scale. Blue: positive values; white: zero; red: negative.
Limitation of the density function approaches
A limitation of the Revised Density definition concerns the use of a “unconventionally” small solvent probe, 0.6 Å, which was optimized to reproduce the electrostatic potential of mean forces of dimers and surface salt-bridges on macromolecules in the TIP3P explicit solvent. It is likely that the use of small probe may result in more hydrophilic interior in loosely packed macromolecules. Thus we also tried to use the traditional solvent probe of 1.4 Å in our training of the revised density function. However our analysis shows that the Revised Density definition can perform no better than the MVDW definition even in the training sets (data not shown). Thus, the limitation of the method to applications with smaller solvent probe radii is clearly an issue that needs further considerations to make it a more general numerical procedure for molecular surface calculations. Nevertheless, since our ultimate motivation in the study was to reproduce as close as possible the explicit solvent energetic and it is unclear how quantitative loosely packed the molecular interior would be without detailed explicit solvent simulations, we delay further improvement to a future study. In addition, it is worth highlighting the intrinsic difference between all density function definitions and the SES definition to represent the molecular surface. Indeed, the multi-body reentry region in the SES definition is very difficult if not possible to reproduce with any additive density function approach.
Concluding Remarks
A revised density function is developed to define the molecular surface for dielectric assignment in the numerical PB methods. The density function is optimized through an exhaustive search using a benchmark data set of reaction field energies computed with the solvent excluded surface for a wide-range of proteins and peptides in both folded and unfolded conformations. A uniformly low average unsigned error of less than 1% in reaction field energies can be achieved for both the training and test sets. The maximum errors and error spreads are also smaller than the modified van der Waals definition upon which the new density function was developed. We further studied the transferability of the revised density function. Our data show that the average unsigned errors change little as the molecular sizes increase, confirming the size independence of the method. We also studied the conformation dependence of the revised density function with unfolded conformations of two proteins and two peptides. It turns out that there is little conformation dependence in the revised density function. Next we studied the convergence and stability of numerical electrostatic forces computed with the revised density function. The analysis shows that the revised density function can improve the convergence and numerical stability by a factor of two over the solvent excluded surface. The analysis of computed molecular surfaces shows that the revised density function can well reproduce the solvent excluded surfaces for the three tested proteins in both folded and unfolded conformations. Finally, we also analyzed the performance of the revised density function in reproducing the surface electrostatic potential. The analysis shows that the agreements are very good for different sized proteins, no matter it is neutral or highly charged.
Nevertheless, it is worth pointing out the limitation of the current development documented here. First, it is important to highlight that the numerical instability of the dielectric boundary forces is still higher than that of the reaction field forces. This is in part due to the use of grid-independent surface polarization charges in the computation of reaction field energy and forces, which improves the convergence and stability in the computed energies and forces. In contrast, the dielectric boundary forces were computed directly with the finite-difference grid potential without further treatment. This is in part responsible for their larger error and uncertainty. We are actively working to improve the convergence and stability of dielectric boundary forces by utilizing the grid-independent surface polarization charges, which would further enhance their numerical performance when combined with the revised density function. In addition, partition of dielectric boundary force elements on the solvent/surface interface to nearby atoms is clearly the next natural step before the method can be applied to routine molecular dynamics simulations. We are actively working on both issues in this group.
Second, our analysis shows that the density approximation does not work well for “conventional” solvent probe of 1.4 Å. Fortunately, our prior comparative analysis indicates that the numerical PB methods with a probe radius of 0.6 Å reproduces the TIP3P solvent best on the tested conformations and systems. It is likely that the use of a small probe may result in more hydrophilic interior in loosely packed macromolecules. This apparent dilemma between a molecular interior being too hydrophilic and the best agreement with TIP3P solvent points to the limitation of the hard-sphere-based strategies to define the dielectric model for numerical PB methods. To overcome this difficulty we may revise the molecular surface calculation into a two-step procedure. First, we shall use a large solvent probe to calculate solvent accessibility of each atom. Of course, this procedure should be optimized to be consistent with solvent accessibility simulated in explicit solvent models. For the solvent inaccessible atoms, we will augment their van der Waals radii with an optimized amount that would effectively fill the molecular interior, resulting in a hydrophobic interior. Second, we will still use the density function optimized with the solvent probe of 0.6 Å to compute the reentry region among the solvent-accessible atoms. The proposed strategy is still within the hard-sphere strategies but may resolve the dilemma discussed to a certain degree.
Supplementary Material
Acknowledgements
This work is supported in part by NIH (GM069620).
References
- 1.Davis ME, McCammon JA. Chemical Reviews. 1990;90:509. [Google Scholar]
- 2.Gilson MK. Current Opinion in Structural Biology. 1995;5:216. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 3.Honig B, Nicholls A. Science. 1995;268:1144. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 4.Sharp KA. Current Opinion in Structural Biology. 1994;4:234. [Google Scholar]
- 5.Bashford D, Case DA. Annual Review of Physical Chemistry. 2000;51:129. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 6.Cramer CJ, Truhlar DG. Chemical Reviews. 1999;99:2161. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 7.Roux B, Simonson T. Biophysical Chemistry. 1999;78:1. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 8.Baker NA. Current Opinion in Structural Biology. 2005;15:137. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 9.Chen JH, Im WP, Brooks CL. Journal of the American Chemical Society. 2006;128:3728. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Feig M, Chocholousova J, Tanizaki S. Theoretical Chemistry Accounts. 2006;116:194. [Google Scholar]
- 11.Im W, Chen JH, Brooks CL. Peptide Solvation and H-Bonds. Vol. 72. San Diego: Elsevier Academic Press Inc; 2006. p. 173. [Google Scholar]
- 12.Koehl P. Current Opinion in Structural Biology. 2006;16:142. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 13.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Communications in Computational Physics. 2008;3:973. doi: 10.4208/cicp.081009.130611a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang J, Tan CH, Tan YH, Lu Q, Luo R. Communications in Computational Physics. 2008;3:1010. [Google Scholar]
- 15.Davis ME, McCammon JA. Journal Of Computational Chemistry. 1989;10:386. [Google Scholar]
- 16.Klapper I, Hagstrom R, Fine R, Sharp K, Honig B. Proteins Structure Function and Genetics. 1986;1:47. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- 17.Luty BA, Davis ME, McCammon JA. Journal of Computational Chemistry. 1992;13:1114. [Google Scholar]
- 18.Nicholls A, Honig B. Journal Of Computational Chemistry. 1991;12:435. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 19.Forsten KE, Kozack RE, Lauffenburger DA, Subramaniam S. Journal of Physical Chemistry. 1994;98:5580. [Google Scholar]
- 20.Holst M, Saied F. Journal of Computational Chemistry. 1993;14:105. [Google Scholar]
- 21.Im W, Beglov D, Roux B. Computer Physics Communications. 1998;111:59. [Google Scholar]
- 22.Rocchia W, Alexov E, Honig B. Journal of Physical Chemistry B. 2001;105:6507. [Google Scholar]
- 23.Bashford D. Lecture Notes in Computer Science. 1997;1343:233. [Google Scholar]
- 24.Gilson MK, Sharp KA, Honig BH. Journal of Computational Chemistry. 1988;9:327. [Google Scholar]
- 25.Luo R, David L, Gilson MK. Journal of Computational Chemistry. 2002;23:1244. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 26.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. J. Comput. Chem. 2002;23:128. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 27.Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, McCammon JA. Computer Physics Communications. 1995;91:57. [Google Scholar]
- 28.Nicholls A, Sharp KA, Honig B. Proteins-Structure Function and Genetics. 1991;11:281. doi: 10.1002/prot.340110407. [DOI] [PubMed] [Google Scholar]
- 29.Wang J, Cai Q, Li ZL, Zhao HK, Luo R. Chemical Physics Letters. 2009;468:112. doi: 10.1016/j.cplett.2008.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cai Q, Wang J, Zhao HK, Luo R. Journal of Chemical Physics. 2009;130:145101. doi: 10.1063/1.3099708. [DOI] [PubMed] [Google Scholar]
- 31.Cai Q, Hsieh MJ, Wang J, Luo R. Journal of Chemical Theory and Computation. 2010 doi: 10.1021/ct900381r. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang J, Luo R. Journal of Computational Chemistry. 2010;31 In press. [Google Scholar]
- 33.Baker N, Holst M, Wang F. Journal Of Computational Chemistry. 2000;21:1343. [Google Scholar]
- 34.Cortis CM, Friesner RA. Journal Of Computational Chemistry. 1997;18:1591. [Google Scholar]
- 35.Holst M, Baker N, Wang F. Journal Of Computational Chemistry. 2000;21:1319. [Google Scholar]
- 36.Chen L, Holst MJ, Xu JC. Siam Journal on Numerical Analysis. 2007;45:2298. [Google Scholar]
- 37.Shestakov AI, Milovich JL, Noy A. Journal of Colloid and Interface Science. 2002;247:62. doi: 10.1006/jcis.2001.8033. [DOI] [PubMed] [Google Scholar]
- 38.Xie D, Zhou S. BIT Numerical Mathematics. 2007;47:853. [Google Scholar]
- 39.Hoshi H, Sakurai M, Inoue Y, Chujo R. Journal of Chemical Physics. 1987;87:1107. [Google Scholar]
- 40.Miertus S, Scrocco E, Tomasi J. Chemical Physics. 1981;55:117. [Google Scholar]
- 41.Zauhar RJ, Morgan RS. Journal of Computational Chemistry. 1988;9:171. [Google Scholar]
- 42.Juffer AH, Botta EFF, Vankeulen BAM, Vanderploeg A, Berendsen HJC. Journal of Computational Physics. 1991;97:144. [Google Scholar]
- 43.Rashin AA. Journal of Physical Chemistry. 1990;94:1725. [Google Scholar]
- 44.Yoon BJ, Lenhoff AM. Journal of Computational Chemistry. 1990;11:1080. [Google Scholar]
- 45.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. Journal of Computational Chemistry. 1995;16:898. [Google Scholar]
- 46.Purisima EO, Nilar SH. Journal of Computational Chemistry. 1995;16:681. [Google Scholar]
- 47.Zhou HX. Biophysical Journal. 1993;65:955. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liang J, Subramaniam S. Biophysical Journal. 1997;73:1830. doi: 10.1016/S0006-3495(97)78213-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Vorobjev YN, Scheraga HA. Journal of Computational Chemistry. 1997;18:569. [Google Scholar]
- 50.Boschitsch AH, Fenley MO, Zhou HX. Journal of Physical Chemistry B. 2002;106:2741. [Google Scholar]
- 51.Lu BZ, Cheng XL, Huang JF, McCammon JA. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:19314. doi: 10.1073/pnas.0605166103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Totrov M, Abagyan R. Biopolymers. 2001;60:124. doi: 10.1002/1097-0282(2001)60:2<124::AID-BIP1008>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 53.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Journal of the American Chemical Society. 1990;112:6127. [Google Scholar]
- 54.Onufriev A, Bashford D, Case DA. J. Phys. Chem. B. 2000;104:3712. [Google Scholar]
- 55.Tsui V, Case DA. Journal of the American Chemical Society. 2000;122:2489. [Google Scholar]
- 56.Onufriev A, Case DA, Bashford D. J. Comput. Chem. 2002;23:1297. doi: 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- 57.Im W, Feig M, Brooks CL. Biophysical Journal. 2003;85:2900. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Feig M, Im W, Brooks CL. Journal of Chemical Physics. 2004;120:903. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 59.Onufriev A, Bashford D, Case DA. Proteins-Structure Function and Bioinformatics. 2004;55:383. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 60.Tanizaki S, Feig M. Journal of Chemical Physics. 2005;122 doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 61.Sigalov G, Scheffel P, Onufriev A. J. Chem. Phys. 2005;122 doi: 10.1063/1.1857811. [DOI] [PubMed] [Google Scholar]
- 62.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. Journal of Chemical Theory and Computation. 2007;3:156. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Grant JA, Pickup BT, Sykes MJ, Kitchen CA, Nicholls A. Physical Chemistry Chemical Physics. 2007;9:4913. doi: 10.1039/b707574j. [DOI] [PubMed] [Google Scholar]
- 64.Davis ME. Journal of Chemical Physics. 1994;100:5149. [Google Scholar]
- 65.Luo R, Moult J, Gilson MK. Journal Of Physical Chemistry B. 1997;101:11226. [Google Scholar]
- 66.Li XF, Hassan SA, Mehler EL. Proteins-Structure Function And Bioinformatics. 2005;60:464. doi: 10.1002/prot.20470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Eisenhaber F, Argos P. Journal of Computational Chemistry. 1993;14:1272. [Google Scholar]
- 68.You T, Bashford D. Journal of Computational Chemistry. 1995;16:743. [Google Scholar]
- 69.Zauhar RJ, Morgan RS. Journal of Computational Chemistry. 1990;11:603. [Google Scholar]
- 70.Swanson JMJ, Mongan J, McCammon JA. Journal of Physical Chemistry B. 2005;109:14769. doi: 10.1021/jp052883s. [DOI] [PubMed] [Google Scholar]
- 71.Tan CH, Yang LJ, Luo R. Journal Of Physical Chemistry B. 2006;110:18680. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 72.Wang J, Tan C, Chanco E, Luo R. Physical Chemistry Chemical Physics. 2010;12 doi: 10.1039/b917775b. In press. [DOI] [PubMed] [Google Scholar]
- 73.Lu Q, Luo R. Journal of Chemical Physics. 2003;119:11035. [Google Scholar]
- 74.Chocholousova J, Feig M. Journal Of Computational Chemistry. 2006;27:719. doi: 10.1002/jcc.20387. [DOI] [PubMed] [Google Scholar]
- 75.Alexov E. Proteins-Structure Function and Bioinformatics. 2003;50:94. [Google Scholar]
- 76.Davis ME, McCammon JA. Journal of Computational Chemistry. 1991;12:909. [Google Scholar]
- 77.Grant JA, Pickup BT, Nicholls A. Journal Of Computational Chemistry. 2001;22:608. [Google Scholar]
- 78.Grant JA, Pickup BT. Journal of Physical Chemistry. 1995;99:3503. [Google Scholar]
- 79.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes: The Art of Scientific Computing. 1992 [Google Scholar]
- 80.Stoer J, Bulirsch R. Introduction to Numerical Analysis. 1992 [Google Scholar]
- 81.Gilson MK, Davis ME, Luty BA, McCammon JA. Journal of Physical Chemistry. 1993;97:3591. [Google Scholar]
- 82.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes: The Art of Scientific Computing. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- 83.Osher S, Fedkiw RP. Level set methods and dynamic implicit surfaces. New York: Springer; 2003. [Google Scholar]
- 84.Sethian JA. Level set methods and fast marching methods : evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science. Cambridge, U.K.; New York: Cambridge University Press; 1999. [Google Scholar]
- 85.Landau LD, Lifshitz EM, Pitaevskii LP. [Google Scholar]
- 86.Ye X, Wang J, Luo R. Submitted to JCP [Google Scholar]
- 87.Sharp KA, Honig B. J. Phys. Chem. 1990;94:7684. [Google Scholar]
- 88.Feig M, Onufriev A, Lee MS, Im W, Case DA, Brooks CL. Journal Of Computational Chemistry. 2004;25:265. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 89.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. Journal of Computational Chemistry. 2005;26:1668. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.