Perceiving the average hue of color arrays

Abstract

The average of a color distribution has special significance for color coding (e.g. to estimate the illuminant) but how it depends on the visual representation (e.g. perceptual vs. cone-opponent) or nonlinearities (e.g. categorical coding) is unknown. We measured the perceived average of two colors shown alternated in spatial arrays. Observers adjusted the components until the average equaled a specified reference hue. Matches for red, blue-red, or yellow-green were consistent with the arithmetic mean chromaticity, while blue-green settings deviated toward blue. The settings show little evidence for categorical coding, and cannot be predicted from the scaled appearances of the individual components.

1. INTRODUCTION

Recently a wide array of studies have explored the perception of “ensemble statistics” of scenes, such as the ability to judge the average value of stimuli composed of distributed features [1]. Early reports showed that observers can accurately estimate the average direction of motion of a field of randomly moving dots [2, 3], the average orientation of a set of lines [4, 5], or the average size of a set of circles [6]. Moreover, these judgments can be made without attention [7]or when elements in the display are rendered invisible, for example by crowding [8]. The average of a stimulus set can also be represented more accurately than the individual members, and observers may be sensitive to changes in the average even when they are unaware of a change in the individual elements [9]. This has led to the suggestion that the visual system might directly encode summary statistics such as the average feature properties in order to allow efficient representations of scenes. Similar summary representations have been found for higher-level properties of images, including the perceived gender, identity, or expression of faces [10–12], or the average direction of point-light walkers simulating biological motion [13]. They have also been shown for other modalities such the perception of sound ensembles [14, 15]. This suggests that ensemble coding is a common and consistent property of sensory representations, and have illustrated the importance of perceiving the average of stimulus distributions in visual coding.

In this study we explored average judgments for color. Despite the recent spate of interest in summary statistics in perception, there has been little corresponding work within the context of color perception. As a first step, we examined how well observers could estimate the average of a pair of colors, and what processes might influence their judgments. The approach we used is different from standard procedures used for testing ensemble coding, which are focused on addressing whether the mean value can be extracted automatically or whether it might be represented with higher fidelity than individual members [1]. In this study we had the more limited aim of asking simply what mean observers select when the component hues are fully available for inspection, in order to explore what this average might be based on.

For color the mean may play a special role. For example, the average color in a scene is a clue to the illuminant and thus an important potential cue for color constancy, allowing the visual system to discount spectral variations in order to assign stable colors to objects [16]. Moreover, mechanisms sensitive to the mean color occur very early in the visual pathway. The receptors themselves adapt to the average color sampled over time by successively scanning the scene, a process that is again fundamental to color constancy [17, 18]. Individuals are also very sensitive to a common vs. non-uniform shift in the chromaticities of a set of colors, and thus can readily detect sudden changes in the mean [19]. Yet how and how well they can actually judge the mean remains unknown.

How colors might be perceptually averaged can potentially reveal the stages and representations on which this averaging depends. Color coding is known to undergo a series of transformations at different levels of the visual system[20]. Within the retina and LGN, the initial signals from the long, medium, and short-wavelength sensitive cones (L, M, and S) are re-organized in terms of three cardinal cone-opponent axes: two that carry chromatic contrast based on comparing either the L and M cones (LvsM) or the S signals opposed by the combined L and M signals (SvsLM), and a third non-opponent dimension conveying lightness or luminance [21]. At cortical levels these are elaborated into “higher-order” mechanisms that include color channels tuned to a variety of different hue and lightness directions, and these may not retain the separable contrasts along the cardinal dimensions [22, 23]. For example, cortical responses and visual performance on some tasks may be weaker for the blue-yellow dimension of color space than for a purplish-greenish direction that has the same LvsM and SvsLM component contrasts, but paired in opposite phase [24–26]. The number of further potential transformations remains unclear. However, it is well known that the red vs. green and blue vs. yellow perceptual opponencies that are thought to define the principal dimensions of our phenomenal experience of color are not aligned with the cardinal axes [27–30]. For example, as suggested above, stimulus variations along a perceptually pure blue-yellow axis do not isolate either of the cardinal chromatic axes and are instead roughly midway between them (i.e. these colors lie along a diagonal in the plane defined by the cardinal chromatic axes). Moreover, opposing unique hues such as red and green are not complementary (on opposite sides of gray) in terms of the cardinal axes. Such differences raise the question of which if any “space” an observer might operate within to estimate the relationships or average of a set of colors.

Finally, the representation of color also includes a number of potential nonlinearities that could influence averaging judgments. For example, cone signals and opponent-cone contrasts may reflect compressive nonlinearities in the neural responses which could bias the linear mean of a set of contrasts (e.g. [31, 32]), though in practice responses to moderate contrasts appear roughly linear [33]. At higher levels, color coding may also be impacted by nonlinearities such as categorical coding, in which the stimulus is represented discretely (e.g. as simply green or blue) rather than as a continuously varying hue. Categorical effects have been reported for color in a number of studies (e.g. [34–37], though they remain controversial and it is unclear under which conditions or tasks they might be manifest [38–40]. A tendency to categorize when averaging colors could again lead to different, nonlinear weightings of the component hues in the stimulus, which should again bias estimates of the average in predictable ways.

Summary judgments of color distributions thus provide a potentially rich context for exploring not only ensemble perception but also many of the properties of color perception itself. In the current work, we examine these summary estimates using pairs of perceptually similar colors (e.g. blue and green), where the task of the observer is to judge the relative balance of the pair. A companion paper explores our ability to judge the metrical relationships between more disparate color categories. Here we focus on how well observers can actually judge the mean of colors, whether these means reflect nonlinearities in color coding, and which level of representation (e.g. cone-opponent or perceptual) might underlie the judgments.

2. METHODS

A. Display

Stimuli were presented on a Sony 500PS CRT monitor controlled by a Cambridge Research Systems VSG 2/5 graphics card, which allows colors to be displayed with high resolution. The monitor was calibrated and gamma-corrected using a Photo Research PR650 spectroradiometer.

B. Participants

Observers included one of the authors (JW) and 16 additional participants who were University of Nevada, Reno students and were unaware of the theoretical aims of the study. Different observers participated in different subsets of experiments, with all observers tested in multiple conditions. Because blue-green judgments have been a focus of recent studies on color appearance and categorical coding, we tested larger numbers of observers for this target color (a total of 13 for the yoked condition and 7 for the fixed hue condition, as defined below). This was in order to fully evaluate the pattern of the settings for this color. For the remaining target colors, smaller subsets of observers were tested, typically with 4 observers assessed for a given condition. All participants had normal color vision as assessed by the Cambridge Colour Test and normal or corrected-to-normal acuity. Participation was with informed consent following protocols approved by the university’s Institutional Review Board.

C. Stimuli

For all experiments the stimulus consisted of an 11 by 11 square array of 0.75 deg uniform circles with a center-to-center spacing of 0.02 deg (Figure 1). The array was shown on a uniform 15 by 20 deg gray background with the chromaticity of (CIE 1931 x,y: 0.31, 0.316) and the same luminance as the array (30cd/m²). Each circle included a narrow black outline to help demarcate it from the background. The array could be composed of a single color common to all elements, or alternated between two different colors. The colors were specified within a scaled version of cardinal axis space, in which the two axes correspond to the LvsM and SvsLM cardinal chromatic directions and chromaticities are given by their angle and distance from the gray neutral point. Signals along the LvsM and SvsLM axes were scaled based on previous studies to roughly equate contrast sensitivity with units corresponding very roughly to multiples of threshold. The relationship between coordinates in our scaled space and the r_mb, b_mb coordinates of the MacLeod-Boynton chromaticity diagram[41] is given by:

$$\text{LvsM}\text{contrast}=({\mathrm{r}}_{\text{mb}}-0.6568)\ast 2754$$ (1)

$$\text{SvsLM}\text{contrast}=({\mathrm{b}}_{\text{mb}}-0.01825)\ast 4099$$ (2)

Fig. 1.

Stimulus Array (color online) – An example of the stimulus array with the elements alternating between the two colors. In one task (yoked hue pairs) the hue angle between the two components remained constant and the pair were varied together to make the setting. In the second task (fixed single component) the color corresponding to the corner elements remained fixed while observers varied the hue of the second component.

Within this space, the cardinal axes corresponded to angles of 0 and 180 deg (+LvsM and −LvsM) and 90 and 270 deg (+S and −S). A common scaling was used for all observers, with luminance defined photometrically. Contrast matches across the different axes (not reported) showed that this nominal scaling roughly equated the perceived suprathreshold contrasts for our observers. In uniform hue conditions contrast was varied at values of 20, 40, 60, or 80 while the hue angle of the components remained the same (in other words, there was no hue difference between the components). The range of contrasts for the uniform condition was measured in part to test whether any shifts in the average hue of a pair could be due to a change in perceived hue with contrast (since the physical mixture of a pair of hues with the same contrast has a lower physical contrast than the components). For the two-component experiments, the contrast was fixed at a value of 80, and the component colors were instead varied only in their hue angle.

D. Procedure

Observers freely viewed the display binocularly from a distance of 114cm in an otherwise dark room. In some trials (yoked hue pairs) the angular difference between the pair of colors remained fixed while observers adjusted the absolute angles of the pair. The two components were separated by angles of 10, 20, 40 or 80 deg for these yoked conditions. In a second set of conditions (fixed single component) one of the component colors was fixed and the observer instead varied the angle of the remaining color. In this case for the different settings the fixed angle was varied in 10 deg increments over a wide range of angles spanning either side of the chosen target color. In both cases the task of the observer was to adjust the pair until the average matched a specified criterion. A specified criterion color was never shown to the observer (and indeed corresponds to different physical stimuli for different observers). Thus the setting was based on an internal reference for the color judgment, which is a standard procedure for measurements of color appearance. Specified criteria included balanced binary hues of blue-green (i.e. an equal perceived mixture of blue and green), red-blue, or green-yellow, or a unique red (i.e. a red that appeared neither bluish nor yellowish). These four hues were selected because for single colors they lie roughly along the 4 poles of the cone-opponent space, and thus allowed us to sample how colors were averaged in terms of the signals along the cardinal axes.

The instructions to the observer were, for example in the blue-green trials, to ‘adjust the pair of colors until the average appears ‘to have an equal amount of blue and green present,’ though the nature of the staircase task required that they simply report whether the average was “too blue” or “too green,” The initial hue angles of the test stimuli were set at random values varied around the 4 poles of the cardinal axes (so that they were in the rough vicinity of the relevant quadrants of color space for each target color). Hue angles of the test stimuli were then varied with a staircase procedure based on the response to the pair (again “too blue” or “too green” for the blue-green judgment). On each trial, the array was displayed for 250 msec, and then returned to a gray screen for 1500 msec during which the observer made their response. This sequence continued until the staircase reversed directions 13 times, with the chosen angle based on the mean of the last 8 reversals. Four repeated settings were made for each hue combination, with the stimulus condition (hue separation or which hue was fixed) counterbalanced across runs., Results reported are based on the means and standard deviations of these 4 repeated settings per observer and condition.

3. RESULTS

A. Yoked Hue Pairs

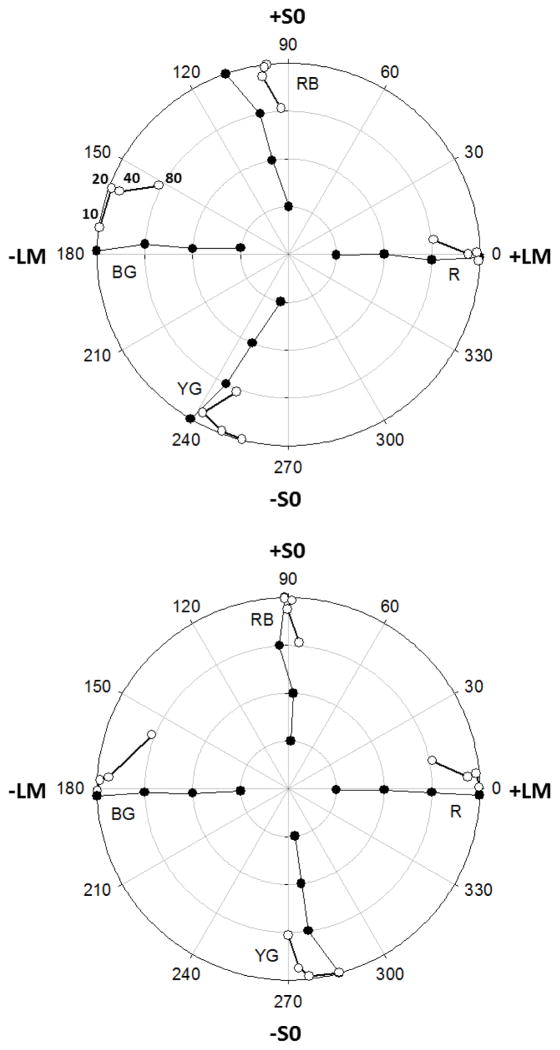
In the first set of experiments we explored the average hue in color pairs that differed by a fixed hue angle and thus were covaried to set the average. Figure 2 illustrates the resulting settings for two representative observers, by plotting the coordinates of the settings in the LvsM and SvsLM plane. The filled symbols show the settings when the array was composed of a single color, with the contrast fixed at a value between 20 and 80. These replicate the basic features found previously for the loci of unique and binary hues in the cone-opponent plane [27, 28]. Unique red is close to the +L pole of the LvsM axis, while the remaining three poles instead correspond to balanced mixtures of blue-green (−L), red-blue (+S), or yellow-green (−S). The two figures also illustrate the large individual differences in hue loci among color-normal observers [27, 42].

Fig. 2.

Results for yoked hue pairs. Examples of the individual settings made by two observers for each of the 4 reference hues (BG blue-green; RB: blue-red: RB; red: R; YG: yellow-green). Filled symbols plot the settings when both components had the same hue (i.e. a hue-angle difference of 0) and were presented at four levels of contrast (20, 40, 60, or 80, corresponding to the increasing concentric circles). Unfilled symbols plot the settings when the pair had a constant fixed contrast of 80 and thus lay along the outermost circle, but differed in hue angle by 10, 20, 40, or 80 deg, with the average for larger differences plotted closer to the origin consistent with the actual chromaticity of the mixture (as indicated for the four blue-green hue pairs in the top panel).

The unfilled symbols plot the settings when the array was composed of two different hues, with the difference varying between 10 and 80 degrees, with the contrast of the two components fixed at 80. To aid visualization, the contrast of the average is arbitrarily given by the actual mean of the two chromaticities in the pair, which obviously plots within the circle on which the two components lie, and closer to the origin the greater their separation. For example, for a hue difference of 80 the mixture has a contrast of 61. (Importantly, however, this is not intended to imply that for the observers the average for the pair necessarily appeared to have a lower average contrast than either component.)

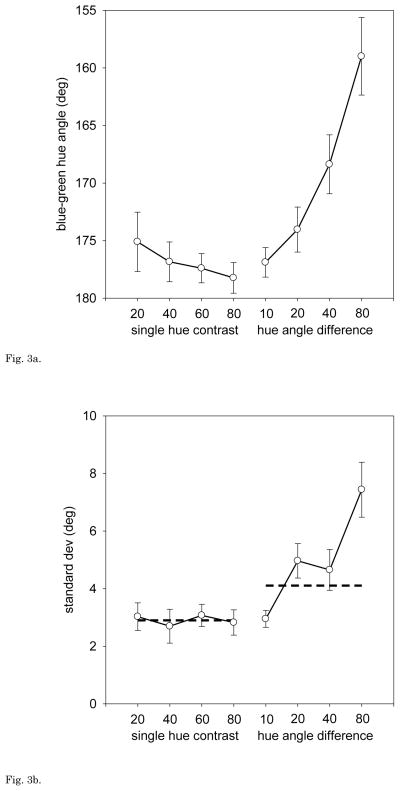
For both observers there are conspicuous biases in the blue-green settings as the average difference between the two component hues increases, and this was a consistent trend across all observers. For example, Figure 3a shows the mean settings for 12 individuals. As the angular difference within the pairs increases, the average rotates toward progressively shorter angles. This corresponds to assigning less weight to blue (or more weight to green) Note that this effect cannot reflect changes in the contrast of the physical mean, since the hue angles chosen with the uniform arrays remain roughly independent of contrast. Instead, there is a strong and consistent nonlinearity in blue-green average judgments, at least when represented within the linear cone-opponent space.

Fig. 3.

Fig. 3a. Yoked Hue Pairs: Mean blue-green settings for 13 observers as a function of the contrast of a uniform-hue array (leftmost points) or the hue-angle difference of pairs with a fixed contrast of 80 (rightmost points). Error bars = ±1 SEM.

Fig. 3b. Yoked Hue Pairs: Average standard deviation of the individual’s settings for the same stimuli, based on 4 repeated settings per condition. Error bars = ±1 SEM. Dashed lines – predicted difference in the standard deviation of the settings for the uniform vs. 2-component arrays if the errors in judging the two components are independent and additive.

The mean shifts with increasing separation were accompanied by more variable judgments of the average. This is shown in Figure 3b, which plots the average standard deviation of the 12 observers’ settings. Variance was significantly greater even when the two components differed only by 20 deg (t = 2.91, df = 22, p = .008). If sensitivity to the average were limited by the uncertainty in judging the hue of the individual components, then the variance should be twice as large for the pairs (Figure 3b, dashed line). However, by a separation of 80 the estimates exceed this value (t = 3.50, df = 11, p = .005). Thus the ability to estimate the average of the two colors shows both systematic biases and increasing error as the difference between the colors increases.

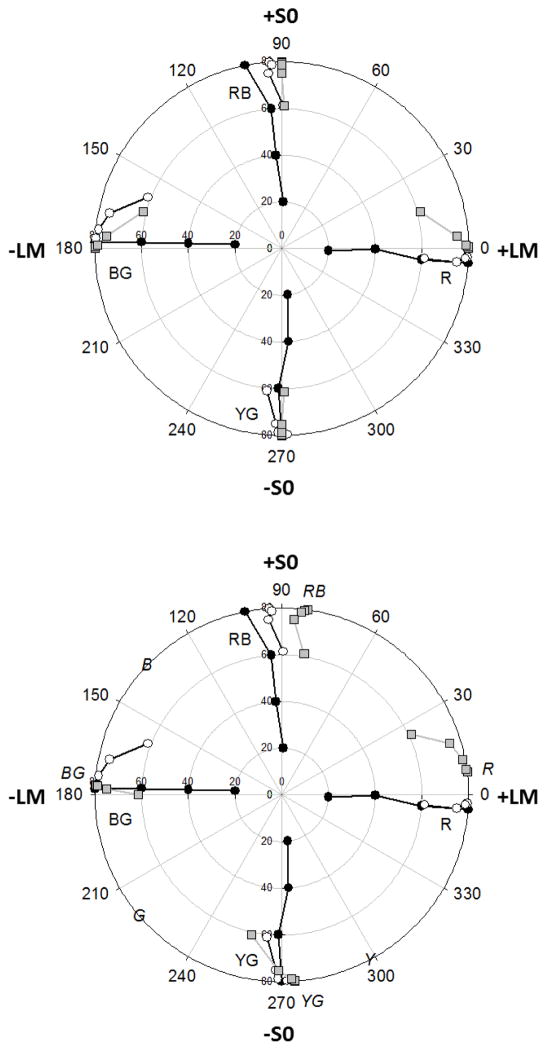
While individual differences were large, we did not find similar consistent biases for the other 3 reference hues examined. This can be seen in Figure 4, which plots the average of the settings for all observers for each of the 4 measured hue loci. Average settings for red remained aligned with the uniform color judgments along the +L axis. The averages for blue-red and yellow-green are instead shifted slightly though again there were large individual differences and thus these overall shifts are not significant.

Fig. 4.

Yoked Hue Pairs: Average settings for the R, RB, BG, or YG hues, based on 4 or more observers tested for each hue. As in Figure 2, filled circles plot the settings for uniform arrays presented at four levels of contrast. Unfilled circles plot the settings for 2-component arrays where contrast was fixed at a value of 80 while hue angle differences between the two components were 10, 20, 40, or 80 deg. Gray squares show the settings predicted if observers are basing their responses on the mean of the log cone-opponent responses (top) or on the average of the perceived red-green and blue-yellow proportions in each component based on hue scaling (bottom). Italic characters in the bottom figure show the loci of the unique and binary hues given by the hue-scaling function.

We considered four possible bases for the observed matches. The first was optical, and assumed that the matches are linear with cone excitations but appear biased in the blue-green region because of chromatic aberration. Wavelength-dependent blurring produces large losses in chromatic contrast in the retinal image, and is a major factor contributing to the fall in chromatic contrast sensitivity with increasing spatial frequency [43]. These aberrations may also be responsible for large size-dependent changes in the relative salience of different chromatic signals in arrays similar to those we used [44]. Obviously, simply blurring the two colors together would not be expected to alter the average. Yet chromatic aberration could impact the balance if it blurred one component more than the other, and the predicted differences in blur are in fact largest for the blue and green pair [45]. Thus we cannot exclude some contribution of this factor. However, it is unlikely to be the only cause of the biases. First, the fundamental spatial frequency of the array was in fact low (0.5 c/deg). Second, if the matches are based on simply the average chromaticity, then the required contrast differences between the blue and green are far too large (e.g. assuming the blue green balance is at 180 deg, the match at 160 deg when the blue and green are 80 deg apart requires that the blue contrast is only 40% of the green contrast:sin(200°) + 0.4sin(120°) = sin(180°)). Instead, direct contrast matches between stimuli at different hue angles suggested that perceived contrast was similar along the different axes. Finally, it cannot be due to blur-induced changes in the perceived hue angle of the stimuli, since the perceived hue of the spots remained stable when we doubled or halved the viewing distance.

The foregoing suggests that at least part of the blue-green bias reflects non-linearities in the cone-opponent responses. For example, suppose that observers’ judgments are based on a compressive nonlinearity such as the log of the cone responses (Figure 4a). This would predict that S cone increments (hue angles >0 deg and < 180degand thus above the LvsM axis) would have weaker effective contrast than S cone decrements (angles >180 deg and <360deg). Predictions based on this assumption (gray squares in Figure 4a) provide a rough approximation to the shifts toward (weaker) blues in the blue-green settings. It also predicts the absence of biases along the S axis itself, where the average instead depends on balancing the L and M responses. This is because along this axis the L and M signals are opposed, and thus the modeled nonlinearities within each largely cancel. This asymmetry is seen in how light adaptation alters the effective color contrast along the LvsM and SvsLM axes [46, 47]. However, this account fails for the red settings, since like the blue-green axis these again depend primarily on balancing the S cone signals and thus should show the same biases as blue-green. Moreover, nonlinearities in the cone-opponent contrasts are more generally an unlikely explanation because as we noted above, under a constant state of adaptation the cone-opponent contrasts appear fairly linear [21, 33, 48].

In the third case, we asked whether the average hues could be predicted from the average appearance of the component colors. That is, observers might first judge the proportion of blue and green in the individual elements, and then adjust these so that these perceived proportions are balanced. This could potentially imply a very late neural locus for the judgments, at a level where the stimuli are coded in terms of their perceptual dimensions. To examine this, we used previous measures of hue scaling functions, in which observers rate the proportion of red vs. green or blue vs. yellow present in the hue. Malkoc, Kay, and Webster [49] sampled these at 15 deg intervals in the LvsM and SvsLM plane, at a contrast similar to the one we used in the current study. We used their average reported function (Figure 3 of their paper) and then used a spline interpolation to estimate the values for intermediate angles. We then calculated the cone-opponent angles that would be required so that the average of the perceived hues of a pair equaled the chosen reference hue. For example, if one spot appeared 30% blue and 70% green, then the second spot would need to appear 70% blue and 30% green to form a balanced blue-green. These predictions are shown in Figure 4b. Note that the hue angles based on the hue scaling are in good agreement with the average hue loci for the uniform arrays measured in the current study. However, these again fail to predict the mixtures, and in particular, in this case predict large biases in the red averages while very little bias for blue-green, the opposite of the pattern we actually observed. Intuitively, these predictions reflect the fact that, as noted on the figure, unique yellow and blue are very different angular distances from unique red (~60 vs. 135 deg respectively). Thus a pair of hues symmetric about the red locus will have a stronger yellow than blue component, and the pair must be biased toward blue to compensate for this. Conversely, the loci of blue and green are at more similar distances from the blue-green boundary (~40 vs. 35 deg away from a blue-green boundary at 180 deg), so that pairs straddling the blue-green locus should remain perceptually balanced.

Finally, because the stimulus is composed of spatially interleaved elements, as a fourth possibility we considered whether the biases in the mean for BG could result from chromatic induction between the components. To account for the BG shifts this would need to be asymmetric and stronger from the blue (i.e. so that blue components caused larger hue shifts in the green elements than vice versa). However, this should again predict that the biases should systematically vary with the spatial frequency of the stimuli and would again be expected to show similar shifts for the unique red settings, if the induction is controlled by separable signals along the cone-opponent axes [50]. Moreover, this account is again based on the assumption that observers base their mean percepts on the phenomenal appearance of the component colors. Induced changes in appearance would therefore need to effectively cancel the biases predicted by the perceived color of the isolated components in the red settings, requiring that the induced bias produce shifts in opposite directions for the BG and R averages (Figure 4b). For these reasons, induction also fails to account for the observed pattern. In summary, whatever the basis for the averaging, these analyses surprisingly suggest that it is not based on simply averaging either the perceived hue of the individual components or on the mean of separable signals along the LvsM and SvsLM cone-opponent axes.

B. Hue Pairs With A Fixed Component

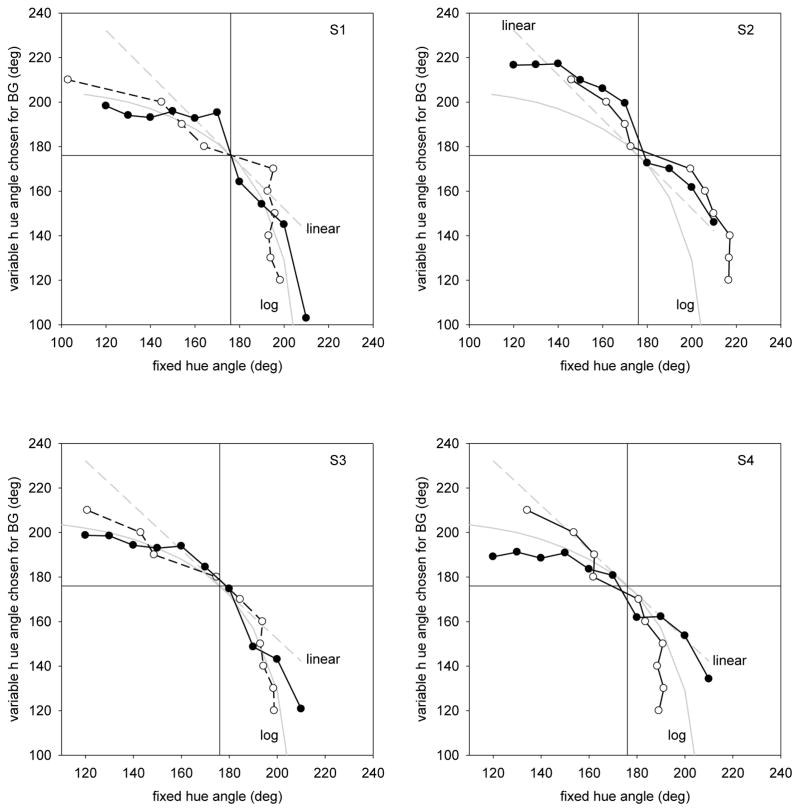
In the second set of experiments, we modified the procedure so that the hue angle of one of the two components remained fixed, while the observer varied the angle of the second component to set a specified average color. Representative results for 4 observers are again shown in Figure 5, which this time plots the chosen variable hue as a function of the fixed hue angle. For the blue-green settings, the fixed component was set to angles ranging from 120 to 210in 10 deg increments. If the average depended on the linear mean of the cone-opponent signals, then the settings should lie along a straight line passing through the blue-green locus (i.e. if the fixed hue were 20 deg off in the green direction then the variable should be set to be 20 deg in the blue direction, etc.) Instead, the matches are clearly curved, again consistent with a weaker response to blue components than the green. In fact as the figure shows, the blue-green settings are again reasonably approximated by assuming the average is based on the log of the S cone signals. However, as we found before, the settings for the remaining three target hues were instead roughly linear. Thus the pattern of results remained similar across the two paradigms.

Fig. 5.

Fixed Single Component: Blue-green settings for 4 individual observers when one of the two color components remained fixed. Filled symbols plot the original measured settings. Unfilled symbols plot the mirror settings by exchanging the abscissa and ordinate. Gray lines plot the settings predicted by averaging the linear or log cone-opponent responses.

We chose the fixed-hue conditions because they allowed us to test for possible categorical biases in the matches. These are predicted to occur if the subject represents the colors discretely in terms of their dominant hue (e.g. treating all hues composed of more than 50% blue as simply “blue”). In the extreme, this would mean that whenever the fixed hue lay on the green side of the blue-green boundary, balancing it would only require setting the variable hue to be just on the blue side of the boundary. In particular, the staircase should converge at the category boundary, where the percept of the average shifts from “too green” to “blue-green.” This extreme is clearly unrealistic, because it also predicts that we would not be able to discriminate between different shades within either category. However, it remains possible that there are categorical biases that might lead the observer to give extra weight to the dominant hue in the stimulus. To test for these, we followed Webster and Kay[39] in assuming that the response to the stimulus was composed of two decisions, an analog response that varied continuously with hue angle and a discrete response that represented the color category. The response for each color in the pair could then be modeled as a weighted average of these two components, with the balance matched by equating the total responses:

$$(1-\mathrm{\alpha }){\mathrm{\Theta }}_{\mathrm{F}}+\mathrm{\alpha }{\mathrm{\Theta }}_{\mathrm{C}1}=(1-\mathrm{\alpha }){\mathrm{\Theta }}_{\mathrm{V}}+\mathrm{\alpha }{\mathrm{\Theta }}_{\text{CB}}$$ (3)

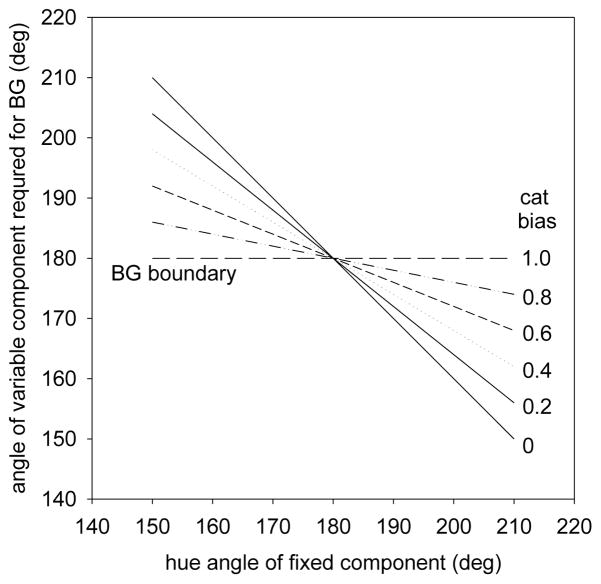
where Θ_F and Θ_V are the responses at the fixed (F) vs. variable (V) hue angles, Θ_C1 and Θ_CB are the categorical responses to the fixed angle (CF) and to the second stimulus as the hue angle crosses the category boundary (CB), and α is the weight given to the categorical response. As α increases, the categorical bias increasingly pulls the setting of the variable hue angle toward the category boundary, leading to an asymmetry where smaller offsets of the variable hue angle from the boundary are required to balance the color of the component with a fixed hue angle.

Figure 6 illustrates the matches for different degrees of categorical bias, assuming the matches follow the linear average of the hue angles. These lie along the negative diagonal if there is no categorical bias, and along the fixed blue-green boundary as the limit of complete categorical coding is approached. As we have seen, the blue-green settings themselves are not linear. Yet regardless of their form, an analog representation of the hues predicts that the same matches will occur whether the green or blue component is fixed. In contrast, any categorical bias should instead lead to an asymmetry in the settings, since the variable angle will be pulled toward the category boundary. That is, a weak blue will be sufficient to match a strong fixed green, yet a weak green will suffice when a strong blue is fixed. In the settings, this asymmetry can be revealed by reflecting the matches about the blue-green boundary – exchanging the x and y values in the plots. Without a categorical effect the two curves should superimpose, while a categorical bias should instead result in a steeper slope for the reflected settings. For the first 3 observers in Figure 5, there is little evidence of a systematic asymmetry between their original and reflected settings. Intriguingly however, the fourth plot shows one observer who shows what appears to be a substantial categorical bias – her reflected settings are consistently steeper. In fact, her settings are reasonably fit by assuming a log compressive S cone response combined with an equally weighted (α = 0.5) categorical response.

Fig. 6.

Fixed Single Component: Predicted settings for different levels of categorical bias, assuming the unbiased settings are based on the arithmetic mean of the hue angles (analog response), and the bias is to instead simply select the matching color at the categorical boundary (categorical response). Settings range from a slope of -1 for no categorical bias to constant settings at the blue-green boundary for a complete bias.

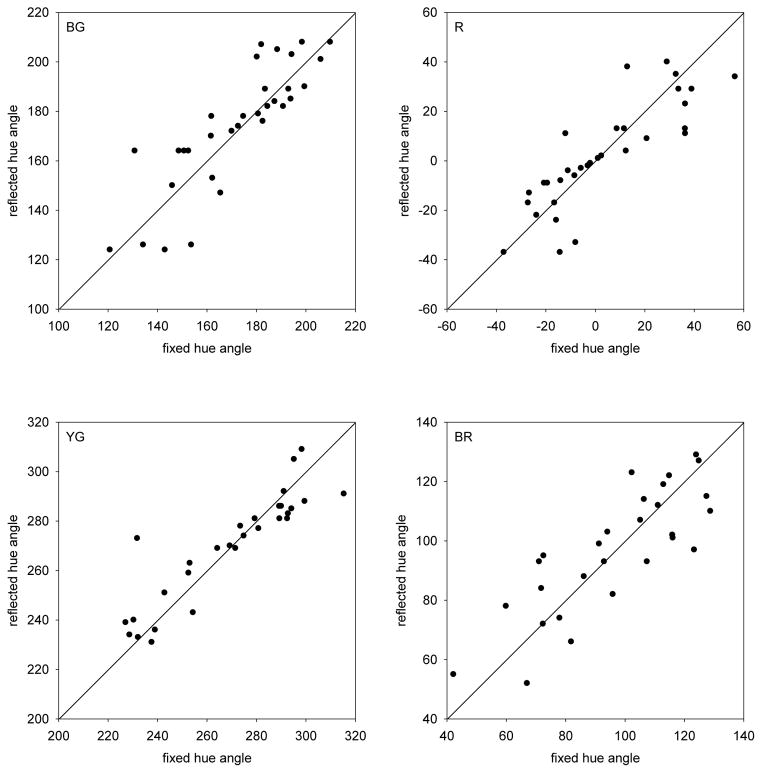
To formally test for categorical effects, for each fixed hue (e.g. 120deg) we compared the chosen setting for that hue (e.g. 200deg), to the setting predicted when the variable hue was instead assumed to be fixed (i.e. start instead with a fixed hue of 200 deg and see if the variable hue was set to 120deg). Again this should reproduce the original fixed hue if the settings are symmetrical, whereas categorical effects should bias the reciprocal setting toward the reference boundary. To estimate the reciprocal matches, the curves shown in Figure 5 were again interpolated with a cubic spline. Figure 7 plots the settings for each of the fixed hue angles vs. their complements. The 4 panels show the results pooled across observers for each reference hue. These settings are variable, for as seen above the judgments of the average color of the pair is itself noisy. However, for each color the settings do not deviate from the trend predicted by a pure analog response to the colors. Thus at least for the average settings across all observers, the results argue against a strong presence of a categorical bias in the judgments.

Fig. 7.

Fixed Single Component: Comparisons between the actual settings of the variable hue angle chosen when one component was fixed (fixed hue angle), and the predicted settings when these match angles were instead taken as the fixed angles and the corresponding matching hue was selected from the reflected function (reflected hue angle). Positive diagonal corresponds to equal symmetric matches in the two cases. Symbols plot the settings for individual observers. Each panel shows the settings for the labeled average hue.

4. DISCUSSION

In this study, we explored the ability of observers to judge the average of a pair of colors, and a first notable result is that they could in fact reliably perform the task (though performance significantly worsened as the color differences increased). A related result was also reported by Fuchida, Cowan and Wyszecki [51] in a similarity judgment where subjects were instead shown a pair of colors and then asked to adjust a variable color until it appeared to bisect the pair while minimizing the perceived difference. In our study we instead used an array of alternating colors and asked observers to judge the average according to an internal reference. The array was chosen in part to highlight the appearance of the stimulus as a texture. We did not test whether different settings might have been found if only two colors were presented or if observers were shown an external reference to match. However, our results and those of Fuchida et al. suggest that observers can in general make such judgments.

While observers were asked to set the pair of colors to a specified “average” hue, our results also do not demonstrate or require that they directly experienced this hue in the stimulus. For an attribute like color the mean could in principle be directly encoded simply by including mechanisms with large receptive fields. In fact something like this happens in color assimilation, in which colors within patterns tend to fuse together. These can lead to percepts in which the blended mean and individual components are simultaneously perceived, and one account for this is that the patterns is encoded by mechanisms operating in parallel at multiple spatial scales[52]. However, the periodicity in our stimuli was again a very low spatial frequency with clear separation between the clearly distinct elements, and assimilation effects were not visible in the arrays. Thus a physiological basis for the averaging is less certain, and perhaps not necessary. An alternative account of the settings is that observers were comparing the “amounts” of different hues, and adjusting the hue angles so that these amounts appeared equal. The “average” for our target hues should occur when the amounts of the two components were equal, and judging this would not require explicitly representing the mixture. Importantly, in the present conditions these comparisons were in principle sufficient for accomplishing the task. That is, to judge whether the mixture was a balanced blue-green, observers could compare the relative quantities of “blueness” vs. “greenness” in the two chromaticities (though as we note below these need not correspond to the labeled “blueness” or “greenness” in the stimuli). In further studies we are exploring larger color differences or judgments, in which the target hue cannot be indirectly inferred from the constituent hues. Observers are very poor at these tasks, and this supports an account in which observers are simply comparing the relative magnitude of the two colors rather than directly computing an average.

Whatever its basis, the balance of angles chosen for the hues revealed strong and consistent biases in the blue-green region. As noted, these may in part be due to chromatic aberration, but also point to neural nonlinearities. These in turn cannot be accounted for by the independent responses along the cardinal cone-opponent axes, since the biases are not separable along these axes. Moreover, they were not predictable from the color appearance of the individual components. We do not currently have an explanation for the pronounced shifts in the blue-green settings compared to the more linear matches along the other axes we examined.

Another aim of our work was to test whether the judgments were susceptible to categorical biases. Categorical effects in color perception remain controversial. A number of studies have found that visual search or color discrimination is faster for pairs of stimuli that fall within different rather than the same linguistic categories [34, 36, 37, 40, 53]. However, others have failed to replicate these effects [38, 39, 54]. Moreover, several authors have noted the possibility that these tasks may reflect linguistic effects on the response rather than the perception of the stimuli [34, 39, 53, 55, 56]. In a recent study we explored categorical effects on color appearance using a perceptual grouping task, specifically to limit the influence of a speeded response on the task[39]. The tendency to group shades of blue and green based on similarity showed very little influence of their relationship to the blue-green boundary. In the present study we similarly used a task in which the emphasis was on the accuracy rather than the speed of the response, to again try to place less weight on factors that might influence the response rather than the percept. Like the perceptual grouping task, for the present averaging task, we found that judging the balance between two colors is not strongly affected by their category, and specifically that observers showed little evidence of over-weighting a hue simply because it fell within a linguistic category. Thus these results again suggest that the actual appearance of color may be impervious to the verbal labels used to classify it. Notably, both the grouping and averaging task made no reference to the hues of the individual components (though we did of course ask observers to adjust the balance in terms of a given color label). In a hue scaling task – where color labels are explicitly used to describe the colors – categorical effects do emerge [39]. As also noted, at least one observer (Figure 4d) did show evidence of a fairly strong categorical bias. Our results do not reveal the basis for these possible individual differences. However, it is tempting to speculate that this observer was to some extent simply labeling the stimuli by their dominant hue, and basing their average on these labels (i.e. without actually “seeing” the stimuli differently). Our paradigm did not manipulate attention in ways that might more clearly isolate preattentive processes in ensemble coding [50]. Yet even when the potential for any type of strategy was available to them, it is notable that most observers showed no evidence that color labeling influenced their judgments.

Categorical effects on color appearance are generally weak. For example, even when they have been found they represent only minor biases in performance. Thus the debate is over whether they show up at all, and not whether they dominate the judgment. Given this, it is not surprising that these effects were largely absent in the present task, especially since the variability in the averaging judgment means that it can only provide a fairly insensitive test for categorical coding. What is much more surprising is that the phenomenal color appearance of the individual stimuli did not even seem relevant to the judgment of the average color. That is, the amount of red vs. green or blue vs. yellow, as reported in tasks such as hue scaling, did not predict how red-green or blue-yellow the ensemble appeared. This dissociation between color appearance and performance has also been reported in a recent study of visual search [57]. The present results suggest that whatever the processes or judgments observers were using to balance the hues, they are largely impervious to how the colors are described, and thus reflect perceptual computations that not only are not be mediated by language, but more importantly may not be mediated by phenomenal color appearance.