Abstract
We implemented and optimized seven finite-difference solvers for the full nonlinear Poisson-Boltzmann equation in biomolecular applications, including four relaxation methods, one conjugate gradient method, and two inexact Newton methods. The performance of the seven solvers was extensively evaluated with a large number of nucleic acids and proteins. Worth noting is the inexact Newton method in our analysis. We investigated the role of linear solvers in its performance by incorporating the incomplete Cholesky conjugate gradient and the geometric multigrid into its inner linear loop. We tailored and optimized both linear solvers for faster convergence rate. In addition, we explored strategies to optimize the successive over-relaxation method to reduce its convergence failures without too much sacrifice in its convergence rate. Specifically we attempted to adaptively change the relaxation parameter and to utilize the damping strategy from the inexact Newton method to improve the successive over-relaxation method. Our analysis shows that the nonlinear methods accompanied with a functional-assisted strategy, such as the conjugate gradient method and the inexact Newton method, can guarantee convergence in the tested molecules. Especially the inexact Newton method exhibits impressive performance when it is combined with highly efficient linear solvers that are tailored for its special requirement.
Introduction
Electrostatic interaction plays a key role in determining the structure and function of biomolecules.1-14 However, modeling of the electrostatic interaction in biomolecules remains a serious computational challenge. The difficulty in modeling a biomolecular system resides in its high dimensionality, especially when explicit solvents are used. Explicit solvents can provide a realistic description of the solution system but require expensive computational resources. In contrast, implicit solvent representation reduces the system degrees of freedom by capturing the average or continuum behavior of the solvent. To model the electrostatic interaction in the salt water solution, the Poisson-Boltzmann equation (PBE) has been widely used:
| (1) |
where ) is the dielectric constant, ) is the electrostatic potential, ρ0 is the solute charge density, λ is the ion-exclusion function with values of 0 within the Stern layer and the molecular interior and 1 outside the Stern layer, e is the unit charge, zi is the valence of ion type i, ci is the number density of ion type i, kB is the Boltzmann constant, and T is the absolute temperature. For a solution with symmetric 1:1 salt, eqn. (1) can be simplified to
| (2) |
where and . Here “out” denotes the outside solvent, I represents the ionic strength of the solution and I = z2c. If the electrostatic potential is weak and the ionic strength is low, the nonlinear PBE can be simplified to the linearized form15
| (3) |
The linearized PBE is easier to solve but it is not very accurate in modeling highly charged biomolecules, such as nucleic acids, while the nonlinear PBE predictions have been shown to yield good agreement with experiments and explicit ion simulations.16-20 Solution of the nonlinear PBE has attracted much attention in the past. Just as linear PBE solvers, these methods can also be grouped into three categories according to how the PBE is discretized, that is, the finite difference method (FDM),17,19,21-27 the finite element method (FEM),28-34 and the boundary element method (BEM).35-37 A combination of the FDM and BEM38 was also reported. Some of these methods have been incorporated into the widely used PB programs, including Delphi,24,26 UHBD,23 PBEQ,24 and APBS.28,31 This study intends to evaluate the existing nonlinear FDM solvers and explore strategies to improve their performance.
After the nonlinear PBE is discretized with the FDM, a nonlinear system is generated as follows
| (4) |
where i, j, and k are the grid indexes along x, y and z axes, respectively. is the dielectric constant between grids (i, j, k) and (i+1, j, k). and are defined similarly. h is the grid spacing in each dimension. φi,j,k is the potential at (i, j, k). qi,j,k is the total charge within the cubic volume centered at (i, j, k). The nonlinear system can then be denoted as
| (5) |
where A is the coefficient matrix for the linear part of the PBE, which is a positive-definite matrix, φ is the potential vector, b is the free charge vector, and N (·) denotes the nonlinear term in the PBE. The discretized form of PBE can be solved by several numerical methods, such as the nonlinear relaxation methods as implemented in Delphi and PBEQ,17,19,21,22,24,26,27 2the nonlinear conjugate gradient method implemented in UHBD,23 the nonlinear multigrid method,25 and the inexact Newton method implemented in APBS,16 The relaxation methods, extended from classical linear methods such as Gauss-Seidel and successive over-relaxation, were first attempted to solve the FDM version of the nonlinear PBE.17,24 However, the convergence of such methods cannot be guaranteed.16 The multigrid method was also attempted,25 but it may diverge on certain applications.16 More robust approaches, such as the conjugate gradient method23 and the inexact Newton method16 were also reported for biomolecular applications. The conjugate gradient method is very slow due to considerable evaluations of the nonlinear term. The inexact Newton method is very attractive and is proven to converge.16,39 More importantly, the inexact Newton method can be combined with highly efficient linear FDM solvers to yield highly efficient methods.
Despite the early introduction of various nonlinear PBE solvers to biomolecular applications, a comparative and extensive analysis of these solvers is still in need. Such an analysis can guide future development and application of nonlinear PBE solvers. In this study we implemented, evaluated, and improved when possible seven nonlinear PBE solvers in the FDM scheme. In the following, the tested algorithms of the nonlinear PBE solvers are first summarized. This is followed by a comprehensive analysis of their convergence and performance with a large number of high-quality crystal structures of DNAs, RNAs, and proteins.
Methods
The discretized nonlinear PBE, eqn. (5), cannot be solved directly for typical biomolecular systems. Even for a linear equation system, the cost to compute the inverse of the coefficient matrix A is prohibitively high. In practice, the discretized PBE is often solved iteratively in the following form
| (6) |
where δφt is an update of φt at the t-th iteration. The conjugate gradient method follows a minimization strategy. It first intends to find an update δφt, which is A-conjugate to all previous updates if the nonlinear term is eliminated. δφt is then scaled to minimize a pre-defined functional. In contrast, the inexact Newton method and the relaxation method are both derivatives of the root-finding Newton method for nonlinear functions, which uses the first-order Taylor expansion of the residual of eqn. (5), g(φ) = Aφ+N(φ)−b, to obtain an appropriate update δφt. The inexact Newton method also requires δφt to be scaled to descend a functional that is closely related to that used in the conjugate gradient method.
Conjugate Gradient Algorithm
Luty et al. first explored to use the nonlinear conjugate gradient (CG) method to solve the nonlinear PBE.23 The nonlinear conjugate gradient method is derived from the linear conjugate gradient method in a straightforward fashion. The CG method always tries to solve a minimization problem. The pre-defined functional G(φ) to be minimized is the integral form of g(φ):
| (7) |
Here . Therefore, the stationary point of G(φ) is also the solution of g(φ) = 0. It is difficult to build conjugacy between subsequent updates, δφt, for a nonlinear equation system. Instead, the Fletcher-Reeves algorithm for the corresponding linear problem is used as an approximation, which was proven to converge.40 Thus, δφt is computed in the following way:41
| (8) |
where , which is used to enforce the A-conjugacy between δφt and all previous updates in the linear case. Here (a, b) denotes the dot product of two vectors a and b. Note that δφt is scaled so that eqn. (6) becomes
| (9) |
where αt is the scaling factor. By tuning αt, the functional G(φ) is minimized. The pseudo-code for the nonlinear CG algorithm is given as follows
For i,j,k from 1 to xm,ym,zm
End for i,j,k
Do until convergence
For i,j,k from 1 to xm,ym,zm
End for i,j,k
Do until convergence
for αt using Newton’s root-finding method
End do
For i,j,k from 1 to xm,ym,zm
End for i,j,k
For i,j,k from 1 to xm,ym,zm
End for i,j,k
t = t + 1
End do
where the superscript 0 represents the initial value and the superscript t represents the value at the t-th iteration. Here the inner Newton iterations are employed to find the scaling factor αt that minimizes G(φ). Luty et al. showed that the nonlinear CG solver was about four times slower than the linear CG solver with otherwise identical conditions.23
Inexact Newton Method
The inexact Newton (NT) method starts from the standard Newton method.42 The first-order Taylor expansion of g(φ) at φ = φt gives
| (10) |
where N′(φ) is the Jacobian matrix of the vector N(φ), and a diagonal matrix in this case. The ideal δφt would make the new φt+1 the root of g(φ)=0. Thus we have
| (11) |
In eqn. (11), the inverse of [A + N′(φt)] is difficult to compute and the corresponding δφt cannot be obtained within a few iterations, but it is actually unnecessary to solve eqn. (11) precisely for δφt . Eqn. (11) is solved iteratively to the extent that a pre-defined functional f (φ) is ensured to decrease in the update direction δφt, or in other words, a descent direction of f(δφt) is found. Although the integral of g(φ) in the above nonlinear CG algorithm is a natural choice for the functional,23 a simpler form is also effective,16
| (12) |
It has been proven that if the following condition is satisfied
| (13) |
a descent direction of f(φ) can always be obtained,16 and the inexact Newton method can converge locally.42 Next a line search along the descent direction is conducted to assure f(φt+1) < f(φt), which can guarantee the global convergence of the inexact Newton method.16 There are various ways to solve eqn. (11) inexactly, such as the multigrid (MG) method, the incomplete Cholesky conjugate gradient (ICCG) method, and the successive over-relaxation (SOR) method. In summary, the NT algorithm can be written as follows.
Do until convergence
Calculate the nonlinear PB residual g(φt).
Calculate the Jacobian matrix N′(φt).
Let AL(φt)=A(φt)+N′(φt).
Iteratively solve a linear problem AL(φt)δφt = −g(φt) for δφt until ||AL (φt) δφt + g(φt)|| < || g (φt)||
Conduct line search along the direction δφt, i.e. looking for αt, to satisfy ||f(φt + αt δφt)|| < || f(φt)||
t = t + 1
End do
The two NT solvers tested in this study are combined with ICCG (NT-ICCG) and MG (NT-MG), respectively, which are employed to solve the inner linear problem for updating the potentials. The ICCG method is an optimized version by Luo et al.43 In the MG method, we applied a four-level v-cycle implementation, where the restriction and prolongation were realized with a three-dimensional, seven-banded version of Alcouffe’s algorithm.44 We employed the SOR method for the MG pre-smoothing and post-smoothing on fine grids, and also for solving the linear problem on the coarsest grid. The relaxation parameter was set as 1.5 on fine grids and 1.9 on the coarsest grid. Both the pre-smoothing and post-smoothing use five SOR steps. Because eqn. (11) is solved inexactly, we adopted this simple and fast algorithm, which would be otherwise unstable and unsuitable to solve a normal linear problem with tight convergence criterion.45 Specifically the convergence criterion for the NT-MG method was set as ||[A + N′(φt)]δφt + g(φt)|| < ||g (φt)||, and the convergence criterion for the NT-ICCG method was set as ||[A + N′(φt)]δφt + g(φt)|| < 0.1×||g (φt)||.
Relaxation Algorithms
Unlike the inexact Newton method, a nonlinear relaxation method uses a matrix B that is approximate to [A + N′ (φt)]−1 in eqn. (11). Specifically, for the nonlinear SOR method,
| (14) |
For the nonlinear Jacobi method,
| (15) |
For the nonlinear Gauss-Seidel (GS) method,
| (16) |
In eqn. (14)-(16), D is a diagonal matrix, L is a strictly lower triangular matrix, so that A = D + L + LT, where LT denotes the transpose of L. Each of the above approximate matrices can be easily inversed and the update (δφt) can be obtained by forward substitutions.
The nonlinear relaxation algorithms are similar to their linear counterparts. The unknowns are updated iteratively in a main loop. At each step, however, a nonlinear term, either a sinh/cosh function22,24,26,27 or a polynomial,17,19,21 has to be evaluated on every grid point. A typical nonlinear relaxation algorithm for the PBE can be summarized as the following pseudo-code.
Do until convergence
For i,j,k from 1 to xm,ym,zm
End for i,j,k
t = t + 1
End do
Here ω is the relaxation parameter, ω = 1 corresponds to the nonlinear GS method, and 1 < ω < 2 corresponds to the nonlinear SOR method. is a diagonal element of the matrix N′.(φ)22 or a corresponding approximate expression.17,19,21,24 The above procedure works well for the nonlinear PBE in many situations but there are cases where the iteration diverges.24 The convergence failures can be reduced by optimizing the relaxation parameter ω and adding the nonlinearity gradually. For example, in the Delphi program, the nonlinear term is added to the PBE by 5% each time and the optimal ω is estimated adaptively based on the average nonlinearity across the whole space.26
In this study, the nonlinear SOR solver uses a constant high-value ω , i.e., ω = 1.9 . Our previous analysis shows that the optimal relaxation parameter for the linear SOR method is between 1.9 and 1.95, depending on the structures.45 We chose ω = 1.9 because it gives a reasonable balance between convergence rate and convergence failure among tested molecules. Reducing ω further can lead to fewer convergence failures but much lower convergence rate. For example, ω=1.8 reduces convergence failures by 24% but simultaneously reduces the convergence rate by 49%. Instead of optimizing ω, we implemented two different strategies to reduce the convergence failures of SOR. In the first revised SOR, termed the adaptive SOR (ASOR) method, we initially use a high-value ω and then gradually lower it if the norm of the residual starts to increase. As will be shown below, ASOR can reduce the convergence failures of the original SOR method and retains its overall convergence rate. The second modified SOR method combines SOR with the same line search used in the two NT methods after δφt is calculated. The “damped” SOR (DSOR) method can also improve the convergence efficiently, though neither can guarantee convergence as will be shown below.
Simulation Details
We implemented seven nonlinear PBE solvers in the PBSA program of the AMBER 10 package,46 including one implementation of GS, three implementations of SOR, one implementation of CG, and two implementations of NT. The relaxation solvers and the conjugate gradient solver all solve the corresponding linear PBE first, and utilize the solution as the initial guess of the solution of the nonlinear PBE.
The dielectric constant was set to 1 within the molecular interior and it was set to 80 within the solvent. The solvent probe was set to be 1.5 Å to compute the solvent excluded surface that was used as the solute/solvent dielectric boundary. The ion probe was set to be 2.0 Å to compute the ion accessible surface that was used as the interface between the Stern layer and the bulk ion accessible solvent region. The finite-difference grid spacing was set as 0.5 Å. The ratio between the longest dimension of the finite-difference grid and that of the solute was set as 1.5. The convergence criterion for the nonlinear system was set to be 10−6 and the ionic strength was set to 150 mM if they are not mentioned otherwise. All floating point data were set in double precision to be consistent with the rest of the Amber 10 package.
We initially collected 588 high-resolution (at least 2 Å) nucleic-acid structures with sequence diversity more than 30% from the Protein Data Bank. We first removed all ligand molecules and those structures with non-natural nucleotides unsupported by the Amber force field. Often the unsupported nucleotides are located in the terminal regions, so that the remaining structures can still be used if the terminal regions are deleted. Finally the test set includes 364 nucleic acids. Hydrogen atoms were added in LEAP of the Amber 10 package.46 These molecules were assigned the charges of Cornell et al.47 and the radii of Tan et al.48 The atom numbers of the nucleic acids range from 250 to 5,569, and the numbers of grid points of the nucleic acids range from 313,551 to 15,218,175. The PDB codes of the nucleic acids are given in the Appendix.
The performance statistics of the seven solvers was collected on a computer cluster of 80 nodes with 1GB memory of 3.0GHz P4 CPUs. For some methods, calculations on the ten largest molecules in the test of 364 nucleic acids require more than 1GB memory, so they were left out in the overall analysis. Next, we tested the two NT solvers with the 22 largest nucleic acids (>2,000 atoms) in the test set, with the ten largest nucleic acids included, on a server node with 8GB memory. We also tested the two NT solvers with the 26 largest proteins (>4,000 atoms) from the Amber test set.46 Finally, we analyzed the effects of different salt properties on the performance of the two NT solvers.
Results and Discussion
Idealized System Test
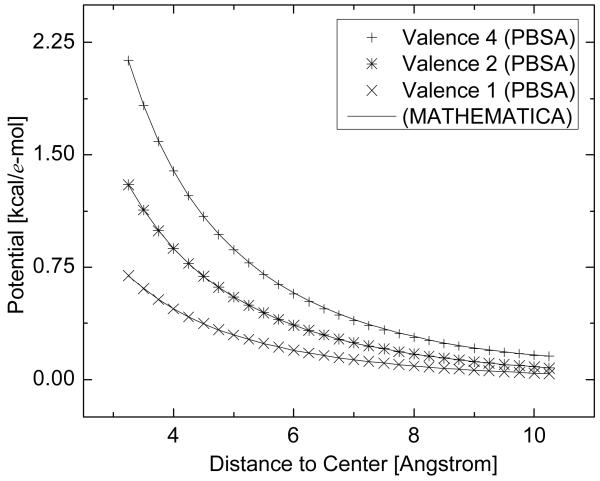
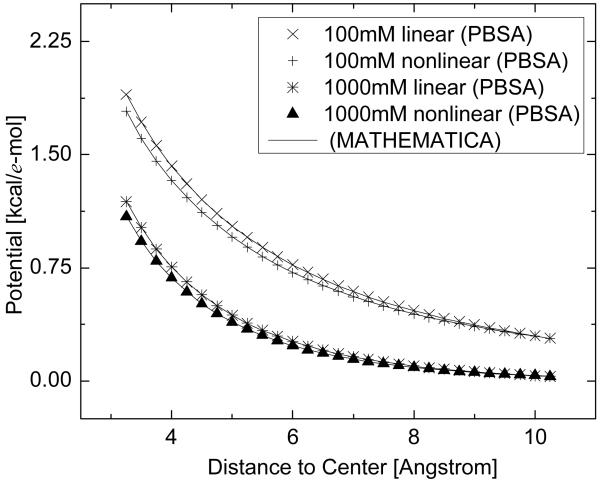
We first tested the nonlinear solvers with an idealized system, i.e., a single ion with radius of 1 Å and multiple charges in the salt-water solution. In this simple system, the grid spacing was set to be 0.25 Å. We compared the numerical solutions of the seven solvers with the solutions obtained from the predictor-corrector Adams method in Mathematica 6.0 under different conditions. Here different charges for the single ion and different ion concentrations were used. Figure 1 shows the results with different charges for the single ion while the ion concentration is 500 mM, and Figure 2 shows the results under different ion concentrations while the charge of the single ion is 2e. Note that the solutions of all seven tested numerical solvers are represented by the same symbol due to their virtually identical numerical values. Both figures demonstrate excellent agreements between the seven implemented solvers and the standard numerical method packaged in Mathematica for the tested systems.
Figure 1.
Comparison between the numerical solutions from PBSA and Mathematica for the idealized system under different charges of the single ion. PBSA: numerical solutions in the PBSA program. MATHEMATICA: numerical solutions from the Mathematica program. The charge of the single ion is set as 1 e, 2 e, and 4 e, respectively. Ion concentration is 500mM and ion valence is 1. Only potential in the ion accessible region is plotted.
Figure 2.
Comparison between the numerical solutions from PBSA and Mathematica for the idealized system under different ion concentrations. Linear: solutions to the linearized PBE. Nonlinear: solutions to the full nonlinear PBE. Ion concentrations are set as 100 mM and 1000 mM, respectively. The charge of the single ion is 2 e and ion valence is 1. Only potential in the ion accessible region is plotted.
Solver Convergence Statistics
We studied the convergence of all the solvers for the 364-nucleic-acid test set, excluding the ten largest molecules due to the memory limitation of the computer cluster. The convergence statistics are shown in Table 1. Three out of the seven solvers can converge within 10,000 steps in all test cases, i.e., the CG method and the two NT methods, each of which makes use of a functional-assisted strategy. The original SOR method fails in most cases but is noticeably improved if ω is adaptively modified: 76% failed cases in the original SOR method converge with the ASOR method. After a damped step size is applied in the DSOR method, 88% failed cases in the original SOR method converge.
Table 1.
Solver Convergence and Relative Performance Statistics in the Test Set of 364 Nucleic Acids, excluding the ten largest ones. Relative performance of a solver for a molecule is defined as the CPU time of the solver over the CPU time of the NT-MG solver for the same molecule. Avg Rel: average relative performance over all tested molecules. Unconv: number of convergence failures.
| Solver | GS | SOR | ASOR | DSOR | CG | NT-ICCG | NT-MG |
|---|---|---|---|---|---|---|---|
| Avg Rel | 47.10 | 3.32 | 3.71 | 5.86 | 21.35 | 1.99 | 1.00 |
| Unconv | 6 | 25 | 6 | 3 | 0 | 0 | 0 |
Since we first solve the corresponding linear problem in the nonlinear SOR solvers, the nonlinearity is weakened. This strategy was found to improve the convergence. Moreover, lower-value ω, or even under-relaxation, can obtain better convergence than high-value ω.24,26 For example, in our test, the GS method converges in more test cases than the original SOR method in spite of its much lower convergence rate. The minimal ω in the ASOR method is equal to 1, so it is expected that the ASOR method has the same number of convergence failures as the GS method, but it converges much faster because over-relaxation is initially used. The DSOR method conducts a line search to descend f(φ) in eqn. (12) but still cannot guarantee convergence because the direction is not necessarily a descent direction. Note that for those test cases that the original SOR method cannot converge, the DSOR method shows better convergence rate than the ASOR method.
There is one way to improve the inexact Newton method, which is to use an appropriate convergence criterion to inexactly solve the inner linear equation at each step. This requires that each convergence criterion be different and deliberately designed to prevent under-solving or over-solving eqn. (11). Over-solving the equation means the convergence criterion is too tight. This is because the descent direction δφt no longer changes much when the appropriate convergence criterion is reached. That is to say, the extra computation in reaching the tighter convergence criterion does not results in noticeable improvement. Under-solving the equation means the convergence criterion is so loose that δφt is no longer a good descent direction, along which the functional can decrease little. This will lead to a significant increase in the Newton iteration steps. The set of convergence criteria is called the forcing terms. A study on local convergence of different sets of forcing terms was conducted in the literature.49 However, it is still hard to design appropriate forcing terms if the initial guess is far away from the solution. Note that NT-MG and NT-ICCG are in different situations. One linear MG cycle can substantially reduce the residual and probably over-solve the equation, while multiple ICCG cycles are necessary to reduce the residual to the same level. Therefore, we used a tighter inner convergence criterion for NT-ICCG (the average relative performance is 53.12 if the same inner convergence criterion as for NT-MG is used), and for the same reason, NT-ICCG is more likely to be improved by optimizing the forcing terms.
Finally, the convergence performance of SOR might be improved if a hybrid method is employed. For example, one would start with SOR and later switch to NT-MG when SOR becomes ineffective. The memory requirement is the same as in the more demanding method, i.e., NT-MG. This hybrid method can definitely guarantee convergence. However, it is useful only if SOR is superior to NT-MG during the initial iteration steps, which is actually not the case. Thus more effort is definitely needed if a hybrid method is to be pursued.
Timing and Memory Requirement of Inexact Newton Methods
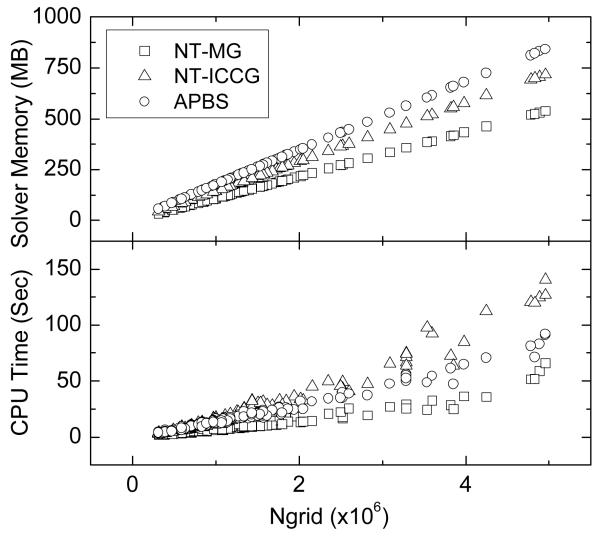
In the following we focus on the two NT methods because of their significantly higher efficiency and robustness. First, we examined the timing and memory requirement of the two NT methods in solving the PB equations for the test set of 364 nucleic acids, excluding the ten largest ones. We utilized the APBS finite-difference solver as a reference in this round. All three solvers were compiled and tested under conditions as identical as possible though it should be pointed out that the APBS solver has been adapted for parallel platforms which may impact its single-CPU performance. Specifically the exactly same discretized nonlinear problems were solved. Figure 3 shows that the memory requirement and solver time of the three solvers are similar for smaller molecules, but their difference becomes obvious when the number of grid points increases. Both the memory and the timing trends for NT-MG are linear over the number of grid points. The memory trend for NG-ICCG is linear, but its timing trend remains linear only for smaller test cases and becomes nonlinear for larger test cases. On average, the APBS solver requires the most memory, the NT-ICCG consumes the most time, and the NT-MG needs less memory and less time than both the NT-ICCG and the APBS solver. Although our simple implementation of MG is superior under current circumstances, a more robust MG solver will probably bring more benefit if the convergence criterion for the nonlinear equation is tighter. In this case, the linear equation should be solved exactly in the last few Newton steps because the linear equation is a very good approximation. Finally it should be noted that the memory usages and the CPU times among the three solvers differ at most by a factor of two. The difference may be overwhelmed by a higher grid resolution and by a different testing condition, such as in molecular dynamics, as our latest analysis has shown.50
Figure 3.
Scaling of solver CPU times and memory usages versus grid numbers for the two inexact Newton methods and the APBS solver in the test set of 364 nucleic acids, excluding the ten largest ones.
Table 2 and Table 3 list the solver time of the two NT methods for the 22 largest molecules in the test set of 364 nucleic acids and the 26 largest proteins in the Amber test set, respectively. Since tested proteins are more compact than tested nucleic acids, the average number of grid points is similar for the two sets of molecules. It is apparent that the solver times are also comparable between the two sets of molecules, i.e., the solver efficiency mostly depends on the number of grid points. More importantly, for these largest tested molecules, NT-MG uses only a third of the time of NT-ICCG. Note that it uses about a half of the time of NT-ICCG in the overall test. This observation is consistent with the intrinsic advantage of the MG method on large systems.
Table 2.
Solver Times (second) of Two Inexact Newton Methods for the 22 Largest Nucleic Acids in the Test Set of 364 Nucleic Acids. Natom: atom number; Ngrid: grid number.
| Nucleic Acids | N atom | N grid | NT-MG | NT-ICCG |
|---|---|---|---|---|
| 1EHZ | 2509 | 7258191 | 51.71 | 131.35 |
| 1EVV | 2509 | 6650175 | 46.76 | 108.97 |
| 1I2Y | 2124 | 3820287 | 18.31 | 51.83 |
| 1NUJ | 3112 | 7498575 | 53.54 | 140.65 |
| 1NUV | 3112 | 7498575 | 53.97 | 142.65 |
| 1Q96 | 2616 | 4887087 | 31.08 | 80.03 |
| 1U8D | 2145 | 3285711 | 20.83 | 44.12 |
| 1ZCI | 2448 | 5980975 | 34.74 | 107.87 |
| 244D | 3120 | 4956175 | 34.81 | 79.97 |
| 2DZ7 | 2032 | 2597023 | 17.35 | 28.18 |
| 2EES | 2145 | 3285711 | 20.43 | 48.83 |
| 2EET | 2147 | 3285711 | 20.89 | 46.78 |
| 2EEU | 2145 | 3285711 | 20.71 | 46.67 |
| 2EEV | 2147 | 3285711 | 20.75 | 48.43 |
| 2G3S | 2580 | 4779775 | 26.27 | 77.83 |
| 2G9C | 2144 | 3285711 | 20.67 | 48.07 |
| 2GWQ | 3128 | 6286383 | 40.55 | 104.68 |
| 352D | 3024 | 4956175 | 34.75 | 90.32 |
| 3BNN | 2696 | 8078175 | 57.32 | 146.12 |
| 3D2V | 4970 | 8299375 | 61.94 | 164.3 |
| 2Z75 | 4646 | 11979711 | 102.47 | 225.23 |
| 3DIL | 5569 | 15218175 | 126.39 | 383.26 |
Table 3.
Solver Times (second) of Two Inexact Newton Methods for the 26 Largest Proteins in the Amber test set.
| Proteins | N atom | N grid | NT-MG | NT-ICCG |
|---|---|---|---|---|
| 1B8O_A | 4348 | 4779775 | 29.91 | 98.38 |
| 1C0P_A | 5566 | 7258191 | 73.34 | 194.19 |
| 1D8V_A | 4211 | 5849375 | 32.19 | 119.25 |
| 1DCI_A | 4281 | 6204975 | 40.45 | 160.39 |
| 1DJ0_A | 4176 | 5759775 | 44.74 | 115.93 |
| 1DS1_A | 4916 | 4869375 | 45.02 | 121.3 |
| 1E19_A | 4874 | 6384175 | 34.93 | 127.91 |
| 1E6Q_M | 7819 | 8816751 | 74.85 | 193.63 |
| 1E6U_A | 4966 | 5180175 | 49.82 | 103.8 |
| 1EZA_0 | 4034 | 4921631 | 29.07 | 69.93 |
| 1EZO_A | 5735 | 8392815 | 49.42 | 147.62 |
| 1F24_A | 6221 | 6286383 | 39.43 | 108.85 |
| 1HZY_A | 5092 | 4869375 | 30.28 | 97.17 |
| 1IXH_0 | 4856 | 5637663 | 36.70 | 87.21 |
| 1MLA_0 | 4485 | 4424175 | 28.18 | 81.41 |
| 1PA2_A | 4441 | 4779775 | 30.43 | 91.16 |
| 1QH4_A | 5983 | 6829375 | 37.72 | 130.39 |
| 1QNR_A | 5129 | 4379375 | 37.47 | 91.42 |
| 1QOP_B | 5895 | 5233167 | 41.56 | 140.93 |
| 1QQF_A | 4365 | 4019679 | 22.28 | 56.62 |
| 1QTW_A | 4380 | 4342767 | 26.85 | 85.04 |
| 1YUB_0 | 4168 | 6768719 | 37.55 | 134.5 |
| 2CTC_0 | 4801 | 4342767 | 28.59 | 71.34 |
| 2OLB_A | 8254 | 7866207 | 53.02 | 148.77 |
| 3SIL_0 | 5804 | 5359375 | 38.29 | 120.5 |
| 7A3H_A | 4578 | 3615183 | 22.25 | 68.95 |
Performance of Inexact Newton Methods versus Convergence Criterion
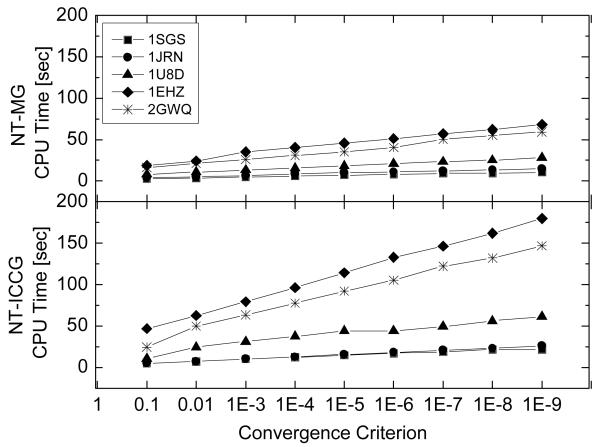
Next the performance of the two NT methods under a variety of convergence criteria ranging from 10−1 to 10−9 was examined. Five nucleic acids of different sizes were selected as test cases in this round, which are 1SGS (1074 atoms), 1JRN (1564 atoms), 1U8D (2145 atoms), 1EHZ (2509 atoms) and 2GWQ (3128 atoms). Figure 4 shows that both methods can improve convergence without any steep jump in the solver time, indicating a constantly smooth convergence behavior. Specifically a linear relationship exists between the solver time and the logarithm of the convergence criterion. The slope, however, increases with the complexity and size of tested molecules.
Figure 4.
Solver CPU times versus convergence criterion for the two inexact Newton methods. Note that the flat region between adjacent convergence criteria results from the same number of iterations required to converge even if the convergence criteria are different, i.e. the residual reduction is more than the specified convergence criterion reduction.
Performance of Inexact Newton Methods versus Ion Concentration
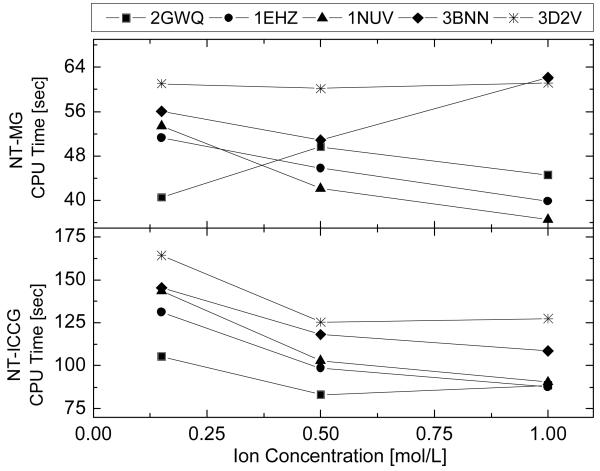
Finally, the effect of the ion concentration was studied and the results are shown in Figure 5. The sample in this test consists five large nucleic acids, which are 1EHZ (2509 atoms), 3BNN (2696 atoms), 1NUV (3112 atoms), 2GWQ (3128 atoms), 3D2V (4970 atoms). Three different ion concentrations were tested, including 150 mM, 500 mM, and 1000 mM. Regardless of ion concentration, the average solver time of NT-MG for the five molecules is more or less constant. On the contrary, the average solver time of NT-ICCG depends on the ion concentration: the solver uses about one-quarter less solver time when the ion concentration is high (≥ 500 mM). This observation indicates that NT-MG is probably more stable than NT-ICCG under different salt conditions in biomolecular applications.
Figure 5.
Solver CPU times versus ion concentrations for the two inexact Newton methods.
We also tested the performance of the two NT methods when the ion valence is changed. However, no clear trend was observed. The average solver times of both the NT-MG method and the NT-ICCG method only increase slightly with the ion valence. This behavior is different from the observation in the analytical test case with MATHEMATICA, where higher ion valence was found to cause convergence difficulty at some testing conditions.
Conclusion
We implemented and optimized seven finite-difference solvers for the nonlinear Poisson-Boltzmann equation, including four relaxation methods, one CG method and two NT methods. We tested the performance of the seven solvers with a large number of nucleic acids and proteins, with special attentions given to the robust NT algorithm. We investigated the role of linear solvers in its performance by incorporating ICCG and MG into the algorithm. Specifically, a four-level v-cycle was applied in the MG method, where the restriction and prolongation were realized with a three-dimensional seven-band version of Alcouffe’s algorithm. In addition, the SOR method was applied for the multigrid pre-smoothing and post-smoothing on fine grids, and also for solving the linear problem on the coarsest grids. We adopted this simple and fast algorithm because the inner linear problem of an NT method does not need to be solved exactly. On the contrary, to accelerate the convergence of our implementation of NT-ICCG, we tightened the convergence criterion of the inner linear solver loop, which would cause our implementation of NT-MG to be unstable. In addition, we explored strategies to optimize the SOR method to reduce its convergence failures without too much sacrifice in its convergence rate. In the ASOR method, ω was designed to decrease when the norm of the residual starts to increase. This method reduces the convergence failures by 76% and retains much of the overall convergence rate of the original SOR method with a high-value ω. In the DSOR method, the damping strategy from the NT method was utilized to optimize the search step length, and was found to reduce the convergence failures by 88%.
Our results show that only the nonlinear methods accompanied with a functional-assisted strategy can guarantee convergence, such as the CG method and the NT method, while the relaxation methods cannot. Especially the NT method exhibits impressive performance when it is combined with highly efficient linear solvers. Therefore our analysis suggests that the functional-assisted strategies be used in existing numerical solvers for biomolecular applications if they intend to solve the nonlinear PBE for biomolecules.
Finally it is instructive to discuss future directions in the optimization of nonlinear solvers for biomolecular applications. First point charges are widely used to represent atomic charge density distributions in current biomolecular models. Unfortunately this practice introduces singularity into the right hand side of PBE. The presence of charge singularity results in discontinuity in the electrostatic potential with large error when the finite-difference method is used. We have developed a new formulation to remove the charge singularity in the linear finite-difference solvers.51 Given the current implementations of the nonlinear solvers, we are in a position to investigate the effect of charge singularity on the performance of the nonlinear finite-difference solvers. In addition, we plan to extend our analysis and optimization of the nonlinear finite-difference solvers in the context of molecular dynamics simulations. It is expected that the efficiency of the nonlinear solvers can be improved in molecular dynamics simulations just as in our prior analysis of the linear solvers.45 However, further development is necessary to fully take advantage of the potential update nature in molecular dynamics to achieve computational efficiency high enough for routine biomolecular applications.
Acknowledgements
We thank Drs. Hong-Kai Zhao (UC Irvine) and Zhi-Lin Li (NC State) for exciting discussions. This work is supported in part by NIH (GM069620 & GM079383).
Appendix
Test Set of 364 Nucleic Acids
The following molecular structures, in both the Amber format and the pqr format, can be downloaded from http://rayl0.bio.uci.edu/rayl/#Database.
100D, 109D, 110D, 118D, 126D, 127D, 131D, 137D, 138D, 151D, 152D, 157D, 158D, 160D, 161D, 165D, 181D, 182D, 184D, 190D, 191D, 192D, 196D, 198D, 1A2E, 1BD1, 1BNA, 1CSL, 1D10, 1D11, 1D12, 1D13, 1D15, 1D23, 1D32, 1D36, 1D37, 1D38, 1D39, 1D43, 1D44, 1D45, 1D46, 1D48, 1D49, 1D54, 1D56, 1D57, 1D58, 1D63, 1D67, 1D78, 1D79, 1D88, 1D8G, 1D8X, 1D96, 1DA0, 1DA9, 1DC0, 1DCG, 1DJ6, 1DL8, 1DN8, 1DNO, 1DNS, 1DNT, 1DNX, 1DNZ, 1DOU, 1DQH, 1EHV, 1EHZ, 1EN3, 1EN8, 1EN9, 1ENE, 1ENN, 1EVP, 1EVV, 1F27, 1FD5, 1FDG, 1FMQ, 1FMS, 1FN2, 1FQ2, 1FTD, 1G4Q, 1I0T, 1I1P, 1I2Y, 1I7J, 1ICG, 1ICK, 1ID9, 1IDW, 1IH1, 1IHA, 1IKK, 1IMR, 1IMS, 1JGR, 1JO2, 1JRN, 1JTL, 1K9G, 1KCI, 1KD3, 1KD4, 1KD5, 1L1H, 1L2X, 1L4J, 1LJX, 1M69, 1M6F, 1M6G, 1M6R, 1M77, 1MF5, 1MSY, 1NLC, 1NQS, 1NT8, 1NUJ, 1NUV, 1NVN, 1NVY, 1O0K, 1OFX, 1OSU, 1P20, 1P4Y, 1P4Z, 1P79, 1PFE, 1PJG, 1PJO, 1Q96, 1Q9A, 1QCU, 1QYK, 1QYL, 1R68, 1RQY, 1RXB, 1S23, 1S2R, 1SGS, 1SK5, 1T0E, 1U8D, 1UB8, 1UE4, 1V9G, 1VAQ, 1VJ4, 1VS2, 1VZK, 1WOE, 1WQY, 1XA2, 1XCS, 1XCU, 1XJX, 1XJY, 1XPE, 1XVK, 1XVN, 1XVR, 1Z3F, 1Z8V, 1ZCI, 1ZEV, 1ZEX, 1ZEY, 1ZEZ, 1ZF0, 1ZF1, 1ZF2, 1ZF3, 1ZF4, 1ZF5, 1ZF6, 1ZF7, 1ZF8, 1ZF9, 1ZFA, 1ZFB, 1ZFC, 1ZFF, 1ZFG, 1ZNA, 1ZPH, 1ZPI, 200D, 212D, 215D, 220D, 221D, 222D, 224D, 232D, 234D, 235D, 236D, 240D, 241D, 243D, 244D, 245D, 248D, 251D, 255D, 258D, 259D, 260D, 272D, 276D, 279D, 284D, 288D, 292D, 293D, 295D, 2A43, 2A7E, 2ADW, 2AVH, 2B0K, 2B1B, 2B2B, 2B3E, 2D47, 2D94, 2D95, 2DCG, 2DES, 2DYW, 2DZ7, 2EES, 2EET, 2EEU, 2EEV, 2F8W, 2G32, 2G3S, 2G9C, 2GB9, 2GPM, 2GQ4, 2GQ5, 2GQ6, 2GQ7, 2GVR, 2GW0, 2GWA, 2GWQ, 2GYX, 2HBN, 2HTO, 2I2I, 2I5A, 2IE1, 2O1I, 2O4F, 2OE5, 2OE8, 2OIY, 2OKS, 2PKV, 2PL4, 2PL8, 2PLB, 2PLO, 2PWT, 2Q1R, 2QEK, 2R22, 2V6W, 2V7R, 2VAL, 2Z75, 307D, 308D, 310D, 312D, 314D, 315D, 317D, 331D, 332D, 334D, 336D, 348D, 349D, 351D, 352D, 354D, 355D, 360D, 362D, 368D, 369D, 370D, 371D, 377D, 385D, 386D, 393D, 394D, 395D, 396D, 397D, 398D, 399D, 3BNN, 3C2J, 3C44, 3CGP, 3CGS, 3CJZ, 3CZW, 3D0M, 3D2V, 3DIL, 3DNB, 3ERU, 3EUM, 413D, 414D, 420D, 423D, 428D, 431D, 432D, 434D, 435D, 437D, 439D, 440D, 441D, 442D, 443D, 452D, 453D, 455D, 463D, 465D, 466D, 472D, 473D, 476D, 477D, 479D, 480D, 482D, 483D, 485D, 5DNB, 7BNA, 9BNA, 9DNA.
References
- 1.Baker NA. Curr. Opin. Struct. Biol. 2005;15:137. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 2.Bashford D, Case DA. Annu. Rev. Phys. Chem. 2000;51:129. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 3.Chen JH, Im WP, Brooks CL. J. Am. Chem. Soc. 2006;128:3728. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cramer CJ, Truhlar DG. Chem. Rev. 1999;99:2161. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 5.Davis ME, McCammon JA. Chem. Rev. 1990;90:509. [Google Scholar]
- 6.Feig M, Chocholousova J, Tanizaki S. Theor. Chem. Acc. 2006;116:194. [Google Scholar]
- 7.Gilson MK. Curr. Opin. Struct. Biol. 1995;5:216. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 8.Honig B, Nicholls A. Science. 1995;268:1144. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 9.Im W, Chen JH, Brooks CL. Adv. Protein Chem. 2006;72:173. doi: 10.1016/S0065-3233(05)72007-6. [DOI] [PubMed] [Google Scholar]
- 10.Koehl P. Curr. Opin. Struct. Biol. 2006;16:142. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 11.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Commun. Comput. Phys. 2008;3:973. [Google Scholar]
- 12.Roux B, Simonson T. Biophys. Chem. 1999;78:1. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 13.Sharp KA. Curr. Opin. Struct. Biol. 1994;4:234. [Google Scholar]
- 14.Wang J, Tan CH, Tan YH, Lu Q, Luo R. Commun. Comput. Phys. 2008;3:1010. [Google Scholar]
- 15.Hill TL. An Introduction to Statistical Thermodynamics. Dover Publications, Inc.; New York: 1986. Dilute Electrolyte Solutions and Plasmas; pp. 321–331. [Google Scholar]
- 16.Holst MJ, Saied F. J. Comput. Chem. 1995;16:337. [Google Scholar]
- 17.Jayaram B, Sharp KA, Honig B. Biopolymers. 1989;28:975. doi: 10.1002/bip.360280506. [DOI] [PubMed] [Google Scholar]
- 18.Prabhu NV, Panda M, Yang QY, Sharp KA. J. Comput. Chem. 2008;29:1113. doi: 10.1002/jcc.20874. [DOI] [PubMed] [Google Scholar]
- 19.Sharp KA, Honig B. J. Phys. Chem. 1990;94:7684. [Google Scholar]
- 20.Ye X, Cai Q, Yang W, Luo R. Biophys. J. 2009;97:554. doi: 10.1016/j.bpj.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Allison SA, Sines JJ, Wierzbicki A. J. Phys. Chem. 1989;93:5819. [Google Scholar]
- 22.Forsten KE, Kozack RE, Lauffenburger DA, Subramaniam S. J. Phys. Chem. 1994;98:5580. [Google Scholar]
- 23.Luty BA, Davis ME, McCammon JA. J. Comput. Chem. 1992;13:1114. [Google Scholar]
- 24.Nicholls A, Honig B. J. Comput. Chem. 1991;12:435. [Google Scholar]
- 25.Oberoi H, Allewell NM. Biophys. J. 1993;65:48. doi: 10.1016/S0006-3495(93)81032-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rocchia W, Alexov E, Honig B. J. Phys. Chem. B. 2001;105:6507. [Google Scholar]
- 27.Xiang ZX, Shi YY, Xu YW. J. Comput. Chem. 1995;16:200. [Google Scholar]
- 28.Baker N, Holst M, Wang F. J. Comput. Chem. 2000;21:1343. [Google Scholar]
- 29.Chen L, Holst MJ, Xu JC. SIAM J. Numer. Anal. 2007;45:2298. [Google Scholar]
- 30.Dyshlovenko PE. Comput. Phys. Commun. 2002;147:335. [Google Scholar]
- 31.Holst M, Baker N, Wang F. J. Comput. Chem. 2000;21:1319. [Google Scholar]
- 32.Sayyed-Ahmad A, Tuncay K, Ortoleva PJ. J. Comput. Chem. 2004;25:1068. doi: 10.1002/jcc.20039. [DOI] [PubMed] [Google Scholar]
- 33.Shestakov AI, Milovich JL, Noy A. J. Colloid Interf. Sci. 2002;247:62. doi: 10.1006/jcis.2001.8033. [DOI] [PubMed] [Google Scholar]
- 34.Xie D, Zhou SZ. BIT. 2007;47:853. [Google Scholar]
- 35.Rashin AA, Malinsky J. J. Comput. Chem. 1991;12:981. [Google Scholar]
- 36.Vorobjev YN, Grant JA, Scheraga HA. J. Am. Chem. Soc. 1992;114:3189. [Google Scholar]
- 37.Zhou HX. J. Chem. Phys. 1994;100:3152. [Google Scholar]
- 38.Boschitsch AH, Fenley MO. J. Comput. Chem. 2004;25:935. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]
- 39.Eisenstat SC, Walker HF. SIAM J Optimiz. 1994;4:393. [Google Scholar]
- 40.Ortega JM, Rheinboldt WC. Convergence of Minimization Methods. In: Rheinboldt WC, editor. Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, Inc.; New York: 1970. pp. 509–512. [Google Scholar]
- 41.Fletcher R, Reeves CM. Comput. J. 1964;7:149. [Google Scholar]
- 42.Dembo RS, Eisenstat SC, Steihaug T. SIAM J. Numer. Anal. 1982;19:400. [Google Scholar]
- 43.Luo R, David L, Gilson MK. J. Comput. Chem. 2002;23:1244. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 44.Alcouffe RE, Brandt A, Dendy JE, Painter JW. SIAM J. Sci. Stat. Comp. 1981;2:430. [Google Scholar]
- 45.Wang J, Luo R. J. Comput. Chem. Submitted. [Google Scholar]
- 46.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Crowley M, Walker RC, Zhang W, Merz KM, Wang B, Hayik S, Roitberg A, Seabra G, Kolossváry I, Wong KF, Paesani F, Vanicek J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Mathews DH, Seetin MG, Sagui C, Babin V, Kollman PA. AMBER 10, University of California; San Francisco: 2008. [Google Scholar]
- 47.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. [Google Scholar]
- 48.Tan CH, Yang LJ, Luo R. J. Phys. Chem. B. 2006;110:18680. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 49.Eisenstat SC, Walker HF. SIAM J Sci Comput. 1996;17:16. [Google Scholar]
- 50.Cai Q, Luo R. In preparation. [Google Scholar]
- 51.Cai Q, Wang J, Zhao HK, Luo R. J. Chem. Phys. 2009;130:145101. doi: 10.1063/1.3099708. [DOI] [PubMed] [Google Scholar]