Modeling Bivariate Longitudinal Hormone Profiles by Hierarchical State Space Models

Abstract

The hypothalamic-pituitary-adrenal (HPA) axis is crucial in coping with stress and maintaining homeostasis. Hormones produced by the HPA axis exhibit both complex univariate longitudinal profiles and complex relationships among different hormones. Consequently, modeling these multivariate longitudinal hormone profiles is a challenging task. In this paper, we propose a bivariate hierarchical state space model, in which each hormone profile is modeled by a hierarchical state space model, with both population-average and subject-specific components. The bivariate model is constructed by concatenating the univariate models based on the hypothesized relationship. Because of the flexible framework of state space form, the resultant models not only can handle complex individual profiles, but also can incorporate complex relationships between two hormones, including both concurrent and feedback relationship. Estimation and inference are based on marginal likelihood and posterior means and variances. Computationally efficient Kalman filtering and smoothing algorithms are used for implementation. Application of the proposed method to a study of chronic fatigue syndrome and fibromyalgia reveals that the relationships between adrenocorticotropic hormone and cortisol in the patient group are weaker than in healthy controls.

1. INTRODUCTION

The hypothalamic-pituitary-adrenal (HPA) axis plays a major role in coping with stress and maintaining the homeostasis of the human body. In responding to external and internal stimuli, the paraventricular nucleus of hypothalamus produces corticotropin-releasing hormone (CRH) and vasopressin (VP), which stimulate the pituitary gland to secrete adrenocorticotropic hormone (ACTH). ACTH in turn stimulates the adrenal cortex to produce cortisol. Cortisol is a major stress hormone and has wide-ranging effects, such as increasing blood sugar, suppressing immune system and regulating the metabolic system. Cortisol then inhibits both the hypothalamus and the pituitary gland in a classical endocrine feedback loop. Dysregulation of the HPA axis, consequently, can trigger the development of multiple pathologies (e.g. Fink et al., 2012, Chapter 29).

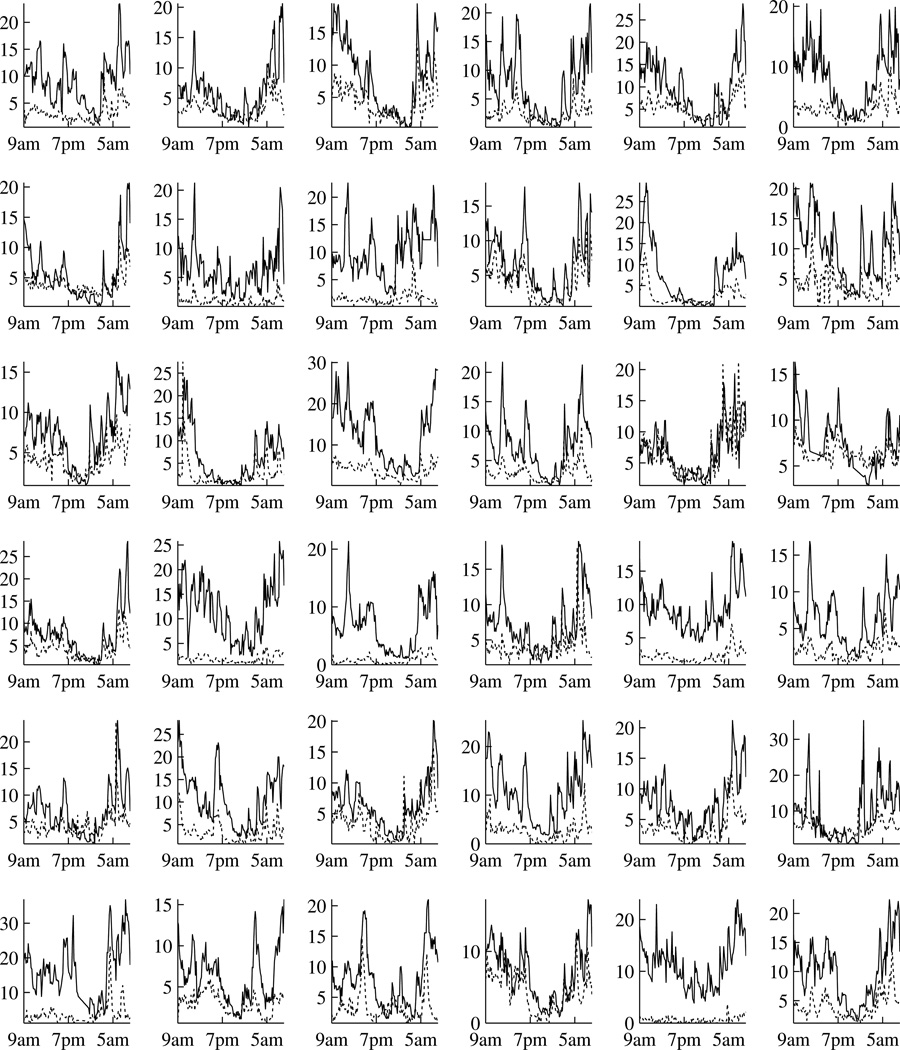
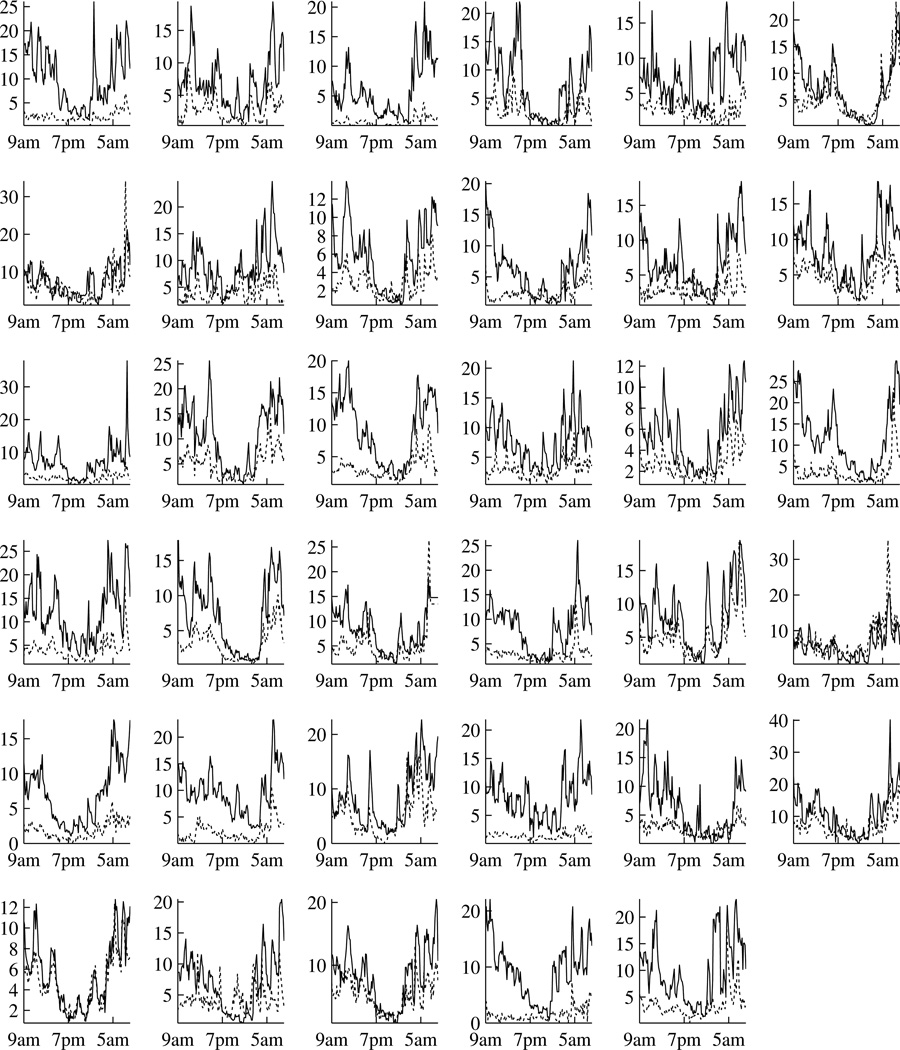
Our particular interest in the HPA axis comes from a study of chronic fatigue syndrome (CFS) and fibromyalgia (FM). While the etiology of CFS and FM remains unclear, dysfunction of the HPA axis is the most common hypothesis. Consequently, evaluation and comparison of HPA function are of primary interest to researchers. A study has been conducted to obtain the plasma ACTH and serum cortisol levels over a 24-hour period from a group of patients with CFS or FM or both and a group of healthy controls (Crofford et al., 2004). The data are displayed in Figure 1 and 2. Both ACTH and cortisol exhibit complex patterns, which from the physiological point of view can be viewed as a result of the combination of burst hormone secretions, distribution and clearance. These complex hormone profiles can be decomposed into two parts: a slowly varying basal concentration which is usually referred to as circadian rhythm, and rapid concentration changes which are referred to as pulses (e.g. Gudmundsson and Carnes, 1997). A general view is that the ACTH circadian rhythm is largely responsible for the cortisol circadian rhythm and the pulses are responsible for the short term feedback loop (e.g. Fink et al., 2012, Chapter 3). For this particular study, we are interested in quantifying the relationships between ACTH and cortisol and our interest is twofold. Firstly, we aim to evaluate whether the cortisol circadian rhythm can be explained by a linear function of ACTH circadian rhythm, and if so to compare this relationship between patients and controls. Secondly, we aim to evaluate and compare the directions and magnitudes of the short term feedback loop. Consequently, a joint modeling of ACTH and cortisol is required. Note that such a joint modeling would allow localization of HPA dysregulation to the pituitary gland, the adrenal gland or their communications, which would not be possible if only a single hormone were studied.

Figure 1.

Individual hormone levels over a 24 hour period at 10-minute intervals for the patient group. Time is from 9am to 9am. Each of the 36 cells is for one subject. Black lines are for cortisol (µg/dl) and gray lines are for ACTH (pg/ml).

Figure 2.

Individual hormone levels over a 24 hour period at 10-minute intervals for the control group. Time is from 9am to 9am. Each of the 35 cells is for one healthy control. Black lines are for cortisol (µg/dl) and gray lines are for ACTH (pg/ml).

Joint modeling the profiles of ACTH and cortisol is challenging. This is not only because of the complex univariate profiles, but also the complex relationships in the pulses. Firstly, the relationships are asymmetric. ACTH has positive feedforward on cortisol, while cortisol has negative feedback on ACTH. Secondly, the effects are lagged in time instead of concurrent. Both the feedforward and the feedback take effects after a certain amount of time instead of instantaneously. Thirdly, the feedforward and feedback are on the pulses rather than on the overall level of the underlying signals. Despite these complexities, methods used in studying their relationships in the biomedical literature are rather simple. For example, one-way analysis of variance has been used to study the temporal effects of ACTH on glucocorticoid (Spiga et al., 2011). These simple methods, obviously, cannot fully capture the relationships between ACTH and cortisol.

From the statistical point of view, ACTH and cortisol profiles can be viewed as bivariate longitudinal data. In the literature, the random effects approach is mostly used in modeling bivariate longitudinal data (Reinsel, 1982; Shah et al., 1997). This approach models each univariate outcome by linear mixed effects models and the relationships across different outcomes by the joint distributions of the random effects. It has subsequently been extended to nonlinear and nonparametric regression functions (Zhou et al., 2008; Wu et al., 2010). The limitation of this approach is that the concurrent correlations are symmetric by definition. On the other hand, time-lagged and asymmetric relationships have been widely studied in time series analysis, such as vector autoregressive (VAR) models (e.g. Box et al., 2008, Chapter 14). Additionally, Guo and Brown (2001) extended multiprocess dynamic linear models to allow flexible relationships among multiple time series. Carlson et al. (2009) developed bivariate de-convolution models for hormone pulses. Aschbacher et al. (2012) developed differential equation based models. These models, however, are generally applicable to a single subject instead of a group of subjects. Zeger and Liang (1991) combined fixed effects and VAR in marginal models to study feedback. Funatogawa et al. (2008) combined linear mixed effects models with VAR to study profiles approaching asymptotes. The limitation of these two approaches is that the relationships are built on the observed values. Consequently, the same relationship structure is forced upon every component of the underlying signal and the error terms. Not only is this relationship structure rigid, but imposing the same autoregressive structure on both the errors and the true signals may lead to model identifiability problems. In a similar approach Sy et al. (1997) modeled asymmetric relationships using bivariate integrated Ornstein-Uhlenbeck processes, which can be viewed as generalizations of autoregressive processes. Latent processes have also been used to model multivariate longitudinal data (e.g. Roy and Lin, 2000; Dunson, 2003), which are limited to multivariate outcomes measuring the same latent trait. Multivariate longitudinal data have also been analyzed by modeling the joint distributions of the error terms (e.g, Rosen and Thompson, 2009), whose focus is on improving the estimation efficiency rather than on quantifying the relationships.

In this paper, we adopt a signal extraction approach to study the relationships between ACTH and cortisol. Both the individual hormone profiles and the between-hormone relationships are viewed as signals to be extracted from noisy observations. For each hormone, we aim to extract group-average circadian rhythms and subject-specific pulsatile activities. Periodic smoothing splines are adopted for the circadian rhythms to account for their complex shapes. Autoregressive processes are adopted for the pulses, which can be derived from compartmental models and are widely used in modeling pulses. Both components can be represented in state space forms and thus can be unified into one hierarchical state space model. The feedforward and feedback in the pulses are then built into the AR components by concatenating the corresponding state vectors. By doing so, they can be modeled as asymmetric and time-lagged on a subcomponent of the underlying signals. Parameters are estimated by maximizing the marginal likelihood. The underlying signals are estimated by posterior means, and confidence intervals can be constructed using posterior variances. Computationally efficient Kalman filtering and smoothing algorithms are adopted for implementations. Note that this approach can be used to model general multivariate longitudinal data to handle both complex univariate profiles and complex between-outcome relationships beyond the ACTH and cortisol data.

The rest of the paper is organized as follows. The ACTH and cortisol data are described in Section 2. The proposed models are presented in Section 3. Estimation and inference are in Section 4. The proposed method is applied to the ACTH and cortisol data in Section 5. A small simulation is performed in Section 6. Some concluding remarks are given in Section 7.

2. THE ACTH AND CORTISOL DATA

CFS is characterized by persistent and unexplained fatigue and affects about 0.5% to 1.5% of the general adult population (e.g. Reeves et al., 2007). FM is characterized by chronic pain and has a prevalence of around 2% (e.g. Arnold, 2010). Although their etiologies remain unclear, the most popular hypothesis is that both syndromes are stress-related. Consequently, the HPA axis has undergone intensive investigations (e.g. Riva et al., 2010; Papadopoulos and Cleare, 2012, and references therein). It is known that ACTH has positive feedforward effects on cortisol and cortisol has negative feedback on ACTH. Dysregulation of the normal relationships between ACTH and cortisol has been conjectured to be part of the pathophysiological processes in CFS and FM. The clinical results, however, are inconsistent. For example the response of cortisol to ACTH in patients has been found to be hypersensitive, blunted, or the same compared to healthy subjects (Parker et al., 2001; Papadopoulos and Cleare, 2012). One possible reason is that most of these studies used a single dose of stressor or suppressor, which were originally designed to evaluate acute stress responses and may not be suitable for chronic stress. The data presented in this paper, on the other hand, provide an opportunity to study the relationships in a more natural setting.

A study was conducted at the University of Michigan General Clinical Research Center. Its overall aim was to study the HPA axis in patients with CFS or FM or both and healthy controls. The data are displayed in Figure 1 and 2, which exhibit circadian rhythms and pulses for both hormones. There were 36 patients and 35 controls. The patients were recruited from outpatient clinics and the controls from local communities. The patients were 18–65 years old, mostly female (32 of 36 subjects), non-smoking, and non-obese. The controls were matched by age, gender and menstrual status when applicable. All subjects were admitted on the evening before the blood sample collection, were provided standard meals at regular times and were at rest. Blood samples were collected at 10-minute intervals over a 24-hour period beginning at 9am and hormone levels were assayed. Consequently, there are 145 equally spaced observations for each subject. See Crofford et al. (2004) for details of the study.

Previous analyses of this study have focused on univariate approaches. Guo (2002) compared the cortisol circadian rhythms by functional mixed effects models. He found that cortisol circadian rhythms of the FM patients and the controls were statistically different. These results were confirmed by a periodic approach (Qin and Guo, 2006). Crofford et al. (2004) first extracted the subject-level parameters by a smoothing base-line plus pulses approach (Guo et al., 1999). They then compared the parameters by Student’s t test and found that cortisol levels in FM patients declined more slowly from acrophase to nadir than in healthy controls, but they were unable to detect any significant difference in the pulsatile activities. To gain insights into the HPA axis from a different angle, we propose to investigate the relationships between ACTH and cortisol.

3. THE MODEL

3.1 The General Model

We will present a bivariate model for the clarity of presentation, but our methods can be readily extended to a general multivariate setting. Let y_i(t_ij) = { y_i1(t_ij) y_i2(t_ij) }^⊤ be the bivariate outcomes of the ith subject at time t_ij for i = 1,⋯, m and j = 1,⋯, n_i. Let X_i(t_ij) and Zi(t_ij) be the design matrices containing experimental conditions and covariates. In this paper, we propose a hierarchical model in state space form

$${\mathbf{y}}_i(t_{ij})={\mathbf{X}}_i(t_{ij})\mathit{\beta }(t_{ij})+{\mathbf{Z}}_i(t_{ij}){\mathit{\alpha }}_i(t_{ij})+{\mathbf{e}}_i(t_{ij}),$$ (1)

$$\mathit{\beta }(t_{ij})={\mathbf{F}}_{\beta }(t_{ij})\mathbf{u}(t_{ij}),$$ (2)

$${\mathit{\alpha }}_i(t_{ij})={\mathbf{F}}_{\alpha }(t_{ij}){\mathbf{v}}_i(t_{ij}),$$ (3)

$$\mathbf{u}(t_{ij})={\mathbf{T}}_u(t_{ij})\mathbf{u}(t_{i,j-1})+{\mathbf{R}}_u(t_{ij}){\mathit{\eta }}_u(t_{ij}),$$ (4)

$${\mathbf{v}}_i(t_{ij})={\mathbf{T}}_{\upsilon }(t_{ij}){\mathbf{v}}_i(t_{i,j-1})+{\mathbf{R}}_{\upsilon }(t_{ij}){\mathit{\eta }}_{\upsilon i}(t_{ij}),$$ (5)

where

$$\mathit{\beta }(t_{ij})={\{{\mathit{\beta }}_1{(t_{ij})}^{\top }{\mathit{\beta }}_2{(t_{ij})}^{\top }\}}^{\top },{\mathit{\alpha }}_i(t_{ij})={\{{\mathit{\alpha }}_{i1}{(t_{ij})}^{\top }{\mathit{\alpha }}_{i2}{(t_{ij})}^{\top }\}}^{\top },\mathbf{u}(t_{ij})={\{{\mathbf{u}}_1{(t_{ij})}^{\top }{\mathbf{u}}_2{(t_{ij})}^{\top }\}}^{\top },{\mathbf{v}}_i(t_{ij})={\{{\mathbf{v}}_{i1}{(t_{ij})}^{\top }{\mathbf{v}}_{i2}{(t_{ij})}^{\top }\}}^{\top },{\mathit{\eta }}_u(t_{ij})={\{{\mathit{\eta }}_{u_1}{(t_{ij})}^{\top }{\mathit{\eta }}_{u_2}{(t_{ij})}^{\top }\}}^{\top },{\mathit{\eta }}_{\upsilon i}(t_{ij})={\{{\mathit{\eta }}_{{\upsilon }_{i1}}{(t_{ij})}^{\top }{\mathit{\eta }}_{{\upsilon }_{i2}}{(t_{ij})}^{\top }\}}^{\top },{\mathbf{F}}_{\beta }(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{F}}_{{\beta }_{11}}(t_{ij})\hfill & \hfill {\mathbf{F}}_{{\beta }_{12}}(t_{ij})\hfill \\ \hfill {\mathbf{F}}_{{\beta }_{21}}(t_{ij})\hfill & \hfill {\mathbf{F}}_{{\beta }_{22}}(t_{ij})\hfill \end{array}\right),{\mathbf{F}}_{\alpha }(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{F}}_{{\alpha }_{11}}(t_{ij})\hfill & \hfill {\mathbf{F}}_{{\alpha }_{12}}(t_{ij})\hfill \\ \hfill {\mathbf{F}}_{{\alpha }_{21}}(t_{ij})\hfill & \hfill {\mathbf{F}}_{{\alpha }_{22}}(t_{ij})\hfill \end{array}\right),{\mathbf{T}}_u(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{T}}_{u_{11}}(t_{ij})\hfill & \hfill {\mathbf{T}}_{u_{12}}(t_{ij})\hfill \\ \hfill {\mathbf{T}}_{u_{21}}(t_{ij})\hfill & \hfill {\mathbf{T}}_{u_{22}}(t_{ij})\hfill \end{array}\right),{\mathbf{T}}_{\upsilon }(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{T}}_{{\upsilon }_{11}}(t_{ij})\hfill & \hfill {\mathbf{T}}_{{\upsilon }_{12}}(t_{ij})\hfill \\ \hfill {\mathbf{T}}_{{\upsilon }_{11}}(t_{ij})\hfill & \hfill {\mathbf{T}}_{{\upsilon }_{22}}(t_{ij})\hfill \end{array}\right),{\mathbf{R}}_u(t_{ij})=\text{block diagonal}\{{\mathbf{R}}_{u_1}(t_{ij}),{\mathbf{R}}_{u_2}(t_{ij})\},{\mathbf{R}}_{\upsilon }(t_{ij})=\text{block diagonal}\{{\mathbf{R}}_{{\upsilon }_1}(t_{ij}),{\mathbf{R}}_{{\upsilon }_2}(t_{ij})\}.$$

Equation (1) defines the hierarchical structure of the underlying signal as a combination of group-averages and subject-specific deviations. Group-averages are indexed by design matrices X_i(t_ij) and the effects β(t_ij) are the features shared by the whole group. Subject-specific deviations are indexed by possibly different design matrices Z_i(t_ij) and the effects α_i(t_ij) are realizations from independent and identically distributed stochastic processes. The underlying signal is observed with serially and mutually independent errors e_i(t_ij) ~N(0, diagonal$\{{\sigma }_{e1}^2,{\sigma }_{e2}^2\}$).

Both β(t_ij) and α_i(t_ij) are dynamic effects, which are specified in state space forms. Equation (2) and (3) are the state space observation equations. Processes u(t_ij) and v_i(t_ij) are known as state vectors, which are transformed into effects β(t_ij) and α_i(t_ij) by the observation matrices F_β(t_ij) and Fα(t_ij). Equation (4) and (5) are the state transition equations. State vectors evolve over time according to the state transition matrices T_u(t_ij) and T_υ(t_ij), and stochastic innovations R_u(t_ij)η_u(t_ij) and R_υ(t_ij)η_υi(t_ij). The stochastic innovations are serially and mutually independent normal random vectors as η_u(t_ij) ~ N(0,Σ_u(t_ij)) and η_υi(t_ij) ~ N(0,Σ_υ(t_ij)) with

$${\mathbf{\Sigma }}_u(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{u_1}(t_{ij})\hfill & \hfill {\mathbf{\Sigma }}_{u_1,u_2}(t_{ij})\hfill \\ \hfill {\mathbf{\Sigma }}_{u_2,u_1}(t_{ij})\hfill & \hfill {\mathbf{\Sigma }}_{u_2}(t_{ij})\hfill \end{array}\right),{\mathbf{\Sigma }}_{\upsilon }(t_{ij})=\left(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{{\upsilon }_1}(t_{ij})\hfill & \hfill {\mathbf{\Sigma }}_{{\upsilon }_1,{\upsilon }_2}(t_{ij})\hfill \\ \hfill {\mathbf{\Sigma }}_{{\upsilon }_2,{\upsilon }_1}(t_{ij})\hfill & {\mathbf{\Sigma }}_{{\upsilon }_2}(t_{ij})\end{array}\right).$$

Processes u(t_ij) and v_i(t_ij) need to be initialized at time zero. Subject specific process v_i(t_ij) is initialized with a proper distribution N(0,Σ_υ(0)). Group-average process u(t_ij), if stationary, can also be initialized with a proper distribution, whose variance Σ_u(0) can be derived from model parameters. When we are completely ignorant about the initial conditions, we can use N(0, κI) with κ → ∞ to indicate the lack of prior information. This is known as diffuse initialization (see, e.g. Durbin and Koopman, 2012, Chapter 5). Equations (1) to (5) define a general bivariate model. Its state space formulation can incorporate many popular methods, such as classical regression models, smoothing splines, autoregressive moving average models (ARMA), structural time series models, multiple processes dynamic linear models, and dynamic factor models (see, e.g. Durbin and Koopman, 2012, Chapter 3).

3.2 Relationships between Group-Averages

We first present an exemplary model for the bivariate group-averages. Period cubic smoothing splines are used for illustration, which will later be adopted to model circadian rhythms in data analysis. The design matrix is a 2 × 2 identity design matrix, denoted as I₂. For the gth group as g = p for patients and g = c for controls, the observation and state transition equations are

$$\left(\begin{array}{c}\hfill {\beta }_{g1}(t_{ij})\hfill \\ \hfill {\beta }_{g2}(t_{ij})\hfill \end{array}\right)=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right){\mathbf{u}}_g(t_{ij}),{\mathbf{u}}_g(t_{ij})={\mathbf{T}}_u(t_{ij}){\mathbf{u}}_g(t_{i,j-1})+{\mathit{\eta }}_u(t_{ij}),$$

where u_g(t_ij) = {β_g1(t_ij) β̇_g1(t_ij) β_g1(0) β̇_g1(0) β_g2(t_ij) β̇_g2(t_ij) β_g2(0) β̇_g2(0)}^⊤, and β̇_gk(t) is the first derivative with respect to t which is scaled to [0, 1]. The state transition matrix T_u(t_ij) = block diagnoal{H_j, I₂, H_j, I₂} and stochastic innovation η_u(t_ij) has variance matrix Σ_u(t_ij) = block diagnoal{λ_g1Σ_j, 0_2×2, λ_g2Σ_j, 0_2×2} with

$${\mathbf{H}}_j=\left(\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{\Delta }{t}_{ij}\hfill \\ \hfill 0\hfill & 1\end{array}\right),{\mathbf{\Sigma }}_j=\left(\begin{array}{cc}\hfill \frac{1}{3}{(\mathrm{\Delta }{t}_{ij})}^3\hfill & \hfill \frac{1}{2}{(\mathrm{\Delta }{t}_{ij})}^2\hfill \\ \hfill \frac{1}{2}{(\mathrm{\Delta }{t}_{ij})}^2\hfill & \hfill \mathrm{\Delta }{t}_{ij}\hfill \end{array}\right),\mathrm{\Delta }{t}_{ij}=t_{ij}-t_{i,j-1}.$$

.

This bivariate periodic smoothing spline is initialized as

$${\mathbf{u}}_g(0)~\mathrm{N}(\mathbf{0},\text{block diagnoal}\{\kappa \left(\begin{array}{cc}\hfill {\mathbf{I}}_2\hfill & \hfill {\mathbf{I}}_2\hfill \\ \hfill {\mathbf{I}}_2\hfill & \hfill {\mathbf{I}}_2\hfill \end{array}\right),\kappa \left(\begin{array}{cc}\hfill {\mathbf{I}}_2\hfill & \hfill {\mathbf{I}}_2\hfill \\ \hfill {\mathbf{I}}_2\hfill & \hfill {\mathbf{I}}_2\hfill \end{array}\right)\}),\kappa \to \infty .$$

This diffuse initialization comes from the Bayesian equivalent model of smoothing splines (Wahba, 1978) and the state space representation of univariate spline is due to Wecker and Ansley (1983). The bivariate extension is immediate. A vector of pseudo data points (0 0 0 0)^⊤ is added at t = 1 to numerically enforce β_gk(0) = β_gk(1) and β̇_gk(0) = β̇_gk(1) for k = 1, 2 (Ansley et al., 1993). The periodic constraint is adopted because conceptually circadian rhythms have a 24-hour period. For these pseudo data points, the observation matrix is

$$F_{\text{add}}=\text{block diagnoal}\{(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}),(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array})\}.$$

Under this state space framework, it is straightforward to evaluate if one groupaverages is a linear function of the other group-averages. For example in the ACTH and cortisol data, we are interested if the cortisol circadian rhythm β_g2(t) is a linear function of the ACTH circadian rhythm β_g1(t) as β_g2(t) = a + bβ_g1(t). This can be formulated as

$${\mathrm{H}}_0:{\beta }_{g2}(t)=a+b{\beta }_{g1}(t),{\mathrm{H}}_a:{\beta }_{g2}(t)=a+b{\beta }_{g1}(t)+f(t),$$

where f(t) is another periodic cubic smoothing spline with a zero intercept. If H₀ is true then f(t) ≡ 0, which is equivalent to the corresponding covariance parameter λ_f = 0. Note that λ_f = 0 falls on the boundary of the parameter space. The likelihood ratio statistic, consequently, no longer follows a chi-square distribution. We will demonstrate how to approximate the null distribution by simulation in data analysis.

3.3 Relationships between Subject-Specific Deviations

In this section we use bivariate autoregressive process of order 1 (BAR(1)) to illustrate how to model relationships between subject-specific deviations. The design matrix is I₂. For the gth group, the observation and state transition equations are

$$\left(\begin{array}{c}\hfill {\alpha }_{gi1}(t_{ij})\hfill \\ \hfill {\alpha }_{gi2}(t_{ij})\hfill \end{array}\right)={\mathbf{I}}_2\left(\begin{array}{c}\hfill {\upsilon }_{gi1}(t_{ij})\hfill \\ \hfill {\upsilon }_{gi2}(t_{ij})\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\upsilon }_{gi1}(t_{ij})\hfill \\ \hfill {\upsilon }_{gi2}(t_{ij})\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\varphi }_{g11}\hfill & \hfill {\varphi }_{g12}\hfill \\ \hfill {\varphi }_{g21}\hfill & \hfill {\varphi }_{g22}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\upsilon }_{gi1}(t_{i,j-1})\hfill \\ \hfill {\upsilon }_{gi2}(t_{i,j-1})\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\eta }_{{\upsilon }_{gi1}}(t_{ij})\hfill \\ \hfill {\eta }_{{\upsilon }_{gi2}}(t_{ij})\hfill \end{array}\right).$$

For example in the ACTH and cortisol data, υ_gi1(t_ij) denotes ACTH pulses and υ_gi2(t_ij) denotes cortisol pulses. The diagossnal elements of the state transition matrix, ϕ_g11 and ϕ_g22, denote the exponential decays of the two hormones. The off-diagonal elements ϕ_g12 and ϕ_g21 are used to model the asymmetric and time-lagged relationships. The time-lagged feedback of cortisol on ACTH is characterized by ϕ_g12, and the time-lagged feedforward of ACTH on cortisol is characterized by ϕ_g21. These relationships can also be symmetric if ϕ_g12 = ϕ_g21. This BAR(1) approach is a simplification of the human body system by compartmental models. Time-lags bigger than one can be incorporated by augmenting the corresponding states into the state vectors.

The innovation vector is distributed as

$$\left(\begin{array}{c}\hfill {\eta }_{{\upsilon }_{gi1}}(t_{ij})\hfill \\ \hfill {\eta }_{{\upsilon }_{gi2}}(t_{ij})\hfill \end{array}\right)~\mathrm{N}(\mathbf{0},{\mathbf{\Sigma }}_{g\upsilon }=(\begin{array}{cc}\hfill {\sigma }_{\upsilon ,g1}^2\hfill & \hfill {\rho }_g{\sigma }_{\upsilon ,g1}{\sigma }_{\upsilon ,g2}\hfill \\ \hfill {\rho }_g{\sigma }_{\upsilon ,g1}{\sigma }_{\upsilon ,g2}\hfill & \hfill {\sigma }_{\upsilon ,g2}^2\hfill \end{array}\left)\right).$$

The innovation covariance matrices Σ_gv are used to model concurrent and symmetric relationships, whose direction and magnitude are captured by ρ_g. From the scientific aspect, this correlation can be used to model certain shared driving force that are not measured directly. For model identifiability consideration, we assume this BAR(1) to be covariance stationary by constraining the eigenvalues of state transition matrix, Φ_g = {ϕ_gkl}_k,l=1,2, to be within the unit circle. One approach is to code the transition matrices as Φ_g = {chol(I₂ + AA^⊤)}⁻¹A, where “chol” denotes cholesky decomposition and “A” is a matrix with arbitrary real numbers. Consequently, v_gi(0) = { υ_gi1(0) υ_gi2(0) }^⊤ has a proper distribution. Its covariance matrix Σ_gv(0) is obtained by solving ${\mathbf{\Sigma }}_{g\upsilon }(0)={\mathbf{\Phi }}_g{\mathbf{\Sigma }}_{g\upsilon }(0){\mathbf{\Phi }}_g^{\top }+{\mathbf{\Sigma }}_{g\upsilon }$. Note that this model is for equally spaced situation. Continuous time BAR(1) would be required for non-equally spaced cases.

To evaluate if the two groups have the same relationship, we will test if the BAR(1) parameters are the same, especially the ϕ_gkl’s. Note that under the null hypothesis the differences of the parameters equal to zero, which are interior points of the parameter space for differences can be either positive or negative. Consequently, the likelihood ratio statistics will follow chi-square distributions.

4. ESTIMATION AND INFERENCE

Parameters are estimated by maximizing the marginal likelihood. When diffuse initialization exists, maximizing the diffuse marginal likelihood is equivalent to restricted maximum likelihood (Harville, 1974; Laird and Ware, 1982; Ansley and Kohn, 1985). With the estimated parameter, effects and state vectors are estimated by posterior means, which in combination with posterior variances can be used to construct confidence intervals. These posterior means are equivalent to best linear unbiased predictions. For diffuse initial state vectors, they are equivalent to the generalized least squares estimates of fixed effects (Sallas and Harville, 1981). The maximized marginal likelihood can be used to construct likelihood ratio tests (LRTs) and Akaike information criterion (AIC). Model selection can be performed using LRTs and AIC with respect to covariance structures. Additional considerations are required when nonparametric curves are involved, for it is in general hard to derive the analytic forms of the null distributions. As an alternative, simulations can be adopted to approximate the null distributions. For implementation, we adopt the computationally efficient element-wise Kalman filtering and smoothing algorithms. A brief description of the algorithms is given in the appendix. Readers are referred to Durbin and Koopman (2012) Chapter 4 and 5 for details. The marginal likelihood can be maximized by the Nelder-Mead’s simplex method.

5. APPLICATION

The group-average circadian rhythms are modeled by periodic cubic smoothing splines as in Section 3.2. The subject-specific pulses are modeled by BAR(1) as in Section 3.3. It has also been observed that there is a potential synchronization of pulsatile activities, which may be due to the similar data collection environment which the pulses could have partially aligned to. This synchronization may cause undersmoothing in the circadian rhythms. To remedy, we add a group level AR(1) process to account for the synchronized pulses. For simplicity consideration the same AR(1) coefficients, namely ϕ_gkk for k = 1, 2, are adopted. This is because the estimates of group-level and subject-level AR(1) coefficients are essentially the same when we do assume them tobe different. The innovation variances are denoted as ${\sigma }_{gk}^2$ for k = 1, 2. Our primary interest, however, is still on smooth circadian rhythms and subject-specific pulses.

5.1 Parameter Estimates

Parameter estimates for BAR(1) are presented in Table 1 under “Proposed Method”. Likelihood ratio tests were performed to compare the subject-specific BAR(1) parameters between the patient and the control group. For all the 7 parameter, the 4 BAR(1) coefficients, and the 3 innovation covariance parameters, the test statistics are 225.82, 65.83 and 84.57, respectively. Consequently, all three p-values are < 0.0001 under ${\chi }_7^2,{\chi }_4^2$ and ${\chi }_3^2$. Thus we conclude that they are significantly different at the 0.05 level.

Table 1.

Parameter Estimates. The two columns under “Proposed method” are for parameter estimates of the proposed method. The three columns under “TSTSA” are the mean values and p-values comparing the mean values under an approach described in Section 5.3

	Proposed Method		TSTSA
Parameter	Patient group	Control group	Patient group	Control group	p-value
ϕ̂g11	0.9060	0.9183	0.7287	0.7597	0.2338
ϕ̂g22	0.8773	0.8253	0.6721	0.7125	0.0458
ϕ̂g12	−0.0354	−0.0436	0	−0.0209	0.1026
ϕ̂g21	0.1081	0.1365	0.4566	0.3717	0.1058
${\mathrm{\sigma ̂}}_{\upsilon ,g1}^2$	0.9927	1.2159	1.4806	1.7322	0.5051
${\mathrm{\sigma ̂}}_{\upsilon ,g2}^2$	3.0217	3.3393	4.5017	3.8733	0.3549
ρ̂g	0.3132	0.2132	0.1724	0.1614	0.7636
${\mathrm{\sigma ̂}}_{\omega ,g1}^2$	0	0.0191
${\mathrm{\sigma ̂}}_{\omega ,g2}^2$	0.9499	0.9369

For parameters that quantify the relationships between ACTH and cortisol, Table 1 shows that ϕ̂_g12 are negative for both groups, which confirms a negative feedback of cortisol on ACTH. Estimates ϕ̂_g21 are positive for both groups, which confirms a positive driving force of ACTH on cortisol. Estimates ρ̂_g are positive for both groups, which suggests that the rapid changes of ACTH and cortisol are positively correlated. Both ϕ̂_p12 and ϕ̂_p21 have smaller absolute values than ϕ̂_c12 and ϕ̂_c21. This suggests that the feedforward and feedback between ACTH and cortisol in patients have been weakened compared to the healthy controls. For the correlations between the innovations, on the other hand, we have ρ̂_p > ρ̂_c. The lag-one cross correlations can be calculated from cov{α_gi(t_ij),α_gi(t_i,j−1)} = Φ_gΩ_υg, where Ω_υg is the stationary variance of α_gi(t_ij). The patient group has smaller lag-one cross-correlations for both cov{α_g1i(t_ij), α_g2i(t_i,j−1)} as 0.2034 versus 0.2464 and cov{α_g2i(t_ij), α_g1i(t_i,j−1)} as 0.3187 versus 0.3729. These results again suggest that the communications between ACTH and cortisol in patients are not as good as those in the healthy controls.

5.2 Posterior Means

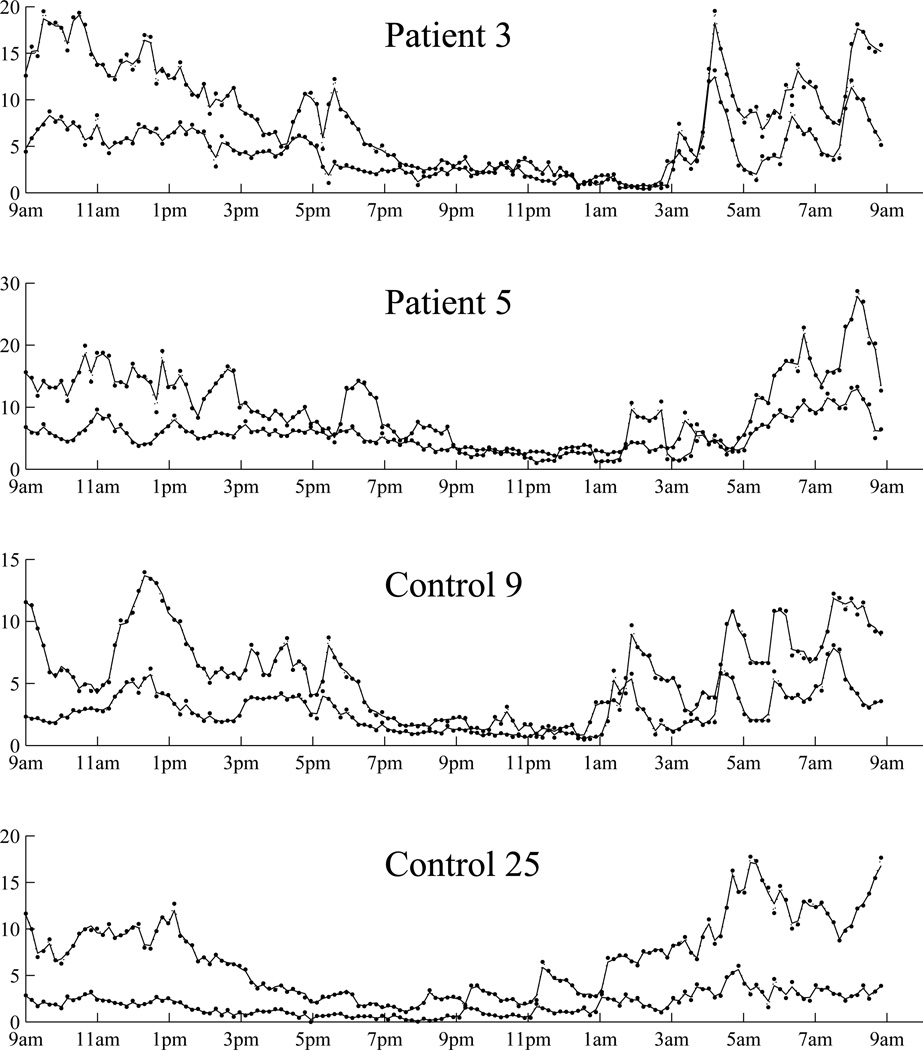
Figure 3 displays individual fittings for two patients and two controls. Fittings for other subjects are similar. We then quantified goodness-of-fit using the conditional coefficient of determination for each subject $(R_{ik}^2)$, adopted from linear mixed effects models (e.g., Liu et al., 2008). It is calculated as $R_{ik}^2=1-{\sum }_j{\{y_{ik}(t_{ij})-{ŷ}_{ik}(t_{ij})\}}^2/{\sum }_j{\{y_{ik}((t_{ij})-{ȳ}_{ik}\}}^2$, for k = 1, 2 as ACTH and cortisol, where ŷ_ik(t_ij) is the posterior mean from the model and ȳ_ik is the arithmetic mean along time. The minimum, median and maximum for each group and each hormone are: (0.9053, 0.9767 0.9966) for patient ACTH, (0.9820, 0.9940 0.9982) for patient cortisol, (0.9615 0.9829 0.9947) for control ACTH and (0.9873 0.9953 0.9983) for control cortisol. Both Figure 3 and $R_{ik}^2$ ’s show that the individual level fittings are reasonably well.

Figure 3.

ACTH (pg/ml) and cortisol (µg/dl) data from two patients and two controls. For each subject, the upper lines are for cortisol, and the lower lines are for ACTH. The original data are displayed by dotted lines with dots, and the fitted values are displayed as solid lines.

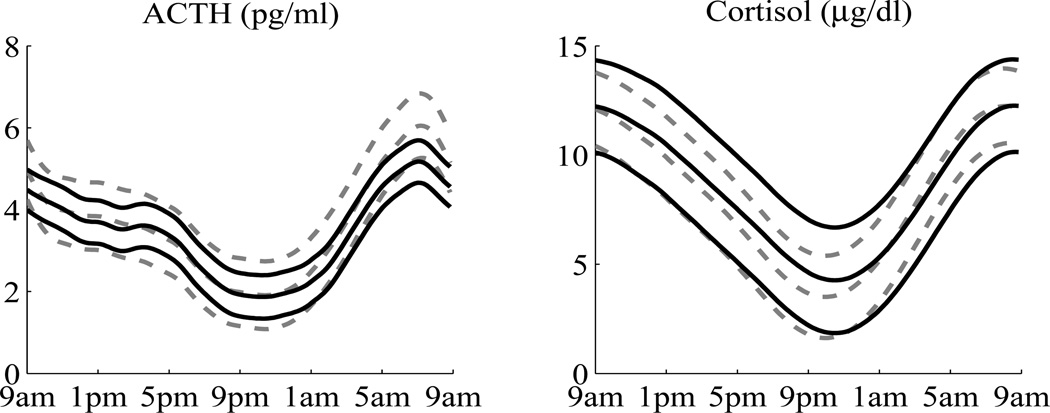
The estimated circadian rhythms with 95% confidence intervals, calculated from the posterior means and variances, are displayed in Figure 4. It shows that the 95% confidence intervals of the controls completely cover the mean curves of the patients, hence their circadian rhythms are not significantly different. The estimated circadian rhythms of cortisol are similar in shape to these of ACTH. One interesting question is whether the cortisol circadian rhythms are mainly linearly driven by the ACTH circadian rhythms. This can be tested as described in Section 3.2. For the patient group, the likelihood ratio statistic is 45.64. Its analytic null distribution, however, is difficult to derive. We instead approximated the null distribution by simulation. One thousand data sets were generated under the reduced model. The circadian rhythms were generated from the posterior distributions that were available from the fitted model, and the pulses were generated using BAR(1) parameter estimates. For each simulated data set, both the reduced model and the full model were fitted. The likelihood ratio statistics were obtained and served as the null distribution. By comparing the observed value of 45.64 to the simulated null distribution, we have P < 0.01. Thus the reduced model is rejected and we conclude that for the patient group the circadian rhythm of cortisol is not a linear function of the circadian rhythms of ACTH. Similar results were obtained for the control group. Since the cortisol circadian rhythms are not mainly linearly driven by ACTH circadian rhythms, we did not compare patients and controls in that aspect.

Figure 4.

Estimated circadian rhythms with 95% confidence intervals. The left panel is for ACTH, the right panel is for cortisol. The solid black lines are for patients, the dashed gray lines are for controls. There are some differences between the patient group and the control group, but the confidence intervals overlap with each other.

5.3 Comparison with Two Other Methods

In this section we compare the proposed method with two other methods. First we compare it with a two-stage time series analysis approach (e.g. Box et al., 2008). In the first stage a BAR(1) was fitted for each subject after detrending individual hormone series. In detrending, a cubic smoothing spline plus AR(1) model was used. In the second stage, the parameter estimates from individual BAR(1) fittings were summarized and compared. Columns under “TSTSA” in Table 1 display the mean values and p-values of comparing the two groups by Student’s t-test. The p-values for all 7 parameters, 4 BAR(1) coefficients and 3 innovation parameters are respectively 0.3772, 0.1431 and 0.6519 by Wilk’s lambda. The results show that the estimates are rather different from the proposed method and most of the p-values are non-significant. One possible reason is that in the detrending step, the trend and the AR process compete for signals. Consequently, the detrended series are likely to be different from the targeted signals. Additionally, the proposed method is a unified modeling approach which usually has better power than multiple-stage approaches.

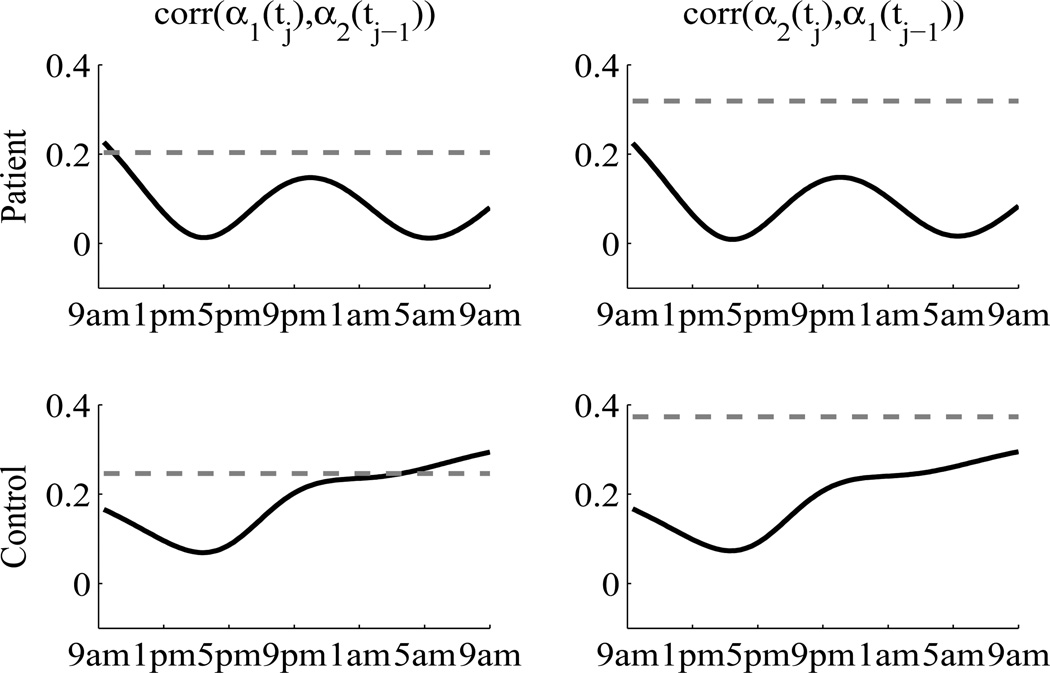
We then compare the proposed method with the random effects approach (Shah et al., 1997). For each hormone, we used cubic smoothing splines for the group-averages and a quadratic random effect for the subject-specific deviations. The quadratic term was chosen by likelihood ratio test comparing to higher and lower order polynomial terms. The joint model of ACTH and cortisol was formulated by modeling the six random regression coefficients with an unstructured covariance matrix. The error terms were assumed to be independent between two hormone. This model was fitted using SAS PROC MIXED (Wang, 1998; Thiébaut et al., 2002). To compare the proposed method with this approach, we again calculated the lag-one cross correlations. The results are displayed in Figure 5. The derived lag-one cross correlations from the random effects approach are time-varying, which is an artifact due the concurrent assumption. This can lead to misunderstanding if over-interpreted (Fieuws and Verbeke, 2004). The figure also shows that the lag-one cross correlations from the random effects approach are in general smaller than those from the proposed method. This is because ACTH and cortisol pulses exhibit comovements only in a short time span. The proposed method uses BAR(1) to capture these comovements, which are thus recognized as signals. The random effects approach, on the other hand, treats these comovements as random fluctuations around the long term trends. Consequently, the lag-one cross correlations were underestimated by the random effects approach.

Figure 5.

Lag-one cross correlations. Solid black lines are from random effects approach. Gray dashed lines are from the proposed method. The upper panel is for the patient group. The lower panel is for the control group.

6. SIMULATION

In this section a small simulation is conducted to investigate the performance of the proposed method with respect to parameter estimation of BAR(1) on top of smooth curves. We then compared the proposed method with the two-stage time series analysis approach mentioned in Section 5.3. Data were generated as

$$\left(\begin{array}{c}\hfill y_{1i}(t_j)\hfill \\ \hfill y_{2i}(t_j)\hfill \end{array}\right)=\left(\begin{array}{c}\hfill f_1(t_j)\hfill \\ \hfill f_2(t_j)\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\alpha }_{1i}(t_j)\hfill \\ \hfill {\alpha }_{2i}(t_j)\hfill \end{array}\right)+\left(\begin{array}{c}\hfill e_{1ij}\hfill \\ \hfill e_{2ij}\hfill \end{array}\right),$$

for outcome 1 and 2, subject i = 1,⋯, 35, and time point j = 1,⋯, n where n = 25, 50, 100. Group level circadian rhythms were generated as f₁(t) = 1.5 + 5cos(2πt) and f₂ = 3 + 10cos(2πt) for t ∈ [0, 1]. BAR(1) components {υ_1i (t_j), υ_2i (t_j)}^⊤ were generated with ${\sigma }_1^2=2,{\sigma }_2^2=4$, ρ = 0.5 and the transition matrix T_υ with six scenarios

$$(1)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill 0.3\hfill \\ \hfill 0\hfill & \hfill 0.6\hfill \end{array}\right),(2)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill -0.3\hfill \\ \hfill 0\hfill & \hfill 0.6\hfill \end{array}\right),(3)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill 0.3\hfill \\ \hfill 0.3\hfill & \hfill 0.6\hfill \end{array}\right),(4)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill -0.3\hfill \\ \hfill -0.3\hfill & \hfill 0.6\hfill \end{array}\right),(5)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill -0.3\hfill \\ \hfill 0.3\hfill & \hfill 0.6\hfill \end{array}\right),(6)\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill -0.1\hfill \\ \hfill 0.1\hfill & \hfill 0.6\hfill \end{array}\right).$$

Independent errors with ${\sigma }_{e1}^2=1$ and ${\sigma }_{e2}^2=2$ were added.

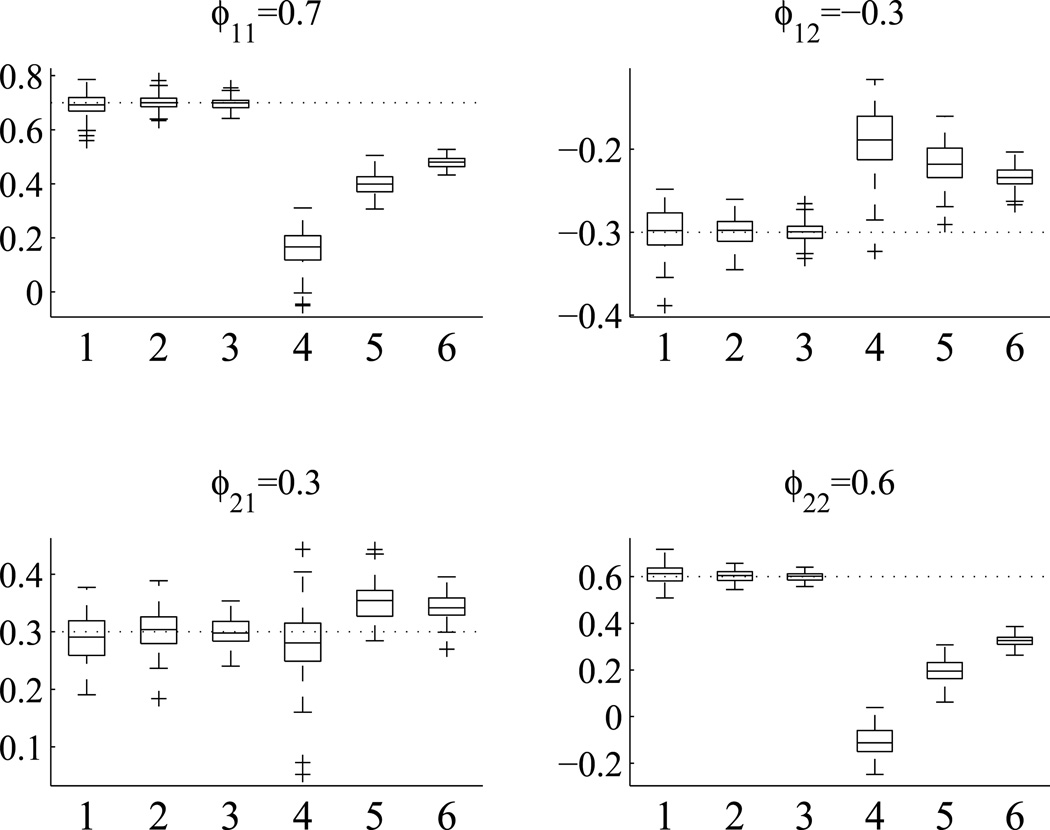
Each combination of T_υ and time point n was repeated 100 times. The results show that for all the BAR(1) parameters, the estimates are around their true values. When n increases, the estimates become more accurate and less variable. The results are obviously expected hence not displayed. We then used scenario 5 to compare the proposed method with the two-stage time series analysis approach. For each of the 100 simulated data sets, the estimates of the BAR(1) coefficients are summarized by the boxplots in Figure 6. The two-stage time series analysis approach shows bigger variations in parameter estimates and with more substantial biases. The biases are more obvious for ϕ₁₁ and ϕ₂₂, less so for ϕ₁₂ and ϕ₂₁. The biases decrease as the number of time points n increases.

Figure 6.

Comparison of BAR(1) coefficient estimates for scenario 5 between the proposed method and the two-stage time series analysis approach. True parameter values are displayed in the titles and by dotted reference lines. For each cell, box 1, 2 and 3 are for the proposed method with n = 25, 50, 100, respectively. Box 4, 5 and 6 are for the two-stage time series analysis approach with n = 25, 50, 100, respectively.

7. DISCUSSION

We have proposed a bivariate hierarchical state space model. The proposed methods can be straightforwardly generalized to multivariate situations. Analyses of the ACTH and cortisol data reveal that the driving forces of ACTH on cortisol and the feedback of cortisol on ACTH were weakened in the patient group. One potential consequence of these weakened communications is that the HPA axis in patients does not respond to external and internal stimuli as well as in healthy subjects. The study analyzed in this paper does not have data on CRH and VP, which are important components of the HPA axis. The proposed models can be easily extended to incorporate CRH and VP, when such data become available.

In this paper we have concentrated on linear Gaussian models. The proposed modeling framework can be generalized to nonlinear and non-Gaussian situations. Estimation and inference of nonlinear and non-Gaussian models would require simulation-based algorithms, such as sequential Monte Carlo methods for non-Gaussian state space methods Durbin and Koopman (2012). One such method is particle filter (Gordon et al., 1993). In this method, sequential random draws are used to approximate the continuous distributions. From these draws, both state estimates and likelihood function can be evaluated.

APPENDIX: ALGORITHMS

The vector form of mixed effects state space models

We first reformulate the proposed models into vector state space forms by collecting items across all m subjects at the same time points

$${\mathbf{y}}_j={\mathbf{F}}_j{\gamma }_j+{\mathbf{e}}_j,$$ (6)

$${\gamma }_j={\mathbf{H}}_j{\gamma }_{j-1}+{\mathbf{R}}_j{\mathit{\eta }}_j,$$ (7)

where j = 1,⋯, n for n distinct time points,

$$y_j=\left(\begin{array}{c}{y}_1(t_j)\\ ⋮\\ y_m(t_j)\end{array}\right),{\gamma }_j=\left(\begin{array}{c}\hfill \beta (t_j)\hfill \\ \hfill {\alpha }_1(t_j)\hfill \\ \hfill ⋮\hfill \\ \hfill {\alpha }_m(t_j)\hfill \end{array}\right),e_j=\left(\begin{array}{c}\hfill e_1(t_j)\hfill \\ \hfill ⋮\hfill \\ \hfill e_m(t_j)\hfill \end{array}\right),{\mathit{\eta }}_j=\left(\begin{array}{c}\hfill {\mathit{\eta }}_u(t_j)\hfill \\ \hfill {\mathit{\eta }}_{\upsilon 1}(t_j)\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathit{\eta }}_{\upsilon m}(t_j)\hfill \end{array}\right),{\mathbf{F}}_j=\left(\begin{array}{ccccc}\hfill {\mathbf{X}}_1(t_j){\mathbf{F}}_{\beta }(t_j)\hfill & \hfill {\mathbf{Z}}_1(t_j){\mathbf{F}}_{\alpha }(t_j)\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill {\mathbf{X}}_2(t_j){\mathbf{F}}_{\beta }(t_j)\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{Z}}_2(t_j){\mathbf{F}}_{\alpha }(t_j)\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{X}}_m(t_j){\mathbf{F}}_{\beta }(t_j)\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{Z}}_m(t_j){\mathbf{F}}_{\alpha }(t_j)\hfill \end{array}\right),{\mathbf{H}}_j=\text{Block diagonal}\{{\mathbf{T}}_u(t_j),{\mathbf{T}}_{\upsilon }(t_j),\cdots ,{\mathbf{T}}_{\upsilon }(t_j)\},{\mathbf{R}}_j=\text{Block diagonal}\{{\mathbf{R}}_u(t_j),{\mathbf{R}}_{\upsilon }(t_j),\cdots ,{\mathbf{R}}_{\upsilon }(t_j)\},$$

and e_j and η_j are serially and mutually independently distributed as

$${\mathbf{e}}_j~\mathrm{N}(\mathbf{0},\text{diagonal}\{{\sigma }_{e1}^2,{\sigma }_{e2}^2,\cdots ,{\sigma }_{e1}^2,{\sigma }_{e2}^2\}){\mathit{\eta }}_j~\mathrm{N}(\mathbf{0},{\mathbf{Q}}_j=\text{block diagonal}\{{\mathbf{\Sigma }}_u(t_j),{\mathbf{\Sigma }}_{\upsilon }(t_j),\cdots ,{\mathbf{\Sigma }}_{\upsilon }(t_j)\}).$$

The initial state vector is distributed as

$${\gamma }_0~\mathrm{N}(\mathbf{0},{\mathbf{P}}_0=\text{block diagonal}\{{\mathbf{\Sigma }}_u(0),{\mathbf{\Sigma }}_{\upsilon }(0),\cdots ,{\mathbf{\Sigma }}_{\upsilon }(0)\}).$$

The vector form needs to be formulated on the finest time grid. The time points across subjects, however, do not need to be equally spaced nor balanced. For each time point, only the available observations across subjects are needed for the filtering and smoothing algorithms. Also note that β(t) and α_i(t) can be recovered from γ_i(t), F_β(t) and F_α(t).

Filtering algorithm

Let z_l (t_j) be the lth element of y_j, Y_l (t_j) = {y (t₁)^⊤ ,⋯, y (t_j−1)^⊤, z₁ (t_j) ,⋯, z_l (t_j)}^⊤ for l = 1,⋯, 2m. Let e_l (t_j) be the lth element of e_j, γ_l (t_j) be the state vector γ(t_j) indexed by z_l(tj), the univariate version state space model of (6) and (7) is

$$z_l(t_j)={\mathbf{F}}_l(t_j){\gamma }_l(t_j)+e_l(t_j),{\gamma }_0(t_j)=\mathbf{H}(t_j){\gamma }_{2m+1}(t_{j-1})+\mathbf{R}(t_j)\mathit{\eta }(t_j),{\gamma }_l(t_j)={\gamma }_{l-1}(t_j),l=1,\cdots ,2m,$$

where F_l(t_j) denotes the lth row of F(t_j).

Define

$${\mathbf{a}}_l(t_j)=\mathrm{E}\{{\gamma }_l(t_j)|{\mathbf{Y}}_{l-1}(t_j)\},{\mathbf{P}}_l(t_j)=\text{var}\{{\gamma }_l(t_j)|{\mathbf{Y}}_{l-1}(t_j)\}.$$

The transition from time j − 1 to j is

$${\mathbf{a}}_0(t_j)=\mathbf{H}(t_j){\mathbf{a}}_{2m+1}(t_{j-1}),{\mathbf{P}}_0(t_j)=\mathbf{H}(t_j){\mathbf{P}}_{2m+1}(t_{j-1}){\{\mathbf{H}(t_j)\}}^{\top }+\mathbf{R}(t_j)\mathbf{Q}(t_j){\{\mathbf{R}(t_j)\}}^{\top },$$

for j = 1,⋯, n, initialized as a_2m+1 (t₀) = 0 and P_2m+1 (t₀) = P₀.

The element-wise filtering algorithm is

$${\epsilon }_l(t_j)=z_l(t_j)-{\mathbf{F}}_l(t_j){\mathbf{a}}_l(t_j),{\upsilon }_l(t_j)={\mathbf{F}}_l(t_j){\mathbf{P}}_l(t_j){\{{\mathbf{F}}_l(t_j)\}}^{\top }+{\sigma }_l^2,{\mathbf{L}}_l(t_j)=\mathbf{I}-{\mathbf{P}}_l(t_j){\{{\mathbf{F}}_l(t_j)\}}^{\top }{\mathbf{F}}_l(t_j){\{{\upsilon }_l(t_j)\}}^{-1},{\mathbf{a}}_{l+1}(t_j)={\mathbf{a}}_l(t_j)+{\mathbf{P}}_l(t_j){\{{\mathbf{F}}_l(t_j)\}}^{\top }{\{{\upsilon }_l(t_j)\}}^{-1}{\epsilon }_l(t_j),{\mathbf{P}}_{l+1}(t_j)={\mathbf{P}}_l(t_j){\{{\mathbf{L}}_l(t_j)\}}^{\top },$$

for l = 1,⋯, 2m, ${\sigma }_l^2={\sigma }_k^2$ with k = l − 2(i − 1), i = ⌈l/2⌉ where ⌈x⌉ denotes the smallest integer ≥ x. The logarithm likelihood is calculated by

$$l(\mathit{\theta }|\mathbf{Y})=\sum _{j=1}^n\sum _{l=1}^{2m}[-\frac{1}{2}\text{log}(2\pi )-\frac{1}{2}\text{log}\{{\upsilon }_l(t_j)\}-\frac{1}{2}{\{{\epsilon }_l(t)\}}^2{\{{\upsilon }_l(t_j)\}}^{-1}],$$

where θ is the parameter vector and Y is the collection of all observations.

Smoothing algorithm

Denote

$$\mathrm{\gamma ̂}(t_j)=\mathrm{E}\{\gamma (t_j)|\mathbf{Y}\},\mathbf{V}(t_j)=\text{Var}(\gamma (t_j)|\mathbf{Y}).$$

Let r_2m (t_n) = 0, N_2m (t_n) = 0, the backward recursion is

$${\mathbf{r}}_{l-1}(t_j)={\{{\mathbf{F}}_l(t_j)\}}^{\top }{\{{\upsilon }_l(t_j)\}}^{-1}{\epsilon }_l(t_j)+{\{{\mathbf{L}}_l(t_j)\}}^{\top }{\mathbf{r}}_l(t_j),{\mathbf{N}}_{l-1}(t_j)={\{{\mathbf{F}}_l(t_j)\}}^{\top }{\{{\upsilon }_l(t_j)\}}^{-1}{\mathbf{F}}_l(t_j)+{\{{\mathbf{L}}_l(t_j)\}}^{\top }{\mathbf{N}}_l(t_j){\mathbf{L}}_l(t_j),{\mathbf{r}}_{2m}(t_{j-1})={\{\mathbf{H}(t_j)\}}^{\top }{\mathbf{r}}_0(t_j),{\mathbf{N}}_{2m}(t_{j-1})={\{\mathbf{H}(t_j)\}}^{\top }{\mathbf{N}}_0(t_j)\mathbf{H}(t_j),$$

for l = 2m,⋯, 1. And the smoothed state vectors and their posterior variances are

$$\mathrm{\gamma ̂}(t_j)={\mathbf{a}}_1(t_j)+{\mathbf{P}}_1(t_j){\mathbf{r}}_0(t_j),\mathbf{V}(t_j)={\mathbf{P}}_1(t_j)-{\mathbf{P}}_1(t_j){\mathbf{N}}_0(t_j){\mathbf{P}}_1(t_j).$$

Readers are referred to Koopman and Durbin (2003) for details of exact diffuse filtering and smoothing.