Automated Segmentation of the Cerebellar Lobules using Boundary Specific Classification and Evolution

Abstract

The cerebellum is instrumental in coordinating many vital functions ranging from speech and balance to eye movement. The effect of cerebellar pathology on these functions is frequently examined using volumetric studies that depend on consistent and accurate delineation, however, no existing automated methods adequately delineate the cerebellar lobules. In this work, we describe a method we call the Automatic Classification of Cerebellar Lobules Algorithm using Implicit Multi-boundary evolution (ACCLAIM). A multiple object geometric deformable model (MGDM) enables each boundary surface of each individual lobule to be evolved under different level set speeds. An important innovation described in this work is that the speed for each lobule boundary is derived from a classifier trained specifically to identify that boundary. We compared our method to segmentations obtained using the atlas-based and multi-atlas fusion techniques, and demonstrate ACCLAIM’s superior performance.

1 Introduction

The human cerebellum is a remarkably complex structure that coordinates numerous vital functions of the human body. It is involved in tasks such as eye-movement, speech, balance, fine motor control, motor learning, and cognition [12, 16]. As in the cerebrum, cerebellar functions tend to be localized to particular regions. As well, cerebellar diseases and degeneration often target specific regions of the cerebellum and are associated with specific patterns of symptoms [23]. The cerebellum has been shown to be affected in diseases ranging from attention-deficit and hyperactivity disorder [14] to chronic alcoholism [17]. Continued research into the nature of these patterns will require accurate estimates of the sizes and shapes of the constituent sub-regions of the cerebellum. Furthermore, more detailed and anatomically meaningful sub-regions will provide the best insight into the particular workings of the cerebellum.

The cerebellar cortex consists of a thin sheet of highly convoluted gray matter wrapped around a central mass of white matter called the corpus medullare (CM). Fissures divide the gray matter into small branches called lobules, numbered from I to X. The most prominent fissures define the boundaries of the lobes of the cerebellum. Lobules I–V form the anterior lobe, VI–VII are the middle lobules, and VIII–X are the caudal lobules. Fig. 1 shows a cartoon representation of the cerebellar lobules, and magnetic resonance images of a control subject and patient annotated with cerebellar lobule labels. Notice the significant gray matter atrophy in the patient.

Fig. 1.

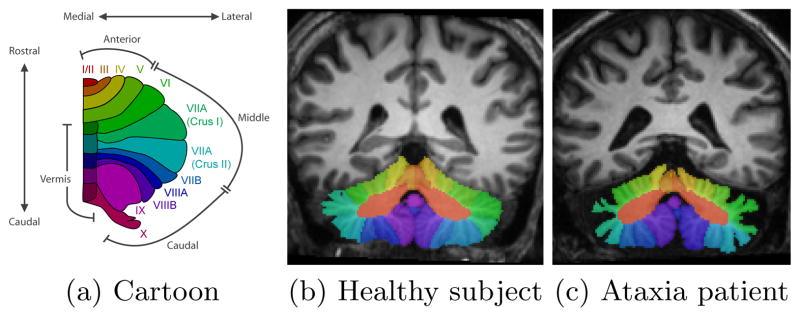
Figures showing (a) a cartoon of the cerebellar vermis and lobules (one hemisphere), and (b) and (c) MR images of the cerebellum labeled by an expert human rater.

Despite the importance of the cerebellar lobules, progress has been slow in developing automated segmentation methods. While several manual and automatic methods [15] exist, the level of human interaction and expertise limits the potential scope of studies. Current automatic segmentation methods for the cerebellar lobules rely on registration with an atlas, for example the SUIT atlas of Diedrichsen et al. [10]. The multi-atlas segmentation framework improves upon single-atlas methods in that they better incorporate inter-subject variability and take advantage of “statistical fusion” techniques [20]. However, neither of these approaches produces adequate segmentation results of the cerebellar lobules. Furthermore, neither of these methods controls the topology of the resulting segmentation; an important capability if subsequent analyses require point correspondences between subjects.

In this work, we describe an Automatic Classification of Cerebellar Lobules Algorithm using Implicit Multi-boundary evolution (ACCLAIM). Given a magnetic resonance (MR) image, ACCLAIM produces a topologically correct and accurate lobule parcellation despite variability due to cerebellar atrophy. The multiple-object geometric deformable model (MGDM) framework [5] is used to find a locally optimal segmentation relative to a topologically correct initialization. MGDM’s capability in enabling the specification of speeds on object boundaries rather than on the objects themselves was key in obtaining desired behavior during evolution.

ACCLAIM applies speed functions derived from a novel boundary classification method to evolve the boundaries between lobule labels. This involves training a classifier to detect individual boundary surfaces between objects. Boundary detection is similar to edge detection, the difference being that while edges are low-level image features without semantic meaning, boundaries are a high-level concept relative to specific objects. For example, while an edge exists at locations between low and high intensity, a boundary exists at the interface between two specific anatomical regions (e.g., different cerebellar lobules, in our case). This aspect of our work shares a philosophy with the work of [19] in the use of low-level, discriminative image features with high-level semantic concepts. Bogovic et al. [5] included a preliminary demonstration of automatic cerebellum parcellation using MGDM but resulted in a coarser parcellation and did not include boundary classification speeds or quantitative validation.

ACCLAIM yields a 28 label cerebellar parcellation of the cerebellum. We group some regions to form a 24 label parcellation to enable direct comparison with SUIT. We validated ACCLAIM using both control subjects and patients with a spinocerebellar ataxia (SCA) type 6: a genetic disease that can cause severe cerebellar atrophy, see Fig. 1. Direct comparisons with atlas and multi-atlas based approaches demonstrate ACCLAIM’s superior performance.

2 Methods

2.1 Subject cohort, Image acquisition, and Preprocessing

A cohort of 15 subjects (9 females) is used for training and validation, with ages ranging from 30 to 71 years. Nine of the subjects have been diagnosed with cerebellar ataxia. The input image to ACCLAIM is a magnetization-prepared rapid gradient echo (MPRAGE) acquired using a 3.0T MR scanner (Intera, Phillips Medical Systems, Netherlands). The parameters of the MPRAGE are: 132 slices, axial orientation, 1.1mm slice thickness, 8° flip angle, TE = 3.9ms, TR = 8.43ms, FOV 21.2 × 21.2 cm, matrix 256 × 256 (resolution: 0.828125 × 0.828125×1.1mm). A human expert rater manually labeled the cerebellar lobules from these images, the results of which we use as ground-truth for training and validation of our method.

ACCLAIM starts by resampling the acquired MR volume to 0.8×0.8×0.8mm voxels using windowed sinc interpolation and then corrects for intensity inhomogeneity using N3 [18]. The intensities are then linearly scaled to the range [0, 1] with all intensities at or above the 99.99^th percentile mapped to unity. SPECTRE [7] is used to mask the brain (cerebrum and cerebellum) and TOADS [4] is used to obtain a mask around the cerebellum and a soft classification of its tissues as gray or white matter.

2.2 Topology and Statistical Atlas

We briefly describe the construction and use of the statistical and topology atlases in ACCLAIM. First, a group-wise registration was performed using all subjects in the cohort using the symmetric image normalization (SyN) algorithm [1]. The ground truth labels were transformed to the group mean, and the probability for each object was computed. We determined the most likely object at each point and resampled that label map to a coarse resolution (2 × 2 × 2mm) in order to ensure that the features of each object will be sufficiently “thick” [2] after being registered to the image to be segmented. Next, we ensured that each object had spherical topology and enforced that all lobule labels are connected to the corpus medullare, and that lobules are connected to the adjacent lobules in the rostral and caudal directions (see Fig. 1(a)). ACCLAIM rigidly registers the topology atlas to the novel subject as an initial segmentation, and uses the registered probabilistic atlas as a prior during parcellation.

The groupwise registration also yields a mean average appearance of the cerebellum which we register to a masked MPRAGE of a novel subject’s cerebellum, also using the SyN algorithm. We ran SyN using cross correlation as the similarity measure, and set the maximum number of iterations at the coarse, medium, and fine levels to 40, 30, and 20, respectively. This coregisters our probabilistic atlas with the subject.

2.3 Multiple-Object Geometric Deformable Model (MGDM)

MGDM is a multiple-object extension to the geometric deformable model framework for active contours [5]. It uses a decomposition of the signed distance functions (SDFs) of all objects that enables efficient evolution of all objects while preventing overlaps or gaps from forming. It also allows speeds to be specified on boundaries between objects as well as on the objects themselves.

The MGDM decomposition of object level sets (ϕ_i), begins by computing a series of “neighbor functions” by:

$$\begin{array}{l}\forall x,L_0(x)=i\text{iff}{\varphi }_i(x)<0\\ L_k(x)=arg\underset{j\ne L_n(x)}{min}{\varphi }_j(x)\forall k>0,0\le n<k\end{array}$$ (1)

These functions can be interpreted as the the current segmentation (L₀) and the set of closest neighboring objects L_k at a point x. These can be used to define a series of distance functions as follows:

$$\begin{array}{l}\forall x,{\phi }_0(x)={\varphi }_{L_1}(x)\\ {\phi }_k(x)={\varphi }_{L_{k+1}}(x)-{\varphi }_{L_k}(x)k>0\end{array}$$ (2)

The first of these φ₀ give the distance to the nearest boundary (i.e., to the closest neighbor). The φ_k functions indicate how much further the k + 1-th neighbor is from x than the k-th neighbor. An important advantage of this decomposition is the fact that only the first few of these functions are required in order to perform the geometric deformable model computations. This is because at any given voxel, storing the first K distance functions allows the SDF for the nearest K + 1 neighboring objects to be exactly reconstructed.

One can think of this decomposition as representing boundaries rather than objects. This enables MGDM to evolve the boundary surfaces between objects rather than the objects themselves. We denote boundaries as unordered pairs of labels, where (i, j) or (j, i) denote the boundary between objects i and j. We also associate every point x with the boundary it is closest to, and can so build a set of points 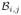associated with boundary (i, j):

$${\mathcal{B}}_{i,j}=\{x:[L_0(x)=i\cap L_1(x)=j]\cup [L_0(x)=j\cup L_1(x)=i]\}.$$ (3)

In other words, the closest boundary is between the current object at x (L₀) and the nearest neighboring object (L₁). This allows MGDM to evolve the distance function at x under speeds defined for the nearest boundary rather than for the object to which x belongs.

As a result, the evolution of the k^th MGDM distance function φ_k is defined by the evolution equation

$$\frac{\partial {\phi }_k(x)}{\partial t}=f_{L_k,L_{k+1}}(x)\mid \nabla {\widehat{\varphi }}_{L_k}(x)\mid ,$$ (4)

where f_Lk,Lk+1 (x) gives the speed for the (L_k, L_k+1) boundary at x and ϕ̂_Lk is the estimate of the distance function for object L_k reconstructed from the set of MGDM distance functions. Furthermore, if L_n = i and L_m = j, and m > n, then the distance to the (i, j) boundary can be computed using:

$${\psi }_{i,j}(x)=\sum _{k=n}^{m-1}{\phi }_k(x).$$ (5)

This capability of MGDM is used in the following section, where we learn a classifier for each boundary. In particular, this enables us to select voxels near the boundary both during training and when detecting a boundary for a novel subject, and in applying appropriate level set speeds according to the nearest boundary.

2.4 Boundary Detection and Evolution

The use of image intensity statistics within objects has been an important technique in the level set literature for finding object boundaries [9, 13]. In the cerebellum, however, image intensity is not sufficient to distinguish the cerebellar lobules from one another because they all share similar intensities. Instead, many classical segmentation approaches use the magnitude of the image gradient, |∇I(x)| as an indicator of a boundary location [8, 22], and develop a level set speed of the form:

$$\begin{array}{c}f(x)=-\mathbf{v}(x)·\nabla \varphi (x),\\ \text{where}f(x)=0\Rightarrow \mid \nabla I(x)\mid >\epsilon \end{array}$$ (6)

where v(x) describes a vector field, most often obtained as the gradient of a stopping or potential function [8], or using gradient vector flow (GVF) [22]. The field is designed such that the speed zero only where an edge is detected. We adopt a similar framework in this work, as a vector is computed at each spatial location x to determine the level set speed.

Rather than detecting edges, we learn the appearance of the (i, j) boundary by training a classifier that discriminates between on-boundary (c_i,j = 1) and off-boundary (c_i,j = 0) image locations for all boundaries. Specifically, we estimate

$$p=p_x(c_{i,j}\mid I)$$ (7)

where p_x(c_i,j|I) denotes the conditional probability that x is on boundary (i, j) given the image intensities I. While machine learning techniques have been used in the past for edge detection, to our knowledge this work is the first to use unique classifiers for each boundary surface. The semantic meaning of these boundaries and the MGDM representation make this approach possible. Our level set speed for the (i, j) boundary is given by the GVF field of the conditional probabilty map, obtained by finding the v_i,j that minimizes:

$$E={\int }_x\mu {\Vert {\mathbf{v}}_{i,j}\Vert }^2+{\Vert \nabla p\Vert }^2{\Vert {\mathbf{v}}_{i,j}-\nabla p\Vert }^2.$$ (8)

The final resulting vector field speed is:

$$f_{i,j}^b(x)=-{\mathbf{v}}_{i,j}(x)·\nabla {\widehat{\varphi }}_i(x).$$ (9)

Note from Eqs. 3 and 4 that $f_{i,j}^b(x)$ only affects the evolution of the distance function φ₀ where x is nearest to the (i, j) boundary (i.e., x ∈ 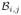). Next, we simplify the conditional probability p_x(c_i,j|I) ≈ p_x(c_i,j|u(x)) where the vector u(x) is a set of features computed at x.

The cerebellar lobules are separated by fissures containing cerebral spinal fluid (CSF), which appear as lines or planes of lower intensity. These fissures can be thinner or wider depending on the particular subject, level of atrophy, and particular fissure. Therefore, we compute these features at a variety of scales as in [21]. We found that the eigenvalues of the image Hessian provide a good trade-off between the number of features and the classification performance. As a result, the feature vector at voxel x is:

$$\mathbf{u}(x)={[{\lambda }_1^{\sigma }(x){\lambda }_2^{\sigma }(x){\lambda }_3^{\sigma }(x)]}_{\sigma \in \{0.5,1.0,2.0,3.0\}}$$ (10)

where ${\lambda }_n^{\sigma }$ is the nth eigenvalue of the Hessian matrix at x at the σ scale. Since each scale yields three eigenvalues, a total of 12 features are used by the classifier.

In this work we used random forests [6] to perform classification and estimate p_x(c_i,j|u(x)). Random forests consist of a set of bootstrap aggregated decision trees and have been shown to achieve robust and accurate classification while avoiding overfitting. We trained an ensemble of 20 decision trees, with each decision node considering a random subset of log₂(M) + 1 of the M total input features (4 of the 12 in our case) as described in [6]. Novel observations are classified by every decision tree in the ensemble. The probability that the observation belongs to a particular class can be computed as:

$$p_x(c_{i,j}\mid \mathbf{u}(x))=\frac{1}{N}\sum _i^N{h}_i(\mathbf{u}(x)),$$ (11)

where h_i(u(x)) ∈ {0, 1} gives the prediction of the ith decision tree. We used the implementation found in the open-source Weka machine learning software [11].

We next create a set of training data 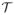from the training subjects 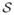. Each observation in the training data for the (i, j) boundary consists of an ordered pair (u(x), c_i,j(x)). At this stage, a decision remains as to which voxels should be included in the training data for a given boundary. One straightforward choice would be to include all voxels, but this could result in voxels being classified as “on-boundary” for multiple boundaries, as well as needlessly increasing computational burden. Rather, we include voxels x within a small window (Δ = 4mm) around a given boundary in the training data for that boundary, with “on-edge” observations being those within a distance δ = 1mm of the boundary. As a result, the training data can be expressed as

$$\mathcal{T}=\{({\mathbf{u}}^s(x),0):\delta <{\psi }_{i,j}^s(x)\le \mathrm{\Delta },s\in \mathcal{S}\}\cup \{({\mathbf{u}}^s(x),1):{\psi }_{i,j}^s(x)\le \delta ,s\in \mathcal{S}\}$$ (12)

where ${\psi }_{i,j}^s(x)$ indicates the distance to the boundary (i, j) at point x for subject s as computed by Eq. 5. We used these data to train the ensemble of decision trees h_i. Next, we describe how ACCLAIM uses these during the segmentation of a novel subject.

In order to take advantage of the ensemble of classifiers, we must compute the vector field defining the level set speeds for all boundaries. First, the conditional probabilities are estimated by:

$$p_x(c_{i,j}\mid \mathbf{u}(x))=\{\begin{array}{rr}\hfill \frac{1}{N}\sum _i^N{h}_i(\mathbf{u}(x)),& \hfill {\widehat{\psi }}_{i,j}(x)\le \mathrm{\Delta }\\ \hfill 0,& \hfill {\widehat{\psi }}_{i,j}(x)>\mathrm{\Delta }\end{array}$$ (13)

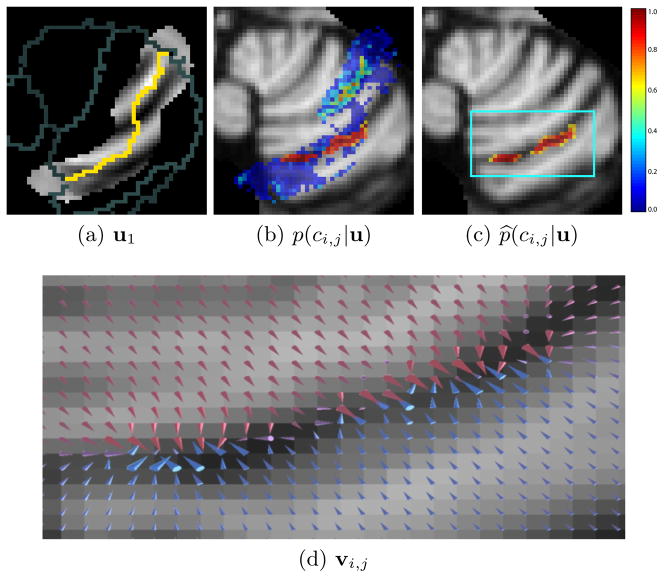
where ψ̂_i,j(x) is the distance to the (i, j) boundary estimated from ACCLAIM’s current segmentation. This estimate is needed only to determine the window in which computations will be performed, and to avoid false positives far from the expected boundary location. An example of a prediction made by our trained random forest classifier p_x(c_i,j|u(x)) is shown in Fig. 2(b). We can observe that voxels for two distinct regions have high probabilities of being on the boundary. We would like to ensure that the anatomical feature that is detected belongs to a single fissure and not to two or more fissures. We applied the fast marching topology correction method of [3] to obtain a corrected probability map p̂_x(c_i,j|u(x)) (shown in Fig. 2(c)), in order to remove extraneous portions of the detected region.

Fig. 2.

A trained classifier is given image features, one of which is shown in (a). The yellow pixels show the current estimate of the boundary to be evolved, while gray pixels show other nearby boundaries. The classifier produces a probability map shown in (b) indicating how likely it is that a given voxel lies on the boundary between two lobules. The topology of this probability map is corrected, the result of which is given in (c). Finally a GVF field is computed from the topologically correct probabilities as shown in (d). The arrows of the GVF are scaled by the square root of their magnitude and colored according to their y component: blues and reds indicate positive and negative y components, respectively.

Finally, the GVF field is computed from the topology corrected probability map by minimizing Eq. 8. A maximum of 20 iterations were allowed with μ = 0.3. Fig. 2(d) visualizes the resulting field.

2.5 Boundary Evolution Speed Functions

ACCLAIM uses level set speeds based on the probabilistic atlas, image intensity, tissue classification, and the boundary classification field. We evolve each boundary using different weights of the speeds, and give two examples here (omitting others for space considerations). First, a tissue boundary between lobules and CSF or WM uses the speed

$$f_{i,j}(x)=(0.1)\kappa -(2.5)[{(I(x)-{\mu }_j)}^2-{(I(x)-{\mu }_i)}^2]-(0.3)[l_j(x)-l_i(x)]-(1.0)[r_{\mathit{CSF}}(x)-r_{GM}(x)]$$ (14)

where i ∈ {Lobule I – VIII}∩j ∈ {Background/CSF}. Second, a lobule-to-lobule boundary uses the speed

$$f_{i^{\prime },j^{\prime }}(x)=(0.3)\kappa -(0.4)[l_{j^{\prime }}(x)-l_{i^{\prime }}(x)]-(1.6)[{\mathbf{v}}_{i^{\prime },j^{\prime }}(x)·\nabla {\varphi }_{i^{\prime }}(x)]$$ (15)

where i′ ∈ {Lobule; I – VIII} ∩ j′ ∈ {Lobule I – VIII}. In these examples, κ denotes the mean curvature of the boundary, l_i(x) denotes the probability of finding object i at x from the probabilistic atlas, μ_i denotes the mean intensity in object i, and r_tissue(x) denotes the membership function of a tissue class.

3 Results

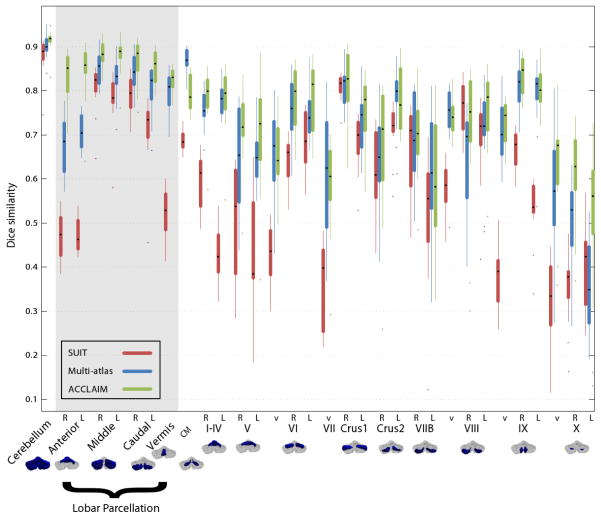
We ran ACCLAIM using each subject in the cohort and compared the results to an expert’s segmentation. The results shown here use all subjects for training, with subject-wise leave-one-out validation planned. We expect cross-validation experiments to produce similar results to those shown because the training procedure for random forests bootstraps the training data. Evaluation was performed at three levels of hierarchy: whole cerebellum, lobe-level (I–V, VI–VII, VIII–X), and lobule-level. We examined the overlap between the true and automatically obtained labels using the Dice similarity coefficient (DSC), and the accuracy of the volumes produced using the intraclass correlation coefficient (ICC). Figure 3 shows a boxplot of the DSC between the expert’s and automatic labels for the three level of hierarchy. As is to be expected, the overlap is lower for smaller labels. We observe that ACCLAIM performs best for the whole cerebellum, the cerebellar lobe labels (in the gray shading), and most of the lobule labels. ACCLAIM’s improvement over the competing methods is perhaps most marked for the small lobules V and X. From Table 1, we see that ACCLAIM produces better or comparable ICCs for most lobules with mean ICC across all lobules of 0.62, 0.31, and 0.71 for SUIT, multi-atlas, and ACCLAIM, respectively.

Fig. 3.

Box plots Dice similarity coefficients.

Table 1.

Inter-rater intraclass correlation coefficients computed relative to the expert human rater. Bold values indicate the method with the highest estimated ICC for a particular label. Values in parentheses give the 95% confidence interval.

Region	Absolute ICC
	SUIT	Multi-atlas	ACCLAIM
I-IVL	0.7473 (0.41, 0.91)	0.4100 (−0.11, 0.78)	0.7865 (0.45, 0.92)
I-IVR	0.5683 (−0.01, 0.85)	0.4427 (−0.10, 0.79)	0.7561 (0.43, 0.91)
VL	0.5595 (0.07, 0.83)	0.4525 (−0.08, 0.78)	0.6584 (0.08, 0.88)
VR	0.7707 (0.30, 0.92)	0.4734 (−0.07, 0.80)	0.7017 (0.33, 0.89)
VIv	0.7648 (0.04, 0.93)	0.3595 (−0.12, 0.74)	0.7613 (0.43, 0.91)
VIL	0.6144 (−0.09, 0.89)	0.6281 (0.20, 0.86)	0.7895 (0.49, 0.92)
VIR	0.8884 (0.70, 0.96)	0.5985 (0.13, 0.85)	0.8349 (0.59, 0.94)
VIIv	0.3602 (−0.12, 0.74)	0.3222 (−0.11, 0.71)	0.6736 (0.29, 0.88)
VIIACrus1L	0.6851 (−0.04, 0.91)	0.3718 (−0.11, 0.75)	0.8371 (0.59, 0.94)
VIIACrus1R	0.8369 (0.58, 0.94)	0.3705 (−0.08, 0.72)	0.8667 (0.65, 0.95)
VIIACrus2L	0.5519 (−0.08, 0.85)	0.2086 (−0.23, 0.62)	0.7027 (0.31, 0.89)
VIIACrus2R	0.7829 (0.48, 0.92)	0.1728 (−0.10, 0.54)	0.8709 (0.50, 0.96)
VIIBL	0.8014 (0.50, 0.93)	0.2968 (−0.19, 0.68)	0.7663 (0.45, 0.91)
VIIBR	0.4279 (−0.07, 0.76)	0.1431 (−0.13, 0.50)	0.3346 (−0.20, 0.71)
VIIIv	0.5068 (0.04, 0.80)	0.1792 (−0.12, 0.55)	0.6504 (0.21, 0.87)
VIIIL	0.6222 (0.14, 0.86)	0.2632 (−0.13, 0.64)	0.8464 (0.61, 0.95)
VIIIL	0.6849 (0.29, 0.88)	0.4651 (−0.02, 0.78)	0.9401 (0.83, 0.98)
IXv	0.2349 (−0.08, 0.63)	0.4248 (−0.04, 0.75)	0.5759 (0.09, 0.84)
IXL	0.7674 (0.15, 0.93)	0.3584 (−0.10, 0.72)	0.8093 (0.52, 0.93)
IXR	0.8400 (0.60, 0.94)	0.2629 (−0.12, 0.64)	0.8390 (0.59, 0.94)
Xv	0.7920 (0.47, 0.93)	−0.0491 (−0.16, 0.20)	0.1733 (−0.37, 0.62)
XL	0.2610 (−0.07, 0.67)	−0.0033 (−0.04, 0.09)	0.4667 (0.00, 0.78)
XR	0.1353 (−0.06, 0.48)	−0.0218 (−0.05, 0.09)	0.7068 (0.10, 0.91)
Mean (Sd)	0.6176 (0.2112)	0.3100 (0.1815)	0.7108 (0.1802)

4 Discussion and Conclusion

In this work, we presented ACCLAIM, a segmentation algorithm for the cerebellar lobules that takes advantage of the MGDM level set decomposition and evolution, boundary-specific speeds, and topology preservation. Tissue memberships, image intensity (based) speeds, and our novel boundary classification speed were used to evolve the boundaries of the cerebellar lobules.

Our novel boundary classification technique enabled us to locate the fissures between pairs of lobules and to design forces that enable MGDM to evolve them to the desired position. A key benefit of our approach is its use of a unique classifier for every boundary in the image, rather than attempting to learn a single classifier that performs well over the entire image. Our approach might still be improved by including a priori known information about boundaries for a particular application. In the case of the cerebellar lobules, for example, a segmentation of the cerebellar white matter branches could be helpful in constraining the regions in which the algorithm should expect a boundary, and could improve initial \window” estimates.

We compared ACCLAIM to a single-atlas method using the SUIT template, and a multi-atlas method using diffeomorphic registration and robust label fusion. Of the three methods tested, ACCLAIM performed best overall, both in terms of the volumes of the labels estimated and the labels’ overlap with those produced by an expert rater. The results in Table 1 suggest that ACCLAIM produces a segmentation with better agreement of lobule volumes than the competing methods. The lobar parcellation shown in the grayed area of Fig. 3 may be the most useful regions to consider when performing automated labeling because their relatively large size and the presence of intensity cues enables them to be reliably labeled. They are also likely to provide sufficient detail for most functional/anatomical studies since the cerebellar lobes differentiate several important functions [12].

In conclusion, ACCLAIM achieves superior segmentations of the cerebellar lobules across a range of control subjects and patients. The label configuration is topologically correct, and can therefore enables subjects to be mapped to a canonical representation and used in sophisticated analyses of shape. When compared to other state-of-the-art automatic methods, our method produces labels with a higher degree of agreement with an expert human rater both in terms of both volume and spatial overlap.

Fig. 4.

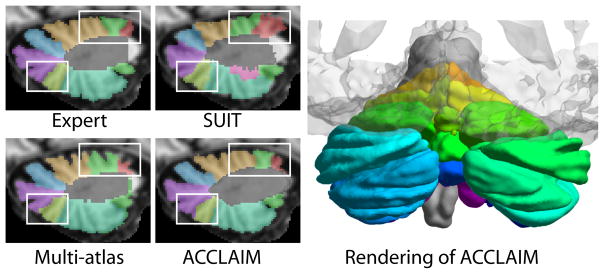
Examples of cerebellar lobule segmenations using the SUIT, multi-atlas, and ACCLAIM methods. Shown also is a rendering of a cerebellar lobule segmentation produced by ACCLAIM, (with a transparent cerebrum for reference).