Automatic Parameterization Strategy for Cardiac Electrophysiology Simulations

Abstract

Driven by recent advances in medical imaging, image segmentation and numerical techniques, computer models of ventricular electrophysiology account for increasingly finer levels of anatomical and biophysical detail. However, considering the large number of model parameters involved parameterization poses a major challenge. A minimum requirement in combined experimental and modeling studies is to achieve good agreement in activation and repolarization sequences between model and experiment or patient data. In this study, we propose basic techniques which aid in determining bidomain parameters to match activation sequences. An iterative parameterization algorithm is implemented which determines appropriate bulk conductivities which yield prescribed velocities. In addition, a method is proposed for splitting the computed bulk conductivities into individual bidomain conductivities by prescribing anisotropy ratios.

1. Introduction

In-silico models of ventricular electrophysiology are widely recognized to be an invaluable adjunct to experimental in-vitro or in-vivo models. Recent advances in medical imaging, image segmentation and image-based finite element (FE) mesh generation [1], along with major advances in the numerical solution of model equations have led to the generation of micro-anatomically accurate and biophysically detailed ventricular models [2]. However, considering the large number of parameters in these models data assimilation and parameterization poses a major challenge.

A minimum requirement in such modeling studies which aim at making case-specific predictions on ventricular electrophysiology is that activation and repolarization sequences are carefully matched. Conduction velocity in the ventricles is orthotropic and may vary in space, thus profoundly influencing shape and location of activation isochrones. Moreover, while anisotropy ratios, on mathematical grounds, are of rather minor relevance when simulating impulse propagation in tissue, they play a prominent role when the stimulation of cardiac tissue via externally applied electric fields is studied.

In this study, we propose an automatic tuning procedure which iteratively refines bidomain bulk conductivities using observed conduction velocities in 1D cable simulations as input. We propose a method for splitting these bulk conductivities into individual bidomain conductivities by prescribing anisotropy ratios and using those experimental data afflicted with the smallest uncertainty.

2. Methods

2.1. Governing equations

The bidomain equations are considered to be among the most accurate descriptions of cardiac bioelectricity at a macroscopic size scale. In the elliptic-parabolic form they are given by

$$\begin{array}{cc}\hfill -\nabla \cdot ({\sigma }_i+{\sigma }_e)\nabla {\varphi }_e=& \nabla \cdot {\sigma }_i\nabla V_m\hfill \\ \hfill \beta C_m\frac{\partial V_m}{\partial t}=& \nabla \cdot {\sigma }_i\nabla {\varphi }_i-\beta I_{ion}(V_m,\eta )\hfill \end{array}$$ (1)

where ϕ_i and ϕ_e are intra- and extracellular potentials, respectively, V_m = ϕ_i – ϕ_e is the transmembrane voltage, σ_i and σ_e are the intra- and extracellular conductivity tensors, respectively, β is the membrane surface-to-volume ratio, C_m is the membrane capacitance per unit area, and I_ion is the membrane ionic current density which depends on V_m and a set of state variables, η. At tissue boundaries, no flux boundary conditions are imposed on ϕ_i and ϕ_e.

In a 1D case where impulse propagation occurs along a thin strand of tissue aligned with an axis ζ, or in the case of a planar wave front moving along an axis ζ, the monodomain equation

$$\beta C_m\frac{\partial V_m}{\partial t}=\nabla \cdot {\sigma }_{m\zeta }\nabla V_m-\beta I_{ion}(V_m,\eta )$$ (2)

is equivalent to the bidomain equation if the monodomain conductivity σ_mζ is chosen to be half the harmonic mean between intracellular and interstitial conductivities, that is,

$${\sigma }_{m\zeta }=\frac{{\sigma }_{i\zeta }{\sigma }_{e\zeta }}{{\sigma }_{i\zeta }+{\sigma }_{e\zeta }}$$ (3)

suggesting that conduction velocity in a full 3D bidomain model at a given location can be matched closely by an equivalent monodomain model using a harmonic mean conductivity tensor.

2.2. Conduction velocity parameterization

Conduction velocity, C^v, is not a parameter in the bidomain equations and as such cannot be directly parameterized. However, assuming a continuously propagating planar wavefront along a given direction, ζ, space and time are related by $\zeta =C_{\zeta }^v·t$ which allows to replace spatial derivatives in Eq. (2) by temporal derivatives

$$\frac{{\sigma }_{m\zeta }}{\beta }\frac{{\partial }^2{V}_m}{\partial {\zeta }^2}=\frac{{\sigma }_{m\zeta }}{C^{v2}\beta }\frac{{\partial }^2{V}_m}{\partial t^2}=C_m\frac{\partial V_m}{\partial t}+I_{ion}(V_m,\eta )$$ (4)

Since membrane properties on the right hand side remain unchanged, V_m remains to be a solution of Eq. (4) as long as σ_mζ/C^v2/β is constant. Thus C^v is governed by the proportionality relation

$$C_{\zeta }^v\propto \sqrt{{\sigma }_{m\zeta }∕\beta }$$ (5)

Ideally, these parameters and their spatial variation would be measured accurately in-vivo for a given subject, however, this is difficult, if not impossible, to achieve. Even when considering ex-vivo measurements, the number of reports in the literature is scarce and the variation in measured values across these studies is vast. These uncertainties inevitably arise due to the significant degree of biological variation and the substantial errors in the measurement techniques themselves.

2.3. Iterative parameterization strategy

Modeling and technical uncertainties may also have an impact on model predictions as well. For instance, C^v also depends on the particular model used to describe cellular dynamics. Uncertainties due to technical factors such as discretization errors are of lesser concern since these are, in general, small (<5%) relative to the uncertainties in model parameters. Therefore, resorting to use overly expensive numerical schemes to minimize discretization errors is not a likely candidate strategy for improving the predictive power of computer simulations. The direct use of experimentally measured conductivity values, is not warranted neither when aiming to achieve good agreement with a specific experiment.

To find a balanced trade-off, we propose a strategy which relies on prescribing C^v directly. This is based on the consideration that C^v is a quantity which is much easier, more robustly and more accurately measurable in-vivo than tissue conductivities. The proposed strategy assumes that C^v predicted by a given computer simulation setup, ${\stackrel{‒}{C}}_{\zeta }^v$, can be represented as a function

$${\stackrel{‒}{C}}_{\zeta }^v={\stackrel{‒}{C}}_{\zeta }^v({\sigma }_{m\zeta },\beta ,I_{ion},\Delta \zeta ,\xi )$$ (6)

which depends on the main factors conductivity along an axis ζ, σ_mζ, surface-to-volume ratio, β, the chosen model of cellular dynamics, I_ion, and technical factors such as spatial discretization, Δζ, and others such as the used spatio-temporal discretization method, convergence criteria and error tolerances, the influence of which shall be summarized by ξ. In most practical scenarios, ξ, I_ion and Δζ are parameters defined by users in the course of selecting a simulation software, an ionic model and a provided mesh to describe the geometry. Thus, only two free parameters, σ_mζ and β, are left which can be tuned to achieve a close match between the pre-specified conduction velocity, C^v, and the velocity, ${\stackrel{‒}{C}}_{\zeta }^v$, predicted by the simulation.

In ventricular models C^v is orthotropic, thus necessitating to find parameters along each of the three eigenaxes. Among the two parameters available for fitting ${\stackrel{‒}{C}}_{\zeta }^v$ , β scales conduction velocity isotropically along all axes ζ. Using (5) and (2), and keeping β at a chosen default value, one can find unique monodomain conductivities along all axes ζ, which yield the prescribed conduction velocities, $C_{\zeta }^v$, by iteratively refining conductivities σ_mζ based on $C_{\zeta }^v$ measured in simple 1D cable simulations. The iterative update scheme we propose is given as

Algorithm 1 Iterative conductivity tuning

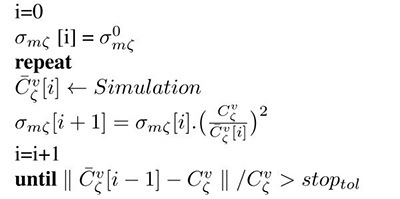
where ${\sigma }_m^0$ is an arbitrary initial guess which is used during the first simulation run.

2.4. Compensation of discretization effects

When using bidomain parameters as chosen based on the proposed strategy, C^v must be independent of the choice of spatial discretization, Δζ. The influence of Δζ is studied in a 1D strand model of 1cm length in which Δζ is varied between 1μm up to 400μm. σ_mζ is iteratively tuned at the 1μm grid to yield a C^v of 0.6m/s, 0.4m/s and 0.2m/s, respectively. At each discretization and for each σ_mζ, propagation is initiated at the left hand side end of the cable and ${\stackrel{‒}{C}}^v$ as well as the spatial extent of the wavefront, ΔX _ζ, is measured at its center. Plots are constructed to show ${\stackrel{‒}{C}}^v$ as a function of Δζ. Finally, each simulation is repeated, replacing σ_mζ, as fitted for the 1μm grid, by ${\stackrel{‒}{\sigma }}_{m\zeta }$, as computed by the iterative tuning loop described in algorithm 1.

2.5. Obtaining bidomain conductivities

Although anisotropy ratios, on mathematical grounds, are of rather minor relevance when simulating impulse propagation in tissue, when the stimulation of cardiac tissue via externally applied electric fields are studied, anisotropy ratios play a prominent role. For this case additional constraints are required to adjust the anisotropy ratio α while keeping conduction velocities unaltered. Using the definition ${\alpha }_{\zeta }=\frac{{\sigma }_i\zeta }{{\sigma }_{e\zeta }}$ to characterize differences in conductivities between intracellular and extracellular space along an axis ζ, and ${\epsilon }_{i\zeta }=\frac{{\sigma }_{il}}{{\sigma }_{i\zeta }},{\epsilon }_{e\zeta }=\frac{{\sigma }_{el}}{{\sigma }_{e\zeta }}$ to characterize differences in conductivity within the same space, but between an axis ζ = t|n relative to the longitudinal axis, ζ = l, we may express the anisotropy ratio ε_l,ζas

$${\epsilon }_{l,\zeta }=\frac{{\epsilon }_{i\zeta }}{{\epsilon }_{e\zeta }}=\frac{{\alpha }_l}{{\alpha }_{\zeta }}$$

Note that we present quantities relative to the longitudinal axes where ζ is then either t or n.

To determine the four individual bidomain conductivities we chose the desired anisotropy ratio ε_lt and the longitudinal conductivity σ_il as these quantities show the smallest variance in the literature [3-5]. Using these constraints the bidomain conductivities are determined using (3) as

$${\sigma }_{ml}^{\ast }=\frac{1}{1+{\alpha }_l}{\sigma }_{il}^{\prime },{\sigma }_{m\zeta }^{\ast }=\frac{1}{1+\frac{{\alpha }_l}{{\alpha }_{\zeta }^{\prime }}}\frac{1}{{\alpha }_{i\zeta }}{\sigma }_{il}^{\prime }$$ (7)

where * denotes quantities which were determined by iterative simulations, as outlined in Algorithm 1, and primed quantities are chosen values. Solving equations (7) for α_l and α_ζ allows to find the bidomain conductivities

$${\sigma }_{il}=1\cdot {\sigma }_{il}^{\prime }{\sigma }_{el}=\frac{1}{a_l}\cdot {\sigma }_{il}^{\prime }$$ (8)

$${\sigma }_{i\zeta }=\frac{1}{{\alpha }_{i\zeta }}\cdot {\sigma }_{il}^{\prime }{\sigma }_{e\zeta }=\frac{{\alpha }_{\zeta }^{\prime }}{{\alpha }_{i\zeta }{a}_l}\cdot {\sigma }_{il}^{\prime }$$ (9)

In the transversely orthotropic case, Eq. (7) is solved with ζ = t, whereas in the orthotropic case Eq. (7) is solved once more with ζ = n.

3. Results

3.1. Monodomain-bidomain equivalence

While the exact equivalence between bidomain and monodomain model using harmonic mean conductivities does not hold in 3D, along the principal eigenaxes the agreement between the models is quite good (Fig. 1). This close agreement suggests that the equivalent monodomain model can be used within the Algorithm 1, yielding a set of conductivities which enforce the prescribed C^v also when using a 3D bidomain model.

Figure 1.

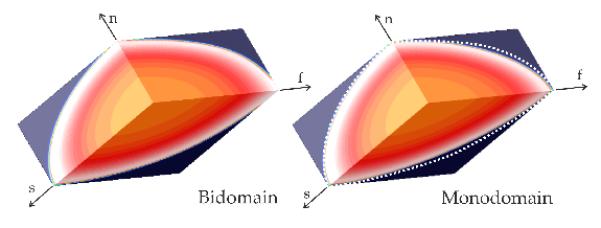
Comparison between bidomain and an equivalent monodomain model in a 3D slab model. White dashed lines in the Monodomain panel indicate position of the wavefront in a bidomain setting for the same instant in time. f, s and n are orthotropic main axes.

3.2. Conduction velocity parameterization

Using the iterative algorithm 1, conductivities were chosen to arrive at the prescribed velocities of $C_{\zeta }^v$ =0.6, 0.4 and 0.2m/s for planar wave fronts traveling along the axes ζ = f, s, n, respectively. Fig. 2A shows how simulated velocities ${\stackrel{‒}{C}}_{\zeta }^v$ are affected when increasing grid resolution Δζ stepwise from 1μm to 400μm. Numerical errors of 5% incurred at different spatial resolutions of Δζ =275μm, 180μm and 90μm for $C_f^v,C_s^v$ and $C_n^v$, respectively. As expected, scaling of simulated velocities with the prescribed velocity, i.e. ${∊}_v={\stackrel{‒}{C}}_{\zeta }^v∕{\stackrel{‒}{C}}_{\zeta }^v∕$, reveals that spatial discretization errors are mainly governed by the ratio Δζ/ΔX _ζ(Fig. 2B). Convergence experiments were repeated for $C_f^v$ =0.6m/s and all discretizations Δζ, but equations were re-parameterized using the automatic parameterization strategy (APS) as described in algorithm 1. While conductivities varied in the range between −6 to +24%, wave fronts propagated with the exact prescribed C^v, independently of Δζ.

Figure 2.

A) Influence of spatial discretization Δζ upon predicted conduction velocities for propagation along the axes f, s and n. B) Deviations in relative velocity, ${∊}_v={\stackrel{‒}{C}}_{\zeta }^v∕C_{\zeta }^v$ depend on the ratio Δζ to spatial extent of wave front, ΔX_ζ. Using APS, predicted C^v (black dotted trace) is independent of Δζ, at the cost of minor variations of the chosen conductivity value, σ_mf (pink trace)

3.3. Choice of individual conductivities

Considering a transversely isotropic scenario, the analytic expressions 9 were used to obtain individual conductivities given three different anisotropy ratios: 1) unequal anisotropy, with ε_l,t = 4.5, 2) equal anisotropy, with ε_l,t = 1, and 3) inverse anisotropy, with ε_l,t = 1/4.5. The propagation patterns and the virtual electrode propagation (VEP) are shown in Fig. 3. Note that during normal propagation differences in anisotropy ratio do not manifest in the activation patterns. However, a different VEP is induced for each anisotropy ratio.

Figure 3.

Anisotropy ratios are chosen without affecting conduction velocity. Upper panels show activation sequences for three different anisotropy ratios. Lower panels show the induced VEPs in response to a strong hyperpolarizing point stimulus for the same given anisotropy ratios.

4. Discussion

In this study an iterative parameterization strategy is proposed that allows to find appropriate tissue conductivities which result then in the prescribed C^v along the orthotropic eigenaxes f, s and n of the tissue, as well as prescribed anisotropy ratios. Computationally cheap 1D equivalent monodomain models can be used in the parameterization loop to determine conductivities which are also suited for bidomain simulations. It is worth noting that parameter variations due to the automatic parameterization strategy, between −6% up to +24% around the nominal values, are well below the experimentally measured variability. The effectiveness of the methods is demonstrated for spatial discretizations of up to 400μm, however, for even coarser discretizations this may not be the case anymore. However, in line with the current trend towards anatomically detailed ventricular models, finer spatial resolution down to average discretizations of around ≈ 100μm are becoming standard to resolve geometric details. With such finer spatial steps Δζ, relative discretization of wave fronts Δζ/ΔX _ζ is less than 0.3 and necessary modifications of conductivity values are below 6%.