Fine Mapping Seronegative and Seropositive Rheumatoid Arthritis to Shared and Distinct HLA Alleles by Adjusting for the Effects of Heterogeneity

Abstract

Despite progress in defining human leukocyte antigen (HLA) alleles for anti-citrullinated-protein-autoantibody-positive (ACPA⁺) rheumatoid arthritis (RA), identifying HLA alleles for ACPA-negative (ACPA⁻) RA has been challenging because of clinical heterogeneity within clinical cohorts. We imputed 8,961 classical HLA alleles, amino acids, and SNPs from Immunochip data in a discovery set of 2,406 ACPA⁻ RA case and 13,930 control individuals. We developed a statistical approach to identify and adjust for clinical heterogeneity within ACPA⁻ RA and observed independent associations for serine and leucine at position 11 in HLA-DRβ1 (p = 1.4 × 10⁻¹³, odds ratio [OR] = 1.30) and for aspartate at position 9 in HLA-B (p = 2.7 × 10⁻¹², OR = 1.39) within the peptide binding grooves. These amino acid positions induced associations at HLA-DRB1^∗03 (encoding serine at 11) and HLA-B^∗08 (encoding aspartate at 9). We validated these findings in an independent set of 427 ACPA⁻ case subjects, carefully phenotyped with a highly sensitive ACPA assay, and 1,691 control subjects (HLA-DRβ1 Ser11+Leu11: p = 5.8 × 10⁻⁴, OR = 1.28; HLA-B Asp9: p = 2.6 × 10⁻³, OR = 1.34). Although both amino acid sites drove risk of ACPA⁺ and ACPA⁻ disease, the effects of individual residues at HLA-DRβ1 position 11 were distinct (p < 2.9 × 10⁻¹⁰⁷). We also identified an association with ACPA⁺ RA at HLA-A position 77 (p = 2.7 × 10⁻⁸, OR = 0.85) in 7,279 ACPA⁺ RA case and 15,870 control subjects. These results contribute to mounting evidence that ACPA⁺ and ACPA⁻ RA are genetically distinct and potentially have separate autoantigens contributing to pathogenesis. We expect that our approach might have broad applications in analyzing clinical conditions with heterogeneity at both major histocompatibility complex (MHC) and non-MHC regions.

Introduction

Rheumatoid arthritis (RA [MIM 180300]) has two distinct subtypes—anti-citrullinated-protein-autoantibody-negative (ACPA⁻ or seronegative) RA and -positive (ACPA⁺ or seropositive) RA—with potentially different genetic risk factors, environmental risk factors, and optimal therapeutic strategies.^1,2 Despite constituting about one-third (∼30%) of RA cases,³ ACPA⁻ RA has been relatively understudied in comparison to ACPA⁺ RA.^4–7 We and others have demonstrated that the widely established method for identifying ACPA⁻ RA subjects on the basis of anticyclic citrullinated peptide (anti-CCP) antibody testing is imperfect in that the absence of antibody is not sufficiently specific to ACPA⁻ RA, whereas its presence is specific to ACPA⁺ RA.^8–10

The lack of a specific test for ACPA⁻ RA can result in heterogeneity in clinical cohorts, which can confound genetic studies for ACPA⁻ disease. For example, ACPA⁻ RA subjects might include ACPA⁺ RA subjects whose ACPAs have not been detected by conventional anti-CCP testing^8–11 or subjects who have other autoantibody-negative inflammatory arthritic conditions, such as ankylosing spondylitis (AS)¹² or other HLA-B^∗27-associated conditions. So, although investigators have reported associations between classical HLA alleles and ACPA⁻ RA,^13,14 it remains unclear whether these associations are distinct from those alleles driving ACPA⁺ disease risk, recently defined by our group.⁶ Additionally, the specific amino acid sites and residues driving ACPA⁻ RA risk have yet to be defined.

To define HLA alleles driving ACPA⁻ RA risk, we first obtained dense SNP genotype data within the major histocompatibility complex (MHC) region by applying the Immunochip custom array³ to ACPA⁻ case and control groups. We then used these data to impute HLA alleles, amino acids, and SNPs with a highly accurate imputation approach.¹⁵ Recognizing that possible clinical heterogeneity within genotyped cohorts might confound associations within the MHC, we developed a statistical approach to correct for the effects of heterogeneity within cohorts; it uses genetic risk scores (GRSs) built from known risk loci for potential confounding diseases as covariates.

We observed that two amino acid positions, HLA-DRβ1 position 11 (in which serine and leucine conferred risk) and HLA-B position 9 (in which aspartate conferred risk), were driving ACPA⁻ RA. These two positions are already known to drive ACPA⁺ RA as well;⁶ however, the specific amino acid residues conferring risk were completely distinct between the two disease subtypes. We also separately tested for associations with ACPA⁺ disease. In addition to confirming known associations at positions 11, 71, and 74 in HLA-DRβ1, position 9 in HLA-B, and position 9 in HLA-DPβ1, we identified an additional association at amino acid position 77 within the binding groove of HLA-A. These results contribute to mounting evidence that ACPA⁺ and ACPA⁻ RA are distinct diseases with certain unique genetic factors.

Material and Methods

Samples

Case-Control Sample Collections

We used data from six case-control collections (UK, US, Dutch, Spanish, Swedish Umeå, and Swedish Epidemiological Investigation of Rheumatoid Arthritis [EIRA], Table S1, available online).³ All individuals provided informed consent and were recruited through protocols approved by institutional review boards. Each collection consisted of individuals who were self-described as white and of European descent, and all cases either met the 1987 American College of Rheumatology diagnostic criteria or were diagnosed by board-certified rheumatologists. We previously genotyped all samples with the Immunochip custom array, which densely covered the MHC region (7,563 SNPs), in accordance with Illumina protocols.

Classifying ACPA⁻ RA in Discovery Samples

From these samples, we defined a total of 2,406 ACPA⁻ RA case and 13,930 control subjects for discovery from five collections (excluding the Swedish EIRA). To do this, we followed standard clinical practice to identify ACPA⁻ RA subjects as those who were not reactive to anti-CCP antibody by using reference cutoff levels defined at local clinical labs. In the UK cohort, we used the commercially available DiastatTM ACPA Kit (Axis-Shield Diagnostics Limited). In the US samples, we used a second-generation commercial anti-CCP enzyme immunoassay (Inova Diagnostics).¹⁶ For Spanish samples, we used the Immunoscan ELISA test (Euro Diagnostica). For the Swedish Umeå and Dutch collections, we used the Immunoscan-RA Mark2 ELISA test (Euro Diagnostica).¹⁷ These assays are the standard commercially available assays that are currently being widely used in clinical practice.

Clinically Homogeneous ACPA⁻ Samples for Replication

To replicate ACPA⁻ results, we sought to define an independent replication data set that was as clinically homogeneous as possible. To this end, we used genotype data on 987 case and 1,940 control subjects who were from the Swedish EIRA cohort and who were identified as anti-CCP antibody negative with the Immunoscan-RA Mark2 ELISA test (Euro-Diagnostica). In addition, to stringently ensure clinical homogeneity, we applied a highly sensitive ACPA typing method developed at the Karolinska Institutet⁸ to test sera for reactivity to four specific citrullinated peptides (α-enolase, vimentin, fibrinogen, collagen type II). We considered samples ACPA⁻ only if they were negative for all four of these tests. After applying this assay, we removed 106 case individuals who were reactive to the sensitive assay, as well as 381 case individuals to whom we did not apply the assay. We also excluded 73 case and 249 control subjects who were positive for HLA-B^∗27. Because HLA-B^∗27 is highly sensitive for AS (>90%), excluding HLA-B^∗27-positive individuals effectively removed the effect of possible confounding from AS or related spondyloarthropathies. The resulting replication collection consisted of 427 case and 1,691 control subjects.

Sample Collections for ACPA⁺ RA

For ACPA⁺ RA, we used 7,279 anti-CCP-positive individuals from all six cohorts (UK, US, Swedish Umeå, Dutch, Spanish, and Swedish EIRA; Table S1). We used all 15,870 control subjects for ACPA⁺ RA analyses.

Statistical Analyses

HLA Imputation

We imputed case and control groups together for 8,961 binary markers representing classical HLA alleles, amino acids, and SNPs by using SNP2HLA,¹⁵ which utilizes the Beagle imputation method.¹⁸ The binary markers included every possible grouping of amino acid residues given a multiallelic amino acid position. We used reference data collected by the Type 1 Diabetes Genetics Consortium;¹⁹ these data consisted of genotypes for 5,863 SNPs tagging the MHC and classical alleles for HLA-A, HLA-B, HLA-C, HLA-DRB1, HLA-DQA1, HLA-DQB1, HLA-DPA1, and HLA-DPB1 at four-digit resolution in 5,225 individuals of European descent.¹⁹

Quantifying Imputation Accuracy

To assess accuracy, we took advantage of typed HLA-A, HLA-B, HLA-C, HLA-DQB1, and HLA-DRB1 alleles for 918 individuals in the UK cohort. We calculated imputation accuracy as the proportion of correctly imputed classical alleles:

$$\frac{{\sum }_i\max \left(\delta \left(g_{i,1}=x_{i,1}\right)+\delta \left(g_{i,2}=x_{i,2}\right),\delta \left(g_{i,1}=x_{i,2}\right)+\delta \left(g_{i,2}=x_{i,1}\right)\right)}{2n},$$

where $g_{i,1}$ and $g_{i,2}$ are genotyped alleles of individual i and x_i,1 and x_i,2 are imputed alleles. For each gene, we used individuals successfully typed for four-digit alleles. The δ function is 1 if the genotyped allele is the imputed allele and 0 otherwise. The term n is the number of samples.

Statistical Framework for Association Testing

We tested associations at all 8,961 binary markers by using probabilistic genotypic dosages that take uncertainty in imputation into account. We used logistic regression under the assumption that each marker conferred a fixed log additive effect across each case-control collection. To account for population stratification, we included ten principal components (PCs) as covariates for each collection. We calculated PCs by using EIGENSOFT v.4.2²⁰ with HapMap Phase 2 samples as reference populations on a subset of SNPs (minor allele frequency > 0.05) filtered for minimizing intermarker linkage disequilibrium (LD).³ This resulted in the following logistic regression model:

$$\log \left({\text{odds}}_i\right)=\theta +{\beta }_a{g}_{a,i}+{\sum }_{j\in \text{collections}}{\delta }_{i,j}\left({\gamma }_j+{\sum }_{k=\mathrm{1...10}}{\pi }_{j,k}{p}_{i,k}\right),$$ (Equation 1)

where a indicates the marker being tested, $g_{a,i}$ is the dosage of a in individual i, and β_a is the additive effect of a. In the collection-specific term, δ_i,j is an indicator variable that is 1 only if individual i is in collection j. The γ_j parameter is the collection-specific effect due to the differences in case-control proportions; it is set to 0 for one arbitrarily selected reference collection. The π_j,k parameter is the effect of the k^th PC, and p_i,k is the k^th PC value for individual i.

Adjusting for Clinical Heterogeneity in ACPA⁻ Discovery

In the discovery analysis for ACPA⁻ disease, we adjusted for possible clinical heterogeneity within the collections. Our approach was to extend Equation 1 to include GRSs of potentially confounding diseases as covariates:

$$\log \left({\text{odds}}_i\right)=\theta +{\beta }_a{g}_{a,i}+{\sum }_{j\in Collections}{\delta }_{i,j}\left({\gamma }_i+{\sum }_{k=\mathrm{1...10}}{\pi }_{j,k}{p}_{i,k}+{\sum }_{h=\mathrm{1...}H}{\alpha }_{j,h}{s}_{i,h}\right),$$ (Equation 2)

where h indicates a confounding disease we want to adjust for and H is the total number of confounding diseases. s_i,h is the GRS of individual i for disease h and is defined as the sum of risk-allele dosages weighted by effect sizes:

$$s_{i,h}={\sum }_l{\beta }_{l,h}{g}_{l,i},$$ (Equation 3)

where l iterates over known risk alleles for h, ${\beta }_{l,h}$ is the effect size of l for h, and $g_{l,i}$ is the dosage of l in individual i. α_j,h is the effect of s_i,h, which approximates the sample proportion of confounding disease in the collection. For a detailed description of the method, see Appendix A.

For our analysis, we adjusted for both ACPA⁺ RA and AS. For the ACPA⁺ RA GRS, l iterated over 47 independent SNPs associated with ACPA⁺ RA (Table S2),³ all four-digit HLA-DRB1 alleles, HLA-B Asp9, HLA-DPβ1 Phe9, and HLA-A Asn77. We estimated β_l from our ACPA⁺ RA case-control data set presented in this paper. To estimate β_l for all four-digit HLA-DRB1 alleles in a multivariate model, we included in the logistic regression all four-digit alleles with allele frequency > 0.1%, except for the reference allele we chose (HLA-DRB1^∗15:01). To avoid reusing the same controls both to estimate β_l and to map ACPA⁻ RA, which could result in bias as a result of overfitting, we estimated β_l for each collection by using the other five collections. Similarly, for the AS GRS, l iterated over HLA-B^∗27 and 19 AS-associated SNPs that passed our quality control (QC) (Table S2).¹² We used reported effect sizes β_l in Cortes et al.¹²

Two-Step Approach for Adjusting for Heterogeneity

Using GRSs as covariates in regression might be overly conservative and could remove true associations if the causal loci are shared between the disease of interest and the confounding disease. To account for the shared genetic structure between the two RA subtypes, we employed an alternative two-step approach: (1) we estimated the confounding proportions α_j,h in Equation 2 by using GRSs based on nonshared loci first, which gave us an unbiased estimate of α_j,h, and then (2) we used this α_j,h as a fixed value in the regression framework presented above. Because we did not definitively know which loci were shared, we used a heuristic to choose nonshared loci by using 38 non-MHC SNPs not associated with ACPA⁻ RA at a nominal significance threshold (p > 0.01)³ (Table S2).

Genomic-Control Inflation Factor

We assessed the genomic-control inflation factor, λ_GC, by testing associations at “reading-writing-ability SNPs” included on the Immunochip platform. Out of 1,469 SNPs, we used 1,250 that passed QC in all six collections. We obtained chi-square statistics at these SNPs by using logistic regression as described above to assess λ_GC.

Forward Conditional Search

Once we identified an associated marker, we forward searched further associations by including the identified marker as a covariate in the logistic regression.

Exhaustive Search

To find the best pair of associations in HLA-DRB1 and HLA-B for ACPA⁻ disease, we examined every possible combination of 495 binary markers within HLA-DRB1 and 774 binary markers within HLA-B (383,130 tests). We extend the single-marker model in Equation 2 to the following two-marker model:

$$\log \left({\text{odds}}_i\right)=\theta +{\beta }_a{g}_{a,i}+{\beta }_b{g}_{b,i}+{\sum }_{j\in collections}{\delta }_{i,j}\left({\gamma }_i+{\sum }_{k=1\dots 10}{\pi }_{j,k}{p}_{i,k}+{\sum }_{h=1\dots H}{\alpha }_{j,h}{s}_{i,h}\right),$$ (Equation 4)

where a and b are the pair of binary markers being tested. We calculated the log-likelihood difference (ΔLL) in model fit due to this pair and assessed significance by comparing the deviance (−2 × ΔLL) to a chi-square distribution with 2 degrees of freedom.

Joint Analysis of Discovery and Replication Data

In order to jointly analyze five discovery collections and a replication cohort for ACPA⁻ disease, we combined them into one logistic regression framework, including GRSs as covariates for five discovery cohorts to adjust for heterogeneity.

Forward Search outside of HLA-DRB1 for ACPA⁺ RA

Because HLA-DRB1 has a very strong effect in ACPA⁺ disease, to examine the associations beyond HLA-DRB1, we conditioned on the HLA-DRB1 effects by including binary variables as covariates corresponding to all four-digit HLA-DRB1 alleles, excluding one allele as a reference (HLA-DRB1^∗15:01). If we forward searched by conditioning on an amino acid position with m residues, such as position 9 of HLA-B, we included binary variables corresponding to the m − 1 residues, excluding the most frequent one.

Testing for Discordant Effect Sizes

Given a multiallelic amino acid position with m residues, we wanted to test whether the effect sizes of m residues were concordant between two different conditions (e.g., ACPA⁻ versus ACPA⁺). To this end, we calculated multivariate odds ratios (ORs) of residues by including in the logistic regression m − 1 binary markers corresponding to m − 1 residues, excluding one residue as the reference. Let a₁, …, a_{m − 1} and b₁, …, b_{m − 1} be the multivariate log ORs in two different conditions. Let v₁, …, v_{m − 1} and u₁, …,u_{m − 1} be their variances. To test discordance of effect sizes between two conditions, we used the statistic

$${\sum }_{i=1\dots m}\frac{{\left(a_i-b_i\right)}^2}{v_i+u_i},$$ (Equation 5)

which is chi-square distributed with m − 1 degrees of freedom under the null.

Assessing Accuracy of Fine Mapping with Simulations

To test the accuracy of our approach to adjust for clinical heterogeneity in fine mapping, we simulated an ACPA⁻ RA case-control study confounded by ACPA⁺ RA. We simulated a large study (50,000 case and 50,000 control subjects) to assess the asymptotic results. We first simulated control subjects by sampling with replacement from the UK control subjects. Then we assumed that specific amino acid positions were conferring risk to ACPA⁻ RA with predefined ORs, and we sampled ACPA⁻ RA subjects from the UK control subjects on the basis of the ORs. Finally, we replaced 26.3% of the case group with individuals randomly sampled from the UK ACPA⁺ RA case group. We performed an association test with and without adjusting for heterogeneity to examine whether we could fine map the risk-conferring amino acid positions correctly. To adjust for heterogeneity, we used GRSs built from the effect sizes estimated from the other five cohorts, excluding the UK cohort.

Results

ACPA⁻ RA Discovery Collection and HLA Imputation

To define HLA alleles driving ACPA⁻ RA risk, we analyzed a discovery data set of 2,406 ACPA⁻ RA case and 13,930 control subjects (from the UK, the US, Spain, Sweden, and the Netherlands, see Table S1) genotyped on the Immunochip custom array with 7,563 SNPs across the MHC region.³ This platform represents greater SNP density than most standard genome-wide-association-study arrays and offers the potential for higher HLA imputation accuracy. Indeed, applying SNP2HLA,¹⁵ we observed an overall imputation accuracy of 96.9% for four-digit HLA alleles in a subset of UK control subjects separately typed for HLA alleles (Table S3). We classified RA samples as ACPA⁻ on the basis of anti-CCP antibody amounts according to standard clinical practice (see Material and Methods). After adjusting for ten PCs, we observed little evidence of population stratification (λ_GC = 0.98, see Material and Methods).

Correcting for Clinical Heterogeneity in ACPA⁻ RA Collections

We considered that other syndromes clinically indistinguishable from ACPA⁻ RA might be embedded within ACPA⁻ RA and thus confound associations. Indeed, in an analysis unadjusted for clinical heterogeneity, we observed that as we defined ACPA⁻ samples by increasing the level of stringency of the anti-CCP cutoff, the frequency of HLA-DRβ1 Val11 (the strongest risk factor for ACPA⁺ disease) decreased in our ACPA⁻ cohort (p = 6.9 × 10⁻⁵), suggesting confounding from ACPA⁺ RA (Figure S1). We also noticed significant association at HLA-B^∗27 (p = 2.8 × 10⁻⁹), a well-known risk factor for AS,^12,21,22 but not at HLA-C^∗06:02 (p > 0.001), a risk factor for psoriatic arthritis.^23–25 However, as in most clinical settings, the phenotypic information that would be essential for identifying and excluding the specific individuals with conditions other than ACPA⁻ RA was not available.

To correct for the effects of heterogeneous samples within our ACPA⁻ cohort, we applied a statistical approach to adjust for confounding diseases (ACPA⁺ RA and AS, Material and Methods). We constructed GRSs representing the log OR for an individual for the confounding disease on the basis of the known-risk-allele dosages weighted by effect sizes.^26–28 Then, adjusting association statistics in a logistic regression model for GRSs could successfully control for the effects of confounding diseases (see Appendix A).

ACPA⁻ RA Is Associated with Ser11 and Leu11 in HLA-DRβ1 and Asp9 in HLA-B

After correcting for clinical heterogeneity as described above, we tested for allelic associations in ACPA⁻ RA. Taking into account multiple hypothesis testing, we considered p < 5.6 × 10⁻⁶ (0.05/8,961 binary MHC-marker association tests) to be significant. After testing all amino acids and classical and SNP alleles, we observed that the strongest association was at amino acid residues at position 11 in HLA-DRβ1 (presence of Ser or Leu, OR = 1.30, p = 1.4 × 10⁻¹³), encoded by HLA-DRB1 (see Figure 1A, Table 1, and Figure S2). This allele exceeded the significance of all other SNPs and classical alleles that we tested. The variation of amino acid residues at this position was attributable to a triallelic SNP (rs9269955, G/C/A) and a quadallelic SNP (rs17878703) at the first and second base positions of the codon, respectively. The association at position 11 was statistically indistinguishable (p > 0.09) from the association at position 13 (presence of Ser, Gly, or Phe, OR = 1.29, p = 4.7 × 10⁻¹³). The most strongly associated classical allele was HLA-DRB1^∗03 (p = 6.7 × 10⁻¹⁰).^13,14 After conditioning on HLA-DRB1^∗03, we observed that Ser11+Leu11 remained highly significant (p = 2.4 × 10⁻⁸), suggesting that HLA-DRB1^∗03 does not fully explain HLA-DRB1 associations. We also observed a separate, strong association 23 kb away from HLA-B at SNP rs9266669 (OR = 1.38, p = 4.0 × 10⁻¹³; Figure 1A). This SNP was statistically indistinguishable (p > 0.01) from the presence of Asp9 in HLA-B (OR = 1.39, p = 2.7 × 10⁻¹²); these two alleles were in tight LD (r² = 0.8). HLA-B Asp9 was almost perfectly correlated with HLA-B^∗08 in our data set (r² = 0.997). The HLA-B^∗08 classical allele, Asp9, and SNP rs9266669 thus could not be distinguished on the basis of genetics alone. Both of these amino acid sites mapped to the binding grooves of their respective HLA receptors (Figure 2).

Figure 1.

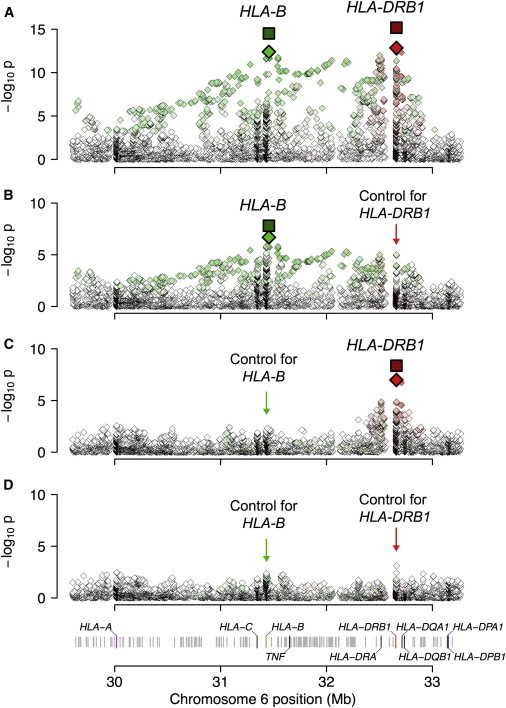
Association Results within the MHC to ACPA⁻ RA

(A) We observed the most significant association at position 11 of HLA-DRβ1 (encoded by HLA-DRB1), where Ser and Leu conferred risk (red diamond). We also observed an independent association at SNP rs9266669, which was statistically indistinguishable from HLA-B Asp9 (green diamond). The dark-red and dark-green squares denote the statistical significance of the two positions in a joint analysis including both discovery and replication data.

(B) Conditioning on HLA-DRβ1 Ser11+Leu11, we found that the association at rs9266669 remained the most significant.

(C) Conditioning on HLA-B Asp9, we found that the association at HLA-DRβ1 Ser11+Leu11 remained the most significant.

(D) Conditioning on both HLA-DRβ1 Ser11+Leu11 and HLA-B Asp9, we did not observe any more statistically significant association within MHC (p > 0.0007).

Table 1.

Effect Estimates for Amino Acids Associated with Risk of ACPA⁻ and ACPA⁺ RA

RA Subtypes	HLA Protein	Amino Acid Position	Amino Acid Residue	OR after Adjustment for Known Associated Positions (95% CI)			Frequency in Control Group	Frequency in Case Group	Classical Alleles
				Discovery	Replication	Joint
ACPA−	HLA-DRβ1	11	Ser+Leu	1.22 (1.14–1.32)	1.22 (1.04–1.43)	1.22 (1.14–1.31)	0.514	0.548	HLA-∗01, HLA-∗03, HLA-∗08, HLA-∗11, HLA-∗12, HLA-∗13, HLA-∗14
	HLA-B	9	Asp	1.27 (1.15–1.40)	1.23 (0.99–1.52)	1.26 (1.15–1.38)	0.131	0.161	HLA-∗08
ACPA+	HLA-A	77	Asn	0.85 (0.81–0.90)			0.343	0.279	HLA-∗01, HLA-∗23, HLA-∗24, HLA-∗26, HLA-∗29, HLA-∗30, HLA-∗36, HLA-∗80

For each amino acid identified in this study, we show the OR and 95% confidence interval (95% CI), unadjusted frequencies in the case and control groups, and corresponding classical HLA alleles. All ORs were conditioned on known associated positions; for ACPA⁻ RA, we estimated ORs of HLA-DRβ1 Ser11+Leu11 and HLA-B Asp9 by conditioning on each other. For ACPA⁺ RA, we estimated the OR of HLA-A Asn77 by conditioning on all alleles at HLA-DRB1, amino acids at HLA-B position 9, and amino acids at HLA-DPβ1 position 9. See Table S7 for the complete table, including previously identified positions.

Figure 2.

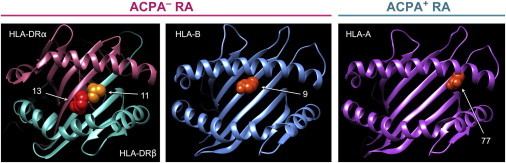
3D Models of Amino Acid Positions Identified in This Study

Key amino acid positions are highlighted as spheres. We used Protein Data Bank entries 3pdo (HLA-DR), 2bvp (HLA-B), and 1x7q (HLA-A) with UCSF Chimera to prepare the figure.³⁰ See Figure S5 for all known associated positions.

The HLA-DRB1 and HLA-B associations were independent of each other and explained most of the MHC association with ACPA⁻ RA. After conditioning on Ser11+Leu11 effects in HLA-DRβ1, we observed that rs9266669 in HLA-B (or Asp9 in HLA-B) remained the most significant association (p = 2.0 × 10⁻⁷, OR = 1.27; Figure 1B). Similarly, we observed that after conditioning on Asp9 in HLA-B, Ser11+Leu11 in HLA-DRβ1 remained the most significant association (p = 1.0 × 10⁻⁷, OR = 1.22; Figure 1C). When we conditioned on both Ser11+Leu11 in HLA-DRβ1 and Asp9 in HLA-B, no further significant association was found (p > 0.0007; Figure 1D).

Because the so-called 8.1 ancestral haplotype²⁹ harbors both HLA-DRβ1 Ser11 and HLA-B Asp9, we considered the possibility that these associations were driven by that haplotype alone and not the individual amino acid sites. Given that our imputation provided phased haplotypes spanning the whole MHC region, we inferred the ancestral haplotype dosage for each individual. Then, using a trivariate logistic regression model including dosages for the 8.1 ancestral haplotype, HLA-DRβ1 Ser11+Leu11, and HLA-B Asp9, we observed that association at the ancestral haplotype was not significant (p = 0.21). In contrast, the other two HLA amino acid variables retained statistical significance even after adjustment for the effect of the 8.1 ancestral haplotype (p = 1.6 × 10⁻⁷ at HLA-DRβ1 Ser11+Leu11 and p = 3.4 × 10⁻³ at HLA-B Asp9). These results suggest that the association was driven primarily by the amino acid sites and not by the effect of the 8.1 haplotype alone.

We further considered that our approach to correcting for heterogeneity might be conservative and might remove shared loci between two subtypes of RA. To address this concern, we developed a two-step alternative approach that estimates the confounding proportion (proportion of misdiagnosed ACPA⁺ RA samples within ACPA⁻ RA cohorts) by using a GRS calculated on the basis of an approximated set of nonshared loci (i.e., known loci associated with ACPA⁺ RA but with p > 0.01 association in ACPA⁻ RA) and then regresses out only this amount from the model (see Material and Methods). The confounding proportion estimates by this approach were comparable to the estimates by the previous approach with the full GRS (mean proportion across cohorts was 26.3% with the full GRS and 28.3% with the nonshared-loci GRS; see Figure S3). Consistent with the previous approach, this two-step approach produced the most significant associations at rs9266669 (p = 1.8 × 10⁻¹³, OR = 1.38 at HLA-B Asp9) and HLA-DRβ1 Ser11+Leu11 (p = 2.3 × 10⁻¹³, OR = 1.27). Again, these two associations were independent (p = 5.4 × 10⁻⁸).

Replicating HLA Associations in a Clinically Homogeneous ACPA⁻ Collection

We wanted to validate these findings in an independent cohort without significant clinical heterogeneity. To this end, we assessed association in an independent data set of 427 phenotypically homogeneous ACPA⁻ individuals and 1,691 control subjects (Swedish EIRA). According to a state-of-the-art commercially unavailable assay,⁸ these ACPA⁻ individuals were negative for not only anti-CCP antibody but also antibodies for four specific citrullinated peptide antigens. We also excluded HLA-B^∗27-positive individuals (>90% sensitive for AS) from case and control groups. We tested for association without any adjustment for heterogeneity. We confirmed associations both at HLA-DRβ1 Ser11+Leu11 (p = 5.8 × 10⁻⁴, OR = 1.28) and at HLA-B Asp9 (p = 2.6 × 10⁻³, OR = 1.34) with comparable effect sizes (Table 1). These associations were again independent of each other. Conditioning on HLA-DRβ1 Ser11+Leu11, we observed an independent effect at HLA-B Asp9 (p = 0.03, OR = 1.23). Conversely, conditioning on HLA-B Asp9, we observed an independent effect at HLA-DRβ1 Ser11+Leu11 (p = 0.007, OR = 1.22).

In a joint analysis of the discovery and replication cohorts, we observed increased significance at both HLA-DRβ1 and HLA-B positions (p = 6.7 × 10⁻¹⁶ and OR = 1.30 for HLA-DRβ1 Ser11+Leu11; p = 5.3 × 10⁻¹⁴ and OR = 1.38 for HLA-B Asp9; Figure 1A and Table S4) and that their effects were independent (p < 2 × 10⁻⁸; Figures 1B and 1C and Table S4). Conditioning on both of these effects, we observed no other independent association throughout the MHC (p > 0.0002).

Exhaustive Search Confirms Associations with Ser11 and Leu11 in HLA-DRβ1 and Asp9 in HLA-B

Because the conditional forward search might miss the best explanations, we exhaustively tested every possible pair of binary markers in HLA-DRB1 and HLA-B in a joint analysis. Out of 383,130 pairs we tested, HLA-DRβ1 Ser11+Leu11 and HLA-B Asp9 in HLA-B (or equivalently HLA-B^∗08 and HLA-B^∗0801) constituted the most significant pair (p = 1.1 × 10⁻²⁰; Table S5), confirming that our model provides the most parsimonious explanation of the data.

Associations Are Independent of Rheumatoid Factor Status

We examined whether the associations we identified were independent of rheumatoid factor (RF) status. We obtained RF data for 1,016 affected individuals in the UK cohort; 470 individuals (46%) were RF⁺, and 546 individuals (54%) were RF⁻. We stratified the samples into two groups on the basis of RF status. The associations were consistent between the two groups in that they showed the same direction of effects at both HLA-DRβ1 Ser11+Leu11 and HLA-B Asp9 (Table S6). We observed that effect sizes tended to be greater in the RF⁺ subjects than in the RF⁻ subjects at both loci (p = 0.02). A thorough investigation of this phenomenon will require larger sample sizes.

Asn77 at HLA-A Is Associated with ACPA⁺ RA

We also mapped associations within the MHC to ACPA⁺ RA in 7,279 ACPA⁺ RA subjects and 15,870 control subjects (see Table S1 and Material and Methods). We observed little evidence of stratification after adjusting for ten PCs (λ_GC = 1.07). We confirmed previously published associations in HLA-DRβ1 at amino acid positions 11 (p < 10⁻⁶⁹²), 71 (p < 10⁻³⁷), and 74 (p < 10⁻²³) (Table S7). Conditioning on HLA-DRB1 alleles, we confirmed associations at Asp9 in HLA-B (p < 10⁻³⁶, OR = 1.93) and Phe9 in HLA-DPβ1 (p < 10⁻¹⁹, OR = 1.31)⁶ (Figure S4). Conditioning on all of these previously known associated positions (the HLA-DRB1 alleles, position 9 in HLA-B, and position 9 in HLA-DPβ1), we observed an independent association with ACPA⁺ RA with the presence of Asn77 in HLA-A (p = 2.7 × 10⁻⁸, OR = 0.85; Figure S4D and Table 1). Similar to the other amino acid sites associated with RA,⁶ position 77 in HLA-A was also located in the binding groove (Figure 2 and Figure S5). We previously observed that Ser77 in HLA-A confers protection in HIV controllers.³¹ After conditioning on this sixth position, we observed no convincing associations (p > 4 × 10⁻⁶).

Discussion

In this study, we observed that associations with ACPA⁻ RA within the MHC were driven by HLA-DRB1 and HLA-B. In addition, we identified the specific residues and specific amino acid sites that parsimoniously explained these associations. These positions mapped to the peptide binding grooves of these receptors, pointing to an important role for antigen recognition. The success of this study was contingent on our ability to distinguish the effects from other conditions contributing to heterogeneity within the case individuals.

Intriguingly, the positions that drove ACPA⁻ risk were the same positions that drove most risk for ACPA⁺ RA as well (Table S8). The risk of Asp9 in HLA-B in ACPA⁻ RA was shared with ACPA⁺ disease but had a more modest effect size (OR = 1.38 in ACPA⁻ versus OR = 1.93 in ACPA⁺). This allele, also associated with myasthenia gravis,³² might affect nonspecific immune reactivity.

In contrast, at position 11 of HLA-DRβ1, different residues drove risk of the two diseases (discordance p < 2.9 × 10⁻¹⁰⁷; Figure 3). For example, Ser11 conferred risk of ACPA⁻ disease (OR = 1.31) but was protective against ACPA⁺ disease (OR = 0.39). On the other hand, Gly11 and Pro11 showed protective effects for both subsets. We speculate that citrullinated antigens that drive ACPA⁺ RA risk might be biochemically distinct from the antigens driving ACPA⁻ RA risk, for example, carbamylated antigens.³³ The different set of risk and protective residues for the two disease subsets might be related to differential binding affinity and reactivity to these autoantigens.

Figure 3.

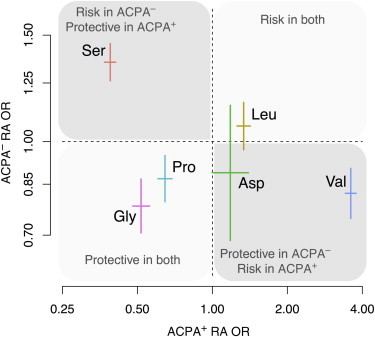
Distinct Effect Sizes of Amino Acid Residues at HLA-DRβ1 Position 11 for ACPA⁻ and ACPA⁺ RA

For each residue, we show the univariate OR (OR with respect to the other residues as a reference) and the 95% confidence interval. Effect sizes were distinct between the two disease subsets (p < 2.9 × 10⁻¹⁰⁷).

In a multicohort study where allele frequencies can differ between cohorts, it is crucial to account for population stratification. For example, the frequency of ancestral 8.1 haplotype differed from 5% to 17% depending on cohorts (Table S9). As described in the Material and Methods, we took two approaches to account for population structure: (1) we stratified the data by country of origin, and (2) we used ten PCs to aggressively adjust for any residual population effects. The effectiveness of this standard approach is reflected in the relatively modest inflation factors for the study (λ_1,000 = 1.00 for ACPA⁻ RA and λ_1,000 = 1.01 for ACPA⁺ RA).

In this study, we addressed the issue of heterogeneity within cohorts. Like for population stratification, if the heterogeneity is present and we fail to adequately adjust for it, spurious associations can occur. For example, without adjusting for heterogeneity, the top ACPA⁻ RA association appeared to be at Leu67 in HLA-DRβ1 (p = 2.9 × 10⁻²⁸). Despite its remarkable significance in our heterogeneous discovery sample, Leu67 failed to replicate when we examined it in our homogenous replication data set (p = 0.26). In contrast, after adjusting for heterogeneity in our discovery data set, we observed the strongest effect at position 11 of HLA-DRβ1 (Table 1); not only did this effect replicate in our homogenous replication data set, but the effect sizes of each amino acid residue at that site were also highly concordant between discovery and replication sets (discordance p > 0.4 after adjustment; Figure S6).

To further demonstrate the potential for accounting for heterogeneity in fine mapping, we performed simulations. We simulated a study under the assumption that HLA-DRβ1 Ser11+Leu11 (OR = 1.30) and HLA-B Asp9 (OR = 1.39) confer risk, which is the model that we found in this study, and included ACPA⁺ RA subjects in 26.3% of affected individuals (Material and Methods). Without adjustment for heterogeneity, the top association was deceivingly at HLA-DRβ1 Leu67 (p < 10⁻³³¹), which was exactly what we observed in discovery cohorts without adjusting for heterogeneity. Using our statistical approach to adjust for heterogeneity, we were able to map the correct positions we simulated; the top associations were HLA-DRβ1 Ser11+Leu11 (p = 1.3 × 10⁻¹⁸⁹), and conditioned on this, rs2853986 (p = 7.2 × 10⁻⁵⁹), which was statistically indistinguishable (p > 0.05) from HLA-B Asp9. We also showed that adjusting for heterogeneity not only removed spurious associations but also provided accurate estimation of the proportion of confounding samples under the null model (Figure S7).

We note that we adjusted for possible confounding from AS by correcting for AS GRSs in discovery cohorts and removing HLA-B^∗27-positive individuals in the replication cohort. This approach effectively adjusted for putative HLA-B^∗27 associations with ACPA⁻ RA if there were any. Currently, it is difficult to distinguish true HLA-B^∗27 associations from confounding from AS. We expect that we will be able to accurately distinguish these two situations as we identify a greater number of non-MHC AS risk loci in the future.

The concern of clinical heterogeneity extends beyond RA to a wide range of diseases where clinical classification might be uncertain because of imperfect diagnostic tests, for example, (1) subclassification of inflammatory bowel disease (MIM 266600) into Crohn disease or ulcerative colitis or (2) distinguishing early bipolar disease (MIM 125480) from major depressive disorder (MIM 608516). We expect that our statistical approach might have application to genetic studies of these conditions as well. The applicability of our approach is contingent on adequate power to detect confounding genetic effects; such power is only possible when sufficient numbers of genetic loci for confounding diseases are known. We also expect that our approach might have utility in better characterizing non-HLA loci of the conditions with clinical heterogeneity.

Our results have important implications for the clinical practice of ACPA⁻ RA. Investigators have long speculated that individuals diagnosed with ACPA⁻ RA might have other inflammatory arthritic conditions, such as AS, that mimic RA and have atypical clinical presentations. Our analysis supports this; we estimated here that each ACPA⁻ RA cohort contained 4%–11% of the affected individuals who most likely had AS and 15%–37% of affected individuals who most likely had ACPA⁺ RA (Table S10 and Figure S3). We note the possibility that other conditions that we did not account for, such as Sjögren syndrome (MIM 270150),³⁴ might have been included within the ACPA⁻ RA samples. These subjects were identified through research protocols, and in clinical practice, these diagnostic uncertainties can be even more pronounced. Clinical misclassifications can be particularly concerning in this setting given that optimal pharmacological treatment and long-term prognosis for these different arthritic conditions vary. Our data not only underscore the need for more accurate clinical tests than the conventional anti-CCP antibody testing but also illuminate the potential role of genetic data in helping categorize individuals with ACPA⁻ inflammatory arthritis.

Appendix A

Asymptotic Mean of Effect-Size Estimate in the Presence of Confounding

We first consider linear regression for quantitative traits. We assume a single locus, which we will extend to multiple loci later. Suppose that two groups of samples are mixed in a cohort. Let x₁ and x₂ be the genotype vectors of the two groups at the locus and y₁ and y₂ be the phenotype vectors. Let β₁ and β₂ be the effect sizes, such that the true model is $y_1=x_1{\beta }_1+{\epsilon }_1$ and $y_2=x_2{\beta }_2+{\epsilon }_2$, where ε₁ and ε₂ are error terms. Without loss of generality, assume that x₁, x₂, y₁, and y₂ have zero mean. Because of sample mixture, what we observe are $x={\left(x_1^T\text{|}{x}_2^T\right)}^T$ and $y={\left(y_1^T\text{|}{y}_2^T\right)}^T$. The standard linear regression formula gives us the least-squares estimate of effect size:

$$\hat{\beta }={\left(x^{T}x\right)}^{-1}{x}^{T}y={\left(x_1^T{x}_1+x_2^T{x}_2\right)}^{-1}\left(x_1^T|x_2^T\right){\left({\left(x_1{\beta }_1+{\epsilon }_1\right)}^T|{\left(x_2{\beta }_2+{\epsilon }_2\right)}^T\right)}^T={\left(x_1^T{x}_1+x_2^T{x}_2\right)}^{-1}\left(\left(x_1^T{x}_1{\beta }_1+x_1^T{\epsilon }_1\right)+\left(x_2^T{x}_2{\beta }_2+x_2^T{\epsilon }_2\right)\right)={\left(x_1^T{x}_1+x_2^T{x}_2\right)}^{-1}\left(\left(x_1^T{x}_1\right)\left({\beta }_1+{\left(x_1^T{x}_1\right)}^{-1}{x}_1^T{\epsilon }_1\right)+\left(x_2^T{x}_2\right)\left({\beta }_2+{\left(x_2^T{x}_2\right)}^{-1}{x}_2^T{\epsilon }_2\right)\right)$$

Given that $E\left[{\left(x_1^T{x}_1\right)}^{-1}{x}_1^T{\epsilon }_1\right]=0$ and $E\left[{\left(x_2^T{x}_2\right)}^{-1}{x}_2^T{\epsilon }_2\right]=0$,

$$E\left[\hat{\beta }\right]={\left(x_1^T{x}_1+x_2^T{x}_2\right)}^{-1}\left(x_1^T{x}_1{\beta }_1+x_2^T{x}_2{\beta }_2\right)$$

If we assume that the minor allele frequency of the variant is the same for the two groups and the genotypes follow Hardy-Weinberg equilibrium, $\left(x_1^T{x}_1\right)/\left(x_2^T{x}_2\right)\approx N_1/N_2$, where N₁ and N₂ are the sample sizes of the two groups. Thus, the effect-size estimate asymptotically converges to an average effect size weighted by the sample sizes of two groups.

This result has the following implication. Suppose that β₁ is the true effect size of interest and β₂ is the effect size for confounding samples. Consider the null model (β₁ = 0). What we observe will be $E\left[\hat{\beta }\right]=\alpha {\beta }_2$, where α is the confounding proportion. Thus, we will have spurious association $\left(E\left[\hat{\beta }\right]\ne 0\right)$. Suppose that we build GRSs with respect to confounding disease as $s=x{\beta }_2$. If we regress out s as a covariate, it will remove spurious association. Moreover, the regression coefficient of s will be an unbiased estimator of α.

Under the alternative model $\left({\beta }_1\ne 0\right)$, using risk score as a covariate might be conservative and remove true association. If we know α a priori, one approach is fixing the coefficient of s to the constant α. That is, we subtract $s\alpha =x{\beta }_2\alpha$ from y. This approach will retain true association. The effect-size estimate can still be conservative, given that what we would want to subtract is actually $x\left({\beta }_2-{\beta }_1\right)\alpha$, which is unknown.

Logistic Regression

Similar results extend to logistic regression. For simplicity, we assume the null model (true OR is 1). Suppose that α% of the case group is confounded by a disease whose OR is $\gamma \ne 1$. Let p be the control minor allele frequency. Then, the asymptotic mean of the observed log OR $\hat{\beta }$ will be

$$E\left[\hat{\beta }\right]=\pi =\log \frac{\left(\alpha p_A+\left(1-\alpha \right)p\right)\left(1-p\right)}{\left(\alpha \left(1-p_A\right)+\left(1-\alpha \right)\left(1-p\right)\right)p},$$

where $p_A=\gamma p/\left(\left(\gamma -1\right)p+1\right)$ is the case minor allele frequency of the confounding disease. Thus, we will have spurious association $\left(E\left[\hat{\beta }\right]\ne 0\right)$.

If γ is small, we can establish an approximate relationship, $\pi \approx \alpha \text{log}\left(\gamma \right)$, which we show by simulations (Figure S8). Thus, using risk score $s=\text{log}\left(\gamma \right)x$ as a covariate, we can not only remove spurious association but also approximate α from the regression coefficient of s.

Generalization to Multiple Loci

We can generalize our approach to multiple loci. Suppose that we know m independent loci associated with the confounding disease. Let ${\beta }_1,\dots ,{\beta }_m$ be their effect sizes. We build GRSs for each individual locus,

$$s_i=x_i{\beta }_{i}i\in \left\{1,\mathrm{...},m\right\},$$

where x_i is the genotype vector at locus i. In order to estimate the confounding proportion α, we look at all loci together by including all s_i in the regression:

$$y=\alpha s_1+\alpha s_2+\dots +\alpha s_m+\epsilon .$$

Application to logistic regression is also straightforward. Because α is invariant across loci, this is equivalent to the model using a combined GRS, $y=\alpha S+\epsilon$, where $S=\sum s_i=\sum x_i{\beta }_i$, which results in the approach presented in the Material and Methods. The advantage of a combined GRS over multiple loci is that it can be less conservative under the alternative model. For example, if we test locus i and include s_i as a covariate, it will remove true association. However, if we include S as a covariate, the information from other loci $\left(s_1,s_2,\dots ,s_{i-1},s_{i+1},\dots ,s_m\right)$ will help in finding correct α and preventing overly regressing out s_i. Another possible way to more strictly prevent overly regressing out GRS can be estimating α with nonoverlapping loci first, as presented in the Material and Methods.

Web Resources

The URLs for data presented herein are as follows:

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• Protein Data Bank (PDB), http://www.rcsb.org/pdb/home/home.do