Direct dose mapping versus energy/mass transfer mapping for 4D dose accumulation: fundamental differences and dosimetric consequences

Abstract

The direct dose mapping (DDM) and energy/mass transfer mapping (EMT) are two essential algorithms for accumulating the dose from different anatomic phases to the reference phase when there is organ motion or tumor/tissue deformation during the delivery of radiation therapy. DDM is based on interpolation of the dose values from one dose grid to another and thus lacks rigor in defining the dose when there are multiple dose values mapped to one dose voxel in the reference phase due to tissue/tumor deformation. On the other hand, EMT counts the total energy and mass transferred to each voxel in the reference phase and calculates the dose by dividing the energy by mass. Therefore it is based on fundamentally sound physics principles. In this study, we implemented the two algorithms and integrated them within the Eclipse TPS. We then compared the clinical dosimetric difference between the two algorithms for 10 lung cancer patients receiving stereotactic radiosurgery treatment, by accumulating the delivered dose to the end-of-exhale (EE) phase. Specifically, the respiratory period was divided into 10 phases and the dose to each phase was calculated and mapped to the EE phase and then accumulated. The displacement vector field (DVF) generated by Demons-based registration of the source and reference images was used to transfer the dose and energy. The DDM and EMT algorithms produced noticeably different cumulative dose in the regions with sharp mass density variations and/or high dose gradients. For the PTV and ITV minimum dose, the difference was up to 11% and 4% respectively. This suggests that DDM might not be adequate for obtaining an accurate dose distribution of the cumulative plan, instead, EMT should be considered.

1. Introduction

For radiation therapy delivered to temporally varying anatomy, such as those in the thorax and abdomen, a dose reconstruction algorithm is required to map the doses at different anatomic phases to a reference phase so that the dosimetric metrics and radiobiological effect can be evaluated in the reference phase. For instance, for lung cancer patients, 4DCT image data can be acquired and sorted into 4, 6, 8 or 10 phases. The tumor and the nearby tissue change in shape and density from phase to phase, which requires determining the dose in each phase and accumulating them to a reference phase. Such a tool is also essential for implementing adaptive radiotherapy (ART), which requires the daily delivered dose to be accumulated (Yan et al 1997, Yan and Lockman 2001, Webb 2008, Wu et al 2011). Accurate dose mapping and accumulation should be based on the correlation between the source and target anatomy, especially when anatomic structures experience deformation from one phase to the other. It requires tracing individual tissue elements in the other phases to the reference phase and bringing the doses deposited during other phases back to the reference phase. This can be achieved by the displacement vector field (DVF) generated by deformable image registration (DIR) between the source and reference images. The DVF establishes a voxel-based correlation between the source and reference image.

In the treatment planning system (TPS), discrete dose values are calculated for the voxels in a 3D grid: each voxel in the grid has a single dose value. During dose mapping, it is possible that tissue elements in the source anatomy are compressed in the target anatomy after tissue deformation. With DVF-based mapping of tissue elements, it is possible that the tissues from multiple dose voxels in the source dose grid go to one voxel in the target dose grid. How does one determine the dose for the target voxel in this scenario? The simplest way is to take the weighted average or interpolated value as the dose for this voxel (Schaly et al 2004, Paganetti et al 2004, Rosu et al 2005). A more physically sound method is to determine the actual energy and mass transferred to that voxel, and then divide the energy by mass to get the dose (Heath and Seuntjens 2006, Siebers and Zhong 2008, Zhong and Siebers 2009, Peterhans et al 2011, Heath et al 2011). In this paper, we call the first method “Direct Dose Mapping” (DDM), and the second “Energy/Mass Transfer Mapping” (EMT).

Since the mechanisms of implementation and the computational work load of the two algorithms are different, researchers implementing ART have raised the question of the difference between the total dose calculated by DDM and EMT. Can interpolation-based Direct Dose Mapping be sufficient for performing dose accumulation for deformable anatomy? Heath et al (2006) compared the interpolation-based dose mapping with the method that incorporating direct voxel tracking into Monte Carlo dose calculation (defDOSXYZ), which can be considered a gold standard for calculating the mapped dose. They found that the former method underestimated the dose up to 2.0% with 0.25 cm cubic voxel size in deformable phantom. Siebers and Zhong (2008) incorporated energy transfer into 4D Monte Carlo dose calculation and compared with that obtained by the interpolation method. In a deformable phantom, the interpolation-based method produced average dose error of 1.1 % along the beam direction and maximum error of 24.9% in the penumbra of a 6 MV beam. When compared with the more accurate Monte Carlo-based energy and mass congruent mapping method (Zhong and Siebers 2009), the DDM method produced an average dose error of 7.3% for a lung IMRT plan when mapping the dose from end-exhale to end-inhale.

Though the EMT technique has been incorporated into Monte Carlo dose calculation through different strategies (Siebers and Zhong 2008, Zhong and Siebers 2009, Peterhans et al 2011, Heath et al 2011), this technique has not yet been implemented in any treatment planning systems for clinical use. Also further comparison of the two dose mapping algorithms with real clinical data is still in need. For this reason, we implemented the two dose mapping algorithms and integrated them within Eclipse treatment planning system through the advanced programming interface (API. See Eclipse API 1.0 User’s Guide issued by Varian Medical Systems, Palo Alto, CA, 2006). We then performed a systematic comparison of the two dose mapping algorithms for lung cancer treatment plans computed with the Anisotropic Analytical Algorithm (AAA).

2. Materials and methods

2.1. Patient and 4DCT dataset

4DCT images of 30 lung stereotactic body radiation therapy (SBRT) patients were retrospectively reviewed under an Institutional Review Board (IRB) approved protocol. The ten patients with the largest lung motion amplitudes were selected for this study. Table 1 shows the tumor location, size in equivalent diameter, and motion amplitude in the superior-inferior (SI), left-right (LR), and anterior-posterior (AP) directions for the ten patients.

Table 1.

The tumor location, size (equivalent diameter), and motion amplitude for the 10 selected cases. RLL-right lower lobe, RML-right middle lobe, LLL-left lower lobe, and LUL-left upper lobe.

Patient No.		1	2	3	4	5	6	7	8	9	10
Tumor location		RLL	LLL	LUL	RLL	RLL	LUL	RML	LUL	RML	RLL
Tumor equiv. diam. [cm]		2.5	3.2	5.0	2.3	5.2	2.7	2.6	2.3	3.1	2.1
Tumor motion amplitude [cm]	SI	0.4	1.2	0.7	0.4	1.0	0.6	1.9	0.4	1.3	0.7
	RL	0.4	0.1	0.1	0.1	0.0	0.1	0.3	0.5	0.2	0.3
	AP	0.4	0.4	0.7	0.4	0.0	0.2	0.3	0.5	0.4	0.5

4DCT images were acquired using Phillips Big Bore CT scanner (Philips Medical Systems, Cleveland, Ohio, USA), and reconstructed into ten phases, CT0, CT10, …, CT90, based on the breathing signals from the Varian Real-Time Position Management (RPM) system (Varian Medical Systems, Palo Alto, CA, USA). Fig. 1 shows an illustration of the respiratory signal sorting, where phase1 and CT0 represents the end-inhale and phase6 and CT50 the end-exhale phase.

Figure 1.

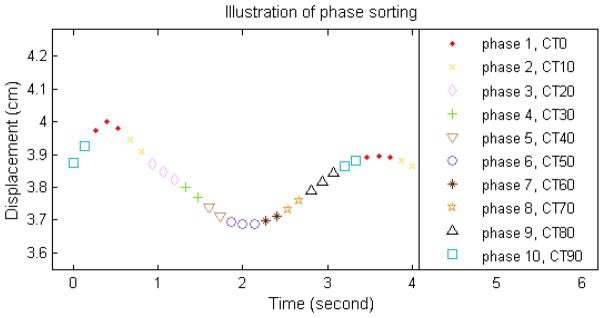
Illustration of sorting of the respiratory motion profile into 10 phases in 4DCT imaging process.

2.2. Treatment plans and dose calculations

For each patient, an internal target volume (ITV) was contoured by a physician such that the gross tumor volume (GTV) was encompassed in all image datasets. The ITV was expanded by 3 mm isotropically to generate the planning target volume (PTV). The end-exhale image (CT50) was selected as reference image because it is the most stable breathing phase. The clinical IMRT plan for lung SBRT delivered with Novalis machine (BrainLAB, Feldkirchen, Germany) was adapted to the reference image. The plan typically consisted of 7 coplanar beams with the MLC moving along the patient lateral direction. The dose was calculated with the Varian Eclipse AAA algorithm using a 2.5 mm dose grid size. (Please note that in Eclipse TPS, the nominal dose grid size denotes the size on the transverse plan, the size in the longitudinal direction is determined by the CT slice thickness. 2 mm CT slice was used in this study. So 2.5 mm dose grid size means dose voxel of 2.5×2.5×2.0 mm³. The same nomenclature is used hereafter.) The plan was then copied to each of the other phase CT images, which were already DICOM-based registered with CT50, and the dose matrices for these image datasets were calculated. Within the Eclipse TPS, since all the phase images have been spatially correlated to each other based on DICOM coordinate reference, the relationship between the x-ray beams and the anatomy in the other phases is automatically configured. Although the image voxels with the same spatial position in different phases are correlated, they do not necessarily correspond to the same tissue element. To align the same tissue element in different respiratory phases, deformable image registration is required.

2.3. Dose matrix transfer and accumulation

The dose matrix on each phase image was transferred to the reference image (CT50) and accumulated as follows:

$$D_{\text{CT}50}^{\text{cum}}=\sum _{p=0,10,\dots ,90}{D}_{\text{CT}p\to \text{CT}50}\times w_p,\text{with}{w}_p=t_p/T.$$ (1)

In the equation, $D_{\text{CT}50}^{\text{cum}}$ is the cumulative dose on CT50 and D_CTp→CT50 is the phase dose matrix transferred from CTp to CT50. The weighting factor W_p is the ratio of the time of the p-th phase (t_p) over the total breathing cycle time (T). In our implementation, all the doses mapped to CT50 had the same dose grid configuration, so that they could be summed up without further interpolation. For the phase-to-phase dose transfer (D_CTp→CT50), two algorithms were implemented: direct dose mapping (DDM) and energy/mass transfer (EMT) mapping.

The Demons deformable image registration algorithm (Thirion 1998) implemented in ITK (Ibáñez et al 2005), a public domain image registration package, was used to establish tissue correlation between two phase images. As an algorithm with multi-level of grid resolution and iterative searching, the Demons was configured with 4 resolution levels. The optimization residues for the four levels were 0.005, 0.005, 0.005 and 0.0001 respectively, the number of iterations for each level was 150 and the standard deviation of the Gaussian smoothing function was 1.0. Zhong et al (2010) have shown that with such configuration of the algorithm, a mean deformation error of 0.76 mm in the lung region can be achieved. The work by Stanley et al (2013) also showed that Demons algorithm is comparable with, even slightly better than the B-spline based deformable multi-pass registration for lung case. Our visual inspection also verified that the registration between the different phase images was of very high quality. Even the subtle anatomy structures within the lung could match very well. To reduce the registration time and computer memory requirements, the image resolution was reduced from 512×512 pixel² (~1×1mm²) to 256×256 pixel² (~2×2mm²). The slice thickness was 2 mm.

The generated displacement vector field (DVF) determines the anatomical mapping between the source and reference image. The mass, energy, and dose belonging to image voxels can be transferred between the registered images based on the DVF. However, the dose information and DVH statistics in a TPS are based on the dose grid which is independent of the image grid. Although the two grids are lined up rectilinearly, the centers of dose and image voxels usually do not overlap. The DDM and EMT algorithms employ different approaches to transfer the dose from the dose to image grids and vice versa.

2.3.1. Direct dose mapping (DDM) algorithm

Since deformable image registration is performed on the image grid, but radiation dose is calculated on dose grid, a transfer of dose value from the dose grid to the image grid is required before performing the DVF-based dose mapping. This transfer was performed using tri-linear interpolation. The dose values in the source image grid were then transferred to the reference image based on the DVF of the registration performed from the source image to the reference image. Specifically, for each image voxel at a position r⃗ in the reference image, the corresponding vector maps this voxel to position r⃗ ′ = T(r⃗) = r⃗ + Δ r⃗) in the source image. Note that the mapped position in the source image is not necessarily at the center of a voxel. The dose at this position in the source image was calculated from its neighboring voxels using a tri-linear interpolation method, and then assigned (pulled back) to the registered reference image voxel, i.e.,

$$D_{\text{CT}p\to \text{CT}50}(\overrightarrow{r})=D_{\text{CT}p}(\overrightarrow{r}+\mathrm{\Delta }\overrightarrow{r}).$$ (2)

This method that pulls the dose from the source image to the reference image is named a “pulling” strategy, as illustrated by Fig. 2. Due to the characteristics of this image registration, this strategy guarantees that every reference image voxel gets a dose value but does not guarantee that every source image voxel dose is transferred exactly once. After the dose in the reference image grid was resolved, interpolation was performed to derive the dose for each voxel in the reference dose grid. Pseudo code of the algorithm with the example of mapping the dose from CTp to CT50 is given in Appendix A. After mapping the doses from all the other phases to the reference phase, the cumulative dose on the reference image was calculated using Eq. (1).

Figure 2.

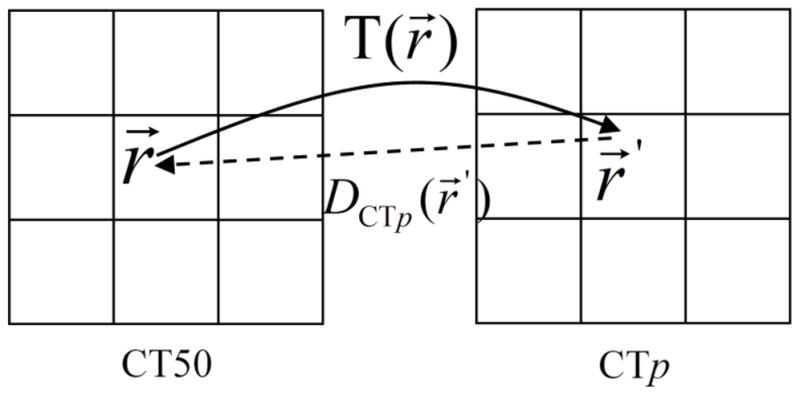
Illustration of “pulling” the dose from source image CTp to reference image CT50. The voxel at position r⃗ in CT50 is mapped to position r⃗′ in CTp and the dose value at r⃗′ is assigned to the voxel at r⃗ in the reference image.

Appendix A.

Pseudo code for mapping the dose from CTp to CT50 with the DDM algorithm:

1. create treatment plan with CT50;

2. copy the plan to CTp, which is DICOM-based registered with CT50, and recalculate the dose;

3. interpolate the dose from dose grid to image grid of CTp;

4. register CT p to CT50 with DIR and generate DVF (function of the DVF: for each image voxel in CT50, the corresponding transfer vector maps the voxel to CTp);

5. for each image voxel centered at r⃗ in CT50

{

// find corresponding point r⃗′ in CTp using the DVF.

$${\overrightarrow{r}}^{\prime }=\mathrm{T}(\overrightarrow{r})=\overrightarrow{r}+\mathrm{\Delta }\overrightarrow{r};$$

// determine the dose at r⃗′ in CTp by interpolation and assign it to CT50.

$$D_{\text{CT}p\to \text{CT}50}(\overrightarrow{r})=D_{\text{CT}p}(\overrightarrow{r}+\mathrm{\Delta }\overrightarrow{r});$$

}

6. interpolate the dose in CT50 image grid to dose grid

2.3.2. Energy/mass transfer (EMT) algorithm

The energy/mass transfer (EMT) algorithm is illustrated with pseudo code in Appendix B, with the example of mapping the dose from CTp to CT50. The essence of the algorithm is to determine the transferred mass and energy to each dose voxel in the reference phase from other phases and obtain the dose by dividing the energy by mass. In this manner, the voxel dose value is calculated by following the definition of dose strictly, avoiding the ambiguity in determining the dose to the voxel when there are multiple dose values from source dose grid mapped to this voxel due to tissue deformation. The algorithm can be outlined in three steps. 1. Deriving the mass and energy values to the image voxels in the source phase; 2. Transferring the mass and energy values from the source image to the reference image based-on the DVF; 3. Converting the mass and energy values from the image grid to the dose grid in the reference phase.

Appendix B.

Pseudo code for mapping the dose from CTp to CT50 with the EMT algorithm:

1. create the optimized treatment plan with CT50;

2. copy the plan to CTp and recalculate the dose;

3. derive the density and mass of the source image voxels in CTp

4. solve the intersection between each source image voxel and the nearby dose voxels and count the energy contained in the image voxels;

5. register CT50 to CTp with DIR and generate the DVF (function of the DVF: for each image voxel in CTp, the corresponding transform vector maps the voxel to CT50);

6. initialize the transferred energy and mass to the dose voxels in CT50 to zeros: $$E_{\text{CT}p\to \text{CT}50}(i)=0,\text{and}{M}_{\text{CT}p\to \text{CT}50}(i)=0;$$

7. for each image voxel centered at r⃗ in CTp

{

7.1 find the transform vector Δr⃗ from DVF;

7.2 transfer the source image voxel at r⃗ to r⃗ + Δr⃗ in CT50;

7.3 solve the intersection between the transferred image voxel at r⃗ + Δr⃗ and the nearby reference dose voxels;

7.4 calculate the energy and mass contribution from the transferred image voxel to each intersected reference dose voxel i: $$\mathrm{\Delta }{E}_{\text{CT}p\to \text{CT}50}(i),\text{and}\mathrm{\Delta }{M}_{\text{CT}p\to \text{CT}50}(i);$$

7.5 for each intersected reference dose voxel i near r⃗ + Δr⃗ in CT50

{

accumulate the transferred energy and mass as $$\begin{array}{l}{E}_{\text{CT}p\to \text{CT}50}(i)=E_{\text{Ct}p\to \text{CT}50}(i)+\mathrm{\Delta }{E}_{\text{CT}p\to \text{CT}50}(i),\\ \text{and}{M}_{\text{CT}p\to \text{CT}50}(i)=M_{\text{CT}p\to \text{CT}50}(i)+\mathrm{\Delta }{M}_{\text{CT}p\to \text{CT}50}(i);\end{array}$$

}

}

8. calculate the transferred dose to CT50 as $D_{\text{CT}p\to \text{CT}50}(i)=\frac{E_{\text{CT}p\to \text{CT}50}(i)}{M_{\text{CT}p\to \mathrm{C}T50}(i)}$

On the source image, the density and mass of each image voxel were derived from the CT Hounsfield value at this voxel. However, the information about the dose value is carried by the dose grid. The energy contained in each image voxel can be extracted through the overlapping between the image and dose voxels. Based on the fact that the image grid and dose grid are aligned rectilinearly, the overlap between each image voxel and the intersected doses voxels can be resolved. Then the contribution of energy to image voxel i from the intersected dose voxels j is calculated as:

$$\mathrm{\Delta }E(\text{dosevoxel}(j)\to \text{image}\text{voxel}(i))=M(i)\times \frac{V(\text{image}\text{voxel}(i)\cap \text{dosevoxel}(\mathrm{j}))}{V(i)}\times D(j),$$ (3)

where M (i) and V (i) are the mass and volume of image voxel i in source image, D( j) is the dose value of dose voxel j, and V (image voxel(i)∩dosevoxel( j)) represents the overlapping volume between image voxel i and dose voxel j. Particularly, $M(i)\times \frac{V(\text{image}\text{voxel}(i)\cap \text{dosevoxel}(\mathrm{j}))}{V(i)}$ is the portion of mass of image voxel i that gets dose value D( j). The total energy contained in image voxel i is the sum of energy contributions from all the intersected dose voxels, i.e., $E(i)={\displaystyle \sum _j}\mathrm{\Delta }E(\text{dosevoxel}(j)\to \text{image}\text{voxel}(i))$, whereV (image voxel(i)∩dosevoxel( j))≠0.

Each source image voxel was “pushed” to the reference phase exactly one time based on the deformation vector, as illustrated by Fig. 3. It should be noted that the center of the “pushed” image voxel does not necessarily fall in the center of an image voxel in the reference phase. However, the “pushed” image voxel is rectilinearly aligned with both the image and dose grid of the reference phase. When pushing each source image voxel, the intersection of the “pushed” image voxel with its neighboring dose voxels of the reference phase was resolved, and the contribution of energy and mass from the “pushed” image voxel to each of the intersected dose voxels was counted. The total energy mapped to a dose voxel i in the reference phase from phase p was counted as:

$$E_{\text{CT}p\to \text{CT}50}(i)=\sum _k{E}_{\text{CT}p}(k)\times \frac{V(\text{pushedimage}{\text{voxel}}_{\text{CT}p}(k)\cap {\text{dosevoxel}}_{\text{CT50}}(i))}{V_{\text{CT}p}(k)},$$ (4)

where E_CTp (k) and V_CTp (k) are the energy and volume of the “pushed” source image voxel k and the overlapped volume between the source image voxel k and the reference dose voxel i V (pushedimage voxel_CTp (k)∩dosevoxel_CT50 (i))≠0. The total mass mapped to the dose voxel is counted similarly. Finally, the dose transferred from phase p to the reference phase is calculated as:

$$D_{\text{CT}p\to \text{CT}50}(i)=\frac{E_{\text{CT}p\to \text{CT}50}(i)}{M_{\text{CT}p\to C\mathrm{T}50}(i)}.$$ (5)

Figure 3.

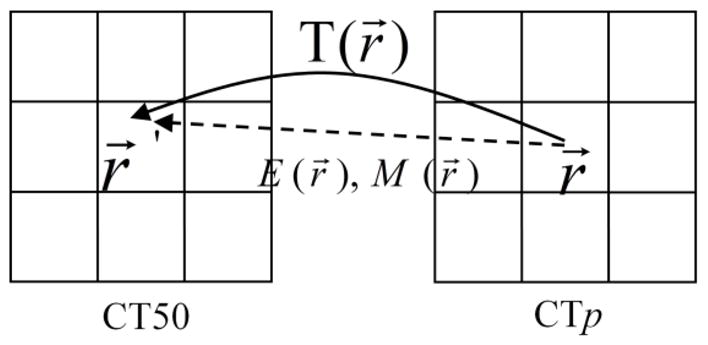
Illustration of “pushing” the energy and mass from the voxel at position r⃗ in source image CTp to r⃗′ in reference image CT50.

2.4. Dosimetric comparison

The difference between the cumulative dose of the DDM and EMT algorithms was evaluated by quantifying the difference in the mean and minimum dose in the PTV and ITV volumes for 10 lung cancer patients. The relative dosimetric difference was calculated as follows:

$$\frac{\text{Cumulative}\text{Dose}\text{of}\text{DDM}-\text{Cumulative}\text{Dose}\text{of}\text{EMT}}{\text{Cumulative}\text{Dose}\text{of}\text{EMT}}\times 100\%.$$

The results of the EMT method were also compared to the reference plan (REF), i.e., the static plan doses calculated on the CT50 phase images. The percentage difference was calculated as follows:

$$\frac{\text{Cumulative}\text{Dose}\text{of}\text{EMT}-\text{Reference}\text{Dose}}{\text{Cumulative}\text{Dose}\text{of}\text{EMT}}\times 100\%$$

Dose volume histograms were compared for the DDM and EMT methods as well as the reference CT50 plans.

The dose to the regions immediately superior and inferior to the PTV volume is more easily affected by the respiratory motion, due to the fact that the regions move in or further away from the radiation field by the motion. To quantify the dosimetric difference between DDM, EMT cumulative plans and the reference plan in these regions, we generated two volumes superior and inferior to the PTV by expanding 2 cm beyond the PTV in these two directions (see Fig. 5(d)). Comparison of the mean dose and DVHs of these regions between DDM, EMT and reference plan will be presented in this paper.

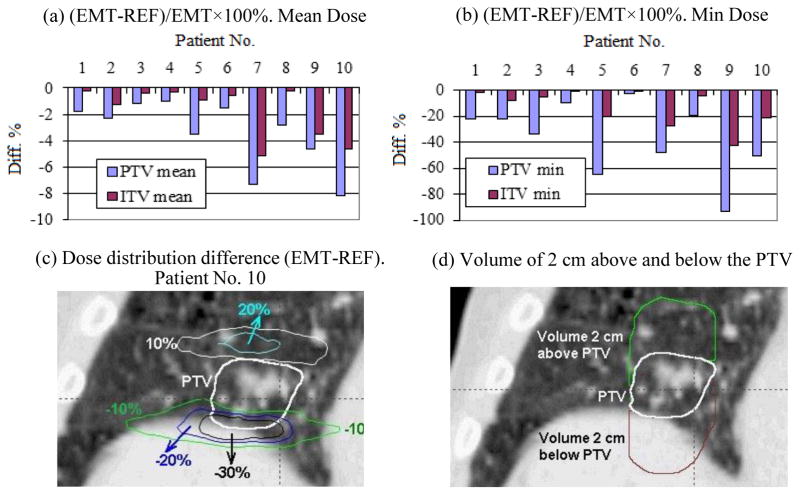
Figure 5.

Difference in the mean and minimum dose of the PTV and ITV between the EMT cumulative plan and the reference static plan (REF) (a and b); an exemplary dose difference of EMT-REF in term of percentage of the prescription dose 48 Gy for patient No. 10 (c); and the regions of 2 cm superior and inferior the PTV (d).

3. Results

3.1. Comparison of the PTV and ITV mean and minimum doses of the EMT and DDM cumulative plans and the reference plan

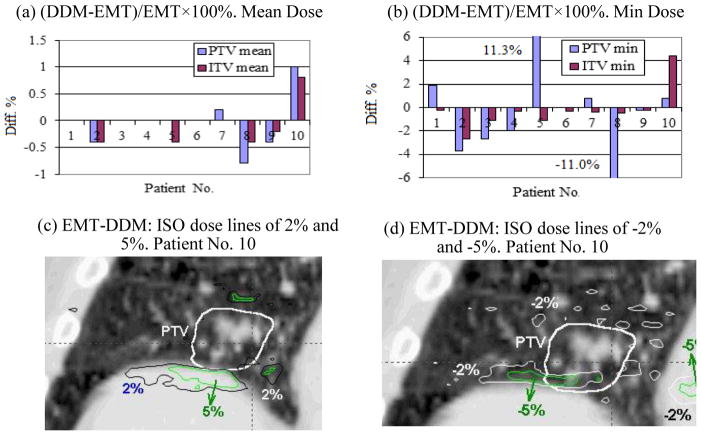
Figure 4 (a) and (b) respectively show the PTV and ITV mean and minimum dose differences in the cumulative plans calculated by the DDM and EMT algorithms. As noted in Fig. 4(a), the PTV mean dose difference is small (<1.0%). The mean and standard deviations (μ±σ) of the mean dose difference was only 0.0 ±0.5% for PTV and −0.1±0.4% for ITV. However, the differences in the minimum doses were measureable; μ±σ= −0.5±5.5% for PTV and μ±σ= −0.2±1.8% for ITV. For the PTV maximum dose (not shown in the charts), the difference between the DDM and EMT cumulative plans was only 0.2±0.2% [0.0~0.5%]; and even less for the ITV. For two patients (No. 5 and No. 8) the difference in PTV minimum dose reached 11%. Patient No. 10 showed relatively large mean dose differences in both the PTV and ITV. The bottom row of Fig. 4 shows the dose distribution difference EMT-DDM for patient No. 10. Fig. 4(c) indicates the regions where the cumulative dose computed with EMT is higher than that of DDM by 2% and 5% of the prescription dose 48 Gy respectively, while Fig. 4(d) shows the regions where EMT dose is lower than the DDM dose by 2% and 5% respectively. The region with the largest dose differences corresponds to the area where the mass density gradient is large (between diaphragm and the lung interface) along the direction with the largest motion amplitude, i.e., the superior-inferior direction (see the discussion section for mathematical proof).

Figure 4.

Dosimetric difference between the DDM and EMT methods for the mean and minimum cumulative doses in the PTV and ITV volumes (a and b), and the iso-dose lines of 2%, 5%, −2%, and −5% of the prescription dose 48 Gy for the subtracted dose EMT-DDM for patient No. 10 (c and d).

Figure 5 shows the comparison between the 4D cumulative doses calculated by the EMT algorithm and the doses of the reference static plans (REF) on the CT50 dataset. The EMT cumulative doses were lower than the reference static doses. The differences in mean dose (μ±σ and range) were −3.4±2.5% [−1.0~−8.2%] for the PTV and −1.7±1.9% [−0.2~−5.2%] for the ITV. The differences in the minimum dose were significantly larger; −36.5±27.7% [−2.1~−92.9%] for the PTV and −12.9±14.0% [−1.4~−42.2%] for the ITV. However, the difference in the PTV maximum dose (not shown in the charts) was only −1.2±2.1% [−6.9~0.7%]; and less for the ITV.

Fig. 5(c) shows the iso-dose curves of 20%, 10%, −10%, −20%, and −30% of the prescription dose 48 Gy for the EMT cumulative dose subtracted by the reference dose for the patient No. 10. The maximum dose difference occurred in the regions immediately superior and inferior to the PTV volume. This is due to the fact that the tumor and the surrounding normal tissues are at the most superior position at the end of exhale phase (CT50), and move inferiorly during other phases. Therefore, relative to the exhale phase, the tissue superior the PTV moves into the radiation field, receiving higher than the reference plan dose. In contrast, the tissue inferior to the PTV moves further away from the irradiation field and gets lower dose.

3.2. Comparison of the mean dose in the 2 cm volumes superior and inferior the PTV of the EMT, DDM and reference plans

Table 2 shows the differences in the mean dose between the DDM and EMT cumulative plans and between the EMT and REF plans for the regions 2 cm superior and inferior the PTV (sees Fig. 5(d)). For the volume of 2 cm superior the PTV, the mean dose differences between DDM and EMT cumulative plans were 0.3±1.4% [−0.7%~4.1%], and the differences between the EMT and REF plans were 13.4±6.7% [3.7~24.5%]. The corresponding quantities for the 2 cm volumes inferior the PTV were 0.0±3.6% [−6.1~7.7%] and −32.7±16.1% [−10.7~−53.5%] respectively.

Table 2.

The difference (%) in the mean dose between the DDM and EMT cumulative plans and between the EMT and REF plans for the 2 cm volumes superior and inferior the PTV (see Fig. 4(d)).

Patient No.		1	2	3	4	5	6	7	8	9	10
2 cm superior PTV	(DDM-EMT)/EMT×100	−0.7	0.6	−0.3	0.0	−0.3	0.3	4.1	−0.5	−0.4	0.0
	(EMT-REF)/EMT×100	12.2	15.7	9.9	15.6	9.8	4.3	17.8	3.7	24.5	20.3
2 cm inferior PTV	(DDM-EMT)/EMT×100	0.6	−1.7	1.8	−1.8	7.7	0	1.9	0.6	−2.6	−6.1
	(EMT-REF)/EMT×100	−29.5	−36.2	−22.9	−11.6	−48.7	−19.3	−47.2	−10.7	−47.1	−53.5

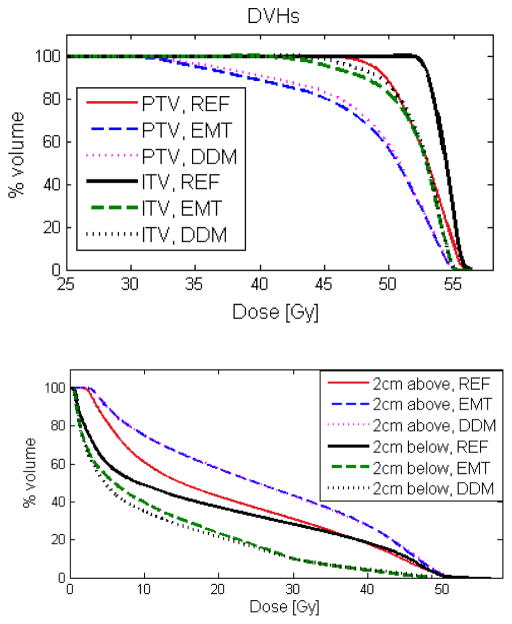
3.3. Comparison of the DVHs

The dose volume histograms (DVH) of the PTV and ITV as well as the volumes superior and inferior to the PTV are presented in Fig. 6 for patient No. 10. For all volumes of interest, the differences in the DVH were small between the DDM and EMT plans, in comparison to the difference from the reference static plan (REF). The dose coverage for the PTV and ITV was largely compromised by the respiration motion for this case. The V₉₅ of PTV for the REF, DDM and EMT plans were 99.9%, 81.6%, and 78.6% respectively, while the V₁₀₀ of ITV were 100%, 91.1%, and 89.8% accordingly. The cumulative dose for the 2 cm volume superior the PTV was significantly higher than that of the reference plan, while it was much lower in the 2 cm volume inferior the PTV.

Figure 6.

The dose volume histograms (DVH) of the PTV and ITV as well as the 2 cm volumes superior and inferior the PTV for the reference static plan (REF) and the EMT and DMM cumulative plans for patient No. 10.

3.4. Impact of dose grid size on the dosimetric difference between EMT and DDM

Typical dose grid sizes in our clinic range from 2 to 5 mm. In addition to 2.5 mm dose grid size, we also investigated the dosimetric differences between the two dose mapping algorithms when using 2 and 5 mm dose grids. Table 3 summarizes the percentage difference for the PTV and ITV mean and minimum dose, between the cumulative plans of the DDM and EMT algorithms, for 2, 2.5, and 5 mm dose grid size respectively. For the PTV and ITV mean dose, the impact of dose grid size on the difference between the two cumulative plans was within 1%. A similar phenomenon was observed for the ITV minimum dose. For the PTV minimum dose, however, the difference between the two cumulative plans depended on dose grid size to some degree. For instance, for patient No. 7, the PTV minimum dose difference between the two cumulative plans changed from 0.8% to 7.4% when the dose grid size was changed from 2.5 mm to 5 mm; for patient No. 9, it changed from −0.2% to −3.2%.

Table 3.

The percentage difference of the PTV and ITV mean and minimum dose between the DDM and EMT cumulative plans ((DDM-EMT)/EMT×100%) for 2, 2.5, and 5 mm dose grid size.

Patient No.	5		7		8			9		10
Grid size: mm	2.5	5	2.5	5	2	2.5	5	2.5	5	2	2.5	5
PTV mean dose	0.0	0.2	0.2	0.6	−0.6	−0.8	−0.4	−0.4	0.0	0.8	1.0	1.2
PTV min dose	11.3	10.0	0.8	7.4	−7.1	−11.0	−10.6	−0.2	−3.2	0.1	0.8	1.8
ITV mean dose	−0.4	−0.2	0.0	0.2	−0.2	−0.4	−0.2	−0.2	0.0	0.6	0.8	1.2
ITV min dose	−1.1	−0.2	0.4	0.7	0.0	−0.5	0.5	0.2	−0.7	4.2	4.4	3.8

4. Discussion

4.1. The prominent difference between the EMT and DDM algorithms

The result of this study showed that, using the direct dose mapping or energy/mass transfer mapping to obtain the cumulative dose for lung cancer treatment with the presence of respiratory motion resulted in small overall differences, i.e., within 1% in the PTV and ITV mean doses. However, the difference in local dose distribution, for instance, the PTV and ITV minimum doses were as high as 11% and 4% respectively. Very prominent differences occurred in the regions with sharp dose or mass density gradients along the superior-inferior direction as observed in Figs 4 (c) and (d). Whether the cumulative dose calculated by DDM is higher or lower than that by EMT depends on the distribution of the dose and mass density at the nearby location, as mathematically illustrated by the following simple example.

Consider the example in Fig. 7 that consists of only two dose voxels, voxel 1 and 2, with mass of m₁ and m₂ and dose of D₁ and D₂ respectively. Suppose that for the two voxels, each has a half of its tissue deformed into a target voxel 2′ after deformation. The dose to voxel 2′ is $\frac{\frac{1}{2}{m}_1{D}_1+\frac{1}{2}{m}_2{D}_2}{\frac{1}{2}{m}_1+\frac{1}{2}{m}_2}$ by the EMT method and $\frac{1}{2}(D_1+D_2)$ by DDM method. The difference of the deformed doses in target voxel 2′ between the two algorithms is

Figure 7.

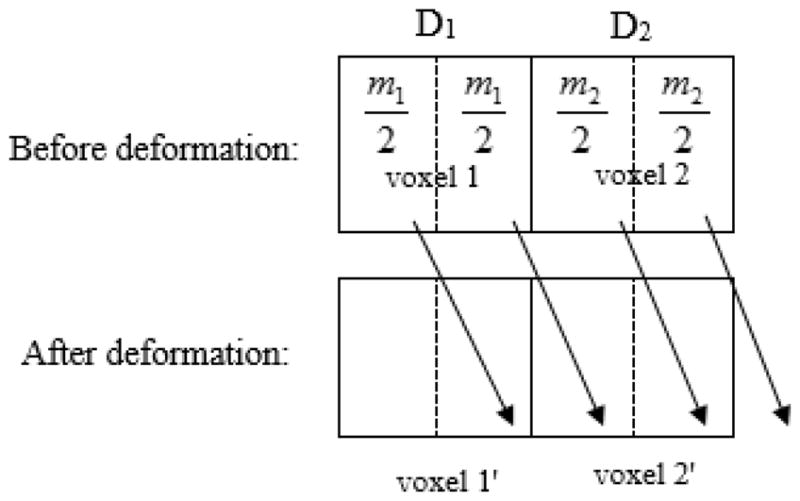
Illustration of tissue deformation with the material of target voxel 2′ mapped from two source voxels, voxel 1 and 2, where the mass is m₁ and m₂, and dose is D₁ and D₂ respectively.

$$\mathrm{\Delta }=\frac{\frac{1}{2}{m}_1{D}_1+\frac{1}{2}{m}_2{D}_2}{\frac{1}{2}{m}_1+\frac{1}{2}{m}_2}-\frac{1}{2}(D_1+D_2)=\frac{(m_1-m_2)(D_1-D_2)}{2(m_1+m_2)}.$$ (6)

$$\text{When}\{\begin{array}{c}{m}_1\ge m_2\\ D_1\ge D_2\end{array}\text{or}\{\begin{array}{c}{m}_1\le m_2\\ D_1\le D_2\end{array},\mathrm{\Delta }\ge 0;\text{otherwise}\text{if}\{\begin{array}{c}{m}_1\ge m_2\\ D_1\le D_2\end{array}\text{or}\{\begin{array}{c}{m}_1\le m_2\\ D_1\ge D_2\end{array},\mathrm{\Delta }\le 0.$$ (7)

The above mathematical analysis shows that for the region featured with higher mass density having higher dose, the deformed dose with EMT algorithm is higher than that with DDM algorithm; for the region featured with lower mass density having higher dose, the deformed dose with EMT algorithm is lower than that with DDM algorithm. In other words, for the region of higher mass density with higher dose, the EMT algorithm favors the higher dose component by assigning it a higher weighting factor than does the DDM algorithm, so that the EMT dose is higher than the DDM dose. Similarly, for the region of higher mass density with lower dose, the EMT algorithm favors the component with lower dose by assigning it a higher weighting factor than does the DDM algorithm, so that the EMT dose is lower than the DDM dose. Furthermore, Eq. (6) also shows that the larger the dose and mass density gradient, the greater the difference between the DDM and EMT mapped doses.

The difference between the DDM and EMT mapped dose is sometimes significant for local dose (e.g., the PTV and ITV minimum dose), but not for the overall dose (e.g., the mean dose). One purpose of the adaptive radiotherapy is to remedy the difference between the actually delivered dose and the planned dose, i.e., to boost the dose in cold spots and reduce the dose in hot spots in the later fractions. In this regard, the EMT algorithm will provide more accurate dose accumulation for individual dose voxels.

4.2. The difference between the cumulative and the reference dose

As shown by Fig. 5 (a) and (b), although the difference in the PTV and ITV mean doses between the DDM and EMT cumulative plans is minimal, the difference between the cumulative plans and the reference plan is up to −5.2% for the ITV mean dose. For the volumes 2 cm superior or inferior to the PTV, the difference in mean dose between the cumulative plan and the reference plan can be very high, up to −53.5% (see Table 2). The magnitude of difference depends on which phase is selected as the reference phase. Since the lung tissue and tumor are at the most superior position during the phase of 50% (end of exhale), which is selected as the reference phase in this study, the difference between the cumulative plan and the reference plan demonstrated in this study is at the maximum. If a phase at the middle between the end of inhale and the end of exhale was selected as the reference phase, the positional deviation of the other phases from the reference phase will be smaller, and the difference between the cumulative and the reference plan dose will likely be smaller also.

4.3. Limits in performing dose mapping and accumulation

Although the energy/mass transfer is a rigorous algorithm, its accuracy depends on other factors, i.e., the accuracy in deformable image registration and conversion from CT Hounsfield value to mass density. In fact, to have a fair comparison between the two dose mapping algorithms, the DVFs for registering the other phase images to the reference image and vice versa should be inverse-consistent (Yan et al, 2010) so that the error related to image registration is consistent. In this study, we used the DVFs of the two directions as what they were, without “forcing” them inverse consistent. The overall inverse consistence error for our DVFs is 1.6±1.2 mm in mean and standard deviation (we measured it by moving the point from the reference image to other image with the forward DVF and then returning the point to the reference image with the backward DVF and then calculating the vector length between the start and end points). This is within the expectation considering the 0.76 mm mean registration error (Zhong et al, 2010). While these issues need to be further considered, they are unlikely to change the conclusions of this study which is focused primarily on the fundamental differences and clinical manifestations of the DDM and EMT dose mapping algorithms.

In implementing the direct dose mapping algorithm, we used the trilinear algorithm to interpolate the dose from the dose to image grids and vice versa. Since we used 2.5×2.5×2.0 mm³ dose voxel size and the typical image voxel size was about 1×1×2 mm³, we expect that trilinear interpolation is sufficiently accurate for this case. Heath and Seuntjens (2006) have investigated the impact of dose grid size on the accuracy of dose mapping with trilinear interpolation and concluded that for a dose grid of 2.5×2.5×2.5 mm³ the warped dose was underestimated by 2% in the worst scenario, compared with the result obtained by a Monte Carlo based dose mapping algorithm defDOSXYZ.

In our implementation of the DDM and EMT algorithm, a single image voxel was moved translationally only; the rotation and deformation were not considered. However, this operation will still induce the deformation of the relatively large tissue volume. Please note that this approximation is adequate for using small image voxel only, for example, 1mm×1mm×2mm as in our work. If the dose mapping is performed with larger image voxel, the deformation of single voxel should be considered. Alternatively, one can reduce the image voxel size by up-sampling the image and ignore the deformation of a single image voxel.

A more rigorous dose accumulation algorithm should also account for the interplay effect between the organ motion and MLC leaf sequence, in addition to the organ motion and deformation effect. This means that the dose deposited for each phase should be computed by the subset of MLC sequences delivered to that specific phase, rather than by the entire MLC sequence delivered in aggregate. We have evaluated the interplay effect on cumulative dose for several patient cases. It was found that, although the interplay effect was significant for individual phases, it “washed out” in dose accumulation over 10 phases. The interplay effect caused less than 1% discrepancy in the PTV and ITV minimum doses, for the cumulative plan with the EMT algorithm (Li et al, 2011).

5. Conclusion

We have implemented two algorithms, direct dose mapping and energy/mass transfer mapping, to accumulate the doses delivered to temporal varying anatomic and tumor volumes. When the two algorithms are employed to accumulate the doses delivered to lung tumor moving with respiration, the difference in the overall cumulative doses, such as the PTV and ITV mean doses, is small. However, the two algorithms were sometimes found to produce noticeably different PTV and ITV minimum doses. Up to 11.3% difference in the PTV and 4.4% in ITV minimum doses, respectively were observed in the cumulative plans. The largest differences occurred in the regions with sharp mass density and/or dose gradient. For the volumes that extended 2 cm beyond the superior or inferior surface of the PTV, up to 7.7% difference in the mean dose between the DDM and EMT cumulative plans was observed.

Since there exists noticeable regional dose difference between and the DDR and EMT algorithms and the latter is based on a more theoretically sound physics principle, we should consider EMT for dose accumulation in the context of adaptive radiotherapy, to achieve the goal to remedy the regional dose discrepancy due to the inter- and intra-fraction motion.