Determining the role of correlated firing in large populations of neurons using white noise and natural scene stimuli

Abstract

The role of correlated firing in representing information has been a subject of much discussion. Several studies in retina, visual cortex, somatosensory cortex, and motor cortex, have suggested that it plays only a minor role, carrying < 10% of the total information carried by the neurons (Gawne and Richmond, 1993; Nirenberg et al., 2001; Oram et al., 2001; Petersen et al., 2001; Rolls et al., 2003). A limiting factor of these studies, however, is that they were carried out using pairs of neurons; how the results extend to large populations wasn’t clear. Recently, new methods for modeling network firing patterns have been developed (Pillow et al., 2008; Nirenberg and Pandarinath, 2010), opening the door to answering this question for more complete populations. One study, Pillow et al. (2008), showed that including correlations increased information by a modest amount, ~20%; however, this work used only a single retina (primate) and a white noise stimulus. Here we performed the analysis using several retinas (mouse) and both white noise and natural scene stimuli. The results showed that correlations added little information when white noise stimuli were used (~13%), similar to Pillow et al.’s findings, and essentially no information when natural scene stimuli were used. Further, the results showed that ignoring correlations did not change the quality of the information carried by the population (as measured by comparing the full pattern of decoding errors). These results suggest generalization: the pairwise analysis in several species show that correlations account for very little of the total information. Now, the analysis with large populations in two species show a similar result, that correlations still account for only a small fraction of the total information, and, most significantly, the amount is not statistically significant when natural stimuli are used, making rapid advances in the study of population coding possible.

Introduction

In the last several years, there has been a great deal of interest in whether correlations in spiking patterns carry important information (e.g., Meister et al., 1995; Nirenberg et al., 2001; Wu et al., 2001; Schneidman et al., 2006; also see reviews by Latham and Nirenberg, 2005; Averbeck et al., 2006). The question arises frequently because the answer has critical bearing on the research approaches that can be used to understand population coding. If these correlations do carry information, then direct, i.e., brute force, approaches for characterizing population activity can’t be used: one simply can’t find the mapping from stimulus to response, as such a mapping would require estimating response distributions in high dimensions – at least N dimensions for N neurons. For populations of more than 3 or 4 cells, the amount of data needed would be impossibly large, and one would have to turn to indirect approaches, such as estimating the response distributions with the correlational structure modeled parametrically.

In contrast, if correlations do not carry unique information, direct approaches become viable even for large populations. Under these conditions, one can characterize the population response distributions from the single neuron distributions. This latter scenario would allow much more rapid advances in the field of population coding.

Much of the work addressing this issue has focused on pairwise analyses. These studies, which include a broad range of neural areas, showed that correlations carry little information – less than 10% of the total information carried by each pair (Gawne and Richmond, 1993; Nirenberg et al., 2001; Oram et al., 2001; Petersen et al., 2001; Rolls et al., 2003). How this result scales with population size, however, is still a subject of debate. One possibility is that as population size increases, each pair will continue to contribute about the same amount of information. Since the number of pairs is proportional to the square of the number of neurons, this scaling behavior predicts that for large populations, correlations could become a substantial or even dominant carrier of information. Another alternative is that as the size of the population grows, only some pairs contribute, or the contributions of the individual pairs become redundant. In these scenarios, the correlations would remain a small contributor to the total amount of information.

Recently, methods for modeling the firing patterns of retinal ganglion cells to white noise stimuli have been developed and used to address this (Pillow et al., 2008). Analysis of the importance of correlations using these models showed that correlations increased information by a relatively small amount, ~20%; however, the work used only a single retina and a white noise stimulus; no natural stimuli were used.

Here we performed the analysis using several retinas, large populations of cells, and both white noise and natural stimuli. The results showed that correlations added little information when white noise stimuli were used (~13%), similar to the results of Pillow et al. (2008), and essentially no information when natural stimuli were used. Thus, the second alternative is more likely the correct one: correlations are a relatively minor contributor to the information carried by populations of neurons - not only for neuronal pairs, but also for whole populations. This is also consistent with a smaller population study with natural scenes in salamander (Oizumi et al., 2010). Thus, correlations likely play a different role in network functioning (e.g., reinforcing network learning (reviewed in Feldman, 2009) or shaping network development (reviewed in Blankenship and Feller, 2010)).

Methods

Defining correlations

Two types of correlations are commonly referred to in the literature. One is called “noise correlation” (Gawne and Richmond, 1993) and is the focus of this paper. Neural responses r=(r₁,…,r_n) are noise-correlated if and only if

$$p(\mathbf{r}\mid x)\ne \underset{i=1}{\overset{n}{\Pi }}p(r_i\mid x),$$

where (r₁,…,r_n) are the individual neural responses that constitute the population response r to the stimulus x.

The second type is called “signal correlation” (Gawne and Richmond, 1993) and differs from noise correlation in that it takes the average over all stimuli. Neural responses are signal-correlated if and only if

$$p\left(\mathbf{r}\right)\ne \underset{i=1}{\overset{n}{\Pi }}p\left(r_i\right).$$

To provide intuition for what these two types of correlations are, we give an example, following from Nirenberg and Latham (2003). Suppose one presents a flash of light while recording from two ON-type ganglion cells that lie far apart on the retina (such that their receptive fields don’t overlap). Because the cells are both ON cells, they will both fire at the onset of the flash. The similarity in their response is an example of signal correlations, and its role in neural coding is clear and not disputed. If, though, the two cells are close enough to receive common input from presynaptic cells (e.g., common photoreceptors, amacrine cells, etc.), then they would show correlations above and beyond the signal correlations. These extra correlations are the noise correlations; their contribution to the information carried by the cells has become the subject of much debate and is the focus of this paper.

Stimuli

The retinas were stimulated with two photopic, grayscale stimuli of identical luminance and contrast: binary spatio-temporal white noise (WN) and a grayscale natural scene movie (NS). The natural scene movie was recorded in New York City’s Central Park, and had a temporal power spectrum of 1/f^2.04, where f is temporal frequency, and a spatial power spectrum of 1/ω^2.09, where ω is spatial frequency. Both were presented at 15 Hz, using an LCD projector driven by a computer running custom software on a real-time version of Red Hat Linux. Luminance was 0.24 μW/cm² on the retina (in the photopic range); root-mean-squared contrast was 0.087 μW/cm². The white noise stimulus covered 10 × 9 squares (with each square corresponding to 160 × 160 μm on the retina); the natural movie stimulus covered 20 × 18 squares (with each square covering 80 × 80 μm on the retina). For each stimulus, we had a training set, which was used to fit model parameters, and a testing set, which was used for evaluating the models and making calculations; the latter were referred to as the “out-of-sample stimuli”.

Measuring degree of correlation

The degree of correlation was measured using the excess correlated fraction (ECF) following Nirenberg et al. (2001). For each pair of cells, the ECF was calculated as follows: first, the “raw fraction” of correlated spikes was determined. This was the number of spikes that occurred within 1 ms of each other divided by the total number of spikes produced by the pair. A second quantity, the “shifted fraction”, was then determined. It was obtained by pairing responses from the two cells when they were presented with the stimulus at different times, i.e., when their responses were shifted by one repeat relative to each other (Perkel et al., 1967). The shifted fraction was then calculated by counting the number of spikes in the shifted pair that occurred within 1 ms of each other and dividing this by the total number of spikes for the pair. The ECF is then the difference between the raw and shifted fraction.

Shift-corrected cross-correlograms were generated in a manner similar to that described above for obtaining the ECF. Briefly, for each pair of neurons, the raw cross-correlogram was first determined from the two cells’ simultaneously-recorded responses. The “shift predictor” was calculated from their responses recorded on separate repeats, and was then subtracted from the raw cross-correlogram to yield the shift-corrected cross-correlogram (Perkel et al., 1967).

Independent and coupled models

Two models were constructed from the neural responses: one in which the neurons were treated as independent, and one in which coupling among the neurons was included. Each model consisted of a set of parameters that were fit by maximizing the log-likelihood of observed spiking data collected for 10 minutes using the training stimulus set (see Stimuli above).

In the independent model (Fig. 2A), the mth neuron’s firing rate was modeled by

$${\lambda }_m^{independent}\left(t\right)=N_m\left[(X\ast L_m\left(t\right))+\sum _i{H}_m(t-{\tau }_m\left(i\right))\right],$$ (1)

where X is the stimulus, * denotes spatiotemporal convolution, L_m is the spatiotemporal impulse response corresponding to the linear filter for the mth neuron, and N_m is a function that describes its nonlinearity. The nonlinearities were parameterized as cubic spline functions with 6 knots. Knots were spaced to cover the range of values given by the linear filter output of the models. H_m is the spike history filter for the mth neuron, and τ_m is the sequence of spike times for the mth neuron.

Figure 2. Schematics of the two input/output models.

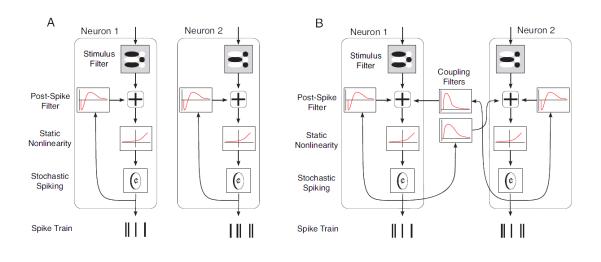
A. The independent model. In this model, each neuron within the population is represented by a separate cascade. To generate each neuron's output, the input is convolved with a linear filter. The output of the convolution is then added to the output of a second filter which is convolved with the cells' spiking history. Finally, a static nonlinearity is applied to the combined linear filter output, yielding a rate function for a Poisson spike generator. B. The coupled model. In the coupled model, the cascades are interconnected - that is, the spiking output of each cell undergoes convolution with neighboring cells' coupling filters, and the result combines additively with the input signal for the neurons.

In the coupled model (Fig. 2B) (Pillow et al., 2008), the influence of neuron k on neuron m is modeled by convolution of a linear filter with the sequence of spikes on neuron k. The outputs of these convolutions for all neighbors k are summed together and added to the stimulus filter output for neuron m, and the sum is then fed into the mth neuron’s nonlinearity function, N_m. Formally, the model is

$${\lambda }_m^{coupled}\left(t\right)=N_m\left[(X\ast L_m)\left(t\right)+\sum _i\left[H_m(t-{\tau }_m\left(i\right))+\sum _{k\ne m}{C}_{m,k}(t-{\tau }_k\left(i\right))\right]\right],$$ (2)

where τ_k is the sequence of spikes times of neuron k.

Each neuron’s linear filter L_m was assumed to be a product of a spatial function (extending through 5 × 5 squares), and a temporal function (extending through 18 time bins, 67 ms each). Dimensionality was further reduced by constraining the temporal function to a linear combination of 10 basis functions (raised cosines), as in Nirenberg et al. (2010), following Pillow et al. (2008). Similarly, coupling filters were parameterized by four raised-cosine basis functions (using additional basis functions was not found to improve fitting), and had a temporal extent of 9 ms (slightly longer than the observed correlogram widths).

Parameters were fit using an expectation maximization procedure, as described by Paninski et al. (2007). The quantity maximized is the log likelihood of the observed spike trains under the model (for a given stimulus). Because the models we’re using produce an output governed by an inhomogeneous Poisson process, the log likelihood of the observed spike trains can be calculated according to the standard formula:

$$Z=\sum _m\left[\sum _{i}log\left[{\lambda }_m\left({\tau }_m\left(i\right)\right)\right]-{\int }_{t=0}^{end}{\lambda }_m\left(t\right)dt\right].$$ (3)

In this equation, λ_m is the instantaneous firing rate of the mth neuron (predicted by either the independent model (eq. 1) or the coupled model (eq. 2)), and Z is the log-likelihood of the population activity in which the mth neuron spikes at times τ_m. Z is a sum of terms, one for each neuron m. The term for the mth neuron (the expression in the larger square brackets) is composed of a sum and an integral. The sum term boosts the log-likelihood if the neuron produces a spike when the model’s instantaneous firing rate (λ_m) is high. The integral is a standard penalty term that prevents models from achieving a high log-likelihood merely by predicting high firing rates overall (Paninski et al., 2007).

To find the parameters that maximize the log likelihood in Eq. 3, we used the following procedure. We began by assuming that the nonlinearity N_m was exponential, since in this case, a global maximum for the log likelihood Z (Eq. 3) is assured (Paninski et al., 2007). After optimizing the linear filters for an exponential nonlinearity (by gradient ascent), the exponential nonlinearity was replaced by a spline, as in Nirenberg et al. (2010). Final model parameters were then determined by alternating stages of maximizing the log likelihood with respect to (i) the spline coefficients and (ii) the filter parameters, until a maximum was reached.

Models were validated by observing their spike-train prediction performance for 10 minutes of novel spiking data, that is, data produced from the retina by out-of sample stimuli (stimuli not used to fit the model).

Recording

Electrophysiological recordings were obtained in vitro from the isolated mouse retina. Recordings of central retinal ganglion cells (RGCs) were performed on a 64 electrode multi-electrode array using methods described previously (Dedek et al., 2008). Spike waveforms were recorded using a Plexon Instruments Multichannel Neuronal Acquisition Processor (Dallas, TX), and a standard spike sorting method (Fee et al., 1996) was used to identify individual cells. Recordings contained 16 to 33 cells per retina; cells that had refractory period violations above 5% were excluded.

Calculating information

For both stimuli (white noise and natural movies) and both models (independent and coupled), we estimated information rates by decoding the population responses and comparing the accuracy of the decoded stimulus with the actual stimulus. Information calculations were performed from data produced by the test stimuli (i.e., data not used to fit the model parameters).

For white noise, we followed the procedure of Pillow et al. (2008): briefly, we used the Bayes’ least squares estimator to decode population responses for both the independent and coupled models. The stimulus variable, x_i, was a 10-element binary vector representing the luminance of a single spatial checker (with spatial location chosen to maximize coverage by the population of recorded cells) over 10 frames. The response variable r was the set of spike trains recorded across all neurons (r₁,…,r_n) for 2 seconds beginning with the first frame of x_i. For each response r, we calculated the likelihood that it would have been elicited by each of the 2¹⁰ possible stimuli x_i. This is the likelihood exp(Z) given by Eq. 3, where the rate functions on the right-hand side are taken from Eq. 1 for the independent model or from Eq. 2 for the coupled model. It is proportional to p(r|x_i), the probability that the stimulus x_i would elicit a population response r. To convert p(r|x_i) to what we need for decoding, the posterior probability p(r|x_i), we use Bayes’ theorem:

$$p(x_i\mid \mathbf{r})\propto p(\mathbf{r}\mid x_i)p\left(x_i\right),$$

where in this case p(x_i) is uniform. The Bayes' least squares estimate of the stimulus given the response r is a probability-weighted sum over all possible stimuli:

$$\widehat{x}=\sum p(x_i\mid \mathbf{r})x_i.$$

Finally, as in Pillow et al. (2008), decoding performance was converted into an estimate of information rate (in bits/sec) via

$$H={\log }_2\left[\det (\langle x_j{x}_j^T\rangle )∕\det (\langle ({\widehat{x}}_j-x_j){({\widehat{x}}_j-x_j)}^T\rangle )\right],$$

where <·> denotes averaging across all responses. Note that the above equation is an estimate of the log of the signal-to-noise ratio (SNR) between the stimulus x and the decoded estimate x̂. Implicit in this estimate is the assumption that the white noise stimulus can be considered to be approximately Gaussian (see Pillow et al., 2008). There are two reasons that we choose to decode a single spatial pixel: 1) this allows for a direct comparison with Pillow et al. (2008), and 2) it facilitates the information calculations under the assumptions of a Gaussian channel. We use short snippets for decoding as it allows us to repeat the decoding calculation for many samples of the response, which is a necessary step for computing the SNR.

For natural scene stimuli, we calculated information by an approach that did not require the Gaussian approximation. The stimulus variable x consisted of the starting point of the 150-frame natural movie sequence, that is, x₀ was the movie that started at frame 0, x₁ was the movie that started at frame 1, etc. Each response r was taken as the spike trains recorded over a single 67 ms segment of the movie. The decoded stimulus was computed as the element from the stimulus set that maximized the posterior probability:

$$\widehat{x}=\arg \max \left[p(x_i\mid \mathbf{r})\right].$$

Mutual information was then calculated between x and x̂ with the standard plug-in estimator of entropy (Antos and Kontoyiannis, 2001). In order to ensure that the stimulus entropy was not a critical factor in our calculations, we also performed this analysis using half of the stimuli (x₀, x₂, x₄, etc.) and a third of the stimuli (x₀, x₃, x₆, etc.). As a further check for robustness, we repeated the calculation with the response variable consisting of longer segments of the spike trains, at lengths of 133 ms and 200 ms (the same was done for the decoding used for confusion matrices described below).

For information estimates, 95% confidence intervals were determined by taking 1000 bootstrap resamples of 200 decoded segments for the white noise stimulus conditions, and by taking 200 bootstrap resamples of 60 decoded segments (for each of the stimuli) for natural scenes.

Finally, we used the natural scene stimuli and responses to construct confusion matrices, as in Pandarinath et al. (2010). Briefly, a confusion matrix gives the probability that a neural response to a presented stimulus will be decoded as that stimulus (Hand, 1981). To find these probabilities, we used the same Bayesian approach as for calculating information. Each recorded response r was decoded by choosing the stimulus x most likely to have produced it, that is, the stimulus for which p(x_i|r) was maximized. Here again, p(x_i|r) was calculated from p(x_i|r) using Bayes theorem, where the prior p(x_i) was uniform . For each presentation of stimulus x_i that resulted in a response r that was decoded as stimulus x_j, the entry at position (i,j) in the confusion matrix was incremented.

Results

Our goal is to determine the extent to which information transmission by a neuronal population – the output cells of the retina – depends on correlations, specifically noise correlations (see Methods). Our strategy is to decode the population responses with two decoders: one that ignores correlations and one that exploits them. The decoding is carried out via a Bayesian framework, and therefore requires a model of the relationship between stimulus and response. The model determines how we treat the correlations: when we decode using an “independent” model, we ignore correlations; when we decode using a “coupled” model, we take them into account (see Methods for descriptions of the models).

To approach this goal, we proceeded in four steps. First, we measured the degree of correlation in our system, the ganglion cells of the mouse retina. Second, we constructed the two input/output models and verified that they perform as expected – that is, that the coupled model predicts correlations while the independent model does not. Third, using each model, we decoded out-of-sample stimuli (i.e., the test stimuli), both white noise and natural scenes. Finally, using the decoding results, we compared the information rates for the two models and assessed the quality of the decoding using confusion matrices.

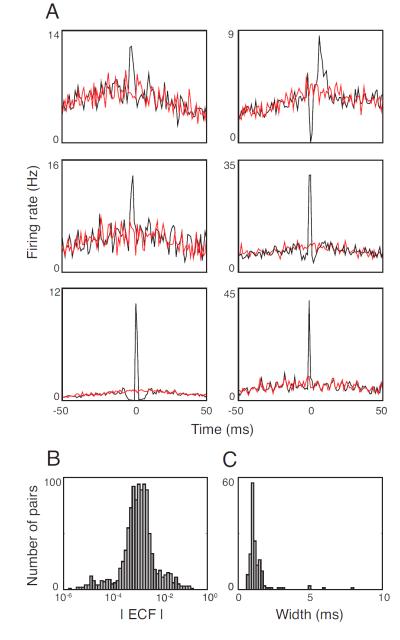
We begin by characterizing the correlations in our model system, the mouse retina (Fig. 1). Fig. 1A shows 6 representative cross-correlograms, covering the range of strengths and timescales. The lower panels summarize the results for the population: Fig. 1B shows the distribution of correlation strengths, quantified by the excess correlated fraction, ECF (Nirenberg et al., 2001, see Methods), and Fig. 1C shows the distribution of correlation timescales. The range of ECF’s encountered (up to 33%) agrees with that previously reported for mouse retina (up to 34% in Nirenberg et al., 2001, and 33% in Jacobs et al., 2009) and other mammalian species (up to 27% in cat (Mastronarde, 1983) and 28% in rabbit (DeVries, 1999)). Similarly, the range of correlation timescales (<1 ms to 5 ms, with a tail out to 11 ms) is also consistent with results reported for other mammalian species, including cat, rabbit, and mouse (Mastronarde, 1983; DeVries, 1999; Nirenberg et al., 2001). Note that the range of ECFs in the retina is broad, and their potential impact, as discussed in the literature, is proposed to occur in two ways: through the cumulative effect of the many small correlations that make up the majority of the correlations, or through groups of highly correlated cells, which, though more rare, could also carry significant information (see Wu et al., 2001; Schneidman et al., 2006; Pillow et al., 2008; Meister et al., 1995; Nirenberg et al., 2001; Chatterjee et al., 2007; also discussed in Latham and Nirenberg, 2005, and Averbeck et al., 2006).

Figure 1. Degree and timescale of correlated activity for pairs of ganglion cells in the mouse retina.

A. Representative cross-correlograms, showing the range of correlation strengths and timescales. As is standard, each plot shows the the firing rate of one cell in the pair relative to the spike times of the cell. Black indicates the raw cross-correlogram; red indicates the shift-predictor (Perkel, Gerstein, and Moore 1967). The difference between these two is the noise correlation, the focus of this paper. B. Distribution of ECFs for all cell pairs in the dataset (n=567 pairs, 3 retinas). C. Distribution of half-widths of the central peak of the cross-correlogram for all cell pairs with ECFs > 0.5% in the dataset (n=157, 3 retinas).

Having established that our dataset is representative of the typical levels of correlated activity in the retina, we constructed the two retinal input/output models mentioned above – the one that ignores correlations (the independent model), and the one that takes them into account (the coupled model). The two models are shown schematically in Fig. 2. The independent model (Fig. 2A) consists of a linear filter, a static nonlinearity, and Poisson spike generation for each neuron (i.e., an LNP cascade) and a post-spike filter for modeling refractoriness. The coupled model (Fig. 2B) consists of the same with an added dependence on the firing of other neurons in the population.

In Figs. 5 and 6, we will show the results of using the models to decode stimuli, but first we show that they have the necessary properties to allow us to test the hypothesis that correlations matter. Specifically, we show that both models predict the average responses well, indicating that they are capturing signal correlations, but only the coupled model predicts the detailed firing patterns and their correlations, indicating that it is capturing both signal and noise correlations, the latter being the correlations that are the subject of so much debate.

Figure 5. The contribution of correlations (noise correlations) to information for white noise and natural stimuli.

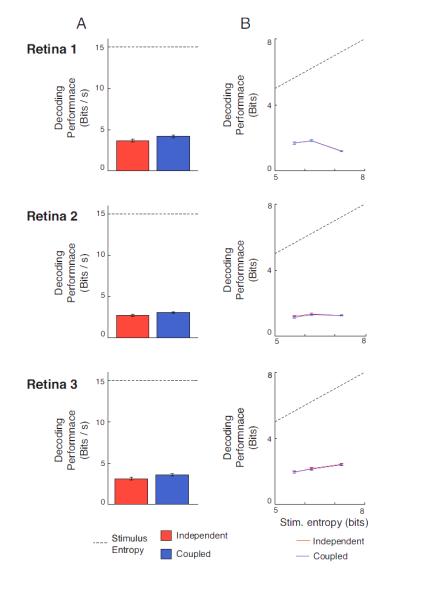
As shown in Figs. 3 and 4, taking correlations into account (via the coupled model) substantially improves the prediction of individual spike trains. However, as shown here, this addition leads to only a modest increase in the amount of information carried. A. Information decoded from populations using white noise stimuli with an independent (red) and coupled (blue) model. The coupled model (which takes noise correlations into account) adds a small amount of information (13% on average). B. Information decoded for populations using natural scene stimuli with an independent (red) and coupled (blue) model. To control for effects due to stimulus entropy, we use three levels of task difficulty (corresponding to the number of stimuli to decode). We find that the coupled model does not add significant information for any of the three difficulties. Error bars show 95% confidence intervals. Population size for Retina 1 was17 cells, for Retina 2 was 13 cells, and for Retina 3 was 26 cells.

Figure 6. Characterization of decoding errors on natural scenes via confusion matrices.

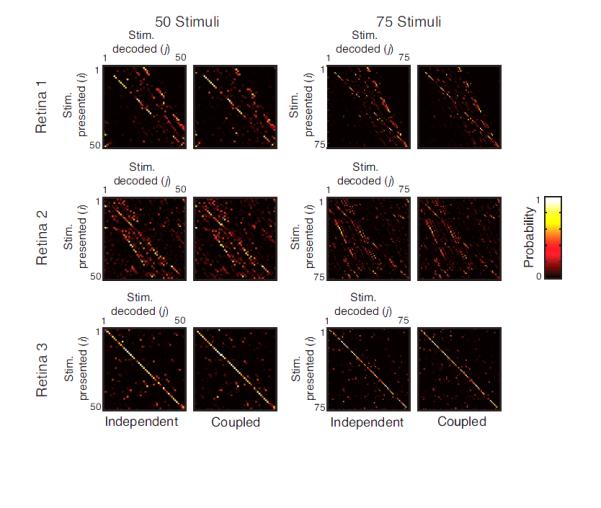
Two confusion matrices are shown. One was constructed with 50 stimuli drawn from the natural scene movies, and the other with 75 stimuli, also drawn from the natural scene movies. The stimuli were 67 ms movie segments. In each matrix, the rows correspond to each presented stimulus, and the columns correspond to the decoded stimulus. The intensity of a pixel in row i and column j corresponds to the probability that the neural response to stimulus i is decoded as stimulus j. On-diagonal elements indicate correct decodings; off-diagonal elements indicate the pattern of errors. Extending the findings of the information calculation (Fig. 5), the confusion matrices are nearly indistinguishable for the independent and coupled models.

Fig. 3 shows the evaluation of the two models using the white noise stimulus. Fig. 3A shows rasters from several representative cells produced by the out-of-sample white noise stimulus (the testing set), along with predictions from the independent and coupled models, and Fig. 3B shows the corresponding average peristimulus time histograms (PSTHs).

Figure 3. Model performance for white noise stimuli.

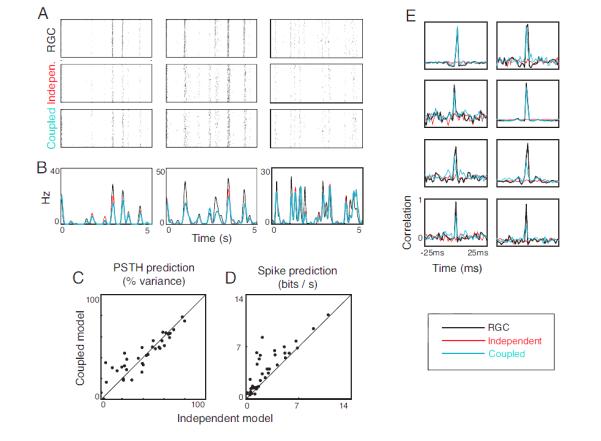
A. Recorded responses from three representative retinal ganglion cells (RGCs) to repeats of an out-of-sample binary white noise stimulus (top), along with responses derived from the independent model (middle) and the coupled model (bottom). B. Corresponding PSTH’s of the ganglion cell responses (black), the independent model output (red), and the coupled model output (blue). C. Quality of PSTH prediction by independent and coupled models across the three retinas. Coupling yields no advantage in predicting the average response. D. Log-likelihoods of ganglion cell responses for the independent and coupled models. The coupled model is better able to explain individual spike trains. E. Representative shift-corrected cross-correlograms for pairs of ganglion cells (black) and for the independent (red) and coupled models (blue). The coupled model is able to capture the correlated activity, while the independent model is not.

Fig. 3C and D summarize the results for the whole dataset. As can be seen in the figures, both models predict the average responses equally well (Fig. 3C). Fig. 3D then shows that, in addition, the coupled model predicts the detailed firing patterns better than the independent model. The increase was quantified by calculating the log likelihood of the observed spike trains, given each model (Methods, Eq. 3). As shown in Fig. 3D, the coupled model consistently achieves the better performance.

Finally, to confirm that the coupled model was achieving the better performance for the right reason, that is, because it was capturing the noise correlations in the spike trains, we calculated cross-correlograms. Each plot in Fig. 3E shows the shift-corrected cross-correlogram of the true responses of a pair of neurons, along with the predictions from the independent and coupled models (the shift-corrected correlograms show only the noise correlations, not the full correlograms which also contain signal correlations as in Pillow et al., 2008 and Oizumi et al., 2010). As shown in the figure, the coupled model provides a good fit to the cross-correlograms, whereas the independent model fails to predict any peaks at all.

Fig. 4 provides a parallel analysis of the two models for natural scene stimuli. As was the case for the responses to white noise, the independent and coupled models provide equally good predictions of the average responses. This is seen in representative rasters (Fig. 4A) and PSTHs (Fig. 4B), and in the summary across all cells in all retinas (Fig. 4C). Also in agreement with the findings for white noise, the coupled model is better able to predict individual spike trains (Fig. 4D) and cross-correlograms (Fig. 4E).

Figure 4. Model performance for natural scene stimuli.

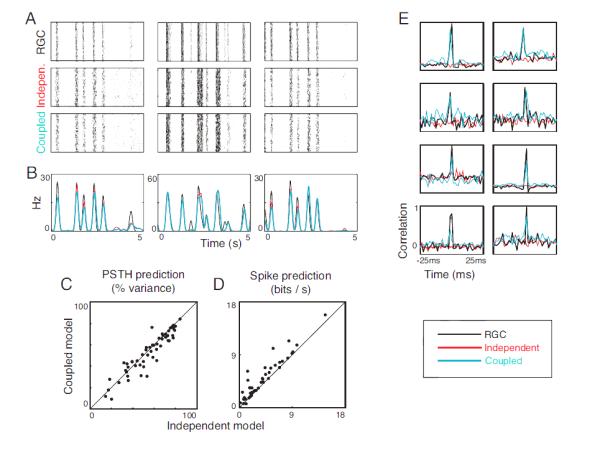
A. Recorded responses of three representative ganglion cells (RGCs) to repeats of an out-of-sample natural scene stimulus (top), along with responses derived from the independent model (middle) and the coupled model (bottom). B. Corresponding PSTH’s of the ganglion cell responses (black), the independent model output (red), and the coupled model output (blue). C. Quality of the PSTH prediction by independent and coupled models for the three retinas. Coupling yields no advantage in predicting the average response. D. Log-likelihoods of ganglion cell responses for the independent and coupled models. The coupled model is better able to explain individual spike trains. E. Representative shift-corrected cross-correlograms for pairs of ganglion cells (black) and for the independent (red) and coupled models (blue). The coupled model is able to capture the correlated activity, while the independent model is not. All of these findings parallel those of Fig. 3, obtained for white noise stimulation.

Having shown that the coupled model captures the noise correlations, we now use a Bayesian decoding framework (given in Methods) to determine how much information these correlations carry.

Fig. 5A shows the results of the decoding analysis for the white noise stimulus in the three retinas. As shown in the figure, capturing the correlations led to only a small increase in decoding performance, about 1 bit/s. On average this amounted to a 13% increase in information.

Fig. 5B extends this analysis to the responses to natural scenes and shows that for these stimuli, the contribution of noise correlations is even less, effectively undetectable. As was the case for white noise, taking noise correlations into account via the coupled model yields superior predictions of spike trains on a trial-by-trial basis (Fig. 4D). But, as shown in Fig. 5B, despite this, taking noise correlations into account yielded no detectable increase in the amount of information that can be decoded about the stimulus. Similar results were obtained when other response lengths were used for decoding (see Methods). Thus, the information in the correlations is essentially redundant to the information in the independent firing patterns, and including them in the decoding does not add information.

The Supplement shows two additional analyses that further support these conclusions: Fig. S1 shows that the results are robust to goodness of fit (as measured by R²), and Fig. S2 shows that the results hold when the analysis is restricted to subpopulations of cells with particularly high mutual correlations.

At this point, we have shown that taking noise correlations into account has minimal effect on the amount of information carried by the population. We now take this one step further, and ask whether they change the kind of information that is carried. To do this, we constructed confusion matrices corresponding to the information calculations for the natural scene stimuli shown in Fig. 5B. Two confusion matrices are shown: one is constructed with 50 stimuli drawn from the natural scene movies, and the other with 75 stimuli, also drawn from the natural scene movies. The stimuli were 67 ms movie segments. These matrices, shown in Fig. 6, indicate which stimuli are correctly decoded, and which ones are mistaken for another. Rows correspond to the presented stimulus; columns correspond to the decoded stimulus. The intensity of a pixel in row i and column j corresponds to the probability that the neural response to stimulus i is decoded as stimulus j. Thus, perfect decoding would result in a bright diagonal line, and off-diagonal elements represent the pattern of decoding errors.

As is clear from Fig. 6, the pattern of decoding for the independent model is the same as the pattern for the coupled model – that is, the pattern of correct classifications (the on-diagonal elements), and the pattern of errors (the off-diagonal elements) are the same for both models. This finding also held for decoding among 150 stimuli and for decoding with longer response durations (133 ms and 200 ms). We conclude that under natural scene stimulation, taking noise correlations into account has little impact not only on the amount of information that is present, but also on the kind of information – that is, it has almost no effect on which stimuli are properly decoded, and which are confused.

Discussion

The question of whether neural responses can be understood or decoded without taking noise correlations into account is crucial to the study of population coding. If cells can’t be treated as independent units, then a recording from one neuron can’t be understood without taking into account the neurons interacting with it. Determining the correlational structure for large populations of neurons is nontrivial: using brute force methods on populations with more than a few neurons is not possible, since the amount of data needed to characterize the population response scales exponentially with the number of cells in the population. Therefore, alternative approaches, such as characterizing the correlational structure parametrically, would be needed. For this reason, the answer to the question of whether noise correlations carry information has direct and significant impact on the direction of research efforts in the field (Nirenberg et al., 2001; Averbeck and Lee, 2004; Latham and Nirenberg, 2005; Averbeck et al., 2006; see Brown et al., 2004 in addition for further discussion of the problems of studying large neuronal populations).

Though this question has already been studied for pairs of neurons, finding that noise correlations add little or negligible amounts of information (Gawne and Richmond, 1993; Nirenberg et al., 2001; Oram et al., 2001; Petersen et al., 2001; Rolls et al., 2003; Levine, 2004), the possibility remained that they could contribute in larger amounts in more complete populations. The concern remained in part because of the matter of scaling: as the number N of neurons in a population grows, the number of pairs of neurons grows in proportion to N². Thus, if the noise correlations from each pair were to contribute non-redundantly to the total information, their contribution would eventually become very large even though the contribution from individual pairs is small. Furthermore, higher-order (non-pairwise) interactions could also contribute in large populations. This study however confirms that neither of these was the case: even in the large populations we used (as high as 26 neurons), noise correlations continued to account for only a small fraction of the total information.

Correlations do not carry significant information in complete subpopulations

Unlike the two previous population studies (Pillow et al., 2008; Oizumi et al., 2010), our analysis included more than one cell class; this was done to allow correlations among different cell types to be included, such as those between ON cells and ON-OFF cells or OFF cells and ON-OFF cells. To relate our results to previous studies, though, we also performed the analysis on two cell type-specific patches (Fig. 7) – a patch of 10 ON cells and a patch of 7 ON-OFF cells. We found that our results still hold for both of these patches, and, in fact, within these single cell type patches, correlations account for even less of the information than in the full mixed populations, possibly because single cell type mosaics do not include the strong correlations that exist between different cell types with overlapping response properties (DeVries, 1999; Greschner et al., 2011) (e.g., between ON and ON-OFF cells).

Figure 7. Information carried by correlations within single-cell mosaics.

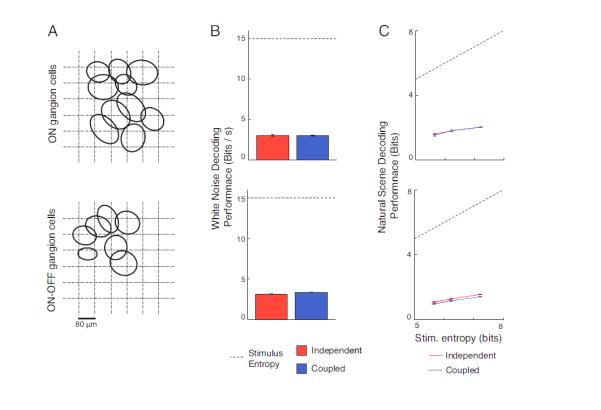
A. The receptive field mosaics for a patch of ON cells (top) and a patch of ON-OFF cells (bottom). The receptive fields were calculated by fitting 2-D Gaussian functions to the spatial kernels of the models, then plotting the contour at height 1/e relative to the peak. B. Information decoded for the white noise stimulus. Calculations were made using only the ON cell patch (top) and only the ON-OFF cell patch (bottom). For each of the patches here, the inclusion of correlations led to a very small increase in information (smaller than for the full retinal populations). C. Information decoded for the natural scene stimulus. For each of the patches here, correlations did not add any significant amount of information, consistent with the results for full populations.

Ignoring correlations does not affect the quality of the information

We emphasize that our analysis went a step beyond determining the contribution of noise correlations to the amount of information: we showed that taking noise correlations into account also does not change the kind of information carried. We showed this using confusion matrices, which delineate which stimuli were correctly decoded, and exactly which errors were made. As shown in Fig. 6, the confusion matrices that emerge when correlations are taken into account are very nearly identical to the confusion matrices that emerge when they are ignored. Thus, taking noise correlations into account does not change either the amount or the quality of the information carried by retinal spike trains.

Conclusions

We have shown that for multiple types of stimuli (white noise and natural scenes), cells in a retinal population can be treated as independent with little or no loss of information. This greatly simplifies, and, therefore, facilitates the study of retinal population coding. The fact that the result holds for natural stimuli is notable because natural stimuli have both local and long range correlations that are not found in white noise, and, as a result, the noise correlations they induce may differ. Hence, generalization of the result from white noise to natural scenes is nontrivial, and, since natural stimuli are the biologically relevant ones, this generalization is critical to know.

One question that naturally arises is whether the conclusions – that population coding can be studied by treating the neurons as independent – will generalize to other regions of the CNS. At the level of pairs of neurons, the contribution of noise correlations is similar between the retina and many cortical areas, including visual, motor, and somatosensory (Oram et al., 2001; Petersen et al., 2001; Rolls et al., 2003), and this contribution is small. While this suggests generalization, it doesn’t assure it. Good parametric models for capturing global input-output relationships will open the door to direct tests along the lines of the ones reported here.

Highlights.

• We examine the role of correlations for carrying information in large populations

• We find that correlations add little information under white noise stimulation

• We find that correlations add no discernible information under natural scenes

• This means neurons may be treated as independent for many applications