Fast, Sequence Adaptive Parcellation of Brain MR Using Parametric Models

Abstract

In this paper we propose a method for whole brain parcellation using the type of generative parametric models typically used in tissue classification. Compared to the non-parametric, multi-atlas segmentation techniques that have become popular in recent years, our method obtains state-of-the-art segmentation performance in both cortical and subcortical structures, while retaining all the benefits of generative parametric models, including high computational speed, automatic adaptiveness to changes in image contrast when different scanner platforms and pulse sequences are used, and the ability to handle multi-contrast (vector-valued intensities) MR data. We have validated our method by comparing its segmentations to manual delineations both within and across scanner platforms and pulse sequences, and show preliminary results on multi-contrast test-retest scans, demonstrating the feasibility of the approach.

1 Introduction

Computational methods for automatically segmenting magnetic resonance (MR) images of the brain have seen tremendous advances in recent years. So-called tissue classification methods, which aim at extracting the white matter, gray matter, and cerebrospinal fluid, are now well established. In their simplest form, these methods classify voxels independently based on their intensity alone, although state-of-the-art methods often incorporate a probabilistic atlas – a parametric representation of prior neuroanatomical knowledge that is learned from manually annotated training data – as well as explicit models of MR imaging artifacts [1–3]. Tissue classification techniques have a number of attractive properties, including their computational speed and their ability to automatically adapt to changes in image contrast when different scanner platforms and pulse sequences are used. Furthermore, they can readily handle the multi-contrast (vector-valued intensities) MR scans that are acquired in clinical imaging, and can include models of pathology such as white matter lesions and brain tumors.

Despite these strengths, attempts at expanding the scope of tissue classification techniques to also segment dozens of subcortical structures have been less successful [4]. In that area, better results have been obtained with so-called multi-atlas techniques – non-parametric methods in which a collection of manually annotated images are deformed onto the target image using pair-wise registration, and the resulting atlases are fused to obtain a final segmentation [4, 5]. Although early methods used a simple majority voting rule, recent developments have concentrated on exploiting local intensity information to guide the atlas fusion process, which is particularly helpful in cortical areas for which accurate inter-subject registration is challenging [6, 7].

Although multi-atlas techniques have been shown to provide excellent segmentation results, they do come with a number of distinct disadvantages compared to tissue classification techniques. Specifically, their non-parametric nature entails a significant computational burden because of the large number of pairwise registrations that is required for each new segmentation. Furthermore, their applicability across scanner platforms and pulse sequences is seldom addressed, and it remains unclear how multi-contrast MR and especially pathology can be handled with these methods.

In this paper, we revisit tissue classification modeling techniques and demonstrate that it is possible to obtain cortical and subcortical segmentation accuracies that are on par with the current state-of-the-art in multi-atlas segmentation, while being dramatically faster. Following a modeling approach similar to [3, 1] for tissue classification, but with a carefully computed probabilistic atlas of 41 brain substructures, we show excellent performance both within and across scanner platforms and pulse sequences. Compared to other methods aiming at sequence adaptive whole brain segmentation, we do not require specific MR sequences for which a physical forward model is available [8], and we segment many more structures without a priori defined contrast-specific initializations as in [2].

2 Modeling Framework

We use a Bayesian modeling approach, in which a generative probabilistic image model is constructed and subsequently “inverted” to obtain automated segmentations. We first describe our generative model, and subsequently explain how we use it to obtain automated segmentations. Because of space constraints, we only describe the uni-contrast case here (i.e., a scalar intensity value for each voxel); the generalization to multi-contrast data is straightforward [3].

2.1 Generative Model

Our model consists of a prior distribution that predicts where anatomical labels typically occur throughout brain images, and a likelihood distribution that links the resulting labels to MR intensities. As a segmentation prior we use a recently proposed tetrahedral mesh-based probabilistic atlas [9], where each mesh node contains a probability vector containing the probabilities for the K different brain structures under consideration. The resolution of the mesh is locally adaptive, being sparse in large uniform regions and dense around the structure borders. The positions of the mesh nodes, denoted by θ_l, can move according to a deformation prior p(θ_l) that prevents the mesh from tearing or folding onto itself. The prior probability of label l_i ∈ {1, …, K} in voxel i is denoted by p_i(l_i|θ_l), which is computed by interpolating the probability vectors in the vertices of the deformed mesh. Assuming conditional independence of the labels between voxels given the mesh node positions, the prior probability of a segmentation is then given by $p(\mathbf{l}\mid {\mathit{\theta }}_l)={\prod }_i^I{p}_i(l_i\mid {\mathit{\theta }}_l)$, where l = (l1, …, l_I)^T denotes a complete segmentation of an image with I voxels.

For the likelihood distribution, we associate a mixture of Gaussian distributions with each neuroanatomical label to model the relationship between segmentation labels and image intensities [1]. To account for the smoothly varying intensity inhomogeneities that typically corrupt MR scans, we model such bias fields as a linear combination of spatially smooth basis functions [3]. Letting d = (d₁, …, d_I)^T denote a vector containing the image intensities in all voxels, and θ_d a vector collecting all bias field and Gaussian mixture parameters, the likelihood distribution then takes the form $p(\mathbf{d}\mid \mathbf{l},{\mathit{\theta }}_d)={\prod }_{i=1}^I{p}_i(d_i\mid l_i,{\mathit{\theta }}_d)$, where

$$p_i(d\mid l,{\mathit{\theta }}_d)=\sum _{g=1}^{G_l}\mathcal{N}\left(d-\sum _{p=1}^P{c}_p{\varphi }_p^i\mid {\mu }_{lg},{\sigma }_{lg}^2\right)w_{lg}$$

and $\mathcal{N}(d\mid \mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp\left(-\frac{{(d-\mu )}^2}{2{\sigma }^2}\right)$. Here G_l is the number of Gaussian distributions associated with label l; and μ_lg, ${\sigma }_{lg}^2$, and w_lg are the mean, variance, and weight of component g in the mixture model of label l. Furthermore, P denotes the number of bias field basis functions, ${\varphi }_p^i$ is the basis function p evaluated at voxel i, and c_p its coefficient. To complete the model, we assume a flat prior on θ_d: p(θ_d) ∝ 1.

2.2 Inference

Using the model described above, the most probable segmentation for a given MR scan is obtained as l̂ = arg max_l p(l|d) = arg max_l ∫ p(l|d, θ)p(θ|d)dθ, where θ = (θ_d, θ_l)^T collects all the model parameters. This requires an integration over all possible parameter values, each weighed according to its posterior p(θ|d). Since this integration is intractable we approximate it by estimating the parameters with maximum weight θ̂ = arg max_θ p(θ|d), and using the contribution of those parameters only:

$$\widehat{\mathbf{l}}=arg\underset{\mathbf{l}}{max}p(\mathbf{l}\mid \mathbf{d})\approx arg\underset{\mathbf{l}}{max}p(\mathbf{l}\mid \mathbf{d},\widehat{\mathit{\theta }})=arg\underset{\{l_1,\dots ,l_I\}}{max}\prod _{i=1}^I{p}_i(l_i\mid d_i,\widehat{\mathit{\theta }}).$$ (1)

The optimization of eq. (1) is tractable because it involves maximizing p_i(l_i|d_i, θ̂) ∝ p_i(d_i|l_i, θ̂_d)p_i(l_i|θ̂_l) in each voxel independently.

To find the optimal parameters we maximize

$$p(\mathit{\theta }\mid \mathbf{d})\propto p(\mathbf{d}\mid \mathit{\theta })p(\mathit{\theta })\propto \left(\prod _{i=1}^I\sum _{l=1}^K{p}_i(d_i\mid l,{\mathit{\theta }}_d)p_i(l\mid {\mathit{\theta }}_l)\right)p({\mathit{\theta }}_l)$$ (2)

by iteratively keeping the mesh positions θ_l fixed at their current values and updating the remaining parameters θ_d, and vice versa, until convergence. For the mesh node position optimization we use a a standard conjugate gradient optimizer, and for the remaining parameters a dedicated generalized expectation-maximization (GEM) algorithm similar to [3]. In particular, the GEM optimization involves iteratively computing the following “soft” assignments in all voxels i ∈ {1, …, I}:

$$q_i^{lg}=\frac{w_{lg}\mathcal{N}(d_i-{\sum }_{p=1}^P{c}_p{\varphi }_p^i\mid {\mu }_{lg},{\sigma }_{lg}^2)p_i(l\mid {\mathit{\theta }}_l)}{{\sum }_{k=1}^K{p}_i(d_i\mid k,{\mathit{\theta }}_d)p_i(k\mid {\mathit{\theta }}_l)},\forall l\in \{1,\dots ,K\},\forall g\in \{1,\dots ,G_l\}$$

based on the current parameter estimates, and subsequently updating the parameters accordingly:

$$\begin{array}{c}{\mu }_{lg}\leftarrow \frac{{\sum }_{i=1}^I{q}_i^{lg}\left(d_i-{\sum }_{p=1}^P{c}_p{\varphi }_p^i\right)}{{\sum }_{i=1}^I{q}_i^{lg}},{\sigma }_{lg}^2\leftarrow \frac{{\sum }_{i=1}^I{q}_i^{lg}{\left(d_i-{\mu }_{lg}-{\sum }_{p=1}^P{c}_p{\varphi }_p^i\right)}^2}{{\sum }_{i=1}^I{q}_i^{lg}},\\ w_{lg}\leftarrow \frac{{\sum }_{i=1}^I{q}_i^{lg}}{{\sum }_{g=1}^{G_l}{\sum }_{i=1}^I{q}_i^{lg}},{(c_1,\dots ,c_P)}^T\leftarrow {({\mathbf{A}}^T\mathbf{SA})}^{-1}{\mathbf{A}}^T\mathbf{Sr},\end{array}$$

where

$$\begin{array}{c}\mathbf{A}=\left(\begin{array}{ccc}{\varphi }_1^1& \dots & {\varphi }_P^1\\ ⋮& \ddots & ⋮\\ {\varphi }_1^I& \dots & {\varphi }_P^I\end{array}\right),\mathbf{S}=\mathit{diag}(s_i),s_i=\sum _{l=1}^K\sum _{g=1}^{G_l}\frac{q_i^{lg}}{{\sigma }_{lg}^2},\\ \mathbf{r}={(r_1,\dots ,r_I)}^T,r_i=d_i-{\stackrel{\sim }{d}}_i,{\stackrel{\sim }{d}}_i=\frac{{\sum }_{l=1}^K{\sum }_{g=1}^{G_l}{s}_i^{lg}{\mu }_{lg}}{{\sum }_{l=1}^K{\sum }_{g=1}^{G_l}{s}_i^{lg}}.\end{array}$$

3 Implementation

We used a training dataset of 39 T1-weighted scans and corresponding expert delineations of 41 brain structures to build our mesh-based atlas and to run pilot experiments to tune the settings of our algorithm. The scans were acquired on a 1.5T Siemens Vision scanner using a magnetisation prepared, rapid acquisition gradient-echo (MPRAGE) sequence (voxel size 1.0 × 1.0 × 1.0 mm³). The 39 subjects are a mix of young, middle-aged, and old healthy subjects, as well as patients with either questionable or probable Alzheimer’s disease [6].

We used 15 randomly picked subjects out of the available 39 to build our probabilistic atlas. The remaining subjects were used to find suitable settings for our algorithm. After experimenting, we decided to restrict sub-structures with similar intensity properties to having the same GMM parameters, e.g., left and right hemisphere white matter are modeled as having the same intensity properties. Further, we experimentally set a suitable value for the number of Gaussians for each label (variable G_l): three for gray matter structures, cerebro-spinal fluid, and non-brain tissues; and two for white matter structures, thalamus, putamen, and pallidum.

To initialize the algorithm, we co-register our atlas to the target image using an affine transformation. For this purpose we use the method described in [10], which uses atlas probabilities, rather than an intensity template, to drive the registration process. As is common in the literature, the MR intensities are log-transformed because of the additive bias field model that is employed [3].

4 Experiments

To validate the proposed algorithm, we performed experiments on two datasets of T1-weighted images that were manually labeled using the same protocol as the training data, each acquired on a different scanner platform and with a different pulse sequence. We also show preliminary results on a third dataset that consists of test-retest scans of multi-contrast (T1- and T2-weighted) images without manual annotations. We emphasize that we ran our method on all three datasets using the exact same settings.

Although our method segments 41 structures in total, some of the structures are not typically validated (e.g., left/right choroid plexus, left/right vessels), thus we here report quantitative results for a subset of 23 structures: cerebral white matter (WM), cerebellum white matter (CWM), cerebral cortex (CT), cerebellum cortex (CCT), lateral ventricle (LV), hippocampus (HP), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA) and amygdala (AM), for both the left and the right side, along with brainstem (BS). In order to gauge the performance of our method with respect to the current state-of-the-art in the field, we also report results for the well-known FreeSurfer package [11] and two multi-atlas segmentation methods: BrainFuse [6], which uses a Gaussian kernel to perform local intensity-based atlas weighing, and Majority Voting [5], which weighs each atlas equally. We note that all three competing methods used the same training data described in section 3, ensuring a fair comparison: FreeSurfer to build its label and intensity models; and the multi-atlas methods to perform the pair-wise atlas propagations and to tune optimal parameter settings. All three competing methods apply the same preprocessing stages to skull-strip the images, remove bias field artifacts, and perform intensity normalization as described in [11]. The proposed method works directly on the input data itself without preprocessing. For our implementation of Majority Voting, we used the pair-wise registrations computed by BrainFuse.

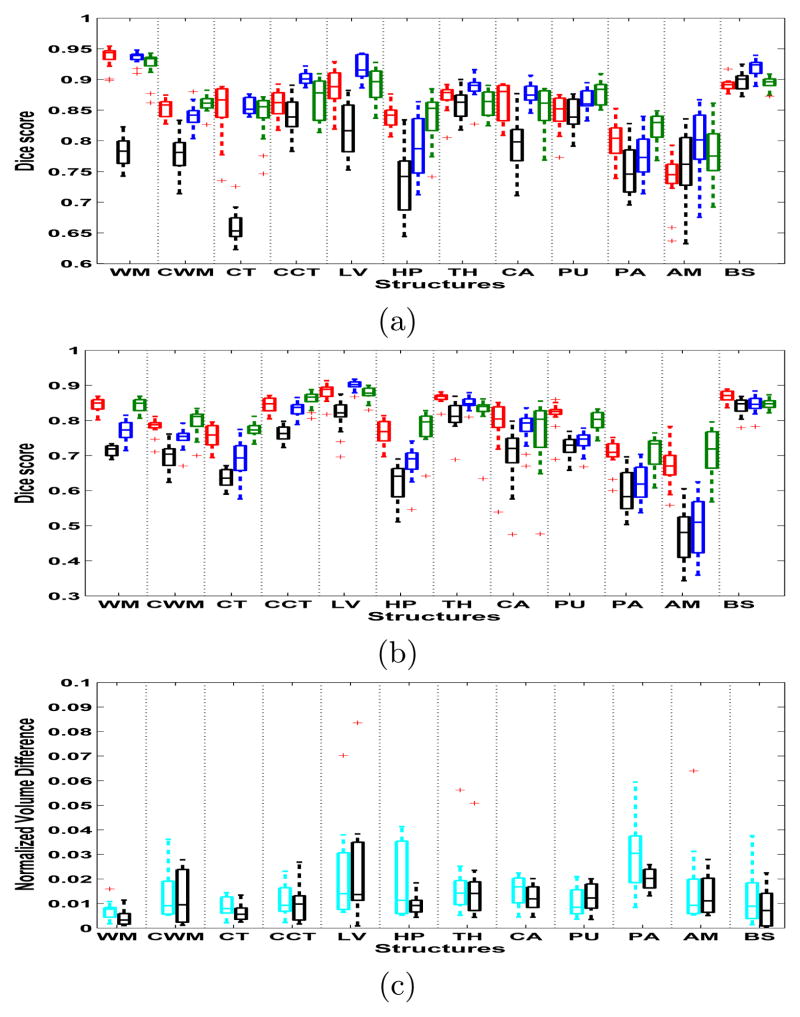
Figure 1(a) shows the Dice scores (averaged across left and right) between the automated and manual segmentations for the four methods on our first dataset, which consists of T1-weighted images of 13 subjects acquired with the same Siemens scanner and MPRAGE pulse sequence as the training data. Note that FreeSurfer, BrainFuse, and Majority Voting are specifically trained for this type of data, whereas the proposed method is not. It can be seen that each method gives quite accurate and comparable segmentations, except for majority voting, which clearly trails the other methods. The mean Dice score across these structures is 0.859 for the suggested method, 0.864 for BrainFuse, 0.853 for FreeSurfer, and 0.793 for Majority Voting. Table 1 shows the execution times for the methods. The experiments were run on a cluster where each node has two quad-core Xeon 5472 3.0GHz CPUs and 32GB of RAM. Only one core was used for the experiments. The multi-atlas methods require computationally heavy pair-wise registrations and thus have the longest run times, followed by FreeSurfer which is somewhat faster. The suggested method is clearly the fastest of the four, being approximately 26 times faster than BrainFuse or Majority Voting and 15 times faster than FreeSurfer. We note that our method is implemented using Matlab with the atlas deformation parts wrapped in C++, and in no way optimized for speed. To conclude our experiments on this dataset, table 2 shows how the number of training subjects in the atlas affects the mean segmentation accuracy of the proposed method, indicating that the method benefits from the availability of more training data.

Fig. 1.

(a) Dice scores of the first dataset (Siemens). FreeSurfer is red, BrainFuse blue, Majority Voting black, and the suggested method green. (b) Dice scores of the second data set (GE). (c) Normalized volume differences: multi-contrast data is cyan, and T1-only black. On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, and outliers are marked with a ‘+’.

Table 1.

Computational times for the four different methods.

Method	Comp. time(h)
BrainFuse	~ 17
Majority voting	~ 16
FreeSurfer	~ 9.5
Suggested method	~ 0.6

Table 2.

Average Dice score across all structures for the first (Siemens) dataset vs. number of training subjects.

Number of subjects	Mean Dice score
5	0.820
9	0.843
15	0.859

Figure 1(b) shows the Dice scores on our second dataset, which consists of 14 T1-weighted MR scans that were acquired with a 1.5T GE Signa scanner using a spoiled gradient recalled (SPGR) sequence (voxel size 0.9375×0.9375×1.5 mm³). The overall segmentation accuracy of each method is decreased compared to the Siemens data, which is likely due to poorer image contrast as a result of the different pulse sequence and a slightly lower image resolution. Both FreeSurfer and our method are able to sustain an overall accuracy of 0.798, while the accuracies of BrainFuse and Majority Voting decrease to 0.746 and 0.70 respectively. The relatively good performance of FreeSurfer, which is trained specifically on the Siemens image contrast, can be explained by its in-built renormalization procedure for T1 acquisitions, which applies a multi-linear atlas-image registration and a histogram matching step to update the class-conditional densities for each structure [12]. The multi-atlas methods, in contrast, directly incorporate the Siemens contrast in the segmentation process, and would likely benefit from a retuning of their parameters for this specific application. Note that the proposed method requires no renormalization or retuning to perform well.

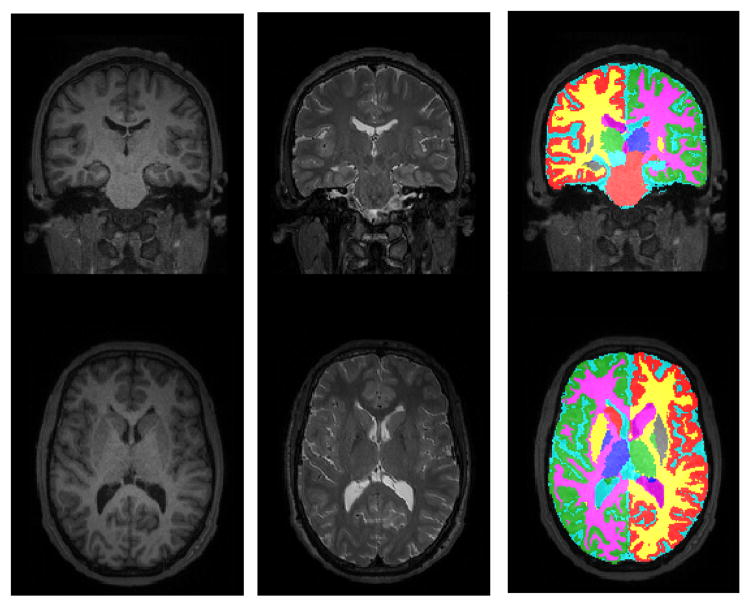
As a preliminary demonstration of the multi-contrast segmentation abilities of our method, figure 1(c) shows a measurement of volume differences between both uni-contrast (T1) and multi-contrast (T1 + T2) repeat scans of five individuals. For each subject, a multi-contrast scan was acquired with an identical Siemens 3T Tim Trio scanner at two different facilities, with a interval between the two scan sessions of maximum 3 months. The scans consist of a very fast (under 5 min total acquisition time) T1-weighted and bandwidth-matched T2-weighted image (multi-echo MPRAGE sequence for T1 and 3D T2-SPACE sequence for T2, voxel size 1.2×1.2×1.2 mm³). The volume difference in a structure was computed as the absolute difference between the volumes estimated at the two time points, normalized by the average of the volumes, both when only the T1-weighted image was used, and when T1 and T2 were used. The figure shows that our method seems to work as well on multi-contrast as on uni-contrast data, opening possibilities for simultaneous brain lesion segmentation in the future. An example segmentation of one of the multi-contrast scans is shown in figure 2.

Fig. 2.

An example of a multi-contrast segmentation generated by the proposed method.

5 Discussion

In this paper we proposed a method for whole brain parcellation using the type of generative parametric models typically used in tissue classification techniques. Comparisons with current state-of-the-art methods demonstrated excellent performance both within and across scanner platforms and pulse sequences, as well as a large computational advantage. Future work will concentrate on a more thorough validation of the method’s multi-contrast segmentation performance. We also plan to use other validation metrics beyond the mere spatial overlap used in this paper, such as volumetric and boundary distance measures.