Summary
The past decade has seen increasing use of the patch clamp technique on neutrophils and eosinophils. The main goal of these electrophysiological studies has been to elucidate the mechanisms underlying the phagocyte respiratory burst. NADPH oxidase activity, which defines the respiratory burst in granulocytes, is electrogenic because electrons from NADPH are transported across the cell membrane, where they reduce oxygen to form superoxide anion (O2−). This passage of electrons comprises an electrical current that would rapidly depolarize the membrane if the charge movement were not balanced by proton efflux. The patch clamp technique enables simultaneous recording of NADPH oxidase-generated electron current and H+ flux through the closely related H+ channel. Increasing evidence suggests that other ion channels may play crucial roles in degranulation, phagocytosis, and chemotaxis, highlighting the importance of electrophysiological studies to advance knowledge of granulocyte function. Several configurations of the patch clamp technique exist. Each has advantages and limitations that are discussed here. Meaningful measurements of ion channels cannot be achieved without an understanding of their fundamental properties. We describe the types of measurements that are necessary to characterize a particular ion channel.
Keywords: Proton current, ion channels, pH, zinc, phagocyte, respiratory burst, NADPH oxidase, electrophysiology, patch clamp
1. Introduction
Ion channels are a diverse group of proteins, representatives of which are found in all plasma membranes. Channels allow the regulated passage of ions across cell membranes, which otherwise have extremely low permeability to ions. Ion channels perform a wide variety of functions in a large number of cellular processes. The development of the voltage-clamp method revolutionized the study of ion channels in excitable cells such as neurons and muscle (1). The patch clamp technique (2) dramatically extended the power of the voltage-clamp approach by making it possible to record current through individual ion channels and to faithfully record currents in the membranes of even the smallest cells. Knowledge of the presence and functions of ion channels in non-excitable cells, such as epithelial cells and immune cells, has mushroomed from virtually nothing a quarter of a century ago to thousands of papers. Researchers now have the luxury of engaging in heated arguments about the functions performed in these cells by ion channels that were not even known to exist a few decades ago. The first patch clamp study on human granulocytes described nonselective cation channels activated by increased intracellular free calcium (3). Subsequently, the patch clamp technique has been used to explore proton, chloride, and potassium currents in neutrophils and eosinophils (4–8), as well as in many other nonexcitable cells.
The phagocyte respiratory burst results in the production of large amounts of O2− via NADPH oxidase activation (9) (see Note 1). The patch clamp technique has proven to be a powerful way to examine the phagocyte NADPH oxidase, and various configurations of this technique have been used to examine the respiratory burst measured as electron current in real time (10,11,5). These techniques have been used to examine the dependence of NADPH oxidase activity on temperature, pHo and pHi, NADPH concentration, and membrane voltage (12–15). The patch clamp approach also enables recording current through voltage-gated proton channels (H+ channels) during oxidase activation. Signaling pathways that regulate and coordinate the activity of NADPH oxidase and proton channels are an area of active investigation (see Note 2). A variety of evidence also implicates Cl− channels in a host of neutrophil functions such as volume regulation, phagocytosis, chemotaxis, and host defense (16–21). Thus, studies of granulocyte ion channels will undoubtedly continue to reveal the mechanisms of important physiological responses of these cells.
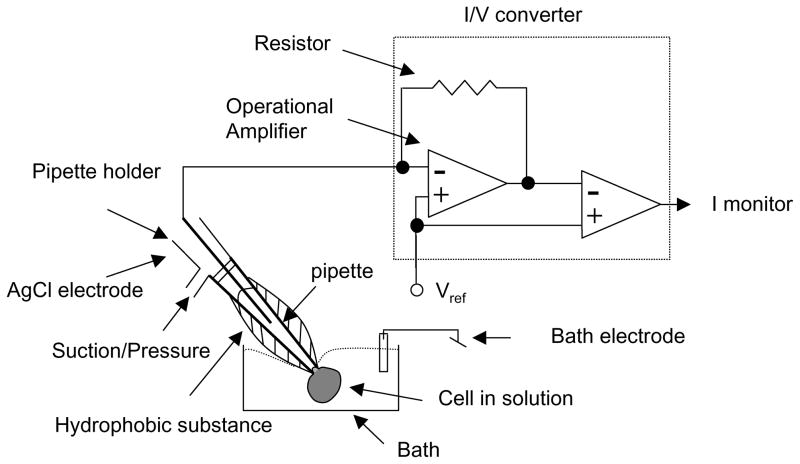
Although conceptually simple, the patch clamp technique is a complicated experimental method. Collecting meaningful data requires appropriate experimental design that is based on a genuine understanding of the properties of ion channels. We hope to introduce the reader to the patch clamp technique and provide an overview of the apparatus required, the general methods involved, and the application of this method to specific electrogenic transporters known to be present in human granulocytes. Figure 1 shows a schematic diagram of the patch clamp setup and circuit. The essence of the patch clamp technique is the formation of an electrically-tight seal between the tip of a pipette and the plasma membrane of a cell. The glass pipette is filled with a solution that may (or may not, depending on the purpose of the experiment) mimic a physiological solution and makes contact with the electrode, shown as a wire. Electrical currents that pass through the membrane are converted into voltage, which is amplified and sent to the data acquisition software (see Note 3).
Fig 1.
A simplified diagram of a cell being studied by a patch clamp is shown (80,75). A cell in a physiological bath solution is sealed to a glass pipette that is filled with a solution that makes contact with the electrode (usually a chlorided silver wire). The small currents due to ion movements across the membrane are measured as a voltage drop across a resistor. The glass pipette is coated with a hydrophobic substance to reduce the pipette/bath solution capacitance.
The patch clamp technique exists in several configurations that are distinguished by the size and orientation of the membrane through which current flow is measured. Whole-cell or perforated-patch configurations allow recording from the entire plasma membrane; in cell-attached or excised patch configurations, only the channels in a small patch of membrane are studied. In the perforated-patch configuration the cytosol is intact; in whole-cell configuration the cytoplasm is replaced by the pipette solution (see Note 4). The choice of solutions depends on the experimental goals. We give examples of solutions that have been used to study granulocytes, but more importantly, we discuss strategies of solution design (see Note 5).
2. Materials
2.1. Patch Clamp Equipment
The equipment comprising a patch clamp setup is listed below. Nearly all of the apparatus can be purchased commercially. It is beyond the scope of this chapter to discuss the relative merits of products of different manufacturers.
Inverted microscope
Perfusion bath and tubes
Pipette electrode headstage
Micromanipulators
Bath temperature control
Pressure/vacuum unit
Vibration isolation table
Faraday cage
Patch clamp amplifier
Computer with relevant data acquisition software
Interface between computer and patch clamp amplifier
Bath electrode
Patch pipette
2.2. Bath (Reference) Electrode
Silver wire
Epoxy resin
Agar powder
Glass or plastic tubing (3 mm bore)
Soldering iron and solder
Bleach or NaOCl
Hot plate
Syringe with wide-bore needle
2.3. Patch Pipette
Glass capillary tubes
Pipette puller
Sylgard 184® (Dow Corning Corp.)
Microscope
Heating filament attached to a power supply
Heat gun
Pipette solution (see next section)
2.4. Solutions
Patch clamp experiments involve exchanging solutions to vary the environment of the cell or membrane patch. The composition of the solutions is predicated on the specific channel of interest and the type of information that is to be extracted from the experiment. For example, the most fundamental measurement of a channel suspected of being K+ selective would be to measure Vrev in solutions with quite different K+ concentrations. Pipette solutions that are intended for whole-cell measurements are often made to approximate cytosolic constituents, with high [K+] and very low [Ca2+]i.
2.4.1. Proton Channel Solutions
To isolate proton currents from other conductances that might be present in the cell membrane, common cations and anions such as Na+, K+ and Cl− may be replaced with larger, less permeant ions such as tetramethylammonium (TMA+), tetraethylammonium (TEA+), or N-methyl-D-glucamine+ and methanesulfonate (MeSO3−), aspartate−, glutamate−, isethionate (HOCH2CH2SO3−), cyanate (CN−), or sulfate (SO42−) (22,7). Occasionally Cs+ is used as an impermeant cation (23), because Cs+ blocks many K+ channels.
Large H+ currents tend to deplete intracellular protonated buffer, increasing pHi. Because proton channels do not inactivate, any decay or “droop” of proton current during maintained depolarization indicates that depletion is occurring and that pHi is increasing significantly (24–26). To prevent or minimize such pHi changes, a large concentration of buffer is required in the pipette solution (27). Many studies have been done with ~100 mM buffer, and concentrations as high as 200 mM buffer with no other cations have been used (14) (see Note 6). Table 1 shows examples of solutions that have been used to study H+ channels (22,6,28).
Buffers should be chosen that have a pKa near the desired pH of the solution, in order to maximize the buffering power of the solution. One consideration is that many buffers bind divalent cations, which creates a problem because inhibition by Zn2+ or Cd2+ is a frequently studied characteristic of proton currents. Because tricine binds Zn2+ with high affinity (29), it removes Zn2+ from solution, so a different buffer would be preferred. Phosphate, a common constituent of solutions that mimic physiological ones, also binds zinc avidly (30). The metal binding constants for several buffers were measured by Cherny & DeCoursey (29).
Examples of buffers that have been used in solutions spanning a wide range of pH are as follows [numbers in brackets are pKa at 20°C]: Homopiperazine-N,N’-bis-(2-ethanesulfonic acid (Homopipes) [4.61]; 2-(N-Morpholino) ethanesulfonic acid (MES) [6.15]; Bis-2-(hydroxyethyl)imino-tris(hydroxymethyl)methane (Bis Tris) [6.5]; Piperazine-N-N-bis(2-ethanesulfonic acid (PIPES) [6.7]; N-N-bis(Hydroxyethyl)-2-aminosulfonic acid (BES) [7.1]; N-(2-hydroxyethyl)-piperazine-N-(2-ethanesulfonic acid) (HEPES) [7.55]; Tris-(hydroxymethyl) amino methanehydrochloride (Tris) [8.3]; 2-(N-cyclohexamino)-ethane sulfonic acid (CHES) [9.3]; and 3-(cyclohexamino)-1-propanesulfonic acid (CAPS) [10.37].
Table 1.
Examples of solutions used for proton channel characterization
| Pipette Solutions | ||||||||
|---|---|---|---|---|---|---|---|---|
| pH | MeSO3 | CsCl | HCl | Base | EGTA | CaCl2 | MgCl2 | Buffer |
| 5.5 | 96 | 80 TMA | 1 | 2 | 100 MES | |||
| 5.5 | 70 | 10 | TEA | 2 | 1 | 100 MES | ||
| 6 | 80 | 130 TMA | 1 | 2 | 100 MES | |||
| 6 | 70 | 10 | TEA | 2 | 1 | 100 MES | ||
| 6.5 | 128 | 75 TMA | 1 | 2 | 100 BIS-TRIS | |||
| 6.5 | 70 | 10 | TEA | 2 | 1 | 100 PIPES | ||
| 7 | 128 | 115 TMA | 1 | 2 | 100 HEPES | |||
| 7 | 70 | 10 | TEA | 2 | 1 | 100 HEPES | ||
| 7.5 | 75 | 50 CsOH | 100 HEPES | |||||
| 8 | 75 | 44 CsOH | 100 TRIS | |||||
| Bath Solutions | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| pH | MeSO3 | CsCl | HCl | Base | BAPTA | EGTA | CaCl2 | MgCl2 | Buffer |
| 5.5 | 96 | 80 TMA | 1 | 2 | 100 MES | ||||
| 6 | 70 | 10 | TEA | 1 | 100 MES | ||||
| 6.5 | 70 | 10 | TEA | 5 | 2 | 100 PIPES | |||
| 6.5 | 35 | 132 CsOH | 10 | 100 PIPES | |||||
| 7 | 70 | 10 | TEA | 5 | 2 | 100 HEPES | |||
| 7.2 | 75 | 30 CsOH | 10 | 11.4 | 100 HEPES | ||||
The table lists examples of solutions used for pipette and bath solutions when recording proton currents in whole cell configuration. Numbers indicate concentration in mM. Where no numbers are given the base was used to titrate the solution to the correct pH.
2.4.2. Potassium Channel Solutions
Solutions for studying K+ channels usually include K+. [K+] can be varied, while maintaining constant ionic strength and osmolality, by replacing K+ with Na+. Tables 2 shows solutions that were used to study K+ channels in granulocytes (31).
Table 2.
Examples of solutions used for K+ channel characterization.
| Pipette Solutions | |||||||
|---|---|---|---|---|---|---|---|
| pH | NaCl | KCl | CaCl2 | MgCl2 | HEPES | Glucose | NaOH |
| 7 | 137.6 | 5 | 2 | 1 | 10 | 6 | 2.4 |
| 7 | 126.6 | 16 | 2 | 1 | 10 | 6 | 2.4 |
| 7 | 117.6 | 25 | 2 | 1 | 10 | 6 | 2.4 |
| 7 | 42.6 | 100 | 2 | 1 | 10 | 6 | 2.4 |
| 7 | 2.6 | 140 | 2 | 1 | 10 | 6 | 2.4 |
| Bath Solutions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| pH | NaCl | KCl | CaCl2 | MgCl2 | Buffer | BAPTA | EDTA | MgATP | Na2ATP | HCL | KOH |
| 7 | 5 | 97.6 | 0.7 | 10 HEPES | 10 | 1 | 42.6 | ||||
| 7 | 3 | 97.6 | 1.6 | 10 HEPES | 10 | 10 | 1 | 2 | 41.5 | ||
| 5.5 | 102 | 0.06 | 0.69 | 10 MES | 10 | 2.5 | 3.6 | 38 | |||
| 8 | 4 | 97.2 | 0.83 | 0.76 | 10 Taps | 10 | 0.5 | 42.6 | |||
The table lists examples of solutions used for pipette and bath solutions when recording proton currents in whole cell configuration. Numbers indicate concentration in mM.
2.4.3 Chloride Channel Solutions
It is possible to replace Cl− with larger, less permeant ions. Table 3 shows examples of bath and pipette solutions that have been used to study Cl− channels (22,7).
Table 3.
Examples of solutions used for K+ channel characterization.
| Pipette Solutions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| pH | NaCl | Na2SO4 | Na-Isethionate | TMA Cl | KCl | CaCl2 | MgCl2 | Mannitol | Base | Buffer |
| 7 | 145 | 2 | 20 BES | |||||||
| 7.2 | 140 | 5 | 2 | 2 | 10 HEPES | |||||
| 7.2 | 140 | 2 | 2 | 10 HEPES | ||||||
| 7.4 | 150 | 5 | 2 | 1 | NaOH | 10 HEPES | ||||
| 7.4 | 150 | 5 | 2 | 1 | 75 | NaOH | 10 HEPES | |||
| Bath Solutions | |||||||
|---|---|---|---|---|---|---|---|
| pH | TMA MeSO3 | NaCl | K-Asp | KCl | EGTA | MgCl2 | Buffer |
| 5.5 | 96 | 1 | 2 | 100 MES | |||
| 7.2 | 5 | 140 | 0.2 | 2 | 10 HEPES | ||
| 7.2 | 5 | 110 | 30 | 0.2 | 2 | 10 HEPES | |
The tables list examples of pipette and bath solutions used for recording proton currents in whole cell configuration. Numbers indicate concentration in mM. Where no numbers are given the base was used to titrate the solution to the correct pH.
2.4.4. Perforated Patch Solutions
Perforated patch recordings are achieved when a pore-forming antibiotic, such as amphotericin or nystatin, is included in the pipette solution. The antibiotic forms pores that allow only small monovalent ions (e.g., Na+, K+, Cl−, or NH4+) to carry current between the pipette and the cell. In order to control pHi, a proton donor/acceptor system such as an ammonium or methylamine gradient can be used (32) (see Note 7). Table 4 shows solutions that were used to change the pH symmetrically and asymmetrically (12). The pH gradient can also be increased in increments by lowering [NH4+]o from 50 mM to 15, 9, 3, and 1 mM (32), although the lowest [NH4+]o controls pHi less effectively (10,32).
Table 4.
Examples of solutions used for perforated patch recordings.
| Solution | TMA MESO3 | (NH4)2SO4 | MgCl2 | CaCl2 | EGTA | Buffer | pH | pHi |
|---|---|---|---|---|---|---|---|---|
| pipette solution | 100 | 25 | 2 | 1.5 | 1 | BES 10 | 7 | N/A |
| Bath 1 | 100 | 25 | 2 | 1.5 | 1 | MES 10 | 5.5 | 5.5 |
| Bath 2 | 100 | 25 | 2 | 1.5 | 1 | MES 10 | 6.5 | 6.5 |
| Bath 3 | 100 | 25 | 2 | 1.5 | 1 | BES 10 | 7.5 | 7.5 |
| Bath 4 | 100 | 25 | 2 | 1.5 | 1 | Tricine 10 | 8.5 | 8.5 |
| Bath 5 | 100 | 1.25 | 2 | 1.5 | 1 | BES 10 | 7 | 6 |
| Bath 6 | 100 | 1.25 | 2 | 1.5 | 1 | Tricine 10 | 8.5 | 7.5 |
| Bath 7 | 100 | 1.25 | 2 | 1.5 | 1 | HEPES | 7 | 6 |
The table lists examples of solutions used for pipette and bath solutions when recording proton currents in perforated patch configuration. Numbers indicate concentration in mM. The pipette solution is the same for all bath solutions. pHi is calculated from Equation 8 (see Note 7).
3. Methods
3.1. Patch Clamp Set-up
In a patch clamp experiment, the pipette is positioned against the cell membrane, and suction is applied to the inside of the pipette until a seal of a very high resistance forms between the membrane and the glass. Hamill et al. (2) called the seal a “gigaohm seal” or “giga seal,” because the resistance between the cell membrane and pipette is preferably in the gigaohm range. “Gigohm” is an accepted alternative spelling. The pipette usually contains a physiological salt solution to mimic the microenvironment of the cell membrane with a wire electrode immersed in the pipette solution.
The typical patch clamp setup consists of an inverted microscope with a small bath placed on the stage. The inverted microscope allows room for the bath, pipette electrode, electrode manipulators, perfusion apparatus, and temperature controller/detector. The bath has a discontinuous solution inlet and outlet to enable exchange of bath solutions. It is impossible to perform normal patch-clamp measurements without exchanging bath solutions. A continuous perfusion system forms a conduction pathway that can act as an antenna that introduces a great deal of noise. A discontinuous perfusion system has a junction where the solution in the chamber does not make contact with fluid in the tubing to avoid this noise source.
Patch-clamp measurements are often performed at “room temperature” which may vary by a few degrees or more dramatically, depending on the building. Both proton and electron currents have unusually strong temperature dependence (33,34,13); consequently, small temperature changes produce dramatic effects. For example, evaporative heat loss from a shallow chamber may lower the temperature in the bath, which will transiently increase when a new solution at room temperature is introduced. As a result, proton currents may transiently increase every time the bath solution is exchanged. Some designs for temperature control involve placing the chamber on a U-shaped piece of thermally conductive metal like copper, with Peltier devices sandwiched between the copper and a metal heat sink (35). When this arrangement is used, care must be taken when decreasing the temperature, because contraction of the U-shaped metal lifts the chamber relative to the pipette, smashing it. Before lowering the temperature, it is advisable to lift the pipette and cell well above the bottom of the chamber.
A reference electrode is placed in the bath and the pipette is attached to micromanipulators that enable positioning the pipette in the bath. Fine movements are required to target the pipette accurately. Both hydraulic (manually controlled) and motorized micromanipulators may be used. The main requirement besides fine control is absence of drift. Cells are small and drift of cellular dimensions can abruptly end an experiment by pulling the pipette away from the cell or by smashing the pipette against the chamber.
The microscope, electrodes, and manipulators are placed on a vibration isolation table to prevent electrode movement. Vibrations from the floor can cause movement artifacts that can introduce noise or break the pipette tip. A commonly used vibration isolation table is an air table in which the legs are supported on pressurized air cylinders. Other tables are made of large, heavy slabs of marble or granite and are placed in room corners to minimize floor vibration. Locating the table in a cellar can also reduce movement artifacts.
The signal from the pipette electrode is amplified by the head-stage amplifier, low-pass filtered and sent to an analogue to digital (A/D) converter, and finally to the computer where it is recognized by data acquisition software. Extraneous electrical noise from power cords to the microscope light, head-stage, electrical thermometer, and micromanipulator motors can be shielded by surrounding them with braided wire. A Faraday cage (a wire screen cage) surrounding the entire microscope or just the microscope stage may be necessary to suppress electrical noise from overhead lights and other environmental electrical sources. Due to the sensitivity of the headstage amplifier, it is important that all metal near the electrode be connected to ground to prevent the detection of line frequencies. It is important to avoid ground loops. Proper grounding is both important and difficult to achieve.
3.2. Electrode Preparation
The electrodes require manual preparation. The bath (reference) electrode can be used for long periods of time, but the patch pipette should be made immediately before use.
3.2.1. Bath (Reference Electrode)
The bath electrode provides the reference point from which voltage is measured. It is important that at each point in the recording apparatus where dissimilar materials meet, at least one current carrier can move freely in each direction. If this is not the case, electrode polarization may occur, in which large sustained currents decay because an opposing electromotive force develops at the offending interface. The most commonly used electrode in patch clamping is the silver-silver chloride electrode, made of a silver wire coated with AgCl. Current flowing into the solution or agar bridge is carried by Cl−. A change in the bath chloride concentration will result in a voltage offset due to a liquid junction potential. Using an agar bridge between the AgCl and the bath solution keeps the concentration of chloride constant near the electrode and minimizes diffusion of the solution in the bridge into the chamber. Because patch-clamp chambers often have small volume (e.g., < 1 mL), the use of saturated KCl in the bridge (typically used in of conventional microelectrodes) is avoided to prevent diffusion of these ions into the bath, which would change their concentrations. Bath electrodes are available for purchase but are often constructed on-site.
Cut the silver wire to a length of about 1 ½ inches and solder it to the end of the wire intended to connect the bath to the setup.
Immerse the silver wire in bleach for several hr or overnight. (see Note 8).
Cut a piece of glass or plastic tubing ~1–2 inches in length, depending on its arrangement in the chamber, and epoxy the tube over the chlorided silver wire. Ensure that the epoxy completely encases the solder and any exposed, un-chlorided silver wire. The tube should extend past the wire by ½ inch.
Heat 4% agar/Ringer’s solution (w/v) in a beaker until the solution begins to boil, then remove from heat.
While the Ringer/agar solution is still hot, take up the solution with the syringe and inject the agar solution into the tube containing the silver wire.
Allow the electrode to cool and the agar to set.
When the electrode is not in use, it should be immersed in the solution used in the bridge and connected to ground.
3.2.2. Patch Pipette
The glass patch pipette contains an electrode, commonly a chlorided silver wire that contacts the pipette solution. The pipette is manufactured using a pipette puller that produces a tip opening a few microns or less in diameter. Commercially available pipette-pulling instruments heat a filament that surrounds the pipette while pulling on either end. The filament may be alternately heated and cooled by an adjustable computer program until the capillary draws out and breaks at the center. The pipette is heat polished to optimize its shape and resistance (36). Lower tip resistance increases the fidelity of recording from whole cells (see Note 9). For small cells with currents of a few hundred picoamperes, a pipette resistance of 2–10 MΩ is typical and reasonable. Cells with larger currents require lower resistance pipettes. Conversely, for recording tiny currents or a small number of channels in excised patches, the tip resistance is not critical (see Note 10). Pipettes are best made immediately before use and should not be kept overnight.
Place the glass capillary tube (see Note 11) in the micropipette puller, and make two pipettes.
Coat the pipette tip is coated with Sylgard, approaching very near the tip. Cure the Sylgard by heating with a heat gun.
Place the pipette on a microscope stage near a heating filament, and pass current through the filament to melt the pipette tip. The current can be adjusted empirically with a variable transformer. This process is observed through the microscope.
Switch off the current through the filament when the tip is rounded and the bore has narrowed to the desired diameter (see Note 12). If the microscope optics permits seeing the tip opening directly, direct observation is the easiest way to judge the progress of heat-polishing (see Note 13).
Back-fill the pipette with a pipette solution, taking care to ensure that no air bubbles are present in the tip of the pipette. Tiny bubbles near the tip can be seen with a dissecting microscope. Bubbles can be dislodged by flicking the pipette shank with a fingertip, or by rubbing the serrated surface of a forceps against the shank of the pipette.
Mount the pipette in the pipette holder, place over the chlorided silver wire electrode, and tighten. When placed in the bath solution, the pipette resistance can be measured.
3.3. Seal Formation
The essence of the patch clamp technique is formation of a high-resistance seal (usually 10–100 GΩ or more) between the cell membrane and the pipette tip. Under optimal conditions, seals can reach the TΩ (1012 Ω) range (37). This high resistance seal allows recordings with very little background noise and small leak currents (i.e., current that flows from the pipette into the bath through the seal, rather than through the membrane). The process of positioning the pipette against the cell with the micromanipulators is similar for all adherent cells but differs when the cells are non-adherent. Filtering the pipette and bath solutions (e.g., at 0.2 μm) may improve seal formation.
3.3.1. Adherent Cells
Mount the pipette in the electrode-holder taking care not to scratch the chlorided surface of the wire and tighten the pipette in place.
Apply positive pressure to the pipette interior and lower the pipette tip into the bath solution.
After the pipette tip enters the bath solution, adjust the offset current to zero.
Position the pipette directly above the cell and lower the pipette toward the cell.
Monitor the access resistance of the pipette by observing the current produced by a small voltage pulse.
When the pipette is near the cell, lower the pipette carefully (a) until the cell is slightly deformed by the pressure of the pipette or (b) until the pipette access resistance begins to increase, and then immediately apply gentle negative pressure (~2–5 inches of water).
3.3.2. Non-Adherent Cells
Perform steps 1–4 as in the method of adherent cells
When the pipette tip is near the cell, reduce the positive pressure to avoid pushing (or “blowing”) the cell away and move the pipette tip near the cell.
Apply negative pressure and suck the cell onto the pipette.
It may not be possible to avoid pushing the cell away by reducing the positive pressure. If this is the case, the pipette can be aligned slightly to the side of the cell. Immediately after moving the pipette in line with the cell, apply negative pressure to pull the cell onto the pipette tip.
3.4. Patch-Clamp Configurations
There are several patch clamp configurations: (1) cell attached patch, (2) inside-out patch, (3) whole cell, (4) outside-out patch, and (5) perforated patch (Fig. 2). Each configuration has advantages and disadvantages that should be considered when deciding which is appropriate for the desired experiment.
Fig. 2.
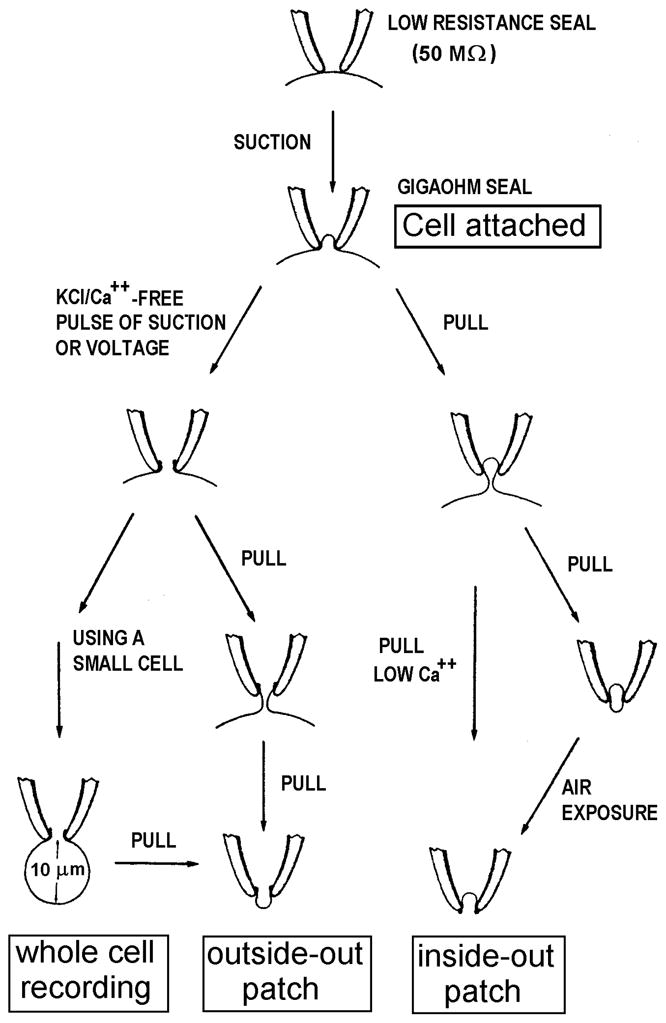
The formation of the four main patch-clamp configurations is illustrated. See text for details. From reference (2).
3.4.1. Cell-Attached Patch
After the pipette has contacted the cell and a GΩ seal has been achieved, the configuration is cell-attached patch.
The currents recorded will reflect only the ion channels in the patch of membrane that spans the tip of the pipette. Single channel events may be detected, because the patch of membrane is very small.
Changing the bath solution will not directly affect channels in the patch, because the cell is still intact. Also because the cell is intact, there is very limited control over the conditions in the cytosol; thus, the pH, ionic composition, and membrane potential will be uncontrolled and unknown.
If the cell has a high membrane resistance, current flowing through a single open channel in the patch may change the membrane potential of the cell substantially, producing a decaying unitary current (38).
Because the pipette is extracellular, applied voltages (and recorded currents) need to be inverted to follow the convention of defining voltage as that inside the cell relative to that outside. The actual membrane potential will be the sum of the command potential and the membrane potential of the cell, which is not known.
Sometimes cells are bathed in an isotonic K+ solution with the intent of clamping the membrane potential near 0 mV, on the assumption that most cells have K+ channels that will perform this function. Most, but not all cells have K+ channels. The patch potential is then simply the inverse of the voltage applied to the pipette.
3.4.2. Inside Out patch
This configuration is achieved by pulling the pipette away from the cell after forming a cell-attached patch in the case of adherent cells, or by lifting the pipette briefly out of the bath solution for non-adherent cells.
It is best to excise the patch into solutions low in Ca2+, because Ca2+ tends to “repair” membranes, producing a sealed vesicle on the end of the pipette, which is useless for recording.
As with the cell-attached patch, an inside-out patch permits recording single channels. The configuration allows complete control over the patch potential and the internal (bath) and external (pipette) solutions.
The bath solution (corresponding with the intracellular solution) can be exchanged easily during experiments.
3.4.3. Whole Cell
To form whole cell configuration from the cell-attached patch configuration, the membrane across the tip of the pipette is ruptured by suction or a brief pulse of high voltage, allowing access to the entire membrane of the cell.
Sometimes it is difficult to rupture the patch. Attaching a large (e.g., 50 mL) syringe to the tubing connected to the pipette interior and rapidly withdrawing the plunger is often effective. After membrane rupture, the pipette solution diffuses rapidly into the cell.
Whole-cell configuration enables recording macroscopic whole-cell currents that reflect all of the channels in the cell, with a defined internal solution. However, in this configuration the cytosol is removed, which may interrupt second messenger pathways that involve diffusible or unknown elements.
3.4.4. Outside-out patch
Outside-out patch configuration occurs when the pipette is pulled away from the cell after forming the whole-cell configuration.
Non-adherent cells tend to follow the pipette, but this may be remedied by pulling the cell away using a second pipette. The membrane ideally reforms across the tip of the pipette with the extracellular surface facing the bath solution.
This configuration is analogous to inside-out configuration, but with the opposite orientation, and has similar benefits and limitations, except that the external solution is readily varied.
The true orientation of the membrane in an excised patch can be verified readily if the membrane contains recognizable channels with known properties, such as voltage-gated channels. A depolarization-activated channel should open upon depolarization in an outside-out patch. This property may seem trivial, but in the real world, strange things do occasionally happen.
3.4.5. Perforated Patch
This configuration is topologically like the cell-attached patch, except the pipette solution contains a pore-forming molecule, such as ATP (39), or an antibiotic like amphotericin (~1 mg/mL) (40) or nystatin (41) that perforates the membrane and allows small ions to permeate. Larger pores that allow entry of larger molecules into the cell are formed by β-escin (42).
Usually the tip of the pipette is dipped into solution lacking the pore-forming molecule to fill the tip before back-filling the pipette. This enables the seal to be formed before the membrane becomes perforated.
The perforated-patch configuration allows electrical access to the cell, but prevents the loss of proteins and large molecules from the cytosol. One can record from all channels in the cell membrane, with the advantage that many signaling pathways remain intact (41,39).
The perforated-patch configuration permits activation of NADPH oxidase in phagocytes (10); in many other cells it prevents the run-down of ionic currents that occurs in conventional whole-cell configuration (43,44).
One problem with the perforated-patch configuration is that the patch may rupture spontaneously, producing a whole-cell configuration (45,13,46).
3.5. Electron Current Recordings
A useful application of the patch clamp technique is to record plasma membrane electron current (Ie) produced by the NADPH oxidase (5). The enzyme is electrogenic and is present at sufficiently large numbers in the plasma membranes of several human phagocytes that it passes currents large enough to be recorded (2–3 pA in neutrophils, 6–15 pA in eosinophils). Electron current can be measured in the perforated-patch configuration (10) or in excised, inside-out patches (11).
3.5.1. Recording Ie in Whole Cells
Schrenzel et al. (5) first reported Ie in phagocytes studied in the whole cell configuration. Eosinophils were patched with a pipette solution consisting of 76 mM CsCl, 50 mM CsOH, 50 mM HEPES, pH 7.6, 10 mM TEACl, 1 mM MgCl2 and 8 mM NADPH. The bath solution mimicked the pipette solution but lacked ATP or NADPH and was at pH 7.1. Under these conditions, the authors reported spontaneous appearance of Ie upon forming whole-cell configuration. The appearance of Ie without agonists suggests that these cells were activated spontaneously, perhaps by adhesion. In later experiments, Ie was observed with 25 μM GTPγs or 5 μM free Ca2+ in the pipette solution (45).
3.5.2. Ie in Perforated Patch
The perforated patch configuration is highly suited to recording electron current. It is possible to record from the same cell before and after stimulation so that each cell is its own control. It appears to be beneficial to have glucose (1 mg/mL) in the bath solution to provide an energy source for the cells. Electron current can be recorded at −40 or −60 mV, voltages sufficiently negative to prevent activation of proton channels (at symmetrical pH) that would obscure the Ie.
After forming a giga-seal, access to the cell increases over time as the amphotericin forms pores in the patch membrane. Depolarizing test pulses that activate H+ current can be used to monitor the access resistance. As electrical access improves, the currents grow larger (see Note 14).
Begin recording when the H+ current is stable.
The most reliable activator of NADPH oxidase is phorbol myristate acetate (PMA), which elicits Ie in almost all cells. (see Note 15).
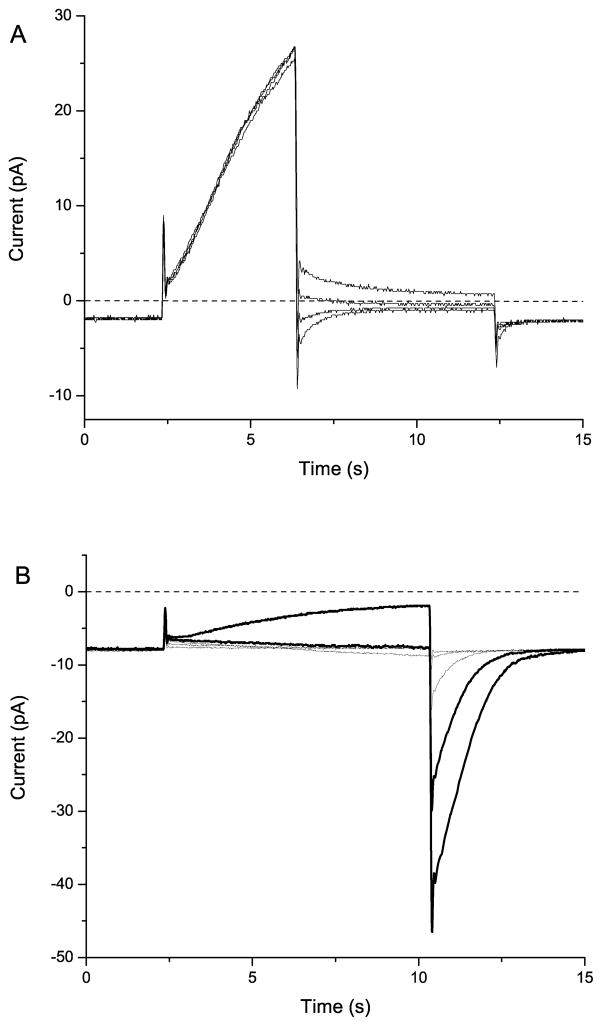
PMA produces a downward deflection of the holding current (Ihold) that usually stabilizes after a few minutes and persists for tens of minutes (Fig. 3).
If the increase in Ihold is due to NADPH oxidase activity, it should be sensitive to diphenylene iodonium (DPI), a well-known inhibitor of the NADPH oxidase (47). If a high concentration of DPI inhibits the presumed Ie only partially, then the DPI-insensitive current is likely due to appearance of a leak conductance.
During perforated patch recording, the patch sometimes ruptures spontaneously, producing whole cell configuration. When this occurs, Ie vanishes rapidly (13), perhaps due to the diffusion of essential components from the cell into the pipette. Ie decreases several times faster when the patch is ruptured (τ = 5.6 s) than when Ie is inhibited by DPI (τ = 25.5 s) (13). (see Note 16).
Fig. 3.
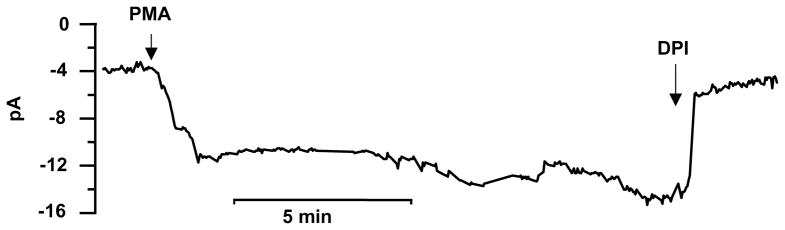
A record from a human eosinophil in the perforated-patch configuration. The holding current is −60 mV. Pipette solution was 100 mM KMeSO3, 1 mM MgCl2, 1mM EGTA, 25 mM (NH4)2SO4, 10 BES and 1 mg/mL amphotericin at pH 7. The bath solution was 100 mM TMAMeSO3, 1 mM EGTA, 2 mM MgCl2, 1.5 CaCl2, 25 mM (NH4)2SO4, and 10 mM BES pH 7. At the times indicated by the arrows, the cell was stimulated with 60 nM PMA and Ie was inhibited by 12 μM DPI.
3.5.3. Ie in Inside-Out Patch
Electron current can be recorded in the inside-out patch configuration (11). A patch of membrane is excised from a stimulated granulocyte in which active oxidase complexes are already assembled. Exposing the internal surface of the patch membrane to NADPH enables electron flow across the membrane through the previously activated NADPH oxidase complexes (see Figure 4 for a representative experiment). (see Note 17).
Fig. 4.
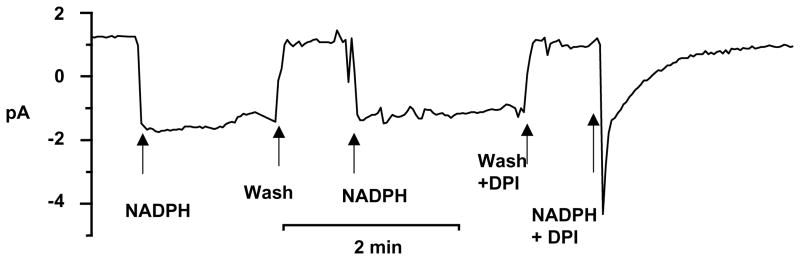
Ie in an inside-out patch of membrane from a human eosinophil at −60 mV. The cell was stimulated with 60 nM PMA in cell-attached patch configuration 5 min before the patch was excised. Pipette solution was 200 mM HEPES, 2 mM MgCl, 2 mM EGTA, titrated to pH 7.5 with TMAMeSO3. The bath solution was the same as the pipette solution with 50 μM GTPγS and 3 mM MgATP added. The arrows indicate the addition of 2.5 mM NADPH or 12 μM DPI.
Patch a granulocyte in the cell-attached patch configuration in Ringer solution (pH 7.4) containing 50 μM GTPγS and 3 mM ATP.
Stimulate the cell by adding 60 nM PMA to the bath solution.
Lift the pipette briefly out of the bath solution to produce an inside-out patch, then quickly replace the pipette in the bath.
Add NADPH to the bath to elicit Ie.
3.6. Ion Channel Recording
3.6.1. Optimizing Conditions to Record Specific Types of Currents
If more than one type of ion channel or electrogenic transporter is present in a cell, as is almost always the case, then the currents that are recorded will be an additive mixture of the various component currents.
To focus on one particular type of channel, the recording conditions may be adjusted to maximize the conductance of interest and to eliminate extraneous currents. To record ionic currents, the permeant ion must be present in appropriate concentrations. To record K+ currents, K+ must be present, although most K+ channels are also permeable to Rb+, NH4+, and usually to a much smaller extent, other cations. To study currents carried by ions that are normally present at small concentrations, such as Ca2+ or H+, it may be helpful to increase their concentration.
-
Eliminating extraneous currents can be achieved by several approaches:
Eliminate all ions permeant through a channel. This may be difficult for channels that are not very selective. For example, many anion channels are notoriously promiscuous, allowing large anions, such as aspartate− or methanesulfonate−, to permeate. Usually, replacing small physiological ions with larger ions of the same sign is sufficient to reduce the current. (see Note 18).
if using impermeant ions is not possible, inhibitors can be used. These should be as specific as possible, so that they do not affect the currents of interest. Many channels have potent and specific inhibitors, often derived from venoms or toxins. (see Note 19).
In some cases, the activation of a conductance can be prevented. To prevent activation of Ca2+-activated channels, intracellular free Ca2+ [Ca2+]i can be buffered to low levels. Voltage-gated channels can be prevented from opening simply by avoiding the voltage range that activates the channels. For example, electron current can be recorded without interference from proton channels at −60 mV, because at symmetrical pH, proton channels do not open at that voltage. Most cells, including neutrophils (7), have volume-regulated anion channels that are activated when osmotic imbalance occurs. Typically, hypotonic solutions cause cell swelling, which activates stretch- or swelling-activated channels. When one first ruptures the membrane patch to begin whole-cell recording, there is often a transient osmotic imbalance thought to be caused by the higher mobility of small anions in the pipette solution than that of the large anionic proteins in the cytoplasm. This diffusional imbalance produces both a Donnan potential (38) and transient activation of stretch-activated anion currents in neutrophils (4,7). These stretch-gated currents usually go away after a few minutes (22).
3.6.2. Requirements for Complete Characterization of an Ion Channel
3.6.2.1. Selectivity-the Reversal Potential Must be Measured!
The selectivity of an ion channel is so important that channels are named for the ions they conduct. Potassium channels are selectively permeable to K+, proton channels are selective for H+, and so forth.
-
Selectivity can be determined only by studying the channel in various ionic conditions to determine which ions permeate. Permeability can be evaluated in two ways.
Create conditions in which there is only a single ionic species (of one sign) on one side of the membrane, and determine whether that ion carries current in the correct direction. Although this approach seems straightforward, a prerequisite is a reliable method to determine whether the current is permeating the channel of interest. If the channel is voltage- and time-dependent, then the kinetics of the currents can be presumed to define the conductance, otherwise using blockers may be necessary. Identification of a channel by pharmacology alone is unacceptable for several reasons. First, truly specific inhibitors are rare. Second, pharmacology can be messy. Some drugs have multiple effects, such as changing the pH or altering metabolism. If the inhibitors are irreversible, or if they act slowly, then positive identification becomes tricky. For example, one published study incorrectly identified volume-regulated anion currents as Na+ currents. The putative Na+ currents consistently ran down after addition of an inhibitor, and the run-down was mistaken for slow and irreversible block.
Selectivity is best determined by measuring the reversal potential, Vrev, and varying the species or concentration of ions in the bath. This approach can give precise information about relative permeability of a channel when many ions are measurably permeant. Addition or removal of impermeant ions should not change Vrev, but changes in the concentration of a permeant ion should. The Vrev of voltage-gated proton currents does not change when the bath is changed among Cs+, K+, TMA+, etc., although changes of a few millivolts are measured in some solutions which disappear when one corrects for liquid junction potentials. If one encounters a channel that indiscriminately conducts all cations or all anions (but does discriminate between ions of opposite charge), then the charge of the permeant ion can be identified by decreasing the ionic strength, replacing ions with uncharged molecules like glucose to maintain the osmolarity (48,49). Sometimes ions that are not permeant indirectly produce changes in Vrev that could be mistaken as an indication of permeability. For example, when the predominant cation in the bath solution is Na+ or Li+, compared with other cations, the measured Vrev of H+ currents shifts in a positive direction (50). Although such a shift would be expected if Na+ were permeant, it is prevented by inhibiting Na+/H+-antiport and therefore is due to increased pHi resulting from exchange of extracellular Na+ for intracellular H+ (50).
How does one measure Vrev? The answer depends on the situation. One principle is to recall that the idea is to determine the reversal potential of a conductance that presumably is due to a population of identical channels. However, all voltage-clamp data includes extraneous conductances that are observed as “leak” currents. If the conductance of interest is, for example, a non-voltage-gated (i.e., the conductance is “on” at all voltages) Ca2+-activated K+ conductance, then one might simply measure the voltage at which the current is zero to estimate Vrev. However, the measured Vrev will be incorrect unless the leak is corrected. Because leak conductances usually reverse near 0 mV, their effect is to decrease the absolute value of the measured Vrev. The larger the leak, the larger the error will be. If a specific inhibitor of the conductance of interest exists, one can subtract the current measured in the presence of blocker from that in its absence. The blocker-subtracted currents should reflect the properties of the conductance of interest. Two dangers exist. First, some drugs block channels in a voltage-dependent manner. In this case, the subtraction will give erroneous results unless block is essentially complete at all voltages. Second, the subtraction procedure introduces errors, because both the “leak’ and conductance of interest may change with time, compromising the subtraction. One must recognize these limitations and accept that the results may have some error. One must be especially careful if two large numbers are subtracted to give a small result. If such a subtraction procedure results in Vrev values that follow the Nernst prediction within 0.1 mV, then one must be extremely suspicious that wish-fulfillment has entered into the data analysis process.
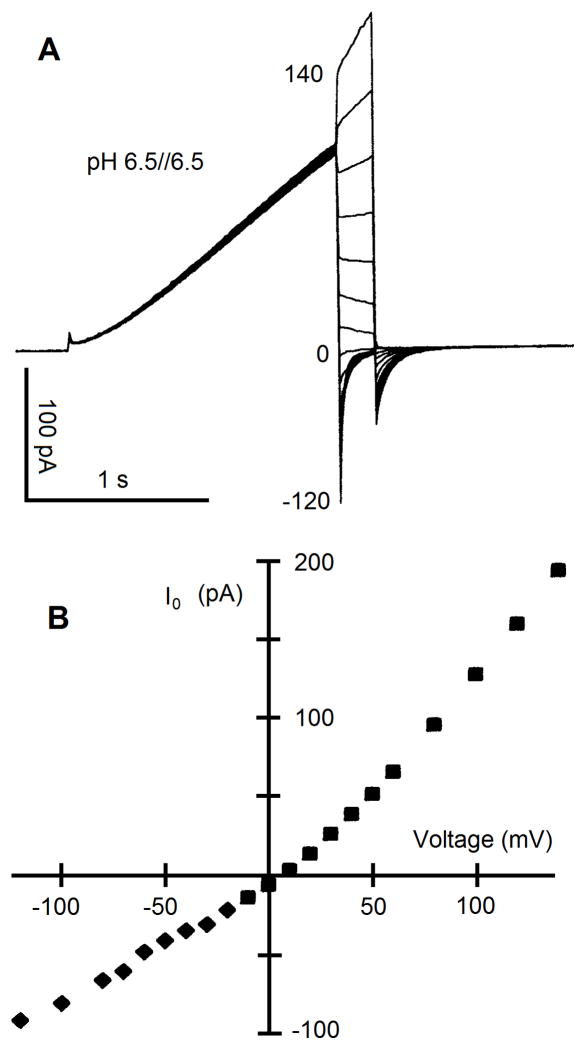
It is relatively easy to measure Vrev for channels that are voltage- and time-dependent. The two situations that may be encountered are illustrated in Figure 5, when Vrev is outside (A) or within (B) the voltage range at which the conductance is activated. The classical method of estimating Vrev of voltage-gated channels, introduced by Hodgkin and Huxley (51) is the “tail current” method (Fig. 5A). The membrane is held at a voltage at which the conductance is off, the “holding” potential, Vhold. A pre-pulse is applied to activate the conductance. Then the voltage is stepped to various voltages at which most channels close, in this example, −10 through +20 mV in 10-mV increments. The object is to determine the voltage at which the resulting “tail currents” vanish; this is Vrev. Often tail currents decay exponentially, and if the initial amplitude is difficult to resolve due to capacity current interference, the current can be fitted by an exponential decay function, which can be extrapolated to the time at the start of the pulse. One could then plot the “instantaneous” current against voltage and interpolate to determine where the currents cross the voltage axis. This would give the wrong answer, +8 mV in our example, because one must always consider the leak current. The conductance of interest in Figure 5A is the voltage-gated proton conductance. At Vhold there is 2 pA of inward current that is unrelated to proton current and therefore considered “leak.” We are not interested in the properties of leak current, except in so far as we want to eliminate their effects. The leak current will be different at each test voltage where tail currents were recorded. The simplest way to eliminate the leak is to look not at the absolute current value at the start of the pulse, but at the amplitude of time-dependent tail current. Generic leak currents are usually time-independent, in contrast with proton currents. When we plot and interpolate the amplitudes of the tail current decay, we find that Vrev is actually +6 mV. The error due to leak was small here because the leak was small and reversed near Vrev for the proton conductance. Much larger errors have been published in reputable journals, including Vrev values that were described as being positive to voltages at which clearly outward tails currents decayed, because leak was not corrected. One presumption in the tail-current-decay-amplitude method is that the same number of channels is open at the end of each prepulse. In the example in Figure 5A, one prepulse activated a smaller fraction of the total conductance, which we can see because the prepulse current was smaller. One can correct for this error retroactively by scaling the tail current according to the proportional decrease in prepulse current (in this example, the correction is negligible). Another presumption is that the tail current decays completely. In Figure 5A, the tail current at +10 mV decayed only partially, resulting in maintained outward current. This can be confirmed by examining the secondary tail current when the voltage is finally returned to Vhold. There is a clear inward tail current after the pulse to +10 mV. One can determine whether complete decay can be expected at a given voltage by simply applying a pulse directly to that voltage to see if current is activated. If Vrev occurs at a voltage at which the conductance of interest is already activated, then a different approach must be used (see below).
Besides leak conductance, what other errors may occur? One systematic error arises from the necessity to activate the conductance in order to generate tail currents. The prepulse that activates the conductance also removes a large number of permeant ions from the cell. The result for proton currents is that the prepulse increases pHi so that the measured Vrev tends to be more positive than the true value (26). This error can be minimized by using high buffer concentrations in the pipette solution and by keeping the prepulse small and brief. However, if the prepulse is too small, the tail currents will be small and difficult to interpret. Although the error cannot be eliminated, it can be recognized. Because of this error, it is more reliable to consider the change in Vrev measured when pHo is varied, rather than the absolute value of Vrev, which will also have errors due to liquid junction potentials. If similar depletion of protonated buffer occurs during each Vrev determination, then the shift in Vrev will be the best indicator of selectivity.
Sometimes, the conductance of interest is already activated at Vrev and therefore decaying tail currents do not occur. One solution is to cave in to error and simply measure the absolute current at various voltages, but this makes leak correction difficult. A simple and preferable alternative is to apply a family of depolarizing pulses, and observe the time dependent turn-on of current at various voltages, as illustrated in Figure 5B. This human eosinophil was activated by PMA in perforated-patch configuration, and there is −8 pA of electron current at Vhold. That this large inward current is not leak can be deduced by noting the small spacing between the currents at the start of the four illustrated test pulses, before much proton current has turned on. During the pulse to −40 mV only leak current and Ie are evident, but the gH is activated detectably at −30 mV, because a small tail current appears upon repolarization. During the pulses to −20 and −10 mV, inward H+ current turns on slowly during the pulses, and large inward tail currents are seen on repolarization. Finally, at 0 mV a large outward current turns on during the pulse. Despite the fact that this is clearly an outward current, its absolute value at the end of the pulse is still negative, because it is superimposed on the larger inward electron current. Only a computer program lacking the most rudimentary insight would declare that Vrev must be positive to 0 mV, simply because the total current at the end of the pulse is inward! It is obvious that Vrev for the voltage- and time-dependent proton conductance that we are interested in, falls between −10 mV and 0 mV (the two darker records), because the time-dependent current is inward and outward, respectively, in the two records. To determine Vrev we can first measure the amplitude of inward current at −10 mV (−1.2 pA) and the outward current at 0 mV (+4.3 pA) that turned on during the pulses. However, simply interpolating between these values on a current-voltage graph, for example, would give the incorrect Vrev value of −8 mV, because the gH activated at these two voltages was a very different fraction of the total gH. We can determine precisely the relative gH that was activated by each pulse from the amplitude of the tail current upon repolarization to −60 mV. We now scale the time-dependent current amplitudes according to the fraction of the gH activated by the prepulse to arrive at the correct answer, −7 mV.
-
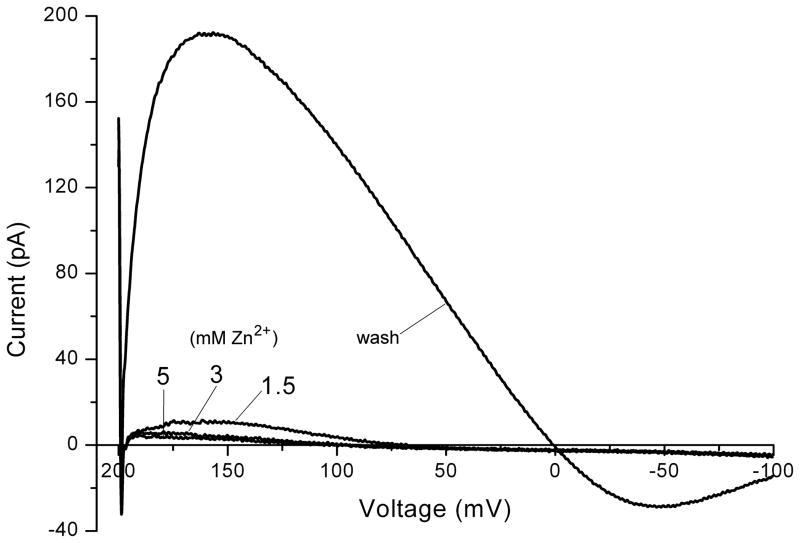
Under some conditions, one may use a “quick-and-dirty” method to determine Vrev. One such method is to use voltage ramps (Fig. 6). Here the voltage in a human eosinophil was ramped rapidly from +200 mV to −100mV. Because H+ current activation is faster at more positive voltages, nearly 200 pA of proton current was activated soon after the start of the ramp. The ramp was fast enough that the conductance was still active at 0 mV, then in the negative voltage range H+ channels closed progressively. When the same ramp was applied after addition of high concentrations of Zn2+, most, but not all of the proton current was abolished. Because a major effect of divalent cations is to shift the voltage dependence of H+ channel activation to more positive voltages (52,53), the currents turned off at much more positive voltages. In the presence of Zn2+, the current negative to +50 mV is almost entirely leak current. Estimating Vrev from voltage ramps suffers from at least three potential errors.
A capacitive artifact produces an offset of the current recorded during a voltage ramp, typically of a few picoamperes, because the capacity current is proportional to dV/dt, which is constant during a voltage ramp. Even if one uses analog capacity correction, the correction is rarely perfect, and can change over time. This offset may be negligibly small, but can be problematic if the currents of interest are comparably small, as may occur in excised patches. The offset increases with the speed of the ramp. A quick way to test whether the offset is a problem is to apply the same ramp (i.e., spanning the same voltage range) but in the opposite direction. If the currents do not superimpose, there is an offset problem. In the ramps in Figure 6, the leak current intersects the X-axis near +70 mV. This may be the result of a small offset, because one expects leak currents to reverse near 0 mV, although this question was not studied systematically. However, the best estimate of Vrev in this experiment is not the point at which the control currents pass through the voltage axis (the zero-current potential), but rather the voltage at which the currents in the absence and presence of Zn2+ intersect, just negative to 0 mV.
Significant numbers of the channel of interest must be open when the voltage passes Vrev to estimate Vrev. For example, voltage-gated proton channels generally open only positive to Vrev and thus Vrev can be estimated only by ramping from positive to negative voltages at a rate slow enough to allow H+ channels time to open, but fast enough so that they do not all close by the time the voltage passes EH. Although it seems obvious that one can measure a meaningful Vrev only if the channels of interest are open at that voltage, papers on human neutrophil electrophysiology have been published in highly reputable journals in which this condition was not met. Naïve authors sometimes simply plot the total current and declare that Vrev is the voltage at which this current crosses the voltage axis, ignoring the fact that they have simply determined Vrev of the leak current!
It is more difficult to separate the conductance of interest from leak or other conductances during ramps than during voltage pulses (see above).
A second “quick-and-dirty” way to estimate Vrev of a voltage-gated channel is to apply a single voltage pulse that activates the conductance, and then repolarize to a voltage at which the channel closes. One can interpolate between the current at the end of the pulse and that at the beginning of the tail current to estimate Vrev (54). This method assumes that the instantaneous current-voltage relationship is linear, i.e., that the open channel conductance is ohmic. Figure 7 illustrates that the instantaneous current-voltage relationship for voltage-gated proton channels is not linear at symmetrical pH, but the rectification is weak enough that the error is not large if the two test voltages are close together. Leak must also be corrected. In some situations, the complete tail current method may be too time-consuming, and a rough estimate is better than none at all. An advantage of this “interpolation” method is that the two measurements are made at essentially the same time. Thus, although depletion would affect the result, the measurement is an accurate reflection of Vrev at that instant. Using the example in Figure 5B, from the outward current at 0 mV, +4.3 pA, and the inward tail current at −60 mV, −34 pA, we interpolate to arrive at −7 mV as an estimate of Vrev which is identical with the result calculated by the more laborious formal methods described above.
Fig. 5.
Determining the reversal potential, Vrev, of a voltage-gated conductance, when Vrev is outside (A) or within (B) the voltage range at which the conductance is activated. (A) Tail current method illustrated by voltage-gated proton currents in a human eosinophil at pHo 7.0 and pHi 7.0. From a holding potential of −60 mV, where H+ channels are closed, a prepulse to +80 mV activates the conductance. The voltage is then stepped to various voltages at which most channels close, −10 to +20 mV in 10-mV increments in this example. Bath solution TMAMeSO3, pipette solution KMeSO3, both with 50 mM NH4+ to control pHi. (B) Determining Vrev from a family of depolarizing pulses. From Vhold = −60 mV, pulses were applied to −40 mV through 0 mV in 10-mV increments, with currents at −10 mV and 0 mV in bold. This human eosinophil was previously activated with PMA, and there is nearly −8 pA of electron current at Vhold. See text for details.
Fig. 6.
Evaluation of Vrev using voltage ramps. Currents during voltage ramps (from +200 mV to −100 mV in 800 ms) in a human eosinophil studied in perforated-patch configuration with KMeSO4 in the pipette solution and TMAMeSO4 in the bath solution, both at pH 7.0 and both with 50 mM NH4+ to clamp pHi near pHo. The predominant conductance is due to voltage-gated proton channels, which are inhibited by Zn2+. The sequence was 1.5 mM ZnCl2, then 5 mM, then 3 mM, then washout with EGTA-containing bath solution. This cell was stimulated with PMA and the DPI was added to inhibit NADPH oxidase.
Fig. 7.
Measurement of the instantaneous current-voltage relationship of proton channels. In A, currents during repeated voltage pulses are superimposed. The first step, the “prepulse,” is to a voltage at which the gH is activated, and then the membrane is stepped to a range of voltages. Ideally, the same number of channels is open at the end of each prepulse, and therefore the current at the start of the test pulse (B) reflects any rectification of the open channel current. If one measured the current-voltage relationship of a single open channel, the result should have the same shape as that plotted in B. If any gating that occurs during the test pulse, typically channels closing at negative voltages, is so rapid that the initial current cannot be resolved, one can fit the decaying current, usually to an exponential decay function, and extrapolate back to the start of the pulse. From reference (90).
3.6.2.2. Rectification
Rectification means that the current flowing through a single open channel is not a linear function of the applied driving force (the applied voltage relative to Vrev).
Rectification can be determined from instantaneous current-voltage curves, like that in Figure 7. Errors can arise if the current at the end of the prepulse is not the same each time, which this can be corrected by scaling, as already described. If the tail currents decay rapidly, their amplitude can be difficult to determine.
Another way to detect rectification is to measure single-channel currents directly at different voltages. The preferred method is to use repeated voltage ramps, and then average segments of ramps containing either one or no open channels, and subtract one from the other. Distinct advantages of this method include: (a) it is efficient, (b) by superimposing records, one can immediately see whether there has been a change in the leak current, (c) one can resolve tiny currents near Vrev more reliably than during sustained voltages pulses, and (d) it is much easier to confirm which channel is which when there are multiple types of channels in the patch. Obviously, this method requires that single channel currents are large enough to detect. Single proton channel currents are in the femtoampere range (37) and thus are not amenable to this method.
3.6.2.3. Activation by Ligands or Voltage, Gating Kinetics
A crucial property of ion channels is the factors that cause them to open.
Some channels are ligand-gated (i.e., they open when a particular substance binds). For example, endplate channels at the neuromuscular junction open when acetylcholine binds. Ca2+-activated channels open when [Ca2+]i increases above resting levels.
Many channels are voltage-gated. The voltage dependence of a channel can be described by applying a family of voltage pulses than span a voltage range in which the channel progresses from being closed to having a high probability of being open (Popen). Ideally, the current is measured after it reaches a steady-state level. In practice, this ideal is often not achieved, especially for proton currents that activate slowly and may decay during prolonged large pulses due to H+ current-induced pHi increases. One can “correct” the current measured before steady-state by fitting the current with a rising exponential, I(t) = Imax (1-e−t/τ), and extrapolating to infinite time. This obviously assumes that an exponential describes the ideal activation behavior, which may not be the case, but may give a reasonable estimate. In this process, one also obtains the time constant (τ or τact) of activation of the current.
In most cells, proton currents activate with a sigmoidal time course, and thus a simple exponential does not accurately describe the kinetics. However, attempts to discover a simple model that fits the currents better have not been productive. Our philosophy is that if the main part of the current can be reasonably well described by a single exponential, then this provides a τact value that gives a rough indication of the rate at which most of the channels open, and it is a parameter that can be easily understood and communicated.
-
The resulting current-voltage relationship can be converted to a conductance-voltage relationship by dividing the current at each voltage (V) by the driving force (V-Vrev). The conductance ideally saturates at large voltages at which Popen is maximal. The single-channel correlate is the Popen-voltage relationship. Both of these relationships tend to be sigmoidal and are often fitted with a Boltzmann function (using proton channels as an example):
[Equation 1] or[Equation 2] The midpoint of the curve, at which the conductance is half maximal, is V½ (in mV) and the slope factor k (in mV) indicates the steepness of the voltage dependence. A smaller value of k means steeper voltage dependence.
3.6.2.4. Single Channel Conductance
Single channel conductance (γ) is important because it determines how much current flows through the open channel. The total current across a cell membrane is described by:
| [Equation 3] |
where (V-Vrev) is the driving force, N is the number of channels in the membrane, and Popen is the probability of any channel being open.
When ion channels open and close, the current increases and decreases in steps of identical amplitude, which sum together when many channels open to form a macroscopic current in which the unitary events cannot be clearly detected.
for many ion channels, γ is large enough that single channel currents can be measured directly.
Detecting single channel currents is usually done using excised patches of membrane, because it is desirable that either one channel or no more than a few channels are present.
There is additional noise when a channel is open, and the total noise increases with each open channel so that it is difficult to resolve unitary events when more than a few channels are open at one time. If multiple types of channels are present, identification becomes very difficult.
Single channel currents can be recorded at constant voltage, during pulses, or during voltage ramps. If there is only one channel in a patch, one can hold the membrane at each voltage for long times and determine mean open and closed times as well as Popen for that voltage. Popen can be efficiently determined by converting the data to an amplitude histogram and comparing the integrals when one or no channel is open.
Giving pulses is useful for voltage-gated channels to derive a sense of whether the channel behaves as expected from macroscopic currents.
Voltage ramps are an excellent way to determine the reversal potential and the voltage dependence of the conductance, i.e., its rectification. Under most circumstances, the open channel current is not ohmic, rather the conductance changes with voltage or rectifies. A voltage ramp is applied repeatedly, and the currents are analyzed afterwards. The average of current segments with no open channels can be subtracted from the average of segments with exactly one channel open to produce the open-channel current-voltage relationship.
-
if the unitary conductance is too small to measure directly, it can be deduced from current fluctuations, or noise. Under stationary conditions (without time-dependence of Itotal, Popen or driving force, etc.), the single channel current (i) can be calculated from the variance, σ2 according to (55):
[Equation 4] The value used for σ2 must have background noise subtracted, which can be determined from identical measurements in the presence of complete pharmacological blockade. If this is not feasible, one can determine background noise at subthreshold voltages, in the case of voltage-gated channels. The only parameter that is difficult to determine is Popen. The macroscopic conductance of a depolarization-activated channel may saturate at large positive voltages, but Popen at saturation may be much less than 1.0. However, by collecting data at different voltages, it is possible to deduce Popen (Fig. 12 of (37)). One can also collect data near Vthreshold where Popen is close to 0, and the error in (1 - Popen) is negligible; this approach, however, produces estimates only within a narrow voltage range. For noise analysis, it is important that the data are collected using an appropriate sampling rate and appropriate filtering. These issues are beyond the scope of this chapter and have been discussed elsewhere at length (56,37).
The transporters involved in the phagocyte respiratory burst have small conductance or transport rates. Proton channels have a conductance of ~15 fS at physiological pH (37), which corresponds with currents of a few femtoamperes, on the order of ~10,000 H+/s, depending on the driving voltage. Store-operated Ca2+ (CRAC) channels may be present in neutrophils (57) and have similarly small conductance (58). In comparison, the NADPH oxidase transports only ~300 e−/s (59,60). It seems teleologically reasonable that in small cells, and especially in the much smaller phagosome, low transport rates would make the transporters more amenable to regulation and fine-tuning of their activity. A single large-conductance channel would produce a drastic and abrupt change in potential and ion concentrations, and thus from a teleological perspective, would be unwieldy (61).
Acknowledgments
This work was supported in part by NIH grants HL61437 and GM087507 and NSF grant MCB-0943362.
Abbreviations
- AA
arachidonic acid
- DPI
diphenylene iodonium
- gH
proton conductance
- O2·−
superoxide anion
- pHi
intracellular pH
- pHo
extracellular pH
- PKC
protein kinase C
- PMA
phorbol myristate acetate
- TEA+
tetraethylammonium ion
- TMA+
tetramethylammonium
- ATP
adenosine triphosphate
- GTPγs
guanosine triphosphate γs
- Vrev
reversal potential
- Vhold
holding potential
- Vthreshold
channel opening potential
- gH
proton conductance
- τact
time constant of activation
- Popen
open probability
- Ihold
holding current
- Ie
electron current
- EH
equilibrium potential for protons
- γ
single channel conductance
Footnotes
The oxidase complex is assembled from two membrane-bound subunits (gp91phox and p22phox) and several cytosolic subunits (p67phox, p47phox, Rac, and p40phox) (9). The NADPH oxidase works by transporting electrons from cytoplasmic NADPH across the membrane, where they reduce O2 to O2·−. This electron movement can be recorded directly as an electrical current (10,5). Because the electron transport is not obligatorily coupled to a compensatory charge movement, it produces a separation of charge that leads to sustained depolarization of the membrane (62) well beyond 0 mV in intact granulocytes (63–66). If this charge movement is not compensated, extreme depolarization results (67,61) that by itself directly opposes electron flux across the membrane (25). In human neutrophils and eosinophils, almost all of this charge compensation is mediated by H+ channels (25,30,61,68,67,69,70,66,71).
H+ channels are membrane proteins that are gated by both voltage and pH. They open with depolarization or an outward pH gradient (defined as ΔpH = pHo - pHi). Increased pHo and/or decreased pHi cause the channels to open at lower voltages. Proton channels have two distinct gating modes, “resting” and “activated,” that are observed before and after stimulation (45,70,10,72). Resting H+ channels open almost exclusively positive to the Nernst potential for protons (EH) and therefore extrude protons from cells. The activated mode occurs concurrently with NADPH oxidase activation, and is manifested as an increased proton conductance, faster channel opening on depolarization, slower channel closing, and a negative shift in the threshold voltage at which the channels open. Enhanced gating of proton channels occurs when the protein is phosphorylated by PKC (73), at a single site, Thr29, on the intracellular N terminus of the protein (74).
The patch clamp allows the recording of small currents and the detection of single channel currents in the cell membrane. Recording small currents with the patch clamp technique requires a large signal-to-noise ratio. The smallest directly-recorded single-channel currents were ~8 fA proton channel currents in human eosinophils (37). Noise in the patch clamp set-up arises from the electronic circuitry, the pipette and holder assembly, the seal and cell membrane, and extraneous mechanical or electrical sources (36,75). Noise interferes with the recordings and should be minimized.
A patch-clamp experiment consists of a number of voltage pulses applied to a cell or membrane patch. Changes in pH, ion concentration, temperature, osmolality, and drug concentration can be exploited to reveal the properties of the channels present. Channels are characterized by the stimulus that causes them to open, their ion permeability, opening and closing kinetics, conductance, and pharmacological sensitivity.
| [Equation 5] |
| [Equation 6] |
| [Equation 7] |
For proton current recording, it is advisable to use a high intracellular buffer concentration to maximize control over pH. Reducing extracellular buffer from 100 mM to 1 mM had very little effect on voltage-gated proton currents (27), because the bath solution represents an effectively infinite sink for protons. Intracellular buffer concentration was more critical, with distinct limitation of H+ current when buffer was reduced from 100 to 10 mM even in excised, inside-out patches (27). Several whole-cell patch-clamp studies in which pHi was determined have revealed that including 5–10 mM buffer in the pipette solution does not adequately control pHi, compared with higher buffer concentrations, e.g., 100–120 mM (53,23,78,79). Even with high buffer, large proton currents can change pH substantially (26); which in a biological sense is fortunate, because extruding acid is a major function of proton channels in many cells.
| [Equation 8] |
A more traditional method is to pass current repeatedly in both directions through a silver wire that is immersed in a Cl−-containing solution (e.g., 0.1 M HCl), to deposit a fine coat of AgCl. Sintered Ag/AgCl electrodes can also be purchased.
The pipette resistance (Rpip) is in series with the membrane resistance of the cell (Rm), and the applied voltage (Vcommand) will be divided according to these relative resistances. The result is that the actual voltage across the cell membrane (Vtrue) is less than the command voltage applied: Vtrue = Vcommand [Rm/(Rm + Rpip)]. It should be noted that the resistance of the cell membrane decreases radically when a pulse that opens ion channels is applied, and therefore the series resistance error increases drastically when a large conductance is activated. Most patch-clamp amplifiers have a “series resistance compensation” circuit that can be adjusted to compensate some fraction of the series resistance. One easily detected manifestation of uncompensated series resistance is non-exponential decay of tail currents that normally decay exponentially.
A pipette filled with solution and placed into a bath solution acts as a capacitor. During a step change in voltage there is a brief transient of current due to charging the pipette (fast) and cell membrane (slow) capacity. The pipette capacitance can be reduced by coating the part of the pipette that will be immersed with a hydrophobic substance, such as Sylgard® (Dow Corning Corp.), thus minimizing contact of the bath solution and the pipette and increasing the distance between the two conductors (the fluid in the bath and pipette) to reduce the capacitance (36). When recording currents, it is necessary to null capacity transients using the analog capacity compensation controls of the patch clamp amplifier.
Many types of glass have been evaluated for use as pipettes (36). Glass with a lower softening temperature is easier to fire polish after pulling and forms blunt pipettes that have low access resistance. Harder glass with a higher softening temperature tends to form long, gradually tapering pipettes with high resistance; hence are a poor choice for whole-cell recording. Hard glass may have other desirable properties, such as lower noise or better sealing proclivity (80). Quartz pipettes have been used to minimize noise (especially in the high frequency range) during single channel recording (81). Some types of glass, especially soft glasses used for whole-cell recording, contain heavy metals that can leach into the solution, affecting the recorded currents (82,83). Such effects can be controlled by including a divalent chelator like EGTA in the pipette solution.
The wire filament is often coated with glass to prevent vaporization and deposition of metal on the pipette tip. Positioning a stream of air blowing toward the filament creates a steep temperature gradient that enables better control over the fire-polishing process.
If the tip opening cannot be seen, the tip resistance can be estimated by a “bubble test” in which a 10 mL syringe is attached to the base of the pipette via a tube. With the tip immersed in methanol and the syringe filled with 10 mL of air, apply pressure until bubbles first start to appear, and then note the amount of air left in the syringe. In one series of measurements, the resistance of the pipette filled with an isotonic KF solution and placed in a Ringer-containing bath was 3–5 MΩ for a bubble test number of 3, 5–8 MΩ for a bubble test number of 2, and 8–17 MΩ for a bubble test number of 1. Actual results may differ, depending on tip geometry and other factors. If the tip is too large, further polishing can be performed.
A more traditional way to monitor the access resistance is to apply a subthreshold test pulse and determine the time constant of decay of the capacity transient (τc). The decay becomes faster as the access resistance (Ra) decreases, because τc = Ra Cm, where Cm is the capacity of the cell (40).
Unlike arachidonic acid (AA), PMA does not perturb the cell membrane. Unlike f-Met-Leu-Phe, PMA needs no priming.
The intactness of the patch membrane can be assessed by including a fluorescent dye (e.g., Lucifer yellow) in the pipette solution (13). The cell will fluoresce if the patch has ruptured. The intactness of the patch can also be assessed by using a dye visible by light microscopy (e.g., eosin) in the pipette solution (45).
Petheö et al. (11) reported that the Ie in this method is susceptible to run-down over time, which was reduced by addition of GTPγS and ATP to the bath (internal) solution. In our hands, Ie often persists in inside-out patches with minimal rundown, without addition of anything to the bath besides saline solution. A speculative explanation for this difference is that our patches might include more cytoskeleton or other cytoplasmic structures that conceivably could influence oxidase stability.
Large, impermeant ions (methanesulfonate−, aspartate−, tetramethylammonium+, N-methyl-D-glucamine+) diffuse more slowly than the smaller physiological ions they replace, and thus significant liquid junction potentials may be present at the tip of the pipette (84,85). Contrary to popular opinion, liquid junction potentials are not corrected by nulling the current at the start of the experiment. If one wants to determine the absolute potential accurately, it is necessary to correct for liquid junction potentials. In many situations, such accuracy is not required, but if one wants to quantitate relative selectivity, for example, accuracy is desirable.
The apparent specificity of inhibitors historically often decreases with the passage of time. For example, charybdotoxin (86) and iberiotoxin (87) were originally thought to be specific for BK channels, but both were later found to also block other Ca2+-activated K+ channels (88) and charybdotoxin also blocks the purely voltage-gated Kv1.3 channel (89).
References
- 1.Hodgkin AL, Huxley AF, Katz B. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J Physiol. 1952;116:424–448. doi: 10.1113/jphysiol.1952.sp004716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hamill OP, Marty A, Neher E, et al. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflügers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 3.von Tscharner V, Prod’hom B, Baggiolini M, et al. Ion channels in human neutrophils activated by a rise in free cytosolic calcium concentration. Nature. 1986;324:369–372. doi: 10.1038/324369a0. [DOI] [PubMed] [Google Scholar]
- 4.DeCoursey TE, Cherny VV. Potential, pH, and arachidonate gate hydrogen ion currents in human neutrophils. Biophys J. 1993;65:1590–1598. doi: 10.1016/S0006-3495(93)81198-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schrenzel J, Serrander L, Bánfi B, et al. Electron currents generated by the human phagocyte NADPH oxidase. Nature. 1998;392:734–737. doi: 10.1038/33725. [DOI] [PubMed] [Google Scholar]
- 6.Gordienko DV, Tare M, Parveen S, et al. Voltage-activated proton current in eosinophils from human blood. J Physiol. 1996;496:299–316. doi: 10.1113/jphysiol.1996.sp021686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stoddard JS, Steinbach JH, Simchowitz L. Whole cell Cl− currents in human neutrophils induced by cell swelling. Am J Physiol. 1993;265:C156–165. doi: 10.1152/ajpcell.1993.265.1.C156. [DOI] [PubMed] [Google Scholar]
- 8.Krause KH, Demaurex N, Jaconi M, et al. Ion channels and receptor-mediated Ca2+ influx in neutrophil granulocytes. Blood Cells. 1993;19:165–173. discussion 173–165. [PubMed] [Google Scholar]
- 9.Babior BM. NADPH oxidase: an update. Blood. 1999;93:1464–1476. [PubMed] [Google Scholar]
- 10.DeCoursey TE, Cherny VV, Zhou W, et al. Simultaneous activation of NADPH oxidase-related proton and electron currents in human neutrophils. Proc Natl Acad Sci USA. 2000;97:6885–6889. doi: 10.1073/pnas.100047297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Petheö GL, Maturana A, Spät A, et al. Interactions between electron and proton currents in excised patches from human eosinophils. J Gen Physiol. 2003;122:713–726. doi: 10.1085/jgp.200308891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morgan D, Cherny VV, Murphy R, et al. The pH dependence of NADPH oxidase in human eosinophils. J Physiol. 2005;569:419–431. doi: 10.1113/jphysiol.2005.094748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Morgan D, Cherny VV, Murphy R, et al. Temperature dependence of NADPH oxidase in human eosinophils. J Physiol. 2003;550:447–458. doi: 10.1113/jphysiol.2003.041525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Petheő GL, Demaurex N. Voltage- and NADPH-dependence of electron currents generated by the phagocytic NADPH oxidase. Biochem J. 2005;388:485–491. doi: 10.1042/BJ20041889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.DeCoursey TE. Interactions between NADPH oxidase and voltage-gated proton channels: why electron transport depends on proton transport. FEBS Lett. 2003;555:57–61. doi: 10.1016/s0014-5793(03)01103-7. [DOI] [PubMed] [Google Scholar]
- 16.Moreland JG, Davis AP, Bailey G, et al. Anion channels, including ClC-3, are required for normal neutrophil oxidative function, phagocytosis, and transendothelial migration. J Biol Chem. 2006;281:12277–12288. doi: 10.1074/jbc.M511030200. [DOI] [PubMed] [Google Scholar]
- 17.Menegazzi R, Busetto S, Dri P, et al. Chloride ion efflux regulates adherence, spreading, and respiratory burst of neutrophils stimulated by tumor necrosis factor-α (TNF) on biologic surfaces. J Cell Biol. 1996;135:511–522. doi: 10.1083/jcb.135.2.511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Matsuda JJ, Filali MS, Moreland JG, et al. Activation of swelling-activated chloride current by tumor necrosis factor-alpha requires ClC-3-dependent endosomal reactive oxygen production. J Biol Chem. 2010;285:22864–22873. doi: 10.1074/jbc.M109.099838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Moreland JG, Davis AP, Matsuda JJ, et al. Endotoxin priming of neutrophils requires NADPH oxidase-generated oxidants and is regulated by the anion transporter ClC-3. J Biol Chem. 2007;282:33958–33967. doi: 10.1074/jbc.M705289200. [DOI] [PubMed] [Google Scholar]
- 20.Volk AP, Heise CK, Hougen JL, et al. ClC-3 and IClswell are required for normal neutrophil chemotaxis and shape change. J Biol Chem. 2008;283:34315–34326. doi: 10.1074/jbc.M803141200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Painter RG, Bonvillain RW, Valentine VG, et al. The role of chloride anion and CFTR in killing of Pseudomonas aeruginosa by normal and CF neutrophils. J Leukoc Biol. 2008;83:1345–1353. doi: 10.1189/jlb.0907658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cherny VV, Henderson LM, DeCoursey TE. Proton and chloride currents in Chinese hamster ovary cells. Membr Cell Biol. 1997;11:337–347. [PubMed] [Google Scholar]
- 23.Demaurex N, Grinstein S, Jaconi M, et al. Proton currents in human granulocytes: regulation by membrane potential and intracellular pH. J Physiol. 1993;466:329–344. [PMC free article] [PubMed] [Google Scholar]
- 24.DeCoursey TE, Cherny VV. Voltage-activated hydrogen ion currents. J Membr Biol. 1994;141:203–223. doi: 10.1007/BF00235130. [DOI] [PubMed] [Google Scholar]
- 25.DeCoursey TE, Morgan D, Cherny VV. The voltage dependence of NADPH oxidase reveals why phagocytes need proton channels. Nature. 2003;422:531–534. doi: 10.1038/nature01523. [DOI] [PubMed] [Google Scholar]
- 26.Musset B, Cherny VV, Morgan D, et al. Detailed comparison of expressed and native voltage-gated proton channel currents. J Physiol. 2008;586:2477–2486. doi: 10.1113/jphysiol.2007.149427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.DeCoursey TE, Cherny VV. Effects of buffer concentration on voltage-gated H+ currents: does diffusion limit the conductance? Biophys J. 1996;71:182–193. doi: 10.1016/S0006-3495(96)79215-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schrenzel J, Lew DP, Krause KH. Proton currents in human eosinophils. Am J Physiol. 1996;271:C1861–1871. doi: 10.1152/ajpcell.1996.271.6.C1861. [DOI] [PubMed] [Google Scholar]
- 29.Cherny VV, DeCoursey TE. pH-dependent inhibition of voltage-gated H+ currents in rat alveolar epithelial cells by Zn2+ and other divalent cations. J Gen Physiol. 1999;114:819–838. doi: 10.1085/jgp.114.6.819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Femling JK, Cherny VV, Morgan D, et al. The antibacterial activity of human neutrophils and eosinophils requires proton channels but not BK channels. J Gen Physiol. 2006;127:659–672. doi: 10.1085/jgp.200609504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tare M, Prestwich SA, Gordienko DV, et al. Inwardly rectifying whole cell potassium current in human blood eosinophils. J Physiol. 1998;506:303–318. doi: 10.1111/j.1469-7793.1998.303bw.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Grinstein S, Romanek R, Rotstein OD. Method for manipulation of cytosolic pH in cells clamped in the whole cell or perforated-patch configurations. Am J Physiol. 1994;267:C1152–1159. doi: 10.1152/ajpcell.1994.267.4.C1152. [DOI] [PubMed] [Google Scholar]
- 33.DeCoursey TE, Cherny VV. Temperature dependence of voltage-gated H+ currents in human neutrophils, rat alveolar epithelial cells, and mammalian phagocytes. J Gen Physiol. 1998;112:503–522. doi: 10.1085/jgp.112.4.503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kuno M, Ando H, Morihata H, et al. Temperature dependence of proton permeation through a voltage-gated proton channel. J Gen Physiol. 2009;134:191–205. doi: 10.1085/jgp.200910213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chabala LD, Sheridan RE, Hodge DC, et al. A microscope stage temperature controller for the study of whole-cell or single-channel currents. Pflügers Arch. 1985;404:374–377. doi: 10.1007/BF00585351. [DOI] [PubMed] [Google Scholar]
- 36.Rae JL, Levis RA. Patch voltage clamp of lens epithelial cells: theory and practice. Mol Physiol. 1984;6:115–162. [Google Scholar]
- 37.Cherny VV, Murphy R, Sokolov V, et al. Properties of single voltage-gated proton channels in human eosinophils estimated by noise analysis and by direct measurement. J Gen Physiol. 2003;121:615–628. doi: 10.1085/jgp.200308813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fenwick EM, Marty A, Neher E. A patch-clamp study of bovine chromaffin cells and of their sensitivity to acetylcholine. J Physiol. 1982;331:577–597. doi: 10.1113/jphysiol.1982.sp014393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lindau M, Fernandez JM. IgE-mediated degranulation of mast cells does not require opening of ion channels. Nature. 1986;319:150–153. doi: 10.1038/319150a0. [DOI] [PubMed] [Google Scholar]
- 40.Rae J, Cooper K, Gates P, et al. Low access resistance perforated patch recordings using amphotericin B. J Neurosci Methods. 1991;37:15–26. doi: 10.1016/0165-0270(91)90017-t. [DOI] [PubMed] [Google Scholar]
- 41.Horn R, Marty A. Muscarinic activation of ionic currents measured by a new whole-cell recording method. J Gen Physiol. 1988;92:145–159. doi: 10.1085/jgp.92.2.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fan JS, Palade P. Perforated patch recording with β-escin. Pflügers Arch. 1998;436:1021–1023. doi: 10.1007/pl00008086. [DOI] [PubMed] [Google Scholar]
- 43.Falke LC, Gillis KD, Pressel DM, et al. ‘Perforated patch recording’ allows long-term monitoring of metabolite-induced electrical activity and voltage-dependent Ca2+ currents in pancreatic islet B cells. FEBS Lett. 1989;251:167–172. doi: 10.1016/0014-5793(89)81448-6. [DOI] [PubMed] [Google Scholar]
- 44.Chung I, Schlichter LC. Criteria for perforated-patch recordings: ion currents versus dye permeation in human T lymphocytes. Pflügers Arch. 1993;424:511–515. doi: 10.1007/BF00374915. [DOI] [PubMed] [Google Scholar]
- 45.Bánfi B, Schrenzel J, Nüsse O, et al. A novel H+ conductance in eosinophils: unique characteristics and absence in chronic granulomatous disease. J Exp Med. 1999;190:183–194. doi: 10.1084/jem.190.2.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Strauss U, Herbrik M, Mix E, et al. Whole-cell patch-clamp: true perforated or spontaneous conventional recordings? Pflügers Arch. 2001;442:634–638. doi: 10.1007/s004240100578. [DOI] [PubMed] [Google Scholar]
- 47.Robertson AK, Cross AR, Jones OTG, et al. The use of diphenylene iodonium, an inhibitor of NADPH oxidase, to investigate the antimicrobial action of human monocyte derived macrophages. J Immunol Methods. 1990;133:175–179. doi: 10.1016/0022-1759(90)90357-2. [DOI] [PubMed] [Google Scholar]
- 48.Barry PH. The reliability of relative anion-cation permeabilities deduced from reversal (dilution) potential measurements in ion channel studies. Cell Biochem Biophys. 2006;46:143–154. doi: 10.1385/CBB:46:2:143. [DOI] [PubMed] [Google Scholar]
- 49.Musset B, Smith SME, Rajan S, et al. Aspartate 112 is the selectivity filter of the human voltage-gated proton channel. Nature. 2011;480:273–277. doi: 10.1038/nature10557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.DeCoursey TE, Cherny VV. Na+-H+ antiport detected through hydrogen ion currents in rat alveolar epithelial cells and human neutrophils. J Gen Physiol. 1994;103:755–785. doi: 10.1085/jgp.103.5.755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hodgkin AL, Huxley AF. The components of membrane conductance in the giant axon of Loligo. J Physiol. 1952;116:473–496. doi: 10.1113/jphysiol.1952.sp004718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Byerly L, Meech R, Moody W., Jr Rapidly activating hydrogen ion currents in perfused neurones of the snail, Lymnaea stagnalis. J Physiol. 1984;351:199–216. doi: 10.1113/jphysiol.1984.sp015241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.DeCoursey TE. Hydrogen ion currents in rat alveolar epithelial cells. Biophys J. 1991;60:1243–1253. doi: 10.1016/S0006-3495(91)82158-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Humez S, Fournier F, Guilbault P. A voltage-dependent and pH-sensitive proton current in Rana esculenta oocytes. J Membr Biol. 1995;147:207–215. doi: 10.1007/BF00233548. [DOI] [PubMed] [Google Scholar]
- 55.Hille B. Ion Channels of Excitable Membranes. 3. Sinauer Associates, Inc; Sunderland, MA: 2001. [Google Scholar]
- 56.Neher E, Stevens CF. Conductance fluctuations and ionic pores in membranes. Annu Rev Biophys Bioeng. 1977;6:345–381. doi: 10.1146/annurev.bb.06.060177.002021. [DOI] [PubMed] [Google Scholar]
- 57.Demaurex N, Monod A, Lew DP, et al. Characterization of receptor-mediated and store-regulated Ca2+ influx in human neutrophils. Biochem J. 1994;297:595–601. doi: 10.1042/bj2970595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zweifach A, Lewis RS. Mitogen-regulated Ca2+ current of T lymphocytes is activated by depletion of intracellular Ca2+ stores. Proc Natl Acad Sci U S A. 1993;90:6295–6299. doi: 10.1073/pnas.90.13.6295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Cross AR, Higson FK, Jones OT, et al. The enzymic reduction and kinetics of oxidation of cytochrome b−245 of neutrophils. Biochem J. 1982;204:479–485. doi: 10.1042/bj2040479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Koshkin V, Lotan O, Pick E. The cytosolic component p47phox is not a sine qua non participant in the activation of NADPH oxidase but is required for optimal superoxide production. J Biol Chem. 1996;271:30326–30329. doi: 10.1074/jbc.271.48.30326. [DOI] [PubMed] [Google Scholar]
- 61.Murphy R, DeCoursey TE. Charge compensation during the phagocyte respiratory burst. Biochim Biophys Acta. 2006;1757:996–1011. doi: 10.1016/j.bbabio.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 62.Henderson LM, Chappell JB, Jones OTG. The superoxide-generating NADPH oxidase of human neutrophils is electrogenic and associated with an H+ channel. Biochem J. 1987;246:325–329. doi: 10.1042/bj2460325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bankers-Fulbright JL, Gleich GJ, Kephart GM, et al. Regulation of eosinophil membrane depolarization during NADPH oxidase activation. J Cell Sci. 2003;116:3221–3226. doi: 10.1242/jcs.00627. [DOI] [PubMed] [Google Scholar]
- 64.Geiszt M, Kapus A, Nemet K, et al. Regulation of capacitative Ca2+ influx in human neutrophil granulocytes. Alterations in chronic granulomatous disease. J Biol Chem. 1997;272:26471–26478. doi: 10.1074/jbc.272.42.26471. [DOI] [PubMed] [Google Scholar]
- 65.Jankowski A, Grinstein S. A noninvasive fluorimetric procedure for measurement of membrane potential. Quantification of the NADPH oxidase-induced depolarization in activated neutrophils. J Biol Chem. 1999;274:26098–26104. doi: 10.1074/jbc.274.37.26098. [DOI] [PubMed] [Google Scholar]
- 66.Rada BK, Geiszt M, Káldi K, et al. Dual role of phagocytic NADPH oxidase in bacterial killing. Blood. 2004;104:2947–2953. doi: 10.1182/blood-2004-03-1005. [DOI] [PubMed] [Google Scholar]
- 67.Demaurex N, Petheõ GL. Electron and proton transport by NADPH oxidases. Philos Trans R Soc Lond B Biol Sci. 2005;360:2315–2325. doi: 10.1098/rstb.2005.1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.DeCoursey TE. During the respiratory burst, do phagocytes need proton channels or potassium channels, or both? Sci STKE. 2004:pe21. doi: 10.1126/stke.2332004pe21. [DOI] [PubMed] [Google Scholar]
- 69.DeCoursey TE. Voltage gated proton channels: molecular biology, physiology and pathophysiology of the HV family. Physiol Rev. 2013 doi: 10.1152/physrev.00011.2012. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.DeCoursey TE. Voltage-gated proton channels find their dream job managing the respiratory burst in phagocytes. Physiology (Bethesda) 2010;25:27–40. doi: 10.1152/physiol.00039.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Henderson LM, Chappell JB, Jones OTG. Superoxide generation by the electrogenic NADPH oxidase of human neutrophils is limited by the movement of a compensating charge. Biochem J. 1988;255:285–290. [PMC free article] [PubMed] [Google Scholar]
- 72.Musset B, Cherny VV, Morgan D, et al. The intimate and mysterious relationship between proton channels and NADPH oxidase. FEBS Lett. 2009;583:7–12. doi: 10.1016/j.febslet.2008.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Morgan D, Cherny VV, Finnegan A, et al. Sustained activation of proton channels and NADPH oxidase in human eosinophils and murine granulocytes requires PKC but not cPLA2α activity. J Physiol. 2007;579:327–344. doi: 10.1113/jphysiol.2006.124248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Musset B, Capasso M, Cherny VV, et al. Identification of Thr29 as a critical phosphorylation site that activates the human proton channel Hvcn1 in leukocytes. J Biol Chem. 2010;285:5117–5121. doi: 10.1074/jbc.C109.082727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Sigworth FJ. Electronic design of the patch clamp. In: Sakmann B, Neher E, editors. Single Channel Recording. 2. Plenum Press; New York: 1995. pp. 95–127. [Google Scholar]
- 76.Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of giant axon of the squid. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Byerly L, Moody WJ. Membrane currents of internally perfused neurones of the snail, Lymnaea stagnalis, at low intracellular pH. J Physiol. 1986;376:477–491. doi: 10.1113/jphysiol.1986.sp016165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kapus A, Romanek R, Qu AY, et al. A pH-sensitive and voltage-dependent proton conductance in the plasma membrane of macrophages. J Gen Physiol. 1993;102:729–760. doi: 10.1085/jgp.102.4.729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Levis RA, Rae JL. Constructing a patch clamp setup. Methods Enzymol. 1992;207:14–66. doi: 10.1016/0076-6879(92)07004-8. [DOI] [PubMed] [Google Scholar]
- 81.Levis RA, Rae JL. The use of quartz patch pipettes for low noise single channel recording. Biophys J. 1993;65:1666–1677. doi: 10.1016/S0006-3495(93)81224-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Cota G, Armstrong CM. Potassium channel “inactivation” induced by soft-glass patch pipettes. Biophys J. 1988;53:107–109. doi: 10.1016/S0006-3495(88)83071-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Rojas L, Zuazaga C. Influence of the patch pipette glass on single acetylcholine channels recorded from Xenopus myocytes. Neurosci Lett. 1988;88:39–44. doi: 10.1016/0304-3940(88)90312-6. [DOI] [PubMed] [Google Scholar]
- 84.Neher E. Correction for liquid junction potentials in patch clamp experiments. Methods Enzymol. 1992;207:123–131. doi: 10.1016/0076-6879(92)07008-c. [DOI] [PubMed] [Google Scholar]
- 85.Ng B, Barry PH. The measurement of ionic conductivities and mobilities of certain less common organic ions needed for junction potential corrections in electrophysiology. J Neurosci Methods. 1995;56:37–41. doi: 10.1016/0165-0270(94)00087-w. [DOI] [PubMed] [Google Scholar]
- 86.Miller C, Moczydlowski E, Latorre R, et al. Charybdotoxin, a protein inhibitor of single Ca2+-activated K+ channels from mammalian skeletal muscle. Nature. 1985;313:316–318. doi: 10.1038/313316a0. [DOI] [PubMed] [Google Scholar]
- 87.Galvez A, Gimenez-Gallego G, Reuben JP, et al. Purification and characterization of a unique, potent, peptidyl probe for the high conductance calcium-activated potassium channel from venom of the scorpion Buthus tamulus. J Biol Chem. 1990;265:11083–11090. [PubMed] [Google Scholar]
- 88.Hermann A, Erxleben C. Charybdotoxin selectively blocks small Ca-activated K channels in Aplysia neurons. J Gen Physiol. 1987;90:27–47. doi: 10.1085/jgp.90.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Sands SB, Lewis RS, Cahalan MD. Charybdotoxin blocks voltage-gated K+ channels in human and murine T lymphocytes. J Gen Physiol. 1989;93:1061–1074. doi: 10.1085/jgp.93.6.1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Cherny VV, Markin VS, DeCoursey TE. The voltage-activated hydrogen ion conductance in rat alveolar epithelial cells is determined by the pH gradient. J Gen Physiol. 1995;105:861–896. doi: 10.1085/jgp.105.6.861. [DOI] [PMC free article] [PubMed] [Google Scholar]