Bayesian statistics: Relevant for the brain?

Abstract

Analyzing data from experiments involves variables that we neuroscientists are uncertain about. Efficiently calculating with such variables usually requires Bayesian statistics. As it is crucial when analyzing complex data, it seems natural that the brain would “use” such statistics to analyze data from the world. And indeed, recent studies in the areas of perception, action, and cognition suggest that Bayesian behavior is widespread, in many modalities and species. Consequently, many models have suggested that the brain is built on simple Bayesian principles. While the brain’s code is probably not actually simple, I believe that Bayesian principles will facilitate the construction of faithful models of the brain.

What is Bayesian statistics?

Bayesian statistics can be seen as a model of the way we understand things. Our sensors are noisy and ambiguous as several possible worlds (or models of how the brain works) could give rise to the same sensor readings. We therefore have uncertainty in our data and cannot be certain which model or hypothesis we should believe in. However, we can considerably reduce uncertainty about the world using previously acquired knowledge and by integrating data across sensors and time. As new data comes in, we update our hypotheses. Bayesian statistics is the rigorous way of calculating the probability of a given hypothesis in the presence of such kinds of uncertainty. Within Bayesian statistics, previously acquired knowledge is called prior, while newly acquired sensory information is called likelihood.

A simple example based on brain-machine interfaces highlights its use. Let’s say we have a monkey opening and closing its hand, while we record from its primary motor cortex [1]. We want to decode how the monkey is moving the hand, maybe to build a prosthetic device. Let us say the monkey wants to open the hand 80% of the time and close it otherwise (prior p(open)=.8). Let us say we record the number of spikes from a neuron related to hand opening which gives 10+−3 spikes (mean+−sd) when the hand is open and 13+−3 spikes when the hand is closed. How could we estimate if the hand should be open based on both the spikes and the prior knowledge?

We can then use Bayes rule:

$$p(\mathit{open}\mid \mathit{spikes})=\frac{p(\mathit{open})p(\mathit{spikes}\mid \mathit{open})}{p(\mathit{open})p(\mathit{spikes}\mid \mathit{open})+p(\mathit{closed})p(\mathit{spikes}\mid \mathit{closed})}$$

If we got 19 spikes and used approximate Gaussian distributions we would have a probability of about 53% that the hand should be closed. This combination of prior and likelihood is a typical application of Bayes rule. All of Bayesian statistics is in some way built upon Bayes rule.

Analyzing neural data with Bayesian statistics gives better results with less data

When it comes to the analysis of the increasingly complex datasets in neuroscience, Bayesian statistics is used ubiquitously [2]. This should be no surprise, after all Bayesian statistics is just the calculus of variables about which we have uncertainty.

I want to go through one illustrative example. In many experiments, the experimentalist is showing visual stimuli while measuring spikes from a neuron. They need to know the receptive field of the neuron, the (to first approximation) linear transfer function from input to spikes. However, the input is high dimensional. For example, a spatial pattern may be described with the brightness values of 10*10 pixels. Estimating the underlying 100 free parameters takes an awful lot of trials, even when choosing the stimuli in an optimal way [3]. However, not all potential receptive fields are equally likely. In fact, from previous experiments we know that receptive fields tend to be small (sparse in space), smooth (sparse spatial derivatives), and localized in frequency space (sparse in frequency). Putting these ideas into a Bayesian prior, it is possible to obtain the same quality of receptive field mapping with a lot less data [4].In a way, a theory borne by previous experiments can radically simplify subsequent experiments enabled by Bayesian ideas.

This example shows the nature of prior knowledge that is typically used. Sparseness in a few dimensions was used, and combined in a soft way with data. The “theory”, if we should call it that, proposed that localized receptive fields are more likely than non-localized. It did not posit that receptive fields should be maximally localized. Formulating theories in such a soft way allows them to be readily combined with data.

Similar applications can be found in many areas of neuroscience. In the field of brain machine interfaces, we have priors about how people want to interact with machines and need to combine this with data from the brain [5]. When analyzing high dimensional data, such as data from multiple simultaneously recorded neurons [4] or imaging [6], Bayesian approaches usually simplify the data analysis by allowing the use of prior knowledge about the relations of variables. When analyzing interactions between molecules there is the need to use prior knowledge about data and to combine data across experiments [7]. Regardless the subfield of neuroscience, when data analysis gets complicated, Bayesian statistics tend to be useful.

Why Bayesian data-analysis matters

Being able to combine data, using previous experiments to set priors for following experiments is the very essence of the scientific method. Being able to quantify such relations in a world characterized by progressive data integration and increasing use of databases is crucial for current and necessary for much of future neuroscience.

Assuming that the brain solves problems close to the Bayesian optimum often predicts behavior

If progressively more complex datasets force neuroscientists to use Bayesian statistics to make sense of their data – it should come as no surprise that animals would have to go down a similar route. After all, the world is complex, perception is noisy and ambiguous and data is scarce. In fact, it is known that without prior information learning is entirely impossible, an idea that is known since the work of Hume [8] and that has been recently formalized in the so-called no free lunch theorems [9]. While there is no doubt that the brain needs to combine noisy information with relevant prior knowledge, how close the way it does this to the optimal Bayesian solution is an issue of intense debate.

Before moving to the discussion of concrete applications we need to clarify what we mean by Bayesian behavior. The sole essence of Bayesian models of behavior is that they predict that behavior is close to the best possible solution to a problem encountered by the animal. Nothing about likelihoods or priors needs to be explicitly represented. For example, chemical stability of synapses over multiple timescales[10], may implement the believe that the past is similar to the presence and that the world evolves over multiple timescales [11]. As far as models of behavior are concerned, they do not make any statement about the nature of the implementation of the underlying statistical calculations[12].

Bayesian models are frequently used to model information integration. Sensory signals get combined with one another or with priors. They are integrated over time or space. Recent research using simple models for such integration has compared actual behavior with predictions of models of optimal integration. Behavior is often close to optimal for cue combination in motor settings, auditory, visual and sensorimotor behavior [13].

Bayesian models have also recently been used to model many high level cognitive phenomena. Some studies construct Bayesian models of how subjects estimate the values of continuous variables [e.g. 14]. Other studies construct Bayesian models of how subjects estimate the structure of the world [15–18]. A thriving community tries to relate actual behavior to predictions of optimal Bayesian behavior.

However, there is an active debate about the explanatory power of Bayesian models. A central criticism of Bayesian theories is that the degrees of freedom in the models allow a new kind of over-fitting, basically allowing the modeler to achieve any predictions they like [19]. The defense by these Bayesian modelers is that there are far fewer degrees of freedom because knowledge about the actual structure of the world makes the set of permissible Bayesian models rather small[20]. Constraining Bayesian models, e.g. by measuring the statistical properties of the real world, seems crucial to strengthen their predictive power.

Why Bayesian models of behavior matter

The question of how “Bayesian” or optimal the brain is, is important in and by itself. Beyond this, understanding the problem that the brain needs to solve is important. Any credible model of how the brain or a part of it works must be able to solve the problems that are defined by the environment. This is a surprisingly high bar. For example, while many Bayesian or optimal control algorithms are used to control robots [21], we find few neuromorphic implementations of such algorithms. Lastly, building Bayesian models of information integration leads to an understanding of the relevant variables and their interplay. This understanding is inspiring a good number of experiments in experimental neuroscience.

Asking how the nervous system could achieve Bayesian behavior leads to new insights about neural codes

Many theories are competing about the representation of uncertainty and computation with it and they generally derive from simple assumptions. For example, in linear Probabilistic Population Codes [PPC, 22] the dearth of spikes in a Poisson model represents uncertainty. In sampling models uncertainty is represented in the sequence of activities [23]. In yet other work it’s the firing rate of specialized neurons that represents uncertainty [24]. Many different codes of uncertainty can be unified through the use of Bayesian statistics and the idea of population codes [25]. Each of the proposed models of the representation of uncertainty is elegant by focusing on just one easily communicable code of uncertainty.

However, uncertainty is just one of the many pieces of knowledge about the world that the brain is representing. And in most cases, when probed carefully, the brain exhibits complicated codes [e.g. 26]. Existing studies that ask how uncertainty is represented all point into the direction of complicated codes [27–32]. Admittedly, there have been too few studies asking how uncertainty is represented so it is hard to be sure. Still, I am aware of no dataset that suggests that, across brain areas, there is a simple, conserved, representation of uncertainty.

Each of the proposed models predict some measured data. Some neurons lower firing rates when uncertainty is higher [22] as predicted by probabilistic population codes. Other neurons increase their firing rate[24]. The fact that activities during sleep resemble activities during natural scene viewing [23] is predicted by sampling models. Moreover, there is a broad range of fMRI findings about the role of uncertainty, that do not clearly support any one model [but see 27 28],. And in some cases where neural responses were probed during a task where uncertainty can be well controlled have shown a rather complex set of neural responses [30]. It seems that the overall representation of uncertainty is complicated.

If we find some data disagreeing with a given theory of neural representation of uncertainty (which would be very easy) should we declare it falsified and move on? I disagree with this conclusion[33]. Instead we can view theories as priors, allowing us to deal with approximately true theories. Instead of a theory that posits that no information is lost (as is the case for all theories of optimal processing) we should use a theory that states that high information loss is less probable than low information loss. Instead of assuming that the neural code for uncertainty is the same in all brain areas (as is generally implied) we might prefer to assume that it is similar in related brain areas. We should work on finding ways of making approximately correct theories useful, by using them as part of the data analysis process.

Future promise

Reformulating existing theories as priors and combining them with other theories and with data should allow making these theories more useful, even if they do not capture the full amount of variance. In fact, such combinations between Bayesian data analysis and computational neuroscience modeling promises a more constructive process for improving theories and for analyzing and optimizing experiments.

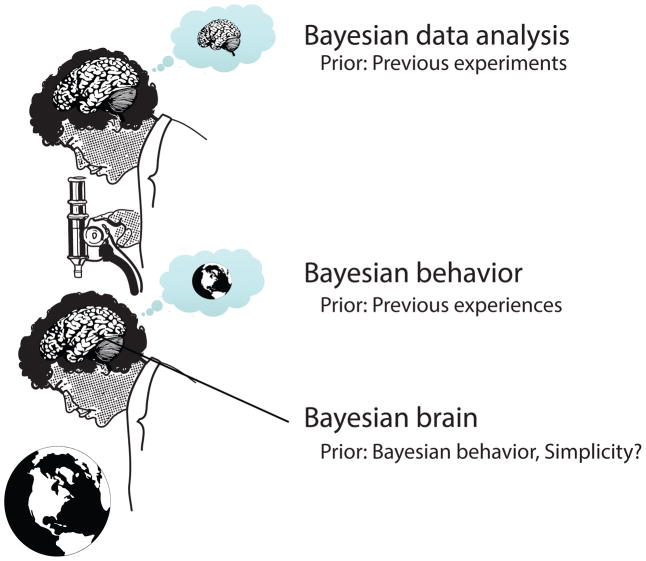
Figure 1.

Scientists try to make sense of the brain. Brains try to make sense of the world. Both processes are statistical. But current theories are focused on simplicity of the neural code, the assumption of which may be wrong.

Highlights.

• Bayesian statistics is a standard tool for modeling and data analysis

• Allows combining past data with new evidence

• In many cases people behave as predicted by Bayesian statistics

• Models should progressively be combined with data