Abstract
In vitro fertilization (IVF) is an increasingly common method of assisted reproductive technology. Because of the careful observation and followup required as part of the procedure, IVF studies provide an ideal opportunity to identify and assess clinical and demographic factors along with environmental exposures that may impact successful reproduction. A major challenge in analyzing data from IVF studies is handling the complexity and multiplicity of outcome, resulting from both multiple opportunities for pregnancy loss within a single IVF cycle in addition to multiple IVF cycles. To date, most evaluations of IVF studies do not make use of full data due to its complex structure. In this paper, we develop statistical methodology for analysis of IVF data with multiple cycles and possibly multiple failure types observed for each individual. We develop a general analysis framework based on a generalized linear modeling formulation that allows implementation of various types of models including shared frailty models, failure specific frailty models, and transitional models, using standard software. We apply our methodology to data from an IVF study conducted at the Brigham and Women’s Hospital, Massachusetts. We also summarize the performance of our proposed methods based on a simulation study.
Keywords: In vitro fertilization, Mixed model, Survival data
1. Introduction
In vitro fertilization (IVF) is an increasingly common method of assisted reproductive technology that by 2003, accounted for 1% of all births in the U.S [1]. In the U.S. the number IVF cycles increased from < 46, 000 in 1995 to > 120, 000 in 2005. The increase in popularity of IVF and its concurrent collection of risk factor and outcome data has motivated a number of research studies to identify and assess factors that impact IVF success rates. Of particular interest have been efforts to evaluate modifiable risk factors, such as obesity and alcohol intake [2, 3, 4], as well as widespread environmental exposures including pesticides, polychlorinated biphenyls (PCBs), and other endocrine disruptors [5, 6, 7].
Our research is motivated by an IVF study conducted by the Brigham and Women’s Hospital (from hereon referred to as the BWH study) and including married couples newly enrolled for IVF treatment between 1994 and 2003 at three clinics in the Boston area. The IVF process involves hormonally controlling the ovulatory process, removing ova (eggs) from the woman’s ovaries and fertilization with sperm. The fertilized egg (zygote) is then transferred to the patient’s uterus with the goal of establishing a successful pregnancy. A successful live-birth occurs only when all the preceding steps were successful.
In the BWH Study, a cycle of IVF treatment usually began with use of a GnRH-a (Gonadotropin-releasing hormone) in a long (down regulation) or short (flare) regimen. Ovarian response was monitored by measuring serum estradiol levels and the number and size of follicles by ultrasound. Generally, when there were two or more follicles with a diameter of equal to or greater than 18 millimeters, human chorionic gonadotropin (hCG) was administered to replicate the pre-ovulatory surge of luteinizing hormone (LH). Transvaginal oocyte recovery generally occurs 36 hours after hCG administration, and the oocytes were then inseminated by mixing them with approximately 50–300 thousand sperm or by intracytoplasmic sperm injection (ICSI). If insemination was successful, the embryos were cultured for several days (ranging from two to five) prior to uterine transfer. Some or all of the embryos were transferred to the uterine cavity via transfer catheter and about 18 days after embryo transfer, a blood pregnancy (β-hCG) test was performed. If the serum β-hCG test was positive, women would then undergo additional testing to monitor the rise in β-hCG levels and a pelvic ultrasound was performed to determine whether there is clinical evidence of a pregnancy (observation of at least one fetal heartbeat). If a clinical pregnancy was detected on ultrasound, follow-up of couples was arranged to document whether the pregnancy ended in a live birth or in miscarriage, ectopic pregnancy, molar pregnancy, or stillbirth. The cycle was considered to be successful only if the pregnancy ended in the delivery of at least one live newborn.
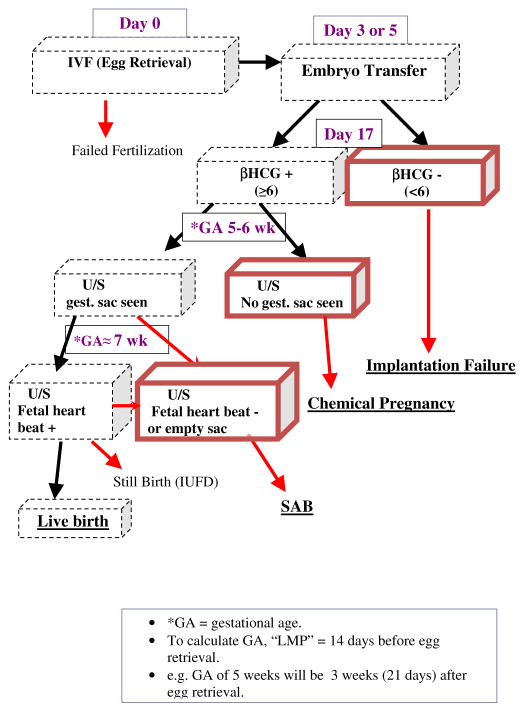
A failure to achieve a live birth can occur at multiple points during the IVF cycle. Among the most common failure types were failed implantation, early fetal loss (this corresponds to a pregnancy that was detected via a rise in hCG levels, but which did not progress to the point where a fetal sac could be detected) and spontaneous abortion (SAB) corresponding to the natural termination of a clinically detectable pregnancy. If a failure occurs, the woman may choose to drop out of treatment or decide to continue for another IVF cycle. In the BWH Study, women could have up to six IVF cycles. Please refer to Figure 1 for a graphical description of a IVF cycle with the three main failure types marked.
Figure 1.
A graphical display of a typical IVF cycle with three main failure types underlined.
The specific questions we are interested in are: (1) What are the covariates (demographic and clinical) that are associated with risk of a IVF failure due to different failure types? (2) Does age contribute to the odds of IVF failure, and if so, is age related to each of the failure types differently? In other words, is there an interaction between age and failure type? (3) Does BMI of a woman contribute to the odds of IVF failure and does the effect of BMI differ across failure types? The complex structure of the IVF data presents several statistical challenges to answer these questions and there is a need for appropriate statistical methodology for the analysis of these complex data.
Many data analysis techniques have been employed to analyze IVF data, ranging from simple binomial tests to sophisticated models designed specifically for use with IVF data. Penman et al. [8, 9] describe methodology for simultaneously modeling the different stages of IVF procedure by considering the stage as an ordinal response, where the response is the highest of these stages successfully achieved and modeling the conditional probability of being in a particular category, given that the response is in the same or higher category. Spiers et al. [10] proposed the ’EU’ (embryo/uterus) model which relies on the fact that successful pregnancy depends upon both the health of the mother (i.e., “uterine receptivity”) and the viability of the transferred embryos (i.e., “embryo quality”). In general, these methods have not fully exploited or adjusted for the repeated measures nature of many IVF data sets.
Pregnancy outcomes are widely-recognized to be correlated within a single woman, such that women with adverse outcomes for previous pregnancies (preterm birth, still birth, SAB, low birth weight, and birth defects) are more likely to have adverse reproductive outcomes in their current pregnancy. The wide range of reproductive outcomes demonstrating such intra-woman clustering has led to the need to consider early reproductive outcomes, and not simply those associated with a recognized pregnancy [11, 12]. Dukic and Hogan [13] extended the EU model to allow for heterogeneity of patients in embryo viability as well as correlation between the embryo viabilities using a hierarchical Bayesian formulation. This was achieved by allowing patient specific effects in the regression model for viability of the embryo. Recently, Missmer et al. [14] extended the EU method to the multiple cycle setting and also discussed simpler approaches based on modeling time to successful pregnancy. The approach in [14] is based on ideas of discrete survival analysis [15, 16], modeling the cycle-specific probability of a successful pregnancy. Such discrete survival models have also been used for modeling the probability of conception at each menstrual cycle for women conceiving naturally [5, 17, 18].
None of these approaches, however, account for the multiple types of IVF failure which are possible within a single cycle for the same woman, as well as the multiple IVF cycles potentially experienced per woman. While there is a rich literature on the analysis of repeated multivariate data [19]–[22], these do not take account of the sequential or time ordered nature of IVF data. Perhaps the most closely related work is that of Chen et al. [23] and Ryan [24] who used correlated multinomial models to analyze multiple outcome data from developmental toxicity studies where littermates are assessed for various types of reproductive failure.
In this paper, we develop statistical methodology for analysis of IVF data when multiple cycles and possibly multiple failure types are observed for each individual. Within each cycle, the three outcomes we consider are mutually exclusive. Our approach accommodates this fact explicitly by modeling the probability of failure occurring at each stage conditional on “success” at the previous stage. For example, the only cycles considered for the outcome of chemical pregnancy are the ones for which there was a successful implantation, and so on. The risk sets are then defined conditional on success at the previous stage. Thus, the model proposed in this article falls in a class of discrete survival models (e.g., [14, 15, 16]), where the probability of failing at each stage is modeled conditional on succeeding in the previous stage.
The rest of the article is organized as follows. In Section 2, we develop a general methodology based on a generalized linear modeling formulation that will allow us to implement various types of models ranging from shared frailty models and failure specific frailty models to transitional models. In Section 3 we demonstrate our proposed methodology by applying it to analyze IVF data, followed by a discussion in Section 4.
2. Model Formulation and Analysis
2.1. Analysis of Multiple Cycle IVF Data
To develop our proposed modeling framework, it is convenient to think of the observable data as corresponding to a set of outcomes (success/failure) observed at each failure opportunity (failed implantation, SAB etc), indexed by the identity of the subject under study, the cycle of observation as well as the nature of the failure at each opportunity. In our subsequent analysis of the BWH Study data, we consider the three most common failure types: implantation failure, chemical pregnancy only or spontaneous abortion (SAB). Let N be the number of subjects in the study and M denote the total number of failure opportunities observed in the data set (the number of rows in the data matrix). Note that in general M > N as one subject may contribute several rows to the data matrix. Suppose that pi denotes the probability that a failure has occurred at the ith failure opportunity, and Fi and Ci denote the failure type and cycle number associated with the ith failure opportunity. The main challenge will be to appropriately account for the correlation induced by having repeated cycles assessed on each woman, as well as having multiple failure types possible within each cycle.
2.1.1. Generalized Mixed Effects Model
One simple approach involves the inclusion of a subject-specific random effect, specifically:
where Ji denotes the identity of the person corresponding to the ith failure opportunity and αJi is a person-specific random effect. Here Xi is the design vector corresponding to the ith failure opportunity.
It is important to note that one woman within one IVF cycle may encounter only one or multiple failure opportunities depending on the outcome of that cycle. For example, suppose a woman experiences implantation failure in one cycle. In this case, the woman can no longer go through the next stages of the cycle anymore and thus only encounters one failure opportunity with observed response Y = 1 indicating a failure. However, if a woman experiences failure at chemical pregnancy stage in a cycle, it is already implied that she has successfully moved past the implantation stage. Thus she encounters two failure opportunities with observed responses Y1 = 0 and Y2 = 1, indicating that the outcome of the first stage was a success but the outcome of the second stage was a failure. Note that in both the cases, we do not record the response of the subsequent failure types/stages since the women can no longer continue the IVF cycle. Thus the generalized linear mixed model described above in fact models the probability of failure at each stage conditional on success at the previous stage. An easy way to structure the observed data in this way is provided in Section 2.2.
By careful definition of covariates in Xi, we can accommodate a wide range of models. Suppose, for example, we wanted a simple model where each of the failure types of interest (failed implantation, chemical pregnancy and SAB) were each separately modeled as linear functions of age. Then we would define
A slightly more complex model would allow for the person-specific random effect to vary by failure type. This can be accommodated by including failure-specific random effects for each woman (ωJi,1, ωJi, 2, ωJi,3). In this case we write
where I(·) denotes the indicator function and where (ω1, ω2, ω3) follows a Normal(0, R) distribution where R is an unknown covariance matrix.
These two models are special cases of the more general mixed effects model
where γ is a vector of appropriate random effects and Ui is a covariate vector of 0’s and 1’s. We provide several examples below to demonstrate the model construction process.
Our particular model of interest is the shared frailty model with age and failure type interaction; that is, we include both the main effect of women’s age as well as interactions between age and the three failure types as our covariates, along with person-specific (but not failure-specific) frailties in the model. To incorporate subject-specific frailties, αJi, we define the covariate vector Ui = (Ui1, …, UiN)T such that for j = 1, …, N, Uij = I(j = Ji) where N is the number of subjects and define γ = (α1, …, αN)T. In the example given in Table 1, when modeling p1 to p7, we will use U1 = …= U7 = (1, 0, …, 0)T. To model the random effects, one typically assumes . In our framework, this translates to .
Table 1.
Demographic Characteristics of Participants of Brigham and Women’s Hospital IVF Study With at Least One Successful Embryo Transfer, Overall and by Failure Type*
| Characteristic, mean (SD) | By Failure Type*
|
Overall (N=2346) | |||
|---|---|---|---|---|---|
| Implantation Failure (N=1227) | Chemical Pregnancy (N=192) | Spontaneous Abortion (N=124) | Live birth (N=760) | ||
| Age | 35.8 (4.4) | 35.21 (4.2) | 35.6 (4.5) | 34.2 (3.9) | 35.2 (4.3) |
| BMI | 24.9 (5.0) | 24.21 (5.3) | 24.6 (5.9) | 23.9 (4.5) | 24.1 (4.9) |
| Gonadotropin dose | 35.5 (18.8) | 32.7 (14.5) | 33.4 (15.8) | 30.2 (13.9) | 33.3 (17.0) |
| Embryos transferred | 2.9 (1.2) | 2.9 (1.3) | 3.2 (1.6) | 2.9 (1.1) | 2.9 (1.2) |
| Previous livebirth, % | 22% | 22% | 25% | 25% | 23% |
| ICSI, % | 27% | 30% | 22% | 32% | 29% |
| Down regulation, % | 66% | 78% | 77% | 84% | 73% |
IVF=in vitro fertilization; BMI=body mass index; ICSI=intracytoplasmic sperm injection
’Failure Type’ indicates the failure point at their first cycle with a successful embryo transfer.
One can easily fit such a model using a generalized linear mixed effects model. An easy way to structure the observed data to facilitate the model fitting is provided in Section 2.2. This can be easily implemented in already available statistical software packages such as PROC GLIMMIX and PROC NLMIXED in SAS, and the ‘nlme’ and ’lme4’ packages in R.
2.1.2. Transitional Models
An alternative to random effects models are transitional models, which in our case correspond to modeling each failure opportunity as a function of what has happened for the same study subject previously. In general, in any given cycle of a woman, one models the probability of a particular failure type by a logistic regression model where the covariate vector includes covariates relating to history of past observations, and present and past covariates for the woman. In particular, conditional on the covariates one can use the transition model
where Xi is the covariate vector, appropriately constructed to capture relevant past history at each failure opportunity.
Note that one could also construct a multiple outcome version of a discrete time survival model by simply including indicator variables of pregnancy stages (I(Fi = 1), I(Fi = 2), I(Fi = 3)), cycle numbers (I(Ci = 1), I(Ci = 2), and so on) and their interactions in Xi in addition to other covariates for that failure opportunity. Thus we would have a different intercept corresponding to a particular cycle and failure type as a woman progresses through multiple cycles. We will use this model in our data analysis as well.
2.2. Observed Data Structure
Let Y be the outcome, a vector of binary failure type indicators for each failure opportunity (implantation failure, chemical pregnancy only or SAB) in each cycle that a woman receives IVF, J the vector of ID codes indicating which woman was being treated, C the vector of cycle numbers that the failure occurred and F the vector of outcome types.
To illustrate, consider data corresponding to two women: woman 1 experiences implantation failure in cycle 1, SAB in cycle 2 but has a live birth in cycle 3 while woman 2 has a live birth in cycle 1. Then woman 1’s contribution to the outcome vector would be recorded as Y = (1, 0, 0, 1, 0, 0, 0), C = (1, 2, 2, 2, 3, 3, 3) and F = (1, 1, 2, 3, 1, 2, 3). The ID vector J would simply take the value 1. The first ‘1’ in the outcome vector is indicator of implantation failure at cycle 1 (we do not record indicators of the other two failure types for cycle 1 as the woman was not in the risk set for those failures). The following two 0’s indicate that the woman did not experience implantation failure or chemical pregnancy only in cycle 2, the following ‘1’ indicates the indicator for SAB in cycle 2, and last three 0’s in Y indicate that the a failure did not happen at any of the three failure opportunities in cycle 3. Woman 2’s contribution to the outcome vector would be recorded as Y = (0, 0, 0), C = (1, 1, 1) and F = (1, 2, 3). The ID vector J would simply take the value 2. For each of the recorded failure opportunities, let X be the measured covariates, such as woman’s age, past reproductive history, Gonadotropin dose used in the IVF procedure, and number of embryos transferred. We record the data in a tabular form as given in Table S1 in Supplementary Materials. In our example, woman 1 contributes 7 rows to the data matrix while woman 2 contributes 3. Notice that the first failure encountered during any IVF cycle becomes the terminal event for that cycle, and thus the woman can no longer advance to future stages.
3. IVF Data Analysis
In this section we demonstrate our proposed methods by applying them to an IVF study conducted at Brigham and Women’s Hospital, the BWH Study. The data set contains 2, 562 women with a total of 4, 785 IVF cycles, each woman having between 1 and 6 cycles, depending on her outcome. In this analysis, we only consider those women who had at least one embryo transferred. There were 2, 346 such women contribution a total of 3, 985 cycles (there were 10 cycles with unknown failpoint and were excluded from our analysis). Among these cycles, 2, 227 resulted in implantation failure (IF), 315 in chemical pregnancy only (CP), 217 in SAB, and 1, 152 in live birth. There were 74 cycles (2% of the total number of cycles) that resulted in failure types other than IF, CP or SAB (e.g., ectopic pregnancy, molar pregnancy, and stillbirth). Hence, we focus on the three most common failure types, namely, IF, CP and SAB. Note that we did not discard the 74 cycles with other failure types. Our data structuring procedure allowed us to keep them in the analysis; we simply do not create separate endpoints for these failure types. After organizing the data, there were a total of 7, 128 failure opportunities. Noting that every woman can have up to three failure opportunities in each IVF cycle she goes through, the total number of failure opportunities for a particular individual across IVF cycles varied from a minimum of 1 to a maximum of 14.
We reiterate that the specific questions we are interested in are: (1) What are the covariates (demographic and clinical) that are associated with risk of a IVF failure due to different failure types? (2) Does age contribute to the odds of IVF failure, and if so, is age related to each of the failure types (FI, CP and SAB) differently? In other words, is there an interaction between age and failure type? (3) Does BMI of a woman contribute to the odds of IVF failure and is there an interaction between BMI and failure type?
Several covariates are measured for each woman. Some covariates are woman-specific, such as body mass index (BMI) at the initial cycle, treatment site (coded 1, 2 or 3), study enrollment period (1994–1998 versus 1999–2003), history of previous livebirth (yes versus no) and age at the initial cycle. Other covariates are cycle-specific, such as ampules of gonadotropin (continuous), GnRH-a regimen (down regulation or flare), whether or not intracytoplasmic sperm injection (ICSI) was used, and number of embryos transferred. Table 1 presents overall and failure type specific summary of these covariates. There were some missing values in some of the covariates. We have excluded the women with such missing covariates from our analysis.
We first fit a model which incorporates the data from repeat IVF cycles and multiple IVF failure types, with a separate intercept for each failure type but assuming common relative effects of all covariates on the failure outcomes (see Table 2). The relatively large value of the intercept associated with implantation failure reflects the fact that this is the most common failure type. The results suggest that a number of factors being associated with the risk of reproductive failure (see further discussion presently).
Table 2.
Evaluation of IVF and Participant Characteristics on IVF Failures in Brigham and Women’s Hospital IVF Study, for Mixed and Transitional Models Assuming Common Covariate Effects on IVF Failure Types
| IVF and Participant Characteristics | Mixed Model | Transitional Model |
|---|---|---|
| OR (95% CI) | OR (95% CI) | |
| Intercepts | ||
| Implantation failure | 1.00 (referent) | 1.00 (referent) |
| Chemical pregnancy | 0.21 (0.18, 0.24) | 0.23 (0.19, 0.28) |
| SAB | 0.20 (0.17, 0.24) | 0.21 (0.17, 0.27) |
| Gonadotropin dose | 1.26 (1.17, 1.36) | 1.27 (1.18, 1.37) |
| Embryos transferred | 0.73 (0.68, 0.78) | 0.73 (0.68, 0.78) |
| Previous livebirth | 0.81 (0.69, 0.95) | 0.80 (0.68, 0.94) |
| Down regulation | 0.79 (0.67, 0.92) | 0.78 (0.66, 0.91) |
| ICSI | 0.99 (0.86, 1.14) | 1.00 (0.87, 1.15) |
| BMI Categories | ||
| < 18.5 | 1.07 (0.73, 1.56) | 1.07 (0.73, 1.57) |
| 18.5 – 25 | 1.00 (referent) | 1.00 (referent) |
| 25 – 30 | 1.03 (0.87, 1.22) | 1.03 (0.87, 1.22) |
| > 30 | 1.00 (0.80, 1.25) | 1.01 (0.80, 1.26) |
| Age Categories | ||
| < 35 | 1.00 (referent) | 1.00 (referent) |
| 35 – 37 | 1.09 (0.92, 1.30) | 1.09 (0.92, 1.30) |
| 38 – 40 | 1.58 (1.31, 1.90) | 1.59 (1.32, 1.92) |
| > 40 | 3.42 (2.67, 4.36) | 3.49 (2.73, 4.47) |
|
| ||
| AIC | 7679.0 | 7694.0 |
IVF=in vitro fertilization; OR=odds ratio; CI=confidence interval; ICSI=intracytoplasmic sperm injection; BMI=body mass index; SAB=spontaneous abortion; AIC=Akaike’s Information Criterion
Although the results in Table 2 do not suggest much association with BMI, we include this variable since it has been reported in the literature as being important. For example, Zhang et al. [25] found that obese women had a significantly lower fertilization rate and fewer oocytes retrieved, but had similar rates of miscarriage and live births as women of normal weight, suggesting the potential of differential effects of obesity on different IVF failure types. Thum et al. [4] and Bellver et al. [3] also observed differential impact of obesity or extreme BMI (>35) on IVF outcomes. To accommodate such potential variation across failure types, we fit two different models incorporating (1) age-failure type interaction terms while adjusting for BMI as a linear covariate, and (2) BMI-failure type interactions adjusting for age as a linear covariate. In the age-failure type interaction model, we use age categories (<35, 35–37, 38–40, >40 years) and include interaction of each failure type with these categories while using age < 35 years as the reference group. In the BMI-failure type interaction model, we used four BMI categories: underweight (BMI< 18.5), normal (18.5 ≤ BMI < 25), overweight (25 ≤ BMI < 30) and obese (BMI ≥ 30), with the normal category as the reference group.
For each of the two scenarios described above, we also implemented transitional models where we included interaction terms involving cycle number (dummy variables representing 1 as reference group, 2, 3 and ≥ 4) and failure types to assess the trajectory of baseline failure probabilities for each failure type across cycles. The logistic mixed effects models were fitted using the glmer() function in R package lme4. The transitional models were fitted using glm() function in R.
The odds ratios (ORs) and their 95% confidence intervals (CIs) for the covariates are reported in Table 2 based on the models assuming common effects of covariates on the three failure types (i.e., without interactions between age or BMI with failure type). We observed estimated intercepts for chemical pregnancy and SAB intercepts which were significantly smaller than 1.0, indicating that the risks of failure due to chemical pregnancy and to SAB were lower than that for implantation failure. In addition, from the results in Table 2, it is clear that having a history of a successful previous live birth, use of GnRH-a in a long regimen (down regulation) and having more embryos transferred significantly reduces the odds of failure. In contrast, a higher dose of gonadotropin and older age (38–40 or over 40 years old) were associated with increased odds of failure. Use of intracytoplasmic sperm injection (ICSI) and BMI category were not found to be significantly associated with IVF failure. The estimated associations were very similar for the mixed and transitional models, and the width of 95% CIs also suggested similar levels of precision for the two types of models.
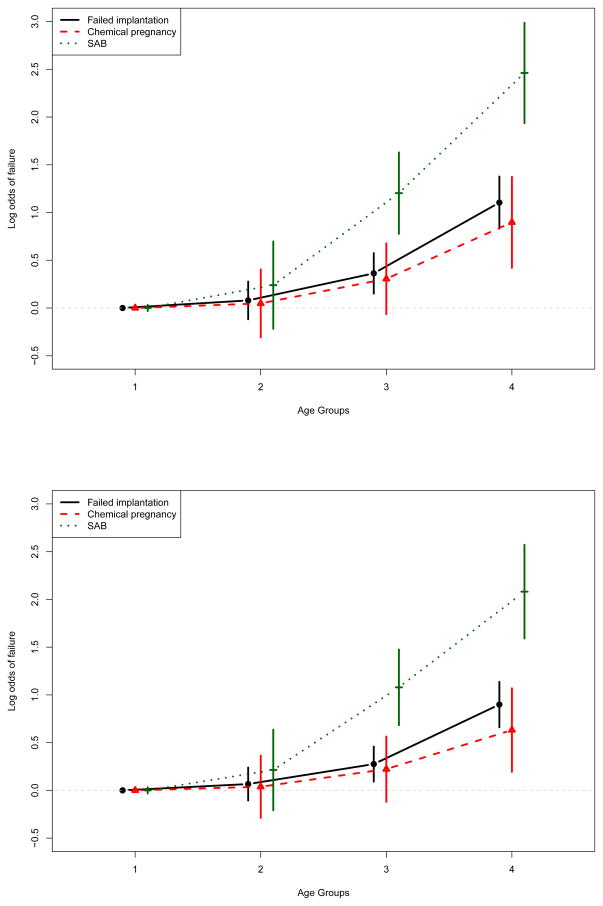
Previous research has indicated significant associations of BMI with fertility outcomes [26, 27], but our initial models did not confirm such associations. Models allowing for separate effects of BMI category on each IVF outcome, shown in Table 3 and Figure S1 (in Supplementary materials), also provided no support for higher risk of IVF failures for women classified as either underweight, overweight, or obese. However, results of models allowing the effect of age to vary over the IVF failure types (Table 3 and Figure 2) indicated that while those in higher age groups had significantly higher odds of failure across all failure types, the association with age was particularly strong for SAB.
Table 3.
Evaluation of IVF and Participant Characteristics on IVF Failures in Brigham and Women’s Hospital IVF Study, for Mixed and Transitional Models Allowing Varying Effects of Covariates on IVF Outcomes
| IVF and Participant Characteristics | Age-failure type interaction
|
BMI-failure type interaction
|
||
|---|---|---|---|---|
| Mixed Model | Transitional Model | Mixed Model | Transitional Model | |
| OR (95% CI) | OR (95% CI) | OR (95% CI) | OR (95% CI) | |
| Intercepts | ||||
| Implantation failure | 1.00 (referent) | 1.00 (referent) | 1.00 (referent) | 1.00 (referent) |
| Chemical pregnancy | 0.22 (0.17, 0.27) | 0.21 (0.17, 0.27) | 0.20 (0.16, 0.24) | 0.20 (0.16, 0.24) |
| SAB | 0.13 (0.10, 0.18) | 0.12 (0.09, 0.17) | 0.19 (0.16, 0.24) | 0.17 (0.13, 0.22) |
| Gonadotropin dose | 1.26 (1.17, 1.36) | 1.20 (1.13, 1.29) | 1.25 (1.16, 1.34) | 1.20 (1.12, 1.28) |
| Embryos transferred | 0.72 (0.67, 0.78) | 0.78 (0.78, 0.83) | 0.74 (0.69, 0.79) | 0.79 (0.74, 0.84) |
| Previous livebirth | 0.80 (0.68, 0.94) | 0.84 (0.73, 0.96) | 0.79 (0.67, 0.92) | 0.82 (0.72, 0.94) |
| Down regulation | 0.79 (0.67, 0.92) | 0.83 (0.72, 0.95) | 0.78 (0.67, 0.91) | 0.81 (0.71, 0.94) |
| ICSI | 0.99 (0.86, 1.14) | 1.01 (0.90, 1.14) | 1.02 (0.89, 1.17) | 1.03 (0.91, 1.16) |
| BMI (continuous) | 0.99 (0.98, 1.01) | 0.99 (0.98, 1.01) | (see Fig S1 in Supplementary Materials) | |
| Age (continuous) | (see Figure 2) | 1.09 (1.06, 1.11) | 1.07 (1.05, 1.09) | |
|
| ||||
| AIC | 7652.0 | 7692.0 | 7701.0 | 7738.4 |
IVF=in vitro fertilization; OR=odds ratio; CI=confidence interval; SAB=spontaneous abortion; ICSI=intracytoplasmic sperm injection; BMI=body mass index; AIC=Akaike’s Information Criterion
Figure 2.
Results of IVF data analysis. Displayed are the log odds ratios for interaction of age group by failure type with 95% confidence intervals for logistic mixed model (top panel) and transitional model (bottom panel).
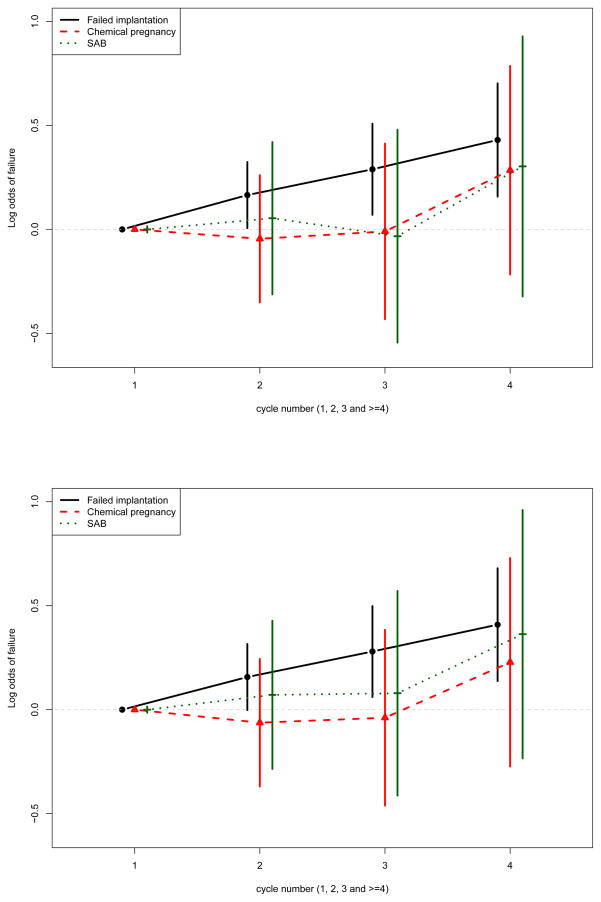
For our transitional model, the inclusion of interaction terms between cycle number (dummy variables representing 1 as reference group, 2, 3 and ≥ 4) and failure types allowed us to assess the trajectory of baseline failure probabilities for each failure types across cycles. As illustrated by the odds ratios presented in Figure 3, we observed a significantly higher odds of failed implantation as a woman undergoes more cycles. This pattern was not as clearly demonstrated for other failure types, although those undergoing a 4th IVF cycle had a suggestion of higher risk of failure for chemical pregnancy and SAB as well. Thus, the transitional model allows for direct estimation of the increased risk of each failure type associated with prior IVF failures.
Figure 3.
Results of IVF data analysis. Displayed are the log odds ratios for IVF cycle number by failure type interaction terms with 95% confidence intervals for age by failure type transitional model (top panel) and BMI by failure type transitional model (bottom panel).
Comparing between the mixed effects and the transitional models, we see that the AIC of the transitional model is slightly higher than that of the mixed effects model. This suggests that transitional model may not offer an improved fit to the data compared to the mixed model. For comparison to the models described above, we also fit simpler models based on the approach most often used to evaluate IVF outcomes [28, 4, 25]. These models consider only the first IVF cycle, and evaluate each of the different IVF failure types separately without accounting for their chronological ordering or intercorrelation. The results of the mixed model and transitional model, both of which allow multiple failure types and control for repeated IVF cycles, provide greater efficiency in estimating covariate effects than does the traditional model which focuses on a single outcome and uses only the first IVF cycle. For example, when assuming a common effect of all covariates on the three IVF failure types or when allowing for varying effects of age or BMI on failure type, there were significant associations of IVF failure with all covariates with the exception of ICSI and BMI. In contrast, when evaluating SAB or chemical pregnancy as separate outcomes (Table S2 in Supplementary Materials), only age >40 shows a significant association with IVF failure.
Allowing for separate effects of covariates on each failure type had no appreciable effect on the precision of parameter estimates over the common covariate effect model in applying our approaches for the BWH IVF study. For example, the estimated ORs and 95% CIs for IVF failure among women with previous live birth were 0.81 (0.69, 0.95) under a common effect of age and 0.80 (0.68, 0.94) for the mixed model with age by failure type interaction. In contrast, the separate models for implantation failure, chemical pregnancy, and SAB based only on first IVF cycles yielded estimated ORs (and 95% CIs) for IVF failure of 0.82 (0.65, 1.02), 0.76 (0.50, 1.16), and 0.72 (0.43, 1.18), respectively, for women with a previous live birth. The estimates for SAB are particularly prone to lack of precision in the single cycle, separate outcome analysis given that only those women with successful implantation failure and verification of a fetal sac (not only a chemical pregnancy) are considered in the “risk set”.
4. Discussion
We have presented a general and flexible framework to analyze IVF data involving multiple repeated ordered outcomes per individual. Our approach is based on generalized linear modeling formulation that allows us to model multiple failure types simultaneously.
There are a few existing approaches such as continuation ratio models [8, 9], or the ‘EU’ (embryo/uterus) model [10], and various extensions [29, 30, 13] that attempt to model IVF data. Penman’s continuation ratio approach views the IVF stage as an ordinal response, where the response is the highest of these stages successfully achieved and models the conditional probability of being in a particular category, given that the response is in the same or higher category. Spiers’ ‘EU’ (embryo/uterus) approach relies on the fact that successful pregnancy depends upon both the health of the mother and the viability of the transferred embryos. Specifically, the ‘EU’ approach formulates the probability of implantation of embryos by modeling each embryo’s own inherent viability and the receptivity of the uterus of the mother. However, this approach does not take the different failure types (following implantation) into account. In general, these methods do not fully exploit the multivariate nature of the data, as opposed to our proposed method. A major advantage of our approach is that our model can account for multiple cycles, with possibly different outcomes, for each woman. We have applied this approach in evaluating association of environmental exposures including chlorinated chemicals with IVF outcomes [7, 31], and it offers promise for evaluating exposures of other types as well as modifiable risk factors on complex reproductive outcomes.
We also identified several factors affecting odds of failure in an IVF cycle by analyzing the BWH IVF study data. It is interesting to note that the estimated odds ratios for some parameters (e.g. failure specific intercepts in Table 3) differ between the age-failure type and BMI-failure type interaction models. However the directionality of the estimates remained unchanged and hence the inference remains qualitatively unchanged. The approach we developed provided greater precision in estimating the effects of covariates than the standard approach of considering only the first IVF cycle and treating each IVF outcome separately. For example, separate analyses of each individual IVF outcome identified no significant association of a previous live birth with IVF failure, while our unified model including all failure types and all IVF cycles provided evidence of a significant protective effect. The flexibility of allowing covariate effects to vary by IVF failure type through the inclusion of interaction terms is an advantage which appeared to result in minimal loss of power in detecting associations.
Motivated by the IVF data set in hand, we focused on three main failure types (failed implantation, chemical pregnancy and SAB). It may happen that a woman experiences an outcome which is not among the three main outcomes. Our approach can easily accommodate this kind of situation. For example, suppose a woman experiences therapeutic abortion (TAB) in cycle 1. In this case, TAB is situated between chemical pregnancy and SAB in the order of failure points. Hence the outcome vector would be recorded as Y = (0, 0), F = (1, 2) and C = (1, 1). The two 0’s in Y indicate that the woman did not experience implantation failure or chemical pregnancy only in cycle 1. Note that we do not record the indicator for SAB in cycle 1 as the woman was not in the risk set for SAB.
Apart from identifying the demographic and clinical factors affecting IVF success, IVF studies offer great promise and potential as an avenue for identifying effects of environmental exposures on IVF outcomes. Participants in IVF studies often provide frequent biological specimens (urine, blood) to allow detection of pregnancies. The availability of these specimens can also be used to evaluate exposures to relatively common endocrine disruptors such as pesticides, phthalates, PCBs, heavy metals such as mercury and lead, and other exposures of interest. The statistical approach we developed here can be used to improve understanding of where in the pathway of reproduction potential insults may have occurred, based on critical windows of exposure. Techniques similar to those outlined for evaluating effects of covariates which may vary across failure types can be applied to assess whether there are differential effects of exposure across IVF outcomes. By incorporating interaction terms between exposure levels and failure types in the mixed or transitional models, additional insights on underlying mechanisms of disruption may be elucidated.
Finally, one important issue is to consider the situation where the number of cycles of a woman is correlated with her failure probabilities, that is, the cluster size is informative of the final outcome. In such situation, the estimates of the covariate effects may be biased and typical estimation procedures such as generalized estimating equations, may not provide valid results. A few techniques have been developed to address this issue. Dunson et al. [32] developed a method for jointly modeling cluster size and multiple categorical and continuous outcomes using a Bayesian approach as a generalization of the standard continuation ratio models. Neuhaus and McCulloch [33] consider the situation where cluster sizes and responses share random effects which are independent of the covariates. Then they show that if one uses maximum likelihood methods that ignore informative cluster sizes, only little bias is observed in the covariate effects that are uncorrelated with the random effects. However, for the covariate effects that are associated with the random effects, the estimators can be biased. In our analysis of the IVF data, we have not modeled the cluster size jointly with the response. In the light of the results of [33], our analysis is still reliable if the covariates are independent of the random effects associated with the cluster size and the IVF outcome. However, the issue of statistically determining whether covariates are dependent of the random effects has not been discussed much in the literature, to the best of our knowledge. We recognize that the issue of informative cluster size is in fact an important issue especially in IVF studies and is a topic for further research in future.
Supplementary Material
Acknowledgments
This research is supported in part by grants R00ES017744 (to Maity), ES000002, ES013967 from the National Institute of Environmental Health Sciences and grant HD32153 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors also thank an anonymous associate editor and two anonymous referees for their helpful comments and suggestions.
References
- 1.Wright VC, Chang J, Jeng G, Macaluso M. Assisted reproductive technology surveillance–United States, 2003. MMWR Surveill Summ. 2006;55:1–22. [PubMed] [Google Scholar]
- 2.Bellver J, Rossal LP, Bosch E, Zuniga A, Corona JT, Melendez F, et al. Obesity and the risk for spontaneous abortion after ooctyes donation. Fertility and Sterility. 2003;79:1136–1140. doi: 10.1016/s0015-0282(03)00176-6. [DOI] [PubMed] [Google Scholar]
- 3.Bellver J, Ayilon Y, Melo M, Goyri E, Pellicer A, Remohi J, Mesequer M. Female obesity impairs in vitro fertilization outcome without affecting embryo quality. Fertility and Sterility. 2010;93(2):447–454. doi: 10.1016/j.fertnstert.2008.12.032. [DOI] [PubMed] [Google Scholar]
- 4.Thum MY, El-Sheikhah A, Raris R, Parikh J, Wren M, Ogunyemi T, Gafar A, Abdalla H. The influence of body mass index to in-vitro fertilisation treatment outcome, risk of miscarriage and pregnancy outcome. Journal of Obstetrics and Gynaecology. 2007;27(7):699–702. doi: 10.1080/01443610701612334. [DOI] [PubMed] [Google Scholar]
- 5.Law DC, Klebanoff MA, Brock JW, Dunson DB, Longnecker MP. Maternal serum levels of polychlorinated biphenyls and 1,1,-dichloro-2,2-bis(p-chlorophenyl)ethylene (DDE) and time to pregnancy. American Journal Epidemiology. 2005;162(6):523–532. doi: 10.1093/aje/kwi240. [DOI] [PubMed] [Google Scholar]
- 6.Buck Louis GM, Lynch CD, Cooney MA. Environmental influences on female fecundity and fertility. Seminars in Reproductive Medicine. 2006;24 (3):147–155. doi: 10.1055/s-2006-944421. [DOI] [PubMed] [Google Scholar]
- 7.Meeker JD, Maity A, Missmer SA, Williams PL, Mahalangaiah S, Ehrlich S, Perry MJ, Cramer DW, Hauser R. Serum concentrations of polychlorinated biphenyls in relation to in vitro fertilization outcomes. Environtal Health Perspectives. 2011;119:1010–1016. doi: 10.1289/ehp.1002922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Penman R, Heller G, Tyler J. Modelling assisted reproductive technology data using an extended continuation ratio model. Sydney, Australia. Statistical Solutions to Modern Problems, Proceedings of the 20th International Workshop on Statistical Modelling; 2005. [Google Scholar]
- 9.Penman R, Heller G, Tyler J. Modelling IVF Data using an Extended Continuation Ratio Random Effects Model. Barcelona. Proceedings of the 22nd International Workshop on Statistical Modelling; 2007. [Google Scholar]
- 10.Speirs AL, Lopata A, Gronow MJ, Kellow GN, Johnston WI. Analysis of the benefits and risks of multiple embryo transfer. Fertility and Sterility. 1983;39:468–471. doi: 10.1016/s0015-0282(16)46933-5. [DOI] [PubMed] [Google Scholar]
- 11.Buck Louis GM, Schisterman EF, Sweeney AM, Wilcosky TC, Gore-langton RE, Lynch CD, Barr DB, Schrader SM, Kim S, Chen Z, Sundaram R on behalf of the LIFE study. Designing prospective cohort studies for assessing reproductive and developmental toxicity during sensitive windows of human reproduction and development - the LIFE Study. Paediatric and Perinatal Epidemiology. 2011;25:413–424. doi: 10.1111/j.1365-3016.2011.01205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Basso O, Olsen J, Bisanti L, Bolumuar F, Kuppers-Chinnow M. Repeating episodes of low fecundability: A multicentre European study. Human Reproduction. 1997;12:1448–1453. doi: 10.1093/humrep/12.7.1448. [DOI] [PubMed] [Google Scholar]
- 13.Dukic V, Hogan JW. A hierarchical Bayesian approach to modeling embryo implantation following in vitro fertilization. Biostatistics. 2002;3:361–377. doi: 10.1093/biostatistics/3.3.361. [DOI] [PubMed] [Google Scholar]
- 14.Missmer SA, Pearson KR, Ryan LM, Meeker JD, Cramer DW, Hauser R. Analysis of multiple-cycle data from couples undergoing in vitro fertilization: methodologic issues and statistical approaches. Epidemiology. 2011;22(4):497–504. doi: 10.1097/EDE.0b013e31821b5351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cox DR, Oakes D. Analysis of Survival Data. London, U.K: Chapman & Hall; 1984. [Google Scholar]
- 16.Cox DG, Hankinson SE, Kraft P, Hunter DJ. No association between GPX1 Pro198Leu and breast cancer risk. Cancer Epidemiology Biomarkers & Prevention. 2004;13(11 Pt 1):1821–1822. [PubMed] [Google Scholar]
- 17.Scheike TH, Jensen TK. A discrete survival model with random effects: An application to time to pregnancy. Biometrics. 1997;53:318–329. [PubMed] [Google Scholar]
- 18.Sundaram R, McLain AC, Buck Louis GM. A survival analysis approach to modeling human fecundity. Biostatistics. 2012;13(1):4–17. doi: 10.1093/biostatistics/kxr015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zeger SL, Liang K-Y. Longitudinal data analysis for discrete and continuous outcomes. Biometrics. 1986;42:121–130. [PubMed] [Google Scholar]
- 20.Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 21.Lefkopoulou M, Moore D, Ryan L. The Analysis of Multiple Correlated Binary Outcomes: Application to Rodent Teratology Experiments. Journal of the American Statistical Association. 1989;84:810–815. [Google Scholar]
- 22.Carey V, Zeger SL, Diggle P. Modelling multivariate binary data with alternating logistic regressions. Biometrika. 1993;80:517–526. [Google Scholar]
- 23.Chen JJ, Kodell RL, Howe RB, Gaylor DW. Analysis of Trinomial Responses from Reproductive and Developmental Toxicity Experiments. Biometrics. 1991;47:1049–1058. [PubMed] [Google Scholar]
- 24.Ryan L. Quantitative Risk Assessment for Developmental Toxicity. Biometrics. 1992;48:163–174. [PubMed] [Google Scholar]
- 25.Zhang D, Zhu Y, Gao H, Zhou B, Zhang R, Wang T, Ding G, Qu F, Huang H, Lu X. Overweight and obesity negatively affect the outcomes of ovarian stimulation and in vitro fertilsation: a cohort study of 2628 Chinese women. Gynecological Endocrinology. 2010;26(5):325–332. doi: 10.3109/09513591003632100. [DOI] [PubMed] [Google Scholar]
- 26.McLain AC, Sundaram R, Cooney MA, Gollenberg AL, Buck Louis GM. Clustering of fecundability within women. Paediatric and Perinatal Epidemiology. 2011;25:460–465. doi: 10.1111/j.1365-3016.2011.01219.x. [DOI] [PubMed] [Google Scholar]
- 27.Pinborg A, Caarslev C, Hougaard CO, Nyboe Andersen A, Andersen PK, Boivin J, Schmidt L. Influence of female bodyweight on IVF outcome: a longitudinal multicentre cohort study of 487 infertile couples. Reproductive Biomedicine Online. 2011;23(4):490–499. doi: 10.1016/j.rbmo.2011.06.010. [DOI] [PubMed] [Google Scholar]
- 28.Li Y, Yang D, Zhang Q. Impact of overweight and underweight on IVF treatment in Chinese women. Gynecological Endocrinology. 2010;26:416–422. doi: 10.3109/09513591003632118. [DOI] [PubMed] [Google Scholar]
- 29.Baeten B, Bouchaert A, Loumaye E, Thomas KA. Regression model for the rate of success of in vitro fertilization. Statistics in Medicine. 1993;12:1543–1553. doi: 10.1002/sim.4780121703. [DOI] [PubMed] [Google Scholar]
- 30.Zhou H, Weinberg CR. Evaluating Effects of Exposures on Embryo Viability and Uterine Receptivity in in vitro Fertilization. Statistics in Medicine. 1998;17:1601–1612. doi: 10.1002/(sici)1097-0258(19980730)17:14<1601::aid-sim870>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 31.Mahalingaiah S, Missmer SA, Maity A, Williams PL, Meeker JD, Berry K, Ehrlich S, Perry MJ, Cramer DW, Hauser R. Association of hexachlorobenzene (HCB), dichlorodiphenyltrichloroethane (DDT), and dichlorodiphenyldichloroethane (DDE) with in vitro fertilization outcomes. Environtal Health Perspectives. 2012;120:316–320. doi: 10.1289/ehp.1103696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dunson DB, Chen Z, Harry J. A Bayesian Approach for Joint Modeling of Cluster Size and Subunit-Specific Outcomes. Biometrics. 2003;59:521–530. doi: 10.1111/1541-0420.00062. [DOI] [PubMed] [Google Scholar]
- 33.Neuhaus JM, McCulloch CE. Estimation of covariate effects in generalized linear mixed models with informative cluster sizes. Biometrika. 2011;98:147–162. doi: 10.1093/biomet/asq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.