Abstract
The accurate staging of liver fibrosis is of paramount importance to determine the state of disease progression, therapy responses, and to optimize disease treatment strategies. Non-linear optical microscopy techniques such as two-photon excitation fluorescence (TPEF) and second harmonic generation (SHG) can image the endogenous signals of tissue structures and can be used for fibrosis assessment on non-stained tissue samples. While image analysis of collagen in SHG images was consistently addressed until now, cellular and tissue information included in TPEF images, such as inflammatory and hepatic cell damage, equally important as collagen deposition imaged by SHG, remain poorly exploited to date. We address this situation by experimenting liver fibrosis quantification and scoring using a combined approach based on TPEF liver surface imaging on a Thioacetamide-induced rat model and a gradient based Bag-of-Features (BoF) image classification strategy. We report the assessed performance results and discuss the influence of specific BoF parameters to the performance of the fibrosis scoring framework.
The excessive accumulation of newly synthesized extra-cellular matrix proteins in the liver tissue results in fibrosis which is the hallmark of chronic liver diseases1. Fibrosis progression is closely related to function failure and neoplastic generation2, therefore monitoring the histo-pathological information connected with liver fibrosis is necessary for the accurate diagnosis of chronic liver diseases and for establishing appropriate therapies. Although the routine histological assessment of liver fibrosis based on biopsy samples is invasive and can be subjected to staining variations, sampling errors and inter- and intra- observer discrepancies, it remains the best standard for fibrosis assessment3. Various non-invasive diagnostic tools, such as serum biomarker assays4 and liver stiffness measurements5, have been reported but none of them can provide histo-pathological information at the tissue and cellular level, which is the most direct and convincing evidence for the diagnosis of liver fibrosis by a pathologist.
Nonlinear microscopy for intrinsic two-photon excitation fluorescence (TPEF)6 and second harmonic generation (SHG)7 imaging has been demonstrated as a useful imaging tool for the qualitative and quantitative assessment of various diseases8,9. TPEF/SHG microscopy can considerably enhance the imaging penetration depth and reduce photobleaching and phototoxicity compared to conventional microscopy. SHG is a nonlinear nonresonant and coherent process that plays an important role in tissue imaging connected to the fact that non-centrosymmetric structures (eg. Collagen) exhibit a nonvanishing second-order susceptibility tensor χ(2) that under the influence of an external electric field generates a nonlinear optical signal at exactly half the wavelength of the excitation source. Conversely, the two-photon excitation of molecules is a nonlinear resonant and incoherent process that involves the simultaneous absorption of two photons whose combined energy is sufficient to induce an electronic transition to an excited electronic state. Excited by these two photons, a fluorophore acts in the same way as if excited by only one photon, emitting a single photon whose wavelength is only determined by its intrinsic characteristics, such as fluorophore type, chemical structure, etc. In TPEF, each excitation photon usually carries half of the energy that is needed to excite the fluorophore, so the wavelength for the two photons is roughly double of the wavelength of the one photon that could have been used in the same purpose8,10. TPEF/SHG microscopy can be used for imaging endogenous signals of tissue structures enabling the assessment of various conditions in non-stained tissue samples, and thus contribute to avoiding observer errors that are related to staining variations.
TPEF/SHG microscopy has already been employed for the qualitative assessment of liver fibrosis11 as histo-pathology features of liver tissue found in conventional histology slides could be successfully visualized in TPEF/SHG images12,13. Quantitative assessment of liver fibrosis through image analysis has also been adopted to complement the conventional qualitative assessment14,15. The advantages of quantitative assessment include the minimization of intra- and inter- observation variations16 and the speed at which a diagnostic can be reached, but most of the available quantitative studies of liver fibrosis are limited to the usage of information from SHG images only. Although the collagen deposition and architecture changes that can be visualized in SHG images are significant signatures of fibrosis progression, the cellular and tissue information in TPEF images are equally important as they provide information on various relevant aspects such as hepatic cell inflammation, apoptosis or portal hypertension. The use of TPEF images for quantitative assessment of liver fibrosis has not yet been studied to its full potential. In a previous study17 it was demonstrated that the bile duct cell proliferation area extracted from the TPEF image is a useful indicator for monitoring fibrosis progression in a bile duct ligation animal model, but it is disease specific and might not be adapted to other liver diseases.
The experiment presented in this study addresses this situation by combining TPEF imaging and a more general computer vision classification method, Bag-of-Features18,19 (BoF) for the purpose of quantification and automatic classification of liver fibrosis samples in a Thioacetamide (TAA)-induced rat model. BoF19 methods are inspired from the Bag-of-Words (BoW) text categorization methods used in information retrieval. By BoW, a document can be classified as belonging to a particular category based on a normalized histogram of word counts. BoF methods, also known as Bag-of-Visual-Words, adapt this text categorization approach to a visual categorization one, by replacing the dictionary of textual words with a dictionary of visual ones, usually referred to as “visual features”. Different BoF methods use different types of visual features, such as textons, raw image data, invariant descriptors of image patches, descriptors of affine invariant interest points, or others. To represent an image, BoF uses a histogram to indicate the number of occurrences of the visual words that take part in a dictionary in the respective image. The dictionary (a.k.a. codebook) is typically built by running a clustering algorithm over a large set of visual features in order to divide them into distinct groups and to identify the representative of each group (e.g., cluster mean). Given a novel training or test image, visual features are detected in it and assigning them their nearest matching terms from the visual vocabulary results in a normalized histogram of the quantized features detected in the image19, which is called the ‘term vector’. The term vector is practically the image representation used in BoF strategies. BoF has been successfully used for tasks such as category-level recognition20,21, object or shape retrieval22,23,24,25, content-based image and video retrieval26,27,28, tracking29,30, pattern mining31, scene classification32,33 or biomedical X-ray image classification34,35. Among the reasons for which this technique has attracted great attention in recent years are simplicity, effectiveness and its modular structure that makes it easily adaptable to a wide range of applications in various fields. In the past decade BoF has been introduced to the field of histopathology image classification36,37 but to the best of our knowledge, it has neither been used for classification of fibrosis stages in liver images, which is the subject of the experiment that we present in this paper, nor in association with the imaging method that we use, TPEF.
Our results clearly demonstrate the utility of TPEF imaging for the quantitative assessment of liver fibrosis, and show that a gradient based BoF strategy can be used to exploit TPEF image content variations connected to the cellular and tissue structure changes associated with fibrosis progression in a diagnostic purpose.
The importance of this experiment is well connected to the potential in vivo application for liver surface scanning of a TPEF/SHG endoscope. The parallel use of such a tool could consistently increase the level of information that is currently collected during a liver biopsy intervention, and could represent a key tool for patients who cannot be subjected to liver biopsy due to various medical conditions. Since the liver surface is surrounded by a thick collagen layer called the Glisson's capsule, the penetration depth of SHG signals in sub-capsule regions attenuates significantly. Thus SHG imaging alone cannot provide enough information when the liver surface is scanned. Hence, studying the suitability of TPEF image analysis for fibrosis assessment is of great importance to future TPEF/SHG endoscopy applications.
Besides illustrating the potential of TPEF liver surface imaging for quantitative liver fibrosis assessment, the experiment that we present highlights the way specific BoF parameters can influence the classification performance in the case of the addressed problem. We aimed at reaching a better understanding of the mechanisms that influence the BoF classification of TPEF liver fibrosis images, by experimenting with specific BoF parameters such as the spacing of the grid by which the features are extracted, the scale of a patch around each grid point that contributes to its descriptor or the size of the codebook. We consider presenting our findings on the BoF parameters influence to the classification performance to be important because to date this is the first study to combine TPEF imaging with BoF, and the first experiment that deals with the classification of TPEF images by exploiting the potential of Scale Invariant Feature Transform (SIFT)38 descriptors.
Results
Qualitative assessment of TPEF/SHG images from liver surface
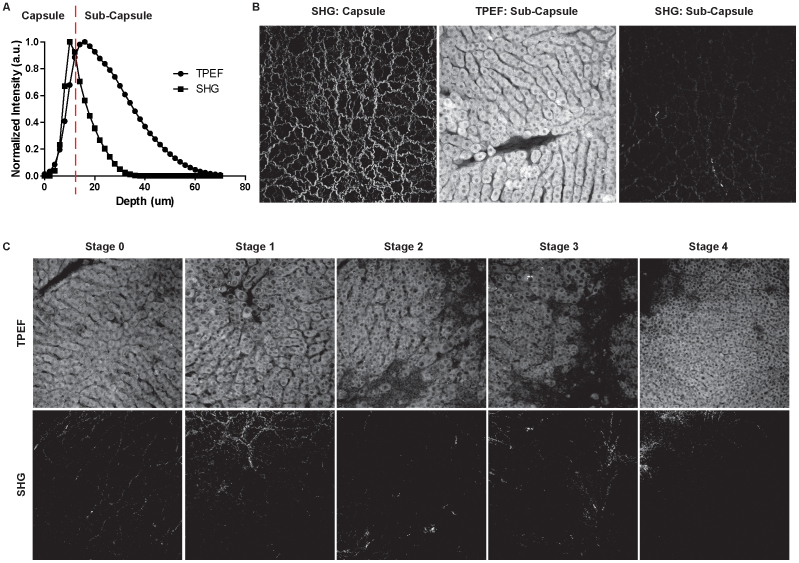
The liver samples were imaged under reflective mode of TPEF/SHG microscopy up to 70 μm from the liver surface. The SHG signals of the Glisson's capsule at the liver surface are strong but attenuate rapidly in the sub-capsule region as shown in Figure 1A, whereas the TPEF signals attenuate more slowly and are much stronger than SHG signals in the sub-capsule regions and therefore can provide more detailed tissue information. The SHG image of the Glisson's capsule as well as the TPEF and SHG images with the highest signal intensity in the sub-capsule region are illustrated in Figure 1B. The cellular structures can be clearly observed in the TPEF image and are complementary to the collagen information in the SHG image. Sub-capsule TPEF and SHG images of liver tissue samples from five fibrotic stages according to the Metavir scoring system are exemplified in Figure 1C; it can be noticed that cellular morphology changes can be successfully observed along fibrosis progression in TPEF images, whereas changes of collagen structures are not obvious due to the low signal intensity in the SHG images.
Figure 1. SHG & TPEF imaging on the liver surface.
(a) SHG & TPEF signal intensity at liver surface in respect to the position of the Glisson's capsule; (b) SHG image collected in the Glisson's capsule region and highest signal intensity TPEF and SHG images collected in the sub-capsule region. The cellular structures that can be observed in the TPEF image are complementary to the collagen information in the SHG image. (c) Pairs of TPEF & SHG images on fibrotic liver tissue from Stage 0 to Stage 4 collected in the sub-capsule region. The TPEF images show that in the normal liver the hepatocytes are well aligned along the sinusoidal spaces. In the course of fibrosis progression, such alignment is destroyed with enlarged nuclei size and nuclei to cell ratio. The tissue structure becomes messy with larger empty spaces occupied by deposited collagen. The collagen structures are not obvious in the corresponding SHG images due to the low signal intensity. Field-of-view size is 450µm x 450µm.
Quantitative assessment of TPEF images from liver sub-capsule region
Further on we present the quantitative assessment results that we obtained by using the DSIFT-BOF strategy presented in the Methods section. The impact of three DSIFT-BOF parameters (grid spacing, bin size and codebook size), that are associated with the spatial and architectural information of the tissue morphology, was investigated in the case of five scenarios. The classification of all fibrosis stages is important for the prognosis of fibrosis progression and for establishing optimal treatment therapies, and for this reason one of the problems towards which we have turned our attention was the classification between all five distinct fibrosis stages, Stage 0 vs. Stage 1 vs. Stages 2 vs. Stage 3 vs. Stage 4 (S0_S1_S2_S3_S4). Additionally, we evaluate the performances of the DSIFT-BOF framework in respect to predicting specific end points in the fibrosis progression, a task that has huge impact in respect to clinical planning. For example, the prediction of significant fibrosis (stages 2–4) versus non-significant fibrosis (stages 0–1) is critical for assessing the need of antiviral therapies, while the detection of cirrhosis (stage 4) versus non-cirrhosis (stages 0–3) is an important indicator for the end stage of fibrosis progression, which is associated to a higher risk of developing liver cancer such as hepatocellular carcinoma. Specific endpoint prediction is evaluated in the frame of four binary classification scenarios: Stage 0 vs. Stages 1, 2, 3, 4 (S0_S1234); Stages 0, 1 vs. Stages 2, 3, 4 (S01_S234); Stages 0, 1, 2 vs. Stages 3, 4 (S012_S34); and Stages 0, 1, 2, 3 vs Stage 4 (S0_S1234).
We evaluate the classification performances of DSIFT-BOF for the five fibrosis classification scenarios mentioned in terms of area under Precision-Recall (PR) curves, PR-area. In a binary decision problem a sample can be classified as either a positive or negative. The decision of the employed classifier can be represented in a structure known as confusion matrix, which consists of four categories: True Positives (TP), samples that are correctly labeled positive, False Positives (FP), samples that are incorrectly labeled as positives, and similarly True Negatives (TN) and False Negatives (FN). The confusion matrix can be used to construct the points of both PR and Receiver Operator Characteristic (ROC) spaces. In PR space, Recall, aka Sensitivity, is plotted on the x-axis while Precision, aka. Positive Prediction Value, on the y-axis. Eq. 1 and Eq. 2 give the definition of each metric. We have generated PR curves by varying the value of the classification criterion as described in the Methods section. The areas under the PR curves were calculated by trapezoidal approximations. The relationships that take place between the PR and ROC curves are very well described in (Davis and Goadrich, 2006)39.
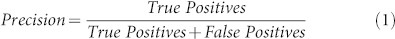 |
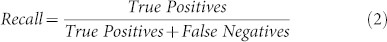 |
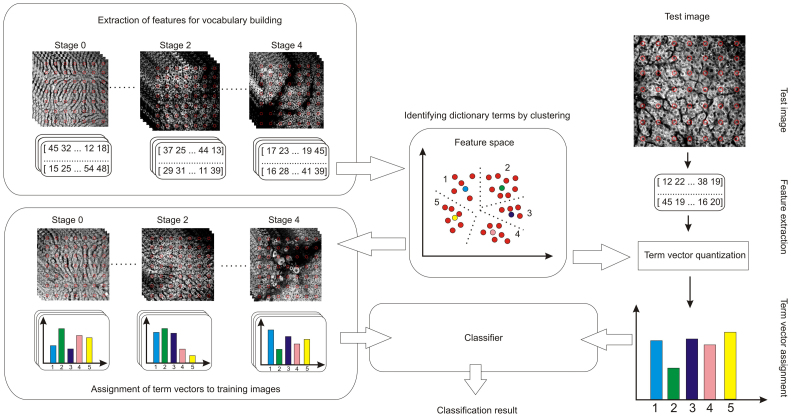
The DSIFT-BOF algorithm (Fig. 2) that we have experimented depends on three variable parameters: the grid spacing, the bin size and the codebook size. The grid spacing is the distance in pixels between extracted features while the bin size refers to the dimension of the SIFT bin38. A schematic illustration of these two parameters is shown in Figure 3. The codebook size is the number of visual words in the dictionary (referred throughout the paper as ‘codeblocks’) employed by the BoF classification framework.
Figure 2. Schematics of the DSIFT-BOF framework.
A codebook feature space is created by extracting DSIFT descriptors at fixed grid locations from all the images that are dedicated to vocabulary building. A codebook is generated by running a clustering algorithm that partitions the codebook feature space into k regions. The centroids of these regions (a.k.a. clusters) represent the codebook terms. The codebook allows for BoF representations, term vectors, to be assigned to training and test images. The term vector is a histogram that indicates the number of occurrences of the codebook terms in an image. Term vectors are assigned to the training images, and will be further on used as ground truth data by a classifier. An image is tested by assigning a term vector to it, and running this term vector through a classifier that uses the term vectors of the training images to indicate its fibrosis stage. The classifier that we use in this experiment is weighted k-NN.
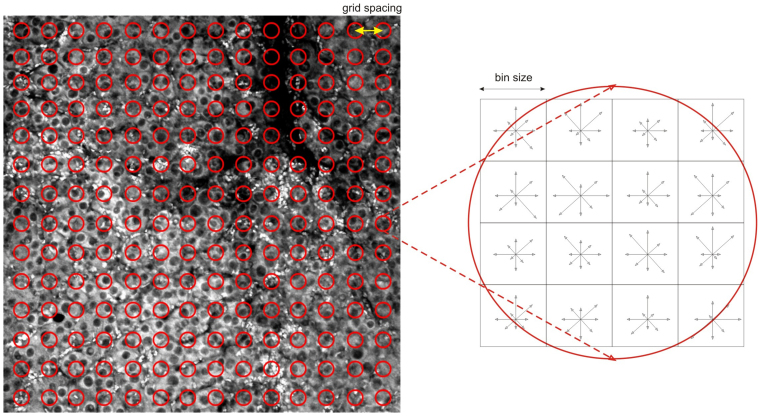
Figure 3. Illustration of grid spacing and DSIFT feature extraction.
For consistency reasons we extract the same number of features from all vocabulary, training or test images. The image locations from where the features are extracted are fixed according to a grid. A sparse grid, equivalent to a low number of features, can be responsible for dismissing important image information, while a dense grid, equivalent to a high number of features, is computationally demanding and may lead to redundant information. The DSIFT descriptors extracted from the grid locations are histogram representations that combine local gradient orientations and magnitudes from a neighborhood around a keypoint, indicated by the bin size. More precisely, the descriptor is a histogram of gradient location and orientation, where location is quantized into a 4 × 4 location grid and the gradient angle is quantized into 8 orientations, one for each of the cardinal directions. The resulting descriptor is a normalized vector with the dimension of 128 elements.
The values of these three parameters that we used in our experiment are presented in Table 1. The case of running DSIFT-BOF for one combination of the three parameters is referred throughout the paper as to a “scenario”. The results that we present are based on a number of 168 scenarios which equals the total number of all possible combinations of the three parameters tested (4 grid spacings × 6 bin sizes × 7 codebook sizes). The influences of grid spacing, bin size and codebook size to the achievable performance are presented in the following sections.
Table 1. The values of the evaluated BoF parameters.
| Parameter | Values |
|---|---|
| Grid spacing | 10, 20, 40, 60 |
| Bin size | 2, 4, 6, 8, 10, 12 |
| Codebook size | 50, 250, 500, 750, 1000, 1250, 1500 |
Grid spacing influence on the DSIFT-BOF performance
Grid spacing, resulting also in the total number of features extracted from an image, refers to the density of extracted features (Fig. 3). The use of various grid spacings has been reported in the literature; for example Lazbenik21 reported using SIFT descriptors38 extracted from a dense grid with a spacing of 8 pixels, and Tamaki40 evaluated the influence of using grid spacing of 5,10,15 pixels. In general, smaller grid spacing performs better as it generates more features but the offered advantage comes at the cost of increased computation time required for clustering, training and classification. We tested regular grids with 10, 20, 40 and 60 pixels spacing. The number of features extracted from an image of 1024 × 1024 pixels by using a grid spacing of 10 pixels is 36 times higher than when using one of 60 pixels (Supplementary Table 1).
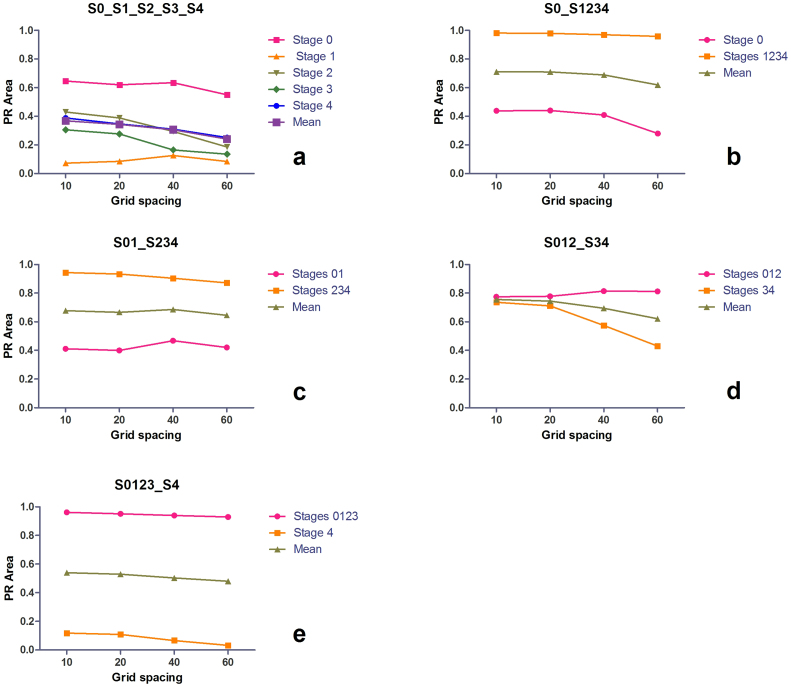
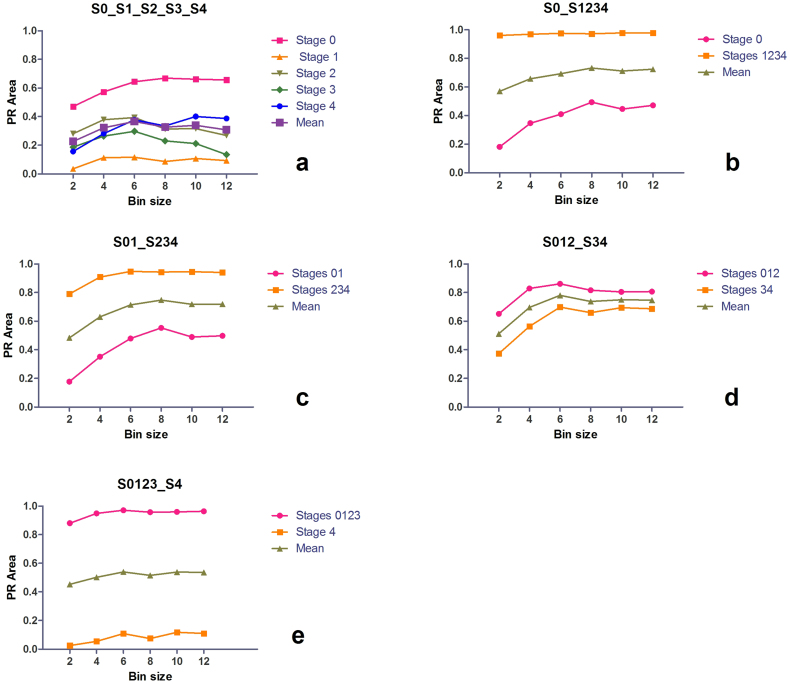
The values of the achieved PR-areas in the case of the ‘S0_S1_S2_S3_S4’ classification scenario are illustrated in Figure 4a. For each grid spacing size we have evaluated 42 scenarios (7 codebook sizes, 6 bin sizes). For all evaluated grid spacings, 10, 20, 40, 60 pixels, the best classification in terms of PR-area is observed for Stage 0 images, and worst classification is observed for Stage 1 images. As expected, the highest mean PR-area value is observed for a grid spacing of 10 pixels that is equivalent to 10′404 features per image, while the lowest PR-area, 52% lower than the maximum, is observed for the highest grid spacing, 60 pixels, which is equivalent to 289 features per image. Even if the differences between the minimum and maximum mean PR-area values are lower, the same trend can be observed also in the case of the four binary classification scenarios evaluated (Fig. 4 b,c,d,e). We observe a 15% decrease in the case of S0_S1234, 5% for S01_S234, 22% for S012_S34 and 12% for S0123_S4. ‘S01’ and ‘S012’ exhibit a different dependence of the grid spacing than the other evaluated binary classes, the PR-area slightly increasing with higher grid-spacing values.
Figure 4. Influence of the grid spacing on liver fibrosis classification performance by DSIFT-BOF.
(a) Stage 0 vs. Stage 1 vs. Stage 2 vs. Stage 3 vs. Stage 4; (b) Stage 0 vs. Stages 1,2,3,4 (c) Stages 0,1 vs. Stages 2,3,4 (d) Stages 0,1,2 vs. Stages 3,4 (e) Stages 0,1,2,3 vs. Stage 4. Grid spacing values refer to the number of pixels between feature locations.
Bin size influence on the DSIFT-BOF performance
One of the important parameters of a descriptor-based BoF method is the dimension of the patch around a keypoint that contributes to its descriptor. In the Scale Invariant Feature Transform (SIFT) method38 the dimension of this patch derives from the size of the bins (Fig. 3), and is related to the SIFT keypoint scale in the Gaussian Scale Space (GSS) by a multiplier. The DSIFT41,42 features used in our framework are not assigned a scale as they are not extracted by using SIFT's Difference-of-Gaussian (DoG) detector but from fixed locations corresponding to a grid. We adopt the concept of SIFT of correlating the bin size with the GSS and use for different bin sizes different representations of the image in the GSS. The GSS representations of the image are obtained by convolving it with an isotropic Gaussian kernel of different standard deviations (Supplementary Fig. 1).
In each particular scenario, the dimension of the patch is the same for all grid keypoints and is directly related to the bin size and smoothing level. We have evaluated six different bin sizes (2, 4, 6, 8, 10, 12 pixels) corresponding to different smoothed instances of the image, and observed how this influences the DSIFT-BOF classification results on TPEF images of liver fibrosis. In previous reports40 it has been proposed to use simultaneously (within the same run) features of different scales, or to include information originating at different scales in the same descriptor. We have chosen however to use features of the same scale within a particular scenario in order to grasp a better understanding of the scale's influence to the results.
Figure 5a presents the achieved PR-areas in the case of S0_S1_S2_S3_S4. For each bin size, we have evaluated 28 scenarios (7 codebook sizes, 4 grid spacings). For all evaluated bin sizes (2, 4, 6, 8, 10, 12), best classification in terms of PR-area is observed for Stage 0 while worst classification is observed for Stage 1. The highest mean PR-area is observed for a bin size of 6 pixels, while the lowest mean PR-area, 62% lower than the maximum, is observed for a bin size of 2 pixels. A similar dependence with the bin size can be observed also in the case of the four binary classification scenarios tested (Fig. 5 b, c, d, e). A bin size of 6 pixels provides a maximum mean PR-area in the case of S012_S34 and S0123_S4, while the position of the maximum PR-area shifts to ‘bin size = 8’ for S0_S1234 and S01_S234. For all classification scenarios evaluated we can observe a consistent rise in the performance between bin size values of 2 and 6 pixels, and low differences between bin sizes ranging from 6 to 12 pixels. For all evaluated scenarios a bin size of 2 pixels provides worst results.
Figure 5. Influence of the bin size on liver fibrosis classification performance by DSIFT-BOF.
(a) Stage 0 vs. Stage 1 vs. Stage 2 vs. Stage 3 vs. Stage 4; (b) Stage 0 vs. Stages 1,2,3,4 (c) Stages 0,1 vs. Stages 2,3,4 (d) Stages 0,1,2 vs. Stages 3,4 (e) Stages 0,1,2,3 vs. Stage 4. Bin size values, given in pixels, refer to the size of the regions that contribute to the bin histograms, which constitute the DSIFT descriptor.
Codebook size influence on the DSIFT-BOF performance
The BoF representation of an image (aka ‘term vector’) consists in a histogram of the visual words defined in a codebook (visual dictionary) that can be found in it, as described in the introductory section. The codebook is built by using a clustering (vector quantization) algorithm, which in our experiment is K-means43. An important parameter to be decided before commencing clustering is the number of codeblocks (aka visual words) that the dictionary contains. Choosing a particular value for this parameter depends on the type and content of the images to be classified as the codeblocks represent key image content components. Using fewer codeblocks has the advantage of potential higher discriminative power, while using more codeblocks has the advantage of potential higher sensitivity. In most applications, a higher number of visual words yields better discrimination between classes, at the expense of higher computational power needed for clustering, which is directly related to the size of the dictionary. Therefore, for deciding upon a dictionary size to be used for a specific application, one should identify the optimum tradeoffs of accuracy and computational efficiency. Even though a higher dictionary size provides better results in most applications on natural image classification18,20, the size of a dictionary was found not to be particularly important in a medical image classification task44. Caicedo et al.36 also report that their SIFT-based codebook required fewer codeblocks to express all different patterns in the histo-pathological image collection that they have tested, and claim their results to be consistent with the rotation and scale invariance properties of the SIFT descriptor. In this section we present our experiments on the codebook size influence to the DSIFT-BOF classification of TPEF liver fibrosis images. Seven codebook dimensions (50, 250, 500, 750, 1000, 1250, and 1500) are evaluated.
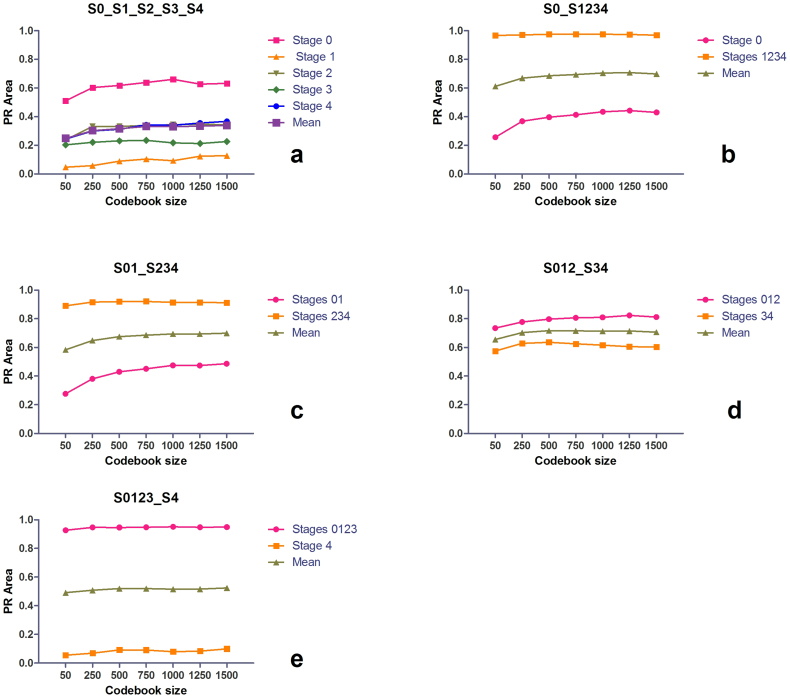
Figure 6a presents the codebook size influence on the S0_S1_S2_S3_S4 classification scenario. For each codebook size, we have evaluated 24 scenarios (6 bin sizes, 4 grid spacings). As in the previous classification experiments, for each of the evaluated codebook sizes, best classification results can be observed for Stage 0 images, while worst results can be observed in the case of Stage 1 images. The highest mean PR-area is observed for a codebook size of 1500, which is 37% higher than the worst case, the one of a 50 element codebook. The mean PR-area differences between codebooks of 750, 1000, 1250 and 1500 elements take values < 1%.
Figure 6. Influence of the codebook size on liver fibrosis classification performance by DSIFT-BOF.
(a) Stage 0 vs. Stage 1 vs. Stage 2 vs. Stage 3 vs. Stage 4; (b) Stage 0 vs. Stages 1,2,3,4 (c) Stages 0,1 vs. Stages 2,3,4 (d) Stages 0,1,2 vs. Stages 3,4 (e) Stages 0,1,2,3 vs. Stage 4.
Except for the case of the S012_S34 scenario, the PR results for the binary classification scenarios illustrate a similar trend, with performance increasing with codebook size (Figure 6 b,c,d,e). The maximum value of the mean PR-area is achieved for codebook dimensions of either 1250 or 1500 elements, with ~1% difference between the two cases. The minimum mean PR-area always occurs for the lowest codebook dimension, 50 elements. The differences between the maximum and minimum PR-area values range from 6% in the case of S0123_S4, to 16% and 20% for S0_S1234 and respectively S01_S234. In the case of S012_S34 the maximum mean PR-area value is achieved for a codebook dimension of 500 elements, 10% higher than the minimum value.
Summary of overall results
The mean PR-area values for all five classification scenarios evaluated, as well as the BoF configurations that yield the minimum and maximum PR-areas for each of the evaluated scenarios are presented in table 2.
Table 2. Mean PR-area values for all five classification scenarios evaluated and the BoF configurations that yield the minimum and maximum PR-areas.
| Classification scenario | Min PR-area | Max PR-area | Mean PR-area | |||
|---|---|---|---|---|---|---|
| Value | BOF configuration (bin/grid/codebook) | Value | BOF configuration (bin/grid/codebook) | Value | ||
| S0_S1_S2_S3_S4: | Stage 0 | 0.1393 | 4/60/50 | 0.8420 | 12/60/1000 | 0.6128 |
| Stage 0 vs. | Stage 1 | 0 | 2/40/250* | 0.2830 | 6/40/1500 | 0.0921 |
| Stage 1 vs. | Stage 2 | 0.0544 | 2/60/500 | 0.6811 | 4/10/750 | 0.3253 |
| Stage 2 vs. | Stage 3 | 0.0295 | 2/40/1250 | 0.5459 | 6/10/1500 | 0.2210 |
| Stage 3 vs. | Stage 4 | 0.0316 | 2/60/1250 | 0.6068 | 12/10/1250 | 0.3235 |
| Stage 4 | Mean | 0.1002 | 2/60/1500 | 0.4825 | 6/20/1500 | 0.3149 |
| S0_S1234: | Stage 0 | 0 | 4/60/50 | 0.6563 | 8/40/1250 | 0.3918 |
| Stage 0 vs. | Stages 1234 | 0.9128 | 2/60/1500 | 0.9911 | 12/40/500 | 0.9719 |
| Stages 1,2,3,4 | Mean | 0.4564 | 2/60/1500 | 0.8186 | 8/40/1250 | 0.6818 |
| S01_S234: | Stages 01 | 0.0063 | 2/60/1250 | 0.7323 | 10/40/1000 | 0.4249 |
| Stages 0,1 vs. | Stages 234 | 0.6927 | 2/60/1500 | 0.9849 | 8/10/1250 | 0.9128 |
| Stages 2,3,4 | Mean | 0.3744 | 2/60/50 | 0.8389 | 10/40/1000 | 0.6688 |
| S012_S34: | Stages 012 | 0.5168 | 2/10/50 | 0.9200 | 6/40/1250 | 0.7948 |
| Stages 0,1,2 vs. | Stages 34 | 0.1436 | 2/60/750 | 0.8726 | 6/10/750 | 0.6128 |
| Stages 3,4 | Mean | 0.3920 | 2/60/250 | 0.8706 | 6/20/1250 | 0.7038 |
| S0123_S4: | Stages 0123 | 0.8272 | 2/60/1500 | 0.9848 | 12/10/1000 | 0.9451 |
| Stages 0,1,2,3 vs. | Stage 4 | 0 | 2/40/50* | 0.2500 | 6/10/750 | 0.0815 |
| Stage 4 | Mean | 0.4149 | 2/40/50 | 0.6148 | 10/20/1500 | 0.5133 |
(*value may occur in other scenarios as well).
Discussion
In the presented experiment we have evaluated a SIFT based BoF framework, DSIFT-BOF, in respect to the potential of BoF methods for classifying liver fibrosis images collected by TPEF imaging. To the best of our knowledge this is the first experiment to combine TPEF imaging with a ‘Bag-of-Features’ image classification strategy and the first experiment to present an approach for the quantitative evaluation of liver fibrosis based on TPEF images collected from the liver surface.
The performed work was aimed at exploiting TPEF data collected on the liver surface in the purpose of assessing fibrosis stages and specific endpoints, at reaching a better understanding of how specific BoF parameters influence the classification performance in regard to the addressed problem and at introducing BoF to the fields of TPEF imaging and liver fibrosis assessment. We assessed the classification performances of the framework for the cumbersome five-class problem (S1_S2_S3_S4_S5) and for four binary classification scenarios important in respect to specific endpoint prediction, such as non-fibrosis and fibrosis (S0_S1234), non-significant fibrosis and significant fibrosis (S01_S234), mild fibrosis and severe fibrosis (S012_S34) and non-cirrhosis and cirrhosis (S0123_4). Best results in terms of mean PR-area are observed in the case of the S012_S34 scenario, while worst results can be observed as expected for the S0_S1_S2_S3_S4 scenario, which is generally considered a difficult classification scenario (Table 2). Taking into account that this experiment represents a first attempt in many regards, the overall results that we obtained (Fig. 4–6, Table 2) are promising and depict the potential of using TPEF imaging on the liver surface as a diagnostic method. The results reveal as well that combining gradient based BoF methods with TPEF imaging and using BoF strategies for quantitatively assessing liver fibrosis stages holds great potential.
The three BoF parameters to which we have focused our attention on are grid spacing, which is equivalent to the number of features extracted per image, bin size, and codebook size. The influence of different grid spacings on the performance of the DSIFT-BOF framework were found to be consistent for the majority of the classification scenarios evaluated, and propose a high density grid as the solution to be preferred despite the higher computational time implied. The worst performances of the classification framework were found to occur when using a bin size of 2 pixels, while best were observed for bin size values of 6 and 8 pixels This situations occurs due to the fact that in the case of low bin sizes neighbor gradients are highly correlated and are very likely to hit the same orientation, so the chance of having orientation bins equal to zero is significant. Such a situation prevents the full dimensionality of the descriptor from being exploited, since a considerable amount of ‘0’ elements will occur, yielding reduced specificity. Increasing the size of the patch that contributes to the descriptor reduces the occurrence of ‘0’ values in the descriptor, making it more discriminative. Our experiments on codebook size influence show that the classification performance is dependent of the codebook size only up to a point. The classification performance improvements are consistent for most scenarios when the codebook size is increased from 50 to 750 elements, but the PR-area differences observed between high dimensional codebooks (eg. 1000, 1250, and 1500) are very low. As higher codebook size means higher computational demand, we can think of a codebook of 1000 elements as providing an optimal ‘computational time/performance’ ratio. The minimum tested codebook dimension (50 elements) performs worst in all scenarios, but since the computational demand for this reduced number of clusters is considerably lower than in the other cases (over ten times lower than in the case of the highest tested codebook size – 1500 elements), it could still be considered an option for real-time, online or mobile applications. The most computationally expensive stage of the suggested DSIFT-BOF algorithm is the k-means clustering procedure. This stage aims to partition n observations (in our case n is sum of all features extracted from all vocabulary images) into k clusters, having each observation belonging to the cluster with the nearest mean. This problem is computationally difficult, NP-hard in general Euclidean space d even for 2 clusters. If k and d are fixed, the problem can be exactly solved in time O(ndk+1 log n)45. In our experiment we use seven codebook dimensions (codebook dimension = k) and the observations are 128-dimensional. A higher PR-area was observed in the binary classification scenarios for the classes containing more stages (eg. non-cirrhosis). Besides being related to image content, this situation is related as well to a statistical reason that influences the weighted k-NN nearest neighbor strategy used for classification. If more fibrosis stages correspond to a class, and the number of associated training images for each class is proportional to the number of fibrosis stages (like in the case of our implementation), there is a higher probability for the k-NN classification criterion to be met for a sample belonging to that particular class. In consequence, in such a situation the classes containing more fibrosis stages are privileged in comparison to the others.
The presented BoF based framework is a modular one, and enhancing any of its components, independently of the others, leads to an enhancement of the overall results. Our future work in this field will focus on enhancing the method by implementing various modifications to the algorithm, such as including orientation and spectral information in the descriptor, using other classifiers more complex than k-NN (such as support vector machines), optimizing the number and the type of images used for vocabulary building and for training or by enabling the automatic selection of optimal BoF parameter configurations. In the same time, our future work aims at developing an advanced iterative approach which will exploit different classifiers, such as Naïve-Bayes, for processing the data resulted after iteratively running a number of BoF scenarios, or even employing methods that combine different classifiers, such as bagging, boosting or stacking46. Finally, another important research direction for the future is designing and exploiting mixed codebooks containing both 2D and 3D features, such as volumetric descriptors47, specific 3D morphological information48, fractal measures (eg. fractal dimension, fractal lacunarity) or spectral information.
The presented experiment brings evidence that the quantification of cellular and tissue information in TPEF images collected from the liver surface is equally important to the characterization of collagen deposition in deeper liver tissue sections by SHG for the assessment of liver fibrosis. We consider this finding extremely important since the liver tissue information provided by the two imaging techniques are complementary, which means that combining the two would yield higher diagnostic sensitivity and specificity. While main emphasis was placed until now on the analysis of SHG images, we have demonstrated the potential use of TPEF imaging for the quantification and automated diagnosis of liver fibrosis.
Besides the fact that to date TPEF data on liver samples has not yet been exploited at its full potential in respect to the liver fibrosis assessment problem, another reason that has motivated our experiment is the possibility to easily extend a TPEF image based algorithm to be used with fluorescence data collected by conventional widefield or confocal microscopy/endomicroscopy. While the availability of TPEF/SHG capable systems is still limited mostly due to the prohibitive costs of femtosecond laser sources, conventional widefield or confocal fluorescence capable systems are available in most institutions where biomedical research is conducted.
Another important aspect of this experiment consists in the fact that TPEF images used this study were collected from the liver surface, which demonstrates the potential application of liver surface scanning with nonlinear endomicroscopy49,50,51. Such techniques could replace in some fibrosis assessment scenarios the more invasive liver biopsy, or could be used in a parallel association with liver biopsy for maximizing the level of information that is collected during an intervention.
The combined TPEF – BOF classification framework proposed in this study provides promising results, and thus holds significant potential in respect to the liver fibrosis assessment problem. In the same time, as multi-photon imaging of tissue/cell is becoming a widely used method to study different medical diseases and conditions52, the proposed framework could represent a consistent solution for other diagnostic scenarios such as TPEF based differentiation between normal, inflammatory and neoplastic lung53, normal and cancerous gastric tissues54 or normal, benign, and cancer affected breast tissues55. The influence of the three DSIFT-BOF parameters that we have evaluated in our experiment is directly connected to the image content in terms of tissue morphology, and for this reason the presented results are mainly relevant for the addressed problem: TPEF based liver fibrosis diagnostic. Irrespectively, TPEF images collected on different types of mammalian tissues, including human tissues, share common contrast mechanism related characteristics and for this reason this study could potentially impact other similar classification experiments that combine TPEF, Bag-of-Features and gradient based descriptors.
Methods
Imaging setup
The non-linear optical microscope used in the experiment for Two-photon Excited Fluorescence (TPEF) data acquisition was based on a confocal imaging system (LSM510Meta, Carl Zeiss, Jena, Germany) coupled to an external tunable mode-locked Ti:Sapphire laser (Mai-Tai broadband, Spectra-Physics, USA)17. The laser line was tuned to a 900 nm wavelength and routed by a dichroic mirror (reflect > 700 nm, transmit < 543 nm), through an objective lens (Plan-Neofluar, 20X, NA = 0.5, Carl Zeiss, Jena, Germany) to the tissue specimen. TPEF signals were collected by the same objective lens in the epi-mode, passing through the dichroic mirror (reflect < 490 nm, transmit > 490 nm) and a 500–550 nm band-pass (BP) filter, before being recorded by a photomultiplier tube (PMT, Hamamatsu R6357, Tokyo, Japan).
Sample preparation
40 male wistar rats were used in this study. 35 rats were treated with thioacetamide (TAA), an organosulfur compound with the formula C2H5NS which is known to produce marked hepatotoxicity in exposed animals. 200 mg/kg of TAA were administered by intraperitoneal injection three times a week for up to 14 weeks to induce liver fibrosis. The wistar rats were sacrificed at time-points of 2, 4, 6, 8, 10, 12 and 14 weeks (n = 5 per time point). Another 5 rats were also sacrificed at week 0, without treatment, as the control group. Cardiac perfusion with 4% paraformaldehyde was performed to flush out blood cells and the liver was fixed in formalin before harvesting.
After harvesting, the entire left lobe of each rat liver was placed on the microscope stage for imaging, and at random sites on the anterior surface of each liver sample TPEF images were collected at multiple depths (z-stacks). For each random site, a representative 2D image to be used in the presented experiment was selected from the corresponding z-stack by using an automatic reference frame estimator56 that relies on image brightness, contrast and sharpness. The dimension of the field of view was 450 μm by 450 μm, and the resolution of the images is 1024 × 1024 pixels.
After performing TPEF imaging, 5 μm thick liver slices were sectioned from the liver lobe and stained with Masson Trichrome (MT) stain kit (ChromaView advance testing, #87019, Richard-Allan Scientific) for fibrosis scoring by an experienced pathologist using the Metavir system57. This system assesses histologic lesions in hepatitis using two separate scores, one for necroinflammatory grade and another for the stage of fibrosis (Stage 0, no fibrosis; Stage 1, portal fibrosis without septa; Stage 2, portal fibrosis with rare septa, Stage 3, numerous septa without cirrhosis; Stage 4, cirrhosis).
DSIFT features
During the past decade strong emphasis has been placed on the detection and description of affine-invariant regions38,58,59,60,61,62,63,64,65,66 as numerous computer vision applications are based on image feature extraction and matching. Among various methods reported in the literature, the Scale-Invariant Feature Transform (SIFT)38 became one of the most preferred choices because of its high accuracy60, relatively low computation time and the availability of open-source implementations. The original SIFT technique provides solutions for both the detection and the description of image keypoints but we have previously shown that sparsely detecting image keypoints by the Difference-of-Gaussian (DoG) method38 proposed in SIFT is influenced by specific acquisition parameters of Laser Scanning Microscopy (LSM) such as photomultiplier amplification and laser beam power67. This means that the number of keypoints that SIFT can automatically detect in LSM images, including TPEF images, can be highly different when these are collected under distinct acquisition configurations. The same situation has been observed68 to take place as well in the case of Speeded-up Robust Features62, another popular gradient based feature detection/description technique. In order to avoid BoF related problems that could occur due to these aspects, such as unbalanced dictionaries or inconsistent term vectors, we have chosen to use a grid approach instead of a feature-detection one, as similar grid based strategies were reported to perform better than feature-detection based strategies in other experiments20,69,70. In a grid based approach the same number of features is extracted from all images from fixed x,y coordinates imposed by a grid, as illustrated in Fig. 3.
The visual features that we have used in our experiment are Dense-SIFT (DSIFT) features41,42, a SIFT38 variant. We have extracted these features by using the ‘vl_dsift’ function for Matlab (The MathWorks, Inc., Natick, Massachusetts, USA) available in the open-source VL-Feat library42, in its exact form, which according to the authors is “roughly equivalent to running SIFT on a dense grid of locations at a fixed scale and orientation”. The description method of DSIFT is similar to the one that SIFT uses: The keypoint descriptor is a histogram representation that combines local gradient orientations and magnitudes from a certain neighborhood around a keypoint. More precisely, the descriptor is in fact a 3D histogram of gradient location and orientation, where location is quantized into a 4 × 4 location grid and the gradient angle is quantized into 8 orientations, one for each of the cardinal directions38. The resulting descriptor is a normalized vector with the dimension of 128 elements. The reason for which we have chosen to use SIFT descriptors instead of other visual features is that these descriptors are simple linear Gaussian derivatives which are more stable to typical LSM image perturbations, such as multiplicative or additive noise, than higher Gaussian derivatives or differential invariants. In the same time, the high dimension of the SIFT descriptors (128 elements) is equivalent to a high potential for the discriminative representation of image regions.
DSIFT-BOF: implementation and evaluation
The experiment that we conducted was aimed at correctly labeling 200 images collected by TPEF on fibrotic mouse liver samples by using a Bag-of-Features (BoF) framework based on DSIFT features, DSIFT-BOF, which is schematically illustrated in Fig. 2. The complete set of 200 images consists of five sub-sets of 40 images each, one sub-set for each of the five METAVIR fibrosis stages: Stage 0 to Stage 4. For training and verification purposes all images used in the study were labeled as corresponding to one of the five fibrosis stages based on the pathologist's evaluation of the MT stained samples that was performed before running the DSIFT-BOF experiment. Previous to running DSIFT-BOF each of the images was processed by Wiener filtering in order to compensate the additive and multiplicative noise which could affect local feature description and hence the results of the method. We have implemented/evaluated DSIFT-BOF and performed the image filtering in a 2012b MATLAB Release (The MathWorks, Inc., Natick, Massachusetts, USA) that was equipped with the open source VL-Feat library42.
In one run of the algorithm, 10 of the 40 images of each sub-set are tested, 15 random images of the remaining ones are used for vocabulary building and the other 15 images from the sub-set are used for training. Training images are used as ground-truth. In order to test all the images in a sub-set, we run DSIFT-BOF algorithm four times, each time testing 10 different images, and using other random combinations of images in the sub-set for vocabulary building and training. This procedure is schematically illustrated in Supplementary Fig. 2.
Further on we present the steps of DSIFT-BOF, referring to a single run. As detailed in the introductory section, a typical BoF strategy requires representing the training and test images as term vectors. A term vector represents a normalized histogram of the visual words in a dictionary (codebook) that are found in an image. Therefore, the first step in the DSIFT-BOF algorithm is to construct the codebook. During a run 15 images from each of the 5 fibrosis image sub-sets are used in this purpose. From each of these images the same number of features, which results from the size of the grid spacing (Supplementary Table 1), is extracted and added to the codebook feature space. Once all features are extracted from the 75 images that are used for vocabulary building, and the codebook feature space is fully populated, we run a square-error partitioning method: k-means clustering43,71 for identifying the centroids (a.k.a. clusters) of the codebook feature space. K-means clustering is a simple nonhierarchical method that aims to partition n observations, in our case the total number of features extracted from the images used for vocabulary building, into k regions in which each observation belongs to the region with the nearest centroid. The centroids of the codebook feature space are identified after running k-means clustering and will represent the elements of the DSIFT-BOF codebook. After the codebook is built, we calculate the term vectors of the training images of each sub-set, and add them to a ‘training pool’. The ‘training pool’ is thus comprised of 75 term vectors, as each of the five sub-sets contribute to it with 15 term vectors. For classifying a test image we calculate its term vector and employ a weighted k-Nearest Neighbor (k-NN) classifier71. In k-NN classification, an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors. As an improvement to k-NN, a distance-weighted k-NN rule can be introduced with the basic idea of weighting close neighbors more heavily, according to their distances to the query. The weight used in the frame of the weighted k-NN classifier that we employed is 1/D, where D is the Euclidean distance between the term vector of a tested image and the term vector of a nearest neighbor. More precisely, after calculating the term vector of the test image, we search its k nearest neighbors (NNs), in terms of Euclidean distance, in the training pool. In each classification scenario, k equals the number of training images associated to the class containing the lowest number of fibrosis stages (the classification scenarios and classes are presented in the ‘Results’ section). For example, in the case of the S01_S234 classification scenario, the number of training images corresponding to the non-significant fibrosis class (stages 0–1) is 30, and 45 for the significant fibrosis class (stages 2–4), thus in this particular case k = 30; similarly, for the S0_S1234 classification scenario k = 15. Further on a classification is assigned to the tested image if a minimum of C NNs out of its total of k NNs belong to a specific class, and their cumulated weight is higher than the cumulated weight of the NNs belonging to the other class(es). If these conditions apply the tested image is classified as belonging to the same class with these minimum C dominant NNs. This weighted k-NN classification procedure is applied for every test image.
As previously mentioned, in order for all the images in the set to be tested, four consecutive runs of DSIFT-BOF were needed. At the end of each of the four runs we have evaluated the assigned classifications for the tested images. We did this by comparing the results with the ground truth information provided by the histo-pathologist as a priori information. Performing this comparison yielded a number of True Positives (TP), False Positives (FP), True Negatives (TN) and False Negatives (FN), for each of the runs (eg. #TP_run1, #TP_run2, #TP_run3, #TP_run4). After all four runs were completed, and all the images in the sub-set had been tested, the results were merged by summing (eg. #TP = #TP_run1 + #TP_run2 + #TP_run3 + #TP_run4). The resulted #TP, #FP, #TN, #FN values were used for calculating the Precision and Recall, explained in detail in the Results section. The Precision-Recall curves are generated by calculating the Precision & Recall for different values of C, the minimal number of dominant NNs required for assigning a classification. More precisely, for generating PR curves, C was varied between 1 and k.
DSIFT-BOF: parameters
The three DSIFT-BOF parameters that are analyzed in the presented experiment are: grid spacing, bin size and codebook size. These parameters and their influence towards the DSIFT-BOF outputs are presented in detail in the ‘Results’ section. The Matlab ‘vl_dsift’ function of the VLFeat open-source platform allows modifying the values for grid spacing and bin size through the following options that it accepts:
‘Step’: This option controls the sampling density, which is the horizontal and vertical displacement of each feature center to the next (‘grid spacing’).
‘Size’: This option controls the scale of the extracted descriptors, i.e. the width in pixels of a spatial bin (‘bin size’).
The codebook size, which corresponds also to the dimension of the term vectors, is configured in the clustering stage of the DSIFT-BOF algorithm (Fig. 2). As previously mentioned, we have employed the k-means method for clustering, which we did by using the fast C implementation of k-means with Matlab interface, VGG K-means72, that can deal with large dimensional matrix. In this implementation the number of clusters can be configured through the option ‘nclus’. The VLFeat open-source platform contains as well an implementation of the k-means methods, ‘vl_kmeans’.
Ethics statement
The Institutional Animal Care and Use Committee (IACUC) approved all animals-related experiments. The reported methods were carried out in accordance with the approved guidelines.
Author Contributions
S.G.S., S.X. and H.Y. conceived the studies and designed them together with G.A.S., R.E.W., P.T.C.S. and G.C. S.G.S. and S.X. implemented and ran the algorithm and performed the data analysis. Q.P. and J.Y. performed tissue imaging. S.G.S., S.X. and H.Y. wrote the paper. All the authors have reviewed the manuscript before submission.
Supplementary Material
Supplementary Info
Acknowledgments
The presented work was supported by the research grant PN-II-PT-PCCA-2011-3.2-1162 funded by the Romanian Executive Agency for Higher Education, Research, Development and Innovation Funding (UEFISCDI), by the SCIEX NMS-CH research fellowship nr. 12.135 awarded to S.G.S. by the Rectors' Conference of the Swiss Universities (CRUS), and in part by the Institute of Bioengineering and Nanotechnology, Biomedical Research Council, A*STAR, grants from Janssen (R-185-000-182-592), Singapore-MIT Alliance Computational and Systems Biology Flagship Project funding (C-382-641-001-091), SMART BioSyM and Mechanobiology Institute of Singapore (R-714-001-003-271) funding to H.Y. The corresponding author thanks Dr. Andrea Vedaldi (University of Oxford) for his detailed clarifications on DSIFT.
References
- Bataller R. & Brenner D. A. Liver fibrosis. J Clin Invest 115, 209–218 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman S. L. Liver fibrosis–from bench to bedside. Journal of hepatology 38, S38–S53 (2003). [DOI] [PubMed] [Google Scholar]
- Bedossa P. & Carrat F. Liver biopsy: the best, not the gold standard. J. Hepatol. 50, 1–3 (2009). [DOI] [PubMed] [Google Scholar]
- Pinzani M., Vizzutti F., Arena U. & Marra F. Technology Insight: noninvasive assessment of liver fibrosis by biochemical scores and elastography. Nat. Rev. Gastroenterol. Hepatol. 5, 95–106 (2008). [DOI] [PubMed] [Google Scholar]
- Martínez S. M., Crespo G., Navasa M. & Forns X. Noninvasive assessment of liver fibrosis. Hepatology 53, 325–335 (2011). [DOI] [PubMed] [Google Scholar]
- Denk W., Strickler J. H. & Webb W. W. 2-Photon Laser Scanning Fluorescence Microscopy. Science 248, 73–76 (1990). [DOI] [PubMed] [Google Scholar]
- Campagnola P. J. & Dong C. Y. Second harmonic generation microscopy: principles and applications to disease diagnosis. Laser Photon. Rev. 5, 13–26 (2009). [Google Scholar]
- So P. T. C., Dong C. Y., Masters B. R. & Berland K. M. Two-photon excitation fluorescence microscopy. Annu. Rev. Biomed. Eng. 2, 399–429 (2000). [DOI] [PubMed] [Google Scholar]
- Campagnola P. Second harmonic generation imaging microscopy: applications to diseases diagnostics. Anal. Chem. 83, 3224 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaspro A. & Robello M. Two-photon excitation of fluorescence for three-dimensional optical imaging of biological structures. J. Photoch. Photobio. B 55, 1–8 (2000). [DOI] [PubMed] [Google Scholar]
- Lee H.-S. et al. Optical biopsy of liver fibrosis by use of multiphoton microscopy. Opt. Lett. 29, 2614–2616 (2004). [DOI] [PubMed] [Google Scholar]
- Yan J. et al. Preclinical study of using multiphoton microscopy to diagnose liver cancer and differentiate benign and malignant liver lesions. J. Biomed. Opt. 17, 0260041–0260047 (2012). [DOI] [PubMed] [Google Scholar]
- Brown C. M. et al. In vivo imaging of unstained tissues using a compact and flexible multiphoton microendoscope. J. Biomed. Opt. 17, 0405051–0405053 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gailhouste L. et al. Fibrillar collagen scoring by second harmonic microscopy: a new tool in the assessment of liver fibrosis. J. Hepatol. 52, 398–406 (2010). [DOI] [PubMed] [Google Scholar]
- Tai D. C. et al. Fibro-C-Index: comprehensive, morphology-based quantification of liver fibrosis using second harmonic generation and two-photon microscopy. J. Biomed. Opt. 14, 044013-044013-044010 (2009). [DOI] [PubMed] [Google Scholar]
- Bedossa P. Harmony in liver fibrosis. J. Hepatol. 52, 313–314 (2010). [DOI] [PubMed] [Google Scholar]
- He Y. T. et al. Toward surface quantification of liver fibrosis progression. J. Biomed. Opt. 15, 056007 (2010). [DOI] [PubMed] [Google Scholar]
- Csurka G., Dance C. R., Fan L., Willamowski J. & Bray C. Visual categorization with bags of keypoints. Paper presented at the 8th European Conference on Computer Vision: Workshop on Statistical Learning in Computer Vision, Prague, Czech Republic. New York: Springer. (2004, May 11–14).
- O'Hara S. & Draper B. A. Introduction to the bag of features paradigm for image classification and retrieval, arXiv:1101.3354v1. (2011).
- Nowak E., Jurie F. & Triggs B. Sampling strategies for bag-of-features image classification. Paper presented at the 9th European Conference on Computer Vision, Graz, Austria. New York:Springer. (2006 May 7–13).
- Lazbenik S., Schmid C. & Ponce J. Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories. Paper presented at the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, USA. Los Alamitos: IEEE Computer Society. (2006, 17–22 June).
- Fehr J., Streicher A. & Burkhardt H. A Bag of Features Approach for 3D Shape Retrieval. Adv. Vis. Comput. 5875, 34–43 (2009). [Google Scholar]
- Lian Z. H., Godil A., Sun X. F. & Zhang H. Non-Rigid 3d Shape Retrieval Using Multidimensional Scaling and Bag-of-Features. Paper presented at the 17th IEEE International Conference on Image Processing, Hong Kong, China. NewYork: IEEE. (2010, September 26–29).
- Lin Z. & Brandt J. A Local Bag-of-Features Model for Large-Scale Object Retrieval. Paper presented at the 11th European Conference on Computer Vision, Hersonissos, Greece. New York: Springer. (2010, September 5–11).
- Sfikas K., Theoharis T. & Pratikakis I. 3D object retrieval via range image queries in a bag-of-visual-words context. Visual Comput. 29, 1351–1361 (2013). [Google Scholar]
- Hao P. Y. & Kamata S. Hilbert Scan Based Bag-of-Features for Image Retrieval. Ieice T. Inf. Syst. E94d, 1260–1268 (2011). [Google Scholar]
- Zhang L. L., Wang Z. Y. & Feng D. G. Content-Based Image Retrieval in P2P Networks with Bag-of-Features. Paper presented at the 2012 IEEE International Conference on Multimedia and Expo Workshops, Melbourne, Australia. New York: IEEE. (2012, July 9–13).
- Andre B., Vercauteren T., Buchner A. M., Wallace M. B. & Ayache N. A smart atlas for endomicroscopy using automated video retrieval. Med. Image Anal. 15, 460–476 (2011). [DOI] [PubMed] [Google Scholar]
- Yang F., Lu H., Zhang W. & Yang G. Visual tracking via bag of features. Iet Image Process. 6, 115–128 (2012). [Google Scholar]
- Can T., Karali A. O. & Aytac T. Detection and tracking of sea-surface targets in infrared and visual band videos using the bag-of-features technique with scale-invariant feature transform. Appl. Optics 50, 6302–6312 (2011). [DOI] [PubMed] [Google Scholar]
- Cruz-Roa A., Caicedo J. C. & Gonzalez F. A. Visual pattern mining in histology image collections using bag of features. Artif. Intell. Med. 52, 91–106 (2011). [DOI] [PubMed] [Google Scholar]
- Bolovinou A., Pratikakis I. & Perantonis S. Bag of spatio-visual words for context inference in scene classification. Pattern Recogn. 46, 1039–1053 (2013). [Google Scholar]
- Li Z. & Yap K. H. An efficient approach for scene categorization based on discriminative codebook learning in bag-of-words framework. Image Vision Comput. 31, 748–755 (2013). [Google Scholar]
- Yang W. et al. Content-Based Retrieval of Focal Liver Lesions Using Bag-of-Visual-Words Representations of Single- and Multiphase Contrast-Enhanced CT Images. J. Digit. Imaging 25, 708–719 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zare M. R., Mueen A. & Seng W. C. Automatic classification of medical X-ray images using a bag of visual words. Iet Comput. Vis. 7, 105–114 (2013). [Google Scholar]
- Caicedo J. C., Cruz A. & Gonzalez F. A. Histopathology Image Classification Using Bag of Features and Kernel Functions. Artif. Intell. Med. 5651, 126–135 (2009). [Google Scholar]
- Situ N., Yuan X. J., Chen J. & Zouridakis G. Malignant Melanoma Detection by Bag-of-Features Classification. Paper presented at the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, Canada. New York: IEEE. (2008, August 21–24). [DOI] [PubMed]
- Lowe D. G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 60, 91–110 (2004). [Google Scholar]
- Davis J. & Goadrich M. The Relationship between Precision-Recall and ROC Curves. Paper presented at the 23rd International Conference on Machine learning, Pittsburgh, USA. New York: ACM (2006, June 25–29).
- Tamaki T. et al. Computer-aided colorectal tumor classification in NBI endoscopy using local features. Med. Image Anal. 17, 78–100 (2013). [DOI] [PubMed] [Google Scholar]
- Vedaldi A. & Fulkerson B. VLFeat: An open and portable library of computer vision algorithms. Paper presented at The International Conference on Multimedia, Firenze, Italy. New York:ACM (2010, October 25–29).
- Vedaldi A. & Fulkerson B. VLFeat: An open and portable library of computer vision algorithms., <http://www.vlfeat.org> (2008). (date of access: 17.02.2014). [Google Scholar]
- MacQueen J. B. Some methods for classification and analysis of multivariate observations. Paper presented at The Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, USA. Berkeley: University of California Press. (1966 January 7).
- Tommasi T., Orabona F. & Caputo B. Cue integration for medical image annotation. Paper presented at the 2007 Cross-Language Evaluation Forum, Budapest, Hungary. New York: Springer. (2007 September 19–21).
- Inaba M., Katoh N. & Imai H. Applications of Weighted Voronoi Diagrams and Randomization to Variance-Based k-Clustering. Paper presented at the 10th ACM Symposium on Computational Geometry, Stony Brook, USA. New York: ACM (1994 June 6–8).
- Witten I. H. & Frank E. Data Mining: Practical Machine Learning Tools and Techniques. (Morgan Kaufman, San Francisco, 2005). [Google Scholar]
- Skibbe H. et al. Fast Rotation Invariant 3D Feature Computation Utilizing Efficient Local Neighborhood Operators. IEEE Trans. Pattern Anal. Mach. Intell. 34, 1563–1575 (2012). [DOI] [PubMed] [Google Scholar]
- Altendorf H. et al. Imaging and 3D morphological analysis of collagen fibrils. J. Microsc. 247, 161–175 (2012). [DOI] [PubMed] [Google Scholar]
- Wu Y., Xi J., Cobb M. J. & Li X. Scanning fiber-optic nonlinear endomicroscopy with miniature aspherical compound lens and multimode fiber collector. Opt. Lett. 34, 953–955 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera D. R. et al. Compact and flexible raster scanning multiphoton endoscope capable of imaging unstained tissue. Proc. Natl. Acad. Sci. USA 108, 17598–17603 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. et al. A compact fiber-optic SHG scanning endomicroscope and its application to visualize cervical remodeling during pregnancy. Proc. Natl. Acad. Sci. USA 109, 12878–12883 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong C. Y. et al. Multiphoton Microscopy: Technical Innovations, Biological Applications, and Clinical Diagnostics. J. Biomed. Opt. 18, 031101–1 (2013). [DOI] [PubMed] [Google Scholar]
- Paylova I. et al. Multiphoton microscopy and microspectroscopy for diagnostics of inflammatory and neoplastic lung. J. Biomed. Opt. 17, 036014 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. X. et al. Establishing diagnostic features for identifying the mucosa and submucosa of normal and cancerous gastric tissues by multiphoton microscopy. Gastrointest. Endosc. 73, 802–807 (2011). [DOI] [PubMed] [Google Scholar]
- Wu X. F. et al. Label-Free Detection of Breast Masses Using Multiphoton Microscopy. Plos One 8, 0065933 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanciu S. G., Stanciu G. A. & Coltuc D. Automated compensation of light attenuation in confocal microscopy by exact histogram specification. Microsc. Res. Tech. 73, 165–175 (2010). [DOI] [PubMed] [Google Scholar]
- Bedossa P. & Poynard T. An algorithm for the grading of activity in chronic hepatitis C. Hepatology 24, 289–293 (2003). [DOI] [PubMed] [Google Scholar]
- Ke Y. & Sukthankar R. PCA-SIFT: A more distinctive representation for local image descriptors. Paper presented at the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, USA. Los Alamitos: IEEE Computer Society (2004, June 27–July 2).
- Mikolajczyk K. & Schmid C. Scale & affine invariant interest point detectors. Int. J. Comput. Vision 60, 63–86 (2004). [Google Scholar]
- Mikolajczyk K. & Schmid C. A performance evaluation of local descriptors. Ieee T. Pattern. Anal. 27, 1615–1630 (2005). [DOI] [PubMed] [Google Scholar]
- Mikolajczyk K. et al. A comparison of affine region detectors. Int. J. Comput. Vision 65, 43–72 (2005). [Google Scholar]
- Bay H., Ess A., Tuytelaars T. & Van Gool L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Und. 110, 346–359 (2008). [Google Scholar]
- Agrawal M., Konolige K. & Blas M. R. CenSurE: Center Surround Extremas for Realtime Feature Detection and Matching. Paper presented at the 10th European Conference on Computer Vision, Marseille, France. New York: Springer (2008, October 12–18).
- Burghouts G. J. & Geusebroek J. M. Material-specific adaptation of color invariant features. Pattern Recogn. Lett. 30, 306–313 (2009). [Google Scholar]
- Burghouts G. J. & Geusebroek J. M. Performance evaluation of local colour invariants. Comput. Vis. Image Und. 113, 48–62 (2009). [Google Scholar]
- Ebrahimi M. & Mayol-Cuevas W. W. SUSurE: Speeded Up Surround Extrema Feature Detector and Descriptor for Realtime Applications. Paper presented at the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Miami, USA. Los Alamitos: IEEE Computer Society (2009, June 20–25).
- Stanciu S. G., Hristu R., Boriga R. & Stanciu G. A. On the Suitability of SIFT Technique to Deal with Image Modifications Specific to Confocal Scanning Laser Microscopy. Microsc. Microanal. 16, 515–530 (2010). [DOI] [PubMed] [Google Scholar]
- Stanciu S. G., Hristu R. & Stanciu G. A. Influence of Confocal Scanning Laser Microscopy specific acquisition parameters on the detection and matching of Speeded-Up Robust Features. Ultramicroscopy 111, 364–374 (2011). [DOI] [PubMed] [Google Scholar]
- Fei-Fei L. & Perona P. A Bayesian hierarchical model for learning natural scene categories. Paper presented at the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, USA. Los Alamitos: IEEE Computer Society (2005, June 20–26).
- Jurie F. & Triggs B. Creating efficient codebooks for visual recognition. Paper presented at the Tenth IEEE International Conference on Computer Vision, Beijing, China. New York: IEEE. (2005, October 17–21).
- Duda O., Hart P. E. & Stork D. G. Pattern classification. (John Wiley & Sons, New Jersey, 2000). [Google Scholar]
- VGG. K-means, <http://crcv.ucf.edu/source/vggkmeans.zip> (date of access: 17.02.2014). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Info