Abstract
Sub-resonances often happen in wireless power transmission (WPT) systems using coupled magnetic resonances (CMR) due to environmental changes, coil movements or component degradations, which is a serious challenge for high efficiency power transmission. Thus self-tuning is very significant to keep WPT systems following strongly magnetic resonant conditions in practice. Traditional coupled-mode ways is difficult to solve this problem. In this paper a two-port power wave model is presented, where power matching and the overall systemic power transmission efficiency are firstly defined by scattering (S) parameters. Then we propose a novel self-tuning scheme based on on-line S parameters measurements and two-side power matching. Experimental results testify the feasibility of the proposed method. These findings suggest that the proposed method is much potential to develop strongly self-adaptive WPT systems with CMR.
In 2007, researchers at the Massachusetts Institute of Technology (MIT) proposed a new scheme for a mid-range wireless power transmission (WPT), namely strongly coupled magnetic resonances (CMR)1,2. By now, three classes of theoretical models have been proposed for WPT systems using CMR, i.e, coupled-mode theory, reflected load theory and lumped circuit model3. CMR is a new concept presenting a potential breakthrough for midrange WPT, but the resonance between the transmitting and receiving coils is a very strict condition of achieving the maximum efficiency. Otherwise, the transmission efficiency will drop dramatically. For engineering applications, once a WPT system using CMR has been designed, its resonant conditions will be fixed. However, physical and geometrical parameters of the WPT system are prone to be affected by environmental changes, coil movements or component degradations, so that their resonant frequencies will shift and sub-resonances often happens. On the other hand, it is inconvenient or impossible to adjust resonant frequencies by hand in most engineering applications. Recently, several adaptive matching methods have been studied to address this issue. These works can be divided into two classes: one is implemented by adjusting the source frequency, and the other is implemented by tuning the impedance of the transmitting loop or the receiving loop at a fixed source frequency. Kim et al4 proposed an automated frequency tracking system for mid-range wireless power transfer. Basic principle was to directly monitor the link efficiency and then adjust the source frequency. However, this method needs to change the source frequency repeatedly because the parasitic capacitance and inductance of the loop have to change with the source frequency. So it is not very convenient. David et al5 used two digitally tuned capacitors to adjust the resonance frequency of the coils. By this way, a high efficiency could be maintained as the receiver moved only within small distances. However, this method is limited for long distance variations. Koizumi et al6 proposed a one-side impedance matching approach on the transmitter side to maintain high power transfer efficiency at varying coil distances. However, the efficiency cannot reach the maximum because the impedance of the receiving coil is not controlled. Beh et al7 proposed another automated matching method at a fixed source frequency using an impedance matching circuit. But the efficiency also cannot reach the maximum because adaptive matching of the receiving loop is not considered. Thus how to realize a self-tuning scheme becomes a significant and urgent problem to be solved.
Early researches including that of MIT were mainly based on coupled-mode theory, reflected load theory or lumped circuit model, but they cannot provide practical design methods for engineers8,9. Recently, researchers in the University of Tokyo proposed one method of impedance matching10,11, which is based on Z parameters of a two-port network model. Its most advantage is that it is not necessary to consider complex circuits inside a WPT system. However, as we all know that it is very difficult to accurately measure voltages and currents to calculate Z parameters for high frequency systems. Thus this kind of impedance matching is very difficult for realizing self-tuning methods. Another problem is that coupling efficiencies are often used to characterize the performance of a WPT system, such as the impedance matching method10,11. Exactly, the true WPT efficiency should be the efficiency of the overall system from the wall outlet to the load. There is much discrepancy between them. As reported by the MIT team8, wireless power transfer efficiency was about 40% while the practical “wall-to-load” efficiency of the overall system was only 15%. In other words, if we optimize a WPT system by the coupling efficiency, the power occupied by the load may be low even though the coupling efficiency is relatively high. It is not the case that we expect.
The goal of this paper is to explore an innovative way to meet the above challenges. Fortunately, power waves are easy to be measured on line for high frequency electric systems, so it is feasible to optimally analyze and design a WPT system using power waves. In this paper, we propose a novel concept of power matching, where the overall systemic power transmission efficiency (SPTE) is defined. Based on the conditions of power matching, a self-tuning scheme is built on two-side power matching. The most advantage is that it can fast tune a WPT system to be strongly resonant and achieve high power transmission efficiencies all the time.
Results
An experimental WPT system shown in Fig. 1 is built to validate the proposed methodology, which is composed of a signal generator, a high frequency amplifier, a DC power source, an oscillograph, a transmitting coil, a receiving coil, a two-side power matching circuit and a load. Physical and geometric parameters of the WPT system are listed in Table 1. A light bulb is selected as the load due to its pure resistance. The transmission distance is denoted as D and we will change D to simulate sub-resonances.
Figure 1. The experimental set-up.
Table 1. Physical and geometric parameters of the WPT system.
| Parameters | Values |
|---|---|
| Radius of the two identical coils (r) | 208 mm |
| Radius of the copper wire (a) | 1 mm |
| Number of turns of each coil (N) | 15 |
| Equivalent inductance of each coil (L) | 154.8 μH |
| Frequency of the power source (f) | 130 KHz |
| Series capacitor (CS, CD) | 9.68 nF |
| Resonant frequency of the coil (f0) | 130 KHz |
| Impedance of the load (RL) | 1000 Ω |
| Impedance of the power source (ZS) | 31 Ω |
When D is changed as 100 mm, 200 mm, 300 mm, 400 mm and 500 mm respectively, the corresponding self-tuning components of the two-side power matching network are calculated as Table 2.
Table 2. Components of the two-side power matching network with different D.
| D (mm) | f0 (KHz) | C1 (nF) | L1 (μH) | C2 (nF) | L2 (μH) |
|---|---|---|---|---|---|
| 100 | 130 | 7.74 | 0.08 | 1.21 | 0.91 |
| 200 | 130 | 4.12 | 0.36 | 0.61 | 1.72 |
| 300 | 130 | 2.20 | 0.68 | 0.38 | 3.78 |
| 400 | 130 | 1.39 | 1.12 | 0.25 | 6.12 |
| 500 | 130 | 0.95 | 1.64 | 0.17 | 8.91 |
Based on Table 2, measured results without/with power matching are listed in Table 3.
Table 3. Comparison of measured results without/with power matching.
| Without power matching | With power matching | |||
|---|---|---|---|---|
| D (mm) | PL (W) | SPTE (%) | PL (W) | SPTE (%) |
| 100 | 6.01 | 51.6 | 10.53 | 90.40 |
| 200 | 1.26 | 10.8 | 9.47 | 81.30 |
| 300 | 0.27 | 2.30 | 6.32 | 54.30 |
| 400 | 0.07 | 0.60 | 5.55 | 47.70 |
| 500 | 0.03 | 0.30 | 3.93 | 33.80 |
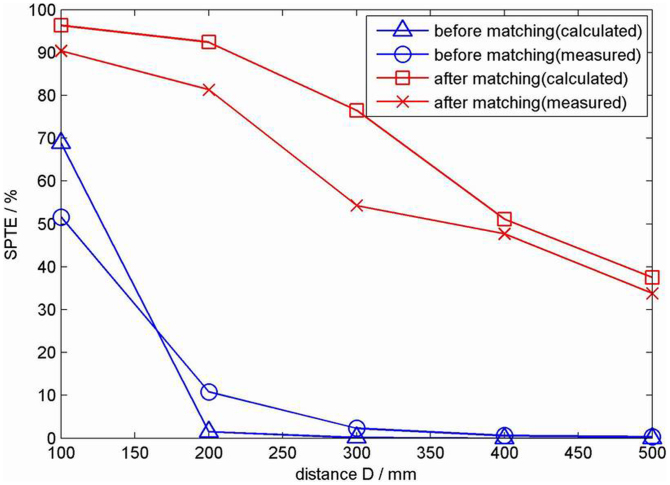
Furthermore, theoretical and measured SPTEs without/with power matching are shown in Fig. 2.
Figure 2. Comparison of theoretical and measured SPTEs without/with power matching.
Discussion
When the distance D becomes very small, the SPTE without power matching is closer to that with power matching. However, the SPTE decreases dramatically with D when there is no power matching. The reason is that strongly coupled magnetic resonance may not be satisfied again when D increases. While a two-side self-tuning power matching network is used, the SPTE decreases slowly with D. Once the distance D becomes large, the SPTE is much more than that without power matching. Thus it demonstrates that power matching is very important for high-efficiency mid-range WPT systems with CMR.
A two-port power wave model is proposed to define the conditions of power matching. This model is built based on power waves instead of standard Z parameters. Power matching is in nature a conjugate matching, while impedance matching reported in previous works is just a real-part matching. If the impedances of the power source and the load are both equal to 50 Ω, power matching will be simplified to impedance matching reported by previous works10,11. Thus impedance matching is just a special case of our proposed method.
Based on the two-port power wave model and power matching, the SPTE is firstly defined as a guideline to evaluate and design a WPT system. The advantage of the SPTE is a “wall-to-load” efficiency of a WPT system, which means that power harvested by the load will reach the maximum value if only the SPTE is the highest. Thus the SPTE is more reliable and feasible to represent the performance of a WPT system than standard coupling efficiencies.
Another innovation of the proposed power matching is that it is a simultaneous two-side matching solution. As we all know that the two-port model of a WPT system is composed of transmitting and receiving ports. Also there are strong dependences between these two ports. In previous impedance matching solutions6, it firstly needs to match the transmitting port, and then the receiving port. Under this case, however, electric properties of the two-port network maybe changes after the receiving port is matched. So it needs to match the transmitting port again. This process maybe needs iterating for many times to achieve a compromise. For the power matching method, on the contrary, electric properties of two ports are both considered to match transmitting and receiving ports simultaneously, so that we can match the whole WPT system for only one time and its tuning time will be reduced dramatically.
The proposed power matching methodology is based on S parameters of the two-port power wave network. Tuning capacitors and inductances in the two-side reversed L-type matching networks can be calculated by S parameters. On the other hand, S parameters can be measured on line using directional couplers, so a self-tuning scheme is firstly carried out by using adjustable capacitances and inductances (such as voltage-controlled or vacuum capacitors), where the values of tuning capacitances and inductances can be adjusted on line based on measured S parameters to retain strong coupled magnetic resonance.
There are some deviations between theoretical and measured SPTEs in Fig. 2. The potential reasons may include, i) Practical self-tuning capacitances and inductances are impossible to exactly be theoretic values due to their precision errors. ii) Although the impedance of the light bulb is assumed to be 1000 Ω, it will change with its temperatures when working. iii) Energy dissipation is unavoidable to happen on high frequency amplifier circuit, two coils and power matching circuits, which is neglected in theoretical calculations.
Methods
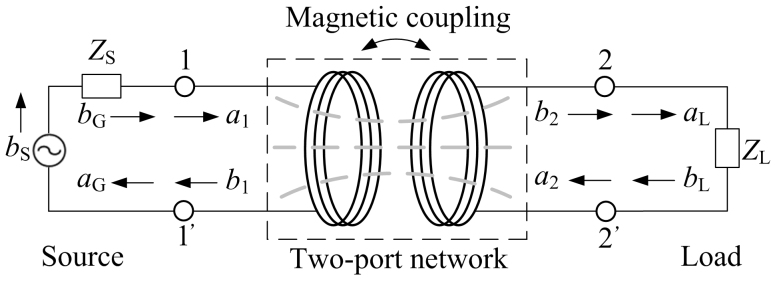
A basic WPT system with CMR is composed of a high frequency power source, a transmitting coil and a receiving coil, which can be equivalent to a two-port network model. However, here power waves are selected as the input and output variables instead of Z parameters. Then a novel two-port power wave model of the WPT system with CMR is presented in Fig. 3. Zs is the characteristic impedance of the power source and ZL is the impedance of the load. bS is the rated power wave of the power source. aG, bG are the input and output power waves of the power source respectively. a1, b1 are the input and output power waves of the 1-1′ port respectively. a2, b2 are the input and output power waves of the 2-2′ port respectively. aL, bL are the input and output power waves of the load respectively.
Figure 3. A two-port power wave model of a WPT system with CMR.
Furthermore, this model can be characterized by S parameters, (S11, S12, S21, S22), as Eq. (1). Its most advantage is that S parameters can be measured on line by directional couplers.
 |
The reflect coefficient of the power source is defined as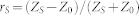 
. The reflect coefficient of the load is defined as 
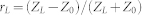. Z0 is the characteristic impedance which is normally 50 Ω.
From a systemic view, we can look both the two-port network and the load as the equivalent load shown in Fig. 4. Then the reflect coefficient of the equivalent load is defined as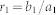 
. Similarly, both the power source and the two-port network can be looked as the equivalent power source. The reflect coefficient of the equivalent load is defined as 
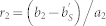, where 
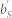is the rated power wave of the equivalent power source.
Figure 4. Systematic views of the power waves-based two-port network model.
The actual power output of the power source is defined as Eq. (2) using power waves
 |
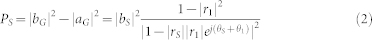bS is always a constant for a given power source, so PS is determined by r1 and rS. Obviously, the maximum value of PS can be achieved only when it satisfies the following condition.
 |
where,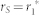 
is called as ‘power matching' of the 1-1′ port.
Similarly, the occupied power by the load is defined as Eq.(4) using power waves
 |
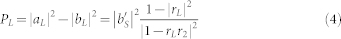The maximum value of PL can be achieved only when it satisfies the following condition.
 |
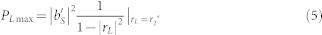where,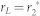 
is called as ‘power matching' of the 2-2′ port.
In order to describe the true power transmission efficiency, here we define a novel performance parameter, G, as shown in Eq. (6).
 |
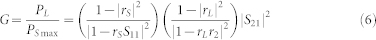Here G is called as the systemic power transmission efficiency (SPTE) and its physical meaning is to measure the usage ratio of the maximum power output of the power source, namely the end-to-end system efficiency. Obviously, PL will also be the maximum when G reaches the maximum value. Interestingly, 
when rS = rL = 0, which is the same as that in Ref.[10, 11].
Based on the two power matching conditions, a self-tuning scheme for the WPT system is shown in Fig. 5, where two reversed L-type matching networks are inserted.
Figure 5. A self-tuning scheme for the WPT system using power matching.
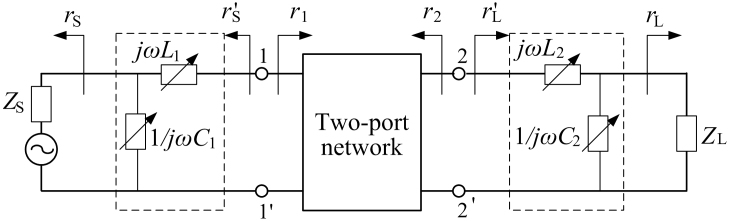
Compared to Fig. 3, the reflect coefficient of the power source is changed from rS to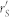 
and the reflect coefficient of the load is changed from rL to 
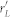in Fig. 5. Furthermore, we will have
 |
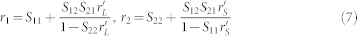By setting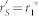 
and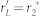 
, we can get
 |
 |
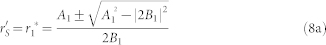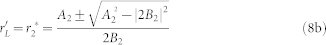where,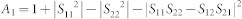 
, 
, 
, 
.
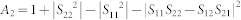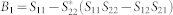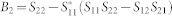At the same time, we have the following equations from Fig. 5.
 |
 |
Based on Eq.(8) and Eq.(9), we can obtain C1, C2, L1, L2. Obviously, each of Ci, Li (i = 1, 2) is the function of S parameters. Coincidentally, on-line measuring S parameters can be easily carried out, so we can use a controller to adjust the variable capacitors and inductances for self-tuning.
Author Contributions
Y.M.Y. and Z.S.C. conceived the study and the experiments. Y.T.L. and Z.S.C. carried out the experiments and data analysis. Z.S.C., Y.T.L. and Y.M.Y. wrote the paper. All contributed to the discussion of the results.
Acknowledgments
This work was supported in part by National Nature Science Foundations of China (Grant Nos. 51275520 and 50805142).
References
- Yan G. Z., Ye D. D., Zan P., Wang K. D. & Ma G. Y. Micro-robot for endoscope based on wireless power transfer. 3577–3581, IEEE international conference on mechatronics and automation, Harbin, (August 5–82007).
- Jung K.-H., Kim Y.-H. & Kim J. Wireless power transmission for implantable devices using inductive component of closed magnetic circuit. Electron. Lett. 45, 21–22 (2009). [Google Scholar]
- Bou E., Alarcon E. & Gutierrez J. A comparison of analytical models for resonant inductive coupling wireless power transfer. 689–693, Progress in electromagnetics research symposium, Moscow, (August 19–232012).
- Kim N. Y. et al. Automated adaptive frequency tracking system for efficient mid-range wireless power transfer via magnetic resonance coupling. 221–224, The 42nd European Microwave Conference, Amsterdam, (October 29–November 12012).
- David S. R., Matthew J. C. & Andrew H. Optimization of wireless power transfer for mobile receivers using automatic digital capacitance tuning. 515–518, The 43rd European Microwave Conference, Nuremberg, (October 6–102013).
- Koizumi M., Komurasaki K., Mizuno Y. & Arakawa Y. Wireless power feeding with strongly coupled magnetic resonance for a flying object. Wireless Engin. Techn. 3, 86–89 (2012). [Google Scholar]
- Beh T. C., Kato M. & Imura T. Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling. IEEE Trans. Indus. Electron. 60, 3689–3697 (2013). [Google Scholar]
- Kurs A. et al. Wireless power transfer via strongly coupled magnetic resonances. Science 317, 83–86 (2007). [DOI] [PubMed] [Google Scholar]
- Karalis A., Joannopoulos J. D. & Soljacic M. Efficient wireless nonradiative mid-range energy transfer. Ann. Phys. 323, 34–48 (2008). [Google Scholar]
- Cheon S. et al. Circuit-model-based analysis of a wireless energy-transfer system via coupled magnetic resonances. IEEE Trans. Indus. Electron. 58, 2906–2914 (2011). [Google Scholar]
- TeckChuan B., Masaki K., Takehiro I. & Yoichi H. Basic study on improving efficiency of wireless power transfer via magnetic resonance coupling based on impedance matching. 2011–2016, IEEE international symposium on industrial electronics, Bari, (July 4–72010).