Information theory of adaptation in neurons, behavior, and mood

Abstract

The ability to make accurate predictions of future stimuli and consequences of one’s actions are crucial for the survival and appropriate decision-making. These predictions are constantly being made at different levels of the nervous system. This is evidenced by adaptation to stimulus parameters in sensory coding, and in learning of an up-to-date model of the environment at the behavioral level. This review will discuss recent findings that actions of neurons and animals are selected based on detailed stimulus history in such a way as to maximize information for achieving the task at hand. Information maximization dictates not only how sensory coding should adapt to various statistical aspects of stimuli, but also that reward function should adapt to match the predictive information from past to future.

Recently Stephen Hawking cautioned against efforts to contact aliens [1], such as by beaming songs into space, saying: “We only have to look at ourselves to see how intelligent life might develop into something we wouldn’t want to meet.” Although one might wonder why we should ascribe the characteristics of human behavior to aliens, it is plausible that the rules of behavior are not arbitrary but might be general enough to not depend on the underlying biological substrate. Specifically, recent theories posit that the rules of behavior should follow the same fundamental principle of acquiring information about the state of environment in order to make the best decisions based on partial data [**2,3]. Further, these principles could also incorporate both the cost of obtaining information and the cost of making complex decisions [**4]. Therefore, validating such theories could help establish frameworks to compare behavior not only in different species and tasks, but also in single cells [5], neurons, intracellular pathways, as well as emergent phenomena at the population level, such as the distribution of blood flow in the brain that anticipates future stimuli [*6] as well as resource allocation within companies and government [7].

In this article, we review recent evidence that behavior in different systems can be described within a common framework whereby actions are chosen to maximize the Shannon mutual information with respect to a variable that quantifies performance in the task at hand. This idea has a venerable history when applied to individual neurons. In this case the mutual information represents how well the neural responses encode incoming stimuli, reviewed in [**2]. The mutual information can be computed as the difference between the entropy of the neural response H(r) and the average entropy 〈H(r|stim)〉_stim of the neural response observed when a given stimulus is repeated multiple times:

$$I=H(r)-{\langle H(r\mid \text{stim})\rangle }_{\text{stim}}$$

Adaptive changes in neural representation can be viewed as a predictive computation about the properties of stimuli to be received in the near future. By properly allocating the inherently limited neural responses through mechanisms such as adjusting the neural gain in single neurons [8,9] or the distribution of the preferred stimulus values for different neurons [10–12], neurons can more accurately encode future stimuli in order to provide more information about them. Indeed, adaptation has been shown to directly increase [13] and maintain [14] information transmission.

The gain of single neuron responses can adapt to increasingly subtle statistical properties, from the mean and variance of incoming stimuli (review of the earlier work is provided in [8,15]), to the detailed structure of sound sequences that extend over minutes [16] or to a power spectrum [17,18] and facial features in the visual system [19,20]. Similarly, maximally informative encoding differs strikingly depending upon higher-order stimulus statistics [21]. For Gaussian inputs, the classic perceptron-like solutions where the neural response depends only on one stimulus dimensions provide maximum information. In contrast, in the case of Laplacian inputs, which approximate many of the inputs derived from the natural sensory environment [**2], the maximally informative solution prescribes that responses of single neurons should depend in specific and nonlinear ways on multiple image components. The corresponding nonlinearities were strikingly similar to those observed experimentally in the primary visual cortex with respect to three cone isolating inputs [*22] as well as the relevant gray scale features [23]. At the level of neural populations, theoretical studies have described how the neural responses and their variability can be coordinated between neurons in such a way as to maximize information transmission [11,12,24,25]. For instance, either positive or negative noise correlations can improve the separability the neural responses to different classes of inputs, if the mean neural responses are negatively or positive correlated across different inputs [26]. These predictions were recently confirmed in experiments addressing changes in neuronal correlations through adaptation [27,28], learning [29] or specific behavioral paradigms, such as parturition [30], where the noise corr. While the neural mechanisms underlying coordination between neurons both in terms of their mean responses and their variability remain to be fully elucidated, the formation of dendritic fields is likely to play an important role. To this end, dendrites of single neurons in the developing cortex were shown to be capable of complex adaptive computations to navigate in shallow chemical gradients to ensure optimal connectivity [31,32]. In the retina, the resulting mosaic is such that even irregularities in the light sensitive regions of retinal ganglion cells carry substantial information [10,33–35].

Yet, the pervasive nature of adaptation and optimality observed at a variety of levels in the nervous system should not be taken for granted. Some statistical parameters, such as kurtosis, do not seem to trigger adaptive changes in neuronal gain [**36,37]. They however can affect the time scale of adaptation to other parameters of the stimulus distribution, such as variance [36]. Furthermore, the ability of neurons to adapt to changes in the variance is not present in newborn neurons and develops slowly over the course of several weeks [38]. This staggering of different adaptive capabilities during development points to the computational cost associated with adaptation itself. It seems possible to quantify this cost in information-theoretic terms, perhaps similarly to how complexity of decisions and rewards was quantified [**4]. This would then make it possible to analyze the trade-off between creating a more fully adapted neural representation versus the gain in information transmission that this representation might provide. Such a framework may help explain when it is better to use automatic forms of adaptation, such as those that are due to built-in nonlinearities in the system [39,40] versus more flexible forms of adaptation where the adaptation time itself reflects the process of statistical inference [**36]. Ultimately, this may provide an explanation for adaptive properties in more natural stimulus ensembles [*41, *42, *43].

It turns out that that information maximization can also accurately describe changes in decision making observed at the behavioral level. Our first example pertains to navigation in a turbulent environment. We know that tiny moths can find their mates over the distances of several kilometers based on encountering just a few pheromone molecules [44]. A computational algorithm for successful navigation in a turbulent environment was recently found [**45] by choosing trajectories that maximize the amount of information about the source location, although individual steps do not always bring the animal closer to the target. These “infotaxis” trajectories reproduced characteristic properties of moth flight, such as cross-wind zigzagging far from the source and following the increasing odorant gradient close to the source. Note that the distinguishing feature of infotaxis is that, at low signal-to-noise conditions, its operation does not rely on time averaged stimulus characteristics, such as mean gradient. This property has its counterparts in neural adaptation, where for example, at low light levels, the gain of retinal ganglion cells can be affected by absorption of single photons [*46], a point to which we will return later.

From a physical perspective, where humans choose to look is a very different type of behavior than moth navigation, yet similar principles appear to be at work. Recent work has explained many aspects of human eye movements [**47], including looking in between two likely locations (“center-of-gravity saccades” [48]) or looking away from the target to eliminate less likely target locations, with an optimization strategy termed ‘ideal observer analysis’. It turns out that the ideal observer analysis in this context can be mapped, in a one-to-one fashion, onto the problem of maximizing the acquisition of information about the target location. Thus, despite different physical constraints and behavioral goals, both the search with eye movements for a visual target and moth navigation using pheromones can be understood as information maximizing search strategies. It is noteworthy that the statistics of our eye movements is also under adaptive control to satisfy the needs of a trade-off between speed and accuracy (such as in reading) [49].

Encouraged by this success of the infotaxis framework [**45,**47], we explored whether it could also account for yet another very different type of animal behavior, namely how a small nematode worm C. elegans decides to stop searching a local area for food Searching for food over areas much larger in scale than the body size is a problem that many different types of species have to solve. A key feature of the infotaxis strategy is that information is continuously gained from both the presence and absence of odorant detection events. The goal is to maximize the function [**45]:

$$\mathrm{\Delta }S(r_{\mathit{new}}\mid r_{\mathit{current}})=-P(r_{\mathit{current}})S_{\mathit{current}}+\lfloor 1-P(r_{\mathit{current}})\rfloor \sum _{n=0}^{\infty }{p}_n(r_{\mathit{new}})\mathrm{\Delta }{S}_n(r_{\mathit{new}}),$$

where P(r) describes the probability to find a source at location r, the entropy of this distribution is denoted as S_current, and the current position of the searcher as r_current. The terms p_n describe the expected probability to observe n odorant hits if the searcher decides to move to a location r_new, whereas terms ΔS_n the corresponding expected change in entropy following these outcomes. By comparison, a chemotaxis search would instead maximize the mean number of expected odorant detection events: ${\sum }_{n=0}^{\infty }{np}_n$. Another important distinction between infotaxis with respect to chemotaxis lies in the computation of p_n(r_new). In the infotaxis model this probability is updated following each odorant detection events and depends of the times where these events have occurred, where for the chemotaxis computation it only depends on the current position. At high odorant concentrations, such as those that often occur close to the source, infotaxis converges to simple chemotaxis. The key difference however is that infotaxis can work at the dilute limit, whereas chemotaxis fails [**45].

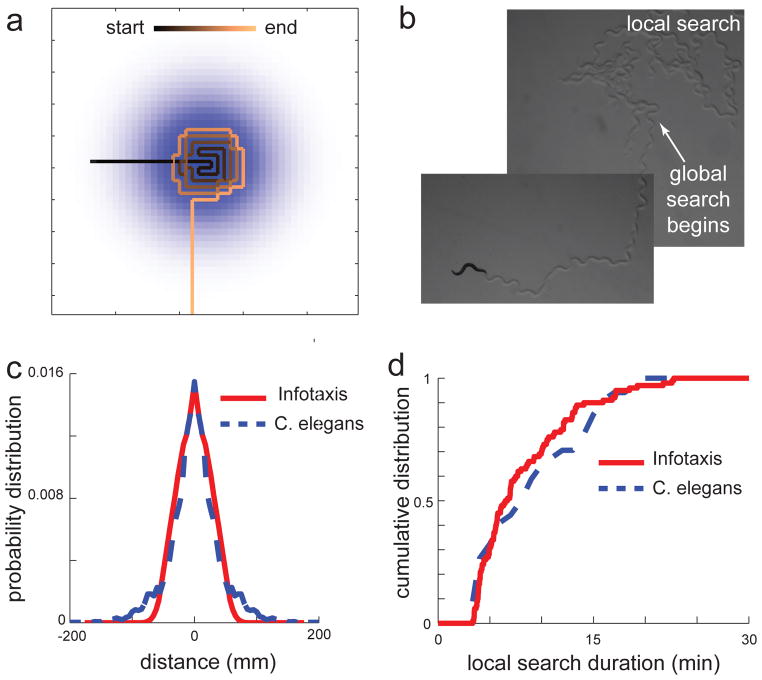
Qualitatively, it is known that when worms are transferred from plates with food to plates without food the animals perform an intense search of a local area [50] for a limited time. Presumably, animals perceived the food to be located nearby based on their prior experience and previous search outcomes. This “local search” lasts for approximately 15 minutes. From a physical perspective, this search problem is similar to the infotaxis navigation considered above. However, an important difference is that in this case there are no odorant cues. Therefore, one might expect that all of the animal’s behavior must be guided by the dynamics implied by its prior beliefs summarized by P(r_current). Surprisingly, the infotaxis solution in this context exhibits an abrupt transition between a local search phase and a global search phase (Figure 1a), provided we allow for the possibility that the source is not located within the modeled area. (the full extent of the distribution in Figure 1a). The corresponding probability p_t(A) evaluated at time t is updated in a Bayesian manner for the next time step: $p_{t+1}(\mathrm{A}\mid 0)=\frac{p_t(0\mid \mathrm{A})p_t(\mathrm{A})}{p_t(0)}$. In the beginning of the search p_t=0(A) = 1. The transition from local search to the global search in the model occurs when p_t(A) reaches zero. This transition matches the worm behavior both qualitatively (Figure 1b) and quantitatively in terms of the distribution of worm positions at the end of the local search phase (Figure 1c). Importantly the same set of parameters in the infotaxis model can also account for the duration of the local search (Figure 1d). This match is achieved without further adjustments in the model because the temporal and spatial scales are related by the known speed of worm movements on the plate (0.2 mm/sec), which remains unaltered during both the local and global phases of the search [50]. A similar optimal allocation of time on a given task to maximize information was also described by a recent theoretical framework that represented human attention as a decision to interrupt the current task or persevere [51].

Figure 1. Information maximization explains transition between tasks in the absence of new sensory stimuli.

(a) Example infotaxis trajectory exhibits a transition from local search to global search. The background color-map shows the initial probability distribution of target locations. Search proceeds following an expectation of odor detection but eventually transitions towards straight motion away from the initial maximum. (b) Similar behavior is observed in the case of C. elegans once they are removed from a patch of bacteria. The initial trajectory has lots of turns. After approximately 15 minutes, the animal stops turning and moves away from the local area. (c) Information maximization accounts for the spatial distribution of worm positions at the end of the local search. (d) Information maximization accounts for the duration of local search in C. elegans.

The infotaxis model makes a number of important predictions that qualitatively differ from the simpler chemotaxis model of navigation. A chemotaxis model is based on the computation of a gradient. It predicts that the animal’s behavioral response will be affected by the magnitude of a drop in odorant concentration. In contrast, the infotaxis model makes predictions based mainly on the relative distribution of food in space rather than on its concentration. If the worms are transferred from plates that have lawns of bacteria (food for C. elegans) that have the same size and different concentrations, then the chemotaxis (but not infotaxis) model would predict a stronger initial response from the animal when it is transferred from a more concentrated lawn. Preliminary evidence in these experiments supports the more involved infotaxis model of behavior. A related prediction is that the duration of the search may depend on the size of the animal, because the trajectory should remain the same in dimensionless units where the width of the prior distribution is normalized by the searcher size. Finally, the search duration is dependent on the diffusion properties of the odorant and would suggest that the search duration may depend on the type of bacteria to which the worms were acclimated prior to removal from food. Verifying these predictions of the infotaxis model would set the precedent that even animals with a relative simple nervous system (302 neurons, in the case of C. elegans) perform computations based on a “mental map” of likely food locations by continuously updating probabilities across the range of spatial locations around them.

Criticisms of information maximization as a behavioral strategy do exist. For example, it has been argued that these strategies do not always guarantee maximum fitness [52]. It is noteworthy that the deviations in optimality when using information maximization have been primarily observed in a dynamic situation where the absolute knowledge of the target position does not guarantee that this position could be reached before the target would move again. In such cases, perhaps the paradox can be resolved by considering maximizing information not only about the current location of the target but also about its future positions, that is predictive coding [53] and predictive information [**4,54]. Interestingly, this has recently been discussed in the context of neuronal responses. Recent analyses show that synergistic effects across multiple neurons are much stronger when one considers predictive information compared to information about preceding stimuli that caused the neural responses [**2], suggesting that the combinatorial power of neural responses across a population is aimed at maximizing information about future events and not the prior sensory inputs. Furthermore, it is true that reward function that guides the animal’s behavior might not correspond directly to information gain, even when integrated to infinite future times. However, to operate as well as possible given the constraints on information acquisition, theoretical arguments indicate that the animal must adjust its internal reward structure to coincide precisely with the predictive information from the past signals about the future trajectories [**4]. This situation was termed as the case “perfectly adapted environment” in [**4], but perhaps another way of describing this type of adaptation would be to emphasize that it target adaptation in the reward function of an agent to the statistics of the environment. One would also expect that the two adaptive processes: adaptation of the encoding function to maximize the reward function and adaptation of the reward functions might be achieved at different time scales [**4]. On short time scales, the optimal behavioral strategy is determined by the current reward structure. However, over longer time scales the reward function adapts to coincide with the available predictive information present in stimuli. A recent review summarizes the experimental evidence supporting this hypothesis [55].

Applying the infotactic perspective to adaptive properties in neural systems, it is worth noting that most of the studies of neural adaptation focused on adaptation to time averaged statistical properties of the stimulus such as mean, variance, covariance or perhaps even higher-order moments. Yet sensory neurons also operate in ‘dilute’ conditions, i.e. at low signal-to-noise ratios. For example, a recent study shows that the gain of retinal ganglion cells can be affected by detection of a single photon [*46]. It is worth noting that infotaxis is a Bayesian approach based on times of individual (often binary) detection events. Given the success of Bayesian approaches in accounting for neural adaptation based on time averaged stimulus properties, such as mean, variance, and kurtosis [36], the more nuanced infotaxis approach might provide a new frontier for understanding adaptive functions in the nervous system.

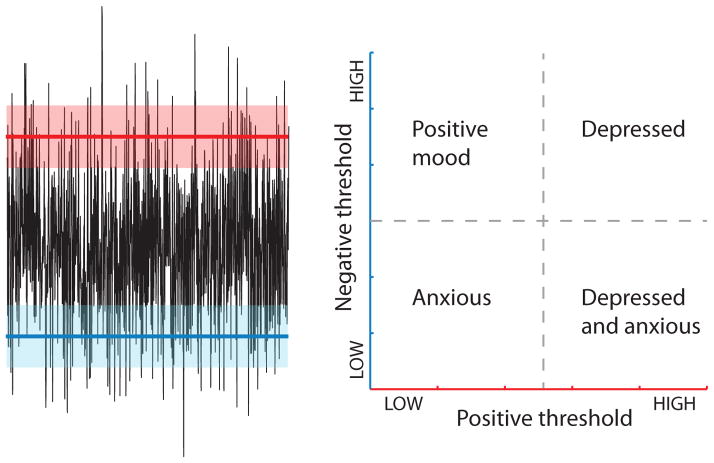
It would be exciting to see if information theory could account for long term adaptive changes in behavior, i.e. mood in the case of humans. There is an emerging view that long lasting mental states, such as depression, anxiety, optimism and pessimism, represent a proper integrative response of an animal to a sequence of events from its prior experiences [**56]. This is an advantageous response from an evolutionary point of view for several reasons. First, many stimuli are ambiguous and lead to reward or punishment with some probability, forcing an animal to make a choice of whether to allocate its effort to pursue a rewarding outcome or to prepare to minimize the consequences of a negative outcome. The threshold for triggering one or the other action cannot be set in a static manner, because the relative costs of false positives and negatives depend on the physical state of the animal and on the state of the environment. Therefore, to make an optimal decision, from a Bayesian point of view [57], the animal has to take into account the outcomes of previous decisions made a recent past, which presumably was characterized by similar states of the animal and its environment. To map this onto mood, a depressed state would then correspond mathematically to having a lower threshold for predicting a negative outcome. It is remarkable that thresholds for betting on positive versus negative outcomes can be changed by similar pharmacological and behavioral modifications in both humans and laboratory rodents [**56]. Furthermore, neural mechanisms underlying emotional states are conserved across a wide variety of organisms, with important homologues between vertebrate and invertebrate species [**56]. In particular, a prominent observation from animal learning studies is that neural mechanisms of reward and punishment are subserved by largely distinct circuits. The analogy to ON- and OFF channels in vision might be more than a mere coincidence. Instead, the separate processing of rewards and punishments might reflect the needs to achieve maximally informative coding under metabolic constraints (Figure 2), following the same arguments that were used in vision to explain the existence of separate ON and OFF pathways [58, *59, 60–61]. It seems likely that information theory could provide a completely novel and quantitative way of characterizing mood and its disorders.

Figure 2. Information theory approach to characterizing mood disorders.

(a) Separate neural mechanisms for encoding rewards and punishments can be explained using similar information-theoretic arguments that were used in sensory coding to explain the separation into OFF and ON channels. (b) Following [**56], variations in positive and negative thresholds corresponds to four basic mood states. The setting of these thresholds can be explained by a Bayesian model based on prior outcomes of the animal-environment interactions [**56].

Unlike in physics, where great successes began with Newton’s realization that the physical laws are the same whether on this planet or in space; in molecular biology, which bloomed with the discovery of a universal genetic code, we do not yet have a unifying framework to work with at the systems and behavioral levels. Information theoretic ideas have been successful at explaining properties of the nervous system from individual neurons to populations of neurons, the building blocks of behavior [**2]. Although the information maximization framework has been tested so far on only in a handful of different types of behavior, it seems well suited for providing such a unifying framework for understanding different facets of behavior, from adaptation in sensory systems to the adaptation of reward circuits on longer time scales so that they can better guide learning.