200 MeV Proton Radiography Studies with a Hand Phantom Using a Prototype Proton CT Scanner

Abstract

Proton radiography has applications in patient alignment and verification procedures for proton beam radiation therapy. In this paper, we report an experiment which used 200 MeV protons to generate proton energy-loss and scattering radiographs of a hand phantom. The experiment used the first-generation proton CT scanner prototype, which was installed on the research beam line of the clinical proton synchrotron at Loma Linda University Medical Center (LLUMC). It was found that while both radiographs displayed anatomical details of the hand phantom, the energy-loss radiograph had a noticeably higher resolution. Nonetheless, scattering radiography may yield more contrast between soft and bone tissue than energy-loss radiography, however, this requires further study. This study contributes to the optimization of the performance of the next-generation of clinical proton CT scanners. Furthermore, it demonstrates the potential of proton imaging (proton radiography and CT), which is now within reach of becoming available as a new, potentially low-dose medical imaging modality.

I. Introduction

With increasing use of proton radiation therapy for cancer patients, research into new imaging methods that can improve the accuracy of proton range estimates in radiation therapy planning have become a high priority. In many cases, protons are particularly desirable for treating cancerous tissue in close proximity to radiosensitive normal tissues, such as at the base of the skull and near the spinal cord. Protons are preferable to photons because their energies are easily tuned and the high dose of the Bragg peak can be localized reducing the threat of damaging otherwise healthy tissue. Accurate treatment of tumors at the base of the skull and near the spinal cord requires accurate knowledge of proton stopping and scattering power.

In order to obtain relative stopping power (RSP), Hounsfield units (HU, i.e. units of x-ray attenuation used in x-ray CT) are transformed using a calibration curve. However, there is no unique relationship between HU and RSP, especially in the regime of RSP=1 (i.e. water, human tissue). This means that errors in proton range are consistently 3–4% of the nominal proton range or even higher in regions containing tissue, bone and air interfaces. A survey at the Annual Meeting 2012 of the American Association of Physicists in Medicine (AAPM) showed that 33% of attendees polled said that range uncertainties are the main obstacle to making proton therapy mainstream [1]. Simulations and first experimental results have shown that by using a proton CT imaging system one may be able to reduce this range uncertainty to about 1% or less without increasing the dose to the patient [2].

Proton radiography has been recognized as being valuable for patient-specific optimization of the calibration from CT HU to RSP, and researchers at the Paul Scherrer Insitute (PSI) have pioneered its technical development and use [4]–[5]. Proton radiography differs in several key aspects from x-ray radiography. While unscattered photons travel in straight line paths, protons undergo multiple Coulomb scattering (MCS) events. This limits spatial resolution since the proton path deviates from the assumed straight lines by up to several millimeters in anatomical objects encountered in medical proton imaging. The accuracy of those path estimates is critical for achieving a high spatial resolution in proton radiography. An advantage of proton radiography is that it may allow us to distinguish small differences in RSP of various tissues better, compared with x-ray radiography at the same dose. Proton radiography also provides us, directly, with the water equivalent thickness (WET) of the object being imaged, which is useful for quality assurance in pre-treatment verification in proton therapy.

II. Experimental Setup

The first generation prototype proton CT scanner, shown in Fig. 1, is based on the design principle described in [6]. It consists of two principal components: The silicon tracker, which tracks individual protons, and the segmented cesium iodide calorimeter used for measuring residual energy of protons.

Fig. 1.

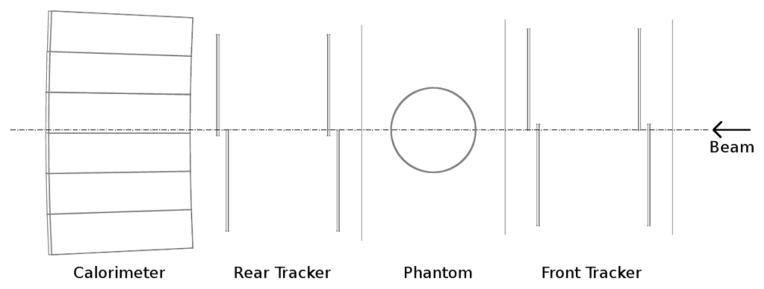
Current proton CT scanner prototype design. The distance between the two planes of the front and rear telescopes is 9.8 cm. The distance between the front and rear tracker is variable.

Eight silicon tracker tiles are arranged into four planes, each 400 μ m thick, with a sensitive area of 8.95 × 17.4 cm². The silicon strip detectors (SSDs) have a strip pitch of 228 μm. The tiles are arranged into two “telescopes,” one upstream and one downstream from the phantom, so that the entry and exit vectors can be determined. The tracking planes interface through a high speed data acquisition system based on field programmable gate arrays (FPGAs).

Each tracking detector has a fast trigger output which is connected to the trigger logic within the FPGA. A trigger decision is then made each clock cycle (50 ns) and the readout sequence begins for the entire system when a coincident event is detected between any two detectors forming an x-y pair. Offline, further data rejection is performed to select events with higher order coincidences only (8-fold, in this case).

The calorimeter is composed of an array of 18 thallium-doped CsI crystals arranged in a 3 × 6 matrix. Each crystal is 12.5 cm long, which is sufficient to stop 200 MeV protons. The residual energy of the protons is converted to light by scintillation, which is read out by photodiodes and converted to a digital value by an analog-digital converter (ADC) at a rate of up to 100 kHz.

For the radiography experiment, the proton flux in the accelerator at LLUMC was tuned to very low values (less than 50k protons per 0.5-second spill) to match the rate capability of the first-generation data acquisition system. The second-generation system (in progress) will allow data acquisition rates of up to 2 MHz.

A realistic hand phantom, consisting of a human hand skeleton embedded in tissue-equivalent plastic, was mounted vertically between the up-stream and down-stream SSDs and imaged with a low-intensity 200-MeV proton cone beam, emanating from the vacuum exit window of one of the proton research beam lines at LLUMC. The entry and exit vectors, as well as the calorimeter response of each individual proton, were measured. This information allowed us to reconstruct the estimated trajectories and water equivalent path length (WEPL) of each proton through the phantom. The WEPL values were derived from the calorimeter response using a calibration process for the first-generation proton CT scanner, which is described in detail in Hurley et al. [8].

III. Reconstruction Software

For the reconstruction of the radiographic images, software previously developed for a full proton CT reconstruction [9] was modified and executed on a quad-core workstation equipped with a Tesla C1060 GPU. The raw data input into the reconstruction software contained the proton tracker coordinates and the calorimeter response for each proton. A cylindrical reconstruction volume, containing the entire hand phantom, was created.

The main steps of the algorithm used for the proton radiography reconstruction were as follows:

1. Read the input data (proton histories) from file.

2. Determine which histories traversed the reconstruction volume and calculate the locations where the proton entered and exited the volume.

3. Assign angular and spatial bins to each history.

4. For histories that traverse the reconstruction volume and belong to the zero-degree angular bin, write data to file.

5. Write scattering angle values in the t and v directions (ϕ_t, ϕ_v) to files corresponding to each pixel.

6. Calculte the total scattering angles, defined with respect to the beam axis, for each proton in each pixel.

7. Plot the median total scattering angle in each pixel to obtain the scattering radiograph.

8. Convert residual energy values to WEPL using the calibration curve.

9. Perform data reduction (“cuts”): For each pixel, define a “mode window” of WEPL that accepts protons within ±30% of the mode, or ±1 cm if 30% is less than 1 cm. Define the “peak” WEPL as the mean of the distribution contained within the mode window.

10. Plot peak WEPL value to obtain the energy-loss radiograph.

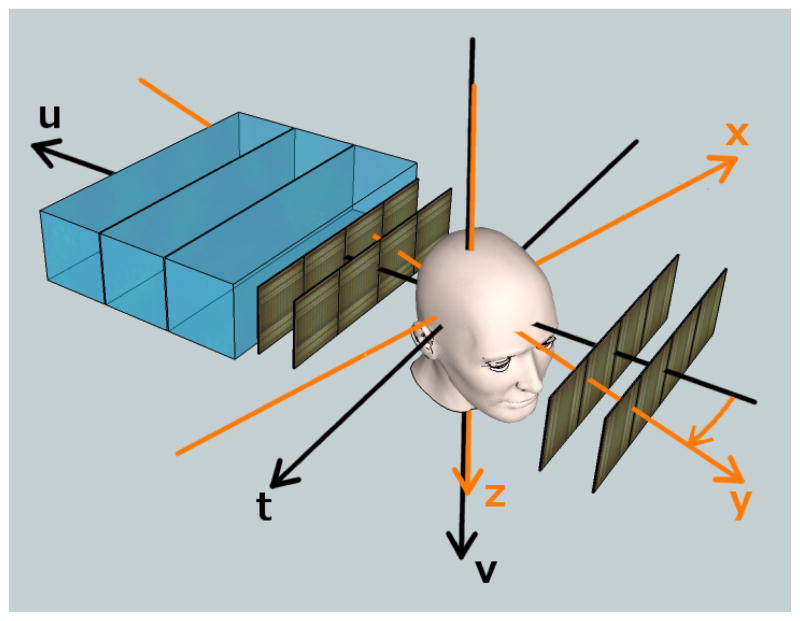
The radiographic reconstruction made use of the phantom-based coordinate system (x,y,z) and the detector-based coordinate system (t, u, v) of the proton CT scanner, as shown in Fig. 2. The system used for reconstruction is defined by the tuv-coordinates, which remain separate from the image system for CT purposes. This system is right-handed with the positive u-axis directed along the beam, and the v-axis directed along the plane of the SSDs in the same direction as the z-axis. The center of the reconstruction volume is located at u = 0. In proton radiography, the t-axis runs in the opposite direction as the x-axis.

Fig. 2.

Two coordinates systems are used in a proton CT scanner, here illustrated in a sketch of the second-generation proton CT scanner. The proton cone beam enters from the right and its central axis is parallel to the u-axis. The phantom can be rotated about the v-axis, but for the radiography experiment, it was kept at 0 degrees (y-axis anti-parallel to the u-axis).

The entry and exit vectors were projected onto the reconstruction volume so that the entry and exit coordinates could be determined. These points were connected by a straight line, for the purposes of radiography, which estimated the path of the proton. The midpoint of the estimated proton path was calculated as the average of the entry and exit coordinates. The proton was then binned into the nearest integer spatial bin (pixel) in t and v.

Cuts in relative angle, defined as the difference between entry and exit angle, were made at 3σ from each pixel’s mean relative scattering angle in both the t and v directions. These cuts were made to exclude events that had very large scattering angles, caused by inelastic nuclear interactions or elastic large-angle scattering events inside the phantom. The software also made cuts in WEPL which is mathematically defined as:

$$L={\int }_{\ell }\mathrm{\varrho }d\ell ,$$ (1)

where ϱ is the ratio of the stopping power of the material to the stopping power of water (i.e. the RSP) and ℓ defines the path of the proton. The WEPL cuts were also made at 3σ from the mean pixel value, and were necessary to exclude histories that were affected by inelastic nuclear interactions or resulted from unresolved coincidence of two or more particles in the calorimeter.

The reconstruction of the radiograph was performed in the t – v plane located at u = 0, at the center of the reconstruction volume.

IV. Proton Energy-Loss Radiography

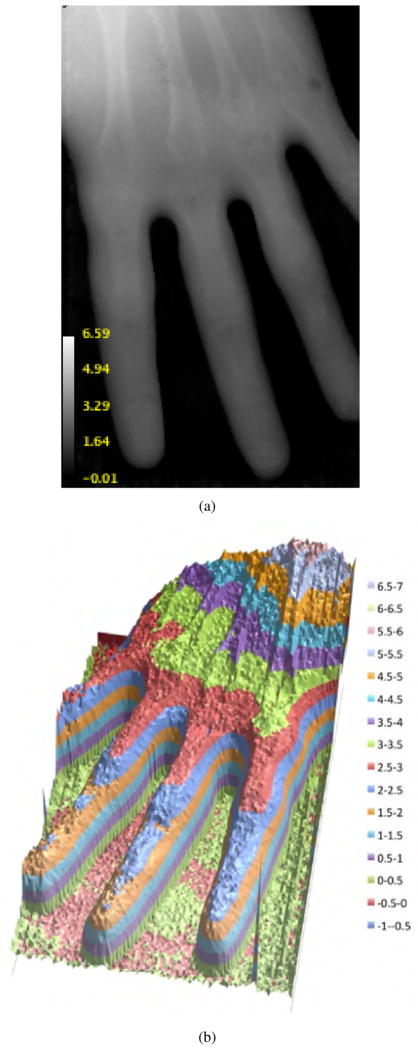
Figs. 3(a) and 3(b) depict two expressions of radiographic images of the hand phantom in terms of WET. ImageJ version 1.45 [10] was used to convert the output text file from the reconstruction software into the image file displayed in Fig. 3(a).

Fig. 3.

3(a) The first radiograph of a hand phantom with 0.5 mm pixels. 3(b) Relief map of WET calculated from the summed-up stopping power of the phantom. The scales for both images are in cm of WET.

A total of about 3.5 million proton events entered the reconstruction volume and were detected by the SSDs with near 100% efficiency. About 2.6 million of these events were selected by excluding pileup events, which were recognized by their larger-than-usual energies deposited in the calorimeter, and by removing events that did not pass through all four tracker planes. Of the 2.6 million events, 67.1% passed cuts in angle and WEPL and were used to construct Figs. 3(a) and 3(b). A pixel size of 0.5 × 0.5 mm² was used to create these images; therefore, each pixel contained the data of approximately 40 protons.

The contrast in 3(a) is low compared with an x-ray radiograph. This is due to the fact that the RSP of bone is only 50%–80% greater than that of water while the x-ray absorption power of bone can be several times greater, depending on the photon energy. The relief-map display of the phantom in Fig. 3(b) more clearly depicts regions of varying WET of the hand, and shows clear structural details.

In order to generate a comparable WET image from x-ray data, an x-ray CT scan of the hand phantom was performed with the 64-slice GE LightSpeed VCT scanner (GE Health-care Technologies, Waukesha, WI), normally used for proton treatment planning in the Department of Radiation Medicine at LLUMC. A Python script written by one of the authors (F. Hurley) was used to convert voxel values to RSP with the Hounsfield-Unit-to-RSP calibration curve provided by the medical physics team. An x-z projection of RSP values was created by summing over pixels with constant x-value in the y-direction for each slice of constant z, and multiplying the sum by the pixel size.

Fig. 4 contains a side-by-side comparison of the transformed x-ray CT scan and the proton radiograph with the same window and level settings. The calibration scales are in centimeters of WET. Table I shows that the WET values averaged over selected regions agree to within about 3%. This is within the realm of what is expected.

Fig. 4.

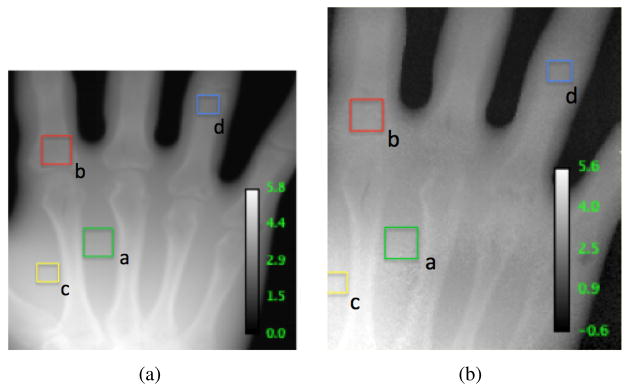
4(a) shows the WET projection image of the hand phantom based on a high-resolution x-ray CT scan. 4(b) shows the corresponding WET proton radiograph displayed in 3(a).

TABLE I.

Comparison of WET_xray and WET_proton for Selected ROIs

ROI	WETxray (cm)	WETproton (cm)	% Diff	Rel. Err.
(a.)	3.6 ± 0.1	3.5 ± 0.1	2.8%	0.7σ
(b.)	2.9 ± 0.1	3.0 ± 0.1	3.3%	0.7σ
(c.)	4.2 ± 0.1	4.2 ± 0.2	0.0%	0.0σ
(d.)	2.5 ± 0.1	2.5 ± 0.0	0.0%	0.0σ

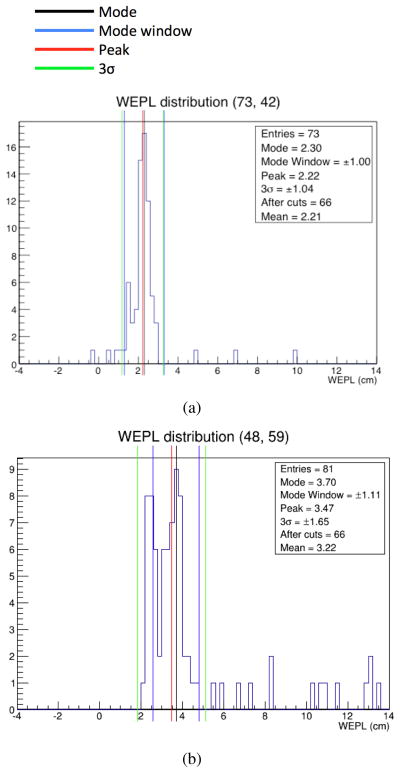
The WEPL distribution of protons before data reduction in each pixel was roughly gaussian, as seen in Fig. 5(a). The distribution was usually right-skewed (high WEPL) which corresponds to the left-skewed (low-energy) distributions in energy. The protons in the tails are protons that underwent nuclear scattering events. These are the events that we eliminated using the appropriate cuts.

Fig. 5.

Distribution in WEPL for pixels described by the coordinates 5(a) (t = 73, v = 42) and 5(b) (t = 48; v = 59) before cuts were made. The black line defines the mode of the distribution and the red line defines the mean or “peak” of the distribution. The blue lines indicate the mode window which contains the particles within ±30% of the mode, and provides the distribution on which the 3σ cuts were based. The green lines indicate the cuts made on this specific pixel. Notice the straggling in the large WEPL range. These values correspond to particles that underwent nuclear interactions. 5(a) illustrates an example of a roughly gaussian WEPL distribution. 5(b) is that for a boundary pixel with a bimodal WEPL distribution.

We did find, however, that a significant percentage of pixels contained non-gaussian WEPL distributions. These distributions, as in 5(b), are bimodal and correspond to pixels that lie on the boundary between two materials of different RSP. In this case, the reconstruction algorithm selected the leftmost mode, and the appropriate cuts were determined based on that value. This, however, reduced spatial resolution. Methods such as averaging the two modes, or “splitting” pixels have been proposed and have yet to be explored.

The image quality of proton radiography in comparison to x-ray radiography would best be studied as described in the work by Depauw and Seco [11]. These investigators used the contrast-noise-ratio (CNR) expressed in units of decibel (dB) in a Monte Carlo study of x-ray and proton radiography with a high-contrast resolution phantom. However, for a similar analysis, the hand phantom used in this study was too non-uniform to provide meaningful data. A phantom better suited for a CNR analysis will be constructed and used in future experiments.

V. Proton Scattering Radiography

The amount that a proton is scattered by MCS between its entry and exit from a phantom is inversely proportional to the product of its velocity and momentum. In the gaussian approximation of MCS, given by Lynch and Dahl [12], the width of the scattering distribution can be described by:

$$\theta =\frac{13.6\text{MeV}}{\beta cp}z\sqrt{\frac{x}{X_o}}[1+0.038log\frac{x}{X_o}]$$ (2)

where θ is the width of the Gaussian approximation for angular deflection in a plane, β, p are the velocity and momentum of the proton, respectively, z is the charge of the proton and x/X_o is the thickness of the material traversed in units of radiation length. We calculate X_o of the material using:

$$\frac{1}{X_o}=\sum \frac{w_j}{X_j}$$ (3)

where the w_j’s are the fractions by weight of each element in a given material and the X_j’s are the radiation lengths of each material. The second term in Eq. 2 tends to be small and can thus be ignored for purposes of estimation. Note that this approximation is good only for relatively thin objects (i.e. 10⁻³ < x/X_o < 100) where the velocity and momentum are assumed to be approximately constant. For a thicker phantom, we would need to account for energy-loss by introducing an integral over x (see [13] for details).

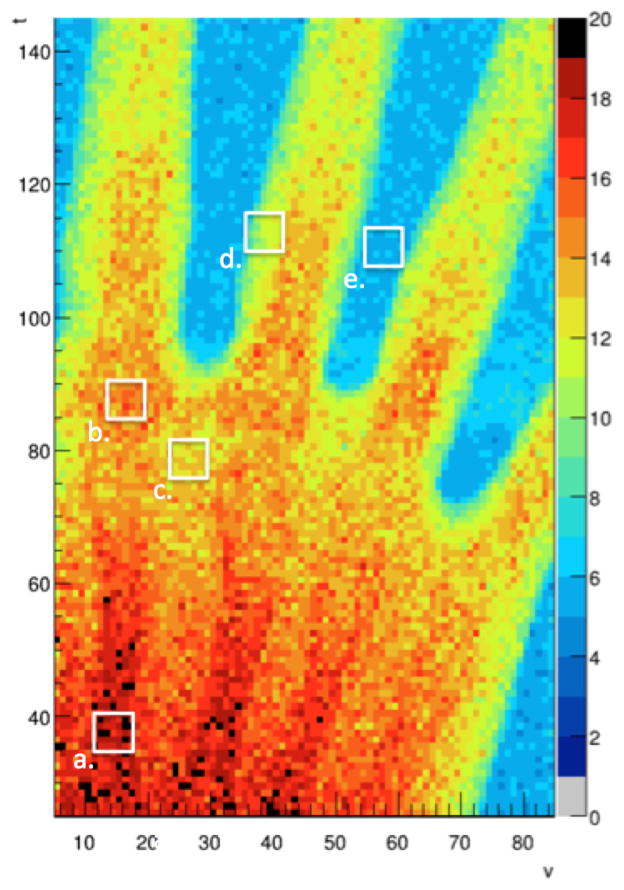
The scattering radiograph of the hand phantom in Fig. 6 was obtained as follows: for each pixel, the scattering angle of each proton history in the t-u and v-u planes was obtained from measurement of the entry and exit directions. The total scattering angle with respect to the u-axis was then calculated as

Fig. 6.

Scattering radiograph of the hand phantom showing the median 3D scattering angle (in mrad) in each voxel. The blue color code corresponds to the scattering of about 5 mrad of 200 MeV protons in the SSDs.

$$\mathrm{\Phi }=\sqrt{{\varphi }_t^2+{\varphi }_v^2}$$ (4)

for every t, v pair. The median Φ in each pixel was plotted as a color map on a two-dimensional graph.

Table II displays the expected and observed median scattering angles for select regions of interest (ROIs) corresponding to Fig. 6. The expected values were calculated using Eq. 2, the measurements of bone and tissue thicknesses obtained from the x-ray CT scan of the phantom, and the radiation lengths of standard bone, soft tissue, water and silicon (Table III).

TABLE II.

Expected and Observed Scattering Angles for 200 MeV Protons (β = .566, p = 644 MeV/c) for Selected ROIs (units in mrad)

ROI	Expected	Observed (Fig. 6)	Relative Difference
(a.)	17	17.8. ± 0.9	0.9σ
(b.)	15	14.1. ± 0.9	1.0σ
(c.)	11	12.3 ± 0.7	1.0σ
(d.)	10	10.3. ± 1.3	0.2σ
(e.)	5	5.2 ± 0.4	0.5σ

TABLE III.

Densities and radiation lengths of materials commonly encountered in proton CT. Data for bone: [15]; data for tissue, water and silicon: [16]

Material	Density (g/cm3)	Radiation Length, Xo (g/cm2)
bone	1.45	16.6
tissue	1.00	38.2
water	1.00	36.1
silicon	2.33	21.8

Table II shows good agreement between expected and observed scattering angles for the hand phantom. All of the selected scattering regions fall within 1σ of the expected value. With the exception of region (b), the measured scattering values were consistently slightly higher than the expected values, which may be explained by the right skew of the distribution in Φ.

Despite the higher noise in the scattering radiograph compared to the energy-loss WET radiograph (Fig. 3(a)), it shows a great amount of structural detail. Skeletal structures such as metacarpal bones and soft tissue can be clearly distinguished. It should also be noted that the overall scattering value of regions (a) and (b) are similar, despite the difference in the structure of the phantom, because region (a) contains a large amount of tissue and a small amount of bone, while region (b) contains a large amount of bone and a very small amount of tissue.

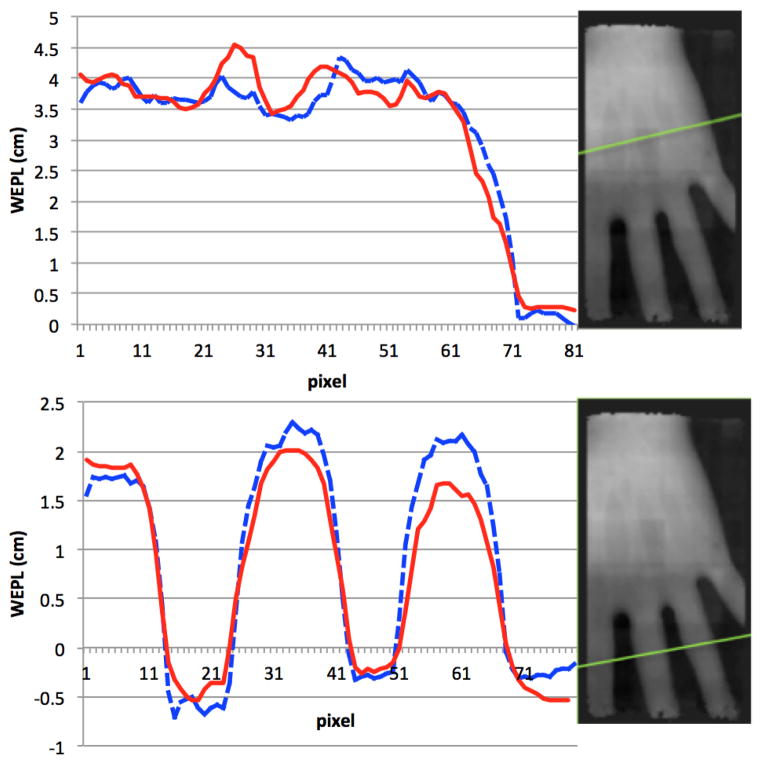
Fig. 7 compares two image profiles for the energy-loss radiograph (dashed curve) and the scattering radiograph, (solid curve) for a pixel size of 1 mm. When the profile of the scattering curve was normalized to the energy-loss profile, we found that the general shapes of the two curves of each plot were very similar, which shows that in this case, regions of greater stopping power were also regions of higher scattering power, as one would expect. Furthemore, qualitative observation of many of these types of line profiles suggest that scattering radiography may yield a higher CNR; however, a phantom better suited for this measurement would be required to confirm this. In this case, proton scattering radiography may prove beneficial for patient alignment based on skeletal features.

Fig. 7.

Normalizing the scattering radiograph (solid curve) to the energy-loss radiograph (dashed curve), we see roughly the same shape and even some subtle features for radiographs with 1-mm pixels. While the quality of the scattering curve is not as good as that of the energy-loss curve, it may still be useful for patient positioning.

While the energy-loss radiograph provides us with WET for energy loss which is most important for quality control in proton range estimation, the scattering radiograph may provide us with the WET for proton scattering power. The usefulness of this information for treatment planning requires further investigation.

VI. Dose to Phantom

As mentioned in section IV, 3.5 million proton events entered the reconstruction volume in this experiment. The fluence near the central axis of the proton cone beam was approximately 24,800 cm⁻². Assuming a proton weighting factor of unity and a total stopping power of 4.5 MeV/cm for 200 MeV protons, the estimated dose delivered to the center of the phantom was approximately 20 μSv which is within the same order of magnitude as the dose delivered in state-of-the art x-ray radiography for a hand or foot [17]. There was no intention to formally study the relationship between dose and image quality in this work. Based on theoretical calculations [18] and early experimental proton CT experience, [19] the dose needed for the same level of image noise could be much lower with proton radiography than was used in this study.

VII. Conclusions and Future Investigations

Our proton radiographs demonstrate the promise of proton imaging (proton radiography and CT) now within reach of becoming a new, potentially low-dose clinical imaging modality. For future investigations, new phantoms will be developed and built in order to systematically study these properties. Region of interest studies of the scattering radiograph indicate strong agreement between our measurements and the predictions made using Lynch and Dahl’s equation. Although the image is lower quality than the energy-loss radiograph, scattering radiography provides information about the proton scattering power of materials, which is inversely proportional to the effective atomic number distribution in the tissue. Energy-loss radiography cannot provide this information since stopping power depends only on Z/A, which is practically identical for most soft tissues and water, leading to very low contrast. Therefore, scattering radiography and tomography will likely have useful applications in proton treatment planning.

Presently, our radiography procedure assumes straight-line trajectories of protons through the phantom. It is likely that we can improve our images by incorporating the most likely path of the proton into our binning algorithm. Additionally, our reconstruction algorithm presently makes angular cuts in the u – v and u – t planes, separately. We believe that by adding these angles in quadrature and cutting based on this total angle (as in Fig. 6) will improve the quality of our event selection. Better yet, instead of removing large-angle scattered protons from our analysis by cuts based on gaussian distributions, we would rather like to include these data by using more appropriate scattering models. In this case, it may be possible to obtain additional information about the elemental composition of tissues using proton radiography and tomography.