Abstract
We carried out free-energy calculations and transient kinetic experiments for the insertion of the right (dC) and wrong (dA) nucleotides by wild-type (WT) and six mutant variants of human DNA polymerase β (Pol β). Since the mutated residues in the point-mutants, I174S, I260Q, M282L, H285D, E288K, and K289M, were not located in the Pol β catalytic site, we assumed that the WT and its point-mutants share the same dianionic phosphorane transition-state structure of the triphosphate moiety of deoxyribonucleotide 5′-triphosphate (dNTP) substrate. Based on this assumption, we have formulated a thermodynamic cycle for calculating relative dNTP insertion efficiencies, Ω = (kpol/KD)mut/(kpol/KD)WT using free-energy perturbation (FEP) and linear interaction energy (LIE) methods. Kinetic studies on five of the mutants have been published previously using different experimental conditions, e.g., primer-template sequences. We have performed a pre-steady kinetic analysis for the six mutants for comparison with wild-type Pol β using the same conditions, including the same primer/template DNA sequence proximal to the dNTP insertion site used for X-ray crystallographic studies. This consistent set of kinetic and structural data allowed us to eliminate the DNA sequence from the list of factors that can adversely affect calculated Ω values. The calculations using the FEP free energies scaled by 0.5 yielded 0.9 and 1.1 standard deviations from the experimental log Ω values for the insertion of the right and wrong dNTP, respectively. We examined a hybrid FEP/LIE method in which the FEP van der Waals term for the interaction of the mutated amino acid residue with its surrounding environment was replaced by the corresponding van der Waals term calculated using the LIE method, resulting in improved 0.4 and 1.0 standard deviations from the experimental log Ω values. These scaled FEP and FEP/LIE methods were also used to predict log Ω for R283A and R283L Pol β mutants.
The ability of nature to fine-tune the fidelity and lesion-bypass abilities of DNA polymerases poses a challenge to theoretical-computational analysis (TCA). The goal of TCA should be to reliably reproduce the biochemical data and eventually provide predictions of structure-function relationships. The complexity of DNA polymerases necessitates choosing approaches that balance theoretical rigor with structural insight by employing sound structural assumptions, linear relationships, and thermodynamic cycles to maximize the cancellation of systematic computational errors. At the same time, a consistent set of biochemical data for primer-template sequences that are identical with those used to obtain crystal structures is needed to support TCA.
Nucleotidyl transfer reaction catalyzed by human DNA polymerase β (Pol β) has been frequently studied by computational methods (1–20) due to small size of Pol β (39 kDa) and its importance for human health (21, 22). The wealth of site-directed mutagenesis data (23–28) on Pol β provides an excellent opportunity to develop robust TCA approaches for prediction of catalytic efficiency of Pol β variants. Recent theoretical studies include the evaluation of contributions of ionized amino acid residues located near Pol β active site on the catalytic efficiency using the semi-microscopic version of Protein Dipoles Langevin dipoles (PDLD/S) method combined with Linear Response Approximation (LRA) method (29), and the identification of the strength of hydrogen bond between N279 and dCTP, as a strong predictor of mutational effects on the catalytic turnover rate for the insertion of dCTP substrate opposite dG (30).
The accurate evaluation of mutation-induced changes in the Pol β catalytic efficiency (kpol/KD) by all-atom molecular dynamics (MD) simulations places extreme demands on consistent description of the electrostatic interactions and thorough sampling of relevant ground- and transition-state (TS) ensembles. Catalytic effects of point mutations that occur near the substrate binding site are especially sensitive to sampling of relevant TS configurations. The TS structure may change in the mutated polymerases because enzymatic catalysis is a robust process, in which alternative mechanisms can occur that involve different amino acid residues or solvent molecules as substitutes for the catalytic role of a wild-type (WT) residue (31). Thus, reliable quantitative predictions of catalytic effects for enzymes with modified active sites necessitate quantum mechanics/molecular mechanics (QM/MM) calculations of all possible alternative reaction mechanisms. Such calculations place extreme demands on computer resources while lacking benefits of the cancellation of systematic computational errors between the WT and mutant enzymes.
The description of short- and long-range electrostatic interactions, and related issues with the treatment of the boundary of the simulated system (32–36), are essential for the calculations of catalytic effects caused by mutations that are in larger distances (> 8 Å) from the α-phosphate of dNTP substrate. Since mutations of these distant residues are less likely to change the catalytic pathway but can sometimes cause significant changes in catalytic efficiency (37–39), these mutants can be utilized to assess and improve the consistency of the computational description of electrostatic effects and TS models. In fact, the comparison of the observed and calculated catalytic effects of distant mutations can be extremely informative even for mutants that cause small catalytic changes. This is because two or more large numbers need to be accurately calculated before they are subtracted to obtain correct near-zero free energy differences. Thus, silent distant mutants can be used to verify a validity of a computational model or to reveal model deficiencies.
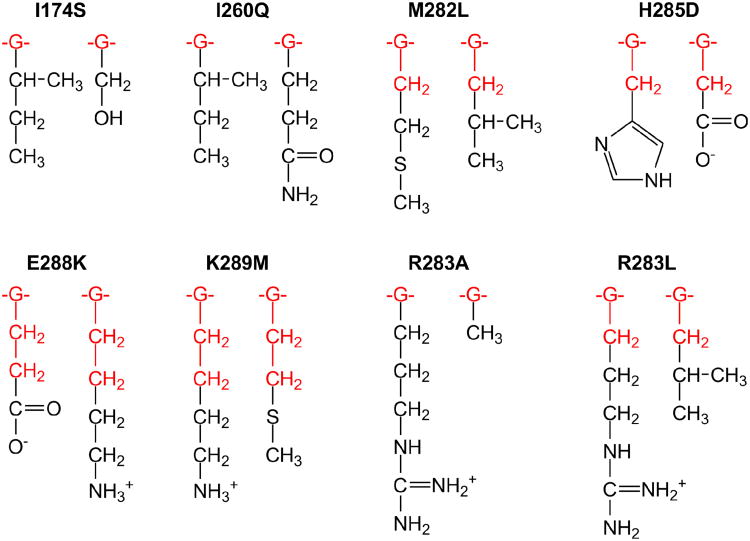
In this paper, we study the catalytic effect of single point mutations in six distant amino acid residues of Pol β, I174S, I260Q, M282L, H285D, E288K and K289M (Figure 1). For these mutants, we calculated and measured, using rapid-quench flow pre-steady state kinetics, the insertion of the right (ℛ) and wrong (W) nucleotides at the 3′-end of the primer DNA strand. We examine the performance of free-energy perturbation (FEP) calculations (40, 41) that are based on ‘alchemistic’ (i.e. non-physical) mutational pathways (42) in the binary Pol β–DNA complex (43) and a postulated chemical TS complex (44).
Figure 1.
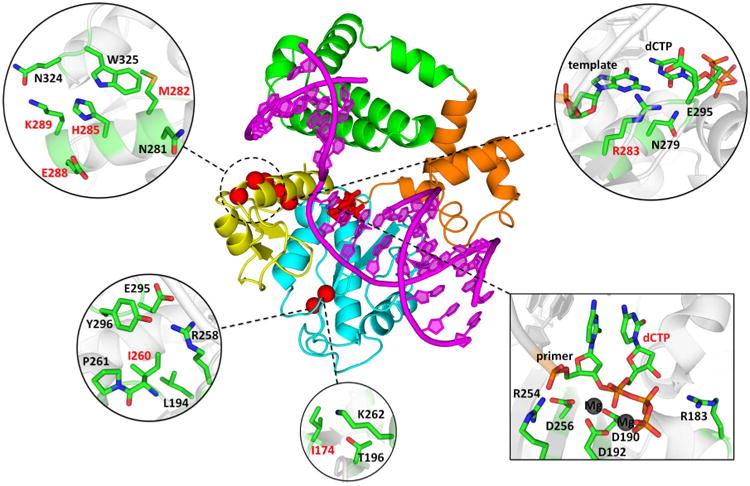
Positions of mutated amino acid residues in the Pol β-DNA-dNTP ternary complex. The primer-template DNA is shown in magenta. The N-terminal lyase domain (green), fingers- (orange), palm- (cyan) and thumb- (yellow) subdomains of polymerase domain are named according to the original Pol β nomenclature (89, 90) in which the polymerase domain is likened to the left hand. The positions of mutated residues are shown in red spheres (centered at Cα atom); dCTP substrate is shown in stick model. Insets show mutated residues and surrounding residues and deoxynucleotides in stick model (colored by atom type: carbon – green; oxygen – red; nitrogen – blue; phosphorus – orange; magnesium – dark grey).
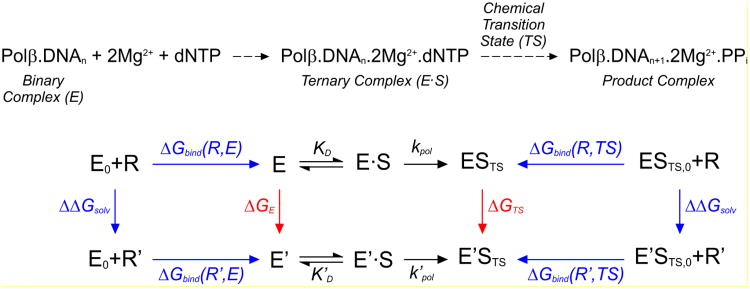
In our attempt to improve agreement between calculated and experimental free energies, we propose and examine two modifications of the FEP computational protocol: (i) scaling FEP free energies by an empirical factor (further referred to as “scaled FEP” method) and (ii) replacing the FEP van der Waals (vdW) term for the interaction of the mutated amino acid residue with its surrounding environment with vdW term calculated using linear interaction energy approximation (LIE) (45). This new method, which is abbreviated as the FEP/LIE method, is based on a modified thermodynamic cycle for alchemistic mutagenesis of Figure 2 (see Materials and Methods). While the electrostatic scaling factor mitigates overestimated electrostatic effects, replacing the FEP vdW term for the interaction of the mutated amino acid residue with surrounding environment by the corresponding term from LIE is aimed at alleviating computational instabilities due to large fluctuations of steric repulsion energies in alchemistic FEP simulations. Both scaled FEP and FEP/LIE methods performed significantly better on the set of six mutants compared to standard FEP and LIE methods. We have used our scaled methods to calculate the catalytic properties of two additional mutants, R283A and R283L, presenting these as new predictions. We have organized the presentation by first discussing conformational dynamics of the thumb subdomain in relation to the insertion of ℛ and W deoxynucleotides. These results are followed by a description of insertion kinetics and energetics for each Pol β mutant, which includes a discussion of the interactions of mutated amino acid residues with nearby protein residues, nucleotides, and water molecules.
Figure 2.
Reaction scheme of the nucleotidyl transfer reaction catalyzed by Pol β (top) and thermodynamic cycle (bottom) for calculating the relative catalytic efficiency, Ω = (kpol/KD)'/(kpol/KD), of a mutant enzyme (see eq 1 to 5). States E0 + R and E0 + R′ correspond to an enzyme that lacks the side-chain of the mutated amino acid residue, and this side-chain (R for WT residue and R′ for the mutant), respectively, each individually solvated in aqueous solution. States E and E′ denote WT and mutant enzymes in aqueous solution, respectively (i.e., for Pol β, E0, E and E′ denote Pol β complex with bound primer-template DNA). States E·S and E′·S correspond, respectively, to WT and mutant enzymes containing a bound substrate (dNTP for Pol β). These enzyme-substrate complexes assume the geometry of the rate-limiting transition state in the states ESTS and E′STS. States ESTS, 0 + R and E′STS,0 + R′ correspond to the side-chain and enzyme-substrate transition states (in which the enzyme lacks the side-chain of the mutated amino acid residue), respectively, each individually solvated in aqueous solution. The free energies evaluated in FEP and LIE calculations are shown in green and blue, respectively.
1. Materials and Methods
1.1. Thermodynamic cycle
The catalytic effect of an enzyme point mutation (mut),
| (1) |
can be expressed using the inner thermodynamic cycle of Figure 2 as
| (2) |
where ΔGE and ΔGTS are the relative free energy of the free WT and mutant enzymes and their transitions states (TS), respectively, and R and T are the universal gas constant and temperature in K. This thermodynamic cycle can be combined with an ‘alchemistic’ (i.e. non-physical) mutational pathway (42) using FEP calculations (40, 41) to assess the catalytic effect of distant mutations that do not change the catalytic mechanism of the enzyme (29). In addition to using FEP calculations, ΔGE and ΔGTS terms are evaluated in this paper using the LIE approximation of Åqvist and coworkers (45), and by a combination of these two approaches.
The FEP calculations involve alchemistic transformation (Movie S1) of the side-chain atoms of the mutated amino acid residue from WT (R) into the mutant (R′) in the binary Pol β-DNA complexes and their corresponding TS complexes. In contrast, LIE requires computation of the relative ‘binding’ free energies of the R′ and R amino acid residue to the binary and the TS structure. These free energies can be calculated for the WT, ΔΔGbind(R), and the mutant, ΔΔGbind(R′), using the outer thermodynamic cycles shown in blue in Figure 2. When also considering that both the energy of forming the covalent bond to the side-chain and the relative solvation free energy of this side-chain in aqueous solution (ΔΔGsolv) cancel out (See Supplementary material – eq. S1-12), we can write
| (3) |
If we define relative binding of a side-chain/amino acid residue R to the E and TS conformations of an enzyme as
| (4) |
eq. 3 can be rewritten as
| (5) |
In the specific case of WT Pol β, TS in Figure 2 can be replaced with a high energy intermediate that structurally mimics dianionic phosphorane transition state for the formation of the new P-O bond. This model has been shown to possess structural and energetic features that were consistent with Pol β fidelity (44).
1.2. Computer simulations
Initial Structure Preparation
In order to reduce the computational ‘cost’ associated with the size of the simulated system, we limited the radius of a sphere, in which motions of all atoms were simulated using MD, to 33 Å. The simulation sphere included most amino acid residues in the fingers sub-domain, entire palm sub-domain (except one extensive surface loop), the whole thumb sub-domain, and the surrounding water molecules. The simulations were initiated using three crystal structures of Pol β: a binary complex with a gapped DNA substrate (PDB code 1BPX), a ternary complex including ddCTP bound opposite dG template (PDB code 2FMP), and a ternary complex containing dG:dAMPCPP mismatch in the active site (PDB code 3C2M). Only the residues 10-335 from the original protein sequence were considered because residues 1-4 and 1-9 are unresolved in the binary structure and the two ternary crystal structures, respectively. The protein coordinates in all crystal structures were aligned using the program PyMol 0.99 (46), and the coordinates of the NH2 atom of R283 of the crystal structure 1BPX were chosen as the origin of the simulation sphere for all simulated systems. This origin permitted the inclusion of the N-terminal thumb sub-domain (Figure 1) and all mutated residues inside the simulation sphere. All crystallographic water molecules were removed and the simulated systems were immersed into a 33 Å radius sphere of TIP3P water molecules generated using the Qprep module of the program Q (47). The water sphere was centered on the center of the simulation system. Those TIP3P water molecules that were not sterically overlapping with the protein or DNA atoms were retained in the starting structures for MD simulations. The 3′-terminal dideoxynucleotide of the primer strand and ddCTP in the 2FMP ternary structure were modified by adding the 3′-O− and 3′-OH groups, respectively. The dAMPCPP in the 3C2M ternary structure was modified by replacing the -CH2- group in the Pα – Pβ bridge by oxygen. One Na+ ion in the active site was replaced by Mg2+ in the 2FMP structure. Additionally, two Mn2+ ions in the active site in the 3C2M structure were replaced by Mg2+ ions. Binary complexes were prepared from the 1BPX, 2FMP and 3C2M structures by removing active site metal ions and dNTPs. Dianionic phosphorane transition state (TS) models were prepared from the 2FMP and 3C2M ternary complexes as described in (44).
MD simulations of WT Pol β were carried out with the following selections of the charged amino acid residues: aspartate (190, 192, 256, 263, 276, 314, 318, 321, 332), glutamate (203, 232, 288, 295, 309, 316, 329, 335), lysine (27, 41, 48, 206, 230, 234, 262, 280, 289, 317, 326, 331), arginine (40, 149, 152, 182, 183, 254, 258, 283, 299, 328, 333) and the charged deoxynucleotides dG (6, 7, 9) and dC (8,10) of the DNA template. In general, this selection of the charged residues is consistent with glutamate, aspartate, lysine and arginine that lie closer than 27 Å from the center of the simulation sphere having charges based on their pKa in water. All residues, including ionizable residues and nucleotides, further than 27 Å from the center of the simulation sphere were electroneutral. The atomic charges of electroneutral phosphate group and ionizable residues are listed in Supplementary Table S1. Eight single amino acid residue mutants, I174S, I260Q, M282L, R283A, R283L, H285D, E288K and K289M were generated from the WT binary and TS structures using PyMOL. The total charge of the simulation sphere was -0.95e for WT and the I174S, I260Q and M282L mutants, -1.95e for the R283A and R283L, H285D, and K289M mutants, and 1.05e for the E288K mutant.
MD simulations
The configurational ensembles for the evaluation of free energies were generated from MD trajectories using the ff94 AMBER force field (48) implemented in the program Q, version 5.01 and 5.06 (47). The ff94 uses identical set of electrostatic and vdW parameters as more recent Amber ff99 (49), ff99SB (50) or ff99SB-ILDN (51) force fields. The torsional parameters that vary among these force fields were fitted and tested in the framework of other important approximations, such us long-range electrostatic treatments or boundary conditions, which are implemented differently in Amber and Q programs. Thus, we decided that the previous reliable performance of the ff94 force field in its Q-implementation out-weights risks of switching to a new parameter library. To compare distribution of φ and ψ dihedral angles in our MD trajectories and the starting X-ray crystal structures we provide examples of Ramachandran plots for binary, ℛTS and WTS complexes in Supplementary Figure S1. The TIP3P water molecules were subjected to the surface-constraint all-atom solvent (SCAAS) type boundary conditions (52, 53) as implemented in the program Q. These constraints were designed to mimic infinite aqueous solution and to produce stable and realistic free energies, while not requiring large dimensions of the simulated systems (as opposed to simulation boxes utilizing periodic boundary conditions).
The structures of the simulated systems were equilibrated by a gradual heating of the simulated system from 5K to 298K in a series of twelve MD simulations with gradually increasing step size (0.01 to 2 fs) and 194.5 ps simulation time in total. Subsequent production LIE and FEP trajectories were generated using 2 fs integration time. The SHAKE algorithm (54), which eliminates integration instabilities associated with stretching vibrations of covalent bonds, was applied to hydrogen atoms of both solute and solvent molecules. The non-bonded interactions were evaluated explicitly for distances shorter than 10 Å. The local reaction field (LRF) method (55) was used to include long-range electrostatic interactions for distances beyond a 10 Å cut-off. The long-range potential was updated every 10 steps. The energies and geometries were sampled every 10 and 250 steps, respectively. Final geometries of the simulated systems were used as starting structures for FEP and LIE simulations.
FEP simulations
The partial atom charges, vdW well depths (ε) and atomic radii of mutated atoms (Figure 3) were changed linearly and concomitantly between the initial and final atom identities. If the end-point atom identity represented a dummy atom (i.e. original atom was annihilated) the charge and ε of such dummy atom were set to zero, and its atomic radius was set to 1.66 Å. Bond lengths and angles of the initial state were retained along the whole mutation pathway, except in cases when an H-atom was mutated to a heavy atom, in which case the typical bond length between the two heavy atoms was used. The initial state for the FEP simulation was chosen to minimize the number of atoms that were grown from a dummy atom (i.e. annihilation was preferred to creation in the forward direction), and the free energies from the forward direction were used. For M282L, FEP simulations were initiated from L-homoisoleucine and ran both to the wild-type methionine and mutant leucine (Supplementary Figure S2).
Figure 3.
Mutated and probe regions that were used in the FEP and LIE simulations, respectively. The atoms shown in black were included in both FEP and LIE regions. The regions mutated in the FEP simulations included additionally -CH2- group(s) and the glycine fragment -G- (NHCHCO) of each amino acid residue (red).
For each mutation, the reported log Ω values were obtained by averaging over two separate FEP simulations, which were initiated from geometries attained after 194.5 ps and 694.5 ps equilibration simulations. The production simulation length varied from 2060 to 4040 ps for each independent FEP simulation. Thus, each reported FEP log Ω value corresponds to total MD trajectory length from 8240 to 16160 ps. Pathways of FEP calculations were subdivided into (2 × 101 − 1) (M282L, Figure S2), 104 (I174S, I260Q, H285D and K289M) or 203 (R283A, R283L and E288K) simulation windows (see Supplementary Table S2), with a sampling time of 20 ps per window. These settings assured that the free energy change per each window stayed under 2 kcal/mol and the difference between forward and reverse simulations (along the same trajectory) was less than 1 kcal/mol for total ΔG. The statistical errors were estimated as standard deviations of four independently calculated log Ω values that included two calculations with FEP windows defined in Table S2 and two calculations with a lower total number of FEP windows.
LIE simulations
For each mutation, two separate 10 ns LIE simulations, one for WT and one for its corresponding mutant, were performed for binary and TS structures (i.e., each LIE log Ω value is based on 40 ns of MD sampling). Free energy changes associated with ‘binding’ of the WT (W) or mutant (R′) residue in Pol β (Figure 2, eq. 3) were calculated from the average electrostatic, <UES(R)>, and van der Waals, <UvdW(R)>, interaction energies of the amino acid residue (R or R′) with its environment as
| (6a) |
| (6b) |
where <UES> and <UvdW> energies were evaluated for selected atoms of the R and R′ amino acid side-chains shown in Figure 3, and empirical factors α = 0.45 and β = 0.43 that were previously determined (56) for the same force field.
The substitution of eq. 6a and 6b into thermodynamic cycle of Figure 2 and cancelling <U>wat terms (See Supplementary material – eq. S1-12) yields
| (7) |
and
| (8) |
Eq. 7 and 8 allow us to directly compare ΔGE and ΔGTS terms calculated using FEP and LIE methods. This comparison can provide insight into the strengths and weaknesses of the FEP and LIE methods as a foundation for their further methodological improvements.
FEP/LIE calculations
The decomposition of the calculated FEP free energy differences to electrostatic (ΔGFEPES) and van der Waals (ΔGFEPvdW) contributions was done using formulas (57)
| (9a) |
| (9b) |
| (9c) |
In addition, using eq 9b and 9c, the total vdW contribution was decomposed into intra- and inter-molecular contributions, ΔGFEPvdW = ΔGFEPvdW,qq + ΔGFEPvdW, qs, where qq and qs subscripts denote interactions among the atoms of the mutated region, and between the mutated atoms and surrounding atoms, respectively. In eq 9, ΔU = Ui+1−Ui represents the potential energy difference between the states in a ‘window’ characterized by coupling parameters λi+1 and λi. β−1=kBT, where kB stands for the Boltzmann constant, and T is the thermodynamic temperature. Notation 〈…〉i indicates averaging over the ensemble of configurations generated by a simulation on the potential energy surface of the state i. The total free energy change, ΔG, was calculated as a sum of the forward free energy differences over an alchemistic mutation pathway that was subdivided into hundred or more windows (Table S2). Although the components of the FEP free energies generally depend on the mutation path, the decompositions based on a ‘natural’ pathway that includes a concomitant linear variation of the charges and vdW well-depths provides electrostatic and vdW free energies that are consistent with the corresponding free energy terms generated by the LIE method (58).
The FEP/LIE free energies (ΔGFL) were calculated using eq. 10,
| (10) |
where χ represents an adjustable scaling factor, and superscripts qq and qs denote interactions among the atoms of the mutated region (Figure 3) and between the mutated atoms and surrounding atoms, respectively. Since the LIE method evaluates only the latter interactions, the vdW FEP free energies were decomposed into the qq and qs components, and the qs component was replaced, in eq. 10, by the corresponding LIE term. In this study, χ = 0.5 was used. FEP/LIE calculations were based on a post-processing of independent FEP and LIE calculations. Thus, depending on mutational pathway (Table S2), the total production simulation times required for the generation of a single log Ω value ranged from 48240 to 56160 ps.
Calculation of the effect of I260Q mutation on dNTP binding
The Kd contribution to the catalytic effect was calculated using the above described FEP/LIE approach with transition state complexes of WT and I260Q mutant structures replaced by ternary complexes.
Structural analysis based on MD simulations
As an integral part of our LIE calculations we monitored the dynamics of the backbone atoms in the thumb sub-domain by evaluating their root-mean-square deviation (RMSD) from the corresponding atoms in 2FMP or 3C2M crystal structures using program VMD 1.87 (59). Global RMSD of the thumb sub-domain was calculated after aligning the C, Cα and N backbone atoms of the residues 153 - 275 in the palm sub-domain; the residues 242 - 250 of the palm loop and residues 160, 212 - 214 in palm α-helices located outside the simulation sphere excluded from this alignment set. Internal thumb RMSD was separately evaluated after aligning the C, Cα and N backbone atoms of the thumb sub-domains. Each reported RMSD value was then obtained by subtracting the internal RMSD from the corresponding global RMSD. The reported magnitude of fluctuations from the mean correspond to two standard deviations, for which ∼95% of simulated points fall within the fluctuation range.
Stability of interactions between substrate and template bases was monitored in LIE simulations of TS complexes by measuring distances between hydrogen bonding donors and acceptors. The presence and stability of the hydrogen bonds was assessed from their average distances and corresponding standard deviations, while angular features were not considered.
1.3. Experimental procedures
Site-directed Mutagenesis, Expression and Purification of Pol β
The human wild-type DNA Pol β cDNA was cloned into the pET28a (Yamtich, J.; Nemec, A.A.; manuscript submitted). I174S, I260Q, M282L, H285D, E288K, and K289M mutations were introduced into the wild-type plasmid using the QuickChange site-directed mutagenesis protocol (Stratagene) with the DNA oligonucleotide primers (Invitrogen) as shown in Table 1. The presence of the mutations was confirmed by sequencing (Keck).
Table 1.
Primer sequences for site-directed mutagenesis.a
| Mutant | Sequence (5′ to 3′) | Direction |
|---|---|---|
| I174S | TGAAGTTAAAAAAGTGGATTCTGAATACAGTGCTACAGTCTGTGG | Forward |
| CCACAGACTGTAGCACTGTATTCAGAATCCACTTTTTTAACTTCA | Reverse | |
| I260Q | ACACAGAAGAATTGATATCAGGTTGCAGCCCAAAGATCAGTATTACTGTGGTG | Forward |
| CACCACAGTAATACTGATCTTTGGGCTGCAACCTGATATCAATTCTTCTGTGT | Reverse | |
| M282L | ACTGGGAGTGATATTTTCAATAAGAATTTGAGGGCTCATGCC | Forward |
| GGCATGAGCCCTCAAATTCTTATTGAAAATATCACTCCCAGT | Reverse | |
| H285D | GAATATGAGGGCTGATGCCCTAGAAAAGGG | Forward |
| CCCTTTTCTAGGGCATCAGCCCTCATATTC | Reverse | |
| E288K | GAGGGCTCATGCCCTAAAAAAGGGTTTCAC | Forward |
| GTGAAACCCTTTTTTAGGGCATGAGCCCTC | Reverse | |
| K289M | GGCTCATGCCCTAGAAATGGGTTTCAC | Forward |
| GTGAAACCCATTTCTAGGGCATGAGCC | Reverse |
Mutated codon is in boldface.
WT and mutant Pol β pET28a plasmids were transformed into the E. coli Rosetta strain (Novagen; gift from Patrick Sung, Yale University). Luria Broth cultures (500mL) were inoculated with a 5mL overnight starter culture and incubated at 37°C until the OD600nm reached approximately 0.6. Isopropyl-D-thioaglactopyranoside (IPTG) was added to a final concentration of 1mM and incubated at 37°C for two hours to induce expression of Pol β. After induction, the bacteria were pelleted and stored at 4°C on ice overnight, and then, purfied as described previously (60). Briefly, bacteria were resuspended in buffer with added protease inhibitors (Roche) and 1mM PMSF and lysed by sonication. The lysate was clarified by centrifugation, and Pol β was purified by fast protein liquid chromatography using a 5mL HiTrap Chelating HP Column (GE Healthcare) charged with NiSO4 using an imidazole gradient followed by a 5mL HiTrap SP HP column (GE Healthcare) using a NaCl gradient. Pol β containing fractions were combined, concentrated to ∼500-700μL, and glycerol was added to a final concentration of 15%. The final protein, which was >90% pure by SDS-PAGE gel analysis, was aliquotted, flash frozen in liquid nitrogen, and stored at 80°C. Final protein concentration was determined using the absorbance at 280nm and the extinction coefficient for Pol β (ε = 21,200 M−1 cm−1).
DNA Substrate for Biochemical Assays
DNA oligonucleotides were purchased from the Keck Oligo Synthesis Resource (Yale University) and purified by PAGE chromatography prior to use. The 5′ end of the primer (U22M) was labeled with 32P, and the three oligonucleotides were annealed to generate the 1bp-gap DNA substrate, 3C2M 45, as described previously (61).
Presteady State Kinetic Anaylsis
Rapid chemical quench kinetics were performed using the KinTek apparatus (62). Single-base gapped DNA substrate 3C2M 45 (Table 2) with a template G at the gap was used. Two reaction mixtures (600nM DNA + 200nM Pol β and 200μM dCTP + 2mM MgCl2) in Reaction Buffer (50mM Tris-Cl pH 8, 100mM NaCl, 2mM DTT, 10% glycerol) were combined (15μL each) in the apparatus, rapidly mixed and quenched with 0.5M EDTA, and combined with 50μL 90% Formamide dye. A time course of reactions from 0.02 to 3.0 seconds was conducted. Final reaction concentrations were 300nM DNA, 100nM Pol β, 100μM dCTP, and 10mM MgCl2 in Reaction Buffer. Completed reactions were separated using denaturing 20% polyacrylamide gel electrophoresis and visualized and quantified using a Storm 860 phosphorimager with ImageQuant software. Kinetic data were plotted and fit using Prism 5 (GraphPad Software, Inc.) to the biphasic burst equation:
Table 2.
DNA substrate sequences.a
| DNA Name | Sequence (5′ to 3′) |
|---|---|
| U22M | GCCTCGCAGCCGGCTGATGCGC |
| D22M | GTCGGTCGATCCAATGCCGTCC |
| 45GM | GGACGGCATTGGATCGACCGACGGCGCATCAGCCGGCTGCGAGGC |
| 3C2M 45 | 5′GCCTCGCAGCCGGCTGATGCGC GTCGGTCGATCCAATGCCGTCC |
| (U22 + D22M + 45GM) | 3′CGGAGCGTCGGCCGACTACGCGGCAGCCAGCTAGGTTACGGCAGG |
Templating base is bold and underlined.
| (11) |
where [E]app is the apparent enzyme concentration, kobs is the observed rate constant of the exponential phase, and kss is the rate constant of the linear (steady-state) phase.
Active Site Titration
Using the KinTek apparatus, Pol β was titrated with increasing concentrations of the 3C2M 45 1bp-gap DNA. 100nM Pol β (final concentration) was reacted with dCTP (100μM final) and MgCl2 (10mM final) in the presence of a series of different concentrations (10 - 300nM) of 1bp-gap DNA for 100ms. The 100ms time point was chosen based the pre-steady state burst data; this is the time required for the polymerization reaction to reach a maximum amplitude without undergoing multiple enzymatic turnovers. Each of the eleven DNA concentrations was used in three or four different reactions. The reactions were analyzed via denaturing PAGE and phosporimager as described above. Kinetic data were fit to the quadratic equation:
| (12) |
where KD(DNA) is the equilibrium dissociation constant for DNA, AS is the percent active sites of the protein preparation, and [DNA] is the concentration of DNA in nM.
Single Turnover Kinetics
In order to examine the misincorporation of dNTP by the mutants in greater detail, single turnover kinetics was employed. Single turnover kinetics allowed for the determination of both the maximum rate of polymerization (kpol) and the dissociation constant for the incoming nucleotide (KD(dNTP)). For correct incorporation, a mixture of 500nM active Pol β and 50nM 3C2M 45 1bp-gap DNA (final concentrations) was reacted with varying concentrations of dCTP (1 - 200μM) and 10mM MgCl2 (final concentrations) in Reaction Buffer. A separate time course from 0.03 to 10 seconds was conducted for each concentration of dCTP using the KinTek apparatus. Reactions were analyzed as above and kinetic data were fit to the single exponential equation:
| (13) |
where A is the amplitude, kobs is the observed rate constant and t is the time. A secondary kinetic plot was constructed by plotting the observed rate constant (kobs) vs [dCTP], which was then fit to the hyperbolic equation:
| (14) |
where kPol is the maximum rate of polymerization and KD(dNTP) is the equilibrium dissociation constant of dNTP.
Misincorporation of incorrect nucleotide (dATP) was conducted in a similar fashion. The misincorporation for Pol β and the mutants is much slower than correct incorporation, so these reactions were performed manually with longer time courses (20 sec - 60 min). Additionally, higher amounts of dATP were used to compensate for the decreased binding of the incorrect nucleotide (generally 2 - 900μM).
2. Results and Discussion
2.1. Global dynamics
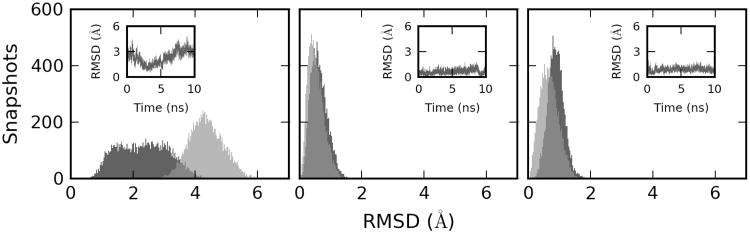
The crystal structures of binary and ternary WT Pol β, which served as starting structures for our simulations, show large differences in the conformation of their thumb sub-domain (thumb, see the sub-domain nomenclature in Figure 1); it is in an open conformation in the binary crystal structure and closes upon dNTP binding (63). The crystal structure that contains the G·dATP mispair (W structure, PDB code 3C2M) has its thumb in a partially open conformation, which is 3.8 Å from its position in the binary crystal structure as measured by the global thumb RMSD metrics that was defined in Methods. Using the same metrics, the crystal structure containing the G·dCTP pair (ℛ structure; PDB code 2FMP) has its thumb 5.1 Å from the binary structure. To assess the structure and dynamics of Pol β mutants, we compared their calculated average thumb positions and fluctuations with these crystallographic RMSD values.
Coordinates of all ℛ and WTS complexes fluctuated near their closed and partially open conformations, respectively (Figure 4; Supplementary Table S3; Supplementary Figures S6 and S7) In contrast, the thumb showed large-amplitude fluctuations (Supplementary Table S3; Supplementary Figures S4) in the simulations of WT and mutant binary complexes that were initiated from the binary crystal structure. Occasionally, these motions brought the thumb into vicinity of its position in the W and ℛ crystal structures. For example, the thumb of the I174S mutant, which showed the largest flexibility, closed at 2.5 ns to within 0.6 Å from its position in the ℛ crystal structure, but later returned to the open position (Figure 4). On the other hand, binary complexes that were generated by the removal of W or ℛ dNTP with both Mg2+ ions from the active site of ternary complexes, remained during our 10 ns simulations near their initial (closed) crystallographic positions (Supplementary Table S4; Supplementary Figures S5 and S6). Here, significant opening of the thumb was observed only for the R283L mutant.
Figure 4.
RMSD of the thumb sub-domain in MD simulations of WT (light grey) and I174S Pol β mutant (dark grey) with respect to the X-ray crystal structure of the closed ternary complex (2FMP). Time evolution of RMSD for the mutant is shown in the insets. Left – MD simulation of the binary complex that was initiated from the X-ray crystal structure of the open binary complex (1BPX); center – MD simulation of ℛ TS initiated from the X-ray crystal structure of the closed ℛ ternary complex (2FMP); right – MD simulation of W TS initiated from the X-ray crystal structure of the partially opened W ternary complex (3C2M).
This indicates that the highest point on the conformational landscape is located near the closed conformation and likely includes the rearrangements of key side-chain interactions described by Sawaya et al. (43) who proposed that closing of the thumb sub-domain is accompanied by loss of R258-D192 interaction and gain of R258-E295 and D192-Mg2+ interactions essential for the formation of a catalytically competent ternary complex. In line with this model, our MD simulations of binary complex of I174S mutant that showed closing/opening movements when viewed from global RMSD perspective, also showed the functional rearrangements taking place in the active site although fully catalytically competent state was not achieved (Supplementary Figure S3).
2.2. Kinetics and energetics of the catalytic turnover
All the biochemical and TCA data presented in this paper were obtained using the same human Pol β and the one-base gapped primer/template DNA that was reported in previous crystallographic studies (43, 64, 65). Such structural consistency is of vital importance because of poorly understood, yet potentially large, effect of DNA sequence on dNTP insertion efficiency. Compare, for example, 130-fold decrease in dCTP insertion efficiency opposite dG by K289M mutant of human Pol β (66) with the 1.1-fold decrease that we measured for the same mutant (Table 3). This likely DNA sequence effect is larger than the acceptable error margin for computer simulations. The observation of such a large DNA sequence effect is not surprising since any change in DNA sequence can be regarded as a mutation of a Pol β/DNA complex. These secondary ‘mutations’ may affect DNA structure near the active site, resulting in a larger kpol/KD effect than those of distant protein mutations. Furthermore, the swap of the biochemical experiments on Pol β from rat and human is also problematic because the primary structures of these proteins differ in 14 amino acid residues. Thus, although a large number of experimental kinetic data for Pol β mutants is available, they do not represent consistent data set that could be used as a benchmark for validation of TCA. The six single-point mutants measured in the present work represent a seed of a consistent mutational database that we hope will grow in the future.
Table 3.
Pre-steady state kinetic constants for insertion of dCTP opposite dG in the template (GC) and dATP opposite dG in the template (GA) by WT Pol β and its mutants.
| Variant | GC | GA | Mutation effect on fidelity | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|||||||
| kPol (s-1) | Kd (μM) | kpol/Kd (s-1. M-1) | kPol (s-1) | Kd (μM) | kpol/Kd (s-1. M-1) | log Ra | log Bb | log Fc | |
| WT | 8.9 ± 0.3 | 1.7 ± 0.3 | 5.2 × 106 | 0.071 ± 0.008 | 210 ± 50 | 340 | 0.0 | 0.0 | 0.0 |
| I260Q | 18.0 ± 1.0 | 12.0 ± 3.0 | 1.5 × 106 | 0.225 ± 0.009 | 32 ± 5 | 7000 | -0.2 | -1.7 | -1.9 |
| H285D | 24.0 ± 1.0 | 4.0 ± 0.9 | 6.0 × 106 | 0.082 ± 0.009 | 120 ± 40 | 683 | 0.4 | -0.6 | -0.2 |
| E288K | 23.0 ± 1.0 | 5.0 ± 1.0 | 4.6 × 106 | 0.110 ± 0.007 | 110 ± 20 | 1000 | 0.2 | -0.7 | -0.5 |
| K289M | 15.6 ± 0.6 | 3.2 ± 0.7 | 4.9 × 106 | 0.059 ± 0.007 | 110 ± 40 | 540 | 0.3 | -0.6 | -0.2 |
| I174S | 22.2 ± 0.6 | 4.5 ± 0.6 | 4.9 × 106 | 0.190 ± 0.010 | 80 ± 20 | 2400 | 0.0 | -0.8 | -0.9 |
| M282L | 16.4 ± 0.7 | 10.0 ± 2.0 | 1.6 × 106 | 0.018 ± 0.001 | 250 ± 40 | 72 | 0.9 | -0.7 | 0.2 |
log R = log[(kpol,GC / kpol,GA)mut / (kpol,GC / kpol,GA)wt]
log B = −log[(Kd,GC / Kd,GA)mut / (Kd,GC / Kd,GA)wt]
log F = log R + log B = log [fidelitymut / fidelitywt]
The observed rate-constant for the extension of the primer strand by a single nucleotide (kpol) and the corresponding dNTP binding constants (Kd) are presented in Table 3. These data show that all studied mutants increase kPol for the insertion of W by two to three fold compared to WT. This increase is compensated by weaker binding so that the catalytic efficiency kpol/Kd is either lowered or unchanged from its WT value, resulting in zero or negative log Ω (eq. 1) values (Table 4). In contrast, W binding is improved in all except one (M282L) mutants, and four of these mutants also show larger kPol compared to WT. Consequently, all mutants except M282L increase the catalytic efficiency for W insertion, resulting in positive log Ω values.
Table 4.
Relative dNTP insertion efficiencies of Pol β point mutants.a
| Mutant | log Ω (GC) | log Ω (GA) | ||||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||
| Experiment | Experiment | |||||||
|
|
|
|||||||
| FEP | FEP/LIE | This Study | Other Studies | FEP | FEP/LIE | This Study | Other Studies | |
| I174S | 1.1 ± 0.5 | 0.2 ± 0.3 | 0.0 ± 0.2 | -0.5b | 0.8 ± 0.4 | 0.1 ± 0.5 | 0.8 ± 0.3 | 0.6b |
| I260Q | 0.0 ± 0.1 | -0.6 ± 0.3 | -0.5 ± 0.2 | -1.0 ± 0.7 | -0.6 ± 0.6 | 1.3 ± 0.2 | ||
| M282L | 0.2 ± 0.6 | -0.4 ± 0.5 | -0.5 ± 0.2 | -0.3c | 0.1 ± 0.3 | -0.1 ± 0.5 | -0.7 ± 0.3 | 0.2d |
| H285D | 1.2 ± 0.4 | 0.1 ± 0.8 | 0.1 ± 0.2 | 0.8 ± 0.9 | -0.5 ± 0.9 | 0.3 ± 0.3 | ||
| E288K | 1.1 ± 0.5 | 0.8 ± 0.6 | -0.1 ± 0.2 | 0.6 ± 0.9 | 0.3 ± 0.9 | 0.5 ± 0.3 | ||
| K289M | -0.8 ± 0.1 | -0.4 ± 0.4 | 0.0 ± 0.2 | -2.1e | -0.9 ± 0.1 | -0.7 ± 0.3 | 0.2 ± 0.4 | |
|
| ||||||||
| R283A | -1.4 ± 0.6 | -1.1 ± 1.2 | -2.4f | 0.0 ± 1.2 | 0.0 ± 1.3 | -0.4f | ||
| R283L | -1.7 ± 0.9 | -1.5 ± 1.2 | 1.5 ± 0.2 | 1.2 ± 1.0 | ||||
Eq 1 – 2, see Figure 2 and Supplementary Table S5 for definitions and magnitudes of underlying ΔGE and ΔGTS values, and Supplementary Tables S6 and S7 for their respective electrostatic and vdW contributions.
Rat Pol β; different sequence (28);
Insertion of dTTP against template dA; rat Pol β; different sequence (80);
Insertion of dGTP against template dA; rat Pol β; different sequence (80);
Different sequence (66);
Rat Pol β; different sequence (86);
Computationally, log Ω values can be calculated from the relative free energies of mutant vs WT in binary (ΔGE) and TS complexes (ΔGTS) (Figure 2; eq. 3 and 5). However, the standard FEP and LIE calculations resulted in large overestimation of log Ω for I174S, I260Q, H285D, E288K and K289M mutants. These mutations involved significant change in the total charge or dipole moment of the side-chain of the altered amino acid residue. We attributed this overestimation to the fact that practical limitations of the applied simulation protocol, including the use of a crystal structure of the WT, the non-polarizable force field, approximations of long-range electrostatic effects, and limited length of MD trajectories, do not allow the protein-water-counterion system to fully adapt to the mutation-induced structural change (for a more detailed discussion of the compensation effects in proteins see ref (34) and references therein). Thus, the large calculated changes in electrostatic energies for these point mutations need to be offset by down-scaling of electrostatic contributions in the FEP and LIE methods.
The decomposition of the FEP free energies into the electrostatic and vdW contributions also showed that, for some mutations, the vdW contributions differed significantly from the corresponding energies obtained by the LIE method. Since the steric energies in alchemistic FEP simulations suffer from poor convergence (67) the LIE vdW energies can be considered significantly more reliable. These considerations led us to propose and test the FEP/LIE method of eq. 10 as a more reliable way to calculate log Ω values. The use of LIE in hybrid free-energy methods was previously suggested by Oostenbrink and Ruiter for the evaluation of protein-inhibitor binding free energies, but their hybrid method combined the electrostatic part of the LIE free energy with the vdW part calculated by the one-step FEP (68, 69).
The optimal magnitude of the electrostatic scaling factor χ was chosen as 0.5, and for the sake of implementation simplicity it was also applied to scaling of the FEP vdW term. This factor was determined with an uncertainty of about ±0.2 due to a limited number of experimental data and sizeable statistical errors of the calculated log Ω values. In the previous FEP study of Xiang et al (29), ΔGE and ΔGTS free energies (Figure 2) were scaled by a factor of 0.67 in order to fit experimental data for D276V, K280G and R283A Pol β mutations. The difference in the scaling factor used in our study and in the study of Xiang et al stems from different force-fields and FEP protocols. The down-scaling of free energies was not required in original mutation studies of Warshel and coworkers (70) or in a previous FEP study of the hydrolysis of (-)-cocaine by mutant butyrylcholinesterase by Yang et al (71), which employed an identical inner thermodynamic cycle as the present study and the study of Xiang et al (29). However, Yang et al did not evaluate protein mutations that would alter the total charge of the mutated residues. Yang et al predicted 1376-fold but observed 102-fold increase in the catalytic efficiency upon the mutation of four amino acid residues. This is actually good agreement because the mutation effect was calculated by adding effects of four subsequent point mutations. Such a good performance suggests that the FEP method in conjunction with the inner part of the thermodynamic cycle of Figure 2 may reliably evaluate effects of individual point mutations in proteins. However, the prediction accuracy can be affected by magnitude of the mutation effects, mutation type and location, the polarity of the substrate, and the accuracy of the TS model.
The FEP/LIE log Ω values calculated for the mutants measured in this study range from −0.7 (large detrimental effect of the mutation on insertion efficiency) to 0.8 (large beneficial effect of the mutation) (Table 4), and fall in most cases to within combined experimental and computational standard deviation from the corresponding experimental values. The largest discrepancy between our FEP/LIE and experimental results was obtained for the insertion of ℛ by E288K where the calculations indicate 6-fold increased insertion efficiency whereas the experimental value showed practically no change. Overall, the calculated data tend to be in a better agreement with the experiment for the ℛ insertion (standard deviation of 0.9 and 0.4 for scaled FEP and FEP/LIE calculations) than W insertion (standard deviation of 1.1 and 1.0 for scaled FEP and FEP/LIE methods, respectively). In both cases, a simple null prediction of zero mutation effect on insertion efficiency, i.e. log Ω = 0 for all mutants would perform better than our all-atom simulations. However, our simulations for the ℛ insertion perform slightly better than the null approximation when the experimental log Ω = -2.4 for R283A mutant from rat Pol β is included in the experimental set.
2.3. Individual mutants
I174S
In rat Pol β, I174S is a mutator mutant with a 3-fold lower insertion efficiency of ℛ (dG ·dCTP) and a 4-fold higher insertion efficiency of W (dG ·dATP) compared to WT (28). Substitution of threonine, aspartate or glycine for isoleucine 174 also imposes mutator character to rat Pol β (28). In our study on the human polymerase, I174S is also a mutator, exhibiting a 7-fold reduced fidelity compared to wild type. This is due to a 7-fold reduced discrimination at the level of ground state nucleotide binding, with no difference in discrimination in kPol (Table 3).
Isoleucine 174 is a solvent exposed amino acid residue that is located in the first β-strand of five-stranded palm β-sheet. Its side-chain protrudes into the interface of the palm and the thumb sub-domain. In the binary crystal structure, isoleucine 174 makes close contact only with a hinge amino acid residue tyrosine 265, which has been recognized to be crucial for the polymerase fidelity (72–74). This interaction, which is of hydrogen bond type, is absent in the ℛ and W crystal structures.
Our simulations of binary and TS complexes retained crystallographic positions of these residues, including, though infrequent, hydrogen bonding between carbonyl group of isoleucine 174 and tyrosine 265 in the binary form but absent in TS simulations. The I174S mutation further weakened interaction of the residue 174 with tyrosine 265 in simulations of the binary complex and induced infrequent hydrogen bonding of serine 174 to lysine 262 in all simulations. Interestingly, the binary form of I174S showed the most pronounced mobility of the thumb sub-domain among all mutants – the full closing and opening motions were observed within 10 ns (Figure 4).
Our scaled FEP calculations showed 8 to 6-fold increase of insertion efficiency upon I174S mutation. In contrast, our FEP/LIE calculations predict a small 1.6- and 1.3-fold increase in the insertion efficiency of ℛ and W, respectively – in agreement with our experimental data for ℛ, but not for W. The 6-fold higher insertion efficiency of W that we observed for this mutant confirms the weak mutator character of this mutant also for human Pol β.
I260Q
I260Q is a well-known mutator mutant of the rat Pol β, exhibiting ∼60-fold increase in mutator frequency relative to the wild-type enzyme (75). Rat Pol β, which differs by 14 amino acid residues from its human variant, was also used to characterize I260H, I260D, I260N, I260E, I260R, I260K mutants (75). However, only one of these point-mutations (I260H) yielded a mutator polymerase, whereas the remaining mutants exhibited impaired in vivo activity (75). A decrease in in vivo activity was also detected for I260M mutant of human Pol β, which is associated with prostate tumor (76). Thus, similarly to the position 174, there seems to be a requirement for hydrophobic amino acid residue at the position 260 for unimpaired function of Pol β. With the human polymerase in our study, I260Q is a mutator mutant with a 72-fold reduced fidelity compared to the wild-type Pol β. Like I174S, this mutator effect is dominated by reduced discrimination at the level of Kd (46-fold), which leads to an increased catalytic efficiency for incorrect insertion (21-fold), and a reduced catalytic efficiency for the correct (dCTP:G) insertion (3-fold) (Table 3).
Isoleucine 260 is located next to the last β-strand of the palm β-sheet. This region, which also includes hydrophobic residues L194, Y271, F272 and Y296, serves as a hinge for the thumb sub-domain opening and closing (63). Isoleucine 260 is solvated by a large number of water molecules in our simulations of the binary complex, but only one or few water molecules remain after the reaction reaches its TS for the ℛ or W dNTP substrate, respectively. The calculated solvation free energies (ΔGsolv = -8.0 vs. -8.1 or -8.6 kcal/mol for binary and ℛ or W TS complexes, respectively; Supplementary Table S8), which include combined effect of both the protein and water environment, indicate that the hydration forces that disappear in the TS are fully compensated by the interactions of isoleucine side-chain with the protein residues.
Glutamine 260 hydrogen bonds with arginine 258 (TS for ℛ) or with glutamine 264 and glutamate 295 (TS for W), but solvent water molecules hinder these interactions in the binary complex. This hydrogen-bonding network has been suggested for mutant rat Pol β to ‘overstabilize’ arginine 258, thus freeing aspartate 192 to coordinate the catalytic Mg2+ ion, hindering the mismatch discrimination, and imposing mutator property to I260Q Pol β mutant (77, 78). In a separate study, Sweasy and coworkers suggested that I260Q affects geometry of the dNTP binding pocket by restricting sub-domain movements (79) but our present calculations do not show any significant difference in the extent of the thumb sub-domain motions between WT and I260Q. However, we observed that the average position of the thumb in the binary complex is significantly more closed in the mutant than in WT (Table S3).
Our FEP/LIE calculations indicate similar 4-fold mutation-induced kpol/Kd decrease for both ℛ and W, in agreement with the experiment for ℛ but not for W, which showed a 20-fold kpol/Kd increase (Table 4). Since this is the largest discrepancy between our calculated and observed data, and the observed effects are dominated by binding contribution (Table 3) we extended our FEP/LIE approach to calculate the effects of I260Q mutation on Kd for binding of ℛ and W dNTP (Table 5). In the thermodynamic cycle for these calculations, the TS structure was replaced by the structure of the ternary complex. To retain total charge of the studied system, the O3′ atom that forms partial bond with Pα in our TS model was left unprotonated in the ternary complex simulations. These simulations significantly improved the agreement with the experiment for W and for the mutation effect on fidelity (Table 5), thus pointing to the TS model for W as the most likely source of the log Ω discrepancy between experiment and theory.
Table 5.
The effect of I260Q mutation on binding of ℛ and W dNTP.
| Approach | log(Kd,wt/Kd,mutant)ℛ | log(Kd,wt/Kd,mutant)W | Kd fidelitya |
|---|---|---|---|
| FEP | -1.9±0.8 | 0.0±0.8 | 1.9±1.1 |
|
| |||
| FEP/LIE | -1.8±1.3 | 0.2±1.4 | 2.0±1.9 |
| Experiment | -0.8±0.5 | 0.8±1.7 | 1.6±1.8 |
Kd fidelity = log(Kd,wt/Kd,mutant)W − log(Kd,wt/Kd,mutant)ℛ
M282L
This mutant, identified in rat Pol β using an in vivo genetic screen, demonstrated increased mutagenesis in both in vivo and in vitro assays (80). In vitro, M282L showed a 7.5-fold higher mutation frequency and 9.5-fold increased frameshift error frequency, relative to the wild-type enzyme (80). Human M282L in the sequence context of our current work, did not exhibit any mutator activity. The efficiencies for both correct and incorrect insertions were less than that of the wild-type polymerase (3 and 5-fold, respectively). The reduced efficiencies in the case of the correct insertion are due to a 6-fold reduction in nucleotide binding, and in the case of incorrect insertion, are due to a 4-fold reduction in polymerization rate.
Methionine 282 is located next to arginine 283 in the thumb-subdomain α-helix N. While arginine 283 can interact with the templating base, the side-chain of methionine 282 is buried in the hydrophobic core of the thumb sub-domain that consists of the L270, F278, I293, I319, F320, I323, and W325 amino acid side-chains. Consistent with structural similarity of Met and Leu side-chains, our simulations did not reveal any structural or dynamical effects of the M282L mutation. Shah et al (80), who reported crystal structure of the polymerase domain of a free rat Pol β M282L protein (PDB code 1JN3), noticed up to 0.9 Å shift of the neighboring amino acid residues R283, L287, I293 and E295 towards the core of the thumb sub-domain and rearrangement of the intra-thumb sub-domain hydrogen bonding network (absence of the hydrogen bond between S275 and N279, presence of the hydrogen bonds between K289 and Q324, and between T292 and R299). Shah et al. related these structural changes with the observed increased stability of the mutant protein against heat denaturation (Tm increased from 42 to 48 °C) and urea unfolding (ΔG decreased from 22.9 to 7.1 kJ mol-1) (80). We did not observe any indication of increased stability of the M282L mutant in our simulations. This apparent discrepancy could stem from the fact that our simulations were not performed for a free Pol β but for its binary and TS complexes.
Our FEP/LIE calculations ranked M282L as the second least influential mutant from the set of the eight mutants, predicting 2.5-fold decrease and 1.3-fold increase in the catalytic efficiency, for ℛ and W, respectively. Here we reached a good agreement with the experiment for ℛ but not for W, the insertion efficiency of which was observed to decrease 5-fold compared to WT.
H285D
In rat Pol β in vivo assays, the H285D mutation confers resistance to 3′-azido-3′-deoxythymidine (AZT) (81), a nucleoside analog drug that causes chain termination after incorporation into DNA. This mutation was proposed to cause loss of the contacts of both the mutated residue and lysine 289 with isoleucine 323 (61). This structural perturbation was suggested to destabilize the C-terminal arm and propagate into the dNTP binding site, leading to increased efficiencies of mispair extension (61), without any increased misincorporation over wild type. The same is true in our current study, as no increased misincorporation was seen. There is a slight reduction in discrimination at the level of Kd for H285D, but this is counteracted by a slight increase in discrimination at the level of kpol. These small changes lead to a slightly increased efficiency of incorrect incorporation compared to the wild-type polymerase, but this effect is not enough to lead to a significant change in fidelity.
Histidine 285 is a solvent exposed amino acid residue located in the thumb sub-domain α-helix N. In the binary crystal structure, the Nε2 atom of histidine 285 is in the hydrogen bonding distance from the O atom of isoleucine 323 (2.3 Å). It also stacks with tryptophan 325, thus contributing to the integrity of the thumb sub-domain. These interactions are weakened in the crystal structures of ternary complexes.
In our simulations of binary complex and the TS for ℛ, histidine 285 did not interact with isoleucine 323. Instead, its Nδ1 atom formed unstable hydrogen bond with lysine 289. Histidine 285 also formed partial stacking interaction with tryptophan 325 in both TS complexes. The integrity of the C-terminal arm did not seem to be compromised in the simulations of the H285D mutant because the Oδ atom of aspartate 285 formed a stable hydrogen bond with lysine 289. Aspartate 285 was additionally stabilized in both TS complexes by a second hydrogen bond (via its other Oδ atom) to the Hε atom of tryptophan 325. Our FEP/LIE calculations reproduced a small 1.3-fold increase in the catalytic efficiency for ℛ, but unlike scaled FEP, disagree with the experiment in the direction of the log Ω change for W (Table 4).
E288K
This mutant was found in a colon tumor (82). In vivo studies showed it to be a mutator polymerase at AT base pairs with no reduced fidelity at GC base pairs, and it was shown to have up to a 6-fold decreased fidelity opposite template A in vitro (83). It was included in our training set because it involves a charge reversal that places stringent demands on the accuracy of the electrostatic calculations. Additionally, the residue 288 has a potential to be biologically important because it forms, in the WT, the salt bridge to lysine 289, whose mutation to methionine has been implied in carcinogenesis (66). In this current study, E288K has the same efficiency of correct incorporation as the wild-type Pol β, and the efficiency of incorrect is increased by about 3-fold. This increased efficiency is due to a 6-fold increase in dATP binding opposite template G compared to wild type.
Glutamate 288 is a penultimate amino acid residue of the thumb sub-domain α-helix N. Its side chain is solvent exposed in binary and both ℛ and W ternary crystal structures. In the latter two, the side chain of glutamate 288 is oriented towards DNA substrate. In our simulations, glutamate 288 forms unstable hydrogen bond with lysine 289 in the binary complex and both ℛ and W TS. Upon the mutation to lysine, lysine 288 hydrogen bonds with the Nδ1 atom of H285 in the binary complex, but reaches towards DNA substrate in the TS complexes. Here it interacts with oxygen atoms in the sugar-phosphate backbone of the complementary strand that lie +4 to +6 nucleotides downstream from the one-nucleotide gap; occasionally, E288K forms hydrogen bond to the O atom of alanine 284. These electrostatic interactions of the mutant in the TS explain the 6- and 2-fold increase of its catalytic efficiency calculated for ℛ and W insertion by FEP/LIE, but this increase was experimentally confirmed only for W insertion. Thus, E288K is a weak mutator mutant. The important question of whether the 8-fold disagreement between our calculated and experimental data for ℛ originates from the wrong structural prediction or from imperfect energetic description could be resolved by the crystal structures of this mutant.
K289M
The K289M mutant was detected in the cDNA of one of six human colorectal carcinomas studied by Wang et al (84). Since the K289M mutant was not detected in a normal mucosa from the same patient and was not detected as a polymorphism in normal individuals (85), it was suggested that this mutant could have a role in carcinogenesis (66). In this study, K289M was not shown to be a mutator mutant. There were no changes in the efficiencies of correct or incorrect insertions. This correlates with the study by Lang, et. al, which showed that K289M mainly misincorporates dCTP opposite template C and dGTP opposite G.
Lysine 289 is the last amino acid residue of the thumb sub-domain α-helix N. Its side chain is solvent exposed in the binary as well as in the ℛ and W ternary crystal structures. However, it forms alternate salt bridge interactions with glutamate 288 and glutamine 324, respectively, in the simulated binary and TS complexes. These interactions are not retained and no new specific interactions of the methionine 289 side-chain are formed during our simulations of the K289M mutant.
This mutation was calculated by the FEP/LIE method to cause about 2.5- and 5-fold decrease of the catalytic efficiency of ℛ and W insertion, respectively. However, the observed kinetics showed no effect on catalytic efficiency for ℛ and a small 1.6-fold increase in the catalytic efficiency for W.
R283A and R283L
Arginine 283 has been found to be essential for Pol β fidelity (24). Substitution of the arginine by alanine, leucine or lysine results in dramatic decrease in catalytic efficiency and fidelity (24). The strongest effect was reported for the alanine mutant: 160- to 4900-fold decrease in catalytic efficiency for insertion of correct, but not incorrect, dNTP and 150- to 6800-fold decrease in fidelity (24, 86, 87). The decreased catalytic efficiency is due to a loss of nucleotide binding affinity and decrease in the rate of nucleotide insertion (24, 25, 86, 87). In their computational study, Yang et al (8) employed molecular dynamics simulations and qualitative analysis of electrostatic potential on energy-minimized structures to identify dynamic and energetic contributions, respectively, to the decreased nucleotide binding affinity of the R283A mutant; this mutant partially opened during the simulation and the electrostatic interaction between R283A and dNTP was weakened relative to WT. Yang et al also noticed a compensatory lysine 280-template interaction in their MD simulation of R283A, which led them to propose that the R283A/K280A double mutant should decrease nucleotide binding affinity and increase misinsertion more than R283A alone (8). On the other hand, our linear-response MD simulations indicated that the R283A/E295A double mutant showed only modest (2 to 10-fold) decrease of fidelity of dATP binding opposite dT, dG, dC and dA in the template (2).
Arginine 283 is located next to methionine 282 in the thumb-sub-domain α-helix N, pointing towards the DNA binding groove. In the crystal structure of the binary complex, the side-chain of arginine 283 is solvent exposed with no close contacts with DNA substrate. In ℛ and W ternary crystal structure complexes, arginine 283 is buried and partially exposed to water solvent, respectively, making contacts to the template strand of the DNA substrate. In the ternary crystal structure with the dG·dCTP nascent base pair, arginine 283 interacts with the O4′ oxygen of deoxyribose of the dG nucleotide located just downstream of the templating base (i.e. opposite the 3′-terminal primer nucleotide) (88). Due to a shift in the template strand caused by dG·dATP mispairing and slight opening of the conformation of the thumb sub-domain, arginine 283 interacts with the N3 atom of the templating dG. Besides the interaction with DNA substrate, arginine 283 has been also proposed to play a role in the transmission of the structural information between the thumb sub-domain and the catalytic site. This transmission likely occurs via the R283-E295-R258-D192-MgA cascade (MgA is the catalytic metal ion), thus helping correlate the presence of the catalytic metal in the active site with the stabilization of the closed conformational state (27, 63).
The dependence of the thumb sub-domain conformation on the arginine 283-DNA interaction observed in the crystal structures is retained in our simulations. Namely, arginine 283 showed stable interactions with the template strand only in the TS complexes, although these contacts were transiently observed also in the simulations of binary complex due to the closing motion of the thumb sub-domain. In the W TS, arginine 283 retains its interaction with the template nucleotide (dG), whereas in the ℛ TS, it interacts also with the dG nucleotide just downstream of the template dG. Positioning of the arginine 283 side-chain for its interaction with DNA in the simulations of TS complexes is supported by the interaction of its guanidyl group with carbonyl and carboxylate groups of isoleucine 293 and glutamate 295. Both R283A and R283L mutations eliminate these favorable interactions with the template strand and, especially in R283A, generate a large void that is filled by water molecules. Yang et al (8) suggested that the impact of the lost interaction of the R283A/L with the template dG could be alleviated by the interaction of K280 with the template dG. In accordance with the proposal by Yang et al, we observed the interaction of K280 with the template dG in the simulations of R283A and R283L mutants as well as in the WT Pol β.
The FEP/LIE calculations indicated a modest adverse effect of the R283A mutation on the catalytic efficiency for the insertion of ℛ (∼13-fold decrease) but no effect on W. Interestingly, the mutation of arginine 283 to a larger leucine was predicted to result in a more dramatic 500-fold decrease of the catalytic efficiency for ℛ, while increasing the insertion efficiency of W 50-fold. However, due to a large size of the arginine side chain, the statistical errors of its calculated mutation effects are the largest among all studied mutant.
Experimental catalytic efficiencies of R283A and R283L mutants are not available for the studied polymerase. Using WT and R283A rat Pol β and a different mispair, Ahn et al. observed 250-fold and 2.5-fold decreased catalytic efficiency for ℛ and W, respectively (86). This dual loss was considered as the main supporting factor for the suggestion that catalytic efficiency for the ℛ insertion and discrimination against W are coupled (24). However, our experiments for I260Q and calculated results for R283L mutator mutants represent examples when the discrimination against W can be weakened in the mutant by both decreasing the efficiency of the ℛ and increasing the efficiency of the W insertion. Moreover, I174S mutant even shows the case when the protein mutation leads to improved W insertion without the loss of the efficiency for the insertion of ℛ.
In conclusion, the alchemistic mutagenesis using scaled FEP or FEP/LIE method represents a potentially robust computational approach that sets the initial bar for quantitative all-atom simulations of distant mutations. Our FEP/LIE method can provide insights from local and global dynamics combined with quantitative free energy contributions, while being more accurate than the scaled FEP method. The calculated log Ω values show significant uncertainties (0.1 to 1.3; Table 4), which are largely due to slow convergence of the FEP calculations. However, we estimate that extending the FEP simulation length by one order of magnitude could halve these uncertainties. On the other hand, if sufficient computational precision was reached, the differences between the experimental and calculated log Ω values could indicate the mutation-induced changes of the TS structure, or differences in the TS structure for the ℛ and W insertion. Actually, the latter is implied by our current data that show significantly better agreement with the experimental kinetics for ℛ than for W insertion.
As illustrated by our calculations of the I260Q mutant, the thermodynamic cycles of Figure 2 can be adapted for calculations of binding contributions Kd(WT)/Kd(mutant) by replacing the TS with the ternary complex. One advantage of such a modification is that the accuracy of the resulting binding contributions does not rely on the assumption of the atomic charges and geometry of the TS state. Further extension of our approach could include log Ω experiments and calculations for the reverse reaction - DNA pyrophosphorolysis - and FEP/LIE examination of mutation effects for several plausible TS structures.
Improvements of the accuracy and efficiency of TCA based on scaled alchemistic mutagenesis could allow reliable saturation mutagenesis by computer simulations. The application of this approach to different DNA contexts could help identify mutants that are most likely to cause the initiation of cancer growth. This goal could become more feasible with the help from experimental biochemists and structural biologists if they augment their efforts to discover new mutagenic Pol β mutants with systematic assays of Pol β mutants that are already known.
Supplementary Material
Abbreviations
- dNTP
deoxyribonucleotide 5′-triphosphate
- FEP
free energy perturbation
- IPTG
Isopropyl-D-thioaglactopyranoside
- LIE
linear interaction energy
- LRF
local reaction field
- MD
molecular dynamics
- Pol β
DNA polymerase β
- ℛ
right
- RMSD
root-mean-square deviation
- SCAAS
surface-constraint all-atom solvent
- TCA
theoretical-computational analysis
- TS
transition state
- vdW
van der Waals
- W
wrong
- WT
wild type
Footnotes
This work was supported by the National Institutes of Health Program Project Grant 5U19CA105010.
Supporting Information Available: Auxiliary equations derived from the thermodynamic cycle of Figure 2, selection of the values of the FEP coupling parameter λ, FEP path used for the alchemistic mutation of methionine 288 to leucine, time evolution of RMSDs of the thumb subdomain, average RMSD (Å) of the thumb subdomain in LIE simulations of binary and TS complexes of Pol β containing ℛ or W dNTP substrate with respect to the crystal structures with open, closed and partially open conformation of the thumb subdomain, relative free energies of Pol β point mutations calculated using the FEP, LIE and FEP/LIE methods, Ramachandran plots for the X-ray and calculated structures of WT Pol β in open, closed and partially-open conformations, histograms of the calculated RMSD of the thumb sub-domain for WT Pol β and its mutants, histograms of hydrogen bonding distances between D192 and R258, and R258 and E295 side-chains. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Abashkin YG, Erickson JW, Burt SK. Quantum chemical investigation of enzymatic activity in DNA polymerase β. A mechanistic study. J Phys Chem B. 2001;105:287–292. [Google Scholar]
- 2.Florian J, Goodman MF, Warshel A. Theoretical investigation of the binding free energies and key substrate-recognition components of the replication fidelity of human DNA polymerase β. J Phys Chem B. 2002;106:5739–5753. [Google Scholar]
- 3.Yang L, Beard WA, Wilson SH, Broyde S, Schlick T. Polymerase beta simulations suggest that Arg258 rotation is a slow step rather than large subdomain motions per se. J Mol Biol. 2002;317:651–671. doi: 10.1006/jmbi.2002.5450. [DOI] [PubMed] [Google Scholar]
- 4.Yang L, Beard W, Wilson S, Roux B, Broyde S, Schlick T. Local deformations revealed by dynamics simulations of DNA polymerase beta with DNA mismatches at the primer terminus. J Mol Biol. 2002;321:459–478. doi: 10.1016/s0022-2836(02)00617-4. [DOI] [PubMed] [Google Scholar]
- 5.Florián J, Goodman MF, Warshel A. Computer simulation studies of the fidelity of DNA polymerases. Biopolymers. 2003;68:286–299. doi: 10.1002/bip.10244. [DOI] [PubMed] [Google Scholar]
- 6.Rittenhouse RC, Apostoluk WK, Miller JH, Straatsma TP. Characterization of the active site of DNA polymerase beta by molecular dynamics and quantum chemical calculation. Proteins. 2003;53:667–682. doi: 10.1002/prot.10451. [DOI] [PubMed] [Google Scholar]
- 7.Radhakrishnan R, Schlick T. Orchestration of cooperative events in DNA synthesis and repair mechanism unraveled by transition path sampling of DNA polymerase beta's closing. Proc Natl Acad Sci U S A. 2004;101:5970–5975. doi: 10.1073/pnas.0308585101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang L, Beard WA, Wilson SH, Broyde S, Schlick T. Highly organized but pliant active site of DNA polymerase beta: compensatory mechanisms in mutant enzymes revealed by dynamics simulations and energy analyses. Biophys J. 2004;86:3392–3408. doi: 10.1529/biophysj.103.036012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang L, Arora K, Beard WA, Wilson SH, Schlick T. Critical role of magnesium ions in DNA polymerase beta's closing and active site assembly. J Am Chem Soc. 2004;126:8441–8453. doi: 10.1021/ja049412o. [DOI] [PubMed] [Google Scholar]
- 10.Radhakrishnan R, Schlick T. Fidelity discrimination in DNA polymerase beta: differing closing profiles for a mismatched (G:A) versus matched (G:C) base pair. J Am Chem Soc. 2005;127:13245–13252. doi: 10.1021/ja052623o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Arora K, Beard WA, Wilson SH, Schlick T. Mismatch-induced conformational distortions in polymerase beta support an induced-fit mechanism for fidelity. Biochemistry. 2005;44:13328–13341. doi: 10.1021/bi0507682. [DOI] [PubMed] [Google Scholar]
- 12.Radhakrishnan R, Arora K, Wang Y, Beard WA, Wilson SH, Schlick T. Regulation of DNA repair fidelity by molecular checkpoints: “gates” in DNA polymerase beta's substrate selection. Biochemistry. 2006;45:15142–15156. doi: 10.1021/bi061353z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lin P, Pedersen LC, Batra VK, Beard WA, Wilson SH, Pedersen LG. Energy analysis of chemistry for correct insertion by DNA polymerase beta. Proc Natl Acad Sci U S A. 2006;103:13294–13299. doi: 10.1073/pnas.0606006103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Alberts IL, Wang Y, Schlick T. DNA polymerase beta catalysis: are different mechanisms possible? J Am Chem Soc. 2007;129:11100–11110. doi: 10.1021/ja071533b. [DOI] [PubMed] [Google Scholar]
- 15.Bojin MD, Schlick T. A quantum mechanical investigation of possible mechanisms for the nucleotidyl transfer reaction catalyzed by DNA polymerase beta. J Phys Chem B. 2007;111:11244–11252. doi: 10.1021/jp071838c. [DOI] [PubMed] [Google Scholar]
- 16.Wang Y, Schlick T. Distinct energetics and closing pathways for DNA polymerase beta with 8-oxoG template and different incoming nucleotides. BMC Struct Biol. 2007;7:7. doi: 10.1186/1472-6807-7-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang Y, Reddy S, Beard WA, Wilson SH, Schlick T. Differing conformational pathways before and after chemistry for insertion of dATP versus dCTP opposite 8-oxoG in DNA polymerase beta. Biophys J. 2007;92:3063–3070. doi: 10.1529/biophysj.106.092106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xiang Y, Goodman MF, Beard WA, Wilson SH, Warshel A. Exploring the role of large conformational changes in the fidelity of DNA polymerase beta. Proteins. 2008;70:231–247. doi: 10.1002/prot.21668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lin P, Batra VK, Pedersen LC, Beard WA, Wilson SH, Pedersen LG. Incorrect nucleotide insertion at the active site of a G:A mismatch catalyzed by DNA polymerase beta. Proc Natl Acad Sci U S A. 2008;105:5670–5674. doi: 10.1073/pnas.0801257105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ram Prasad B, Warshel A. Prechemistry versus preorganization in DNA replication fidelity. Proteins. 2011;79:2900–2919. doi: 10.1002/prot.23128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dobashi Y, Shuin T, Tsuruga H, Uemura H, Torigoe S, Kubota Y. DNA polymerase beta gene mutation in human prostate cancer. Cancer Res. 1994;54:2827–2829. [PubMed] [Google Scholar]
- 22.Srivastava DK, Husain I, Arteaga CL, Wilson SH. DNA polymerase beta expression differences in selected human tumors and cell lines. Carcinogenesis. 1999;20:1049–1054. doi: 10.1093/carcin/20.6.1049. [DOI] [PubMed] [Google Scholar]
- 23.Menge KL, Hostomsky Z, Nodes BR, Hudson GO, Rahmati S, Moomaw EW, Almassy RJ, Hostomska Z. Structure-function analysis of the mammalian DNA polymerase beta active site: role of aspartic acid 256, arginine 254, and arginine 258 in nucleotidyl transfer. Biochemistry. 1995;34:15934–15942. doi: 10.1021/bi00049a008. [DOI] [PubMed] [Google Scholar]
- 24.Beard WA, Osheroff WP, Prasad R, Sawaya MR, Jaju M, Wood TG, Kraut J, Kunkel TA, Wilson SH. Enzyme-DNA interactions required for efficient nucleotide incorporation and discrimination in human DNA polymerase beta. J Biol Chem. 1996;271:12141–12144. doi: 10.1074/jbc.271.21.12141. [DOI] [PubMed] [Google Scholar]
- 25.Werneburg BG, Ahn J, Zhong X, Hondal RJ, Kraynov VS, Tsai MD. DNA polymerase beta: pre-steady-state kinetic analysis and roles of arginine-283 in catalysis and fidelity. Biochemistry. 1996;35:7041–7050. doi: 10.1021/bi9527202. [DOI] [PubMed] [Google Scholar]
- 26.Kraynov VS, Werneburg BG, Zhong X, Lee H, Ahn J, Tsai MD. DNA polymerase beta: analysis of the contributions of tyrosine-271 and asparagine-279 to substrate specificity and fidelity of DNA replication by pre-steady-state kinetics. Biochem J. 1997;323(Pt 1):103–111. doi: 10.1042/bj3230103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kraynov VS, Showalter AK, Liu J, Zhong X, Tsai MD. DNA polymerase beta: contributions of template-positioning and dNTP triphosphate-binding residues to catalysis and fidelity. Biochemistry. 2000;39:16008–16015. doi: 10.1021/bi0008480. [DOI] [PubMed] [Google Scholar]
- 28.Yamtich J, Starcevic D, Lauper J, Smith E, Shi I, Rangarajan S, Jaeger J, Sweasy JB. Hinge residue I174 is critical for proper dNTP selection by DNA polymerase beta. Biochemistry. 2010;49:2326–2334. doi: 10.1021/bi901735a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xiang Y, Oelschlaeger P, Florián J, Goodman MF, Warshel A. Simulating the effect of DNA polymerase mutations on transition-state energetics and fidelity: evaluating amino acid group contribution and allosteric coupling for ionized residues in human pol beta. Biochemistry. 2006;45:7036–7048. doi: 10.1021/bi060147o. [DOI] [PubMed] [Google Scholar]
- 30.Martínek V, Bren U, Goodman MF, Warshel A, Florián J. DNA polymerase beta catalytic efficiency mirrors the Asn279-dCTP H-bonding strength. FEBS Lett. 2007;581:775–780. doi: 10.1016/j.febslet.2007.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yep A, Kenyon GL, McLeish MJ. Saturation mutagenesis of putative catalytic residues of benzoylformate decarboxylase provides a challenge to the accepted mechanism. Proc Natl Acad Sci U S A. 2008;105:5733–5738. doi: 10.1073/pnas.0709657105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Warshel A, Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr Opin Struct Biol. 1998;8:211–217. doi: 10.1016/s0959-440x(98)80041-9. [DOI] [PubMed] [Google Scholar]
- 33.Simonson T, Carlsson J, Case DA. Proton binding to proteins: pKa calculations with explicit and implicit solvent models. J Am Chem Soc. 2004;126:4167–4180. doi: 10.1021/ja039788m. [DOI] [PubMed] [Google Scholar]
- 34.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim Biophys Acta. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 35.Warshel A, Dryga A. Simulating electrostatic energies in proteins: perspectives and some recent studies of pKas, redox, and other crucial functional properties. Proteins. 2011;79:3469–3484. doi: 10.1002/prot.23125. [DOI] [PubMed] [Google Scholar]
- 36.Morgan BR, Massi F. Accurate estimates of free energy changes in charge mutations. J Chem Theory Comput. 2010;6:1884–1893. doi: 10.1021/ct900565e. [DOI] [PubMed] [Google Scholar]
- 37.Jackson SE, Fersht AR. Contribution of long-range electrostatic interactions to the stabilization of the catalytic transition state of the serine protease subtilisin BPN'. Biochemistry. 1993;32:13909–13916. doi: 10.1021/bi00213a021. [DOI] [PubMed] [Google Scholar]
- 38.Rajagopalan PTR, Lutz S, Benkovic SJ. Coupling interactions of distal residues enhance dihydrofolate reductase catalysis: mutational effects on hydride transfer rates. Biochemistry. 2002;41:12618–12628. doi: 10.1021/bi026369d. [DOI] [PubMed] [Google Scholar]
- 39.Rod TH, Radkiewicz JL, Brooks CL. Correlated motion and the effect of distal mutations in dihydrofolate reductase. Proc Natl Acad Sci U S A. 2003;100:6980–6985. doi: 10.1073/pnas.1230801100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zwanzig RW. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J Chem Phys. 1954;22:1420–1426. [Google Scholar]
- 41.van Gunsteren WF, Daura X, Mark AE. Computing of free energy. Helv Chim Acta. 2002;85:3113–3129. [Google Scholar]
- 42.Kollman P. Free energy calculations: Applications to chemical and biochemical phenomena. Chem Rev. 1993;93:2395–2417. [Google Scholar]
- 43.Sawaya MR, Prasad R, Wilson SH, Kraut J, Pelletier H. Crystal structures of human DNA polymerase beta complexed with gapped and nicked DNA: evidence for an induced fit mechanism. Biochemistry. 1997;36:11205–11215. doi: 10.1021/bi9703812. [DOI] [PubMed] [Google Scholar]
- 44.Klvaňa M, Jeřábek P, Goodman MF, Florián J. An abridged transition state model to derive structure, dynamics, and energy components of DNA polymerase β fidelity. Biochemistry. 2011;50:7023–7032. doi: 10.1021/bi200790s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hansson T, Marelius J, Aqvist J. Ligand binding affinity prediction by linear interaction energy methods. J Comput Aided Mol Des. 1998;12:27–35. doi: 10.1023/a:1007930623000. [DOI] [PubMed] [Google Scholar]
- 46.DeLano WL. The PyMOL molecular graphics system. DeLano Scientific; Palo Alto, CA, USA: 2002. [Google Scholar]
- 47.Marelius J, Kolmodin K, Feierberg I, Aqvist J. Q: a molecular dynamics program for free energy calculations and empirical valence bond simulations in biomolecular systems. J Mol Graph Model. 1998;16:213–225. 261. doi: 10.1016/s1093-3263(98)80006-5. [DOI] [PubMed] [Google Scholar]
- 48.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 49.Cheatham TE, Cieplak P, 3rd, Kollman PA. A modified version of the Cornell et al. force field with improved sugar pucker phases and helical repeat. J Biomol Struct Dyn. 1999;16:845–862. doi: 10.1080/07391102.1999.10508297. [DOI] [PubMed] [Google Scholar]
- 50.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, Shaw DE. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.King G, Warshel A. A surface constrained all-atom solvent model for effective simulations of polar solutions. J Chem Phys. 1989;91:3647–3661. [Google Scholar]
- 53.Sham YY, Warshel A. The surface constraint all atom model provides size independent results in calculations of hydration free energies. J Chem Phys. 1998;109:7940–7944. [Google Scholar]
- 54.Ryckaert JP, Ciccotti G, Berendsen HJ. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics. 1977;23:327–341. [Google Scholar]
- 55.Lee FS, Warshel A. A local reaction field method for fast evaluation of long-range electrostatic interactions in molecular simulations. The Journal of Chemical Physics. 1992;97:3100–3107. [Google Scholar]
- 56.Bren U, Martínek V, Florian J. Free energy simulations of uncatalyzed DNA replication fidelity: structure and stability of T.G and dTTP.G terminal DNA mismatches flanked by a single dangling nucleotide. J Phys Chem B. 2006;110:10557–10566. doi: 10.1021/jp060292b. [DOI] [PubMed] [Google Scholar]
- 57.Bren M, Florián J, Mavri J, Bren U. Do all pieces make a whole? Thiele cumulants and the free energy decomposition. Theor Chem Acc. 2007;117:535–540. [Google Scholar]
- 58.Bren U, Martínek V, Florián J. Decomposition of the solvation free energies of deoxyribonucleoside triphosphates using the free energy perturbation method. J Phys Chem B. 2006;110:12782–12788. doi: 10.1021/jp056623m. [DOI] [PubMed] [Google Scholar]
- 59.Humphrey W, Dalke A, Schulten K. VMD - Visual Molecular Dynamics. J Mol Graphics. 1996;14.1:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 60.Murphy DL, Jaeger J, Sweasy JB. A triad interaction in the fingers subdomain of DNA polymerase beta controls polymerase activity. J Am Chem Soc. 2011;133:6279–6287. doi: 10.1021/ja111099b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Murphy DL, Kosa J, Jaeger J, Sweasy JB. The Asp285 variant of DNA polymerase beta extends mispaired primer termini via increased nucleotide binding. Biochemistry. 2008;47:8048–8057. doi: 10.1021/bi702104y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Johnson KA. Conformational coupling in DNA polymerase fidelity. Annu Rev Biochem. 1993;62:685–713. doi: 10.1146/annurev.bi.62.070193.003345. [DOI] [PubMed] [Google Scholar]
- 63.Pelletier H, Sawaya MR, Wolfle W, Wilson SH, Kraut J. Crystal structures of human DNA polymerase beta complexed with DNA: implications for catalytic mechanism, processivity, and fidelity. Biochemistry. 1996;35:12742–12761. doi: 10.1021/bi952955d. [DOI] [PubMed] [Google Scholar]
- 64.Batra VK, Beard WA, Shock DD, Krahn JM, Pedersen LC, Wilson SH. Magnesium-induced assembly of a complete DNA polymerase catalytic complex. Structure. 2006;14:757–766. doi: 10.1016/j.str.2006.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Batra VK, Beard WA, Shock DD, Pedersen LC, Wilson SH. Structures of DNA polymerase beta with active-site mismatches suggest a transient abasic site intermediate during misincorporation. Mol Cell. 2008;30:315–324. doi: 10.1016/j.molcel.2008.02.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lang T, Maitra M, Starcevic D, Li SX, Sweasy JB. A DNA polymerase beta mutant from colon cancer cells induces mutations. Proc Natl Acad Sci U S A. 2004;101:6074–6079. doi: 10.1073/pnas.0308571101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Beutler TC, Mark AE, van Schaik RC, Gerber PR, van Gunsteren WF. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem Phys Lett. 1994;222:529–539. [Google Scholar]
- 68.Oostenbrink C. Efficient free energy calculations on small molecule host-guest systems - a combined linear interaction energy/one-step perturbation approach. J Comput Chem. 2009;30:212–221. doi: 10.1002/jcc.21116. [DOI] [PubMed] [Google Scholar]
- 69.de Ruiter A, Oostenbrink C. Efficient and accurate free energy calculations on trypsin inhibitors. J Chem Theory Comput. 2012 doi: 10.1021/ct200750p. in press. [DOI] [PubMed] [Google Scholar]
- 70.Alden RG, Parson WW, Chu ZT, Warshel A. Calculations of electrostatic energies in photosyntetic reaction centers. J Am Chem Soc. 1995;117:12284–12298. [Google Scholar]
- 71.Yang W, Pan Y, Zheng F, Cho H, Tai HH, Zhan CG. Free-energy perturbation simulation on transition states and redesign of butyrylcholinesterase. Biophys J. 2009;96:1931–1938. doi: 10.1016/j.bpj.2008.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Opresko PL, Sweasy JB, Eckert KA. The mutator form of polymerase beta with amino acid substitution at tyrosine 265 in the hinge region displays an increase in both base substitution and frame shift errors. Biochemistry. 1998;37:2111–2119. doi: 10.1021/bi9722711. [DOI] [PubMed] [Google Scholar]
- 73.Shah AM, Li SX, Anderson KS, Sweasy JB. Y265H mutator mutant of DNA polymerase beta. Proper teometric alignment is critical for fidelity. J Biol Chem. 2001;276:10824–10831. doi: 10.1074/jbc.M008680200. [DOI] [PubMed] [Google Scholar]
- 74.Shah AM, Maitra M, Sweasy JB. Variants of DNA polymerase Beta extend mispaired DNA due to increased affinity for nucleotide substrate. Biochemistry. 2003;42:10709–10717. doi: 10.1021/bi034885d. [DOI] [PubMed] [Google Scholar]
- 75.Starcevic D, Dalal S, Sweasy J. Hinge residue Ile260 of DNA polymerase beta is important for enzyme activity and fidelity. Biochemistry. 2005;44:3775–3784. doi: 10.1021/bi047956x. [DOI] [PubMed] [Google Scholar]
- 76.Starcevic D, Dalal S, Sweasy JB. Is there a link between DNA polymerase beta and cancer? Cell Cycle. 2004;3:998–1001. [PubMed] [Google Scholar]
- 77.Tang KH, Niebuhr M, Tung CS, Chan HC, Chou CC, Tsai MD. Mismatched dNTP incorporation by DNA polymerase beta does not proceed via globally different conformational pathways. Nucleic Acids Res. 2008;36:2948–2957. doi: 10.1093/nar/gkn138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Roettger MP, Bakhtina M, Tsai MD. Mismatched and matched dNTP incorporation by DNA polymerase beta proceed via analogous kinetic pathways. Biochemistry. 2008;47:9718–9727. doi: 10.1021/bi800689d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Dalal S, Starcevic D, Jaeger J, Sweasy JB. The I260Q variant of DNA polymerase beta extends mispaired primer termini due to its increased affinity for deoxynucleotide triphosphate substrates. Biochemistry. 2008;47:12118–12125. doi: 10.1021/bi8011548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Shah AM, Conn DA, Li SX, Capaldi A, Jäger J, Sweasy JB. A DNA polymerase beta mutator mutant with reduced nucleotide discrimination and increased protein stability. Biochemistry. 2001;40:11372–11381. doi: 10.1021/bi010755y. [DOI] [PubMed] [Google Scholar]
- 81.Kosa JL, Sweasy JB. 3′-Azido-3′-deoxythymidine-resistant mutants of DNA polymerase beta identified by in vivo selection. J Biol Chem. 1999;274:3851–3858. doi: 10.1074/jbc.274.6.3851. [DOI] [PubMed] [Google Scholar]
- 82.Donigan KA, Sun K, Nemec AA, Murphy DL, Cong X, Northrup V, Zelterman D, Sweasy JB. Human POLB gene is mutated in high percentage of colorectal tumors. J Biol Chem. 2012;287:23830–23839. doi: 10.1074/jbc.M111.324947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Murphy DL, Donigan KA, Jaeger J, Sweasy JB. The E288K Colon Tumor Variant of DNA Polymerase Beta Is a Sequence Specific Mutator. Biochemistry. 2012 doi: 10.1021/bi3003583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wang L, Patel U, Ghosh L, Banerjee S. DNA polymerase beta mutations in human colorectal cancer. Cancer Res. 1992;52:4824–4827. [PubMed] [Google Scholar]
- 85.Mohrenweiser HW, Xi T, Vázquez-Matías J, Jones IM. Identification of 127 amino acid substitution variants in screening 37 DNA repair genes in humans. Cancer Epidemiol Biomarkers Prev. 2002;11:1054–1064. [PubMed] [Google Scholar]
- 86.Ahn J, Werneburg BG, Tsai MD. DNA polymerase beta: structure-fidelity relationship from Pre-steady-state kinetic analyses of all possible correct and incorrect base pairs for wild type and R283A mutant. Biochemistry. 1997;36:1100–1107. doi: 10.1021/bi961653o. [DOI] [PubMed] [Google Scholar]
- 87.Beard WA, Shock DD, Vande Berg BJ, Wilson SH. Efficiency of correct nucleotide insertion governs DNA polymerase fidelity. J Biol Chem. 2002;277:47393–47398. doi: 10.1074/jbc.M210036200. [DOI] [PubMed] [Google Scholar]
- 88.Osheroff WP, Jung HK, Beard WA, Wilson SH, Kunkel TA. The fidelity of DNA polymerase beta during distributive and processive DNA synthesis. J Biol Chem. 1999;274:3642–3650. doi: 10.1074/jbc.274.6.3642. [DOI] [PubMed] [Google Scholar]
- 89.Sawaya MR, Pelletier H, Kumar A, Wilson SH, Kraut J. Crystal structure of rat DNA polymerase beta: evidence for a common polymerase mechanism. Science. 1994;264:1930–1935. doi: 10.1126/science.7516581. [DOI] [PubMed] [Google Scholar]
- 90.Pelletier H, Sawaya MR, Kumar A, Wilson SH, Kraut J. Structures of ternary complexes of rat DNA polymerase beta, a DNA template-primer, and ddCTP. Science. 1994;264:1891–1903. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.