Efficient estimation of the distribution of time to composite endpoint when some endpoints are only partially observed

Abstract

Two common features of clinical trials, and other longitudinal studies, are (1) a primary interest in composite endpoints, and (2) the problem of subjects withdrawing prematurely from the study. In some settings, withdrawal may only affect observation of some components of the composite endpoint, for example when another component is death, information on which may be available from a national registry. In this paper, we use the theory of augmented inverse probability weighted estimating equations to show how such partial information on the composite endpoint for subjects who withdraw from the study can be incorporated in a principled way into the estimation of the distribution of time to composite endpoint, typically leading to increased efficiency without relying on additional assumptions above those that would be made by standard approaches. We describe our proposed approach theoretically, and demonstrate its properties in a simulation study.

1 Introduction

In many medical studies, the time to the first of two or more events—termed the time to composite endpoint—is of primary interest. For example, in cardiovascular clinical trials, the target of inference is often some aspect(s) of the distribution of time to death or myocardial infarction (MI), whichever occurs first. We consider the common situation in which some subjects withdraw from the study prematurely, before experiencing an event. In particular, we focus on a setting in which data on the occurrence of a subset of the components of the composite endpoint are available by other means even after a subject has withdrawn from the study. For example, the vital status of all subjects at the end of the study can sometimes be obtained from a national death index. That is, even for those who withdraw, we know whether or not they died before the end of the study, and if so when, but whether or not they experienced any of the other events included in the composite endpoint remains unknown. We show how this additional information can be incorporated in a principled way into the estimation of the distribution of time to composite endpoint, leading to increased efficiency.

The article is organised as follows. In section 2 we formally describe the setting and introduce the notation and some concepts from semiparametric theory used in the remainder of the work. In section 3 we set out the model that would be assumed if there were no withdrawals, and hence the analysis that would be carried out with the full data. We consider withdrawal in section 4, first describing standard approaches to dealing with it, and then in section 5 we describe our suggested improved approach. In section 6 we give the results of a simulation study demonstrating the properties of our approach, followed in section 7 by some concluding discursive remarks.

2 Setting, notation and preliminary definitions

2.1 Setting, full and coarsened data

Suppose that the recruitment of n subjects into a study occurs over r years, and that the study ends after d years, where d > r. At the end of the study, any subject who has not yet experienced either of the events of interest is administratively censored. Let C_i ∈ (d − r, d] be the time between recruitment (henceforth time 0) and administrative censoring for subject i (i = 1, …, n).

For simplicity, and in keeping with our motivating example, we restrict our description to the case where the composite endpoint is composed of two events (MI and death), only one of which (MI) is affected by withdrawal due to the availability of registry data on the other event (death). However, the approach can be extended to the case where the composite endpoint consists of more than two events.

Had there been no withdrawal or censoring, let T_i ∈ (0, ∞) be the time at which subject i would have experienced the first of the two events of interest. Then, in the presence of censoring (but in the absence of withdrawal) let $U_i^{\ast }=min(T_i,C_i)$ be the time at which subject i either would have experienced the first of the two events of interest, or would have been administratively censored, whichever would have occurred first.

Let ${\mathit{\Delta }}_i^{\ast }=0$ if $U_i^{\ast }=C_i$, i.e. if $U_i^{\ast }$ is a censoring time, ${\mathit{\Delta }}_i^{\ast }=1$ if $U_i^{\ast }<C_i$ and the event is a death, and ${\mathit{\Delta }}_i^{\ast }=2$ if $U_i^{\ast }<C_i$ and the event is an MI.

Let D_i ∈ (0, C_i] be the death time or censoring time for subject i, whichever occurs first.

Let Γ_i = 0 if D_i = C_i, i.e. if D_i is a censoring time, and Γ_i = 1 if D_i < C_i, i.e. if D_i is a death time.

Let $W_i\in (0,U_i^{\ast })\cup \{\infty \}$ be the time at which subject i withdraws from the study. By convention, we denote the withdrawal time to be ∞ if subject i does not withdraw, i.e. if subject i is observed to experience the event or is administratively censored before withdrawal.

At baseline, and possibly at subsequent occasions during follow-up, a vector of covariates is observed. At each time $t\in [0,U_i^{\ast }]$, we write the history of the vector of covariates available at time t as X̄_i(t).

Let $U_i=min(U_i^{\ast },W_i)$. Let ${\mathit{\Delta }}_i={\mathit{\Delta }}_i^{\ast }$ if $U_i=U_i^{\ast }$ and Δ_i = −1 if U_i = W_i. These are the composite endpoint times and classification we would observe when there are withdrawals.

Note that, since the national death registry data are available on everyone, D_i and Γ_i are observed on all subjects, even if withdrawal or the other event (MI) occurs before death, i.e. even if U_i < D_i.

The full data (in the absence of withdrawal) for subject i are thus:

$${\mathcal{F}}_i=\{C_i,U_i^{\ast },{\mathit{\Delta }}_i^{\ast },{\overline{\mathbf{X}}}_i(U_i^{\ast }),D_i,{\mathit{\Gamma }}_i\}$$

and the actual observed data (with withdrawals) are:

$${\mathcal{O}}_i=\{C_i,U_i,{\mathit{\Delta }}_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}.$$

Moreover, we define the level-r coarsened data [10] for subject i to be:

$$G_r({\mathcal{F}}_i)=\{C_i,I(U_i^{\ast }<r),I(U_i^{\ast }<r)U_i^{\ast },I(U_i^{\ast }<r){\mathit{\Delta }}_i^{\ast },{\overline{\mathbf{X}}}_i\{min(r,U_i^{\ast })\},D_i,{\mathit{\Gamma }}_i\}.$$

If subject i withdraws at time r < ∞, then 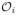= G_r( 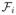). Note that G_∞( ) = .

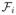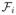2.2 Counting processes

We adopt the counting processes [2] notation throughout, and write

$$N_i^{\ast }(t)=I(U_i^{\ast }\le t,{\mathit{\Delta }}_i^{\ast }\in \{1,2\})$$

for the counting process associated with the composite endpoint in the absence of withdrawal.

Similarly, in the presence of withdrawal, we define the following counting process:

$$N_i(t)=I(U_i\le t,{\mathit{\Delta }}_i\in \{1,2\}),$$

The risk sets at time t, both in the presence and absence of withdrawal, are define as follows:

$$Y_i^{\ast }(t)=I(U_i^{\ast }\ge t),$$

and

$$Y_i(t)=I(U_i\ge t).$$

2.3 Semiparametric theory and an outline of the approach to be employed

Put briefly, the approach we will take is to specify a model for the coarsening mechanism, that is a model for the hazard of withdrawal given the observed data; this constitutes a semiparametric model for the observed data, since all other aspects of the joint distribution of the observed data are left unspecified. We then use the theory of augmented inverse probability weighted estimation set out by Robins, Rotnitzky and Zhao [9], and further explained by Tsiatis [10], to define a class of estimators that are consistent under the assumption that the data were generated from a density belonging to this semiparametric model. Furthermore, we use the same theory to obtain the most efficient estimator in this class. In this section, we briefly review some key definitions from semiparametric theory that will be required in later sections of the paper. More details can be found in [10].

Definition 1 (Parametric, semiparametric and non-parametric models)

A model 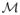for a set of i.i.d. observations Z₁, Z₂, …, Z_n is a set of densities

$$\mathcal{M}=\{p(z,\theta ):\theta \in \mathit{\Theta }\}$$

that could have given rise to the data, indexed by a parameter θ.

• If θ is finite-dimensional, then 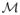is parametric.

• If θ can be partitioned as

  $$\theta ={({\beta }^T,{\eta }^T)}^T$$

  where β is a finite-dimensional parameter of interest, and η is an infinite-dimensional nuisance parameter, then 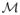is semiparametric. In practice, such models arise when η can be any real-valued function, such as the baseline hazard function in Cox’s proportional hazards model (strictly speaking, any positive real-valued function of time). For this reason, we will write η as η(·) when η is infinite-dimensional.

Finally, if 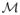contains all possible densities for Z then it is nonparametric.

Definition 2 (Semiparametric estimator)

Given a semiparametric model 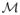, a semiparametric estimator β̂ of the q-dimensional parameter of interest β is one which is consistent and asymptotically normal in the sense that

$$\widehat{\beta }-\beta \stackrel{\mathcal{P}\{\beta ,\eta (·)\}}{\to }0$$

and

$$n^{\frac{1}{2}}\left(\widehat{\beta }-\beta \right)\stackrel{\mathcal{D}\{\beta ,\eta (·)\}}{\to }N(0,{\mathit{\sum }}^{q\times q}\{\beta ,\eta (·)\})$$

for all densities p{z, β, η(·)} ∈ 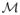, where $\stackrel{\mathcal{P}\{\beta ,\eta (·)\}}{\to }$ denotes convergence in probability and $\stackrel{\mathcal{D}\{\beta ,\eta (·)\}}{\to }$ denotes convergence in distribution when the density of Z is p{z, β, η(·)}.

Definition 3 (Asymptotically linear estimator, influence function)

An estimator β̂ of β is asymptotically linear if it can be written as

$$n^{\frac{1}{2}}\left(\widehat{\beta }-{\beta }_0\right)=n^{-\frac{1}{2}}\sum _{i=1}^n\phi (Z_i)+o_p(1)$$ (1)

where β₀ is the true value of β, o_p(1) is a term that converges in probability to zero as n → ∞, and φ(Z_i) is a (q × 1) random vector with expectation zero under the truth (i.e. E_θ0{φ(Z_i)} = 0) and E_θ0{φ(Z_i)φ(Z_i)^T} is finite and nonsingular.

φ(Z_i) is known as the i^th influence function of β̂.

Note that by the central limit theorem and Slutsky’s theorem, (1) implies that

$$n^{\frac{1}{2}}\left(\widehat{\beta }-{\beta }_0\right)\stackrel{\mathcal{D}\{{\beta }_0,{\eta }_0(·)\}}{\to }N\left(0,E_{{\theta }_0}\left\{\phi (Z_i)\phi {(Z_i)}^T\right\}\right).$$

Thus the asymptotic properties of an asymptotically linear estimator are governed by its influence function.

Definition 4 (Parametric submodel)

Given a semiparametric model 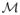, a class of densities 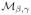indexed by the finite-dimensional parameter (β^T, γ^T)^T is a parametric submodel o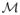f if 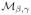⊂ 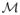and p{z, β₀, η₀(·)} ∈ 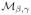, where p{z, β₀, η₀(·)} is the true density that generated the data.

Definition 5 (Efficient influence function for a parametric model)

Given a parametric model 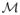indexed by finite-dimensional θ = (β^T, γ^T)^T, the efficient influence function φ_eff (Z) is given by:

$${\phi }_{\text{eff}}(Z)={[E\{S_{\text{eff}}(Z,{\theta }_0)S_{\text{eff}}^T(Z,{\theta }_0)\}]}^{-1}{S}_{\text{eff}}(Z,{\theta }_0)$$

where S_eff (Z, θ₀), the efficient score, is given by

$$S_{\text{eff}}(Z,{\theta }_0)=S_{\beta }(Z,{\theta }_0)-E\{S_{\beta }(Z,{\theta }_0)S_{\gamma }^T(Z,{\theta }_0)\}{[E\{S_{\gamma }(Z,{\theta }_0)S_{\gamma }^T(Z,{\theta }_0)\}]}^{-1}{S}_{\gamma }(Z,{\theta }_0)$$

where

$$S_{\beta }(z,{\theta }_0)={\frac{\partial logp(z,\theta )}{\partial \beta }|}_{{\theta }_0}$$

and

$$S_{\gamma }(z,{\theta }_0)={\frac{\partial logp(z,\theta )}{\partial \gamma }|}_{{\theta }_0}.$$

Using Hilbert space theory [10] it can be shown that φ_eff (Z) is the influence function with the smallest variance amongst the set of all influence functions for regular asymptotically linear (RAL) estimators for the parametric model 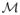. The definition of regular is given in chapter 3 of [10], and essentially excludes pathological super-efficient estimators. The variance of φ_eff (Z) is, by definition,

$${[E\{S_{\text{eff}}(Z,{\theta }_0)S_{\text{eff}}^T(Z,{\theta }_0)\}]}^{-1}.$$

Definition 6 (Semiparametric efficiency bound, local and global semiparametric efficiency)

The semiparametric efficiency bound for a semi-parametric model 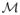is the supremum of ${[E\{S_{\text{eff}}(Z,{\theta }_0)S_{\text{eff}}^T(Z,{\theta }_0)\}]}^{-1}$ over all parametric submodels 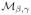of .

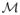Any semiparametric RAL estimator β̂ with the variance of its influence function achieving this bound at the true density p{z, β₀, η₀ (·)} is said to be locally efficient.

If the variance of its influence function achieves this bound for any density p{z, β, η(·)} in 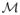, then β̂ is said to be globally semiparametric efficient.

3 Full data model, estimation and inference

Our aim is to make inference about the distribution of T_i in the population from which our sample of n subjects is taken, summarised by the survivor function:

$$S(t)=Pr(T_i>t),$$

the hazard function:

$$\lambda (t)=\underset{\mathit{\Delta }t\to 0}{lim}\frac{1}{\mathit{\Delta }t}Pr(t\le T_i<t+\mathit{\Delta }t\mid T_i\ge t),$$

and/or the cumulative hazard function:

$$\mathit{\Lambda }(t)={\int }_0^t\lambda (u)du,$$

which are related as follows:

$$S(t)=exp\{-\mathit{\Lambda }(t)\}=exp\left\{-{\int }_0^t\lambda (u)du\right\}.$$ (2)

In the absence of withdrawal, we would do so using the full data

$$\{{\mathcal{F}}_i:i=1,\dots ,n\}$$

under the assumption that these are i.i.d. observations from some density, with no restriction on the form of that density, except that censoring is independent, C_i ⫫ T_i: call this model .

Under this assumption, we can use the Nelson–Aalen estimator [7,1] of the cumulative hazard function, and corresponding Breslow estimator [3] of the survivor function. The Nelson–Aalen estimator of dΛ(t) is given by the solution to:

$$\sum _{i=1}^n\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}=0,$$

which leads to the following full-data estimator of Λ(t):

$${\widehat{\mathit{\Lambda }}}^{\text{full}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\sum }_{i=1}^n{Y}_i^{\ast }(u)}.$$ (3)

Indeed, it can be shown that Λ̂^full(t) is the only semiparametric estimator of Λ(t) for , and thus it is (trivially) both locally and globally semiparametric efficient [10].

The Breslow estimator of S(t) is then given by:

$${\widehat{S}}^{\text{full}}(t)=exp\left\{-{\widehat{\mathit{\Lambda }}}^{\text{full}}(t)\right\}.$$

A variance estimator for Λ̂^full(t) [1] is given by:

$$\widehat{\text{Var}}\left({\widehat{\mathit{\Lambda }}}^{\text{full}}(t)\right)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\{{\sum }_{i=1}^n{Y}_i^{\ast }(u)\}}^2}$$

and thus 95% confidence intervals for Λ(t) and S(t) can be constructed as

$$\left[{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\sum }_{i=1}^n{Y}_i^{\ast }(u)}\mp 1.96\sqrt{{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\{{\sum }_{i=1}^n{Y}_i^{\ast }(u)\}}^2}}\right]$$

and

$$\left[exp\left\{-{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\sum }_{i=1}^n{Y}_i^{\ast }(u)}\mp 1.96\sqrt{{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i^{\ast }(u)}{{\{{\sum }_{i=1}^n{Y}_i^{\ast }(u)\}}^2}}\right\}\right],$$

respectively.

4 Standard approaches to dealing with withdrawal

4.1 Complete case (CC) estimator

Suppose we assume that withdrawal is independent. More specifically, the assumption is as follows:

$$\underset{\mathit{\Delta }t\to 0}{lim}\frac{1}{\mathit{\Delta }t}Pr(t\le W_i<t+\mathit{\Delta }t\mid W_i\ge t,U_i^{\ast },{\mathit{\Delta }}_i^{\ast })=I(U_i^{\ast }\ge t)\kappa (t).$$ (4)

Note that for independent censoring we stated the assumption simply as C_i ⫫ T_i. The only reason that the two assumptions differ in form (and we do not say analogously that $W_i⫫U_i^{\ast }$) is due to the convention that W_i = ∞ if $W_i>U_i^{\ast }$, whereas for censoring, a finite value of C_i exists even when C_i > T_i.

We write 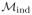for the model defined by (4) and the assumption of independent censoring. Under the assumptions of 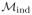we can treat withdrawal as an additional source of independent censoring, which leads to the complete case (CC) estimator.

The CC estimator of dΛ(t) is given by the solution to:

$$\sum _{i=1}^n\{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)\}=0,$$ (5)

which leads to the following complete case estimator of Λ(t):

$${\widehat{\mathit{\Lambda }}}^{\text{CC}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\sum }_{i=1}^n{Y}_i(u)}.$$ (6)

The CC estimator of S(t) is then given by:

$${\widehat{S}}^{\text{CC}}(t)=exp\left\{-{\widehat{\mathit{\Lambda }}}^{\text{CC}}(t)\right\}.$$ (7)

To see why these estimators are consistent under (4), we first note that

$${dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)=I(W_i>t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}$$

and thus that

$$\begin{array}{l}E\{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)\}=E[I(W_i>t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}]\\ =E(E[I(W_i>t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}\mid U_i^{\ast },{\mathit{\Delta }}_i^{\ast }])\\ =E[Pr(W_i>t\mid U_i^{\ast },{\mathit{\Delta }}_i^{\ast })\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}].\end{array}$$ (8)

Next note that it follows from (4) and (2) that:

$$\begin{array}{l}Pr(W_i>t\mid U_i^{\ast },{\mathit{\Delta }}_i^{\ast })=exp\left\{-{\int }_0^{t}I(U_i^{\ast }\ge u)\kappa (u)du\right\}\\ =exp\left\{-{\int }_0^{min(t,U_i^{\ast })}\kappa (u)du\right\}\\ =I(U_i^{\ast }\ge t)exp\left\{-{\int }_0^t\kappa (u)du\right\}+I(U_i^{\ast }<t)exp\left\{-{\int }_0^{U_i^{\ast }}\kappa (u)du\right\}.\end{array}$$ (9)

Substituting into (8),

$$E\{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)\}=E\left(\right[I(U_i^{\ast }\ge t)exp\left\{-{\int }_0^t\kappa (u)du\right\}+I(U_i^{\ast }<t)exp\left\{-{\int }_0^{U_i^{\ast }}\kappa (u)du\right\}]\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}).$$ (10)

But

$$I(U_i^{\ast }\ge t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}={dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)$$

and

$$I(U_i^{\ast }<t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}=0$$

and so (10) simplifies to give:

$$\begin{array}{l}E\{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)\}=E\left[exp\left\{-{\int }_0^t\kappa (u)du\right\}\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}\right]\\ =exp\left\{-{\int }_0^t\kappa (u)du\right\}E\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}\\ =0\end{array}$$ (11)

as required, by the consistency of the Nelson–Aalen estimator for the full data (3).

As before, a variance estimator for Λ̂^CC(t) is given by:

$$\widehat{\text{Var}}\left({\widehat{\mathit{\Lambda }}}^{\text{CC}}(t)\right)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\{{\sum }_{i=1}^n{Y}_i(u)\}}^2}$$

and thus 95% confidence intervals for Λ(t) and S(t) can be constructed as

$$\left[{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\sum }_{i=1}^n{Y}_i(u)}\mp 1.96\sqrt{{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\{{\sum }_{i=1}^n{Y}_i(u)\}}^2}}\right]$$

and

$$\left[exp\left\{-{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\sum }_{i=1}^n{Y}_i(u)}\mp 1.96\sqrt{{\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\{{\sum }_{i=1}^n{Y}_i(u)\}}^2}}\right\}\right],$$

respectively.

Although Λ̂^CC(t) is a semiparametric estimator of Λ(t) under model 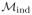, it is not the only semiparametric estimator, in contrast with what we noted for Λ̂^full(t) under model . Furthermore, Λ̂^CC(t) is neither locally nor globally semiparametric efficient under 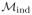; this is intuitively apparent since (5) does not utilise the data on (D_i, Γ_i) for those who withdraw. In section 5 we show how estimating functions such as the one in (5) can be augmented to include these additional data without restricting the model further than 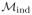, thus— for judicious choices of the augmentation term—improving efficiency. First, however, we consider relaxing the assumption of independent withdrawal.

4.2 Inverse probability weighted complete case (IPWCC) estimator

In many situations, independent withdrawal is implausible. We may wish to relax this to an assumption of covariate-driven withdrawal at random, which is that:

$$\underset{\mathit{\Delta }t\to 0}{lim}\frac{1}{\mathit{\Delta }t}Pr(t\le W_i<t+\mathit{\Delta }t\mid W_i\ge t,{\mathcal{F}}_i)=I(U_i^{\ast }\ge t)\lambda \{t,{\overline{\mathbf{X}}}_i(t)\}$$ (12)

i.e. the hazard of withdrawal at time t conditional on the full data is allowed to depend on the full data, but only as a function of t and X̄_i(t) and only if the event has not already occurred, since the hazard of withdrawal is zero after that. Note that (12) is an example of a coarsening at random [6,10] mechanism, since $\{I(U_i^{\ast }\ge t),{\overline{\mathbf{X}}}_i(t)\}\subset G_t({\mathcal{F}}_i)$.

We write 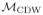(where CDW stands for covariate-driven withdrawal) for the model defined by (12) and the assumption of independent censoring.

The complete case estimators (6) and (7) are, in general, not consistent under model 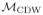. The reason for this is that (9) is replaced by a function of X̄_i(t), which can no longer be taken out of the expectation in (11), leading to a non-zero expectation whenever X̄_i(t) is correlated with $U_i^{\ast }$, as is typically the case.

Re-weighting the complete case estimating equation (5), however, gives rise to a consistent estimator under (12). Specifically, consider the following:

$$\sum _{i=1}^n\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}=0,$$ (13)

which leads to the following inverse probability weighted complete case estimator of Λ(t):

$${\widehat{\mathit{\Lambda }}}^{\text{IPWCC}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n\frac{{dN}_i(u)}{Pr\{W_i\ge u\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u)\}}}{{\sum }_{i=1}^n\frac{Y_i(u)}{Pr\{W_i>u\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u)\}}}.$$ (14)

The IPWCC estimator of S(t) is then given by:

$${\widehat{S}}^{\text{IPWCC}}(t)=exp\{-{\widehat{\mathit{\Lambda }}}^{\text{IPWCC}}(t)\}.$$ (15)

These are consistent estimators since

$$\begin{array}{l}E\{\frac{{dN}_i(t)=d\mathit{\Lambda }(t)Y_i(t)}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}\}=E\left\{\frac{I(W_i>t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}\right\}=E\left[E\left\{\frac{I(W_i>t)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}|{\mathcal{F}}_i\right\}\right]\\ =E\left[\frac{Pr(W_i>t\mid {\mathcal{F}}_i)\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}\right]\\ =E\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\}=0\end{array}$$

as required, by assumption (12) and the consistency of the Nelson–Aalen estimator for the full data (3).

Similarly to what was noted in the previous section, although Λ̂^IPWCC(t) is a semiparametric estimator of Λ(t) under model 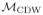, it is not the only one, and is neither locally nor globally semiparametric efficient; this is intuitively apparent for the same reason, i.e. that (13) does not utilise the data on (D_i, Γ_i) for those who withdraw. We return to this issue in later sections.

Another issue is that the probabilities $Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}$ are not known to us, and thus (13) cannot be solved, making (14) and (15) infeasible estimators. In practice, therefore, we must specify a model for

$$Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}=K\{t,{\overline{\mathbf{X}}}_i(t);\gamma \}$$ (16)

in terms of parameters γ to be estimated from the observed data. Equations (13), (14) and (15) then become

$$\sum _{i=1}^n\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{K\{t,{\overline{\mathbf{X}}}_i(t);\widehat{\gamma }\}}=0,$$ (17)

$${\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{IPWCC}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n\frac{{dN}_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u);\widehat{\gamma }\}}}{{\sum }_{i=1}^n\frac{Y_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u);\widehat{\gamma }\}}}$$ (18)

and

$${\widehat{S}}^{\mathrm{f}-\text{IPWCC}}(t)=exp\{-{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{IPWCC}}(t)\},$$ (19)

respectively, where γ̂ are the estimators of γ obtained from fitting model (16) to the observed data, and f-IPWCC stands for feasible IPWCC.

A natural choice for this model is Cox’s proportional hazards model, leading to maximum partial likelihood estimators γ̂ of γ [4,5]. Let 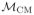be the set of densities for which model (16) holds; here, CM stands for ‘coarsening model’.

It can be shown [10] that Λ̂^f-IPWCC(t) and Ŝ^f-IPWCC(t) are consistent estimators for the model 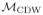∩ 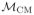. Furthermore, provided that the parameters γ of the coarsening model are estimated sufficiently efficiently (where the precise definition of ‘sufficiently efficiently’ in this context is discussed in [10]), these estimators have a smaller asymptotic variance than their infeasible counterparts, Λ̂^IPWCC(t) and Ŝ^IPWCC(t), respectively. In other words, even if the coarsening probabilities were known to us, we can obtain a more efficient estimator by estimating them from the data; this can seem counter-intuitive at first glance. It is not counter-intuitive, however, if we think a little more deeply: the weights are employed to correct for any imbalance between the complete and incomplete cases; what matters is the imbalance present in our sample, and not the imbalance present in the population from which that sample was taken.

We have not discussed variance estimation since we will do so in greater generality in section 5.

4.3 IPWCC estimator including (D, Γ)

Thus far we have made no use of data on the observed endpoint {D_i, Γ_i} for those who withdraw. The simplest way in which these additional data can be incorporated is by changing model (16) to

$$Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}=\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\stackrel{\sim }{\gamma }\}$$ (20)

As long as there exists a choice of γ̃ = g(γ) as a function of γ, such that

$$\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i,D_i,{\mathit{\Gamma }}_i;g(\gamma )\}\equiv K(t,{\overline{\mathbf{X}}}_i;\gamma )\forall t,{\overline{\mathbf{X}}}_i,D_i,{\mathit{\Gamma }}_i,\gamma ,$$ (21)

then the subset of 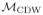for which model (20) holds is the same as the subset for which model (16) holds, i.e. it is the subset 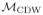∩ 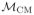. In practice, if (16) is, say, a Cox proportional hazards model, then specifying (20) to be the same except for the addition of Γ_i and Γ_iD_i (and/or any other functions of Γ_i and D_i) as variables in the linear predictor would satisfy this requirement, since setting their coefficients in (20) to zero would recover model (16), i.e. γ̃ = g(γ): = (γ^T, 0, 0)^T.

Under model (20) for the weights, (17), (18) and (19) become

$$\sum _{i=1}^n\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}=0,$$ (22)

$${\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{IPWCC}-\text{ext}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n\frac{{dN}_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}}{{\sum }_{i=1}^n\frac{Y_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}}$$ (23)

and

$${\widehat{S}}^{\mathrm{f}-\text{IPWCC}-\text{ext}}(t)=exp\left\{-{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{IPWCC}-\text{ext}}(t)\right\},$$ (24)

respectively, where $\widehat{\stackrel{\sim }{\gamma }}$ are the estimators of γ̃ obtained from fitting model (20) to the observed data, and f-IPWCC-ext stands for extended feasible IPWCC, in the sense that model (16) has been extended to model (20).

Under condition (21), Λ̂^f-IPWCC-ext(t) and Ŝ^f-IPWCC-ext(t) are consistent estimators for the model ∩ .

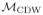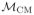Moreover, provided that (20) is correctly specified, they are consistent under a relaxation of (12) to

$$\underset{\mathit{\Delta }t\to 0}{lim}\frac{1}{\mathit{\Delta }t}Pr(t\le W_i<t+\mathit{\Delta }t\mid W_i\ge t,{\mathcal{F}}_i)=I(U_i^{\ast }\ge t)\nu \{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}$$ (25)

i.e. that the hazard of withdrawal at time t conditional on the full data is allowed to depend on the full data as a function of t, X̄_i(t), D_i and Γ_i, provided that the event has not already occurred, with the hazard of withdrawal being zero after that. Note that (25) is also an example of a coarsening at random mechanism, since $\{I(U_i^{\ast }\ge t),{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}\subset G_t({\mathcal{F}}_i)$.

We call assumption (25) covariate-and-death-time-driven with-drawal at random and write 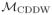(where CDDW stands for covariate-and-death-driven withdrawal) for the model defined by (25) together with the assumption of independent censoring. Furthermore, we write 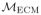for the set of densities for which (20) holds; here, ECM stands for ‘extended coarsening model’, to distinguish it from the coarsening model (16).

Since death potentially occurs after withdrawal, it is difficult to imagine a situation in which (25) precisely holds without the stronger assumption (12) also holding. However, suppose that neither assumption holds, since there is an unmeasured factor Z_i influencing both the propensity to withdraw (even after conditioning on X̄_i) and the propensity to die (also after conditioning on X̄_i), then, although (25) would not hold (since Z_i is unmeasured), assuming (25) rather than (12), and hence using estimators Λ̂^f-IPWCC-ext(t) and Ŝ^f-IPWCC-ext(t) rather than Λ̂^f-IPWCC(t) and Ŝ^f-IPWCC(t), would often lead to a reduction in bias, since the conditional association between Z_i and {D_i, Γ_i} given X̄_i means that some of the effect of Z_i is captured by {D_i, Γ_i}. However, this is not necessarily the case, as explained in greater detail in the Appendix. This is the ‘bias-reduction’ argument for preferring Λ̂^f-IPWCC-ext(t) and Ŝ^f-IPWCC-ext(t) over Λ̂^f-IPWCC(t) and Ŝ^f-IPWCC(t).

There is also an argument in terms of efficiency. Under model 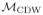∩ 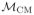and condition (21), provided that the parameters γ̃ of the extended coarsening model are estimated sufficiently efficiently, Λ̂^f-IPWCC-ext(t) and Ŝ^f-IPWCC-ext(t) have a smaller asymptotic variance than their non-extended counterparts, Λ̂^f-IPWCC(t) and Ŝ^f-IPWCC(t), respectively. In other words, even if we knew assumption (12) to be true, we could obtain more efficient estimators by estimating the weights from the extended model (20) rather than model (16). The intuition is the same as for why the feasible IPWCC estimators are more efficient than their infeasible counterparts: even though in truth the coefficients for Γ_i and Γ_iD_i, say, in (20) would be zero, their non-zero estimates in any finite sample improves efficiency.

In summary, Λ̂^f-IPWCC(t) and Λ̂^f-IPWCC-ext(t) are both semiparametric estimators for Λ(t) under model 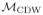∩ 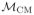, with Λ̂^f-IPWCC-ext(t) more efficient than Λ̂^f-IPWCC(t), but neither achieves the semiparametric efficiency bound, as we see in the next section. In addition, Λ̂^f-IPWCC-ext(t) is a semi-parametric estimator under model 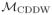∩ 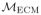, but again it does not achieve the semiparametric efficiency bound. In the next section, we derive more efficient estimators in these classes.

For completeness, there are of course infeasible counterparts to the extended feasible IPWCC estimators, namely:

$$\sum _{i=1}^n\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}}=0,$$ (26)

$${\widehat{\mathit{\Lambda }}}^{\text{IPWCC}-\text{ext}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n\frac{{dN}_i(u)}{Pr\{W_i>u\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}}{{\sum }_{i=1}^n\frac{Y_i(u)}{Pr\{W_i>u\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}}$$ (27)

and

$${\widehat{S}}^{\text{IPWCC}-\text{ext}}(t)=exp\left\{-{\widehat{\mathit{\Lambda }}}^{\text{IPWCC}-\text{ext}}(t)\right\}.$$ (28)

5 Proposed improved approach

5.1 Augmented inverse probability weighted estimator

For further efficiency gains, without requiring further assumptions, we can use estimators based on augmented versions of the IPWCC estimating equations given above. Consider augmenting equation (13) to:

$$\sum _{i=1}^n[\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\}}+{\int }_0^t\frac{{dM}_i(u)}{Pr\{W_i>u\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u)\}}h\{u,G_u({\mathcal{F}}_i)\}]=0$$ (29)

where, roughly speaking, for Δu small,

$${dM}_i(u)=[I(u\le W_i<u+\mathit{\Delta }u)-\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}\mathit{\Delta }uI(W_i\ge u)]I(U_i^{\ast }\ge u)$$

and h{u, G_u( 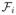)} is an arbitrary function at time u of G_u( ).

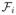Under (12),

$$\underset{\mathit{\Delta }u\to 0}{lim}\frac{1}{\mathit{\Delta }u}E\{{dM}_i(u)\mid G_u({\mathcal{F}}_i)\}=0,$$

and thus the estimator derived as a solution to (29) is consistent under model .

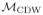The semiparametric theory explained by Tsiatis [10] shows that all semi-parametric estimators of dΛ(t) under model 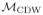are of the form shown in (29). In general, the theory shows that given an estimator dΛ̂^full(t) of dΛ(t) under model , re-weighting (as in (13)) and then augmenting (as in (29)) leads to a class of semiparametric estimators under model 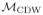, indexed by the choice of h{u, G_u( )}, and also by the choice of dΛ̂^full(t). However, in our setting, since is nonparametric, there is only one semiparametric estimator dΛ̂^full(t), and thus the solutions of the estimating equation (29) for different choices of h{u, G_u( 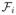)} constitute all the semiparametric estimators of dΛ(t).

Furthermore, the theory [10] shows that the most efficient estimator in the class of all semiparametric estimators (29) is given by the choice:

$$h_{\text{opt}}\{u,G_u({\mathcal{F}}_i)\}=E\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\mid G_u({\mathcal{F}}_i)\}$$ (30)

i.e. for each u, it is the conditional expectation of the full data estimating function (3), given the coarsened data at level u.

In the Appendix, we evaluate the conditional expectation in (30) and show that it is equal to

$$\frac{I(C_i<t)I(U_i^{\ast }>u)}{H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}(I(D_i=t)H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}+\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}.[dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}-d\mathit{\Lambda }(t)H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}])$$ (31)

where I(D_i = t) is used as shorthand for lim_Δt→0 I(t ≤ D_i < t + Δt),

$$H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}=exp\left[-{\int }_0^u\mu \{r,{\overline{\mathbf{X}}}_i(r),D_i,{\mathit{\Gamma }}_i\}dr\right],$$

$$H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}={\int }_{\stackrel{\sim }{\mathbf{x}}\in \overline{\mathcal{X}}(t)}H\{t,{\overline{\mathbf{X}}}_i(t)=\stackrel{\sim }{\mathbf{x}},D_i,{\mathit{\Gamma }}_i\}{f}_{\overline{\mathbf{X}}(t)\mid \overline{\mathbf{X}}(u),D,\mathit{\Gamma }}\{\stackrel{\sim }{\mathbf{x}},{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}d\stackrel{\sim }{\mathbf{x}}$$ (32)

and

$$dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}=H\{t+\mathit{\Delta }t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}-H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\},$$

where μ{u, X̄_i(u), D_i, Γ_i} is the cause-specific conditional hazard of the incompletely-observed event (MI, in our example) given X̄_i(u), D_i, and Γ_i, that is,

$$\mu \{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}=\underset{\mathit{\Delta }u\to 0}{lim}Pr\{u\le U_i^{\ast }<u+\mathit{\Delta }u,{\mathit{\Delta }}_i^{\ast }=2\mid U_i^{\ast }\ge u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\},$$ (33)

and

$$f_{\overline{\mathbf{X}}(t)\mid \overline{\mathbf{X}}(u),D,\mathit{\Gamma }}\{\stackrel{\sim }{\mathbf{x}},{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}$$

is the conditional density of X̄_i(t) given X̄_i(u), D_i and Γ_i, with X̄_i(u), D_i and Γ_i evaluated at their observed values, and X̄_i(t) between u and t evaluated according to x̄, one possible value of X̄_i(t) in the space 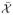(t) of all possible values of X̄_i(t). Equation (32) is discussed in greater detail in section 5.4.

Substituting (31) for h{u, G_u( 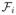)} in (29), and simplifying (details given in the Appendix) leads to the following estimating equation:

$$\sum _{i=1}^n(\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{K\{t,{\overline{\mathbf{X}}}_i(t)\}}+I(C_i>t)[I(C_i>D_i)I(D_i=1)J_i(t)-\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}\{J_i^{\prime }(t)-d\mathit{\Lambda }(t)J_i(t)\}\left]\right)=0$$ (34)

where

$$K\{t,{\overline{\mathbf{X}}}_i(t)\}=Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t)\},$$

$$J_i(t)=\frac{I(U_i\le t,{\mathit{\Delta }}_i=-1)H\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}{K\{U_i,{\overline{\mathbf{X}}}_i(U_i)\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}+{\int }_0^{min\{t,U_i\}}\frac{dK\{u,{\overline{\mathbf{X}}}_i(u)\}H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{K^2\{u,{\overline{\mathbf{X}}}_i(u)\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}$$

and

$$J_i^{\prime }(t)=\frac{I(U_i\le t,{\mathit{\Delta }}_i=-1)dH\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}{K\{U_i,{\overline{\mathbf{X}}}_i(U_i)\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}+{\int }_0^{min(t,U_i)}\frac{dK\{u,{\overline{\mathbf{X}}}_i(u)\}dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{K^2\{u,{\overline{\mathbf{X}}}_i(u)\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}.$$

Details of the calculation leading to (34) are given in the Appendix.

Thus the augmented inverse probability weighted (AIPW) estimator of Λ(t) is given by:

$${\widehat{\mathit{\Lambda }}}^{\text{AIPW}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n\left[\frac{{dN}_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}+A_i(u)\right]}{{\sum }_{i=1}^n\left[\frac{Y_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}+B_i(u)\right]}$$ (35)

where

$$A_i(u)\equiv A_i(u,C_i,U_i,{\mathit{\Delta }}_i,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i):=I(C_i>u)[I(C_i>D_i)I(D_i=u)J_i(u)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>u)\}{J}_i^{\prime }(u)]$$

and

$$B_i(u)\equiv B_i(u,C_i,U_i,{\mathit{\Delta }}_i,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i):=I(C_i>u)J_i(u)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>u)\}.$$

Correspondingly,

$${\widehat{S}}^{\text{AIPW}}(t)=exp\left\{-{\widehat{\mathit{\Lambda }}}^{\text{AIPW}}(t)\right\}.$$ (36)

These estimators are semiparametric efficient under model .

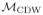Replacing K{t, X̄_i(t)} by

$$\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}=Pr\{W_i>t\mid U_i^{\ast }\ge t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}$$

throughout leads to semiparmetric efficient estimators Λ̂^AIPW-ext(t) and Ŝ^AIPW-ext(t) under model .

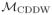Since 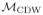⊂ 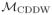, then the set of semiparametric estimators for 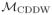must be contained within the set of semiparametric estimators for 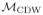. To see why the inclusion reverses direction, recall that the definition of a semiparametric estimator (Definition 2) concerns a criterion which must be satisfied for all densities in the model; thus the smaller the model, the easier it is for these criteria to be met. Consequently, Λ̂^AIPW-ext(t) and Ŝ^AIPW-ext(t) can be at most as asymptotically efficient as Λ̂^AIPW(t) and Ŝ^AIPW(t), respectively, in contrast to what was noted earlier for the non-augmented estimators. However, there are typically finite sample efficiency gains from using the extended versions, even when the true density comes from .

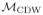5.2 Feasible estimation

Typically, none of K{t, X̄_i(t)}, K̃{t, X̄_i(t), D_i, Γ_i}, H{t, X̄_i(t), D_i, Γ_i} or f_{X̄(t)|X̄(u), D, Γ} {x̄, X̄_i(u), D_i, Γ_i} is known to us, and thus parametric models must be specified for these, and their parameters estimated from the observed data.

We write the posited models as:

$$K\{t,{\overline{\mathbf{X}}}_i(t)\}=K\{t,{\overline{\mathbf{X}}}_i(t);\gamma \},$$ (37)

$$\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}=\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\stackrel{\sim }{\gamma }\},$$ (38)

$$H\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}=H\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\eta \}$$ (39)

and

$$f_{\overline{\mathbf{X}}(t)\mid \overline{\mathbf{X}}(u),D,\mathit{\Gamma }}\{\stackrel{\sim }{\mathbf{x}},{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}=f_{\overline{\mathbf{X}}(t)\mid \overline{\mathbf{X}}(u),D,\mathit{\Gamma }}\{\stackrel{\sim }{\mathbf{x}},{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\nu \}$$ (40)

We call (37) the coarsening model, (38) the extended coarsening model, (39) the cause-specific model, since it is derived from the cause-specific hazard for the incompletely-observed outcome, and (40) the time-updated covariates model.

As before, we write 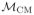for the set of densities for which model (37) holds, and 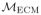for the subset of densities for which model (38) holds. In addition, we write 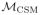for the set of densities for which model (39) holds and 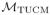for the set of densities for which model (40) holds.

5.3 Double robustness and semiparametric efficiency

It can be shown [10] that Λ̂^f-AIPW(t) and Ŝ^f-AIPW(t) are semiparametric under the model 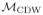∩ { 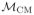∪ ( 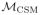∩ 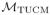)} and that Λ̂^f-AIPW-ext(t) and Ŝ^f-AIPW-ext(t) are semiparametric under the model ∩ { ∪ ( ∩ )}.

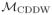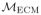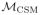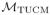Furthermore, Λ̂^f-AIPW(t) and Ŝ^f-AIPW(t) are semiparametric efficient under the model 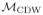∩ ∩ 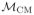∩ 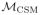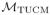and Λ̂^f-AIPW-ext(t) and Ŝ^f-AIPW-ext(t) are semiparametric efficient under the model ∩ ∩ ∩ .

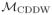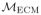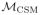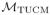In other words, if we correctly specify either the coarsening model or both the cause-specific and time-updated covariates models, then the AIPW estimator will be consistent. This property is known as double robustness and is especially important in our setting, where it is probably unrealistic to hope that the cause-specific and time-updated covariates models are correctly specified; under only the assumption that the coarsening model is correctly specified, the AIPW estimator is consistent. Furthermore, if we correctly specify all three models, then the AIPW estimator is optimal in terms of asymptotic efficiency. In practice, when the cause-specific and time-updated covariates models are not correctly specified, experience suggests that augmentation will lead to efficiency gains as long as these models are not too badly incorrectly specified [10]. We report on such a setting in section 6.

5.4 The challenge posed by time-updated covariates

Note that the AIPW estimators described above are substantially simplified when there are no time-updated covariates, i.e. when X̄_i(t) can be replaced by X̄_i. The simplification follows from the fact that we could write

$$H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}=H\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i\}=H\{t,{\overline{\mathbf{X}}}_i,D_i,{\mathit{\Gamma }}_i\}$$

and the integration in (32) would not be required, and neither would the specification of the TUCM model (40).

Especially if X̄_i(t) were high-dimensional, correctly specifying model (40) would be almost impossible (which in itself is not too problematic since we are protected by the double robustness) and the integral (32) would be very difficult to evaluate analytically, meaning that Monte Carlo simulation would be needed in practice.

One option in the presence of time-updated covariates would be to include them in the coarsening model (where they are not problematic) but to omit them from the cause-specific model, and to specify this only in terms of the baseline covariates. It is implausible that this model would then be correctly specified, but we could rely on the double robustness property for consistency, and hope that efficiency gains would still be seen, even without correct specification of this model.

5.5 Variance estimator

In order to assess the accuracy of our proposed AIPW estimator we also need to derive an estimator of its asymptotic variance. To do so we first derive the corresponding influence function for the increment of the cumulative hazard function dΛ̂^f-AIPW-ext(t) and then use the result that the asymptotic variance of dΛ̂^f-AIPW-ext(t) is equal to the sample variance of the estimated influence functions.

The details are given in the Appendix, where we derive our proposed estimator of the asymptotic variance of Λ̂^f-AIPW-ext(t) as the sample variance of the following n quantities:

$${\int }_0^t\frac{\frac{{dN}_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(u)-\frac{d{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ext}}(u)Y_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}-d{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ext}}(u){\widehat{B}}_i(u)}{n^{-1}{\sum }_{i=1}^n\left[\frac{Y_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{B}}_i(u)\right]}$$

where

$${\widehat{A}}_i(u)=I(C_i>u)\left[I(C_i>D_i)I(D_i=u){\widehat{J}}_i(u)-\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>u)\}{\widehat{J}}_i^{\prime }(u)\right],$$ (41)

$${\widehat{B}}_i(u)=I(C_i>u){\widehat{J}}_i(u)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>u)\},$$ (42)

$${\widehat{J}}_i(t)=\frac{I(U_i\le t,{\mathit{\Delta }}_i=-1)H\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i;\widehat{\eta },\widehat{\nu }\}}{\stackrel{\sim }{K}\left\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i;\widehat{\eta }\}}+{\int }_0^{min\{t,U_i\}}\frac{d\stackrel{\sim }{K}\left\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\eta },\widehat{\nu }\}}{{\stackrel{\sim }{K}}^2\left\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\eta }\}}$$

and

$${\widehat{J}}_i^{\prime }(t)=\frac{I(U_i\le t,{\mathit{\Delta }}_i=-1)dH\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i;\widehat{\eta },\widehat{\nu }\}}{\stackrel{\sim }{K}\left\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i,\widehat{\stackrel{\sim }{\gamma }}\right\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i;\widehat{\eta }\}}+{\int }_0^{min\{t,U_i\}}\frac{d\stackrel{\sim }{K}\left\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\eta },\widehat{\nu }\}}{{\stackrel{\sim }{K}}^2\left\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i,\widehat{\stackrel{\sim }{\gamma }}\right\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i,\widehat{\eta }\}}$$

From this estimator of the variance of Λ̂^f-AIPW-ext(t), confidence intervals for both Λ̂^f-AIPW-ext(t) and Ŝ^f-AIPW-ext(t) can be derived analogously to what was done in section 4.

6 Simulation study

We generated 1000 datasets, each with a sample size of 100, according to the following data generating process.

There is one binary baseline covariate, X, with Pr (X = 1) = 0.5. There are no time-dependent covariates. Subjects enter the study uniformly at random over 2 years, so r = 2, with administrative censoring at 5 years (d = 5).

Conditional on X, time to MI is simulated from a Weibull distribution with shape parameter 0.5 and scale parameter {10 exp (1.5 − 3X)}.

Conditional on X, time to death is simulated from an exponential distribution with hazard 0.24 exp (−1.5 + 3X). This time to death is compared with time to MI. If MI occurs first then the time to death is discarded, and the time to death is re-generated as the MI time plus a further time, with this further time being generated from an exponential distribution with hazard 0.6 exp (−1.5 + 3X).

Conditional on X, withdrawal is simulated from an exponential distribution with hazard exp (−1.5 + X).

In the full data, this leads to 30% censoring, 37% death as first event and 33% MI as first event. 34% of subjects withdraw.

In total we see a death time on 61% of patients. About one-sixth of these are deaths as first events that we didn’t observe in the study because of withdrawal, but that we see later from the registry data; the other five-sixth are divided approximately equally between deaths as first events that we did observe (before withdrawal) and deaths that were second events after an MI had occurred.

We compare six estimators of the survivor distribution:

1. the full data estimator, Ŝ^full(t).

2. the complete case estimator, Ŝ^CC(t).

3. the IPWCC estimator, Ŝ^f-IPWCC(t), with only X used to predict the weights using a Cox proportional hazards model with X the only variable in the linear predictor. Note that this coarsening model (model CM) is correctly specified.

4. the IPWCC estimator, Ŝ^f-IPWCC-ext(t), with X and {D, Γ} used to predict the weights, using a Cox proportional hazards model with X, Γ and Γ D included as separate linear terms in the linear predictor. Note that this extended coarsening model (model ECM) is correctly specified, although the inclusion of {D, Γ} was not needed to guarantee this.

5. the AIPW estimator, Ŝ^f-AIPW(t). X alone is used in the model for the weights (and thus CM is correctly specified) with X and {D, Γ} used in the cause-specific MI model (CSM). The CSM is a Cox proportional hazards model with just three variables, X, Γ and Γ D entered as linear terms in the linear predictor. Note that this model (CSM) is not correctly specified given the data generating process described above.

6. the AIPW estimator, Ŝ^f-AIPW-ext(t). X and {D, Γ} are used in both the model for the weights (and thus ECM is again correctly specified, but more elaborate than necessary) and also for the cause-specific MI model, as described for the previous estimator. Again, therefore, the cause-specific model is not correctly specified given the data generating process described above.

We compare each of the six estimators at values of t = 0.5, 1.5, 2.5, 3.5 and 4.5 years, and the results are given in Table 1. The mean value of Ŝ(t) across all 1000 simulations is given in the third column. The sample standard deviation of these 1000 simulated estimates are given in the fourth column, to represent the actual standard errors of the estimators; these are to be compared with the mean of the estimated standard errors (according to the methods described above for estimating the standard errors of each estimator, using the delta method to convert this to the standard error of the survivor function), given in column five. The sixth column gives the percentage increase in actual standard error for each estimator compared with the full data estimator. Finally, the last column gives the percentage of estimated 95% confidence intervals that included the true value of S(t) (calculated from the full data estimator for one simulated dataset with a sample size of 10⁷).

Table 1.

The results of the simulation study

Years	Estimator of survivor function	Mean	Standard Error		% increase in actual SE compared with full data	Coverage of 95% CI
			Actual	Estimated
	full	0.623	0.0488	0.0481	–	94.4%
	CC	0.633	0.0500	0.0497	2.5%	93.2%
0.5	f-IPWCC	0.624	0.0508	0.0509	4.1%	93.9%
	f-IPWCC-ext	0.624	0.0502	0.0510	2.9%	94.0%
	f-AIPW	0.623	0.0499	0.0497	2.2%	94.1%
	f-AIPW-ext	0.623	0.0497	0.0497	1.9%	93.9%
	full	0.431	0.0480	0.0492	–	94.9%
	CC	0.465	0.0542	0.0547	12.9%	89.9%
1.5	f-IPWCC	0.433	0.0543	0.0583	13.1%	95.9%
	f-IPWCC-ext	0.432	0.0521	0.0587	8.5%	96.9%
	f-AIPW	0.431	0.0506	0.0529	5.4%	96.0%
	f-AIPW-ext	0.431	0.0509	0.0531	5.9%	95.9%
	full	0.360	0.0462	0.0476	–	95.9%
	CC	0.404	0.0548	0.0563	18.7%	88.7%
2.5	f-IPWCC	0.364	0.0520	0.0607	12.5%	97.3%
	f-IPWCC-ext	0.364	0.0513	0.0612	11.1%	97.3%
	f-AIPW	0.360	0.0488	0.0523	5.7%	96.1%
	f-AIPW-ext	0.361	0.0491	0.0525	6.2%	95.9%
	full	0.320	0.0450	0.0466	–	95.4%
	CC	0.366	0.0578	0.0582	28.6%	89.0%
3.5	f-IPWCC	0.327	0.0547	0.0616	21.6%	97.0%
	f-IPWCC-ext	0.328	0.0525	0.0618	16.7%	97.0%
	f-AIPW	0.321	0.0493	0.0520	9.7%	96.6%
	f-AIPW-ext	0.323	0.0491	0.0520	9.2%	96.7%
	full	0.293	0.0484	0.0481	–	95.5%
	CC	0.340	0.0667	0.0631	37.9%	85.8%
4.5	f-IPWCC	0.303	0.0614	0.0650	26.9%	95.4%
	f-IPWCC-ext	0.307	0.0577	0.0646	19.3%	96.1%
	f-AIPW	0.294	0.0552	0.0546	14.1%	95.4%
	f-AIPW-ext	0.295	0.0549	0.0546	13.5%	95.0%

The results of this simulation study are in accordance with what the theory suggests. The complete case estimator is inconsistent, since withdrawal depends on X, but is treated as independent by the complete case estimator, i.e. the true density that generated the data is not contained within 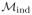. The bias is greater at later values of t. We would expect all other estimators to be consistent, since the true density is contained within 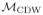∩ , and the results given in Table 1 are in accordance with this, with some small sample bias for the IPWCC estimators at larger values of t. Even the small sample bias is very small for the AIPW estimators.

As we would expect with quite a high (34%) percentage of withdrawal, there is a loss of efficiency due to incomplete information, as high as 30–40% for the CC and f-IPWCC estimators at t = 4.5 years. There are modest efficiency gains from using the extended coarsening model, with between 1 and 8% of the efficiency losses recovered. Substantially more (over a half) of the efficiency losses are recovered by using the augmented estimators, with both estimators performing similarly. We note that these efficiency gains were seen, even though the cause-specific model (CSM) was incorrectly specified; furthermore, both AIPW estimators perform similarly, suggesting little efficiency gain in this instance from including death in the coarsening model, since the augmentation is providing this increased efficiency, even with a misspecified CSM.

All variance estimators, including that for the AIPW estimators proposed in section 5.5, perform well, and lead to close to 95% coverage of the confidence intervals, except in the case of the CC estimator, where the bias is responsible for under-coverage. For the weighted estimators, the variance estimators are slightly conservative, leading to slight over-coverage; this is in accordance with the theory stating that ignoring the estimation of the weights leads to conservative inferences.

Further simulation studies, with alternative withdrawal mechanisms, and a time-dependent covariate, are included in the Appendix. The code used for all simulation studies, including that for implementing the AIPW estimator, is available from the corresponding author upon request.

7 Discussion

In this paper, we have used the powerful semiparametric theory of augmented inverse probability weighted estimating equations to show how partial information on components of a composite endpoint can be incorporated into the estimation of the time to composite endpoint in a principled way, when other components of the composite endpoint are not observed due to withdrawal.

In this setting, standard approaches would typically ignore the additional post-withdrawal information and assume withdrawal either to be independent or covariate-driven; if the latter, then some further modelling would be required, e.g. a model for the hazard of withdrawal conditional on covariates. One appeal of our approach is that, although further models are required (for the cause-specific hazard of the incompletely-observed event, and for the evolution of the time-updated covariate process, if this is to be modelled), the consistency of our estimator does not rely on having correctly specified these models. Efficiency gains are guaranteed if the additional models are correctly specified, and typically will be seen even if this is not the case.

Although the approach can deal in theory with time-updated covariates, in practice incorporating these into the cause-specific model for the incompletely-observed event will be problematic, since further models are required, along with the calculation of a typically intractable integral. A pragmatic solution would be to omit time-updated covariates from the cause-specific model, but further work is required to understand the sacrifice involved in doing so.

The theoretical properties of the proposed approach were demonstrated in a simulation study, where the AIPW estimator was seen to recover up to 50% of the efficiency lost through withdrawal in the standard approaches.

Future work will involve extending this approach to allow the comparison of the distributions of time to composite endpoint in two independent groups, via a log-rank test.

Appendix

A cautionary note on the bias-reduction properties of including death in the model for withdrawal

On page 13, it was suggested that including the fully-observed death information (Γ, D_i) in the model for withdrawal can reduce (but not eliminate) bias when the covariate-driven withdrawal (CDW) assumption is violated, even if the covariate-and-death-driven withdrawal (CDDW) assumption is also violated. We now elaborate on this argument, explaining why it will not always be the case, and that including the death information could increase bias in some settings.

A graphical representation [8] is used. Let T_MI represent the (possibly latent, due to death) time to MI. Bias due to withdrawal will occur when W and T_MI are correlated. We allow the times to the two events to be potentially correlated due to an effect of MI on mortality, and also due to unmeasured common causes (Z) of both. Under covariate-driven withdrawal, it is assumed that the set-up is as follows:

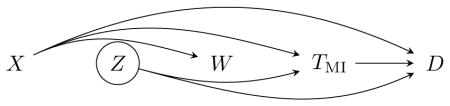
It is easily seen in this case that W and T_MI are conditionally independent given X, which is the motivation for including X in the model for withdrawal.

Furthermore, in the (highly artificial) setting in which the death time ‘causes’ withdrawal, then W and T_MI are conditionally independent given X and D (this is covariate-and-death-driven withdrawal):

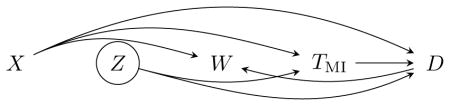
When CDW does not hold, a far more plausible alternative to CDDW is a setting such as this:

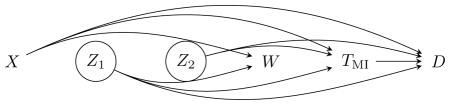
Z₁ are unmeasured common causes of withdrawal, death and MI, and Z₂ are unmeasured common causes of death and MI, independent of withdrawal. The problematic path is W ← Z₁ → T_MI since this leads to a residual association between W and T_MI even after conditioning on X. The motivation given on page 13 for conditioning on D in this setting is that D is also affected by Z₁ and thus acts as a proxy for Z₁, thereby reducing some of the bias due to this residual association. However, in the presence of Z₂, D is a collider on the path W ← Z₁ → D ← Z₂ → T_MI, and so conditioning on the death information, opens up this path, creating an additional source of conditional association between W and T_MI. As argued by Vansteelandt et al [11], longer induced paths tend to lead to weaker associations than shorter paths, and so, in practice, we would expect including the death information to be beneficial for bias reduction in many settings. One could easily construct counter-examples, however, in which the bias created by conditioning on the death information outweighs the reduction in bias achieved by using D as a proxy for Z₁.

Evaluating the conditional expectation that gives h_opt

The first technical omission from the main manuscript was the evaluation of

$$h_{\text{opt}}\{u,G_u({\mathcal{F}}_i)\}=E\{{dN}_i^{\ast }(t)-d\mathit{\Lambda }(t)Y_i^{\ast }(t)\mid G_u({\mathcal{F}}_i)\}.$$

First we write

$${dN}_i^{\ast }(t)={dN}_i^{\ast }(t,1)+{dN}_i^{\ast }(t,2),$$

where $N_i^{\ast }(t,1)$ and $N_i^{\ast }(t,2)$ are the separate counting processes for death and MI, respectively.

We now show how the expression given in (31) in the main manuscript is derived by evaluating $E\{{dN}_i^{\ast }(t,1)\mid G_u({\mathcal{F}}_i)\},E\{{dN}_i^{\ast }(t,2)\mid G_u({\mathcal{F}}_i)\}$ and $E\{Y_i^{\ast }(t)\mid G_u({\mathcal{F}}_i)\}$, separately.

Starting with ${dN}_i^{\ast }(t,1)$, this takes the value 1 if and only if there is a death at time t, no censoring before t, no event of any kind before u (this is all information available to us in G_u( 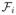)), and finally, there should be no MI between u and t; this is not known to us in G_u( 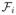) and so its probability given G_u( 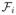) must be calculated. Given no death or censoring before t (and hence u), H {u, X̄_i(u), D_i, Γ_i} is the conditional probability of no MI either by time u, given X̄_i(u), D_i, Γ_i and H {t, X̄_i(u), D_i, Γ_i} is the conditional probability of no MI by time t, given X̄_i(u), D_i, Γ_i. Thus given no death or censoring before t, and no MI before u, the conditional probability of no MI by time t, given X̄_i(u), D_i, Γ_i is

$$\frac{H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}.$$

This leads to the following expression:

$$E\{{dN}_i^{\ast }(t,1)\mid G_u({\mathcal{F}}_i)\}=I(D_i=t)I(C_i>t)I(U_i^{\ast }>u)\frac{H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}.$$ (43)

Similarly, ${dN}_i^{\ast }(t,2)$ takes the value 1 if and only if there is an MI at time t, no censoring before t, no event of any kind before u and either (a) no death observed (so censoring occurs before death) or (b) a death observed, but after t. Only the first piece of information (MI at time t) is not contained in G_u( 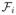) and hence its probability given G_u( ) is calculated. This leads to the following expression:

$$E\{{dN}_i^{\ast }(t,2)\mid G_u({\mathcal{F}}_i)\}=I(C_i>t)I(U_i^{\ast }>u)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}\frac{dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}.$$ (44)

Finally, $Y_i^{\ast }(t)$ takes the value 1 if and only if there is no censoring before t, no event of any kind before u, and either (a) no death observed (so censoring occurs before death) or (b) a death observed, but after t (this is all information available to us in G_u( )), and finally, there should be no MI between u and t; this is not known to us in G_u( ) and so its probability given G_u( ) must be calculated. This leads to the following expression:

$$E\{Y_i^{\ast }(t)\mid G_u({\mathcal{F}}_i)\}=I(C_i>t)I(U_i^{\ast }>u)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}\frac{H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}.$$ (45)

Putting (43), (44) and (45) together leads directly to the expression given in (31) of the main manuscript, as required.

Evaluating the martingale integral to obtain (34)

The next omission from the main manuscript was to show that upon substituting the above into

$$\sum _{i=1}^n\left[\frac{{dN}_i(t)-d\mathit{\Lambda }(t)Y_i(t)}{K\{t,{\overline{\mathbf{X}}}_i(t)\}}+{\int }_0^t\frac{{dM}_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}h(u,G_u({\mathcal{F}}_i))\right]=0$$

we obtain the equation given in (34).

The key part is to evaluate

$${\int }_0^t\frac{{dM}_i(u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}h\{u,G_u({\mathcal{F}}_i)\}$$

where, roughly speaking, for Δu small,

$${dM}_i(u)=[I(u\le W_i<u+\mathit{\Delta }u)-\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}\mathit{\Delta }uI(W_i\ge u)]I(U_i^{\ast }\ge u).$$

We do this by evaluating each of the following expressions separately:

$${\int }_0^t\frac{I(W_i=u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{{dN}_i^{\ast }(u,1)\mid G_u({\mathcal{F}}_i)\},$$ (46)

$${\int }_0^t\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}I(W_i\ge u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{{dN}_i^{\ast }(u,1)\mid G_u({\mathcal{F}}_i)\},$$ (47)

$${\int }_0^t\frac{I(W_i=u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{{dN}_i^{\ast }(u,2)\mid G_u({\mathcal{F}}_i)\},$$ (48)

$${\int }_0^t\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}I(W_i\ge u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{{dN}_i^{\ast }(u,2)\mid G_u({\mathcal{F}}_i)\},$$ (49)

$${\int }_0^t\frac{I(W_i=u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{Y_i^{\ast }(u)\mid G_u({\mathcal{F}}_i)\}du$$ (50)

and

$${\int }_0^t\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}I(W_i\ge u)}{K\{u,{\overline{\mathbf{X}}}_i(u)\}}E\{Y_i^{\ast }(u)\mid G_u({\mathcal{F}}_i)\}du$$ (51)

where I(W_i = u) is used as shorthand for lim_Δu→0 I(u ≤ W_i < u + Δu).

First we note that the integrands in (46), (48) and (50) take a non-zero value only at u = W_i, and as such only if 0 < W_i ≤ t. For such a subject, U_i = W_i and hence (46), (48) and (50) can be re-written (using (43), (44) and (45) above) respectively as:

$$I(U_i\le t,{\mathit{\Delta }}_i=-1)I(D_i=t)I(C_i>t)\frac{H\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}{K\{U_i,{\overline{\mathbf{X}}}_i(U_i)\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}},$$ (52)

$$I(U_i\le t,{\mathit{\Delta }}_i=-1)I(C_i>t)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}·\frac{dH\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}{K\{U_i,{\overline{\mathbf{X}}}_i(U_i)\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}$$ (53)

and

$$I(U_i\le t,{\mathit{\Delta }}_i=-1)I(C_i>t)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}·\frac{H\{t,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}{K\{U_i,{\overline{\mathbf{X}}}_i(U_i)\}H\{U_i,{\overline{\mathbf{X}}}_i(U_i),D_i,{\mathit{\Gamma }}_i\}}.$$ (54)

In expressions (47), (49) and (51), note that the integrand includes I(W_i ≥ u) and also (from each conditional expectation term) $I(U_i^{\ast }\ge u)$. When multiplied together, these give I(U_i ≥ u), and hence the integrand can be nonzero only between 0 and U_i if U_i < t. Thus we can write the integral as being from 0 to min (t, U_i). This leads to the following simplifications of (47), (49) and (51) respectively:

$$I(D_i=t)I(C_i>t){\int }_0^{min(t,U_i)}\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{K\{u,{\overline{\mathbf{X}}}_i(u)\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}du,$$ (55)

$$I(C_i>t)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}·{\int }_0^{min(t,U_i)}\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}dH\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{K\{u,{\overline{\mathbf{X}}}_i(u)\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}du,$$ (56)

and

$$\begin{array}{l}I(C_i>t)\{I(C_i\le D_i)+I(C_i>D_i)I(D_i>t)\}.\\ {\int }_0^{min(t,U_i)}\frac{\lambda \{u,{\overline{\mathbf{X}}}_i(u)\}H\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}{K\{u,{\overline{\mathbf{X}}}_i(u)\}H\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i\}}du.\end{array}$$ (57)

Putting (52)–(57) together, and using the shorthands J_i(t) and $J_i^{\prime }(t)$ defined in the main manuscript, we obtain (34) as required.

More details on the variance estimator

We start by explicitly writing the feasible extended AIPW estimator of dΛ(t) (but analogous expressions for all other estimators could be used and a similar logic followed) as:

$$d{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ext}}(t)=\frac{{\sum }_{i=1}^n\left[\frac{{dN}_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(t)\right]}{{\sum }_{i=1}^n\left[\frac{Y_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{B}}_i(t)\right]}$$

where Â_i(t) and B̂_i(t) are as defined in equations (41) and (42) of the main manuscript.

Thus, subtracting dΛ(t) from both sides,

$$d{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ex}t}(t)-d\mathit{\Lambda }(t)=\frac{{\sum }_{i=1}^n\left[\frac{{dN}_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(t)-\frac{d\mathit{\Lambda }(t)Y_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}-d\mathit{\Lambda }(t){\widehat{B}}_i(t)\right]}{{\sum }_{i=1}^n\left[\frac{Y_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{B}}_i(t)\right]}.$$

Let

$$\mathit{\Phi }(t)=\underset{n\to \infty }{lim}{n}^{-1}\sum _{i=1}^n\left[\frac{Y_i(t)}{\stackrel{\sim }{K}\left\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}}+{\widehat{B}}_i(t)\right].$$

Then

$$n^{\frac{1}{2}}\left\{d{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ext}}(t)-d\mathit{\Lambda }(t)\right\}=\frac{n^{-\frac{1}{2}}{\sum }_{i=1}^n\left[\frac{{dN}_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(t)-\frac{d\mathit{\Lambda }(t)Y_i(t)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(t),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}-d\mathit{\Lambda }(t){\widehat{B}}_i(t)\right]}{\mathit{\Phi }(t)}+o_p(1)$$

which means that

$$n^{\frac{1}{2}}\left\{{\widehat{\mathit{\Lambda }}}^{\mathrm{f}-\text{AIPW}-\text{ext}}(t)-\mathit{\Lambda }(t)\right\}=n^{-\frac{1}{2}}\sum _{i=1}^n{\int }_0^t\frac{\left[\frac{{dN}_i(u)}{\stackrel{\sim }{K}\{t,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(u)-\frac{d\mathit{\Lambda }(u)Y_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}-d\mathit{\Lambda }(u){\widehat{B}}_i(u)\right]}{\mathit{\Phi }(u)}+o_p(1).$$

Thus the i^th influence function of Λ̂^f-AIPW-ext is

$${\int }_0^t\frac{\left[\frac{{dN}_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}+{\widehat{A}}_i(u)-\frac{d\mathit{\Lambda }(u)Y_i(u)}{\stackrel{\sim }{K}\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\}}-d\mathit{\Lambda }(u){\widehat{B}}_i(u)\right]}{\mathit{\Phi }(u)}.$$

Finally, replacing Φ(u) by its estimator,

$$\widehat{\mathit{\Phi }}(u)=n^{-1}\sum _{i=1}^n\left[\frac{Y_i(u)}{\stackrel{\sim }{K}\left\{u,{\overline{\mathbf{X}}}_i(u),D_i,{\mathit{\Gamma }}_i;\widehat{\stackrel{\sim }{\gamma }}\right\}}+{\widehat{B}}_i(u)\right],$$

and dΛ(u) by its estimator, dΛ̂^f-AIPW-ext(u), we obtain the estimated i^th influence function, and the sample variance of these n estimated influence functions becomes our estimator of the variance of Λ̂^f-AIPW-ext(t), as stated in the main manuscript.

Additional simulation studies

We conducted three additional simulation studies, similar to that presented in the main manuscript, but exploring changes to a few key aspects. In the first two additional simulation studies, the set-up is exactly as before, except that withdrawal is simulated differently.

In the first set of additional simulations, withdrawal is simulated from an exponential distribution with hazard exp (−1.5 + X − Γ + 0.1Γ D), i.e. the hazard of withdrawal depends on both X and death, in such a way that the extended coarsening model (ECM), which is the same Cox PH model used in the simulations in the main manuscript, is correctly specified. In the second set of additional simulations, this hazard of withdrawal is instead $exp\left(-1.5+X+0.2\sqrt{\mathit{\Gamma }D}\right)$ so that the ECM is incorrectly specified.

Finally, in the third set of additional simulations, X is instead a time-dependent covariate, measured at baseline, and again at 2 years after recruitment, if the subject is still in the study. X(0) is simulated in the same way as X in the previous simulation studies, and X(2) is simulated as a Bernoulli random variable with mean 0.3 + 0.4X(0). The endpoints and withdrawal are all simulated as in the original simulation study, except that, if an endpoint and/or withdrawal have not occurred before 2 years, the further time to endpoint and withdrawal, respectively, are simulated from the same distributions as originally used, but with X(2) used in place of X(0). In other words, the distributions all remain the same, except that rather than depending on the baseline value of X, they depend on the most recently observed value, X(0) during the first two years, and X(2) thereafter. In the analyses of these simulated dataset, a time-updated Cox model with X(t) as the only covariate is used for the coarsening model (and this is correctly specified) and a time-updated Cox model with X(t) and Γ and Γ D is used for the extended coarsening model (which is again correctly specified, but more elaborate than necessary). Only the baseline value X(0) is used in the cause-specific model for MI, in accordance with the suggestion made on page 18 of the main manuscript.

The same six estimators of the survivor distribution are compared as previously, with the results shown in Tables 2–4, using the same format as in the main manuscript.

Table 2.

The results of the first set of additional simulations

Years	Estimator of survivor function	Mean	Standard Error		% increase in actual SE compared with full data	Coverage of 95% CI
			Actual	Estimated
	full	0.622	0.0479	0.0481	–	93.7%
	CC	0.622	0.0494	0.0492	3.1%	95.1%
	f-IPWCC	0.621	0.0493	0.0494	2.9%	95.1%
	f-IPWCC-ext	0.622	0.0489	0.0493	2.2%	94.6%
	f-AIPW	0.621	0.0484	0.0488	1.1%	94.9%
	f-AIPW-ext	0.622	0.0484	0.0488	1.0%	94.5%
	full	0.431	0.0479	0.0492	–	94.9%
	CC	0.432	0.0514	0.0526	7.2%	94.9%
	f-IPWCC	0.426	0.0505	0.0531	5.4%	95.9%
	f-IPWCC-ext	0.431	0.0495	0.0529	3.3%	96.1%
	f-AIPW	0.430	0.0489	0.0509	1.9%	95.7%
	f-AIPW-ext	0.431	0.0491	0.0509	2.4%	95.6%
	full	0.361	0.0464	0.0477	–	96.0%
	CC	0.359	0.0506	0.0531	8.9%	96.6%
	f-IPWCC	0.352	0.0487	0.0537	4.9%	96.8%
	f-IPWCC-ext	0.361	0.0481	0.0535	3.5%	97.2%
	f-AIPW	0.359	0.0474	0.0504	2.0%	96.1%
	f-AIPW-ext	0.360	0.0477	0.0504	2.8%	96.3%
	full	0.320	0.0452	0.0466	–	95.6%
	CC	0.315	0.0524	0.0542	15.7%	94.8%
	f-IPWCC	0.308	0.0505	0.0546	11.6%	95.0%
	f-IPWCC-ext	0.322	0.0496	0.0541	9.5%	97.0%
	f-AIPW	0.320	0.0481	0.0503	6.3%	96.0%
	f-AIPW-ext	0.321	0.0489	0.0504	8.0%	95.8%
	full	0.293	0.0487	0.0481	–	94.9%
	CC	0.285	0.0601	0.0587	23.4%	93.7%
	f-IPWCC	0.279	0.0580	0.0589	19.1%	94.3%
	f-IPWCC-ext	0.299	0.0556	0.0574	14.2%	96.7%
	f-AIPW	0.294	0.0531	0.0527	9.0%	95.6%
	f-AIPW-ext	0.294	0.0545	0.0532	12.0%	95.5%

Table 4.

The results of the third set of additional simulations

Years	Estimator of survivor function	Mean	Standard Error		% increase in actual SE compared with full data	Coverage of 95% CI
			Actual	Estimated
	full	0.623	0.0479	0.0481	–	94.3%
	CC	0.632	0.0491	0.0497	2.5%	93.6%
	f-IPWCC	0.623	0.0500	0.0510	4.3%	94.9%
	f-IPWCC-ext	0.624	0.0499	0.0509	4.2%	94.8%
	f-AIPW	0.622	0.0487	0.0498	1.6%	95.2%
	f-AIPW-ext	0.622	0.0487	0.0498	1.6%	95.1%
	full	0.433	0.0492	0.0492	–	95.1%
	CC	0.467	0.0541	0.0546	9.9%	91.6%
	f-IPWCC	0.436	0.0539	0.0582	9.5%	96.6%
	f-IPWCC-ext	0.437	0.0550	0.0582	11.7%	95.8%
	f-AIPW	0.433	0.0513	0.0528	4.2%	95.4%
	f-AIPW-ext	0.434	0.0512	0.0528	4.0%	95.4%
	full	0.280	0.0430	0.0445	–	96.7%
	CC	0.314	0.0559	0.0566	30.1%	90.2%
	f-IPWCC	0.283	0.0528	0.0576	22.8%	96.0%
	f-IPWCC-ext	0.285	0.0553	0.0577	28.7%	95.1%
	f-AIPW	0.279	0.0484	0.0520	12.7%	96.0%
	f-AIPW-ext	0.280	0.0482	0.0522	12.3%	96.2%
	full	0.217	0.0396	0.0412	–	95.1%
	CC	0.255	0.0576	0.0569	45.6%	91.0%
	f-IPWCC	0.224	0.0529	0.0569	33.7%	95.8%
	f-IPWCC-ext	0.226	0.0550	0.0569	38.8%	94.0%
	f-AIPW	0.216	0.0462	0.0485	16.7%	95.9%
	f-AIPW-ext	0.217	0.0460	0.0487	16.1%	96.1%
	full	0.189	0.0401	0.0419	–	96.0%
	CC	0.229	0.0622	0.0603	54.9%	88.4%
	f-IPWCC	0.199	0.0561	0.0590	39.9%	94.9%
	f-IPWCC-ext	0.201	0.0577	0.0591	43.7%	94.3%
	f-AIPW	0.186	0.0495	0.0502	23.3%	95.7%
	f-AIPW-ext	0.187	0.0498	0.0507	24.1%	96.4%

The relative performance of the estimators as demonstrated in these additional simulation studies is similar to what was seen in the simulation study in the main manuscript. In addition, we note that in Tables 2 and 3 (the first two of the additional scenarios), the f-IPWCC estimator is biased, as well as the CC estimator. This is because the coarsening model (without death) is incorrectly specified. The f-AIPW estimator does not appear to suffer from the same bias, suggesting that the double robustness property (despite both models being wrong in this instance) leads to reduced bias here. A similar pattern is seen for f-IPWCC, f-IPWCC-ext, f-AIPW and f-AIPW-ext in Table 3, although some bias is still seen for all estimators, since the ECM is no longer correctly specified. Finally, substantial efficiency gains are seen from using AIPW even in the final scenario with time-updated covariates, when only the baseline measurement of the covariate was included in the cause-specific model.

Table 3.

The results of the second set of additional simulations

Years	Estimator of survivor function	Mean	Standard Error		% increase in actual SE compared with full data	Coverage of 95% CI
			Actual	Estimated
	full	0.623	0.0490	0.0481	–	94.4%
	CC	0.634	0.0504	0.0499	2.8%	93.2%
	f-IPWCC	0.621	0.0515	0.0517	4.9%	94.5%
	f-IPWCC-ext	0.623	0.0505	0.0515	3.1%	94.3%
	f-AIPW	0.622	0.0503	0.0502	2.5%	94.3%
	f-AIPW-ext	0.623	0.0501	0.0501	2.2%	94.4%
	full	0.431	0.0485	0.0492	–	94.4%
	CC	0.475	0.0565	0.0552	16.6%	86.7%
	f-IPWCC	0.433	0.0566	0.0605	16.8%	96.2%
	f-IPWCC-ext	0.433	0.0549	0.0611	13.4%	97.1%
	f-AIPW	0.432	0.0508	0.0537	4.8%	95.9%
	f-AIPW-ext	0.431	0.0516	0.0542	6.5%	95.7%
	full	0.360	0.0474	0.0476	–	95.4%
	CC	0.420	0.0578	0.0572	22.0%	80.5%
	f-IPWCC	0.371	0.0548	0.0631	15.5%	96.8%
	f-IPWCC-ext	0.368	0.0545	0.0645	14.9%	98.0%
	f-AIPW	0.364	0.0500	0.0528	5.4%	95.4%
	f-AIPW-ext	0.363	0.0511	0.0534	7.6%	95.4%
	full	0.319	0.0455	0.0465	–	95.2%
	CC	0.386	0.0597	0.0593	31.2%	78.9%
	f-IPWCC	0.340	0.0560	0.0636	23.1%	95.7%
	f-IPWCC-ext	0.335	0.0551	0.0653	21.2%	96.8%
	f-AIPW	0.323	0.0502	0.0525	10.5%	95.7%
	f-AIPW-ext	0.324	0.0504	0.0528	10.9%	95.6%
	full	0.292	0.0483	0.0482	–	95.2%
	CC	0.364	0.0674	0.0639	39.6%	74.4%
	f-IPWCC	0.321	0.0617	0.0664	27.7%	93.1%
	f-IPWCC-ext	0.315	0.0604	0.0682	25.1%	94.8%
	f-AIPW	0.294	0.0559	0.0558	15.8%	94.7%
	f-AIPW-ext	0.296	0.0549	0.0558	13.8%	94.7%