Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Mar 3;30(11):3041–3050. doi: 10.1021/la5002754

A Versatile Self-Assembly Strategy for the Synthesis of Shape-Selected Colloidal Noble Metal Nanoparticle Heterodimers

Tina A Gschneidtner †, Yuri A Diaz Fernandez †, Svetlana Syrenova ‡, Fredrik Westerlund †, Christoph Langhammer ‡,*, Kasper Moth-Poulsen †,*
PMCID: PMC3982509  PMID: 24580549

Abstract

graphic file with name la-2014-002754_0010.jpg

The self-assembly of individual nanoparticles into dimers—so-called heterodimers—is relevant for a broad range of applications, in particular in the vibrant field of nanoplasmonics and nanooptics. In this paper we report the synthesis and characterization of material- and shape-selected nanoparticle heterodimers assembled from individual particles via electrostatic interaction. The versatility of the synthetic strategy is shown by assembling combinations of metal particles of different shapes, sizes, and metal compositions like a gold sphere (90 nm) with either a gold cube (35 nm), gold rhombic dodecahedron (50 nm), palladium truncated cube (120 nm), palladium rhombic dodecahedron (110 nm), palladium octahedron (130 nm), or palladium cubes (25 and 70 nm) as well as a silver sphere (90 nm) with palladium cubes (25 and 70 nm). The obtained heterodimer combinations are characterized by transmission electron microscopy (TEM), scanning electron microscopy (SEM), scanning transmission electron microscopy–energy dispersive X-ray spectroscopy (STEM-EDX), dynamic light scattering (DLS), and zeta-potential measurements. We describe the optimal experimental conditions to achieve the highest yield of heterodimers compared to other aggregates. The experimental results have been rationalized using theoretical modeling. A proof-of-principle experiment where individual Au–Pd heterodimers are exploited for indirect plasmonic sensing of hydrogen finally illustrates the potential of these structures to probe catalytic processes at the single particle level.

1. Introduction

Since the pioneering work of Faraday1 in the 19th century, the optical properties of noble metal nanoparticles (NPs) have been extensively studied both theoretically and experimentally.2−4 Phenomena like strong absorption and intense light-scattering produced by these particles are well understood and have found many applications.2,5,6 Silver (Ag) and gold (Au) NPs show localized surface plasmon resonance (LSPR) in the UV–vis7 or the near-IR regions8 of the electromagnetic spectrum that depends on their size and shape. The plasmonic electron oscillation can be localized on single particles or distributed over several NPs in close vicinity to each other through interparticle coupling of the individual particle plasmonic modes. The collective plasmonic properties of NP assemblies can be synergistic, and they are strongly dependent on the distance between the NPs, on the chemical composition of the NPs, and of the surrounding medium.9−11 Moreover, plasmonic metal NPs have found a wide range of applications, ranging from single molecule electronic devices,12,13 drug delivery,14 and photodynamic therapy systems.15

By combining two different materials or different particle shapes of the same material within the same single nanostructure, as in focus here, new properties of the coupled system can be obtained16 and new applications emerge.17−20 For example, one can envision sensing of a catalytic process by using the plasmonic unit as a probe for a reaction on the adjacent catalyst particle at the individual catalyst particle level.21−23

In the field of indirect sensing applications for materials science and catalysis, it has been shown that ensembles of AuNPs can be used to probe catalytic processes and other kinds of phenomena like phase transitions, hydrogen absorption, or nanoparticle sintering taking place in/on adjacent functional particles of different material.24 The process of interest in/on the functional particles affects the plasmon resonance of the Au “sensor” NP and can thus be investigated by monitoring specific changes in the plasmon peak and produce a quantitative response.11,23,25

One potential route to produce such nanoparticle arrangements is by self-assembly of the components. The mechanisms driving the self-assembly of nanoparticles have been extensively studied.26−29 Theoretical formulations rely on the effect of the pairwise interaction energy on the self-diffusion of the colloidal particles, and therefore considerable efforts have been devoted to the understanding of the interactions involved in this process.30−33 Exploiting the balance between repulsive and attractive interactions in colloidal systems, it has been possible to control the self-assembly of NPs into discrete structures.33,34 In this context, the assembly of NP homodimers, that is dimeric structures of the same metal, and their optical properties have been studied before.35,36 Examples in which NPs in solution were selectively assembled have been presented by Mirkin et al.19 and Alivisatos et al.37 using DNA as linker molecules. Enrichment of the dimer population have been achieved by different methods.38,39

The situation for the assembly of heterodimer structures is very different. While a plethora of methods for synthesis of NPs of different sizes, shapes, and materials exist,40−43 just a few methods for controlled assembly of NPs into well-defined heteroaggregates have been established.44−46 Specifically, the selective formation of heterodimers from NPs of different materials remains a challenging goal. Chen et al.47 synthesized bimetallic NPs by using nanoscopic phase separation of different metals due to the embedment of surface ligands. Pietryga et al.48 described the synthesis of quantum dot–dielectric–metal hybrids where a silicon shell on top of the gold nanostructure was used to attach quantum dots. An alternative method lies in the use of bimetallic nanocrystals by means of seed-grow processes to obtain heterogeneous NPs. Following this approach, Xia et al.49 described the overgrowing of Au structures on presynthesized Pd cubes. Zhang et al.50 reported the synthesis of au-nanorods on Ag and CdSe seeds, while Lombardi et al.10 demonstrated direct self-assembly of heterodimers formed by Au and Ag@SiO2 NPs, highlighting the relevance of this method to investigate single NP spectroscopic properties. The self-assembly methods currently available for bottom-up building of NP heterodimers are quite specific and require advanced experimental approaches. A general and simple method to address this challenge has been missing in the literature, probably due to the very delicate balance of interactions involved in the self-assembly process that cannot be easily adapted from system to system.

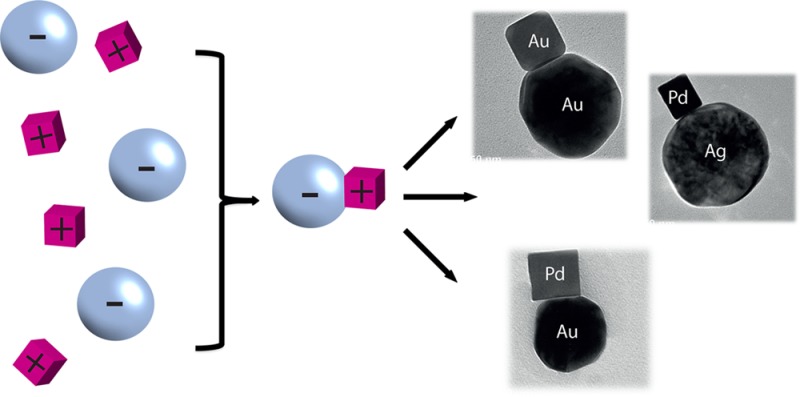
In the present work, we have developed a versatile synthetic strategy for combining two different metal NPs (of the same metal or two different metals) via electrostatic interaction. By using oppositely charged particles, heterodimer combinations of individual NPs of different sizes, shapes, and compositions, as exemplified in Figure 1, were obtained. The aggregation process can be controlled to produce the highest possible yield of dimers by tuning the ratio between the two kinds of NP components. The experimental results are rationalized with the aid of theoretical calculations. The basic function of our system as an indirect plasmonic sensor for catalytic processes occurring on a single NP is illustrated in a proof-of-principle experiment. The reversible catalytic uptake of hydrogen in a palladium NP is sensed by a neighboring Au-NP by observing a change in its plasmonic peak.

Figure 1.

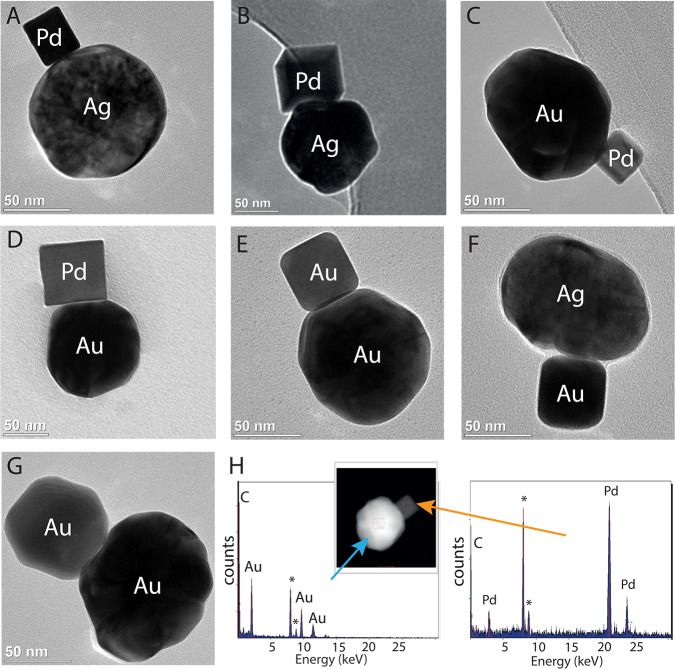
Figure 1

Open in a new tab

TEM images of different NP heterodimers prepared by electrostatic self-assembly: (A) Ag (spherical90 nm) and Pd (cube25 nm); (B) Ag (spherical90 nm) and Pd (cube70 nm); (C) Au (spherical90 nm) and Pd (cube25 nm); (D) Au (spherical90 nm) and Pd (cube70 nm); (E) Au (spherical90 nm) and Au (cube35 nm); (F) Ag (spherical90 nm) and Au (cube35 nm); (G) Au (spherical90 nm) and Au (rhombic octahedron50 nm); (H) EDX-STEM elemental analysis of dimer Au (spherical90 nm)–Pd (cube25 nm). The peaks of Cu, arising from the TEM grid, are marked with an asterisk.

2. Results and Discussion

2.1. Electrostatic Self-Assembly of NPs Heterodimers

The synthesis strategy of material- and shape-selected NP heterodimers developed in this work exploits the electrostatic interactions between oppositely charged NPs (Scheme 1). Starting from two classes of NPs, here called NP-A (negatively charged) and NP-B (positively charged), controlled aggregation can be achieved by tuning the experimental conditions.

Scheme 1. Synthetic Procedure Used To Prepare NPs Heterodimers via Electrostatic Interactions.

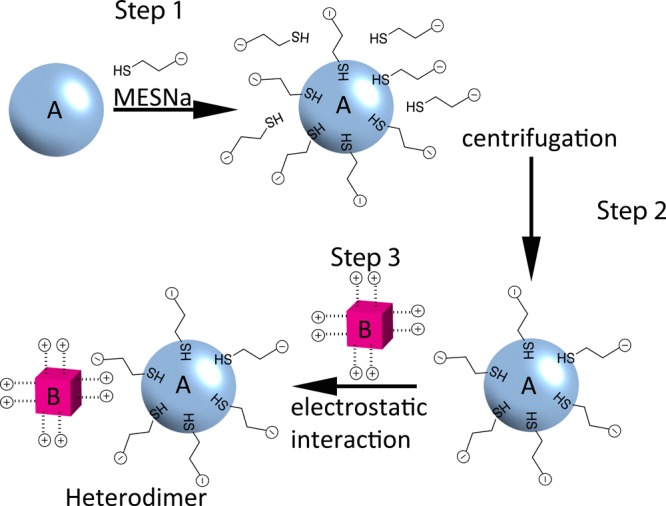
Scheme 1

Open in a new tab

Step 1: functionalization of NP-A with sodium 2-mercaptoethanesulfonate (MESNa) through ligand exchange. Step 2: purification of functionalized NP-A from excess of coating agent by centrifugation. Step 3: controlled self-assembly of NP-A and NP-B through electrostatic interactions. NP-B were synthesized according to procedures published before.40,41,51

Class NP-A constitutes negatively charged NPs capped by sodium 2-mercaptoethanesulfonate (MESNa) in trisodium citrate. Noble metal particles can be synthesized with citrate as the capping agent in high yields and with narrow size distributions. For this reason extended libraries of Ag and Au colloidal solutions stabilized by citrate, with average sizes varying from tens to hundreds of nanometers, are commercially available. The citrate ligand is very labile and therefore suitable for ligand exchange with stronger ligands (e.g., thiols, here MESNa). We chose commercially available spherical Ag and Au NPs stabilized by citrate, with average size 90 nm as the starting material for class NP-A. The stabilizing citrate layer was substituted through an exchange reaction with MESNa. The excess of thiol capping agent and residual citrate was removed by centrifugation and redispersion of the colloids in deionized water. The residual concentration of citrate in the final NP-A solution was between 30 and 45 μM, while the concentration of MESNa was 3 μM and therefore is negligible (details on the experimental procedures leading to these final concentrations are presented in Supporting Information SI1).

The second class, NP-B, is composed by NPs capped with a cationic surfactant. We used well-established protocols for the synthesis of NPs coated by cetyltrimethylammonium bromide (CTAB) or chloride (CTAC).40,41,51 These synthetic procedures lead to NPs with well-defined shapes, surface crystallographic facets, and narrow size distributions in high yields. The excess of surfactant can be removed by several centrifugation–redispersion cycles, but a minimum concentration of surfactant is needed to achieve stability of NP-Bs.52

The surface charge and the hydrodynamic radii of the nanoparticles were evaluated by zeta-potential and dynamic light-scattering (DLS) measurements. The data obtained confirm that under our experimental conditions the class NP-As are negatively charged, while NP-Bs present a positive surface charge due to the stabilization with cationic surfactants (Table 1).

Table 1. Summary of the Effective Hydrodynamic Radii (R) for All NPs and Their Corresponding Zeta-Potential Values.

NP R (nm) zeta-potential (mV) NP R (nm) zeta-potential (mV)
Au 46 –44.3 (1) Pd(octahedron) 63 56.6 (1.5)
Ag 45 –42.1 (1) Pd(rhom.dodeca) 55 41.2 (2)
Pd(cube small) 13 66.7 (1.5) Au(rhombic) 25 36.6 (1)
Pd(cube big) 35 50.4 (1.5) Au(cube) 18 47.1 (1.5)
Pd(truncated cube) 60 58.7 (1)      
Open in a new tab

The controlled electrostatic self-assembly of NP heterodimers can occur only under experimental conditions that guarantee the mutual stability of the two kinds of NPs used. We have observed that the presence of cationic surfactants destabilizes the negatively charged NP-A. Similarly, positively charged NP-Bs are destabilized by citrate, which is negatively charged. For this reason, in a wide range of capping agent concentrations, each type of NP is incompatible with the capping agent of the other type. We have explored the phase diagram of the NPs to find the conditions that allow mutual stability of the oppositely charged NPs (further discussion below, section 2.2). Under these “stability zone” experimental conditions, we have performed self-assembly experiments leading to the preferential formation of heteroaggregates.

In order to facilitate the differentiation (in TEM and SEM) between heterodimers and self-aggregates, we combined NP-A and NP-B with distinctly different shapes and sizes. Representative examples of these combinations are Ag sphere (90 nm) with Pd cubes (25 and 70 nm), Ag sphere (90 nm) with Au cube (50 nm); Au sphere (90 nm) with Pd cubes (25 and 70 nm); Au sphere (90 nm) with Au cube (35 nm) and Au rhombic octahedron (50 nm) (Figure 1A–G, additional representative micrographs are presented in SI3). Furthermore, EDX analysis by STEM was carried out to evaluate the chemical composition of the heterodimeric structures (Figure 1H, SI2). For all the combinations of NP-A and NP-B investigated, EDX in STEM characterization confirmed that the heteroaggregates were formed by NPs of different metals, as expected from the analysis of TEM and SEM micrographs. The average gap between the NPs in the heterodimers was found to be between 0.8 and 1.9 nm, suggesting that these structures can be used in sensing and plasmonic applications (see SI8, Figure 1; details on the determination of interparticle distances are presented in SI1). The maximum yields of heterodimers were ranging from 30% to 40% for the combinations of NPs investigated (experimental details in SI1 and representative data are presented as SI4).

To further demonstrate the versatility of our method, we assembled heterodimers consisting of PdNPs of different shapes linked to Au spheres. For this purpose we prepared three types of palladium particles stabilized by CTAB having different morphologies that correspond to specific crystallographic surface facets (truncated cubes, rhombic dodecahedron, octahedron), as described by Xu et al.41 The self-assembly of these particles with Au spheres (NP-A) into heterodimers was successful with yields of about 30%. In high-magnification SEM images the three-dimensional features of the Pd surfaces can clearly be observed (Figure 2).

Figure 2.

Figure 2

Open in a new tab

High-magnification SEM image of NP heterodimers formed by self-assembly of Au spheres90 nm and PdNPs: (a) octahedron130 nm, (b) truncated cube120 nm, (c) rhombic dodecahedron110 nm. The insets schemes show the surface crystallographic facets for each Pd structure: purple (111), blue (110), and green (100).

2.2. Origin of Mutual Stability of Oppositely Charged NPs

In order to rationalize the conditions that lead to controlled self-assembly of NP-A and NP-B, we have investigated the nature of the interactions involved in the aggregation process. According to the extended Derjaguin–Verway–Landau–Overbeek theory (DVLO), the interaction energy between two nanoparticles A and B can be divided into three contributions:26,53

2.2. 1

The last term in eq 1 (VsolvAB) is the solvation repulsion potential, describing a short-range repulsive interaction that depends on the properties of the solvent. This interaction, even at very short interparticle distances, is of the same order of magnitude as the thermal energy and decays very fast as the interparticle distance increases. The second term (VVdW) accounts for the contribution of van der Waals and London attraction forces to the interaction energy. This contribution can be neglected for long distances but becomes significant as the interparticle distance decreases, reaching more than 10 kBT. The first term in eq 1 ( VelecAB) is related to electrostatic interactions between the electric double layers of the NPs and depends on the electric surface potential of the NPs (i.e., the zeta-potential).53 This contribution determines the limiting behavior of the interaction energy for large interparticle distances, and the sign depends on the surface charges of the particles. In the case of particles with the same charge, this interaction is repulsive (Velec > 0) and creates an energy barrier for aggregation, while for particles oppositely charged, the electrostatic contribution is attractive (VelecAB < 0). A detailed description of the analytical expressions describing these interactions can be found in SI7.

The zeta-potential values (Table 2) give a good estimation of the surface potentials of the NPs.53 We determined the zeta-potential of class NP-A (negatively charged NPs) in the presence of different concentrations of CTAB and CTAC, within the range used in the self-assembly experiments (SI5-A). The data suggest that the absolute value of the surface electric potential of NP-A is reduced in the presence of cationic surfactant molecules, leading to destabilization of the colloidal solution if the concentration of surfactant is sufficiently high. Similarly, the zeta-potential for NP-B is decreased by addition of citrate ions (SI5-B). Combining these two results, we can infer that the appropriate ratio between the particle stabilizers, CTAB/CTAC and citrate, leads to conditions in which both kinds of NPs are stable.

Table 2. Zeta-Potential of NP-A and NP-B after Addition of CTAB/CTAC to NP-A or Citrate to NP-B in the Concentrations Used for the Self-Assembly Experiments.

  zeta-potential (mV)
heterodimer NP-A–NP-B NP-Aa NP-Bb
Au–Pd(cube small) –18.6 (1) 20.6 (1.5)
Au–Pd(cube big) –15.1 (2) 20.3 (1.5)
Au–Pd(truncated cube) –13.0 (2) 24 (2)
Au–Pd(octahedron) –13.0 (2) 21 (1)
Au–Pd(rhom.dodeca.) –13.0 (2) 36.3 (2)
Au–Au(rhombic) –8.4 (1) 30 (1)
Au–Au(cube) –8.4 (1) 30 (1)
Ag–Pd(cube small) –18.3 (2) 18.8 (2)
Ag–Pd(cube big) –12.4 (2) 19.5 (2)
Ag–Au(cube) –5.4 (1) 28.5 (1)
Open in a new tab
a

After adding CTAB/CTAC as in self-assembly experiments.

b

After adding citrate as in self-assembly experiments.

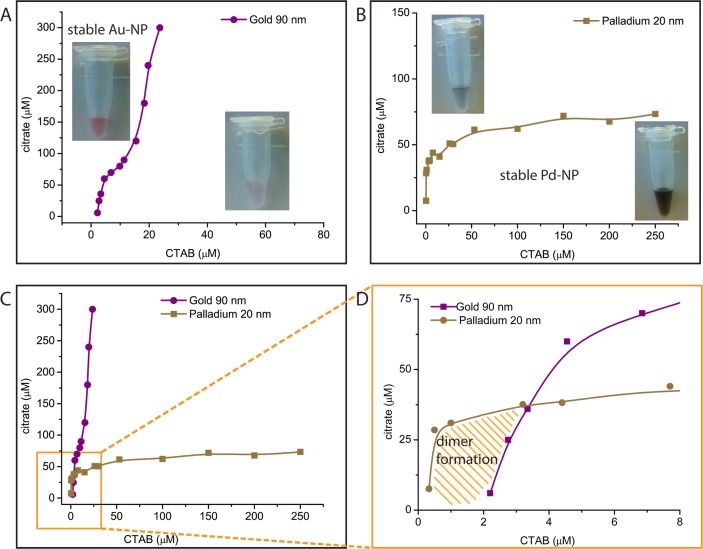
It is generally accepted that there is a minimum residual concentration of surfactant needed to achieve stability of CTAB or CTAC capped NPs.52 At the same time, according to our stability experiments, there is also a maximum concentration threshold of cationic surfactant above which, negatively charged NP-A colloids undergo self-aggregation. Considering the concentration of citrate, there is also a maximum concentration of this salt above which the NPs stabilized by cationic surfactants become unstable (see SI5 and SI7). Therefore, we can define a stability concentration zone in which NP-A and NP-B are both stable (for experimental details see SI1). For the case of Au sphere90 nm with Pd cube25 nm, the stability zone is very narrow and is delimited by the stability curve of Au-NPs (Figure 3a) and Pd-NPs (Figure 3b) at different concentrations of citrate and CTAB, respectively. Figure 3d is the stability phase diagram of the binary system of NPs as a function of the concentrations of their respective stabilization agents. Controlled self-aggregation occurs only within the stability zone, and therefore the determination of these experimental conditions is crucial to achieve high yields of dimeric structures formed by electrostatic self-assembly.

Figure 3.

Figure 3

Open in a new tab

Stability phase diagrams as a function of concentration of capping agents for (A) Au sphere90 nm, (B) Pd cube25 nm, and (C) the combination of Au sphere90 nm and Pd cube25 nm. (D) Detailed view of the stability zone (zoom-in of the square marked in (C)).

The colloidal solution phase diagrams presented in Figure 3 can be rationalized considering the interaction energy involved in self- and heteroaggregation processes. Since van der Waals and London forces are short-range attractive interactions, the electrostatic potential energy constitutes the long-range driving force for the formation of aggregates for NPs of different charge (heteroaggregates) and generates the energy barrier for aggregation of NPs of the same charge (homoaggregates). This is the situation we have observed within the stability zone presented in Figure 2, leading to controlled self-assembly. Conversely, if the electrostatic repulsion potential is not enough to create an aggregation barrier higher than the thermal energy, the system undergoes massive aggregation, as observed experimentally outside the stability zone in Figure 3 (see SI7 for further discussion).

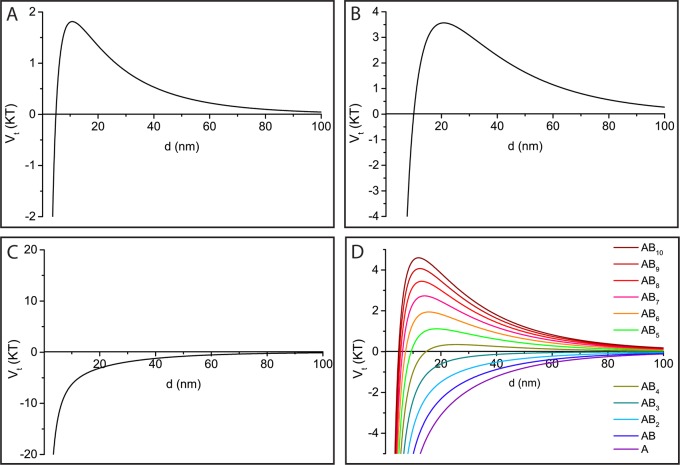
To further elucidate the nature of the experimentally determined stability zone, the pairwise interaction energy profiles as a function of the interparticle distance for Au Spheres90 nm and Pd cubes25 nm were calculated considering the same conditions as for the self-assembly experiments. This analysis provides additional information regarding the specific conditions that lead to controlled self-assembly (Figure 3, see SI7 for further details on the calculations). The homopair interaction profiles describe predominantly repulsive interactions for large interparticle distance, accounting for the dominant effect of the electrostatic contribution (Figure 4a,b). For short distances, the potential energy for homodimers reaches a maximum and drops into the attraction regime due to the van der Waals forces operating at short range. The energy barrier for homoaggregation is higher than the thermal energy for both kinds of NPs, and for this reason, under our experimental conditions, the formation of aggregates of the same kind of particles is disfavored. Conversely, the heteropair interactions are predominantly attractive at every distance (Figure 4c); therefore, the formation of heteroaggregates has no energy barrier and occurs spontaneously. Furthermore, considering that the depth of the attractive potential at short distances is more than 10 kBT, the aggregation process can be considered irreversible. Hence, in our case, the formation of aggregates can be understood as a kinetic process that is controlled by the collision rate of the nanoparticles in the solution.

Figure 4.

Figure 4

Open in a new tab

Interaction energy vs interparticle separation for representative NPs: (A) homodimer Pd cube25 nm with Pd cube25 nm; (B) homodimer Au sphere90 nm with Au sphere90 nm; (C) heterodimer Au sphere90 nm with Pd cube25 nm; (D) multimer Pd cube25 nm with different Au sphere90 nm–Pd cube25 nm (ABn) multimers. The legend in (D) describes the composition of the multimers considering one NP A (Au sphere90 nm) and different numbers of NPs B (Pd cube25 nm).

For similar detailed theoretical considerations for all the dimer combinations investigated in the present work we refer to the Supporting Information (SI7). In essence, the sum of all obtained theoretical results suggests that under our experimental conditions the energy barriers for self-aggregation disfavor the formation of homodimers, while for heteroaggregation, the interactions are attractive and constitute the driving force for the formation of heteroaggregates.

2.3-. Analysis of the Populations of Aggregates

The electrostatic self-assembly of two kinds of oppositely charged NPs, for the reasons discussed in the previous section, should predominantly lead to the formation of heteroaggregates. In principle, the number and composition of these heteroassemblies of NPs depend on the entity of the interactions involved and on the density-number of each kind of particle in solution. We have used TEM and SEM imaging as complementary techniques to evaluate the populations of different NP aggregates during the self-assembly experiments. For TEM sample preparation, a droplet of NP solution was spread and dried on a TEM copper grid, while SEM samples were prepared by spin-coating of the NP solution on silicon wafer substrates (see SI3 for details). The relative yields of different types of aggregates determined for each sample by TEM and SEM image analysis were similar for each combination at each NP-A:NP-B ratio, irrespective of the different procedures used for sample preparation. Thus, the similarity between these two data sets suggests that the yields obtained from our TEM and SEM analysis are representative of the distribution of aggregates in solution.

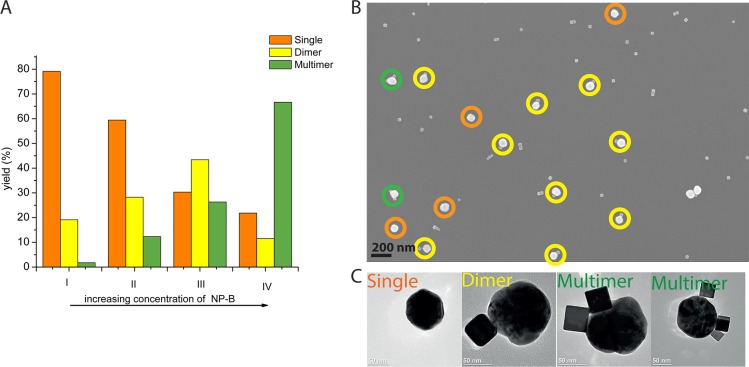
The analyzed TEM and SEM images of the samples produced by self-assembly experiments showed populations of aggregates containing different numbers of NP-A and NP-B (Figure 5b). For all the combinations of NPs investigated here, the fraction of homoaggregates was very low, reflecting the repulsive nature of the interactions among NPs of the same type. Similarly, more than 95% of the NP heteroaggregates in the samples contained only one NP-A. These results are supported by the analysis of the repulsion energy barriers for Au spheres90 nm and Pd cubes25 nm, suggesting that homoaggregates and heteroaggregates containing more than one NP-A are energetically disfavored (see SI7 for further discussion). Taking these facts into account, we have defined three statistical classes of clusters based on aggregates containing one NP-A.

Figure 5.

Figure 5

Open in a new tab

(A) Statistics of aggregates populations for the targeted dimer combination Au sphere90 nm (cNP ≈ 2.17 × 1010 NP/mL) and Pd cube25 nm at different NP concentrations: I: cNP ≈ 3.49 × 1011 NP/mL; II: cNP ≈ 6.98 × 1011 NP/mL; III: cNP ≈ 1.40 × 1012 NP/mL; IV: cNP ≈ 2.09 × 1012 NP/mL. (B) Representative SEM image of the population of aggregates (scale bar 200 nm, circles highlight different classes: orange = single, yellow = dimer, green = multimer). (C) High-magnification TEM images of representative single, dimer and multimers (scale bar 50 nm).

The first class is called “singles” and consists of isolated NP-A’s. The second class is heterodimers, containing one NP-A and one NP-B. The third class accounts for small aggregates containing one NP-A and more than one NP-B, here called multimers (see Figure 5c). We have performed a statistical analysis of the populations of aggregates obtained from SEM and TEM analysis for each combination of NPs by considering at least four independent experiments for each case. In each experiment several hundred particles were counted. Representative yields for the three classes of aggregates, in self-assembly experiments using different ratios of NP-B and NP-A, are presented in Figure 5a (additional data are presented in SI4). Aggregates containing more than one NP-A were considered large aggregates and counted separately. For the NP combinations investigated here, these large aggregates accounted for less than 5% of the populations. This observation is also supported by DLS data showing that, in solution, there are no detectable large aggregates (see SI6).

Using this approach, we have explored a range of concentrations of NPs in order to determine the concentration ratio for NP-A and NP-B leading to the highest yield of heterodimers for each combination of NPs. Considering, for example, the combination of spherical Au NPs (sphere90 nm, NP-A) and Pd nanocubes25 nm, (NP-B), single Au-NPs were mostly observed for low concentrations of palladium cubes (Figure 5A). Increasing the concentration of palladium cubes, a highest yield of 43% dimers was obtained. Further increase of the concentration of NP-B leads to larger amounts of multimeric structures in which several Pd-NPs surround the spherical Au-NP.

From the theoretical point of view, the formation of multimers can be understood considering a stepwise aggregation process. We have calculated the pairwise interaction energy for the combination of Au NPs (sphere90 nm, NP-A) and Pd nanocubes25 nm (NP-B) forming multimers (Figure 4D, for further details on calculations see SI7). In this case, the electrostatic interactions between the multimers ABn and one NP-B are attractive for low NP-B-occupancy numbers (A, AB, AB2, and AB3). However, they become repulsive if the number of NP-B’s in the multimer is larger than 3. Moreover, the energy barrier for aggregation becomes higher than the thermal energy for occupancy numbers larger than 4. Therefore, we can conclude that the formation of multimers with large number of NP-B’s is energetically disfavored, and the yield of such structures is expected to be low. This theoretical result is consistent with the results observed during the self-assembly experiments and DLS characterization.

In the presence of irreversible aggregation, the formation of NP aggregates can be related to the collision rates depending on the NPs interaction energy and on the cross section of collision. If we consider that the driving force for aggregation has an effective volume of action (νa), and assuming that the average distance between two NPs of type A is sufficiently large, we can infer that if n NP-B are within effective volume of action of one particle NP-A, they will lead to the formation of an aggregate of the type ABn. Under these conditions, the relative amounts of single NPs as well as dimeric and multimeric aggregates can be expressed as

2.3-. 2
2.3-. 3
2.3-. 4

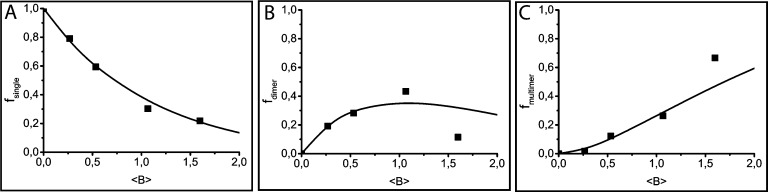
where [B] is the concentration of NP-B and va is the effective volume of action of NP-A that can be obtained from the experimental data (see SI7 for more details). The agreement between the theoretical data (calculated from eqs 2–4) and the experimental values determined in the self-assembly experiments suggests that this set of equations accurately describes the formation of the aggregates, especially for low concentrations of NP-B (Figure 6).

Figure 6.

Figure 6

Open in a new tab

Experimental (dots) and theoretical (lines) population abundance for (A) single Au sphere90 nm, (B) heterodimers Au sphere90 nm–Pd cube25 nm, and (C) multimers Au sphere90 nm–Pd cube25 nm; as a function of the average number of Pd cube25 nm in the effective volume of action of Au sphere90 nm (⟨B⟩ = [B]va).

The major features of these equations can be seen in Figure 6. The fraction of single NP-A’s decreases monotonically while increasing the concentration of NP-B (Figure 6a). The relative abundance of dimeric heteroaggregates (AB) initially increases and reaches a maximum when the average number of NP-B’s within the effective volume of action is equal to 1 (Figure 6b). It is interesting to notice that according to eq 3, the relative yield of dimeric aggregates is theoretically expected to be lower than 37%. Therefore, we can conclude that the maximum yields of dimers obtained in the optimal experimental conditions (ranging from 30 to 40%) corresponds to the theoretical limit of our electrostatic self-assembly method. Moreover, these yields are comparable with other state-of-the-art methods for self-assembly of NP heterodimers.54

The Poisson-fluctuation model describing the population of single NP-A’s as well as dimeric and multimeric aggregates was found to be universal for the combinations of NPs A and B investigated. Further theoretical discussion and additional simulation data for representative systems are presented in SI7.

The dimer yields and the population distributions discussed above were calculated considering the population of clusters containing one NP-A (Au90 nm or Ag90 nm), which is the sensing unit, giving the plasmonic signal within the self-assembled structures. This statistical description based on NP-A is convenient for tailored structures for single NPs plasmonic-sensing experiments (heterodimers). Furthermore, for single-particle spectroscopic applications, the heterodimer yields obtained (30–40%) allows collection of significant amounts of experimental data for each sample. The single NP experiments described in section 2.4 are of high scientific interest and can, using our self-assembly approach, be implemented for any type of heterodimer, irrespective of the chemical composition or specific chemical reaction probed.

Considering the cluster populations by NP-B composition, it is also possible to express the calculated yields with respect to NP-B. For all the self-assembly experiments we have used at least an excess of 1 order of magnitude of NP-B with respect to the concentration of NP-A; therefore, the yields of heterodimers considering the NP-B distribution are lower than 10%. This statistical mismatch between the absolute values for the two distributions has no influence on the general interpretation of our results, considering that the higher achievable yields of dimers over other heteroclusters is obtained under the same experimental conditions for both distributions.

2.4. Proof-of-Principle Single Particle Hydrogen Sensing Experiments

In the last part of this work we demonstrate the built-in sensor function of our shape-selected heterodimer assemblies by a proof-of-principle hydrogen sensing experiment.55 Specifically, we recorded the uptake of hydrogen by a single palladium cube adjacent to an Au nanosphere90 nm. The experiment was performed on the “as-synthesized” NPs after a 1 min cleaning step in 50 W oxygen plasma to remove surfactants from the synthesis. SEM/TEM investigations concluded that the particles kept their integrity under this treatment. The experiment consisted of measuring single-dimer scattering spectra in a dark-field microscope fiber-coupled to a spectrometer equipped with a CCD camera (details of the instrument setup and procedures are presented in SI1). As shown in Figure 7 for two representative individual heterodimers, deposited onto a thermally oxidized Si wafer substrate, we observed a significant change in the scattering spectra in pure Ar gas and after exposure to 80 mbar of hydrogen in Ar carrier gas at room temperature. This is presumably due to the formation of the Pd hydride phase (PdHx) in the cubes and the concomitant change of their volume and refractive index.

Figure 7.

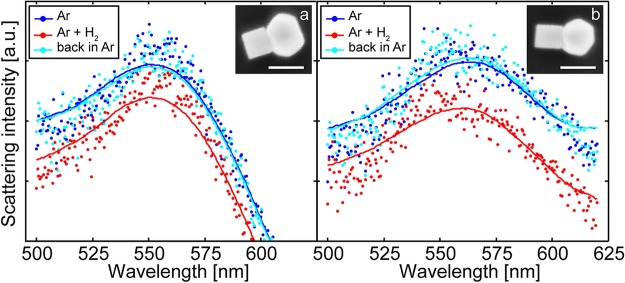
Figure 7

Open in a new tab

Single-particle scattering spectra from two representative (a, b) Au sphere–Pd cube heterodimers in Ar gas (dark blue), under 250 mbar of hydrogen partial pressure in Ar (red) and back in pure Ar (turquoise). The inset shows an SEM image of the respective dimer probed in each measurement. The scale bars in the SEM images are 100 nm.

The detection of these changes occurs via the enhanced electric field that is formed around the Au plasmonic unit and its coupling to the Pd, through which the electronic and volume changes occurring in the Pd upon hydrogen sorption are transformed into different resonance conditions of the LSPR. Since the dielectric properties of the Pd and PdHx phases are significantly different,56,57 the transition between them is reflected in a significant change in the scattered intensity and increase of the full width at half-maximum (Δfwhm) of the LSPR peak (∼10 nm for the heterodimer in Figure 7a and ∼20 nm for the heterodimer in Figure 7b) due to the increased damping in PdHx. The shifts in peak position are smaller than Δfwhm (∼1 and ∼6 nm for the heterodimers in Figures 7a and 7b, respectively) but still appreciable. The reason for the relatively small peak shifts observed are related to a compensation effect between the dielectric changes (inducing spectral blue-shift) and the volume increase of the Pd upon hydrogen sorption (inducing spectral red-shift).58 Thus, depending on the specifics of the Au–Pd particle arrangement and respective sizes and shapes, it is possible that the effective peak shift is very small (or even zero) while other readout parameters (like scattering intensity or fwhm) exhibit a strong signal.

We have demonstrated that the hydride formation process is completely reversible upon exposing the structures to pure Ar gas again after hydrogenation, as expected for the Pd–H system.59 These results suggest that the heterodimeric structures obtained by our self-assembly strategy provide an efficient way to couple functional (e.g., catalytic) and plasmonic units to build single-particle sensors following the indirect nanoplasmonic sensing principle.25,60 Moreover we can conclude that full catalytic activity of the functional dimer entity is retained, despite the necessity of surfactants during dimer synthesis. We attribute the observed differences in the general shape of the scattering spectra of different heterodimers to the slightly different shapes and sizes of the probed dimers as well as to possible differences in the gap size between the NP units.

3. Conclusions

We have developed a versatile colloidal synthesis method to assemble noble metal NP heterodimers based on electrostatic interactions. We have been able to combine metallic NPs of different sizes, shapes, and chemical compositions and have analyzed them in detail by means of SEM, TEM, STEM-EDX, DLS, and zeta-potential measurements. The phase diagrams of the relevant individual dimer components were investigated to derive a stability zone where both components were stable in solution despite opposite surface charge, in order to find the optimal conditions for selective self-assembly of the targeted heterodimers. Using this approach, we have successfully assembled plasmonic heterodimers of Au and Ag spheres90 nm paired with Au30 nm cubes and Au50 nm rhombic dodecahedron. Furthermore, we have also combined catalytic Pd NPs of different sizes and shapes (cubes25 nm/70 nm; rhombic dodecahedron110 nm, truncated cubes120 nm, octahedron130 nm) with plasmonic spherical AuNPs (90 nm). The heterodimers for different combinations of NPs were obtained in yields ranging from 30 to 40%. The demonstrated electrostatic assembly mechanism was explained using theoretical modeling. This analysis proved that the maximum theoretical yields for dimeric heterostructures was achieved in the presented experiments by tuning the experimental conditions in the narrow mutual-stability zone for the binary NP system and used surfactants. Finally, we successfully tested our assembled structures in a proof-of-principle experiment for single particle sensing of hydrogen uptake. Thus, the experimental and theoretical results presented here demonstrate that the electrostatic self-assembly strategy developed can be used as a general approach to build discrete nanostructures that combine plasmonic and other metallic functional/catalytic nanoparticles with narrow interparticle gaps and with excellent control on constituent particle size, composition, and shape. This opens up for exciting possible applications in the field of plasmonic sensing and plasmon enhanced catalysis.

Acknowledgments

This work was funded by the Areas of Advance in Materials Science and in Nanoscience and Nanotechnology at Chalmers University of Technology. C.L. acknowledges financial support from the Swedish Research Council Project 2010-4041. We thank Prof. Johan Bergenholtz, Gothenburg University, Sweden, for the access to the DLS and zeta-potantial instrumentation.

Glossary

Abbreviations

NP

nanoparticle

MESNa

sodium 2-mercaptoethanesulfonate

CTAB

cetyltrimethylammonium bromide

CTAC

cetyltrimethylammonium chloride.

Supporting Information Available

Experimental details; representative STM-EDX, SEM, TEM, population of aggregates, zeta-potential and DLS data; theoretical considerations. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Contributions

T.A.G. and Y.A.D.F. contributed equally to this work.

Supplementary Material

la5002754_si_001.pdf (2.7MB, pdf)

References

  1. Faraday M. Experimental Relations of Gold (and Other Metals) to Light. Philos. Trans. R. Soc. London 1857, 147, 145–181. [Google Scholar]
  2. Kelly K. L.; Coronado E.; Zhao L. L.; Schatz G. C. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar]
  3. Guerrero-Martínez A.; Grzelczak M.; Liz-Marzán L. M. Molecular Thinking for Nanoplasmonic Design. ACS Nano 2012, 6, 3655–3662. [DOI] [PubMed] [Google Scholar]
  4. Pallavicini P.; Taglietti A.; Dacarro G.; Diaz-Fernandez Y. A.; Galli M.; Grisoli P.; Patrini M.; Santucci De Magistris G.; Zanoni R. Self-Assembled Monolayers of Silver Nanoparticles Firmly Grafted on Glass Surfaces: Low Ag+ Release for an Efficient Antibacterial Activity. J. Colloid Interface Sci. 2010, 350, 110–116. [DOI] [PubMed] [Google Scholar]
  5. Romo-Herrera J. M.; Alvarez-Puebla R. A.; Liz-Marzán L. M. Controlled Assembly of Plasmonic Colloidal Nanoparticle Clusters. Nanoscale 2011, 3, 1304–1315. [DOI] [PubMed] [Google Scholar]
  6. Halas N. J.; Lal S.; Chang W.-S.; Link S.; Nordlander P. Plasmons in Strongly Coupled Metallic Nanostructures. Chem. Rev. 2011, 111, 3913–3961. [DOI] [PubMed] [Google Scholar]
  7. Kreibig U.; Vollmer M.. Optical Properties of Metal Clusters; Springer: Berlin, 1995. [Google Scholar]
  8. Pallavicini P.; Chirico G.; Collini M.; Dacarro G.; Donà A.; D’Alfonso L.; Falqui A.; Diaz-Fernandez Y. A.; Freddi S.; Garofalo B.; et al. Synthesis of Branched Au Nanoparticles with Tunable Near-Infrared LSPR Using a Zwitterionic Surfactant. Chem. Commun. 2011, 47, 1315–1317. [DOI] [PubMed] [Google Scholar]
  9. Shanthil M.; Thomas R.; Swathi R. S.; Thomas K. G. Ag@SiO2 Core-Shell Nanostrucutres: Distance-Dependent Plasmon Coupling and SERS Investigation. J. Phys. Chem. Lett. 2012, 3, 1459–1464. [DOI] [PubMed] [Google Scholar]
  10. Lombardi A.; Grzelczak M. P.; Crut A.; Maioli P.; Pastoriza-Santos I.; Liz-Marzán L. M.; Fatti N.; Del Vallée F. Optical Response of Individual Au-Ag@SiO2 Heterodimers. ACS Nano 2013, 7, 2522–2531. [DOI] [PubMed] [Google Scholar]
  11. Shegai T.; Johansson P.; Langhammer C.; Käll M. Directional Scattering and Hydrogen Sensing by Bimetallic Pd-Au Nanoantennas. Nano Lett. 2012, 12, 2464–2469. [DOI] [PubMed] [Google Scholar]
  12. Dadosh T.; Gordin Y.; Krahne R.; Khivrich I.; Mahalu D.; Frydman V.; Sperling J.; Yacoby A.; Bar-Joseph I. Measurement of the Conductance of Single Conjugated Molecules. Nature 2005, 436, 677–680. [DOI] [PubMed] [Google Scholar]
  13. Gschneidtner T. A.; Diaz Fernandez Y. A.; Moth-Poulsen K. Progress in Self-Assembled Single-Molecule Electronic Devices. J. Mater. Chem. C 2013, 1, 7127–7133. [Google Scholar]
  14. Parveen S.; Misra R.; Sahoo S. K. Nanoparticles: a Boon to Drug Delivery, Therapeutics, Diagnostics and Imaging. Nanomedicine 2012, 8, 147–166. [DOI] [PubMed] [Google Scholar]
  15. Chatterjee D. K.; Fong L. S.; Zhang Y. Nanoparticles in Photodynamic Therapy: An Emerging Paradigm. Adv. Drug Delivery Rev. 2008, 60, 1627–1637. [DOI] [PubMed] [Google Scholar]
  16. Tedsree K.; Li T.; Jones S.; Chan C. W. A.; Yu K. M. K.; Bagot P. A. J.; Marquis E. A.; Smith G. D. W.; Tsang S. C. E. Hydrogen Production from Formic Acid Decomposition at Room Temperature Using a Ag-Pd Core-Shell Nanocatalyst. Nat. Nanotechnol. 2011, 6, 302–307. [DOI] [PubMed] [Google Scholar]
  17. Ghosh S. K.; Pal T. Interparticle Coupling Effect on the Surface Plasmon Resonance of Gold Nanoparticles: From Theory to Applications. Chem. Rev. 2007, 107, 4797–4862. [DOI] [PubMed] [Google Scholar]
  18. Zhao J.; Zhang X.; Yonzon C. R.; Haes A. J.; Van Duyne R. P. Localized Surface Plasmon Resonance Biosensors. Nanomedicine 2006, 1, 219–228. [DOI] [PubMed] [Google Scholar]
  19. Mucic R. C.; Storhoff J. J.; Mirkin C. A.; Letsinger R. L. DNA-Directed Synthesis of Binary Nanoparticle Network Materials. J. Am. Chem. Soc. 1998, 120, 12674–12675. [Google Scholar]
  20. McFarland A. D.; Van Duyne R. P. Single Silver Nanoparticles as Real-Time Optical Sensors with Zeptomole Sensitivity. Nano Lett. 2003, 3, 1057–1062. [Google Scholar]
  21. Novo C.; Funston A. M.; Mulvaney P. Direct Observation of Chemical Reactions on Single Gold Nanocrystals Using Surface Plasmon Spectroscopy. Nat. Nanotechnol. 2008, 3, 598–602. [DOI] [PubMed] [Google Scholar]
  22. Seo D.; Park G.; Song H. Plasmonic Monitoring of Catalytic Hydrogen Generation by a Single Nanoparticle Probe. J. Am. Chem. Soc. 2012, 134, 1221–1227. [DOI] [PubMed] [Google Scholar]
  23. Larsson E. M.; Langhammer C.; Zorić I.; Kasemo B. Nanoplasmonic Probes of Catalytic Reactions. Science 2009, 326, 1091–1094. [DOI] [PubMed] [Google Scholar]
  24. Larsson E. M.; Syrenova S.; Langhammer C. Nanoplasmonic Sensing for Nanomaterials Science. Nanophotonics 2012, 1, 249–266. [Google Scholar]
  25. Liu N.; Tang M. L.; Hentschel M.; Giessen H.; Alivisatos A. P. Nanoantenna-Enhanced Gas Sensing in a Single Tailored Nanofocus. Nat. Mater. 2011, 10, 631–636. [DOI] [PubMed] [Google Scholar]
  26. Hogg B. Y. R.; Healy T. W.; Fuerstenau D. W. Mutual Coagulation of Colloidal Dispersions. Trans. Faraday Soc. 1966, 33, 1638–1651. [Google Scholar]
  27. Wang J.; Xia H.; Zhang Y.; Lu H.; Kamat R.; Dobrynin A. V.; Cheng J.; Lin Y. Nucleation-Controlled Polymerization of Nanoparticles into Supramolecular Structures. J. Am. Chem. Soc. 2013, 135, 11417–11420. [DOI] [PubMed] [Google Scholar]
  28. Zakaria H. M.; Shah A.; Konieczny M.; Hoffmann J. A.; Nijdam A. J.; Reeves M. E. Small Molecule- and Amino Acid-Induced Aggregation of Gold Nanoparticles. Langmuir 2013, 29, 7661–7673. [DOI] [PubMed] [Google Scholar]
  29. Chegel V.; Rachkov O.; Lopatynskyi A.; Ishihara S.; Yanchuk I.; Nemoto Y.; Hill J. P.; Ariga K. Gold Nanoparticles Aggregation: Drastic Effect of Cooperative Functionalities in a Single Molecular Conjugate. J. Phys. Chem. C 2012, 116, 2683–2690. [Google Scholar]
  30. Bentz J. Electrostatic Potential Around a Charged Sphere with Cation Binding. J. Colloid Interface Sci. 1981, 80, 179–191. [Google Scholar]
  31. Ohshima H. Electrostatic Interaction Between Two Dissimilar Spheres with Constant Surface Charge Density. J. Colloid Interface Sci. 1995, 170, 432–439. [Google Scholar]
  32. Zhou S.; Zhang G. Approximate Analytical Expressions for Electrical Potential Distribution and Surface Charge Density/surface Potential Relationship for Planar, Cylindrical, and Spherical Entities Immersed in a General Electrolyte Solution. Colloids Surf., A 2011, 385, 28–39. [Google Scholar]
  33. Grzelczak M.; Vermant J.; Furst E. M.; Liz-Marzán L. M. Directed Self-Assembly of Nanoparticles. ACS Nano 2010, 4, 3591–3605. [DOI] [PubMed] [Google Scholar]
  34. Lattuada M.; Hatton T. A. Synthesis, Properties and Applications of Janus Nanoparticles. Nano Today 2011, 6, 286–308. [Google Scholar]
  35. Gunnarson L.; Rindzevicius T.; Prikulis J.; Kasemo B.; Käll M.; Zou S.; Schatz G. C. Confined Plasmons in Nanofabricated Single Silver Particle Pairs: Experimental Observations of Strong Interparticle Interaction. J. Phys. Chem. B 2004, 109, 1079–1087. [DOI] [PubMed] [Google Scholar]
  36. Reinhard B. M.; Siu M.; Agarwal H.; Alivisatos a P.; Liphardt J. Calibration of Dynamic Molecular Rulers Based on Plasmon Coupling Between Gold Nanoparticles. Nano Lett. 2005, 5, 2246–2252. [DOI] [PubMed] [Google Scholar]
  37. Loweth C. J.; Caldwell W. B.; Peng X.; Alivisatos a. P.; Schultz P. G. DNA-Based Assembly of Gold Nanocrystals. Angew. Chem., Int. Ed. 1999, 38, 1808–1812. [DOI] [PubMed] [Google Scholar]
  38. Wang Y.; Chen G.; Yang M.; Silber G.; Xing S.; Tan L. H.; Wang F.; Feng Y.; Liu X.; Li S.; et al. A Systems Approach Towards the Stoichiometry-Controlled Hetero-Assembly of Nanoparticles. Nat. Commun. 2010, 1, 87–94. [DOI] [PubMed] [Google Scholar]
  39. Busson M. P.; Rolly B.; Stout B.; Bonod N.; Larquet E.; Polman A.; Bidault S. Optical and Topological Characterization of Gold Nanoparticle Dimers Linked by a Single DNA Double Strand. Nano Lett. 2011, 11, 5060–5065. [DOI] [PubMed] [Google Scholar]
  40. Wu H.-L.; Kuo C.-H.; Huang M. H. Seed-Mediated Synthesis of Gold Nanocrystals with Systematic Shape Evolution from Cubic to Trisoctahedral and Rhombic Dodecahedral Structures. Langmuir 2010, 26, 12307–12313. [DOI] [PubMed] [Google Scholar]
  41. Niu W.; Zhang L.; Xu G. Shape-Controlled Synthesis of Single-Crystalline Palladium Nanocrystals. ACS Nano 2010, 4, 1987–1996. [DOI] [PubMed] [Google Scholar]
  42. Scarabelli L.; Grzelczak M.; Liz-Marzán L. M. Tuning Gold Nanorod Synthesis through Prereduction with Salicylic Acid. Chem. Mater. 2013, 25, 4232–4238. [Google Scholar]
  43. Lohse S. E.; Burrows N. D.; Scarabelli L.; Liz-Marzán L. M.; Murphy C. J. Anisotropic Noble Metal Nanocrystal Growth: The Role of Halides. Chem. Mater. 2014, 26, 34–43. [Google Scholar]
  44. Bidault S.; Abajo F. J. G.; De Polman A. Plasmon-Based Nanolenses Assembled on a Well-Defined DNA Template. J. Am. Chem. Soc. 2008, 130, 2750–2751. [DOI] [PubMed] [Google Scholar]
  45. Brown L. V.; Sobhani H.; Lassiter J. B.; Nordlander P.; Halas N. J. Heterodimers: Plasmonic Properties of Mismatched Nanoparticle Pairs. ACS Nano 2010, 4, 819–832. [DOI] [PubMed] [Google Scholar]
  46. Sheikholeslami S.; Jun Y.-W.; Jain P. K.; Alivisatos A. P. Coupling of Optical Resonances in a Compositionally Asymmetric Plasmonic Nanoparticle Dimer. Nano Lett. 2010, 10, 2655–2660. [DOI] [PubMed] [Google Scholar]
  47. Feng Y.; He J.; Wang H.; Tay Y. Y.; Sun H.; Zhu L.; Chen H. An Unconventional Role of Ligand in Continuously Tuning of Metal-Metal Interfacial Strain. J. Am. Chem. Soc. 2012, 134, 2004–2007. [DOI] [PubMed] [Google Scholar]
  48. Khanal B. P.; Pandey A.; Li L.; Lin Q.; Bae W. K.; Luo H.; Klimov V. I.; Pietryga J. M. Generalized Synthesis of Hybrid Metal-Semiconductor Nanostructures Tunable from the Visible to the Infrared. ACS Nano 2012, 6, 3832–3840. [DOI] [PubMed] [Google Scholar]
  49. Lim B.; Kobayashi H.; Yu T.; Wang J.; Kim M. J.; Li Z.-Y.; Rycenga M.; Xia Y. Synthesis of Pd-Au Bimetallic Nanocrystals via Controlled Overgrowth. J. Am. Chem. Soc. 2010, 132, 2506–2507. [DOI] [PubMed] [Google Scholar]
  50. Liang S.; Liu X.-L.; Yang Y.-Z.; Wang Y.-L.; Wang J.-H.; Yang Z.-J.; Wang L.-B.; Jia S.-F.; Yu X.-F.; Zhou L.; et al. Symmetric and Asymmetric Au-AgCdSe Hybrid Nanorods. Nano Lett. 2012, 12, 5281–5286. [DOI] [PubMed] [Google Scholar]
  51. Niu W.; Li Z.-Y.; Shi L.; Liu X.; Li H.; Han S.; Chen J.; Xu G. Seed-Mediated Growth of Nearly Monodisperse Palladium Nanocubes with Controllable Sizes. Cryst. Growth Des. 2008, 8, 4440–4444. [Google Scholar]
  52. Becker R.; Liedberg B.; Käll P.-O. CTAB Promoted Synthesis of Au Nanorods--Temperature Effects and Stability Considerations. J. Colloid Interface Sci. 2010, 343, 25–30. [DOI] [PubMed] [Google Scholar]
  53. Kim T.; Lee C.-H.; Joo S.-W.; Lee K. Kinetics of Gold Nanoparticle Aggregation: Experiments and Modeling. J. Colloid Interface Sci. 2008, 318, 238–243. [DOI] [PubMed] [Google Scholar]
  54. Lombardi A.; Grzelczak M.; Crut A.; Mioli P.; Isabel P.-S.; Liz-Marzán L. M.; Del Fatti N.; Vallée F. Optical Response of Individual Au–Ag@ SiO2 Heterodimers. ACS Nano 2013, 7, 2522–2531. [DOI] [PubMed] [Google Scholar]
  55. Langhammer C.; Zorić I.; Kasemo B.; Clemens B. M. Hydrogen Storage in Pd Nanodisks Characterized with a Novel Nanoplasmonic Sensing Scheme. Nano Lett. 2007, 7, 3122–3127. [DOI] [PubMed] [Google Scholar]
  56. Switendick A. C. Electronic-Structure and Total Energy Calculations for Transition-Metal Hydrides. J. Less-Common Met. 1987, 130, 249–259. [Google Scholar]
  57. Ameen Poyli M.; Silkin V. M.; Chernov I. P.; et al. Plasmonic Sensing of Hydrogen Uptake in Palladium Nanodisks. J. Phys. Chem. Lett. 2012, 3, 2556–2561. [DOI] [PubMed] [Google Scholar]
  58. Tittl A.; Kremers C.; Dorfmuller J.; Chigrin D. N.; Giessen H. Spectral Shifts in Optical Nanoantenna-Enhanced Hydrogen Sensors. Opt. Mater. Express 2012, 2, 111–118. [Google Scholar]
  59. Fukai Y.The Metal-Hydrogen System; Springer-Verlag: Berlin, 1993. [Google Scholar]
  60. Langhammer C.; Larsson E. M.; Kasemo B.; Zoric I. Indirect Nanoplasmonic Sensing: Ultrasensitive Experimental Platform for Nanomaterials Science and Optical Nanocalorimetry. Nano Lett. 2010, 10, 3529–3538. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la5002754_si_001.pdf (2.7MB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES