Fluorescence excitation and ultraviolet absorption spectra and theoretical calculations for benzocyclobutane: Vibrations and structure of its excited S₁(π,π^*) electronic state

Abstract

The fluorescence excitation spectra of jet-cooled benzocyclobutane have been recorded and together with its ultraviolet absorption spectra have been used to assign the vibrational frequencies for this molecule in its S₁(π,π^*) electronic excited state. Theoretical calculations at the CASSCF(6,6)/aug-cc-pVTZ level of theory were carried out to compute the structure of the molecule in its excited state. The calculated structure was compared to that of the molecule in its electronic ground state as well as to the structures of related molecules in their S₀ and S₁(π,π^*) electronic states. In each case the decreased π bonding in the electronic excited states results in longer carbon-carbon bonds in the benzene ring. The skeletal vibrational frequencies in the electronic excited state were readily assigned and these were compared to the ground state and to the frequencies of five similar molecules. The vibrational levels in both S₀ and S₁(π,π^*) states were remarkably harmonic in contrast to the other bicyclic molecules. The decreases in the frequencies of the out-of-plane skeletal modes reflect the increased floppiness of these bicyclic molecules in their S₁(π,π^*) excited state.

INTRODUCTION

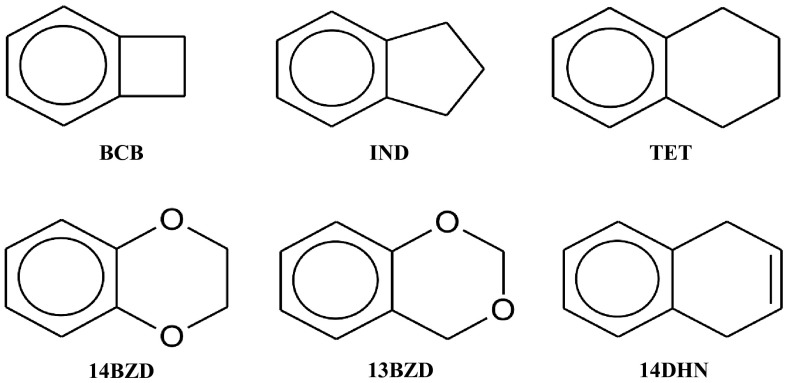
In recent years we have investigated the structures, conformations, and molecular vibrations of bicyclic molecules in their ground and excited states. Among these are indan (IND),¹ tetralin (TET),² 1,4-benzodioxan (14BZD),^{3, 4, 5} 1,3-benzodioxan (13BZD),⁶ and 1,4-dihydronaphthalene (14DHN).⁷ In the present study we report our results on the S₁(π,π^*) electronic excited state of benzocyclobutane (BCB) utilizing fluorescence excitation spectroscopy (FES) and ultraviolet absorption spectroscopy (Scheme ch1). The vibrational study of the BCB S₀ ground state is reported in Ref. 8.

Figure .

Bicyclic molecules of interest.

The focus of these studies has been not only to determine the structures and vibrational data for these molecules but also to understand what effect the π→π^* transition has on the rigidity and conformations of the molecules. Each of these molecules has a ring-flapping vibration whose frequency decreases dramatically in the S₁(π,π^*) excited states. In addition, many of the vibrational frequencies and bond distances reflect the weakening of the π-bonding in the electronic excited states. The five-membered ring of indan (IND) is puckered with a barrier to planarity of 488 cm⁻¹ (1.40 kcal/mole) in its S₀ ground state. This drops to 441 cm⁻¹ (1.26 kcal/mole) in its excited state. The six-membered ring in tetralin (TET) is twisted with a barrier to planarity of about 6000 cm⁻¹ (17 kcal/mole) in its S₀ electronic ground state and this drops to about 3500 cm⁻¹ (10 kcal/mole) in its S₁(π,π^*) state. For 1,4-benzodioxan (14BZD) the calculated twisting barrier values are 11.7 kcal/mole for the ground state and 9.2 kcal/mole for the S₁(π,π^*) excited state. 1,4-Dihydronaphthalene (14DHN) is planar and relatively floppy in its S₀ state but becomes even more so in its S₁(π,π^*) state. Benzocyclobutane (BCB), the molecule of interest here, is expected to remain planar in both its S₀ and S₁(π,π^*) states, but the difference in the rigidity of the molecule between the two electronic states as reflected by its out-of-plane vibrations will be the focus of the work. BCB has a highly strained four-membered ring attached to the benzene ring and what its effect is on the low-frequency vibrations will be investigated.

EXPERIMENTAL

The BCB sample (98% purity) was purchased from Aldrich Chemical Company and further purified by vacuum distillation. Ultraviolet absorption spectra of the vapor at ambient temperatures were recorded on a Bomem DA8.02 Fourier transform spectrometer using a deuterium lamp source, a quartz beamsplitter, and a silicon detector in the 20 000 to 50 000 cm⁻¹ region. Approximately 3 Torr of sample was contained in a 20 cm glass cell with quartz windows. A resolution of 1 cm⁻¹ was used and 4000 scans were averaged. The fluorescence excitation spectra (FES) were recorded using a Continuum Powerlite 9020 Nd:YAG laser which pumped a Continuum Sunlite optical parametric oscillator (OPO) and an FX-1 ultraviolet extension unit. The laser was scanned under computer control and the fluorescence was detected with a photomultiplier tube whenever resonance with a vibronic level was achieved. The FES were obtained at 0.5 cm⁻¹ resolution and recorded under supersonic jet-cooled conditions. More details on the laser system are provided in Refs. ^{9, 10, 11, 12, 13, 14, 15, 16}.

COMPUTATIONS

In the present study, geometry optimizations and harmonic vibrational frequency computations for BCB in its lowest singlet excited state, S₁(π,π^*), as well as in its ground state, were performed using the complete-active-space self-consistent-field (CASSCF) method with the aug-cc-pVTZ basis sets. The active space for the CASSCF computations consisted of six π electrons distributed in six π orbitals on the six-membered ring of BCB, as depicted in Figure 1. All CASSCF(6,6)/aug-cc-pVTZ computations were performed using the GAMESS program.^{17, 18} A scaling factor of 0.905 was used for excited state calculated frequencies.¹⁹ The MacMolPlt²⁰ program was used to visualize the excited state vibrational motions of BCB.

Figure 1.

Molecular orbital diagram for the π and π^* orbitals of BCB.

We have previously reported our electronic ground state results for BCB.⁸ MP2/cc-pVTZ calculations were used to compute the structures of BCB and related molecules using the Gaussian 09 package.²¹ The geometrical parameters calculated in the present work for the BCB electronic ground state using the CASSCF method were very similar to the previous MP2/cc-pVTZ results.⁸ In the previous work B3LYP/cc-pVTZ calculations were utilized to compute the vibrational spectra and these were compared to the experimental vapor and liquid phase infrared and Raman spectra. Frequencies for the ground state below 1450 cm⁻¹ were scaled with a factor of 0.985, frequencies in the 1450–2000 cm⁻¹ region were scaled by a factor of 0.973, and frequencies above 2000 cm⁻¹ by 0.961 based on previous work.^{22, 23, 24, 25, 26} The Semichem AMPAC/AGUI 9.2²⁷ along with the potential energy distribution (PED) was used to assign the vibrations for the electronic ground state.

In addition to the computational results reported here, we have also carried out CIS/6-311++G(d,p) calculations for the excited state of BCB. Since the calculated bond distances and angles did not differ significantly from our results from the CASSCF computations, the results are not presented here.

STRUCTURES

Figure 2 shows the calculated structure of BCB for both its ground (S₀) and S₁(π,π^*) excited states using the CASSCF(6,6)/aug-cc-pVTZ level. The determinants with the largest contributions to the CASSCF wave function for the S₁(π,π^*) state of BCB correspond to excitation from the π₃ to π₄^* orbitals and from the π₂ to π₅^* orbitals. As a result, the electronic excitation from the S₀ to S₁(π,π^*) states increases all the C–C bonds of the benzene ring. Note that the C–C bonds between the benzene ring and the CH₂ group are slightly shorter in the S₁(π,π^*) state than in the ground state. This may be due to an increased hyperconjugative interaction between the C–H σ bonding orbitals on the methylene group and the half-filled π bonding orbitals.

Figure 2.

Calculated structures of BCB in its S₀ ground and S₁(π,π^*) excited states (CASSCF(6,6)/aug-cc-pVTZ).

Figure 3 shows the structures for both IND and TET with selected bond distances and angles from the MP2/cc-pVTZ calculations performed on the ground state.⁸ Selected bond distances and angles of IND¹ and TET² in their S₁(π,π^*), electronic excited state are also shown. The calculations performed for IND in the excited state¹ utilized the CIS/6-31G(d) basis set, whereas the basis set used for the excited state calculations for TET² was CIS/6-311++G(d,p). Figure 1 presents a representation of the molecular orbitals of BCB so that the π→π^* electronic transition can be visualized. As discussed in Ref. 8, the structure for the ground state is quite typical for what is expected for a bicyclic molecule containing the benzene ring. Namely, the carbon-carbon bond distances are all 1.39 ± 0.01 Å for BCB as well as for IND and TET. The ∠C–C–C angles in the benzene ring are all 120° ± 1° for IND and TET, but the small ring angles of the four-membered ring in BCB cause the ∠C–C–C angle at the carbon joined to the external ring to open up to 122°. In the S₁(π,π^*) excited states, as expected, all of the C–C bonds in the benzene rings increase. For BCB they are 1.43 ± 0.01 Å reflecting an average increase of 0.03 Å. For IND they are 1.42 ± 0.02 Å with an increase of 0.02 Å and for TET they are 1.42 ± 0.01 Å, also with an increase of 0.02 Å. This shows that greater angle strain in the external ring of BCB results in somewhat larger increases in the carbon-carbon bond lengths of the benzene ring. It is also interesting to note that the C–C bond from the benzene ring to an external carbon decreases slightly in the S₁(π,π^*) excited state by 0.006 Å for BCB and by 0.009 Å for IND and TET.

Figure 3.

Calculated structures of IND and TET in their S₀ ground and S₁(π,π^*) excited states. The S₀ structures were calculated using MP2/cc-pVTZ.⁸ The S₁ structure for IND¹ utilized CIS/6-31G(d). The S₁ structure for TET² utilized CIS/6-311++G(d,p).

RESULTS AND DISCUSSION

Figure 4 presents the fluorescence excitation spectrum (FES) of jet-cooled BCB and its ultraviolet (UV) absorption spectrum of BCB at room temperature in the −320 to 1700 cm⁻¹ region, relative to the electronic band origin $0_0^0$ at 37 093.6 cm⁻¹.

Figure 4.

Fluorescence excitation spectrum and ultraviolet absorption spectrum of BCB. The $0_0^0$ band origin is at 37 093.6 cm⁻¹.

Table 1 compares the BCB electronic band origin to those of related molecules. The BCB transition frequency is the highest among these except for 13BZD which shows the effect of attaching an oxygen atom to the benzene ring. Figure 5 shows the UV spectrum expanded in the −340 to 25 cm⁻¹ region. A number of assignments are shown in the Figures 45. Table 2 presents a summary of the vibrational assignments for the ground and excited states of BCB. The ground state data were presented in Ref. 8 whereas the excited state data have been derived from Table 3, which presents the experimental FES and UV absorption data for the most significant transitions. A more complete listing of the spectral data is available in Table S1 in the supplementary material.²⁸ Figure 6 presents an energy map for several of the low-frequency vibrations of BCB in its ground and excited electronic states. This energy map is consistent with the data and assignments of Table 3. Table 2 also shows the calculated frequencies for both the S₀ and S₁(π,π^*) states. As can be seen, these provide excellent guidance for assigning the experimental spectra. In order to allow comparison with the related molecules, Table 4 shows a listing of selected vibrational frequencies of BCB, IND, TET, 14BZD, 13BZD, and 14DHN in their ground (S₀) and excited (S₁) states.

Table 1.

Observed electronic transition frequencies (cm⁻¹) and average calculated benzene ring bond distances (Å) of BCB and related molecules.

		Average benzene ring bond distance
	Transition frequency	S0	S1(π,π*)	Reference1
BCB	37 093.6	1.3952	1.4293	This work
IND	36 903.7	1.3952	1.4164	1
TET	36 789.7	1.3962	1.4155	2
14BZD	35 563.1	1.3912	1.4195	3, 4, 5
13BZD	38 885.6	1.3942	1.4056	6
14DHN	36 788.6	1.3932	…	7

¹References for transition frequencies and S₁ state bond distances. All S_o state bond distances are from Ref. 8.

²MP2/cc-pVTZ.

³CASSCF(6,6)/aug-cc-pVTZ.

⁴CIS/6-31G(d).

⁵CIS/6-311++G(d,p).

⁶CIS/6-311+G(d,p).

Figure 5.

UV absorption spectra of BCB in the −340 to 21 cm⁻¹ region. The $0_0^0$ band origin is at 37 093.6 cm⁻¹.

Table 2.

Vibrational frequencies (cm⁻¹) of BCB in its ground and excited electronic states.

			S0		S1(π,π*)
			Experimental1	Calculated1	Experimental2	Calculated3
A1	ν11	CH sym. stretch	3077	3061	3068	3045
	ν2	CH sym. stretch	3052	3043	3015	3024
	ν3	CH2 sym. stretch	2949	2928	2845	2876
	ν4	Benzene C–C stretch	1605	1599	1643	1679
	ν5	Benzene C–C stretch	1466	1461	1491	1484
	ν6	CH2 deformation	1444	1440	1402	1454
	ν7	Benzene C–C stretch4	1344	1345	1370	1360
	ν8	CH wag4	1195	1203	1167	1170
	ν9	CH2 wag4	1182	1189	1208	1209
	ν10	CH wag	1152	1160	1113	1112
	ν11	Benzene C–C stretch	1001	1009	892	843
	ν12	4 mem. ring C–C stretch	895	893	900	868
	ν13	4 mem. ring C–C stretch4	765	782	740	713
	ν14	Benzene angle bend	539	542	464	465
A2	ν15	CH2 antisym. stretch	2966	2957	…	2893
	ν16	CH2 twist	1170	1169	1150	1169
	ν17	CH2 rock	1054	1034	966	962
	ν18	CH out-of-plane wag	993	981	656	635
	ν19	CH out-of-plane wag	865	873	549	502
	ν20	Benzene ring twist	670	710	440	450
	ν21	Benzene ring twist	486	485	314	312
	ν22	Skeletal twist	208	189	153	157
B1	ν23	CH stretch	3066	3052	…	3039
	ν24	CH stretch	3031	3035	…	3012
	ν25	CH2 sym. stretch	2942	2923	…	2866
	ν26	Benzene C–C stretch	1596	1593	1500	1502
	ν27	Benzene C–C stretch	1458	1455	1364	1366
	ν28	CH2 deformation	1429	1427	1426	1438
	ν29	CH wag in-plane	1282	1292	1266	1261
	ν30	CH2 wag	1208	1218	1188	1174
	ν31	CH wag in-plane	1132	1138	972	972
	ν32	4 mem. ring C–C stretch4	1091	1089	1085	1083
	ν33	Benzene ring bend4	855	854	819	825
	ν34	Benzene ring bend	634	637	564	567
	ν35	Skeletal deformation	404	409	366	375
B2	ν36	CH2 antisym. stretch	2975	2972	…	2911
	ν37	CH2 twist	1068	1079	1035	1038
	ν38	CH out-of-plane wag	928	936	567	568
	ν39	CH2 rock4	781	785	493	483
	ν40	CH out-of-plane wag4	715	720	737	747
	ν41	Benzene ring bend	386	397	245	250
	ν42	Ring flap	209	213	105	109

¹Reference ⁸.

²The experimental frequencies given for vibrations of A₂, B₁, and B₂ symmetry in the S₁(π,π^*) electronic excited state were determined from overtone or combination bands.

³CASSCF(6,6)/aug-cc-pVTZ calculations. Scaling factor: 0.905.

⁴Represent pairs of coupled vibrations.

Table 3.

Fluorescence excitation and UV spectra (cm⁻¹) of BCB selected bands.

FES1		UV1		Assignment	Inferred2	Calculated3
		−276	ms	${21}_1^1{42}_1^1$	−172 – 105 = −277
		−262	ms	${22}_1^1{42}_2^2$	−54 – 204 = −258
		−209	ms	${22}_2^0{42}_0^2$	−417 + 209 = −208
		−183	ms	${20}_0^1{22}_3^0$	440 – 624 = −184
		−172	ms	${21}_1^1$	314 – 486 = −172
		−154	s	${22}_1^1{42}_1^1$	−54 – 105 = −159
		−144	s	${41}_1^1$	245 – 386 = −141
		−114	ms	${22}_2^2$	301 – 417 = −116
		−105	s	${42}_1^1$	105 – 209 = −104
		−86	m	${40}_1^1{42}_1^1$	20 – 105 = −85
		−76	s	${14}_1^1$	464 – 539 = −75
		−71	mw	${34}_1^1$	564 – 634 = −70
		−54	mw	${22}_1^1$	153 – 208 = −55
		−48	mw	${20}_0^1{21}_1^0$	440 – 486 = −46
		−38	s	${35}_1^1$	366 – 404 = −38
		−28	mw	${35}_1^1{42}_2^4$	−38 + 8 = −30
		−18	mw	${18}_0^1{20}_1^0$	656 – 670 = −14
0	vs	0	vs	$0_0^0$
		8	mw	${42}_2^4$	420 – 411 = 9
		20	w	${40}_1^1$	737 – 715 = 22
		63	mw	${19}_0^1{21}_1^0$	549 – 486 = 63
		105	ms	${42}_1^3$	209 – 105 = 104
				${21}_0^1{22}_1^0$	314 – 208 = 106
209	ms	209	ms	${42}_0^2$		2 × 109 = 218
301	w	301	w	${22}_0^2$		2 × 157 = 314
420	vw	420	mw	${42}_0^4$	2 × 209 = 418
463	mw	464	vw	${14}_0^1$		465
466	mw	467	m	${21}_0^1{22}_0^1$	314 + 153 = 467
485	m	484	mw	${41}_0^2$		2 × 250 = 500
626	vw	626	mw	${21}_0^2$		2 × 312 = 624
733	ms	731	mw	${35}_0^2$		2 × 375 = 750
				${27}_0^1{34}_1^0$	1364 – 634 = 730
740	s	740	s	${13}_0^1$		713
875	m	875	mw	${20}_0^2$		2 × 450 = 900
893	ms	892	w	${11}_0^1$		843
900	s	900	s	${12}_0^1$		868
940	mw	940	vw	${35}_0^2{42}_0^2$	731 + 209 = 940
949	w	949	w	${14}_0^1{41}_0^2$	464 + 485 = 949
				${13}_0^1{42}_0^2$	740 + 209 = 949
977	vw	978	w	${40}_0^1{41}_0^1$	737 + 245 = 982
986	vvw	987	w	${39}_0^2$		2 × 483
1094	m	1094	ms	${19}_0^2$		2 × 502 = 1004
1113	mw	1113	m	${10}_0^1$		1112
1130	m	1129	w	${34}_0^2$		2 × 567 = 1134
1133	ms	1133	m	${38}_0^2$		2 × 568 = 1136
1169	w	1167	m	$8_0^1$		1170
1208	s	1208	s	$9_0^1$		1209
		1246	vw	${21}_0^4$	2 × 626 = 1252
1313	mw	1313	w	${18}_0^2$		2 × 635 = 1270
1343	mw	1342	vw	${38}_0^2{42}_0^2$	1133 + 209 = 1342
		1363	mw	${12}_0^1{14}_0^1$	900 + 464 = 1364
1370	m	1370	mw	$7_0^1$		1360
1404	mw	1402	w	$6_0^1$		1454
1457	w	1458	vw	${35}_0^4$	2 × 731 = 1462
1470	w	1471	w	${40}_0^2$		2 × 747 = 1494
				${13}_0^1{35}_0^2$	740 + 731 = 1471
1477	s	1477	ms	${13}_0^2$	2 × 740 = 1480
1493	mw	1491	w	$5_0^1$		1484
1517	m	1517	w	${11}_0^1{21}_0^2$	892 + 626 = 1518
1593	vw	1594	vvw	${14}_0^1{34}_0^2$	464 + 1129 = 1593
1597	w	1599	vvw	${14}_0^1{38}_0^2$	464 + 1133 = 1597
1623	mw	1623	mw	${11}_0^1{35}_0^2$	892 + 731 = 1623
		1629	vw	${11}_0^1{13}_0^1$	892 + 740 = 1632
				$8_0^1{14}_0^1$	1167 + 464 = 1631
1633	w	1633	w	${33}_0^2$		2 × 825 = 1650
1640	w	1639	vw	${12}_0^1{13}_0^1$	900 + 740 = 1640
1644	s	1643	s	$4_0^1$		1679
1646	w	1646	mw	${32}_0^1{34}_0^1$	1085 + 564 = 1649
		1765	w	${11}_0^1{20}_0^2$	892 + 875 = 1767
		1785	w	${11}_0^2$	2 × 892 = 1784
		1793	m	${11}_0^1{12}_0^1$	892 + 900 = 1792
		1810	mw	${10}_0^1{42}_2^0$	2222 – 411 = 1811
		1833	mw	$7_0^1{14}_0^1$	1370 + 464 = 1834
				${13}_0^1{19}_0^2$	740 +1094 = 1834
		1871	m	${13}_0^1{38}_0^2$	740 + 1133 = 1873
		1904	w	${32}_0^1{33}_0^1$	1085 + 819 = 1904
		1910	vw	$8_0^1{13}_0^1$	1167 + 740 = 1907
		1931	w	${17}_0^2$		2 × 962 = 1924
		1943	m	${31}_0^2$		2 × 972 = 1944
		1946	m	$9_0^1{13}_0^1$	1208 + 740 = 1948
		1957	vvw	$5_0^1{14}_0^1$	1491 + 464 = 1955
		2003	w	${10}_0^1{11}_0^1$	1113 + 892 = 2005
		2015	vw	${10}_0^1{12}_0^1$	1113 + 900 = 2013
		2031	mw	${35}_1^1{37}_0^2$	−38 + 2069 = 2031
		2041	m	${10}_0^1{14}_0^2$	1113 + 927 = 2040
		2053	vw	${31}_0^1{32}_0^1$	972 + 1085 = 2057
				${13}_0^1{18}_0^2$	740 + 1313 = 2053
		2069	vw	${37}_0^2$		2 × 1038 = 2076
		2092	vvw	$4_0^1{14}_0^1$	1633 + 464 = 2097
		2105	mw	$7_0^1{13}_0^1$	1370 + 740 = 2110
		2116	m	${10}_0^2{42}_1^1$	2222 – 105 = 2117
		2153	vvw	$8_0^1{39}_0^2$	1167 + 987 = 2154
		2222	vw	${10}_0^2$	2 × 1113 = 2226
				$5_0^1{35}_0^2$	1491 + 731 = 2222
		2239	w	${14}_0^2{18}_0^2$	927 + 1313 = 2240
				${10}_0^1{34}_0^2$	1113 + 1129 = 2242
		2256	vw	${34}_0^4$	2 × 1129 = 2258
		2300	vvw	${16}_0^2$		2 × 1169 = 2338
		2376	vw	${30}_0^2$		2 × 1174 = 2378
		2384	w	$4_0^1{13}_0^1$	1643 + 740 = 2383
		2411	vvw	${14}_0^1{31}_0^2$	464 + 1943 = 2407
		2521	vvw	${29}_0^2$		2 × 1261 = 2522
		2531	w	$6_0^1{34}_0^2$	1402 + 1129 = 2531
		2605	vvw	${13}_0^2{34}_0^2$	1477 + 1129 = 2606
		2606	vvw	${13}_0^2{38}_0^2$	1477 + 1133 = 2610
		2679	vw	${13}_0^1{31}_0^2$	740 + 1943 = 2683
		2725	vw	${27}_0^2$		2 × 1366 = 2732
		2845	w	$3_0^1$		2876
		2851	w	${28}_0^2$		2 × 1438 = 2876
		2999	w	${26}_0^2$		2 × 1502 = 3004
		3015	vvw	$2_0^1$		3024
		3068	vvw	$1_0^1$		3045

¹Relative to $0_0^0$ band at 37 093.6 cm⁻¹; the relative intensities are indicated s-stong, m-medium, w-weak, v-very.

²Inferred from other spectroscopic transitions (FES, IR, Raman, and ultraviolet).

³CASSCF(6,6)/aug-cc-pVTZ calculations. Scaling factor: 0.905.

Figure 6.

Energy map for the low frequency vibrations of BCB in its S₀ ground and S₁(π,π^*) excited states. The levels at 417 and 411 cm⁻¹ are in Fermi resonance.

Table 4.

Skeletal vibrational frequencies (cm⁻¹) of BCB and related molecules in the ground (S₀) and excited (S₁) state.

		S0						S1(π,π*)
		BCB	IND	TET	14BZD	13BZD	14DHN	BCB	IND	TET	14BZD	13BZD	14DHN
A1	Benzene C–C stretch	1605	1589	1581	1599	1587	1571	1646	(1627)	(1640)	(1502)	(1608)	(1625)
	Benzene C–C stretch	1466	1474	1496	1500	1503	1497	1491	(1493)	(1531)	(1498)	(1559)	(1518)
	Benzene C–C stretch	1344	1318	1295	1307	1309	1288	1370	(1409)	(1435)	(1391)	(1381)	1337
	Benzene C–C stretch	1001	1025	1035	1028	1035	1041	892	(934)	971	994	(1051)	951
	Benzene angle bend	539	610	578	566	588	586	464	460	480	531	525	459
A2	Benzene ring twist	670	(714)1	700	717	712	703	440	485	521	(502)	682	(447)
	Benzene ring twist	486	499	501	553	536	510	314	345	330	363	374	(360)
	Skeletal twist	208	178	142	166	158	148	153	137	94	140	102	92
B1	Benzene C–C stretch	1596	1610	1598	1602	1614	1603	1500	(1446)	(1449)	(1566)	(1665)	(1415)
	Benzene C–C stretch	1458	1460	1437	1462	1460	1460	1364	(1394)	(1406)	(1437)	(1481)	(1406)
	Benzene ring bend	855	832	804	834	853	885	819	(821)	(764)	888	(750)	867
	Benzene ring bend	634	579	586	643	698	765	564	535	545	(530)	(574)	(707)
B2	Benzene ring bend	386	412	436	(466)	430	427	245	273	270	(370)	255	298
	Ring flap	209	248	257	297	274	231	105	176	(140)	(119)	194	115
	Reference	8	1	2	3, 4, 5	6	7	This work	1	2	3, 4, 5	6	7

¹Frequencies in parentheses are calculated values.

There are a number of noteworthy features regarding the BCB vibrations. The molecule is rigidly planar in its S₀ ground state but still has two very low-frequency out-of-plane ring modes, ν₂₂ (A₂) skeletal twisting between the two rings at 208 cm⁻¹ and ν₄₂ (B₂) ring flapping at 209 cm⁻¹. The near coincidence of these frequencies was demonstrated by observation of their infrared and Raman band types.⁸ From the UV spectrum in our present study we find that the overtone levels of these vibrations are in Fermi resonance and occur at 411 and 417 cm⁻¹ with mixed 2ν₂₂ and 2ν₄₂ character. Aside from the Fermi interaction, as can be seen in Figure 6, both ν₂₂ and ν₄₂, as well as two other relatively low frequency vibrations ν₄₁ (B₂), the benzene ring out-of-plane bending, and ν₂₁ (A₂), the benzene ring twisting, are all nearly harmonic. This is quite different from the other bicyclic molecules under discussion where the external rings display highly anharmonic character. As can be seen in Table 4, the skeletal twisting frequency for BCB is the highest at 208 cm⁻¹ whereas for the other five molecules it is in the 142–178 cm⁻¹ range. On the other hand, the ring-flapping vibration, which is also a reflection of the rigidity of the molecule, has the lowest value of 209 cm⁻¹ while the frequencies for the related molecules are between 231 and 297 cm⁻¹. This is in part be due to coupling with the out-of-plane benzene ring bending of the same symmetry which in fact is lower for BCB (386 cm⁻¹) than for the related molecules (412–466 cm⁻¹). Of particular interest for us is what happens to the vibrational frequencies in the S₁(π,π^*) excited states of all these molecules. And, specifically, we are most interested in the low-frequency out-of-plane modes. Table 4 shows, as expected, that for the most part the benzene ring modes show modest frequency decreases in the S₁(π,π^*) states as the extent of π bonding is decreased. The out-of-plane modes, however, show the greatest changes. For BCB the skeletal twisting drops from 208 to 153 cm⁻¹ while the related molecules show drops of 26–56 cm⁻¹ for the same mode. The ring-flapping frequency of BCB drops even more dramatically from 209 to 105 cm⁻¹. Similarly, large frequency drops of 72–178 cm⁻¹ occur for the other bicyclic molecules. The out-of-plane benzene ring modes which are ν₂₀ (A₂), ν₂₁ (A₂), and ν₄₁ (B₂) for BCB also show sizable frequency differences between the S₀ and S₁(π,π^*) states due to the decrease in ring rigidity resulting from the π → π^* transition. For BCB the frequency decreases are 670–440 cm⁻¹, 486–314 cm⁻¹, and 386–245 cm⁻¹, respectively. The other bicyclic systems show similar decreases.

CONCLUSIONS

Ab initio computations have been carried out to calculate the structure of benzocyclobutane in its S₁(π,π^*) excited state and to compare it with the S₀ ground state. The results were compared to similar computational results for the ground and excited states of five related molecules. The ab initio calculations were also helpful in assigning the fluorescence excitation and ultraviolet absorption spectra. The majority of the vibrational frequencies, including all of the low-frequency modes, were assigned for the excited state and compared to the ground state data. Of special interest were the large frequency decreases of the out-of-plane skeletal and benzene ring modes in the excited state reflecting the decreased molecular rigidity resulting from a decrease in the π bonding.