Electromechanical characterization of $\text{Pb}\left({\text{In}}_{0.5}{\text{Nb}}_{0.5}\right){\text{O}}_3–\text{Pb}\left({\text{Mg}}_{1/3}{\text{Nb}}_{2/3}\right){\text{O}}_3–{\text{PbTiO}}_3$ crystals as a function of crystallographic orientation and temperature

Abstract

Relaxor based $\text{Pb}\left({\text{In}}_{0.5}{\text{Nb}}_{0.5}\right){\text{O}}_3–\text{Pb}\left({\text{Mg}}_{1/3}{\text{Nb}}_{2/3}\right){\text{O}}_3–{\text{PbTiO}}_3$ ternary single crystals (PIN-PMN-PT) were reported to have broader temperature usage range $\left(T_{R\text{-}T}\right)$ and comparable piezoelectric properties to $\text{Pb}\left({\text{Mg}}_{1/3}{\text{Nb}}_{2/3}\right){\text{O}}_3–{\text{PbTiO}}_3$ (PMNT) crystals. In this work, the orientation dependent dielectric, piezoelectric and electromechanical properties for PIN-PMN-PT crystals were investigated along $⟨001⟩$ and $⟨110⟩$ directions. The electromechanical couplings $k_{33}$ and $k_{32}$ for $⟨110⟩$ poled crystals were found to be 0.91 and 0.91, respectively, with piezoelectric coefficients $d_{33}$ and $d_{32}$ on the order of 925 and −1420 pC/N. Of particular significance was the mechanical quality factor $Q_{33}$ for $⟨110⟩$ oriented crystals, which was found to be $\ge 500$, much higher than the Q values of $⟨001⟩$ oriented relaxor-PT crystals $\left(Q\sim 70–200\right)$. The temperature dependence of the piezoelectric properties exhibited good temperature stability up to their ferroelectric phase transition $T_{R\text{-}T}\sim 125°\text{C}$, indicating $⟨001⟩$ and $⟨110⟩$ oriented PIN-PMN-PT are promising materials for transducer applications, with the latter for high power resonant devices where low loss (high Q) was required.

INTRODUCTION

Recently, extensive research has been carried out on relaxor-PT ferroelectric single crystals. As reported, domain engineered $\text{Pb}\left({\text{Zn}}_{1/3}{\text{Nb}}_{2/3}\right){\text{O}}_3–{\text{PbTiO}}_3$ (PZNT) and $\text{Pb}\left({\text{Mg}}_{1/3}{\text{Nb}}_{2/3}\right){\text{O}}_3–{\text{PbTiO}}_3$ (PMNT) crystals oriented along the pseudocubic $⟨001⟩$ direction exhibit high electromechanical coupling factors and piezoelectric coefficients for longitudinal mode. Electromechanical coupling factors on the order of $>0.90$ and piezoelectric coefficients higher than 1200 pC/N are common for all relaxor-PT single crystals.^{1, 2, 3, 4} The transverse piezoelectric response for relaxor-PT perovskite crystals is more complicated, where it has been reported that there are four different vibration modes showing good piezoelectric characteristics. These modes are $\left(001\right)/⟨100⟩$, $\left(001\right)/⟨110⟩$, $\left(110\right)/⟨001⟩$, and $\left(110\right)/⟨-110⟩$, where the first number indicates the electrode face and the second number is the acoustic wave propagation direction.⁵ It has been demonstrated that the highest transverse piezoelectric coefficients are obtained from crystals poled along $⟨110⟩$ and vibrated along the $⟨001⟩$ direction,^{5, 6, 7, 8, 9, 10} with small signal $d_{32}$ coefficients on the order of $\sim -1500\text{\hspace{0.5em}pC}/\text{N}$ and electromechanical coupling factor $k_{32}\sim 0.90$ in PZNT and PMNT crystals.

Regardless of the excellent piezoelectric properties found in PZNT and PMNT ferroelectric crystals, the crystals exhibit relatively low Curie and ferroelectric phase transition temperatures $\left(T_{R\text{-}T}\sim 60–95°\text{C}\right)$, limiting the operating temperature range. Thus, numerous studies are focusing on exploring new high performance ferroelectric crystals with higher Curie and ferroelectric phase transition temperatures. Based on the reported data in polycrystalline relaxor-PT systems, crystal growth has been carried out on the $\text{Pb}\left({\text{Sc}}_{0.5}{\text{Nb}}_{0.5}\right){\text{O}}_3–{\text{PbTiO}}_3$, $\text{Pb}\left({\text{In}}_{0.5}{\text{Nb}}_{0.5}\right){\text{O}}_3–{\text{PbTiO}}_3$, $\text{Pb}\left({\text{Yb}}_{0.5}{\text{Nb}}_{0.5}\right){\text{O}}_3–{\text{PbTiO}}_3$, and ${\text{BiScO}}_3–{\text{PbTiO}}_3$ systems, using high temperature solution and/or flux Bridgman methods.^{11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} Though the crystals obtained were confirmed to exhibit high $T_{C}s$ and $T_{R\text{-}T}s$, their implementations were restricted by the crystal size and/or crystal quality. More recently, solid state crystal growth of PMN-PZ-PT^{22, 23, 24} and melt Bridgman growth of PIN-PMN-PT^{25, 26, 27} ternary single crystals have been reported, showing broadened temperature usage range $T_{R\text{-}T}>100°\text{C}$. These crystals can be grown to large size and of high quality. In addition to the efforts to improve $T_{R\text{-}T}$, higher mechanical Q values in the relaxor-PT ferroelectric crystals have been observed in recent studies. The Q was found to be a function of composition and crystallographic directions, while maintaining electromechanical coupling on the order of 0.90.²⁸

In this work, ternary PIN-PMN-PT single crystals with high $T_{R\text{-}T}$$\left(>125°\text{C}\right)$ were selected for further investigation along different crystallographic orientations $⟨001⟩$ and $⟨110⟩$ for longitudinal/transverse modes. The temperature dependence of the dielectric, piezoelectric, and electromechanical behaviors were explored for use at elevated temperature.

EXPERIMENTAL

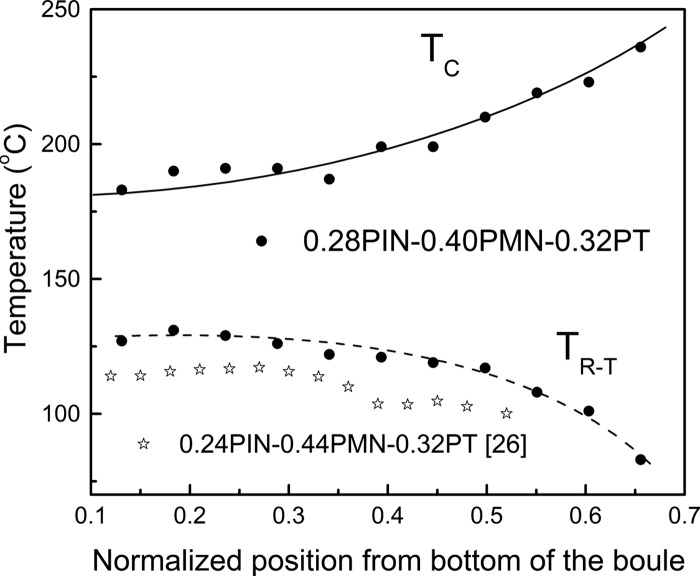
Ternary $x\text{PIN-}\left(1-x-y\right)\text{PMN-}y\text{PT}$$\left(x>0.2\sim 0.4;y>0.28\sim 0.33\right)$ rhombohedral single crystals grown by Bridgman method were investigated in detail. These crystals demonstrated improved temperature stability and broadened operating temperature range.²⁷ Due to the different segregation ratio of the ions in crystal, the grown single crystal boules exhibited compositional variation along the growth direction. The composition along the growth direction was determined by electronic probe microanalysis, the PIN variation was found to be less than 2% from the bottom to the top of the crystal boule (100mm in length and 50mm in diameter). In contrast, the variations are found to be on the order of 5% and 7% for PMN and PT, respectively. Figure 1 shows Curie temperatures $\left(T_C\right)$ and rhombohedral to tetragonal phase transition $\left(T_{R\text{-}T}\right)$ temperatures for $⟨001⟩$ poled crystals, cut from different positions along the growth direction of a nominal 0.28PIN–0.40PMN–0.32PT crystal. 20%–30% of the crystal boule belongs to the tetragonal phase due to the high PT content. It was found that the Curie temperature ranged from 175 to $230°\text{C}$, while $T_{R\text{-}T}$ fell in the range of $138-90°\text{C}$ along the growth direction. Compared to 0.24PIN–0.44PMN–0.32PT crystal from Ref. 26, the $T_{R\text{-}T}$ was found to be increased by $15–20°\text{C}$. It was observed that one third of the grown 0.28PIN-0.40PMN-0.32PT crystals possessed $T_{R\text{-}T}$ in the range of $120–130°\text{C}$ and exhibited high piezoelectric properties.

Figure 1.

Curie temperature and ferroelectric phase transition temperature along the growth direction for 0.28PIN–0.40PMN–0.32PT single crystal.

In this work, the 0.28PIN-0.40PMN-0.32PT crystals were grown using the modified Bridgman technique. The crystals were oriented using real-time Laue X-ray and cut to obtain longitudinal rods and transverse bars with the aspect ratios following IEEE piezoelectric standards.^{21, 29} All the samples were oriented along $⟨001⟩$ and $⟨110⟩$ directions and vacuum sputtered gold was applied as the electrodes. For the transverse mode, configurations used in this study were bars with electrodes on (001) or (110) faces and length (vibration) along $⟨100⟩/⟨110⟩$ and $⟨001⟩/⟨-110⟩$ directions. All samples were poled by applying 10 kV/cm dc electric field at a temperature of $140°\text{C}$. High field polarization and strain measurements were performed on the $⟨001⟩$ and $⟨110⟩$ oriented plate samples at room temperature at a frequency of 1Hz, using a modified Sawyer–Tower circuit and linear variable differential transducer driven by a lock-in amplifier. Room temperature dielectric, piezoelectric, electromechanical properties, and the mechanical loss (inverse of Q) were determined for longitudinal and transverse modes according to IEEE standards, by using HP4194A Impedance-phase gain analyzer. The dielectric temperature dependence was measured using a multifrequency LCR meter (HP4284A), connected to a computer controlled temperature chamber. The high temperature piezoelectric and electromechanical characteristics were obtained from an impedance analyzer connected to a temperature chamber. In order to minimize the stress effects on the samples during the measurement, thin silver wires were attached on the electrodes using a small amount of high temperature conductive silver.

RESULTS AND DISCUSSION

Dielectric properties

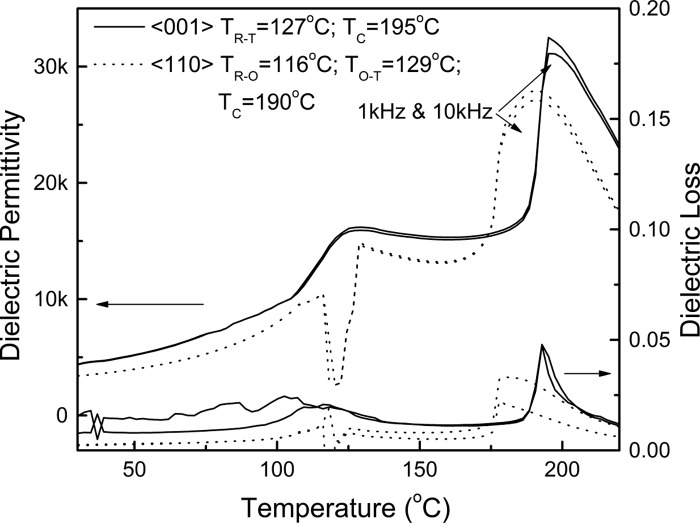
Figure 2 shows the dielectric behavior as a function of temperature for $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT single crystals, measured at frequencies of 1 and 10 kHz, respectively. The Curie temperature $T_C$ and ferroelectric phase transition temperatures can be determined by the temperature where the dielectric permittivity reaching its peak values. Thus, the $T_C$ and rhombohedral to tetragonal phase transition temperature $T_{R\text{-}T}$ were found to be on the order of 195 and $127°\text{C}$ for $⟨001⟩$ poled samples, respectively. In contrast, two ferroelectric phase transformations were observed below its Curie temperature for $⟨110⟩$ poled sample. A relatively low dielectric permittivity $\left(\sim 2700\right)$ in the temperature range of 116 and $129°\text{C}$ was found, which is believed to be related to an orthorhombic phase, bounded by a lower temperature domain engineered pseudorhombohedral phase and higher temperature tetragonal phase.^{10, 30} Thus, the two ferroelectric phase transformation temperatures can be confirmed to be rhombohedral to orthorhombic phase transition $T_{R\text{-}O}\sim 116°\text{C}$ and orthorhombic to tetragonal phase transition $T_{O\text{-}T}\sim 129°\text{C}$, while the Curie temperature was similar to $⟨001⟩$ poled samples.

Figure 2.

Dielectric permittivity and dielectric loss as a function of temperature for $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT single crystals, measured at 1 and 10 kHz frequencies.

High field ferroelectric properties

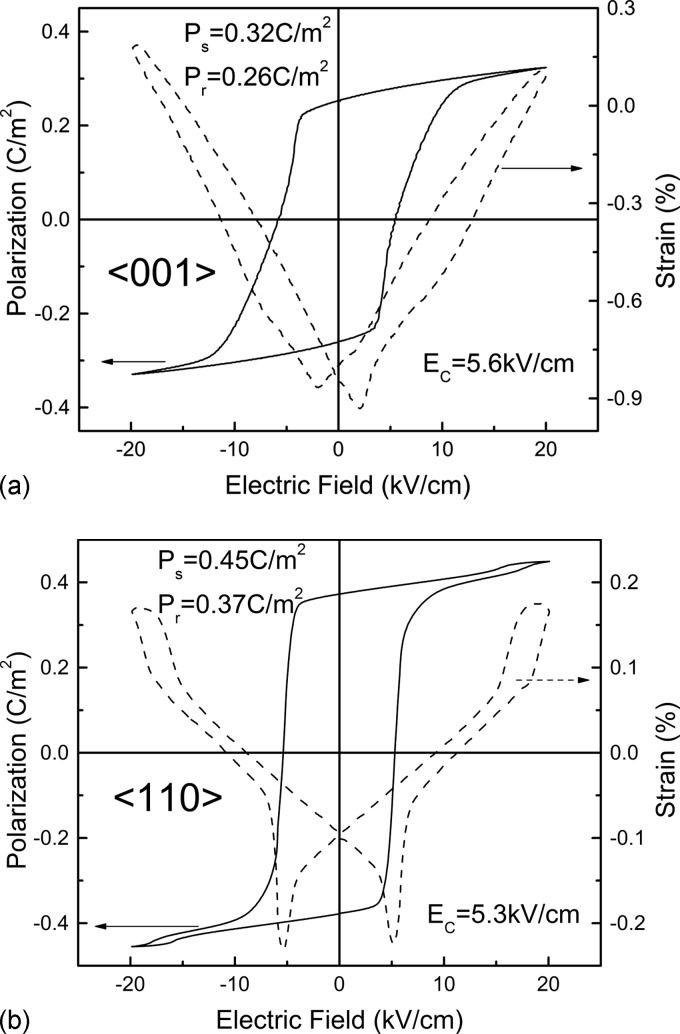
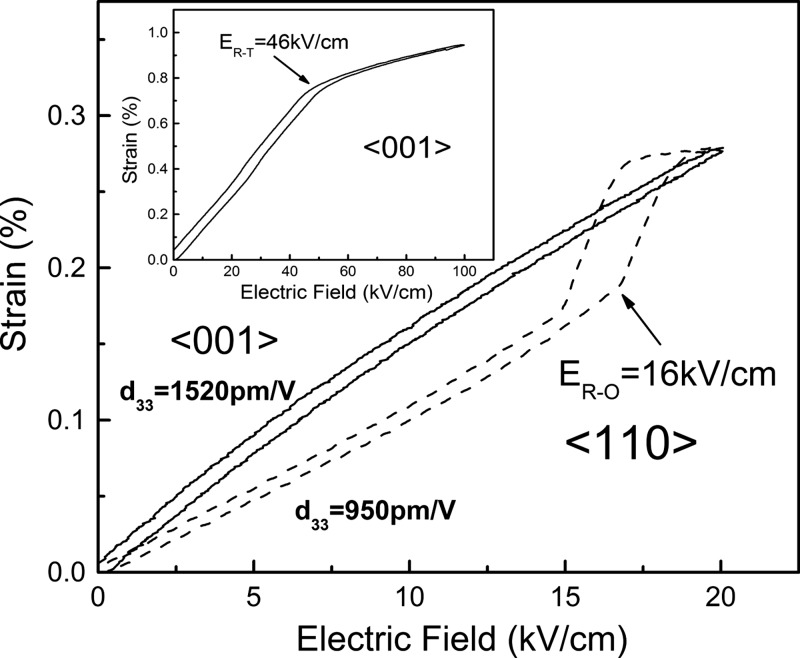
Figure 3 shows polarization hysteresis and butterfly strain loops for $⟨001⟩$ [Fig. 3a] and $⟨110⟩$ oriented [Fig. 3b] PIN-PMN-PT single crystals, respectively. It was found that the coercive field $E_C$, on the same order of $\sim 5\text{\hspace{0.5em}kV}/\text{cm}$ for both orientations, much higher than the binary PMNT counterpart $\left(\sim 2.5\text{\hspace{0.5em}kV}/\text{cm}\right)$. However, the spontaneous and remnant polarizations exhibited anisotropic behavior, with remnant polarization $P_r$ on the order of $0.26\text{\hspace{0.5em}C}/{\text{m}}^2$ for $⟨001⟩$ orientation, much lower than the value of the $⟨110⟩$ orientation $\left(P_r=0.37\text{\hspace{0.5em}C}/{\text{m}}^2\right)$. In rhombohedral ferroelectric single crystals, the spontaneous polarization is along the crystallographic $⟨111⟩$ direction. For the domain engineered single crystals along $⟨001⟩$ and $⟨110⟩$ directions, the $P_r$ will be lower than the value along the polar axis $⟨111⟩$, following $P_{r⟨001⟩}\sim 1/\sqrt{2}{P}_{r⟨110⟩}\sim 1/\sqrt{3}{P}_{r⟨111⟩}$.^{1, 8} As expected, the ratio of the obtained $P_r$ along $⟨001⟩$ and $⟨110⟩$ directions was indeed very close to the theoretical value. The unipolar strain behavior as a function of electric field for the $⟨001⟩$ and $⟨110⟩$ directions are given in Fig. 4. The slope of the strain electric field curve for the $⟨110⟩$ orientation was found to be $\sim 950\text{\hspace{0.5em}pm}/\text{V}$, lower than the value of $⟨001⟩$ orientation $\sim 1520\text{\hspace{0.5em}pm}/\text{V}$, both values are similar to the piezoelectric $d_{33}$ obtained according to IEEE standards (as listed in Table 1). The electric field induced phase transformation for $⟨001⟩$ orientation was found to occur at an electric field of $\sim 46\text{\hspace{0.5em}kV}/\text{cm}$ (as shown in the small inset of Fig. 4), while the rhombohedral to orthorhombic phase transformation occurred at a field of $\sim 16\text{\hspace{0.5em}kV}/\text{cm}$ for $⟨110⟩$ orientation, much lower than the threshold for $⟨001⟩$ oriented crystals. The lower threshold electric field indicates the polarization rotation is much easier to be induced through an intermediate phase $M_B$ (“structure bridge” which is anhysterestic in character) when the field applied along $⟨110⟩$ direction, as observed in PMNT crystals.^{30, 31}

Figure 3.

Bipolar polarization hysteresis and strain butterfly loops for $⟨001⟩$ (a) and $⟨110⟩$ (b) oriented PIN-PMN-PT single crystals.

Figure 4.

Unipolar strain behavior as a function of electric field for $⟨001⟩$ and $⟨110⟩$ oriented crystals, showing the electric field induced phase transformation.

Table 1.

Longitudinal and transverse piezoelectric and electromechanical properties for $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT crystals.

PIN-PMN-PT		$K_{ij}$	Loss(%)	$k_{ij}$	$d_{ij}$ (pC/N)	$s_{jj}{}^E$$\left({\text{pm}}^2/\text{N}\right)$	$Q_{ij}$
Longitudinal$ij=33$	001	4400	0.4	0.92	1500	68.0	160
	110	3400	0.2	0.91	925	34.8	500
$ij=31$$ij=31\left(45°\right)$$ij=32$$ij=31$	001/100	4400	0.4	0.50	−700	51.2	150
	001/110	4400	0.4	0.81	−800	25.0	150
	110/001	3400	0.2	0.91	−1420	83.1	200
	110/−110	3400	0.2	0.74	590	21.5	210

Room temperature piezoelectric properties of the PIN-PMN-PT crystals

The main properties for longitudinal and transverse modes at room temperature are listed in Table 1. The dielectric permittivity was found to be on the order of 4400 and 3400 for $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT crystals, respectively, while the dielectric losses were 0.4% and 0.2%, respectively. The longitudinal electromechanical coupling factor $k_{33}$ was found to be 0.92 for $⟨001⟩$ samples, slightly higher than that of $⟨110⟩$ poled crystals $\left(\sim 0.91\right)$. The piezoelectric $d_{33}$ was on the order of 1500 pC/N for the $⟨001⟩$ cut, higher than the value for $⟨110⟩$ oriented sample $\sim 925\text{pC}/\text{N}$. Of particular significance was the mechanical quality factor Q, being greater than 500 for $⟨110⟩$ poled crystals, much higher than the values along $⟨001⟩$$\sim 160$. The low dielectric loss and high Q along the $⟨110⟩$ direction are believed to relate to the different engineered domain patterns as compared to $⟨001⟩$ orientation, as observed in all relaxor-PT single crystals.²⁸ The typical extensional transverse modes for perovskite ferroelectric crystal were summarized in Table 1, where the first number indicates the poling direction and the second number gives the vibration orientation. Unlike $⟨001⟩$ poled samples, a large discrepancy between the piezoelectric $d_{31}$ and $d_{32}$ was observed in $⟨110⟩$ poled crystals. The optimal transverse properties were found for $\left(110\right)/⟨001⟩$ cut (polarized along $⟨110⟩$ with vibration along $⟨001⟩$ direction), with electromechanical coupling factor $k_{32}$ on the order of 0.91 and corresponding piezoelectric $d_{32}$ on the order of −1420 pC/N. Higher mechanical Q values were also observed in the transverse mode for samples poled along $⟨110⟩$ direction. It was found that the elastic compliances $s_{ij}$, which is relate to the speed of sound in the materials, exhibited strong anisotropic characteristics for both longitudinal and transverse modes, revealing that the acoustic wave propagating along the $⟨110⟩$ direction was much higher than the $⟨001⟩$ direction. The velocity difference is assumed to be related to the engineered domain configurations and the chemical bonds along different orientations, where a more compact crystal lattice should have higher velocity. This is under further investigation.

Piezoelectric properties as function of temperature

Figure 5 presents the temperature dependent characteristics of the longitudinal electromechanical coupling [Fig. 5a] and piezoelectric [Fig. 5b] properties for $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT crystals. The $k_{33}$ for $⟨001⟩$ poled crystals was found to be on the order of 0.91 at $-50°\text{C}$, increasing to 0.94 at $125°\text{C}$, the ferroelectric phase transition temperature, above which, the $k_{33}$ decreased to only 0.78. In contrast, the coupling for the $⟨110⟩$ poled crystals was $>0.90$ at $-50°\text{C}$, slightly increased to 0.93 at a temperature of $116°\text{C}$, above which, $k_{33}$ dropped due to the $R\text{-}O$ phase transformation. The $O\text{-}T$ phase transition at $130°\text{C}$ was also observed in the coupling measurement. The piezoelectric coefficient $d_{33}$, shown in Fig. 5b, followed a similar trend as found in the electromechanical coupling behavior, reaching its peak value at the ferroelectric phase transition temperatures.

Figure 5.

Longitudinal electromechanical coupling factor $k_{33}$ (a) and piezoelectric coefficient $d_{33}$ (b) as a function of temperature for $⟨001⟩$ and $⟨110⟩$ poled single crystals.

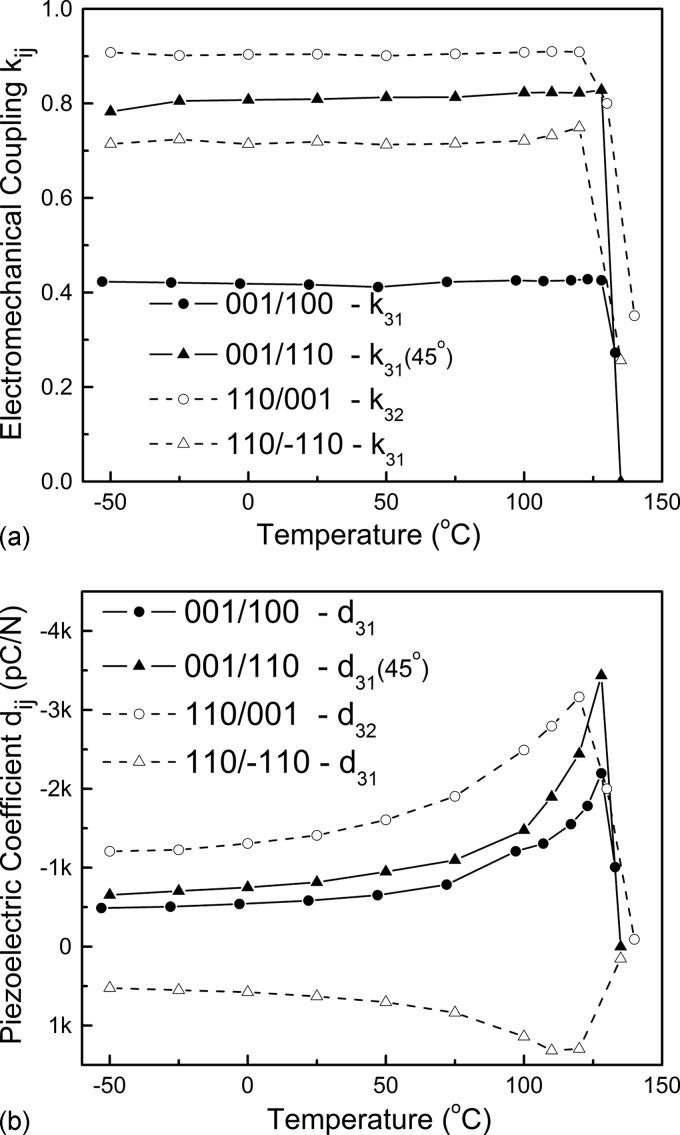
Figure 6 gives the temperature dependent behavior of the transverse electromechanical coupling [Fig. 6a] and piezoelectric [Fig. 6b] properties for $⟨001⟩$ and $⟨110⟩$ poled samples along different vibration directions. It was found that the electromechanical coupling factors $k_{ij}$ for different poling and vibration directions followed similar tendency, maintaining their values in the temperature range from $-50°\text{C}$ to $T_{F\text{-}F}$ (ferroelectric phase transition temperature). The coupling factors were found to drop sharply above the phase transition temperature, where the crystals transformed to the tetragonal and/or orthorhombic phases. The piezoelectric coefficients $d_{31}$ and $d_{32}$ (considering the symmetry $\text{mm}2$ in $⟨110⟩$ oriented crystal, the value of $d_{31}$ is assumed to be positive, while $d_{32}$ is negative) showed similar temperature dependent behavior as found for the transverse coupling, reaching peak values close to the ferroelectric transition temperature, above which, the transverse piezoelectric response disappeared. From the temperature dependent properties, both $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT crystals exhibited very stable temperature dependent characteristics when compared to PMNT crystals, with a $30–40°\text{C}$ higher usage temperature range.

Figure 6.

Transverse electromechanical coupling factor $k_{31}/k_{32}$ (a) and piezoelectric coefficient $d_{31}/d_{32}$ (b) as a function of temperature for $⟨001⟩$ and $⟨110⟩$ poled single crystals.

CONCLUSION

In conclusion, the dielectric, piezoelectric, electromechanical, and mechanical properties were investigated as a function of orientation and temperature for PIN-PMN-PT single crystals. The longitudinal electromechanical coupling for $⟨110⟩$ poled crystals showed similar value as for $⟨001⟩$ orientation, while the transverse piezoelectric for $\left(110\right)/⟨001⟩$ cut exhibited much higher values when compared to $⟨001⟩$ poled crystals. Of particular significance is the low dielectric loss and high mechanical quality factor for $⟨110⟩$ poled samples, which relates to the engineered domain configurations. Together with its broadened usage temperature range ($30–40°\text{C}$ higher than the binary PMNT crystal), the $⟨001⟩$ and $⟨110⟩$ poled PIN-PMN-PT crystals show promise for transducer and actuator applications, with the $⟨110⟩$ poled crystals being an excellent candidate for high power applications where low losses are required.