Abstract
Design and fabrication of electronic biosensors based on field-effect-transistor (FET) devices require understanding of interactions between semiconductor surfaces and organic biomolecules. From this perspective, we review practical considerations for electronic biosensors with emphasis on molecular passivation effects on FET device characteristics upon immobilization of organic molecules and an electrostatic model for FET-based biosensors.
INTRODUCTION
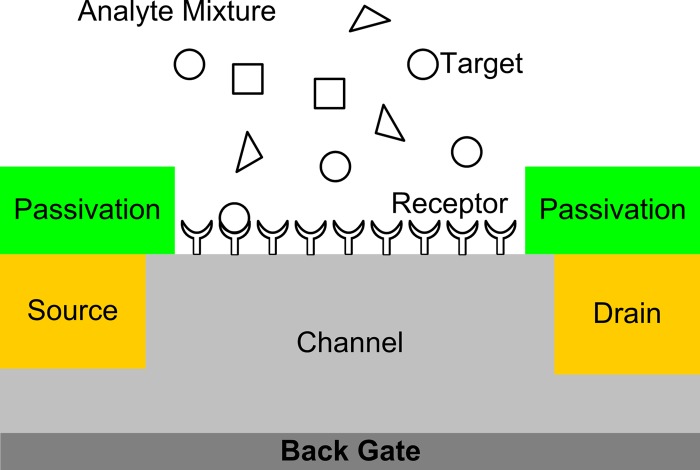
Label-free detection of bioanalytes using field-effect-transistor (FET)-based sensors is an attractive technology to realize point-of-care or home-care diagnosis systems because of its potential for enabling small, low-cost, high-sensitivity detectors with integrated microelectronics for signal detection, processing, and output. A number of different studies have demonstrated conductance-based sensors employing a molecular receptor layer immobilized on the surface of a semiconductor device, as illustrated schematically in Fig. 1. The receptor molecules provide the means to achieve highly selective sensing because they can be engineered to have much higher binding affinities with the desired target molecules than the other species in the analyte solution. Various device geometries have been reported, including planar FETs, nanowire (NW) FETs, and carbon nanotube (CNT) FETs.1, 2, 3, 4, 5, 6, 7, 8, 9 Most of the one-dimensional biosensors expose the semiconducting NW or CNT directly to biological solutions immediately after appropriate surface functionalization, whereas previously reported planar FET biosensors have traditionally passivated the semiconductor surfaces with solid dielectrics (e.g., , SiN, etc.) to protect front-end complementary metal-oxide semiconductor processes from biological materials and solutions.1, 9 Such (soft) surface passivation provides flexibility in designing sensor devices by taking advantage of abundant, facile chemical synthesis schemes for functionalizing semiconductor and CNT surfaces.10, 11 However, design and fabrication of such FET biosensors require reliable biofunctionalization of semiconductor surfaces.
Figure 1.
Schematic of FET biosensor. The device consists of source and drain regions and a channel region. The channel region is functionalized with receptor molecules and exposed to an analyte solution. The receptor molecule is designed to bind specifically to certain target species in the analyte solution which induces changes in the electrical properties of the channel region. The source and drain regions are isolated from the analyte by a passivation material.
Detection of “target” analytes with biofunctionalized FETs involves diffusion of target analytes in solution onto the sensor surfaces, interaction of the analyte with the surface, and resultant modulation of device characteristics. Immobilized target molecules are located at least a few nanometers above the semiconductor surfaces and are surrounded by counterions in the analyte solution; therefore net in situ electrostatic effects and their influence on device channel conductivity must be modeled to estimate sensor device characteristics. In addition, device sensitivity is limited by the diffusion of target analytes to the sensor surface under low concentration conditions; therefore device geometry needs to be optimized to maximize device sensitivity in the presence of counterions in biological solutions. The effect of device dimensions on detection limit has been discussed, addressing the difficulty of femtomolar detection within a practical incubation time.12 Furthermore, optimization of the device structure and operating conditions can also affect FET-biosensor performance, as will be discussed later in details. Although detection of target analytes with functionalized FET devices has typically been demonstrated by real-time measurement of conductivity modulation, such optimization requires comparison of complete FET characteristics upon exposure of the sensor to analyte, which may offer additional insights into the mechanisms by which direct electrical sensing can be achieved. Hence, the combination of thorough electrical characterization and development of electrostatic models which consider environmental as well as device issues will also be critical in manufacturable FET-biosensor development.
In this review article, we discuss practical device considerations for FET biosensors, addressing the issues mentioned above. In Sec. 2, molecular passivation of Si and GaAs surfaces is overviewed with emphasis on biosensor applications. These case studies highlight general considerations relating to chemical and electrical surface passivation, which are critical for sensing applications. Molecular passivation effects on FET device characteristics are presented in Sec. 3. Next, physical models related to biosensor response are reviewed in details in Sec. 4. Finally, comments on selectivity and nonspecific adsorption are considered in Sec. 5.
MOLECULAR FUNCTIONALIZATION OF SILICON AND GALLIUM ARSENIDE SURFACES
A variety of compounds including silicon carbide, nitride materials, and diamond have been proposed as potential channel materials for FET biosensors. In this paper, we will consider the functionalization of Si and GaAs in details. Silicon is an attractive material for FET-based sensors due to its technological relevance and maturity.13 The processing and physical insights that have been developed for integrated circuit fabrication can be adapted to sensors. GaAs is another attractive material for biosensing applications because it can be covalently functionalized by direct thiol linkages. Many receptors of interest for biosensing applications have been modified with thiol groups for applications such as labeling with gold nanoparticles. This technology can be readily applied to the modification of the GaAs surface for FET-based sensors. Another attractive feature of GaAs is that it is a technologically relevant material for optoelectronics and high-performance applications; therefore processing techniques such as molecular beam epitaxy are well developed for this substrate, leading to a wealth of possible device structures. For these reasons, we choose these two semiconductors as case studies to consider functionalization effects; however the observations presented here can be generalized to a wide variety of semiconductor channel materials.
Silicon functionalization
To date, biofunctionalization of silicon has often been most achieved by using siloxane chemistry on oxidized silicon surfaces. Amine-terminated siloxane moieties such as 3-aminopropyltriethoxy-silane are attached to a hydroxyl-terminated silicon oxide surface using solution-phase techniques or vacuum desiccations. The films are typically cured at an elevated temperature, which induces crosslinking of the molecular layer. This results in a crosslinked film that is intermittently covalently attached to the oxide surface through silicon-oxygen bonds. Receptors are then attached to the resulting amine-terminated films. Although laboratory demonstrations have successfully been realized using this platform,3 there are several fundamental physical reasons that this modification scheme is not optimal for FET-based sensors. Biological buffers typically contain salts with small ions such as sodium, which are known to be mobile in silicon oxide. These mobile oxide charges are known to cause large threshold voltage shifts and other reliability issues that degrade metal-oxide-semiconductor field-effect transistor (MOSFET) performance; therefore silicon oxide surfaces should not be exposed in the active sensing region of such devices.14 In order to maximize sensor electrostatic response, it is desirable to maximize the insulator capacitance . The presence of the silicon native oxide in addition to the molecular layer adds an additional dielectric component between the target analyte and the active channel region, thereby reducing . The sensor response is also affected by the presence of interface traps. In the case of functionalized oxide surfaces, such traps can occur at the silicon/oxide interface, within the oxide, and at the oxide-molecule interface; therefore it is very important to have a high quality, well-characterized oxide. Because of these potential complications, it is desirable to eliminate the interfacial oxide layer for FET sensor structures.
Organic layers can be bound to silicon surface by direct silicon-carbon attachment chemistry. A variety of approaches including thermal, ultraviolet, radical, and electrochemical methods have been demonstrated on single crystal (111) and (100) silicon surfaces as well as on porous silicon.15, 16, 17, 18 Many small aliphatic and aromatic species have been successfully and covalently attached to silicon surfaces and chemically characterized. Silicon surfaces can be hydrogen terminated by etching in appropriate- fluorinated solutions; however these systems oxidize and degrade relatively quickly in ambient conditions.19 For steric reasons, covalently bound molecular layers other than methyl groups cannot pack densely enough to passivate every site on the silicon surface. The optimal packing density for alkene and small aromatic molecules is in the range of 50%.20 In spite of this, interface trap densities as low as have been inferred from surface recombination velocity measurements of as-modified methyl and alkene-terminated silicon (111) surfaces in air, and trap densities of have been determined for metallized alkene-terminated (111) Si surfaces using capacitance and conductance measurements.21, 22 These results indicate that small aliphatic molecules can offer exceptional electrical passivation for such surfaces. These low trap-density surfaces have been realized by grafting high quality monolayers to the Si surface and characterizing them using a variety of surface-science techniques. Most receptors for biological recognition are much bulkier and more complex than these simple molecules. Obtaining well-passivated surfaces with a variety of directly bound receptors is nontrivial. Problems that can arise from nonideal monolayer formation are shown schematically in Fig. 2. Bulky molecules that do not pack sufficiently can leave voids [Fig. 2d] in the monolayer, which offer incomplete electrical and chemical passivation. Such voids are prone to biofouling [Fig. 2f] and surface oxidation [Fig. 2g], both of which compromise the electrical response of the sensor. The receptor molecules must be designed such that they have a high specificity for the target to avoid nonspecific interactions [Fig. 2c] and well-defined bonding to the semiconductor surface to prevent nonspecific surface-receptor interactions [Fig. 2a]. Moreover, the passivation layer must have excellent chemical stability as substrate/monolayer reactions can cause formation of surface and suboxide [Figs. 2g, 2e] and surface radicals [Fig. 2b].23, 24
Figure 2.
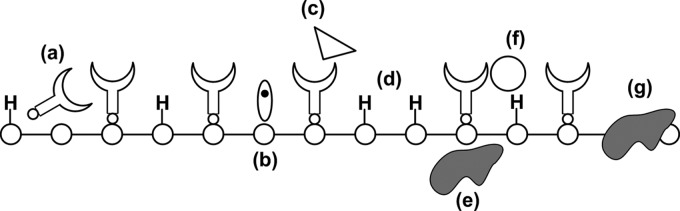
Nonideal modified semiconductor surface. For steric reasons, the receptor molecules cannot occupy every site on the semiconductor surface, leaving many surface atoms with termination such as hydrogen. Additional nonidealities include (a) nonspecific interaction of the receptor molecules with the surface, (b) dangling bonds or semiconductor surface radicals, [(c) and (f)] nonspecific interaction of the surface with analytes, (d) voids and defects in the receptor molecule film, (e) suboxide, and (g) surface oxide.
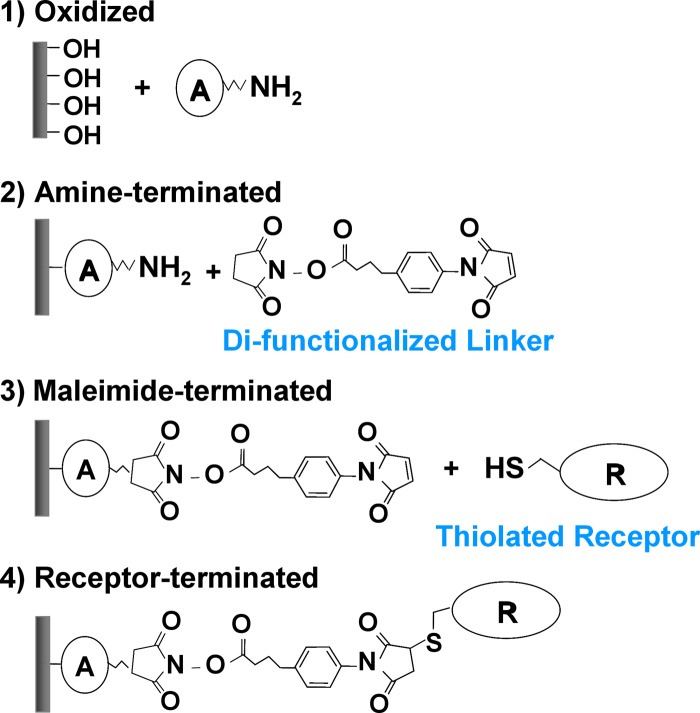
Any surface passivation schemes that are utilized for sensing applications must be carefully studied to ensure that such defects are not occurring in significant enough quantity to affect device performance. In order to functionalize devices in a manner that satisfies both the electrical and chemical recognition requirements for sensor performance, sequential reaction of appropriate well-passivated surfaces with receptors of interest is a promising approach. Figure 3 shows one example of such a functionalization scheme for Si surfaces, which typically involves two consecutive molecular immobilization steps to achieve amine termination and maleimide termination before attaching thiolated receptor molecules.11 Although receptor molecules are traditionally the focus of biosensor functionality, selection of linker molecules (e.g., component A in Fig. 3) can greatly affect the overall sensor device performance, depending on their packing density, bonding stability, and electronic/electrochemical properties. Surface passivation with linker molecules can induce significant modulation of device characteristics due to their intrinsic molecular dipoles/net charges or interactions with semiconductor surface states. In addition, since bulky receptor molecules usually result in poor packing density and a large number of unpassivated sites on the semiconductor surface, the semiconductor surface may be exposed to polar ions and nonspecific charged biomolecules in biological solutions. Therefore, selection of appropriate linker molecules is critical for minimizing nonspecific reactions of analyte material with the surface, thereby preventing “false” positives. Receptors such as DNA, antibodies, proteins, and carbohydrates have been attached to appropriate aliphatic-modified silicon surfaces.25, 26, 27, 28, 29 Sensitive, label-free detection of biological material has been demonstrated using oxide-free silicon NW FET structures.8, 30 Such devices demonstrate improved sensitivity compared to oxygen-containing interfaces.31
Figure 3.
An example of Si surface functionalization scheme for immobilization of thiolated receptor molecules. The component A can have an arbitrary chemical structure, which greatly affects the quality of molecular passivation and device characteristics.
Gallium arsenide functionalization
Direct covalent attachment of thiolated molecules onto GaAs surfaces has made GaAs an attractive substrate for high-quality molecular passivation. Sulfur passivation and self-assembled monolayers of alkanethiols [e.g., 1-octadecanethiol (ODT)] on GaAs (100) have been extensively investigated using atomic force microscopy, x-ray photoelectron spectroscopy (XPS), and Fourier transform infrared reflection absorption spectroscopy to study morphology, surface composition, and molecular conformation, respectively.23, 32, 33, 34, 35, 36, 37 The chemical composition of the GaAs surface can be tuned by chemical etching or by heating the substrate with varying As/Ga ratios. It has been observed from XPS measurements that sulfur can bond to both Ga and As surface atoms; however it bonds primarily to As on surfaces with large As/Ga ratios.32 HCl etching of native oxide on GaAs results in As-rich surfaces; therefore subsequent thiol modification takes place primarily via As–S bonding. Highly organized dense ODT monolayers can be formed on GaAs (100) by simple solution-cast self-assembly techniques, resulting in significant suppression of GaAs surface oxidation.34 For steric reasons, thiolated biomolecules, which typically have more than 1000 molar weight, cannot form dense surface passivation layers. In order to make a chemically stable, nonbiofouling surface, it is necessary to form a well-packed molecular passivation layer to immobilize biologically sensitive receptor molecules. A close analogy to this type of heterogeneous molecular layers can be found in cell membranes. The cell membrane is a semipermeable lipid bilayer which is typically about 5–10 nm thick and consists of two monolayers of fatty acids which function as cellular barriers to polar solutes. Membrane proteins either inserted into or anchored onto the lipid bilayer provide communication between the interior and exterior of the cell, so-called membrane transport. Considering this natural biosensing mechanism of cell membranes, it is of particular interest to develop methodologies for forming chemically sensitive molecular passivation schemes that are conceptually similar to cell membrane structures. Investigation of DNA hybridization in mixed monolayers of alkanethiols and DNA self-assembled on gold surfaces has confirmed the preservation of the biological activity in such artificial heterogeneous systems.38, 39 Heterogeneous molecular layers composed of ODT and a peptide sequentially self-assembled on GaAs (100) have been also studied by angle-resolved XPS, investigating a degree of surface oxidation, surface composition, and surface coverage of the mixed monolayers formed in different solvent systems.40 It has been experimentally shown that this mixed monolayer can protect GaAs surfaces from polar ions while retaining the original recognition property of the peptide.41
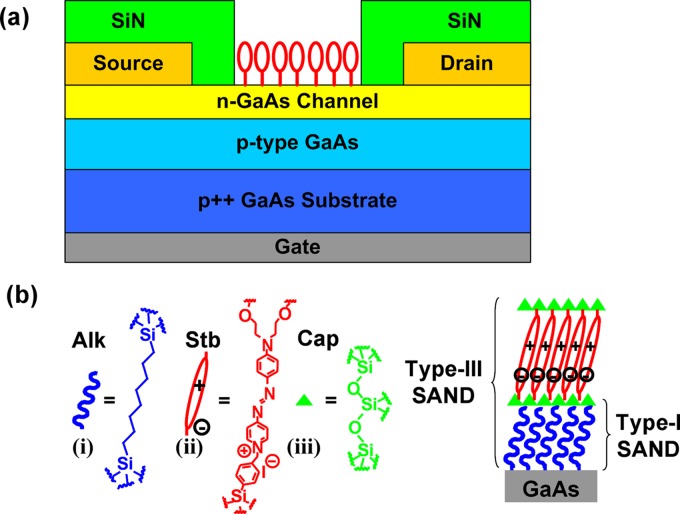
In addition to chemical passivation and bioactivity, reliable electrical passivation of semiconductor surfaces is necessary to achieve good response for FET sensors. This is particularly important for GaAs because of large inherent surface state densities near midgap and the resulting surface Fermi level pinning.42 Also, it has been shown that a physically well-organized monolayer such as ODT self-assembled on GaAs does not guarantee high-quality electrical passivation, leaving the surface Fermi level pinned at midgap.43 Recently, unpinning of GaAs surface Fermi level has been demonstrated by applying silane chemistry to hydroxyl-terminated GaAs surfaces.44, 45 A thin oxide layer with hydroxyl termination is formed by treating GaAs surfaces with and organic multilayers of self-assembled organic nanodielectrics (SAND) were sequentially deposited on the GaAs surface using solution-cast self-assembly techniques reported previously.46 The SAND consists of a sequence of three building blocks, as shown in Fig. 4: (i) α, ω-alkyl double silane (Alk), (ii) highly polarizable push-pull chromaphore layer (Stb) that has strong dipole moment, and (iii) capping layer (Cap) to planarize, crosslink, and seal pinholes.46 These building blocks can be combined into three distinct films: type I , type II, and type III . GaAs metal-insulator-semiconductor field-effect transistors were fabricated using three stacks of type-III SAND as a gate insulator, and an order of magnitude reduction in interface trap density was reported with enhanced capacitance-voltage modulation and typical depletion-mode FET output characteristics.45 In fact, these materials have been utilized as gate insulators for organic thin film transistors (TFTs) and flexible NW FETs, demonstrating the stability and robustness of such organic multilayers.46, 47, 48, 49 Investigation of such molecular layers in planar FET device configurations may provide insights into reliable molecular passivation methodologies for FET biosensors.
Figure 4.
(a) GaAs JFET device structure. (b) Molecular structures of type-I and type-III SANDs with components Alk, Stb, and Cap.
MOLECULAR PASSIVATION EFFECTS ON DEVICE CHARACTERISTICS
The primary sensing mechanism for FET biosensors has been attributed to changes in net surface charge density upon conjugation of receptor and target analytes, which modulates the semiconductor surface potential, thereby modulating channel conductivity and inducing shifts . In addition to this effect, it is important to consider changes in interfacial traps and/or surface states due surface functionalization and immobilization of target analytes. The presence of surface states reduces semiconductor surface potential modulation. Minimizing this effect requires an interface trap density well below the , which is typically associated with Fermi level pinning. Given typical atomic surface densities (a few times ), this implies that suitable passivation layers must be able to electrically passivate the vast majority of the surface atomic bonds. Alternate, potentially improved detection mechanisms can be achieved by considering dynamic electronic interactions between conduction carriers and surface states generated by target analytes. Hence, it is essential to investigate the effects of immobilized organic molecules on semiconductor device characteristics in terms of fixed surface charges , surface states from semiconductor surfaces , and surface states from molecules . It will also be critical to understand changes in these variables over time to determine the reliability of molecular passivation for time frames and environments of interest.
For this type of investigation, planar devices are preferred over NW or CNT devices because changes in and can be more accurately estimated from measured device characteristics such as threshold voltage , subthreshold slope , and hysteresis using well-established device physics. While many NW sensor studies to date have reported two-terminal device characteristics, three-terminal characteristics provide important information that can be used to quantify the nature of the response. For example, is sensitive to molecular charge states as well as device structure and interface trap states. Given the time dynamics of molecular diffusion, it is typically possible to obtain current-voltage characteristics in a short time compared to overall molecular response. Understanding the interactions between semiconductors and immobilized organic molecules via three-terminal planar devices will lead to more sophisticated design and optimization of FET-based NW biosensors. In this section, modulation of device characteristics due to immobilized organic molecules is discussed with emphasis on surface potential change due to net surface charges, surface state control, and dynamic electronic interactions between semiconductors and immobilized organic molecules.
Surface potentials of functionalized semiconductors
Planar field-effect devices have been considered for chemical and biological sensors since the first demonstration of ion-sensitive field-effect transistors (ISFETs) as sensors.50 In typical ISFET sensors, the gate insulator (e.g., ) is exposed to an electrolyte solution with its traditional metallic gate replaced by a reference electrode inserted into the electrolyte solution. Surface hydroxyl groups are neutralized, protonized, or deprotonized depending on the of the solution, resulting in modulation of the double-layer capacitance, thereby inducing changes in surface potential at the semiconductor-insulator interface.50 Similar behaviors have been observed in silicon-on-insulator (SOI) resistors and Si NW transistors in which Si surfaces with thin native oxides were exposed to the electrolyte solution.3, 51 Recently, Estrela and Migliorato9 reported a positive of u using poly-Si TFTs with extended metal gates passivated by . The same device functionalized with physisorbed enzyme penicillinase showed a negative of 11 mV/mM as penicillin G concentration increases. Electrical label-free detection of DNA hybridization has also been demonstrated using FET devices. Surface potential changes due to increased negative charges on the gate of a FET resulted in channel conductance modulation upon immobilization of single-stranded probe DNA and hybridization with complementary DNAs.6, 9, 43, 52, 53 As illustrated in the above demonstrations, the response of FET-based sensor structures to target analytes with net charge can be governed by induced changes in charge density leading to a change in surface potential at a semiconductor surface. Essentially, the change in molecular charge density induces band bending at the surface. The electrostatic properties of semiconductor surfaces modified by molecular dipole layers, a topic of great relevance for sensor development, have received considerable attention recently. The manner in which molecular electronic charge distributions interact with surfaces can be studied by grafting molecular species with systematically varying dipoles but nominally similar other properties to surfaces and probing the surface potential. Samples can be realized by modifying surfaces using the same attachment chemistry and linker ligands but systematically varying the electronegativity of the head groups. He et al.54 fabricated SOI transistors with exposed top Si surfaces and demonstrated systematic changes in by modifying the H-terminated Si surface with a series of molecules which are covalently attached on Si surfaces via Si–C bonding but have different head groups. The ideal surface potential of a semiconductor with a molecular dipole layer, assuming that no molecular depolarization takes place, is given by , where N is the density of molecules, μ is the dipole moment per molecule, θ is the tilt angle of the molecule relative to the surface normal, and is the permittivity of the molecule. The of as-modified semiconductors has been measured experimentally using contact potential difference (CPD), a Kelvin probe technique on dry samples, and inverse photovoltage on samples in electrolyte.55, 56 CPD measurements have been performed on many molecule-substrate systems and indicate that the can be near ideal or deviate greatly from its ideal value due to depolarization and that collective effects can occur due to molecule-molecule interactions, charge transfer, and molecular conformational changes.55, 57, 58 It has also been demonstrated using electrostatic force microscopy that asymmetric molecules self-assembled on a gold surface induce surface potential change up to 250 meV.59 The in situ measurements of molecularly modified surfaces in electrolyte exhibit much less than the dry systems likely due to electrolyte screening effects, which will be discussed in conjunction with the electrostatic model in Sec. 4. These techniques can be applied to biofunctionalized semiconductor surfaces, thereby offering insight into fundamental properties of the molecular layers which have important implications for ligand selection and sensor design.
Control of interfacial traps by molecular passivation
Many studies on molecular passivation of Si and GaAs surface states have been based on two-terminal metal-molecule-semiconductor structures; however the results can be applied to the design of passivation schemes for FET channels. In one prior study, a 2.5 nm thick 1-octadecene monolayer was formed on hydrogen-passivated n-type and p-type Si (111) via Si–C bonding by ultraviolet illumination, top contact was formed by Al evaporation, and capacitance-voltage characterization and admittance spectroscopy were performed.60 Significant reduction in the interface trap density was observed only in case of , indicating a substantial effect of Si dopant-type on the Si/1-octadecene interface. Subsequent experiments by the same authors confirmed that dense 1-octadecene monolayers are formed on n-, p-, and -silicon but not on -silicon, stressing out the important role of surface Fermi level position during the monolayer formation.61 In addition, passivating Si/SiGe/Si heterostructures with 1-octadecene monolayers before Au top metal deposition reduced surface states, resulting in a decrease in surface charges from interfacial traps and an increase in carrier concentration in the Si/Ge/Si quantum-well structure.62 For GaAs, it has been shown that sulfur passivation prior to metal contact evaporation can unpin the GaAs surface, resulting in increased modulation of Schottky barrier height with GaAs doping.63 In contrast, Raman scattering measurements have revealed that ODT passivation of GaAs surfaces is not effective in reducing surface states even though ODT forms a physically well-organized monolayer on GaAs surfaces and suppresses oxide regrowth.64 These results highlight the importance of considering electrical as well as chemical passivation effects for surface-dominated devices.
However, metal deposition on top of molecular layers often leads to distortions in the organic molecules and/or formation of direct metal contacts to the substrate through pinholes in the molecular layers, and it is desirable to characterize molecule-semiconductor interfaces with unmetallized test structures. For this purpose, we proposed using junction field-effect transistors (JFETs) with a back gate and exposed areas for selective functionalization of semiconductor surfaces and studied the SAND passivation effects on device characteristics of GaAs JFETs.44 The device structure of a GaAs JFET along with the molecular structures of type-I and type-III SANDs is shown in Fig. 4. The GaAs JFETs have a common back gate that controls the n-type channel conductance by modulating the junction depletion width, thereby modulating the effective channel width. The n-type channel layer is exposed for surface functionalization and the source and drain regions are passivated with silicon nitride. Next, as-fabricated JFETs were exposed to (1:1) to terminate the exposed GaAs surface with hydroxyl groups, and type-I and type-III SANDs were deposited by the sequential solution-cast self-assembly technique that was briefly described in Sec. 2B.
Measured transfer characteristics of representative GaAs JFETs before and after functionalization with type-I and type-III SANDs are shown in Fig. 5 and changes in and from the forward sweep are summarized in Table 1. Assuming that the GaAs surface states that govern electrical characteristics are acceptorlike interface traps,65 the reduction in GaAs surface states by molecular passivation is expected to result in negative and steeper because acceptorlike traps are negatively charged when occupied by an electron and neutral when empty, which qualitatively explains the type-III SAND passivation effect on and . Even though surface states cannot be directly measured with this type of device structures, a well-established two-dimensional (2D) device simulation (MEDICI) can be used to estimate before and after surface passivation by fitting experimental data (Fig. 5).44 The estimated values for as-fabricated type-I and type-III SAND devices are shown in Table 1. It should be noted that net surface charges exist only in case of type-III SAND passivation due to the presence of the negative ions in the Stb layer. Even though type-III SAND is formed by deposition of Stb and Cap layers on top of type-I SAND and both molecular multilayers have the same nominal interface to GaAs via the Alk layer, type-III SAND is more efficient in reducing than type-I SAND, as indicated by different directions in . Biofunctionalization of semiconductor surfaces typically involves deposition of organic multilayers, and this example illustrates that surface states need to be carefully inspected upon each functionalization step.
Figure 5.
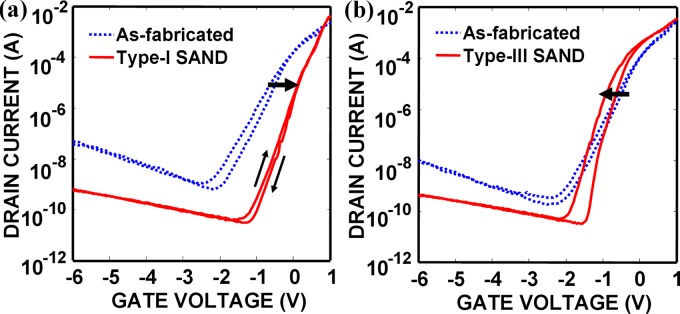
Transfer characteristics of GaAs JFETs functionalized with (a) type-I SAND and (b) type-III SAND. The direction of shifts is indicated by thick arrows. In addition, compared to hysteresis of as-fabricated devices, type-I SAND modification suppresses hysteresis while type-III SAND passivation results in a larger hysteresis. The sweep rate is 500 mV/s.
Table 1.
Changes in and of surface-modified GaAs JFETs and estimated and from 2D device simulation (MEDICI).
| (V) | (mV/decade) | |||
|---|---|---|---|---|
| As fabricated | ⋯ | 0 | ||
| Type-I SAND | 0 | |||
| Type-III SAND |
On the other hand, we observed that ODT passivation of GaAs JFETs provides far less effective electrical passivation compared with SAND passivations.44 This is in contrast with ODT passivation of InAs surfaces which has been found to be very effective in decreasing interface trap electron donor states, improving and mobility of InAs NW transistors,66 which can be attributed to difference in thiol bonding to InAs and GaAs. Previous XPS measurements revealed that ODT molecules are bound to InAs NWs through In–S bonding, whereas in case of HCl-cleaned GaAs, they are attached to As-rich GaAs surfaces via As–S bonding.32, 66 Additional systematic studies on the relationship between the structure of molecule-semiconductor interfaces and electrical passivation will be necessary to facilitate the design of FET sensor systems.
Dynamic electronic interactions between a semiconductor channel and immobilized organic molecules
As demonstrated in Sec. 3B, static control over semiconductor surface properties is important; however sensing is inherently a dynamic process. It is crucial to characterize and understand charge trapping processes in order to evaluate passivation schemes for biosensor applications. In the case of SAND passivation of GaAs considered above, type-I SAND passivation nearly quenches hysteresis by reducing the number of surface states; however, type-III SAND passivation increases hysteresis and results in a steeper , as shown in Fig. 5. Hysteresis also exists in unpassivated devices due to the large GaAs surface state density. The mechanism behind this phenomenon is not clear; however it is possible that increased hysteresis may result from trapping of charge carriers in the Stb layer. Such reversible charge trapping mechanisms have been investigated in various experimental setups. Capacitance and conductance measurements in electrolyte-molecule-semiconductor (EMS) systems can provide information on charge trapping dynamics in immobilized molecules.67, 68 In Ref. 67, redox-active 4-ferrocenylbenzyl alcohol and nonredox-active analog 4-biphenylmethanol were covalently attached on hydrogenated surfaces via an alkylsiloxane bond, and the modified surfaces were exposed to an conducting electrolyte. Capacitance and conductance of the EMS capacitors were measured at various frequencies (25 Hz–1 kHz) and peaks in capacitance and conductance associated with trapping and detrapping of electrons in the molecules were observed only in the sample functionalized with redox-active molecules below 100 Hz. Several groups have also reported on charging/discharging effects of redox-active molecules immobilized on prefabricated NW FETs, demonstrating nonvolatile memory functions with relatively long retention times.69, 70 Gate voltage pulses of different amplitudes were applied to charge and discharge immobilized redox-active molecules, and surface depletion width, i.e., NW channel conductance, was modulated depending on the amount of charges trapped in the molecules. The same charge trapping/detrapping effects were also observed by applying voltage pulses between source and drain at a fixed small gate bias.70
Interestingly, the above-mentioned NW FETs functionalized with redox-active molecules have the same device structure as typical NW-FET biosensors. Understanding such dynamic electronic interactions between a semiconductor channel and immobilized probe molecules can lead to enhanced selectivity of FET biosensors by enabling signature analysis because specific changes in hysteresis before and after conjugation of probe molecules and target analytes can occur even in the presence of other nonspecific molecules with comparable charges. Such signature analysis that utilizes hysteresis modulation would require careful design and optimization of device structures and operating conditions, particularly in the presence of considerable semiconductor surface state densities. It was recently shown that in case of depletion-mode FET devices such as GaAs JFETs, a large increase in net negative surface charge due to conjugated target analytes can nearly quench hysteresis by increasing the surface depletion width and lowering the n-type conduction path from the GaAs surface (i.e., lowering the probability of charge trapping into the surface states) even though the device functionalized with probe molecules exhibited considerable hysteresis due to inherent GaAs surface states.41 Hence, effects from charge trapping/detrapping can be masked in case of depletion-mode FET biosensors involving net surface charge modulation upon probe-target conjugations, implying that FET device structures need to be carefully selected and optimized for specific probe-target interactions. Different device structures and operating modes for FET biosensors will be discussed in details in Sec. 4C.
PHYSICS OF SENSOR RESPONSE
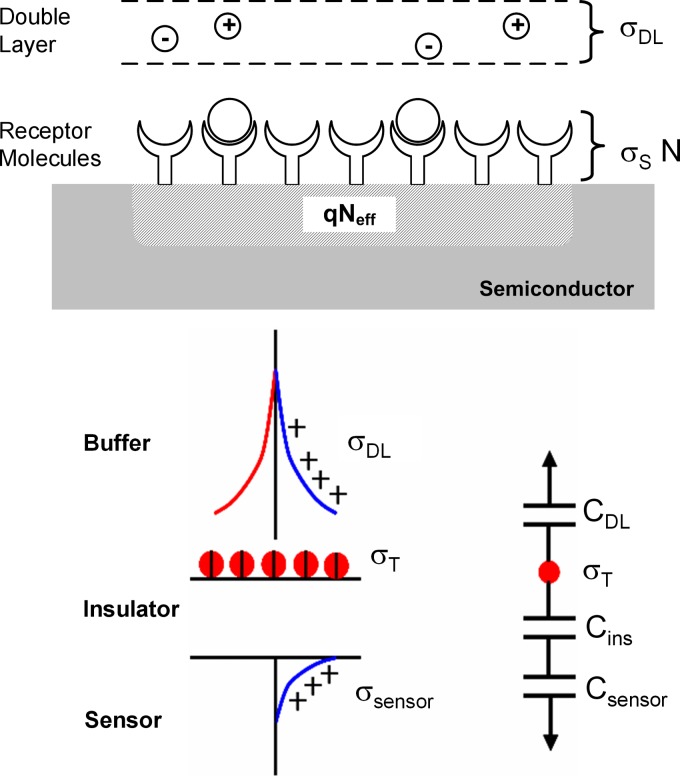
The response of a biosensor involves three elements: (i) transport of target molecules to the sensor surface and subsequent conjugation with the functionalized receptor molecules (Fig. 1), (ii) electrostatic interaction between the net charge of the biomolecule, the counterions in the buffer, and the semiconductor surface, and (iii) modulation of device characteristics due to change in device electrostatics (Fig. 6). In Sec. 4, we review the existing theoretical understanding of these issues.
Figure 6.
Schematic illustrating charge sharing in a biosensor. The net charge of the adsorbed biomolecules on the sensor surface is shared between the sensor and the counterions present in the buffer . The independent parameter is the charge in the biomolecules and the potential of the molecular layer is determined by the relative values of the capacitances shown in the schematic.
Dynamics of biomolecule adsorption
Time dynamics of molecule capture on a sensor surface is essentially a two step process: transport of the target molecules to the sensor surface and the subsequent conjugation with the receptor molecules. The diffusion-capture (DC) model is widely used to describe this process. The model assumes that the molecule transport is diffusion limited and the target-receptor conjugation is treated as a first-order chemical reaction. The model equations are
Equation 1a represents the diffusion of target molecules to the sensor surface where D and ρ are the diffusion coefficient and concentration of target biomolecules (analyte) in solution, respectively. Equation 1b represents the capture of biomolecules by the receptors on sensor surface, where N is the density of conjugated receptors, is the total density of receptors on the sensor surface, and are the capture and dissociation constants, and is the concentration of target analyte particles at the sensor surface.
Many authors have provided solutions for DC equations under different limiting conditions. To list a few, Chandrasekhar71 treated the dynamics under infinite capture rate at the surface , Kankare and Vinokurov72 provided detailed analysis for sensors with different geometries, Kusnezow et al.73 used a two compartment model to decouple the equations and provided solutions under steady diffusion flux. More recently, a general solution for the DC equations valid for conditions relevant for nanobiosensors was provided in Ref. 74 based on the perturbation approach introduced in Ref. 12, showing that the general solution reduces to the reaction-limited response or diffusion-limited response under appropriate conditions. When a steady-state concentration of the target analyte exists at the sensor surface due to high target molecule concentrations or high diffusivity, the dynamics of analyte capture is limited by the surface conjugation reaction rate and the response reduces to the well-known Langmuir response [analytical solution of Eq. 1b, , where is the equilibrium concentration of conjugated molecules]. In the low analyte concentration limit, the dynamics is essentially diffusion limited and the sensor response is given by a unique scaling law: , where k is a constant and is the fractal dimension of the adsorbing sensor surface.75 Most of the recently reported results on ultrasensitive detection of biomolecules are in the diffusion-limited regime.12, 75 The model establishes that in this regime, the detection limits of single NW or nanotube sensors are orders of magnitude better than planar devices, while the performance of NW and nanotube network sensors varies between these two limits depending on the density of nanotubes and the associated percolation threshold.12, 75
Several attempts have been made to overcome the diffusion limit in biomolecule detection by accelerating molecule transport to the sensor surface (e.g., introducing fluid flow). However, a recent article by Sheehan and Whitman76 has shown that improvements obtained under realistic flow conditions diminish as the sensor size is scaled to nanometer dimensions, a regime where the electrostatic sensitivity and molecule capture efficiency are expected to be at their maximum. Preconcentration of tagged molecules has been achieved by many groups based on the concepts of ac electrokinetics;77, 78 however the effectiveness of these methods for electronic detection of biomolecules under physiological buffer conditions is yet to be demonstrated.
Electrostatics of sensor system
In Sec. 4A, we described the DC model for biomolecule adsorption on sensor surface. In electrical detection, however, the measured signal is the conductance change in the sensor, which is not always directly proportional to the density of captured molecules. The nonlinearity in signal transduction comes about in part because of electrostatic screening considerations due to the presence of counterions in the buffer (electrolyte) solution.
The conductance modulation of the sensor is determined by the net induced charge in the semiconductor. The fundamental relation, which is valid under all operating conditions, is the charge conservation of the system74 given by (see Fig. 6)
| (2) |
where is the induced charge density in the sensor and is the charge supported by the electrical double layer in the buffer. The right-hand side (RHS) denotes the net charge of the target molecules [, where is the charge of an individual target molecule and N is obtained by solving Eq. 1]. It is important to note that although the electrostatics of the biosensor can be treated as an equivalent capacitance system shown schematically in Fig. 6, the independent parameter is . The double layer charge depends nonlinearly on the potential of the adsorbed molecule layer and is obtained by solving the Poisson–Boltzmann (PB) equation for an electrolyte system, which will be discussed in more details later. for planar sensors is given by79
| (3) |
where is the Debye–Huckel screening length in the electrolyte , where is the buffer concentration in molar units, is Avogadro’s constant, is the dielectric constant of electrolyte, q is the charge of an electron , and , where is the Boltzmann constant and T is the temperature.
The charge induced in the sensor is determined by the series combination of the insulator (solid or organic) and semiconductor capacitance
| (4) |
where is the capacitance associated with the molecular layer on the semiconductor surface and any interfacial insulating layer such as oxide. is the capacitance due to a surface depletion region in the semiconductor; therefore it is dependent on the semiconductor surface potential. A detailed treatment of this for several modes of device operation will be discussed in Sec. 4C. Depending on the buffer concentration and the device parameters, the charge shared by the sensor and electrolyte varies according to Eq. 2. A self-consistent solution of Eqs. 2, 3, 4 is required to estimate and hence the sensor electrostatic response. The fraction of conjugated molecule charges induced in the semiconductor channel of the sensor is always less than unity due to electrolyte screening ( and have the same polarity). Furthermore, it should be noted that even if the captured target molecules are held close to the sensor surface, the buffer can still screen the charge, a fact not well appreciated in traditional sensor literature.
Modulation of device characteristics
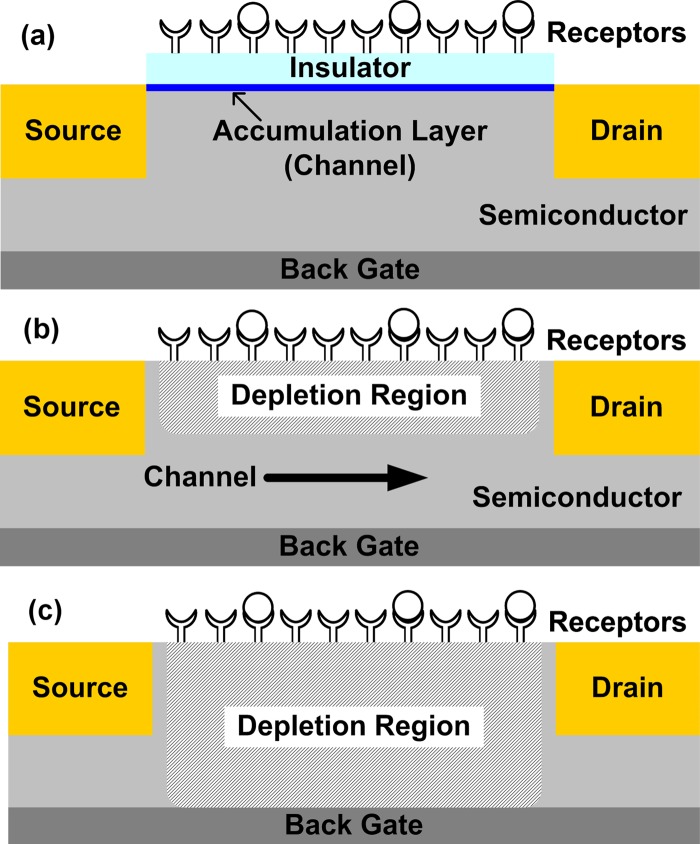
We mentioned in Sec. 4B that conductance modulation of sensor is related to the amount of induced charge. In this section, we analyze the induced change in channel conductivity for a metal-semiconductor field-effect transistor (MESFET)-type sensor under various modes of operation. For this purpose, we consider the case illustrated in Fig. 1, which is representative of many of the conductance-based nanosensors reported to date. The structure employs a doped semiconductor channel and contacts suitable for the desired sign of carrier—i.e., either the opposite doping-type to the channel for inversion-mode MOSFETs, the same doping-type as the channel for MESFET-like devices or metal contacts with appropriate work functions, which are often used in NW FETs. The specific device structure and molecular receptor-type/density configure the sensor into a specific operational state (accumulation, inversion, and depletion) before its exposure to target species. “Response” will involve differential change with respect to this “initial” state. Within this framework, several operating modes of the device can be analyzed, including accumulation (or inversion) of carriers at the semiconductor surface, and depletion of carriers near the surface. Since the device dimensions of such sensors are typically much larger than carrier mean free paths, the drift-diffusion model can be successfully used to model the channel conductivity.14 Molecule conjugation on the sensor surface causes depletion or accumulation of the sensor depending on the relative polarity of the target molecule with respect to the channel doping. Back gate bias can also be applied to electrostatically control the sensor, thus affecting its response. A convenient way to characterize the regime of operation of sensor is in terms of the sensor capacitance . We define the regimes as follows (Fig. 7): (i) accumulation mode—this mode is characterized by the condition . Since in this case [from Eq. 4], the sensor response varies linearly with the induced surface potential. In this regime, the semiconductor surface has an accumulation layer and the binding of target analytes modulates the number of carriers present in that layer, as shown schematically in Fig. 7a. (ii) depletion mode—this mode of operation is characterized by a partially depleted semiconductor channel and the binding of target analytes modulates the depletion width [Fig. 7b]. The ratio of depends on the doping density. (iii) fully depleted mode—in this regime, the entire semiconductor channel is depleted due to either the charge of biomolecules or the applied gate bias, and the binding of target analytes modulates the degree of channel pinchoff [Fig. 7c]. This regime is characterized by the condition and the sensor response varies exponentially with (subthreshold characteristics). We now summarize the sensor response in these different regimes.
Figure 7.
Operation modes of FET-based biosensors: (a) accumulation mode, (b) depletion mode, and (c) fully depleted mode.
In the accumulation mode, the source-drain current flows in the accumulation layer [Fig. 7a]. The carrier concentration in this layer and thus the channel conductance vary linearly with the surface potential. Based on an analytic solution of Eq. 1, Ref. 74 has shown that the sensor response in this regime is given by
| (5) |
where are geometry-dependent constants. Interestingly, the model predicts that the sensor response varies logarithmically with the target molecule concentration, the buffer concentration, with time, and linearly with the (logarithmically with hydrogen ion concentration). This logarithmic dependence on various parameters is due to the electrolyte screening. It should be emphasized that the observed signal (i.e., the conductance change) shows entirely different characteristics when compared with the dynamics of molecule capture on sensor surface. The predicted trends are observed in a wide variety of experimental results.74 The dependence of sensor response on various system parameters such as device dimensions and molecule conjugation affinity is of paramount interest in optimizing the sensor systems and further discussion is available in Ref. 81. An electrostatic model for sensor response in the limits of low doping density and small changes in surface potential is discussed in Ref. 82.
In the depletion mode, the source-drain current flows in the nondepleted portion of the channel [Fig. 7b]. The channel resistance is given by , where is the semiconductor resistivity, is the channel length, and is the cross-sectional area of the channel. Since the cross-sectional area of the channel modulated by the induced change is the depletion width due to the binding of the charged target molecules, the device characteristics are significantly influenced by the choice of doping density. For highly doped devices, the depletion depth can be very small and the condition holds true. In this case, the sensor response is predicted by Eq. 5.74 For moderate doping densities, may become comparable to and a self-consistent numerical solution of Eqs. 2, 3, 4 is necessary. The response with respect to analyte concentration, , and buffer ion concentration is expected to be similar to the trends predicted by Eq. 5, however, with a reduced magnitude. Detailed discussions on the response of biosensors to and electrolyte screening effects are available in Refs. 83, 84, 85.
In the fully depleted mode, the entire semiconducting region is under depletion either due to the charge of biomolecules or due to the applied back gate bias [Fig. 7c]. In this mode, the FET is in the subthreshold region of operation; therefore the channel conductivity varies exponentially with surface potential. In this regime, apart from the sensor conductance, other parameters such as and can be used to detect molecule conjugation on the sensor surface. In addition to inducing charge (, where is the effective fixed charge density), the molecules adsorbed on the sensor surface can create surface states . The response of the device in this fully depleted mode can be used to determine the contribution of surface states to device characteristics.
In full depletion-mode devices, is associated with the amount of majority carriers that the gate is required to deplete. For a given doping and device geometry, any external factors that help lower the integrated amount of majority carriers in the device will result in steeper . We will provide a simple analysis for of fully depleted back-gated devices which was originally discussed in Ref. 41. Solution of Poisson’s equation indicates that the potential in the semiconducting region is given by a quadratic equation of the form , where a, b, and c are constants and can be determined from the boundary conditions shown in Fig. 8. Since the channel is fully depleted, the current I through the device is given by . in terms of a, b, and c is given as . for back-gated devices is defined as
Using the boundary conditions shown in Fig. 8 and accounting for the band bending at the top interface (while evaluating ), can be shown to be
| (6) |
Here, t, , ε, and are the thickness, doping, dielectric constant of the semiconducting region, and the effective surface charge, respectively. Also,
and
where is the valence-band density of states, is the intrinsic carrier concentration, and is interfacial trap density. Equation 6 reduces to classical limits in which (a) with , and (b) increases with increasing , given that . In addition, Eq. 6 also predicts a counterintuitive decrease in with increasing (and nonzero ), an experimentally verified result.41 Finally it can be noted that for large and , of the back-gated depletion-mode devices follows the scaling relationship
a conclusion supported by detailed numerical simulations.41
Figure 8.
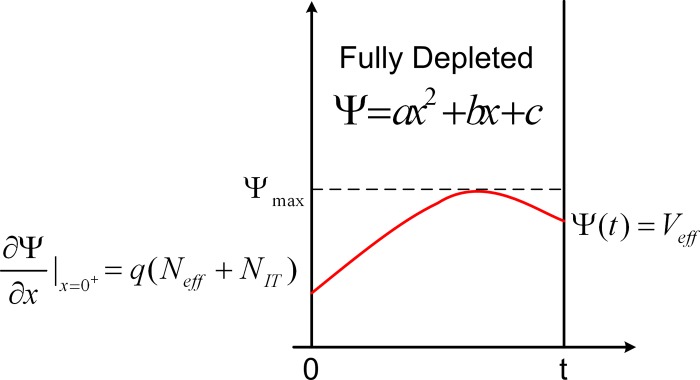
The potential distribution in a fully depleted semiconductor channel. The origin of x-axis indicates the top semiconductor-insulator interface and is the effective back gate potential at the bottom semiconductor-insulator interface. The boundary conditions for the potential profile are indicated.
We would like to stress the significance of the above result in comparison to inversion mode, minority carrier devices such as traditional top-gated MOSFETS. For such inversion mode devices, is related to the rate of increase in minority carriers in the channel with the gate voltage.14 Hence, the presence of surface states always degrades (i.e., increases) . Typical MOSFET analyses relate improvements in to the reduction in surface states , i.e., the reduction in is due to reduction in , the capacitance due to surface states.14 Fixed charge at the interface does not affect but introduces a threshold voltage shift in device characteristics. However, as seen in the previous discussion, both fixed charge and interface states can degrade for depletion-mode back-gated devices.
An interesting debate among the sensor community is regarding the efficiency of molecule detection among these three modes of operation of a sensor as discussed above, in other words, “given a fixed density of conjugated molecules, which of the three modes would be an optimum detection scheme?” A widely held belief is that the fully depleted scheme could be more sensitive because the sensor response varies exponentially with . This argument overlooks the fact that for the fully depleted mode, is often very small, hence most of the charge due to the conjugated biomolecules can be compensated by the electrolyte double layer . is inversely proportional to the depth of depletion region [see Fig. 7c]; therefore scaling the body thickness semiconductor channels to nanoscale is expected to improve sensor response. Recent measurements support this observation by indicating that the response of nanoscale thickness FET devices to can be maximized by optimizing the bias conditions.86 Detailed solution of Eqs. 2, 3, 4 along with the transport through the sensor is helpful in addressing this optimization issue. Another aspect of practical interest is dry versus wet measurements. It is often argued that the counterion screening in wet measurements can be reduced if the detection is done in air, i.e., after draining out the buffer solution. While it is true that draining the buffer reduces the total counterions, it could also result in a reduced density of conjugated molecules on the sensor surface due to dissociation of weakly bound pairs during the draining process. Recent analysis of experiments involving DNA detection shows that the net induced charge in the semiconductor reduces by a factor of 2 during device drying,80 which indicates significant dissociation. As such, more detailed measurements are required to assess the tradeoff between reduced counterion screening and increased dissociation of conjugated molecules in dry measurements.
Finite size effects
The phenomenological models described in Secs. 4A and 4B provide important insights regarding sensor response in terms of various system parameters; however, parameters such as the finite size of molecules and their separation from the sensor surface are neglected in the analytical models. These considerations assume significance as the devices are scaled to molecular dimensions; therefore the electrostatics must be treated by numerically solving the nonlinear PB equation87
| (7) |
where Ψ is the electrostatic potential and r is the spatial coordinate. The sinh term denotes the contribution due to a 1-1 electrolyte (e.g., ), whose ions are assumed to follow the Boltzmann distribution. The RHS denotes the fixed charge due to the biomolecule and denoting the partial charge and location of the atoms within the biomolecule.
Numerical solutions of the PB equation have been widely used for studying the electrostatics of biomolecules88 and conductance modulation of FET-based sensors;89, 90 however, the importance of proper implementation of boundary conditions and the numerical solution methodology relevant for biosensors was not discussed until Ref. 81. In this scheme, the electrostatics of the molecule over a grounded metal plane is considered. The structure of the biomolecule is obtained from the protein data bank.90 The charge distribution of biomolecules is mapped from the force field parameters of molecular dynamics simulators (CHARMM, GROMACS, etc.).89 The simulation results indicated that at higher ion levels in the buffer solution, the incremental change in conductance obtained by increasing DNA strand length diminishes due to the electrostatic screening by the ions. More importantly, the reported results indicated that electrostatic consideration alone is highly unlikely to differentiate DNA strands of similar length but with different base-pair sequences.
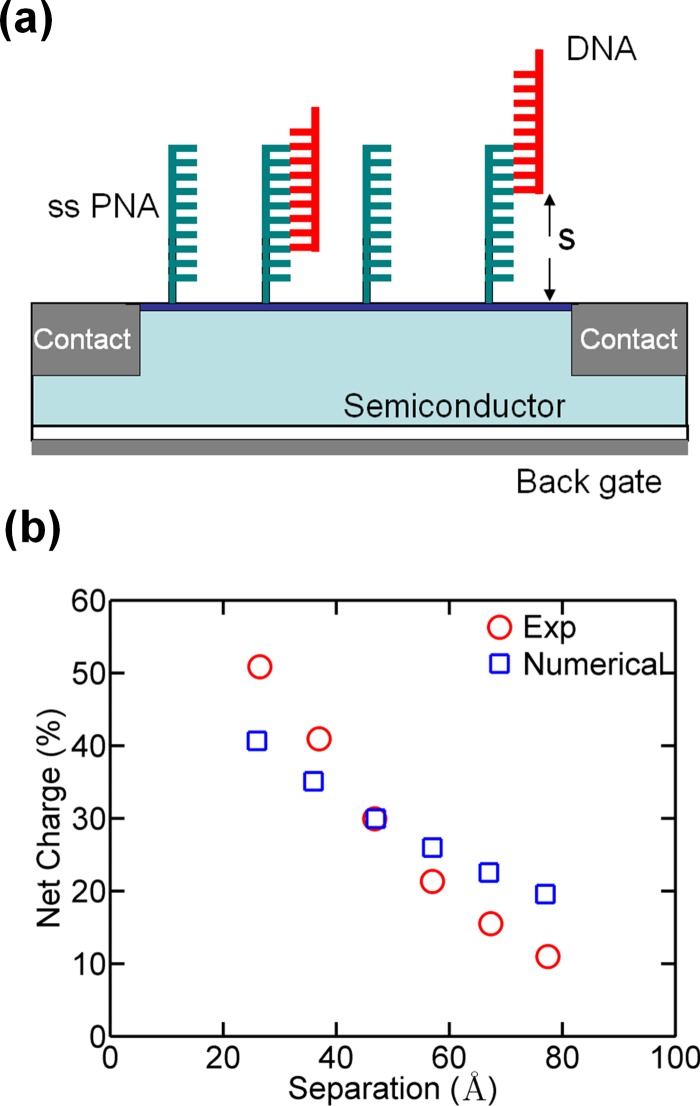
Here, we use the PB solver reported in Ref. 81 to illustrate the effect of finite separation of molecules from the sensor surface and to compare our simulations with recently reported experimental results. Zhang et al.91 did a detailed study on the dependence of target DNA separation from the sensor surface. In this work, Si NW FETs were functionalized with six types of peptide nucleic acid (PNA) capture probes, each of which has varying hybridization binding sites for the target DNA strand to control the distance between the sensor surface and the captured target DNA [Fig. 9a]. This was achieved by changing the PNA sequence but maintaining the net charge a constant. Resistance changes in Si NWs were recorded for each type after DNA hybridization, which showed that the sensor response varies exponentially with the sensor surface-target molecule separation [red circles in Fig. 9b]. The same trend is also observed in our numerical simulations from the PB solver (blue squares).
Figure 9.
(a) Schematic illustrating DNA conjugation on sensor surface. The separation of the target DNA from the sensor surface was varied by changing the length of the complimentary binding sequence (Ref. 91). (b) Comparison between experimental and numerical results [simulation of the nonlinear PB equation (Eq. 7)]. The simulation data have been normalized with respect to experimental results.
SELECTIVITY AND NONSPECIFIC ADSORPTION
A key focus of this paper is the importance of molecular passivation by using appropriate passivation schemes. As has been mentioned, otherwise, small molecules may reach the sensor surface through the opening of the passivation layers and may result in false positive signals. From a theoretical perspective, selectivity of biosensors depends on two parameters: (i) the affinity of receptor molecules to the corresponding targets and (ii) the available unmodified sensor surface, where nonspecific adsorption known as biofouling can take place (Fig. 2). The first effect is characterized by the parameters and in the reaction equation in Sec. 4A. Better selectivity can be obtained by employing sequences of higher conjugation affinity, for example, PNA receptors have higher binding efficiency with DNA molecules than DNA receptors. Accordingly, experimental results indicate that PNA functionalization improves DNA detection limits.6, 92, 93 For a surface modified only by receptor molecules, biofouling is entirely determined by the geometry of these molecules. The finite size of receptor molecules introduces steric hindrance issues, hence uniform surface coverage of receptor molecules is impossible, resulting in exposed regions of different shapes on the sensor surface. Nonspecific adsorption can take place in these exposed regions.
The random sequential adsorption (RSA) model94, 95, 96, 97 can be used to study the finite size effects of molecule adsorption on surfaces. In this model, the molecules of finite size are assumed to irreversibly attach on the surface and no overlap between adjacent molecules is allowed. RSA model indicates that due to steric hindrance issues, the maximum achievable surface coverage is only 54%. At this maximum surface coverage limit, voids of size larger than the individual molecule size are negligible. If not enough time is allowed during surface passivation, the surface coverage will be suboptimum. In this case, significant scale-invariant gaps may exist which are several times larger than the molecule size. These exposed voids act as potential hot spots for biofouling. The fragmentation of the available area for adsorption has profound impacts on the achievable receptor density , exposed voids for biofouling, and the fraction of the receptor sites available for target conjugation.98
CONCLUSION
Formation of reliable molecular passivation of semiconductor surfaces is critical for realization of FET-based biosensors. Development of device models that explain the physical mechanisms of signal transduction in such devices plays a crucial role in development and optimization of passivation methodology. We presented a review of molecular functionalization of Si and GaAs surfaces with emphasis on the importance of electrical and chemical passivation. The physics of sensor response for a MESFET-type structure was also discussed. The models demonstrate that electrolyte screening and capacitance considerations are crucial to realizing a high-sensitivity device.
ACKNOWLEDGMENTS
We thank Professor Tobin J. Marks for valuable discussion on self-assembled organic dielectrics. This work was supported in part by NASA under the Institute for Nanoelectronics and Computing (Grant No. NCC 2-1363), NSF (Grant Nos. ECS-0506802 and FCS-0506802), and DARPA/ARO (Grant No. W911NF-05-0187). The modeling work was performed with financial support from NIH (Grant No. R21-EB006308) and using computational resources of Network for Computational Nanotechnology (NCN). A.S. is supported by a NSF graduate research fellowship.
References
- Hofmann F., Frey A., Holzapfl B., Schienle M., Paulus C., Schindler-Bauer P., Kuhlmeier D., Krause J., Hintsche R., Nebling E., Albers J., Gumbrecht W., Plehnert K., Eckstein G., and Thewes R., IEEE International Electron Devices Meeting, 2002. (unpublished), p. 488.
- Zheng G., Patolsky F., Cui Y., Wang W. U., and Lieber C. M., Nat. Biotechnol. 10.1038/nbt1138 23, 1294 (2005). [DOI] [PubMed] [Google Scholar]
- Cui Y., Wei Q., Park H., and Lieber C. M., Science 10.1126/science.1062711 293, 1289 (2001). [DOI] [PubMed] [Google Scholar]
- Wang W. U., Chen C., Lin K. -H., Fang Y., and Lieber C. M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0406368102 102, 3208 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C., Curreli M., Lin H., Lei B., Ishikawa F. N., Datar R., Cote R. J., Thompson M. E., and Zhou C., J. Am. Chem. Soc. 10.1021/ja053761g 127, 12484 (2005). [DOI] [PubMed] [Google Scholar]
- Hahm J. -I. and Lieber C. M., Nano Lett. 10.1021/nl034853b 4, 51 (2004). [DOI] [Google Scholar]
- Patolsky F., Zheng G., Hayden O., Lakadamyali M., Zhuang X., and Lieber C. M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0406159101 101, 14017 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern E., Klemic J. F., Routenbert D. A., Wyrembak P. N., Turner-Evans D. B., Hamilton A. D., LaVan D. A., Fahmy T. M., and Reed M. A., Nature (London) 10.1038/nature05498 445, 519 (2007). [DOI] [PubMed] [Google Scholar]
- Estrela P. and Migliorato P., J. Mater. Chem. 10.1039/b612469k 17, 219 (2007). [DOI] [Google Scholar]
- Daniel S., Rao T. P., Rao K. S., Rani S. U., Naidu G. R. K., Lee H. -Y., and Kawai T., Sens. Actuators B 10.1016/j.snb.2006.06.014 122, 672 (2007). [DOI] [Google Scholar]
- Kumar A., Larsson O., Parodi D., and Liang Z., Nucleic Acids Res. 28, e71 (2000). 10.1093/nar/28.14.e71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair P. R. and Alam M. A., Appl. Phys. Lett. 88, 233120 (2006). 10.1063/1.2211310 [DOI] [Google Scholar]
- Elibol O. H., Morisette D., Akin D., and Bashir J. P. D., Appl. Phys. Lett. 10.1063/1.1630853 83, 4613 (2003). [DOI] [Google Scholar]
- Sze S. M., Physics of Semiconductor Device, 2nd ed. (Wiley-Interscience, New York, 1981). [Google Scholar]
- Linford M. R., Fenter P., Eisenberger P. M., and Chidsey C. E. D., J. Am. Chem. Soc. 10.1021/ja00116a019 117, 3145 (1995). [DOI] [Google Scholar]
- Boukherroub R., Curr. Opin. Solid State Mater. Sci. 10.1016/j.cossms.2006.03.006 9, 66 (2005). [DOI] [Google Scholar]
- Buriak J. M., Chem. Rev. (Washington, D.C.) 10.1021/cr000064s 102, 1271 (2002). [DOI] [PubMed] [Google Scholar]
- Allongue P., de Villeneuve C. H., Pinson J., Ozanam F., Chazalviel J. N., and Wallart X., Electrochim. Acta 10.1016/S0013-4686(98)00020-6 43, 2791 (1998). [DOI] [Google Scholar]
- Higashi G. S., Chabal Y. J., Trucks G. W., and Raghavachari K., Appl. Phys. Lett. 10.1063/1.102728 56, 656 (1990). [DOI] [PubMed] [Google Scholar]
- Sieval A. B., van den Hout B., Zuilhof H., and Sudhölter E. J. R., Langmuir 10.1021/la001494g 17, 2172 (2001). [DOI] [Google Scholar]
- Royea W. J., Juang A., and Lewis N. S., Appl. Phys. Lett. 10.1063/1.1312203 77, 1988 (2000). [DOI] [Google Scholar]
- Kar S., Appl. Surf. Sci. 10.1016/j.apsusc.2005.09.029 252, 3961 (2006). [DOI] [Google Scholar]
- McGuiness C. L., Blasini D., Masejewski J. P., Uppili S., Cabarcos O. M., Smilgies D., and Allara D. L., ACS Nano 1, 30 (2007). [DOI] [PubMed] [Google Scholar]
- Scott A., Hacker C., and Janes D. B., J. Phys. Chem. C 112, 14021 (2008). [Google Scholar]
- Rohde R. D., Agnew H. D., Yeo W. -S., Bailey R. C., and Heath J. R., J. Am. Chem. Soc. 10.1021/ja062012b 128, 9518 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Smet L. C. P. M., Pukin A. V., Sun Q. -Y., Eves B. J., Lopinski G. P., Visser G. M., Zuilhof H., and Sudhölter E. J. R., Appl. Surf. Sci. 252, 24 (2005). 10.1016/j.apsusc.2005.01.107 [DOI] [Google Scholar]
- Eves B. J., Fan C., and Lopinski G. P., Small 10.1002/smll.200600103 2, 1379 (2006). [DOI] [PubMed] [Google Scholar]
- Strother T., Cai W., Zhao X., Hamers R. J., and Smith L. M., J. Am. Chem. Soc. 10.1021/ja9936161 122, 1205 (2000). [DOI] [Google Scholar]
- Liao W., Wei F., Qian M. X., and Zhao X. S., Sens. Actuators B 101, 361 (2004). 10.1016/j.snb.2004.04.006 [DOI] [Google Scholar]
- Streifer J. A., Kim H., Nichols B. M., and Hamers R. J., Nanotechnology 10.1088/0957-4484/16/9/075 16, 1868 (2005). [DOI] [Google Scholar]
- Bunimovich Y. L., Shin Y. W., Yeo W. -S., Amori M., Kwong G., and Heath J. R., J. Am. Chem. Soc. 10.1021/ja065923u 128, 16323 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin J., Geib K. M., and Wilmsen C. W., J. Vac. Sci. Technol. B 10.1116/1.585744 9, 2337 (1991). [DOI] [Google Scholar]
- Cho Y. and Ivanisevic A., J. Phys. Chem. B 10.1021/jp0515737 109, 12731 (2005). [DOI] [PubMed] [Google Scholar]
- McGuiness C. L., Shaporenko A., Mars C. K., Jppili S., Zharnikov M., and Allara D. L., J. Am. Chem. Soc. 10.1021/ja058657d 128, 5231 (2006). [DOI] [PubMed] [Google Scholar]
- Shaporenko A., Adlkofer K., Johansson L. S. O., Ulman A., Grunze M., Tanaka M., and Zharnikov M., J. Phys. Chem. B 108, 17964 (2004). 10.1021/jp040474a [DOI] [Google Scholar]
- Adlkofer K., Shaporenko A., Zharnikov M., Grunze M., Ulman A., and Tanaka M., J. Phys. Chem. B 107, 11737 (2003). 10.1021/jp0356719 [DOI] [Google Scholar]
- Ye S., Li G. F., Noda H., Uosaki K., and Osawa M., Surf. Sci. 10.1016/S0039-6028(03)00239-5 529, 163 (2003). [DOI] [Google Scholar]
- Herne T. M. and Tarlov M. J., J. Am. Chem. Soc. 10.1021/ja9719586 119, 8916 (1997). [DOI] [Google Scholar]
- Steel A. B., Herne T. M., and Tarlov M. J., Anal. Chem. 10.1021/ac980037q 70, 4670 (1998). [DOI] [PubMed] [Google Scholar]
- Wampler H. P., Zemlyanov D. Y., Lee K., Janes D. B., and Ivanisevic A., Langmuir 10.1021/la703543g 24, 3164 (2008). [DOI] [PubMed] [Google Scholar]
- Lee K., Nair P. R., Park H. H., Zemlyanov D. Y., Ivanisevic A., Alam M. A., and Janes D. B., J. Appl. Phys. 10.1063/1.2936853 103, 114510 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seker F., Meeker K., Kuech T. F., and Ellis A. B., Chem. Rev. (Washington, D.C.) 10.1021/cr980093r 100, 2505 (2000). [DOI] [PubMed] [Google Scholar]
- Remashan K. and Bhat K. N., Thin Solid Films 10.1016/S0040-6090(98)01414-X 342, 20 (1999). [DOI] [Google Scholar]
- Lee K., Lu G., Facchetti A., Janes D. B., and Marks T. J., Appl. Phys. Lett. 92, 123509 (2008). 10.1063/1.2899965 [DOI] [Google Scholar]
- Lin H. C., Ye P. D., Xuan Y., Lu G., Facchetti A., and Marks T. J., Appl. Phys. Lett. 10.1063/1.2358202 89, 142101 (2006). [DOI] [Google Scholar]
- Yoon M. -H., Facchetti A., and Marks T. J., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0501027102 102, 4678 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hur S. H., Yoon M. H., Gaur A., Shim M., Facchetti A., Marks T. J., and Rogers J. A., J. Am. Chem. Soc. 10.1021/ja0553203 127, 13808 (2005). [DOI] [PubMed] [Google Scholar]
- Ju S., Lee K., Janes D. B., Yoon M. H., Facchetti A., and Marks T. J., Nano Lett. 10.1021/nl051658j 5, 2281 (2005). [DOI] [PubMed] [Google Scholar]
- Halik H. K. M., Zschieschang U., Schmid G., Dehm C., Schutz M., Maisch S., Effenberger F., Brunnbauer M., and Stellacci F., Nature (London) 10.1038/nature02987 431, 963 (2004). [DOI] [PubMed] [Google Scholar]
- Bergveld P., Sens. Actuators B 10.1016/S0925-4005(02)00301-5 88, 1 (2003). [DOI] [Google Scholar]
- Nikolaides M. G., Rauschenbach S., and Bausch A. R., J. Appl. Phys. 10.1063/1.1650880 95, 3811 (2004). [DOI] [Google Scholar]
- Sakata T. and Miyahara Y., ChemBioChem 10.1002/cbic.200400253 6, 703 (2005). [DOI] [PubMed] [Google Scholar]
- Fritz J., Cooper E. B., Gaudet S., Sorger P. K., and Manalis S. R., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.232276699 99, 14142 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- He T., He J., Lu M., Chen B., Pang H., Reus W. F., Nolte W. M., Nackashi D. P., Franzon P. D., and Tour J. M., J. Am. Chem. Soc. 10.1021/ja063571l 128, 14537 (2006). [DOI] [PubMed] [Google Scholar]
- Haick H., Ambrico M., Ligonzo T., Tung R. T., and Cahen D., J. Am. Chem. Soc. 10.1021/ja058224a 128, 6854 (2006). [DOI] [PubMed] [Google Scholar]
- Hartig P., Dittrich T., and Rappich J., J. Electroanal. Chem. 524–525, 120 (2002). 10.1016/S0022-0728(02)00764-7 [DOI] [Google Scholar]
- Deutsch D., Natan A., Shapira Y., and Kronik L., J. Am. Chem. Soc. 10.1021/ja068417d 129, 2989 (2007). [DOI] [PubMed] [Google Scholar]
- Gershewitz O., Grinstein M., Sukenik C. N., Regev K., Ghabboun J., and Cahen D., J. Phys. Chem. B 10.1021/jp035764q 108, 664 (2004). [DOI] [Google Scholar]
- Howell S., Kuila D., Kasibhatla B., Kubiak C. P., Janes D. B., and Reifenberger R., Langmuir 10.1021/la0157014 18, 5120 (2002). [DOI] [Google Scholar]
- Kar S., Miramond C., and Vuilaume D., Appl. Phys. Lett. 10.1063/1.1351530 78, 1288 (2001). [DOI] [Google Scholar]
- Miramond C. and Vuillaume D., J. Appl. Phys. 10.1063/1.1767984 96, 1529 (2004). [DOI] [Google Scholar]
- Antonova I. V., Soots R. A., Guliaev M. B., Prinz V. Y., Kagan M. S., and Kolodzey J., Appl. Phys. Lett. 10.1063/1.2775083 91, 102116 (2007). [DOI] [Google Scholar]
- Carpenter M. S., Melloch M. R., Cowans B. A., Dardas Z., and Delgass W. N., J. Vac. Sci. Technol. B 10.1116/1.584612 7, 845 (1989). [DOI] [Google Scholar]
- McGuiness C. L., Shaporenko A., Zharnikov M., Walker A. V., and Allara D. L., J. Phys. Chem. C 111, 4226 (2007). 10.1021/jp065173a [DOI] [Google Scholar]
- Yamada T. and Horio K., Proceedings of Simulation of Semiconductor Processes and Devices, 1996. (unpublished).
- Hang Q., Wang F., Carpenter P. D., Zemlyanov D., Zakharov D., Stach E. A., Buhro W. E., and Janes D. B., Nano Lett. 8, 49 (2008). 10.1021/nl071888t [DOI] [PubMed] [Google Scholar]
- Li Q., Mathur G., Homsi M., Surthi S., Misra V., Malinovskii V., Schweikart K. -H., Yu L., and Lindsey J. S., Appl. Phys. Lett. 10.1063/1.1500781 81, 1494 (2002). [DOI] [Google Scholar]
- Li Q., Surthi S., Mathur G., Gowda S., Misra V., Sorenson T. A., Tenent R. C., Kuhr W. G., Tamaru S., Lindsey J. S., Liu Z., and Bocian D. F., Appl. Phys. Lett. 10.1063/1.1584088 83, 198 (2003). [DOI] [Google Scholar]
- Li C., Fan W., Lei B., Zhang D., Han S., Tang T., Liu X., Liu Z., Asano S., Meyyappan M., Han J., and Zhou C., Appl. Phys. Lett. 10.1063/1.1667615 84, 1949 (2004). [DOI] [Google Scholar]
- Duan X., Huang Y., and Lieber C. M., Nano Lett. 10.1021/nl025532n 2, 487 (2002). [DOI] [Google Scholar]
- Chandrasekhar S., Rev. Mod. Phys. 10.1103/RevModPhys.15.1 15, 1 (1943). [DOI] [Google Scholar]
- Kankare J. and Vinokurov I. A., Langmuir 15, 5591 (1999). 10.1021/la981642r [DOI] [Google Scholar]
- Kusnezow W., Syagailo Y., Rüffer S., Klenin K., Sebald W., Hoheisel J. D., Gauer C., and Goychuk I., Proteomics 6, 794 (2006). 10.1002/pmic.200500149 [DOI] [PubMed] [Google Scholar]
- Nair P. R. and Alam M. A., Nano Lett. 10.1021/nl072593i 8, 1281 (2008). [DOI] [PubMed] [Google Scholar]
- Nair P. R. and Alam M. A., Phys. Rev. Lett. 10.1103/PhysRevLett.99.256101 99, 256101 (2007). [DOI] [PubMed] [Google Scholar]
- Sheehan P. E. and Whitman L. W., Nano Lett. 10.1021/nl050298x 5, 803 (2005). [DOI] [PubMed] [Google Scholar]
- Wang Y., Stevens A. L., and Han J., Anal. Chem. 10.1021/ac050321z 77, 4293 (2005). [DOI] [PubMed] [Google Scholar]
- Wang Y. and Han J., Lab Chip 10.1039/b717220f 8, 392 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grahame D. C., Chem. Rev. (Washington, D.C.) 10.1021/cr60130a002 41, 441 (1947). [DOI] [PubMed] [Google Scholar]
- Elibol O. H., Nair P. R., Reddy B., Go J., Bergstrom D. E., Alam M. A., and Bashir R. (unpublished).
- Nair P. R. and Alam M. A., IEEE Trans. Electron Devices 10.1109/TED.2007.909059 54, 3400 (2007). [DOI] [Google Scholar]
- Sorensen M. H., Mortensen N. A., and Brandbyge M., Appl. Phys. Lett. 10.1063/1.2779930 91, 102105 (2007). [DOI] [Google Scholar]
- Bergveld P., v. Hal R. E. G., and Eijkel J. C. T., Biosens. Bioelectron. 10.1016/0956-5663(95)96887-5 10, 405 (1995). [DOI] [Google Scholar]
- Fung C. D., Cheung P. W., and Ko W. H., IEEE Trans. Electron Devices 10.1109/T-ED.1986.22429 33, 8 (1986). [DOI] [Google Scholar]
- Landheer D., McKinnon W. R., Aers G., Jiang W., Deen M. J., and Shinwari M. W., IEEE Sens. J. 10.1109/JSEN.2007.901047 7, 1233 (2007). [DOI] [Google Scholar]
- Elibol O. H., Reddy B., and Bashir R., Appl. Phys. Lett. 10.1063/1.2920776 92, 193904 (2008). [DOI] [Google Scholar]
- McQuarrie D., Statistical Mechanics (Harper & Row, New York, 1976). [Google Scholar]
- Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.181342398 98, 10037 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitzinger C. and Klimeck G., J. Comput. Electron. 10.1007/s10825-006-0139-x 6, 387 (2007). [DOI] [Google Scholar]
- Landheer D., Ares G., Mckinnon W. R., Deen M. J., and Ranuarez J. C., J. Appl. Phys. 10.1063/1.2008354 98, 044701 (2005). [DOI] [Google Scholar]
- Zhang G. J., Zhang G., Chua J. H., Chee R. E., Wong E. H., Agarwal A., Buddharaju K. D., Singh N., Ghao Z., and Balasubramanian N., Nano Lett. 10.1021/nl072991l 8, 1066 (2008). [DOI] [PubMed] [Google Scholar]
- v. Gunsteren W. F. and Berendsen H. J. C., Biomos BV, GROMOS-87 manual, 1987.
- Li Z., Chen Y., Li X., Kamins T. I., Nauka K., and Williams R. S., Nano Lett. 10.1021/nl034958e 4, 245 (2004). [DOI] [Google Scholar]
- Evans J. W., Rev. Mod. Phys. 10.1103/RevModPhys.65.1281 65, 1281 (1993). [DOI] [Google Scholar]
- Hinrichsen E. H., Feder J., and Jossang T., J. Stat. Phys. 10.1007/BF01011908 44, 793 (1986). [DOI] [Google Scholar]
- Swendsen R. W., Phys. Rev. A 24, 504 (1981). 10.1103/PhysRevA.24.504 [DOI] [Google Scholar]
- Talbot J., Tarjus G., Tassel P. R. V., and Viot P., Colloids Surf., A 10.1016/S0927-7757(99)00409-4 165, 287 (2000). [DOI] [Google Scholar]
- Nair P. R., Ph.D. Dissertation, Purdue University (2009). [Google Scholar]