The Between-Population Genetic Architecture of Growth, Maturation, and Plasticity in Atlantic Salmon

Abstract

The between-population genetic architecture for growth and maturation has not been examined in detail for many animal species despite its central importance in understanding hybrid fitness. We studied the genetic architecture of population divergence in: (i) maturation probabilities at the same age; (ii) size at age and growth, while accounting for maturity status and sex; and (iii) growth plasticity in response to environmental factors, using divergent wild and domesticated Atlantic salmon (Salmo salar). Our work examined two populations and their multigenerational hybrids in a common experimental arrangement in which salinity and quantity of suspended sediments were manipulated to mimic naturally occurring environmental variation. Average specific growth rates across environments differed among crosses, maturity groups, and cross-by-maturity groups, but a growth-rate reduction in the presence of suspended sediments was equal for all groups. Our results revealed both additive and nonadditive outbreeding effects for size at age and for growth rates that differed with life stage, as well as the presence of different sex- and size-specific maturation probabilities between populations. The major implication of our work is that estimates of the genetic architecture of growth and maturation can be biased if one does not simultaneously account for temporal changes in growth and for different maturation probabilities between populations. Namely, these correlated traits interact differently within each population and between sexes and among generations, due to nonadditive effects and a level of independence in the genetic control for traits. Our results emphasize the challenges to investigating and predicting phenotypic changes resulting from between-population outbreeding.

GROWTH rate, the increase in body size per unit time, can vary substantially within and among populations. It can be directly or indirectly linked to fitness through life-history traits such as age at maturity or fecundity (Roff 1992; Stearns 2000). Rapid growth can increase survival probability and enable early reproduction but is usually traded off against later maturity with a higher fecundity (Lester et al. 2004). Furthermore, plasticity in growth can serve as a buffer for responding to environmental variation (Wright 1932; Schlichting and Pigliucci 1998). Consequently, the relationship between growth rate and age at maturity within wild populations might be shaped by local adaptation (Law 1979) or by anthropogenic selection and exploitation (Hutchings and Fraser 2008; Enberg et al. 2012).

Intentional or unintentional anthropogenic translocations increase outbreeding among formerly isolated populations and can result in genotypic and phenotypic changes in local populations that affect individual fitness (Rhymer and Simberloff 1996; Allendorf et al. 2001). A common example is the escape of domesticated aquaculture fish into environments inhabited by their wild counterparts (Naylor et al. 2005; Morris et al. 2008). As with many other livestock species, domesticated fish are normally selected for rapid growth (Gjedrem 2000). In wild or hatchery populations not under directed selection for rapid growth, increased growth rate generally leads to younger age at maturity (e.g., Alm 1959; Thorpe et al. 1983; Taranger et al. 2010). However, maturation is concomitant with a reduction in somatic growth. Thus, to make aquaculture production economical, rapid growth and late age at maturity are, intentionally or unintentionally (as a correlated response to selection for rapid growth), selected for in combination by many breeders (Gjedrem 2000; Thorpe 2004; Taranger et al. 2010). Domesticated individuals destined for consumption markets resulting from such selection programs can exhibit rapid growth and attain late maturity (but see examples for domestication-propagated early maturation in Wright et al. 2012) contrary to patterns naturally exhibited in many species (Roff et al. 2006).

The Atlantic salmon (Salmo salar, Linnaeus 1758) is among the top 10 aquaculture species in terms of worldwide production, with annual production since 2009 exceeding 1 million tons in its native range (Fao 2013). At the same time, many wild populations are in decline and some assessed as endangered (Cosewic 2006; ICES 2010). Linked to domesticated–wild outbreeding, widespread changes to the neutral genetic population structure of wild populations have been reported (Bourret et al. 2011; Glover et al. 2012). Domesticated fish can also introduce allelic combinations into wild populations that change presumably wild-adapted traits, such as age at maturity, reducing fitness as a result (McGinnity et al. 2003).

Trait-linked fitness consequences resulting from outbreeding are predictable across offspring generations under an additive genetic architecture between populations. This is because the average offspring phenotype in each mixed-origin generation will be as similar to the average phenotype of each parental population as the proportions of their allelic contributions. However, when a nonadditive genetic architecture is present, i.e., under the prevalence of dominance or epistasis, phenotypes and associated offspring fitness in different mixed-origin generations may not be as readily predictable (Lynch 1991). Furthermore, a nonadditive genetic architecture can result in initially neutral or positive fitness effects (e.g., first-generation heterosis), allowing for the propagation of domesticated allelic combinations, but which are then followed by negative fitness effects in later generations (Edmands 2007). Hence, a nonadditive genetic architecture might bear the greatest threat to the persistence of wild populations, especially those already experiencing decline. Accordingly, the knowledge of the between-population genetic architecture is crucial in predicting trans-generational fitness consequences arising from outbreeding.

The genetic architecture of divergence in domesticated–wild growth has been investigated in several studies on fishes, but with disparate conclusions. Some studies concluded that growth between populations has an overall additive genetic basis (Tymchuk and Devlin 2005; Tymchuk et al. 2006; Fraser et al. 2010) whereas others detected nonadditive genetic components for growth (McClelland et al. 2005; Tymchuk et al. 2007; Vandersteen et al. 2012). The presence of nonadditive components is supported by transcript-level studies between domesticated and wild populations (Normandeau et al. 2009; Debes et al. 2012; Devlin et al. 2013) but the relationship between transcriptional and morphological phenotype is still largely unknown (Gibson and Weir 2005). Given these disparate conclusions, the genetic architecture of the differences in growth between domesticated and wild populations remains unknown in fishes.

Complicating matters further, results from studies of the between-population genetic architecture based on overall-population growth phenotypes are not easily interpreted. This is especially true for indeterminate growers, such as fish. Fish do not exhibit a genetically determined final size that can be analyzed without confounding genotypes with other temporally acting life-stage-dependent or environmental influences on growth (reviewed by Enberg et al. 2012). In recent studies for example, the direction of between-population dominance for size at age fluctuated between populations across time (McClelland et al. 2005), or the genetic architecture for size differed between being additive and nonadditive with age and environment (Vandersteen et al. 2012). Such temporal and environmental incongruence about the inferred genetic architecture might be explained by nonaccounted changes in growth expression differing between populations. Growth can change between life-history stages, can differ by sex, or can vary among environments (Parker and Larkin 1959; Winkelman and Peterson 1994; Gjedrem 2000; Tymchuk et al. 2007), and one or all of these might differ between analyzed populations. Therefore, analyses of size or growth, and inferences about their between-population genetic architecture, can be misleading if factors other than genotype are largely unaccounted for.

In this study, we investigate the between-population divergence between a wild, endangered S. salar population and its locally occurring domesticated counterpart. Individuals of the wild population mature earlier and grow more slowly relative to those of the domesticated population (present study; Fraser et al. 2010). We describe body sizes and maturation probabilities among the two populations and three multigenerational crosses between them to assess growth among crosses and their environmental plasticity in response to a 2 × 2 factorial design of artificial environments (presence/absence of natural suspended sediments; two water salinities). These four controlled environmental conditions are tested because they mimic water conditions of river (fresh, clear), estuary (fresh, turbid; salty, turbid), and the sea (salty, clear), all of which are experienced by the wild population during its migration between river and sea. We decompose differences in individual growth trajectories underlying environmental, life stage, and genotypic influences by using mixed-model analyses. Our study aims to provide insight into the genetic architecture associated with domesticated–wild divergence in (i) maturation probabilities at the same age, (ii) size at age and growth while accounting for maturity status and sex, and (iii) growth plasticity in response to environmental factors. Although we do not directly evaluate the fitness consequences of domesticated–wild outbreeding, our study provides insight into multigenerational fitness consequences by making inferences about the detailed between-population genetic architecture of the investigated traits. We do this by adopting an approach that combines cross-means analysis and that of individual growth trajectories.

Materials and Methods

Populations

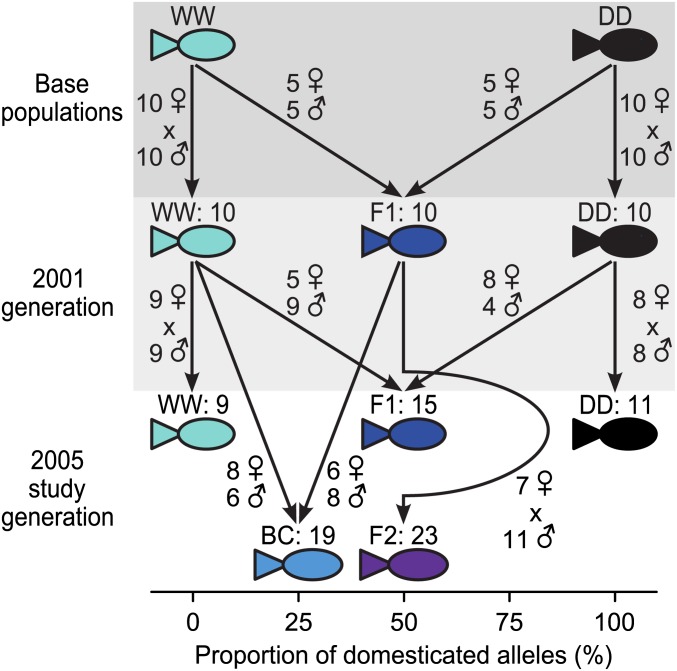
The wild population (WW) originated from the Stewiacke River (45.140°, −63.377°), and the domesticated population (DD) from the Saint John River (45.267°, −66.067°), Canada. The WW population belongs to the endangered inner Bay of Fundy (iBoF) metapopulation (Cosewic 2006). The grandparents of the WW base population were caught as juveniles in the wild, kept at a hatchery for a live gene banking program, and drawn in 2001 from a broodstock of several hundred individuals (details in O’Reilly and Harvie 2009). The source strain of the DD fish was founded in 1989 on 50–100 wild-caught individuals and underwent three generations of individually based selection for rapid growth (Glebe 1998) prior to providing breeders for our DD base population in 2001. The parents of both parental populations and their reciprocal first-generation hybrids (F1) were created in 2001 (Lawlor et al. 2008; Figure 1) and were grown to maturity at Dalhousie University, Halifax, Canada. This laboratory-raised 2001 generation provided the parents for the 2005 fish generation used in this study (Figure 1).

Figure 1.

Graphical representation of the multigenerational crossing design between wild and domesticated S. salar. The number of generated families is indicated for each generation after the colon following each cross abbreviation with wild, WW (turquoise); reciprocal WW parent backcross, BC (light blue); reciprocal first-generation hybrid, F1 (dark blue); second-generation hybrid, F2 (purple); domesticated salmon, DD (black). Also indicated is the number of dams (Venus symbol) and sires (Mars symbol) used to generate each cross in a given generation.

Crossing design, preexperimental conditions

In 2005, WW, DD, and F1 parents were crossed, creating WW, DD, reciprocal F1, second-generation hybrid (F2 = F1 × F1), and the reciprocal WW parent backcross (BC = F1 × WW). Crosses were created as either full-sib families or as a mix of full-sib and half-sib families (Figure 1) and parents were reused within and between crosses whenever possible. Inbreeding up to cousins was avoided by genotyping (see Fraser et al. 2010 for details). All offspring families were grown in a common laboratory. Individuals from each cross were kept from 5 months after initiating of feeding onward in at least four different tanks, as described by Fraser et al. (2010).

Experimental protocol

In July 2008, parr (freshwater individuals prior to seaward migration) were separated from smolts (individuals physiologically capable of migrating to the sea) based on external criteria (parr markings vs. silver coloration in smolts) with only smolts retained for the experiment. This was conducted to provide standardized life-stage phenotypic estimates as post smolts and parr differ in body shape and growth rate. In September 2008, 200 randomly selected individuals from each cross were anesthetized, using eugenol, measured (wet mass ±5 g, fork length ±1 mm), and tagged on both sides of the head with individual alphanumerically marked VIalpha tags (Northwest Marine Technology). After a 28-day recovery period, fish were again anesthetized, identified, measured, and distributed among eight round tanks (1800 liter, flow through system) with 25 fish of each of the five crosses per tank (totaling 1000 fish). For each cross, an equal size distribution was allocated to each tank to avoid a possible cross-by-size bias among tanks. The amount of human disturbance, illumination (natural photoperiod), water quality, flow, temperature, and oxygen saturation was kept constant across tanks with daily correction adjustments.

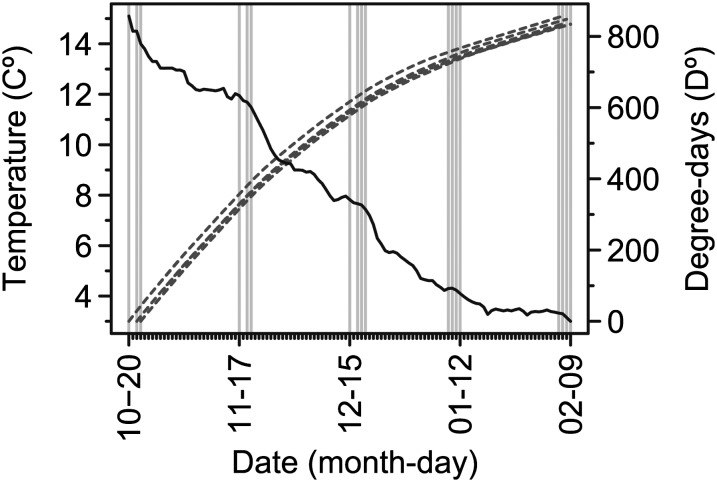
After a recovery period of 5 days, a 2 × 2 factorial arrangement of the environmental factors Salinity and Sediment was randomized to the eight tanks. For Salinity, four tanks were provided with either fresh water (level “fresh”: S = 0 PSU) or brackish water (level “salt”: S = 18 PSU) using a flow-through system. For Sediment, four tanks received daily either a pulse of suspended sediments (level “sediments”: 200 mg/liter with a turbidity of 32 NTU at S = 18 PSU) or clear water (level “clear,” turbidity of 0 NTU) poured in by hand. The applied intertidal sediments were previously collected from upper mudflats of the iBoF and had been air dried. The suspended sediment concentration applied corresponded to that naturally occurring in the iBoF (Gordon 1994), but decreased after the application with a half time of 1.8 hr. Water temperature (range 3–15.1°, mean 7.8°, Figure 2), oxygen saturation (range 79–97%, mean 91%), and salinity (range 0–18.9 PSU) were measured daily for each tank. Once daily after the sediment application, fish were fed ad libitum with four sizes of commercial pellet feed (Corey Aquafeeds, Canada) to accommodate all fish sizes. The daily feed amount, equal for each tank, was determined on the basis of fish-feeding behavior. All individuals were anesthetized, identified, and measured as previously at 26- to 28-day intervals until the end of the experiment (Figure 2). Mortalities were replaced with same-cross individuals for which no data were recorded. At the termination of the experiment, immature and mature individuals, and the sex of mature individuals, were readily identified by gamete stripping.

Figure 2.

Chronology of sampling events and water temperature. Shown are average daily temperatures across all tanks (solid black line), cumulative degree-days for each tank (dotted, gray lines), and data for the five sampling periods (vertical gray lines) across the experimental duration between October 2008 and February 2009.

Statistical analyses

Data from dead individuals and those with lost tags were excluded, yielding data on 934 individuals. As we planned to predict model means across environmental levels (see below), we first evaluated if excluded data or the (unplanned) incidences of sexual maturation by sex had the potential to cause any analytical bias by inequality of individual counts among experimental design levels. We analyzed log-transformed (Ln) number of individuals per Cross-by-Maturity level in each tank by the linear mixed model (LMM),

$$\text{Number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{Individuals}=\mu *\text{Salinity}*\text{Sediment}*\text{Cross}*\text{Maturity}*\text{Tank}$$ (1)

for which μ is a reference mean (the mean in a clear and fresh environment for females of the wild cross), Salinity is the fixed effect of the salt treatment, Sediment is the fixed effect of the sediments treatment, Cross are the fixed effects of the remaining four crosses, and Maturity are the fixed effects for being immature or a male. The asterisks connecting terms indicate interaction effects among terms in addition to their simple effects. Tank represents the random deviation effects for the eight tanks from the respective four treatment combination means of salinity and sediment.

Maturation probabilities

Occurrence of sexual maturation was combined for both sexes and regarded as individual binary of maturation probability (mature vs. immature). We were primarily interested in differences in size-adjusted maturation probabilities among crosses. However, maturation in S. salar is usually affected by processes occurring ∼6–12 months predating spawning time (reviewed by Thorpe et al. 1998)—a time frame that predated our experimental manipulations that coincided with spawning time—but can be controlled later in males (Fjelldal et al. 2011). We thus tested if maturation probability was also influenced by our experimental manipulations. The generalized linear mixed model (GLMM) with logit-link function and binomial residual distribution used for analyses of individual maturation probability binaries was

$$\begin{array}{l}\text{Maturation}\hspace{0.17em}\text{Probability}=\mu +\text{Cross}*\text{Length}+\text{Cross}*{\text{Length}}^2\\ +\text{Cross}*\text{Salinity}*\text{Sediment}+\text{Tank,}\end{array}$$ (2)

for which μ is a reference mean (the mean of the wild cross in a clear and fresh environment, at average length), Length is the fixed continuous effect of length (fork length at the start of the experiment, Ln-transformed, mean centered; representing the reference slope of maturation probability across length for the wild cross), and Length² is its corresponding squared term. Interactions of Cross with either length covariate represent the respective slope effects for the remaining four crosses. All other terms are as in (1).

Size at age and growth

We defined growth rate as the slope of size (fork length or body mass) across time. We Ln-transformed mass and length to meet the assumption of a linear relationship between time and size-proportional growth, normalize residual distributions, and meet normality assumptions for the cross-means analysis (see below). Furthermore, geometric group means were closer to original-scale group medians than arithmetic means, indicating a better representation of population means on the transformed scale. Mean-centered cumulative degree-days (D°, averaged across tanks for each sampling period) was used as a continuous Time covariate because thermal units predict growth in poikilothermic fish better than calendar days (Neuheimer and Taggart 2007) and ambient-based water temperature changed temporally (Figure 2). The resulting slope represents the (temperature-adjusted) specific growth rate (SGR).

To simultaneously analyze size and SGR for all levels of the experimental design we used LMMs. The experiment was analyzed as a completely randomized split plot design in which tanks represented experimental main units (whole plots, term Tank) to which the levels of the 2 × 2 Salinity-by-Sediment factorial (environments) were randomized. Fish individuals were regarded as experimental subunits (subplots, term ID) to which the levels of the 5 × 3 Cross-by-Maturity factorial (genotypes) were randomized. As we analyzed SGR on the basis of temporally repeated measurements of the same fish individuals in the same tanks (a longitudinal design for ID and Tank), we accounted for the correlation at both levels. Therefore, to account for the environmental correlation we including the random-effects terms Tank and Tank-by-Time, and similarly for individual correlations we included the random-effects terms ID and ID-by-Time.

We were primarily interested in comparing the linear slopes of the fixed part of the models (that represent SGRs) among environmental and genotypic levels, and this comparison was valid only under a linear relationship between size and time. In our study, a graphical examination of growth trajectories indicated deviations from linear relationships, some of which varied across time and at several levels of the experimental design (i.e., among environments and genotypes; see Results). Therefore, we modeled these nonlinear growth components nonparametrically by fitting random cubic splines and nonsmooth trend deviations to all longitudinal design terms (Verbyla et al. 1999; Welham 2009). As a result, SGR was allowed to vary among measurement intervals and was estimated as an interval-duration weighted average for each level of the design; this served as an approximation to nonlinear growth trajectories. The model analyzing individual size (for either mass or length) across time was:

$$\begin{array}{l}\text{Size}=\mu +\text{Salinity}*\text{Sediment}*\text{Cross}*\text{Maturity}*\text{Time}+\text{Tank}*\text{Time}+\text{ID}*\text{Time}+\text{spl}\left(\text{Time}\right)/\left(\text{Sediment}*\text{Salinity}*\text{Cross}*\text{Maturity}\right)+\text{spl}\left(\text{Time}\right):\text{Tank}+\text{spl}\left(\text{Time}\right)\text{:ID}+\text{dev}\left(\text{Time}\right)/\left(\text{Sediment}*\text{Salinity}*\text{Cross}*\text{Maturity}\right)+\text{dev}\left(\text{Time}\right)\text{:Tank},\end{array}$$ (3)

for which μ is a reference mean (in a clear and fresh environment for females of the wild cross, at midexperimental Time), Time is the fixed continuous effect of degree-days (mean centered; representing the reference slope of size across degree-days in a clear and fresh environment for females of the wild cross), ID represents the random deviation effects of individuals from the respective 15 genotype combination means of the interaction of Cross and Maturity, spl(Time) represents random splines, dev(Time) represents random trend deviations, and the terms following the colon or slash are nested within each of these effects; i.e., they represent spline and trend deviation terms from linear size trajectories for environments, genotypes, or environment-by-genotype interactions. All other terms are as in (1) and all interactions with Time represent terms for SGR. As individual body size and SGR random deviations might be correlated, we also estimated the covariance between the two. For all terms encompassing among-individual variances (all terms encompassing ID), we evaluated if modeling the (co)variances separately for each of the 15 Cross-by-Maturity levels improved the models. This was conducted to test a priori assumptions of heteroscedasticity among Cross-by-Maturity levels as a consequence of population outbreeding (Hayman 1958; Mather and Jinks 1982; Piepho and Möhring 2010) and of sexual maturation.

Under our longitudinal setting, the choice of a representative covariance structure was crucial for obtaining standard errors that enabled valid hypotheses testing on fixed effects. We chose the structure for among-individual (co)variances across time, as indicated above, among 13 covariance models (Supporting Information, Table S3).

Model fitting and hypothesis testing

Analyses by GLMMs were conducted under Laplace approximation to the likelihood using glmmADMB (Skaug et al. 2012) and analyses by LMMs were conducted under residual maximum likelihood using ASReml-R 3.0 (Butler et al. 2009); both R-packages were executed in R 2.15.3 (R Core Team 2013).

First, the random part of each model was fitted while all fixed-effects terms were included in the model. At this stage, we selected the among-individual covariance structure of growth models (Table S3), while we kept all random effects in the model that did not converge to zero. Next, for a model with chosen among-individual covariance structure, all nonsignificant random terms were removed (likelihood-ratio tests, LRTs; positively constrained variances P > 0.1, unconstrained covariances P > 0.05), except for both Tank error terms and the overall spline term. Random spline terms were tested prior to random nonsmooth trend deviations (Verbyla et al. 1999; Welham 2009). Both Tank error terms, representing the environmental treatment errors, tended to converge to zero when positively constrained and were thence set to be unconstrained for fixed-effects hypotheses testing and marginal predictions (Nelder 1954; Molenberghs and Verbeke 2011).

Second, the fixed part of each model was fitted while keeping all previously chosen random-effects terms in the model. Nonsignificant fixed-effects terms were stepwise removed (P > 0.05; LMMs, conditional Wald F-tests, adjusted after Kenward and Roger 1997; GLMMs, LRTs), highest order first, unless their removal violated marginality (Nelder 1994). Distribution and homoscedasticity of model residuals, and of other random effects, were validated using diagnostic plots. Tests of selected multiple fixed-effects contrasts were conducted by Student’s t-tests in which degrees of freedom (d.f.) were approximated as for F-tests and P-values were adjusted after Benjamini and Yekutieli (2001) to control for the false discovery rate.

Cross-means analysis

Using cross-means analysis, we investigated the between-population genetic architecture for size at midexperimental degree-days (size at age) and for SGRs, of either mass or length. We tested the overall mean ($\widehat{\mu }$), the diallelic additive ($\widehat{d}$), and dominant ($\widehat{h}$) outbreeding effects. Further, we tested three digenic, diallelic epistatic effects: additive-by-additive ($\widehat{i}$), additive-by-dominant ($\widehat{j}$), and dominant-by-dominant ($\widehat{l}$). Traditionally, cross-means analysis has been conducted by a stepwise weighed least-squares (WLS) regression on cross means (outlined by Cavalli 1952; Lynch and Walsh 1998). Analysis of cross means directly by a more recent LMM methodology accounts for variation arising from the experimental design (Piepho and Möhring 2010). In our models, two cross-means terms occur: intercepts (cross sizes at age) and slopes (cross SGRs). As we are not aware of any study attempting to estimate outbreeding effects for intercepts and slopes simultaneously and are unaware of effects on inferences, we used two approaches: (i) a traditional WLS approach on model-predicted cross means and (ii) a direct LMM approach. Large differences in sample sizes for Cross-by-Maturity levels across environments were detected (see Results). As a consequence, we predicted marginal cross means and their standard errors for WLS analyses from Maturity-specific LMMs and conducted the direct LMM approach using Maturity-specific LMMs. Predicting from Maturity-specific models reduced a potential bias of cross means by Maturity when averaging across environments for the WLS approach and ensured a better representation of the covariance structures for the direct LMM approach (deviations from linear growth trajectories differed among maturity groups; see Results). This meant we removed the Maturity term from (3) and selected three models for each trait, each conditional for one of the three Maturity levels.

Our WLS approach was similar to that outlined by Cavalli (1952): we added outbreeding effects stepwise as regression terms (with coefficents after Hayman 1958) to a linear model with cross means as a response and using respective squared standard errors as data weights, until obtaining an adequate fit to the cross means. We defined “adequate” by P > 0.05 for an approximately χ²-distributed lack-of-fit test statistic (residual sum of squares, RSS), with d.f. equaling the number of cross means minus the number of model parameters. Significance of outbreeding effects was approximated by dropping each term from the model and evaluating the associated change in RSS based on the χ² distribution with one d.f.

Our LMM approach was similar to that of Piepho and Möhring (2010): we added outbreeding effects terms directly to each Maturity-specific LMM (after removing the cross-means term to be evaluated, i.e., the slope or intercept term), and the model fit to the cross means was assessed by including a fixed lack-of-fit-term. Adequate was defined by P > 0.05 for the lack-of-fit term (conditional Wald F-tests, adjusted as above). Significance of outbreeding effects terms was evaluated using F-tests after removing the lack-of-fit term. To test significances of the outbreeding effects for SGRs (= model slopes), intercepts were allowed to vary by Cross; for sizes (= model intercepts), slopes were allowed to vary by Cross. Estimating effects for SGR and size simultaneously resulted in conflicts because model effects for both terms affect each other. We did not attempt to estimate genetic cross variances as (i) our sample sizes were small, resulting in unreliable estimates (Piepho and Möhring 2010), (ii) variances between parental populations and F1 differed, which is a violation of an important assumption (Cavalli 1952), and (iii) we were missing the DD parent backcross, which contributes estimates of epistatic variances.

Under both approaches, we first tested if $\widehat{\mu }$ and $\widehat{d}$ and then if $\widehat{\mu }$, $\widehat{d}$, and $\widehat{h}$ adequately fit cross means. Only when all simple effects resulted in a lack-of-fit, we fitted epistatic effects (Hayman 1958). Five cross means allowed us to fit up to four outbreeding effects simultaneously, making it necessary to assess the fit of epistatic effects sequentially. As adding an epistatic effect can affect the estimate and significance of a simple effect and vice versa (Hayman 1958), we never dropped any nonsignificant term from nonadequate models, and that is also why we used conditional rather than traditionally used sequential tests to assess the significance of each term. When several adequate models with equal numbers of parameters occurred, we chose the model with the higher P-value for the lack of fit.

Results

We obtained data on 934 individuals (numbers across experimental level in Table S1, raw data are available as supporting information, File S1 and File S2). Omitted individual data were due to missing identifications (56 out of 1000 individuals), lack of growth (one likely sick individual), and altogether nine mortalities from all five crosses and four environments. Significant differences in individual numbers were not observed by Cross, environments, or for their interactions (Table S2). However, maturity groups (which were not under our control) were represented by different frequencies (Maturity: F_2/56 = 48.8, P < 0.001), and these additionally differed among crosses (Cross-by-Maturity: F_8/56 = 20.6, P < 0.001). Furthermore, this differential Cross-by-Maturity representation varied across environments (Salinity-by-Sediment-by-Cross-by-Maturity: F_8/56 = 2.9, P = 0.008).

Maturation probability

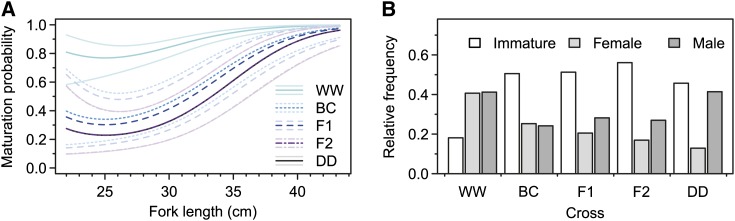
Maturation probability (mature vs. immature) was not affected by the interaction of Cross with any length covariate, by environments, or by any of the interaction terms. Furthermore, among-tank variance was not different from zero (${\chi }_1^2$ = 0, P = 1). Hence, maturation probability was regarded as an observational trait and estimated with different intercepts only among levels of Cross and with common length slopes for all crosses. Under the final model, maturation probability generally increased with length (${\chi }_1^2$ = 82.8; P < 0.001), albeit a small increase in probability at the smallest sizes was accounted for by the squared length term (${\chi }_1^2$ = 12.4, P < 0.001; Figure 3A). Maturation probability at the overall geometric mean for length (30.7 cm) differed among crosses (${\chi }_4^2$ = 121.5, P < 0.001) and was higher for wild S. salar than for all other crosses, which had very similar maturation probabilities (Figure 3A).

Figure 3.

Predicted combined maturation probability and observed frequencies of maturity groups. (A) Predicted maturation probabilities combined for both sexes for each of the five crosses between wild and domesticated S. salar as a function of retransformed fork length at the start of the experiment. Line colors and types are differentiating among the five crosses as given in the key and thinner, pale lines show respective approximate 95% confidence intervals. Lines for DD and F2 have equal positions. (B) Observed relative frequency for each of the three maturity groups for each cross. All cross abbreviations are as in Figure 1.

When overall frequencies of sexes among mature individuals were investigated (while ignoring body sizes), a sex-bias toward mature males occurred in most crosses, except for WW and BC with equal sex frequencies, and this bias was highest in DD (Figure 3B). Under the assumption of within-cross equality of sex frequency (including the unknown sex of immature individuals), presumed female maturation probabilities appeared to be close to additive with the highest probability in WW (Figure 3B). In contrast, the presumed male maturation probabilities were equal in both parental populations at ∼40%, whereas in all mixed-origin crosses probabilities appeared to be 25–35% lower (Figure 3B).

Size at age and growth

Among fixed-effects terms in growth models, most of the higher-order interactions were nonsignificant and therefore removed. The same fixed-effects terms were retained in overall models for both traits (Table 1). Also, overall and Maturity-specific models (which were modeled for the subsequently conducted cross-means analysis) mostly agreed with each other for retained fixed-effects terms (Table 1 and Table 2). Three exceptions were present. First, the significant Salinity-by-Cross interaction term in overall models for SGR of both traits was nonsignificant in all Maturity-specific models. Second, the Salinity effect for SGR was nonsignificant in both overall models, but significant in both immature individual-specific models. Third, a significant Sediment effect for SGR in the overall models was nonsignificant for the female-specific length model (F_1/7.6 = 4.6, P = 0.065).

Table 1. Fixed-effects terms in the final models for either body mass or fork length of crosses between wild and domesticated S. salar.

		Mass	Length
Term	d.f.	d.d.f.	F	P	d.d.f.	F	P
Sediment	1	4	6.4	0.065	4.5	6.4	0.052
Salinity	1	4	0.5	0.536	4.4	1.0	0.367
Cross	4	434.2	111	<0.001	422.6	199	<0.001
Maturity	2	230.1	42.1	<0.001	388.5	24.8	<0.001
Time	1	5.2	>1000	<0.001	1.8	>1000	0.001
Salinity:Cross	4	440.2	0.9	0.480	431.4	0.7	0.623
Cross:Maturity	8	232.9	1.8	0.078	233.6	1.6	0.120
Sediment:Time	1	6.4	150	<0.001	11.2	21.3	<0.001
Salinity:Time	1	6.7	0.5	0.522	9.3	0.2	0.636
Cross:Time	4	443.6	111	<0.001	390.2	58.8	<0.001
Maturity:Time	2	5.8	74.0	<0.001	108.9	547	<0.001
Salinity:Cross:Time	4	456.1	4.3	0.002	438.1	3.0	0.019
Cross:Maturity:Time	8	246.1	5.2	<0.001	214.4	2.3	0.024

Interaction effects terms are indicated by a connecting colon. Degrees of freedom (d.f.) and denominator d.f. (d.d.f.) are given for each term along with F-statistic and P-value.

Table 2. Fixed-effects terms in the final maturity-group-specific models for either body mass or fork length of crosses between wild and domesticated S. salar.

		Immature			Females					Males
Term	d.f.	d.d.f.	F	P	d.d.f.	F		P	d.d.f.	F	P
Body mass
Sediment	1	5.2	1.7	0.251	4.0	0.2		0.694	6.2	0.4	0.556
Salinity	1	4.6	1.7	0.251	—	—		—	—	—	—
Cross	4	153.1	32.4	<0.001	83.3	35		<0.001	134.1	37.0	<0.001
Time	1	6.7	>1000	<0.001	6.3	>1000		<0.001	6.8	928	<0.001
Sediment:Time	1	6.8	234	<0.001	6.0	47.9		<0.001	6.7	9.6	0.017
Salinity:Time	1	3.7	30.1	0.007	—	—		—	—	—	—
Cross:Time	4	140.6	74	<0.001	78.9	19.1		<0.001	133.2	30.7	<0.001
Fork length
Sediment	1	4.7	7.5	0.041	—	—		—	5.5	0.2	0.642
Salinity	1	4.8	0.1	0.804	—	—		—	—	—	—
Cross	4	154.4	78.7	<0.001	83.2a	59.4		<0.001	132.8	60.5	<0.001
Time	1	0.7	>1000	0.016	9.3a	520		<0.001	13.5	>1000	<0.001
Sediment:Time	1	5.3	28	0.003	—	—		—	10.8	21.3	0.001
Salinity:Time	1	6.0	6.7	0.041	—	—		—	—	—	—
Cross:Time	4	141.2	35.1	<0.001	77a	8.3		<0.001	126.1	17.2	<0.001

Interaction effects terms are indicated by a connecting colon. Degrees of freedom (d.f.) and denominator d.f. (d.d.f.) are given for each term along with F-statistics and P-value.

^aThe whole plot Tank error term was negative, exceeded the residual variance, and was omitted as this made the model nonestimable. Note that in the same model whole plot treatment terms were nonsignificant and therefore also omitted.

Random-effects terms modeling smooth and nonsmooth deviations from linear growth trajectories differed between the overall and the Maturity-specific models and also between Maturity-specific models for mass or length [retained model random terms along with their (co)variance estimates can be found in Table S4 and Table S5].

Effects of environments

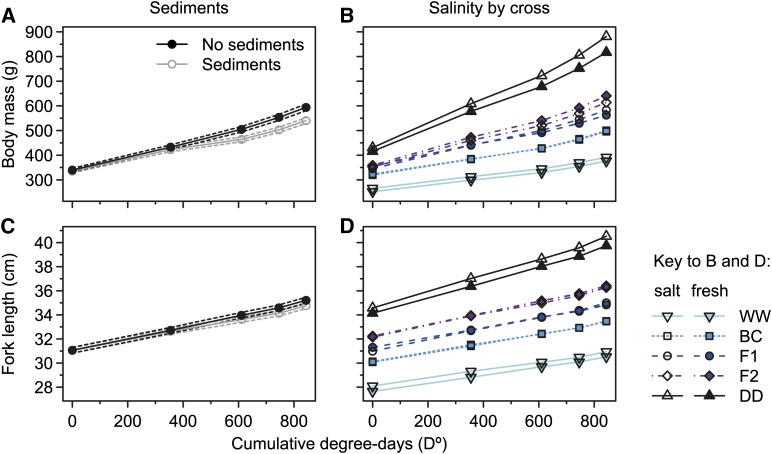
Effects in response to environmental treatments on size at age for mass or length (age at midexperimental degree-days) were nonsignificant, but significant effects on SGRs were detected. Salinity had no overall effect on SGRs of mass and length, but Cross-by-Salinity effects on SGR for both traits were detected (Table 1 and Figure 4, B and D). This was exhibited as Salinity effect on SGR that was different from zero only in F1 hybrids (five pairwise contrasts, given as mass/length; F1, t_456.1/t_438.4 = 3.0/3.0, P_(adjusted) = 0.034/0.029; all others, t_456.1/t_438.4 = 0.3–1.8/0.2–1.3, P_(adjusted) = 0.46–1/1) for which the overall SGR in salt water was 22 and 11% higher (mass, length) relative to fresh water.

Figure 4.

Effects of environments on growth trajectories for body mass and fork length. Marginal predictions for growth trajectories of retransformed body mass (A) and fork length (C) are shown in the absence and presence of a daily pulse of suspended sediments, differentiated by line color as indicated in the key of A. Dashed lines represent ∼95% confidence intervals. Predicted average growth for each of the five crosses is shown for retransformed body mass (B) and fork length (D) in fresh water and salt water, differentiated by symbols and line colors and types as indicated in the key. All cross abbreviations are as in Figure 1.

Suspended sediments had effects on SGRs of both traits that were similar among crosses (Table 1). In the presence of suspended sediments, average SGR was 25 and 19% lower (mass, length) relative to the clear environment. However, graphical examination of average growth trajectories for treatments deviating nonparametrically from linear slopes allowed the identification of two details (Figure 4, A and C). First, the presence of a response delay relative to treatment start could be identified. Second, the presence of an only temporary reduction in SGR in response to suspended sediments could be identified, which appeared to have been shorter but stronger for mass than for length (Figure 4, A and C).

Effects of cross and maturity group

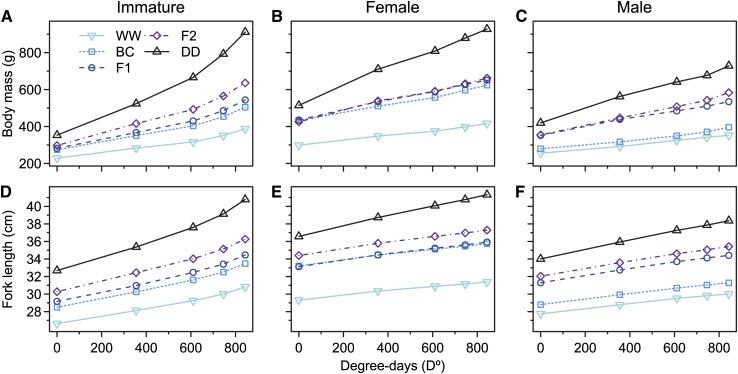
As Cross-by-Maturity effects were detected for both size at age and SGR, these results are reported for the Maturity-specific models. The order among crosses for size at age and SGR of both traits was constant during the experiment with DD > F2 > F1 > BC > WW (Figure 5). Average size at age for both traits was considerably smaller for WW individuals within each maturity group than for individuals of all other crosses, except for male BCs (Figure 5 and Figure 6). Initially, for all crosses mature individuals were larger than immature individuals. Mature individuals exhibited much lower SGRs relative to immature individuals and nearly linear average growth trajectories on the retransformed scale. In contrast, initially smaller, immature individuals exhibited exponential-like growth trajectories. As a consequence, patterns for initial and final sizes among maturity groups differed (Figure 5).

Figure 5.

Effects of cross by maturity group on growth trajectories for body mass and fork length. Marginal predictions of growth trajectories for retransformed body mass (A, B, C) and fork length (D, E, F) are shown for immature individuals (A and D), mature females (B and E), and mature males (C and F). Growth trajectories for crosses are differentiated by colors, line, and symbol types as indicated in the key of A. All cross abbreviations are as in Figure 1.

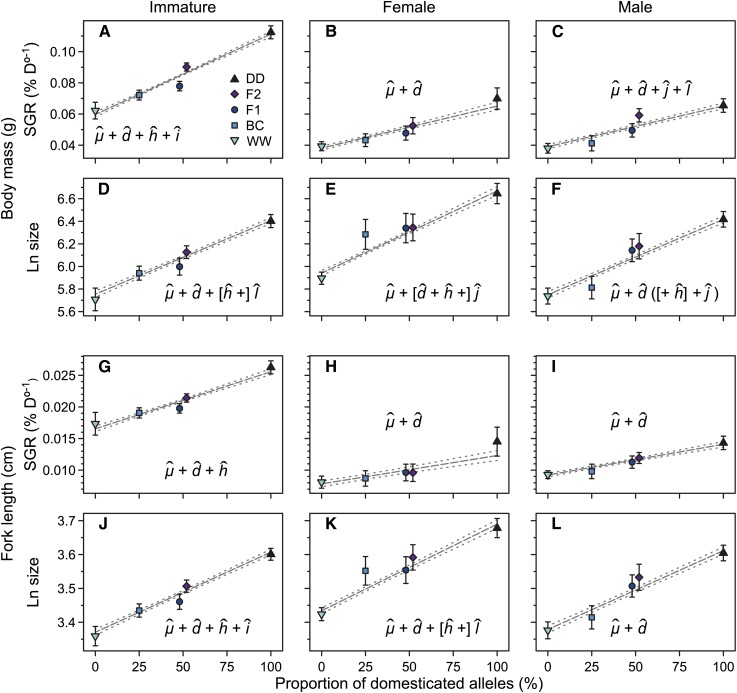
Figure 6.

Cross means for specific growth rate (SGR) and size at age for the three maturity groups. Marginal predictions from maturity-specific models for means of SGRs (A, B, C, G, H, I) and sizes (D, E, F, J, K, L) are shown for body mass (A–F) and fork length (G–L). Means of crosses are differentiated by colors and symbols as indicated in the key of A. Error bars represent ∼95% confidence intervals. Cross means for F1 and F2 hybrids have been offset to improve depiction. All cross abbreviations are as in Figure 1. For each trait, the estimated outbreeding effects, abbreviated as in the text, are indicated. Effects in brackets were nonsignificant and have been removed from the final models. The model for F differed between WLS and LMM approaches and terms in parentheses were assessed only under the WLS approach. The grey lines with dashed 95% confidence intervals represent predicted cross positions under an additive outbreeding effect model.

Cross-means analysis of size and growth

All Maturity-specific cross means were predicted by averaging across environments as no interaction effects of environments with Cross were detected (Table 2). Results based on WLS and LMM approaches led to mostly equal inferences, but effect standard errors under the traditional WLS approach tended to be smaller (Table 3 and Table 4). As a major difference between approaches, the model for male body mass fit solely the additive effect under the LMM approach but fit the additive and additive-by-dominant effects combination under the WLS approach (Table 3 and Figure 6F).

Table 3. Estimated outbreeding effects for size at age of body mass (Ln of grams) and SGR of body mass (% °D^-1).

Effect	Mean ± SE	d.d.f. (d.f.)	F1/d.d.f. (${\chi }_{\text{d.f.}}^2$)	P	Lack-of-fit
Immature
$\widehat{\mu }$ (size)	6.126 ± 0.022 (6.124 ± 0.018)	—	—	—	F2/218.2 = 0.8, P = 0.467 (${\chi }_2^2$= 1.5, P = 0.484)
$\widehat{d}$ (size)	−0.358 ± 0.026 (−0.359 ± 0.022)	112.8 (1)	188 (187)	<0.001 (<0.001)
$\widehat{l}$ (size)	−0.090 ± 0.033 (−0.091 ± 0.028)	200.8 (1)	7.0 (7.5)	0.009 (0.006)
$\widehat{\mu }$ (SGR)	0.0899 ± 0.0012 (0.0899 ± 0.0010)	—	—	—	F1/160.4 = 0.4, P = 0.517 (${\chi }_1^2$= 0.7, P = 0.409)
$\widehat{d}$ (SGR)	−0.0258 ± 0.0016 (−0.0258 ± 0.0012)	127.9 (1)	261 (297)	<0.001 (<0.001)
$\widehat{h}$ (SGR)	−0.0118 ± 0.0023 (−0.0122 ± 0.0016)	160.7 (1)	27.0 (37.7)	<0.001 (<0.001)
$\widehat{i}$ (SGR)	−0.0142 ± 0.0039 (−0.0152 ± 0.0028)	193.1 (1)	13.5 (19.5)	<0.001 (<0.001)
Female
$\widehat{\mu }$ (size)	6.308 ± 0.020 (6.289 ± 0.017)	—	—	—	F3/77.2 = 0.6, P = 0.618 (${\chi }_3^2$= 2.0, P = 0.572)
$\widehat{j}$ (size)	0.392 ± 0.075 (0.384 ± 0.021)	64.8 (1)	177 (231)	<0.001 (<0.001)
$\widehat{\mu }$ (SGR)	0.0520 ± 0.0012 (0.0516 ± 0.0017)	—	—	—	F3/83.8 = 1.7, P = 0.166 (${\chi }_3^2$= 6.4, P = 0.092)
$\widehat{d}$ (SGR)	−0.0135 ± 0.0016 (−0.0135 ± 0.0023)	90.1 (1)	70.7 (71.6)	<0.001 <0.001
Male
$\widehat{\mu }$ (size)	6.082 ± 0.018 (6.102 ± 0.021)	—	—	—	F3/110 = 2.3, P = 0.085 (${\chi }_2^2$= 3.5,P = 0.172)
$\widehat{d}$ (size)	−0.334 ± 0.025 (−0.579 ± 0.108)	161.9 (1)	181 (28.8)	<0.001 (<0.001)
($\widehat{j}$ (size))a	(−0.240 ± 0.111)	(1)	(4.7)	(0.031)
$\widehat{\mu }$ (SGR)	0.0592 ± 0.0021 (0.0592 ± 0.0019)	—	—	—	F1/96.9 = 1.0, P = 0.320 (${\chi }_1^2$= 0.8,P = 0.376)
$\widehat{d}$ (SGR)	−0.0351 ± 0.0064 (−0.0359 ± 0.0057)	88.6 (1)	30.6 (30.8)	<0.001 <0.001
$\widehat{j}$ (SGR)	−0.0229 ± 0.0065 (−0.0224 ± 0.0058)	95.7 (1)	12.5 (11.5)	0.001 (0.001)
$\widehat{l}$ (SGR)	−0.0073 ± 0.0024 (−0.0080 ± 0.0021)	80.9 (1)	9.6 (11.1)	0.003 (0.001)

The effects are predicted F2 cross mean ($\widehat{\mu }$), and additive ($\widehat{d}$), dominant ($\widehat{h}$), additive-by-additive ($\widehat{i}$), additive-by-dominant ($\widehat{j}$), and dominant-by-dominant ($\widehat{l}$) outbreeding effects. Given are effects with standard errors (SE), and probabilities (P) for being different from zero, for immature, female, or male S. salar. Estimates from the LMM approach are given with respective denominator degrees of freedom (d.d.f.) and F-statistic; estimates from the WLS approach (values in parenthesis) are given with respective degrees of freedom (d.f.) and ${\chi }^2$ statistic.

^aOnly under a WLS approach the additive effect did not fit to the cross means (${\chi }_3^2$ = 8.2; P = 0.042).

Table 4. Estimated outbreeding effects for size at age of fork length (Ln of centimeters) and SGR of fork length (% °D^-1).

Effect	Mean ± SE	d.d.f. (d.f.)	F1/d.d.f. (${\mathit{\chi }}_{\text{d.f.}}^2$)	P	Lack-of-fit
Immature
$\widehat{\mu }$ (size)	3.509 ± 0.009 (3.508 ± 0.005)	—	—	—	F1/180.4 = 0.4, P = 0.552 (${\chi }_1^2$ = 0.3 P = 0.591)
$\widehat{d}$ (size)	−0.121 ± 0.007 (−0.119 ± 0.004)	96.6 (1)	267 (244)	<0.001 <0.001
$\widehat{h}$ (size)	−0.047 ± 0.014 (−0.046 ± 0.008)	190.9 (1)	11.2 (10.4)	0.001 0.001
$\widehat{i}$ (size)	−0.072 ± 0.022 (−0.073 ± 0.012)	233.2 (1)	10.8 (10.4)	0.001 0.001
$\widehat{\mu }$ (SGR)	0.0211 ± 0.0002 (0.0211 ± 0.0002)	—	—	—	F2/152.2 = 0.9, P = 0.426 (${\chi }_2^2$ = 1.9 P = 0.382)
$\widehat{d}$ (SGR)	−0.0041 ± 0.0004 (−0.0042 ± 0.0004)	181.8 (1)	98.2 (107)	<0.001 (<0.001)
$\widehat{h}$ (SGR)	−0.0011 ± 0.0003 (−0.0011 ± 0.0003)	184.2 (1)	12.1 (14.1)	0.001 (0.001)
Female
$\widehat{\mu }$ (size)	3.602 ± 0.014 (3.602 ± 0.009)	—	—	—	F2/83.6 = 0.3, P = 0.698 (${\chi }_2^2$ = 0.7 P = 0.696)
$\widehat{d}$ (size)	−0.126 ± 0.008 (−0.126 ± 0.005)	57.4 (1)	231 (227)	<0.001 (<0.001)
$\widehat{l}$ (size)	−0.051 ± 0.016 (−0.051 ± 0.010)	113.3 (1)	10.4 (10.2)	0.002 (0.001)
$\widehat{\mu }$ (SGR)	0.00950 ± 0.00068 (0.01018 ± 0.00045)	—	—	—	F3/80.8 = 2.0, P = 0.124 (${\chi }_3^2$ = 4.9 P = 0.178)
$\widehat{d}$ (SGR)	−0.00224 ± 0.00044 (−0.00248 ± 0.00066)	126.3 (1)	25.3 (24.3)	<0.001 (<0.001)
Male
$\widehat{\mu }$ (size)	3.495 ± 0.007 (3.495 ± 0.010)	—	—	—	F3/106.1 = 2.3, P = 0.089 (${\chi }_3^2$ = 6.5 P = 0.090)
$\widehat{d}$ (size)	−0.116 ± 0.008	162.8 (1)	215 (201)	<0.001 (<0.001)
	−0.116 ± 0.012
$\widehat{\mu }$ (SGR)	0.01172 ± 0.00024 (0.01168 ± 0.00019)	—	—	—	F3/113.5 = 0.8, P = 0.520 (${\chi }_3^2$ = 2.3 P = 0.512)
$\widehat{d}$ (SGR)	−0.00243 ± 0.00030 (-0.00243 ± 0.00026)	146.9 (1)	68.0 (67)	<0.001 (<0.001)

The effects are predicted F2 cross mean ($\widehat{\mu }$), and additive ($\widehat{d}$), dominant ($\widehat{h}$), additive-by-additive ($\widehat{i}$), additive-by-dominant ($\widehat{j}$), and dominant-by-dominant ($\widehat{l}$) outbreeding effects. Given are Effects with standard errors (SE), and probabilities (P) for being different from zero, for immature, female, or male S. salar. Estimates from the LMM approach are given with respective denominator degrees of freedom (d.d.f.) and F-statistic; estimates from the WLS approach (values in parenthesis) are given with respective degrees of freedom (d.f.) and ${\chi }^2$ statistic.

Cross means of immature individuals for SGRs of both mass and length fit different combinations of additive and nonadditive effects (Table 3 and Table 4). The nonadditive outbreeding effects were expressed either as differential deviations from an additive pattern between the first (F1) and second generation (F2, BC) of outbreeding (size of length, SGR of mass and length; dominance; Figure 6, A, G, and J), or as deviations from an additive pattern expressed only in the second generation of outbreeding (size of mass; dominant-by-dominant, Figure 6D), with additional differences between F2 and BC (size of length and SGR of mass; additive-by-additive epistasis; Figure 6, A and J). Female cross means for SGRs of both traits were best explained by additive effects, whereas cross means for size at age fitted additive and epistatic effects (Table 3, Table 4, and Figure 6, B, E, H, K). Epistatic effects were exhibited either as equal mean sizes among F1, F2, and BC (size for mass; additive-by-dominant; Figure 6E), or as deviations from an additive pattern expressed only in the second generation of outbreeding (size of length; dominant-by-dominant, Figure 6K). For male individuals, cross means for size at age and SGR of length were best explained solely by the additive effect (Table 3, Table 4, and Figure 6, I and L). Depending on the method used, male cross means for size of mass fit either the additive effect (LMM approach) or the combination of additive and additive-by-dominant effects (WLS approach; Table 3, Table 4, and Figure 6F). Male cross means for SGR of mass fit a combination of additive, epistatic additive-by-dominant, and dominant-by-dominant effects (Table 3 and Table 4); deviations from an additive pattern exhibited different directions for F2 and BC.

Discussion

Our analyses revealed the presence of both additive and nonadditive outbreeding effects for two investigated traits: size at age and growth rate. In immature individuals, nonadditive effects comprised one-quarter to one-half of the total effects on means. As a result, the consequences of outbreeding can be difficult to predict, which might be problematic for conservation efforts or animal breeding initiatives. On the other hand, outbreeding among individuals from different populations might allow natural populations to reach adaptive peaks by a trial and error mechanism (Wright 1932). Considering that combined outbreeding effects for both growth and maturation might create new phenotypes from combinations of the two traits, some of which might result in higher fitness in certain environments, nonadditive outbreeding effects could represent an important means of generating evolutionary change in wild populations. However, a successful trial and error mechanism might require that populations (i) have a steady effective number of breeders and (ii) receive a balanced number of immigrants. In our particular model organism, S. salar, neither might be the case, as many populations are experiencing decline (Cosewic 2006; ICES 2010) and receive elevated numbers of immigrants in the form of aquaculture escapees (reviewed by Glover et al. 2012).

From a general perspective, this study illustrates how the consequences of outbreeding can differ among maturity groups of mature male, mature female, and immature individuals. A population’s average size at age is the sum of products of maturity group frequencies with maturity group mean sizes at age. As a result, studies on the genetic architecture of body size that are based on average size at age can be biased if different frequencies of maturity groups between populations remain unaccounted for. Furthermore, the study of growth rate can also be biased if the maturation process is unaccounted for because maturation causes temporally changing growth rates that usually differ between sexes as a result of differential costs of reproduction (Hutchings 2006). These findings might well extend to other species having indeterminate growth, such as many invertebrates, fish, amphibians, and reptiles (Heino and Kaitala 1999), and to those species that allocate large amounts of energy to female gametes and exhibit variability in age at maturity, such as birds (Newton 1989).

We did not detect differences in environmental plasticity for growth among crosses; in other words, reaction norms were of similar shape among crosses. Many previous studies have reported genetically based differences in reaction norms and it is often assumed that these differences reflect local or evolutionary adaptation (reviewed by Hutchings 2011; Reusch 2014). However, despite considerable differences in growth rate between populations and between sediment treatments, we did not find evidence of genetic differences in the plastic responses by salmon to changes in suspended sediments (or water salinity). As a result, we were unable to examine whether outbreeding affects reaction norms.

Size at age and growth

One question of general interest is whether the between-population epistatic variation for size at age and growth rate detected here is also expressed within populations. There is evidence to suggest that reductions in population abundance can be associated with the potential conversion of epistatic to additive variation (Goodnight 1988). Past natural colonization or bottleneck events, or anthropogenic selection programs, might propagate a conversion of epistatic to additive variation, and outbreeding might reverse this process (Whitlock et al. 1993).

For mature individuals, we detected differential outbreeding effects for size at age and growth rate. Such incongruence of effects for size and growth rate (the latter should underlie the former) is likely to have been caused by a mix, or either, of two processes. First, probability of maturity is likely to be a function of size at age, quite possibly at ages younger than the ages at which our experimental fish were challenged in the laboratory. Second, divergence in growth rates of mature (or maturing) individuals among crosses might have differed before and during the experiment. Large observed differences in growth rates between mature and immature individuals were expected because of growth-related changes associated with maturation. Nevertheless, growth rate for length of males and females and mass of females was additive, whereas growth rate for mass of males and growth rate of immature individuals for both mass and length was nonadditive. These differences suggest that nonadditive growth components between populations can be conditionally expressed for life stage and sex; this might be responsible for the inferred different outbreeding effects for size at age and growth rate.

Size and age at maturity

In nature, the fastest-growing individuals within populations typically mature first (Alm 1959; Hutchings 1993) and among-population differences can be attributed to phenotypic plasticity, different genetically based maturation schedules, or both (Enberg et al. 2012). Our within-cross observations were consistent with the common pattern that fastest growing individuals mature first. However, this was contradicted by among-cross observations for females; an increasing percentage of domesticated allelic combinations resulted in an increasing size at age but also in a decreasing female maturation probability. This contrasts with typically observed natural patterns and strongly suggests a level of independence between the genetic basis of growth and maturation probability. Furthermore, a different cross-means pattern in male vs. female maturation probabilities indicates sex specificity in genetic architecture. Such sex specificity was somewhat expected because of differential sex-specific resource demands during maturation and their respective evolutionary constraints (Roff 1992; Hutchings 2006; Taranger et al. 2010). However, as a limitation to our conclusions, differences in sex ratios might be present among crosses.

In mature females, we inferred an epistatic additive-by-dominant architecture for size at age because backcrosses were as large as F1 and F2 hybrids; conversely, these latter two crosses fit the midparental value. Hence, the epistatic basis for the female size pattern can be attributed to the strong size deviation of the backcrosses. It is possible that this pattern of size at age resulted from a combination of population divergence in growth rate and divergence in size-specific female maturation probability. Accordingly, it is difficult to infer which of these traits dominates the epistatic female size-at-age pattern. However, it is possible that mere additive and dominance effects for the different traits in combination have caused the observed additive-by-dominant effect pattern.

Phenotypic trait combinations or interactions might also have had effects on the inferred genetic architecture of correlated traits. This consideration challenges the assumption that an epistatic genotype underlies an epistatic phenotype. Nevertheless, an epistatic effect size-at-age pattern was absent in male backcrosses (only under the LMM approach; see below), but male backcrosses exhibited an opposing trend relative to female backcrosses by being smaller than expected under additivity. Backcrosses and F2 hybrids possess 50 and 100% chromosomes, respectively, which have been recombined between populations during meiotic crossover in F1 hybrid parents. For many species, recombination differs strongly in rates and in sites between sexes (Mank 2009), which is also true in our model organism (Moen et al. 2008), and this has the potential to create sex-specific epistasis. Furthermore, generally larger effects of genetic drift on X-chromosomes vs. autosomes have been suggested to play important roles in speciation (Whitlock and Wade 1995). Similar mechanisms may underlie the presence of sex-specific outbreeding effects, here primarily observed in wild-parent backcrosses where recombined chromosomes function under a wild allelic background, in contrast to the F2 hybrid. Unfortunately, logistical space limitations prohibited us from generating and evaluating the domesticated-parent backcross. Hence, we could not evaluate if epistatic effects are also evident for the missing backcross or if these effects differ for parental population genetic backgrounds. In nature, the wild-parent backcross is more likely to occur than the domesticated-parent backcross. Therefore, having evaluated the wild-parent backcross, this appears, at least from a conservation perspective, to have been more important.

We used two approaches to disentangle the between-population genetic architecture. For the traditional WLS approach, relative to the direct LMM approach, standard errors were generally smaller and this might have led to the choosing of a more complicated model for male body mass by the WLS approach. We posit that the WLS approach might have resulted in too liberal results given our limited sample sizes. We suggest this because hypothesis testing under the direct LMM approach is based on sample-size adjusted tests, whereas for the WLS approach it is based on large sample approximations. As a consequence, preference might be afforded to the results we obtained by the direct LMM approach, using F-tests with adjusted denominator degrees of freedom.

One caveat associated with our work is that we did not account for correlations among individuals arising from kinship. That is, we were unable to account for family-level biases that are known to affect population-level inferences (Jourdan-Pineau et al. 2012). We expect that the significance of large differences in means between populations is unlikely to change when accounted for kinship. However, the sensitive cross-means analyses might have been influenced by a potential family bias or unduly liberal tests resulting from unaccounted positive correlations among individuals. Such potential effects might be especially relevant for test statistics that are close to significance thresholds, as is the case for the above-mentioned epistatic effect for male body mass under the WLS approach. Despite this, our strongest result, the contrasting size deviations from an additive pattern between female and male backcrosses, is unlikely to be affected by any unaccounted effects.

Combined effects from divergence of growth and size and age at maturation

Growth rate, size at age, and size and age at maturity are life-history traits of fundamental importance to fitness (Roff 1992; Stearns 2000). In this study, investigated traits either influence each other (such as growth rate affects size and maturation probability and vice versa) or are a result of trait combinations (such as size or age at maturity is a result of maturation probability and growth rate). Some traits appear to underlie a large share of nonadditive effects between populations. A previous metaanalysis indicated that nonadditive effects might generally be much stronger for life-history traits than for morphological traits and the authors suggested that additive genetic variation might be reduced more strongly in the former by natural selection (Roff and Emerson 2006). We suggest that nonadditive effects resulting from trait combinations, such as how growth rate and size-specific maturation probability combined define size at age of mature individuals (and also average age at maturity), might also contribute to a higher occurrence of nonadditive effects in some life-history traits relative to “simpler” morphological traits (see also Brodie Iii 2000).

Our results underscore the challenges in predicting morphological and life-history trait changes resulting from outbreeding because of temporally changing correlations between single traits (such as size at age with growth rate) or because the expression of single “traits” can result from combinations of other traits (Barton and Turelli 1989; Brodie Iii 2000). As growth expression differs among environments and crosses, and size-specific maturation probability differs among crosses and between sexes, size and age at maturity among crosses and between sexes will be very difficult to predict. In nature, temporally changing feeding opportunities and variable environments will likely induce phenotypic plasticity for growth beyond the scope of our study and this may further alter maturation schedules among crosses and between sexes. Overall changes in age at maturity by outbreeding appear unpredictable because a nonadditive genetic architecture underlies growth rate and, at least for females, size-related maturation patterns can have opposing effects within vs. between crosses.