A population health approach to reducing observational intensity bias in health risk adjustment: cross sectional analysis of insurance claims

Abstract

Objective To compare the performance of two new approaches to risk adjustment that are free of the influence of observational intensity with methods that depend on diagnoses listed in administrative databases.

Setting Administrative data from the US Medicare program for services provided in 2007 among 306 US hospital referral regions.

Design Cross sectional analysis.

Participants 20% sample of fee for service Medicare beneficiaries residing in one of 306 hospital referral regions in the United States in 2007 (n=5 153 877).

Main outcome measures The effect of health risk adjustment on age, sex, and race adjusted mortality and spending rates among hospital referral regions using four indices: the standard Centers for Medicare and Medicaid Services—Hierarchical Condition Categories (HCC) index used by the US Medicare program (calculated from diagnoses listed in Medicare’s administrative database); a visit corrected HCC index (to reduce the effects of observational intensity on frequency of diagnoses); a poverty index (based on US census); and a population health index (calculated using data on incidence of hip fractures and strokes, and responses from a population based annual survey of health from the Centers for Disease Control and Prevention).

Results Estimated variation in age, sex, and race adjusted mortality rates across hospital referral regions was reduced using the indices based on population health, poverty, and visit corrected HCC, but increased using the standard HCC index. Most of the residual variation in age, sex, and race adjusted mortality was explained (in terms of weighted R2) by the population health index: R2=0.65. The other indices explained less: R2=0.20 for the visit corrected HCC index; 0.19 for the poverty index, and 0.02 for the standard HCC index. The residual variation in age, sex, race, and price adjusted spending per capita across the 306 hospital referral regions explained by the indices (in terms of weighted R2) were 0.50 for the standard HCC index, 0.21 for the population health index, 0.12 for the poverty index, and 0.07 for the visit corrected HCC index, implying that only a modest amount of the variation in spending can be explained by factors most closely related to mortality. Further, once the HCC index is visit corrected it accounts for almost none of the residual variation in age, sex, and race adjusted spending.

Conclusion Health risk adjustment using either the poverty index or the population health index performed substantially better in terms of explaining actual mortality than the indices that relied on diagnoses from administrative databases; the population health index explained the majority of residual variation in age, sex, and race adjusted mortality. Owing to the influence of observational intensity on diagnoses from administrative databases, the standard HCC index over-adjusts for regional differences in spending. Research to improve health risk adjustment methods should focus on developing measures of risk that do not depend on observation influenced diagnoses recorded in administrative databases.

Introduction

Per capita medical spending and utilization varies extensively among healthcare regions, as reported in the Dartmouth Atlas of Healthcare, the NHS Atlas of Variation, and the Spanish Atlas of Variability.^{1 2 3} These variations have raised major concerns about the effectiveness and equitable distribution of healthcare services, and led naturally to an important question: “To what extent can variations be explained by differences in illness of the regions’ populations?”^{4 5 6 7 8 9 10 11 12 13}

When the distribution of illness differs substantially from region to region, risk adjustment can allow an “apples to apples” comparison of spending and utilization. The traditional approach to risk adjustment is to remove statistically the variation in illness associated with age and sex. This makes intuitive sense and fits the data: the relation between growing older and increased illness is incontrovertible and there are conditions (childbirth) or illnesses (prostate cancer) that only occur in one sex. The development and use of accurate risk adjustment is more than an academic exercise. In the United States, risk adjustment is fundamental to healthcare reform initiated by the Affordable Care Act.^{14 15} Risk adjustment is central to the formulas used to allocate resources within the English National Health Service and to risk equalization between competing insurers in the Netherlands.^{16 17 18}

With the advent of modern computers and “big data” transaction files such as the US Medicare administrative and NHS hospital episode statistics databases, new methods of adjusting for variation in illness among population groups have been developed using the International Classification of Diseases (ICD) diagnosis codes recorded in these administrative databases.^{18 19} Each system accomplishes risk adjustment in roughly the same manner: a comorbidity score is developed for each individual in the database and then used statistically to adjust spending, mortality, and utilization rates for illness. Certain methods have become standard in the United States for developing comorbidity scores. The Iezzoni chronic condition count and the Charlson comorbidity index were developed primarily to control for risk in observational studies of health outcomes and are now used to adjust for illness in public reports of hospital mortality.^{20 21} The Centers for Medicare and Medicaid Services—Hierarchical Condition Categories (HCC) score was initially developed to adjust payments to health insurers under the US Medicare Program, but it is also used to adjust mortality and utilization rates for public reports of health quality and outcomes research.^{21 22}

The validity of these newer methods of risk adjustment rests on the assumption that the diagnoses recorded in the administrative databases accurately reflect the underlying burden of illness in a region’s population. In other words, these methods assume that the frequency of diagnosis is independent of intensity of observation related to a region’s supply of medical care. Several recent studies have questioned this assumption. The first, a natural experiment, followed Medicare beneficiaries who migrated from one region of the United States to another.²³ Those who went from a region with low healthcare spending to one with high spending experienced more visits to physicians, referrals, diagnostic tests, and imaging exams. Each of these encounters with the medical system became an opportunity to identify or code more clinical conditions. Those who migrated to regions with lower intensity of care acquired fewer diagnoses. However, mortality rates over a three year follow-up were similar for migrators regardless of the different rates of “new” conditions they acquired.

The second, a cross sectional study showed a strong positive association between the intensity of patient observation, as measured by visit rates to physicians and the proportion of a region’s population with a diagnosis of chronic illness.²⁴ This “observational intensity” effect was not simply the consequence of poorer health: greater observational intensity led to healthier people being labeled “chronically ill,” with a commensurate decline in case fatality rates (the proportion of patients diagnosed as chronically ill who died). Despite the higher proportion of the population with a diagnosis of chronic illness, the age, sex, and race adjusted mortality rates among regions were similar.

The third study evaluated the extent of observational intensity bias associated with risk adjustment using the standard HCC, Iezzoni, and Charlson comorbidity indices, and suggested an approach to reduce this bias.^{19 20 21 25} Application of the standard indices resulted in implausible changes in adjusted mortality rates in regions of high and low visits. For example, in regions with high rates of visits, adding the HCC index to age, sex, and race adjustment caused a 10% downward swing in adjusted mortality and an upward swing of over 12% in regions with low rates of visits. However, the observational intensity biases of the standard indices could be reduced through a statistical adjustment to correct for variation in visit rates. The visit corrected comorbidity indices proved better risk adjusters than the standard indices: they reduced overall variation in age, sex, and race adjusted mortality; they also explained more of the residual variation in age, sex, and race adjusted mortality than the standard indices.

For the current study we developed two new approaches to risk adjustment based on data that is clearly independent of observational intensity. Our first approach used a single measure of deprivation: the percent of the population below poverty as defined by the US census. The second approach used a composite index of population health: self reported illness, obesity, smoking status, and the regional incidence of admission to hospital for hip fractures and strokes. We compared the ability of each approach to reduce the residual variation in age, sex, and race adjusted mortality and spending per capita across regions; explain these residual variations; and avoid implausible swings in mortality and spending rates in regions with high and low visit rates. We then considered the implications of our study for risk adjustment in the US and the National Health Service.

Methods

Data

The study population included a 20% sample of Medicare beneficiaries residing in 306 hospital referral regions in the United States in 2007, identified from the 2007 Centers for Medicare and Medicaid Services denominator file.¹ Hospital referral regions were empirically developed based on patient origin studies to define the geographic region served by tertiary hospitals. We restricted the analysis to fee for service beneficiaries who were either fully enrolled in part A and part B throughout 2007 and who were 65-99 years old on 31 December 2007, or fully enrolled beginning 1 January 2007 until their death that year and who were 65-99 years old at their time of death. We excluded beneficiaries enrolled in risk contract Medicare Advantage plans because their administrative databases are incomplete. The final sample totaled 5 153 877 beneficiaries.

Mortality and spending adjusted for age, sex, and race

The numerator for mortality rates was the number of deaths from any cause in calendar year 2007 among the study population (based on death dates obtained from the Medicare denominator file). The numerator for spending rates per capita was the 2007 price adjusted total reimbursement for this population. Price adjustment removes reimbursements for graduate medical education, extra payments made to hospitals serving low income populations (“disproportionate share” payments), and differences in wages.²⁶

We used a standard adjustment approach estimated at the individual level (n=5 153 877). We initially adjusted solely for age, sex, and race at the level of the individual beneficiary using linear regression models (SAS GENMOD procedure) incorporating 20 indicator variables to represent all age, sex, and race combinations (a logistic regression model yielded similar results). In addition to the individual level categorical variables (with means set equal to zero) we included the 306 hospital referral regions as classification variables for regional effects. We then used the hospital referral region level coefficient estimates to construct age, sex, and race adjusted measures of mortality and price adjusted expenditures at the hospital referral region level.

Mortality and spending adjusted for risk

We compared four approaches to risk adjustment that used different indices of illness. The first approach used the standard HCC method. We calculated patient level HCC risk scores, employing coding algorithms that are used by the Centers for Medicare and Medicaid Services to adjust payments for Medicare Advantage plans.²⁷ For each beneficiary we assigned HCCs using diagnoses coded on their 2007 part A hospital discharges, part B evaluation and management services, part B procedures, and visits from the outpatient administrative databases. The algorithm to compute the HCC score incorporates administrative database diagnoses at the individual level as well as age, sex, and disability status.

The second approach corrected the HCC index to reduce observational intensity bias using the physician visit rate during the last six months of life as a proxy.²⁵ At the regional level, the visit rate, whether calculated on an annualized basis or for the last six months of life, was highly correlated with the risk score, while uncorrelated with age, sex, and race adjusted mortality. We calculated the visit corrected HCC index by ordinary least squares regression analysis in which the dependent variable was the individual level risk score; the independent variable was physician visit at the regional level. The residual from this regression—the difference between the observed and predicted risk score—is the visit corrected HCC index. It represents the component of illness that is not explained by frequency of physician visits.

The third approach to risk adjustment was based solely on poverty: the percentage of the population aged 65 and over below the federal poverty level as defined by the US census for 2000. This is measured at the zip code level for black and non-black Americans and assigned to all beneficiaries according to their race and zip code of residence.

The fourth approach used data on population health using five measures. Two of these are annual rates for hip fractures and strokes at the hospital referral region level, which were computed for Medicare beneficiaries who were aged 65-99 and part A entitled in 2006 using the 2006 part A hospital administrative database for primary diagnosis for hip fracture and diagnosis related groups for stroke. We computed age, sex, and race adjusted rates at the hospital referral region level for two subgroups, the young old (65-79), and the very old (80-99), and applied to each age group within the hospital referral regions. The other three were county level measures of obesity, smoking status, and self reported illness (measured by average number of poor physical health days per month) from the 2010 Behavioral Risk Factor Surveillance System (BRFSS) (www.countyhealthrankings.org). These three were selected through first identifying as candidate variables those measures that are independent of a physician’s diagnosis (for example, “Now thinking about your physical health, which includes physical illness and injury, for how many days during the past 30 days was your physical health not good?”), and avoiding those that may be influenced by intensity of observation (for example, “Have you ever been told by a doctor that you have diabetes?”). Once the candidate questions were identified we used statistical power to select the final BRFSS measures to include in our model. All of these risk adjustors were assigned to individuals in our study population according to their county of residency; for a small number of beneficiaries with non-linking county data, we used a measure at hospital referral region level.

Evaluation

We used standard statistics to describe the variation in age, sex, and race adjusted mortality rates and age, sex, race, and price adjusted rates of spending per capita across the 306 hospital referral regions. The ability of the four risk adjustment indices to reduce variation in the distribution of the adjusted mortality and spending rates among the 306 regions was measured by the interquartile range, the extremal ratio, and the coefficient of variation. We evaluated their ability to explain variation in adjusted rates of mortality and spending using the coefficient of determination (the R² statistic). We present both weighted R² (by hospital referral region population) and unweighted R² in the figures and tables, but use the weighted measure in the text. An F test was used to judge whether the predictive measures were jointly significant at the 5% level. A bootstrap method was used to calculate confidence limits for the R² statistic.

Our measure for observational intensity is the average per capita Medicare physician visit rates (all evaluation and management services) in the last six months of life at the hospital referral region level. To ensure that no direct relation could exist between our proxy for intensity of observation and our outcomes (mortality or spending) we measured physician visits in the prior year (2006). We evaluated the effect of adjustment method on predicted mortality and spending rates in regions with high and low rates of visits by aggregating hospital referral regions in fifths of equal population size based on physician visit rates.²⁸ For these estimates, we ran a series of regression models similar to the regional models but incorporated the fifths as the classification variable instead of hospital referral region.

Results

Ability to explain variation in age, sex, and race adjusted mortality

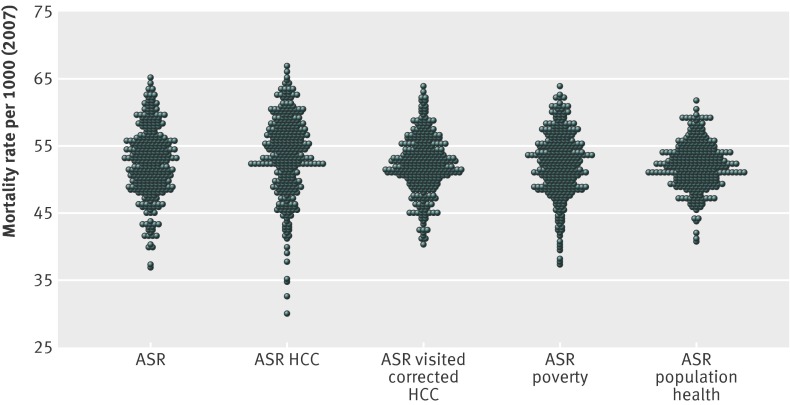
Figure 1 and table 1 show the distribution and summary statistics for Medicare mortality rates across the 306 hospital referral regions using the four risk adjustment indices. The coefficient of variation from that of age, sex, and race adjustment alone was 9.7 (the standard deviation was 9.7% of the mean). This value was lowered 33% to 6.5 for the population health index, 17% to 8.1 for the visit corrected Hierarchical Condition Categories (HCC) index, and 7% to 9.1 for the poverty index. Adjustment using the standard HCC method increased variation in mortality rates by 14% (coefficient of variation=11.0).

Fig 1 Distribution plots of 2007 mortality rates per 1000 Medicare beneficiaries in each of 306 hospital referral regions for age, sex, and race (ASR) alone, ASR HCC (Hierarchical Condition Categories), ASR visit corrected HCC, ASR poverty, and ASR population health

Table 1.

 Descriptive statistics of the effect of four risk adjustment indices on variation in Medicare mortality rates per 1000 population in 2007 across 306 hospital referral regions

Statistics	ASR adjusted mortality	ASR HCC adjusted mortality	ASR HCC visit corrected mortality	ASR poverty adjusted mortality	ASR population health adjusted mortality
Median (interquartile range)	52.9 (49.4-55.9)	54.5 (50.1-57.7)	52.2 (50.1-55.0)	52.7 (49.3-55.6)	52.3 (50.2-54.3)
Mean	52.7	53.7	52.3	52.5	52.3
Coefficient of variation	9.7	11.0	8.1	9.1	6.5
Extremal ratio	1.77	2.24	1.59	1.52	1.70
Coefficient of variation % change from ASR	—	13.9	−16.7	−6.5	−32.5

ASR=age, sex, and race; HCC=Hierarchical Condition Categories.

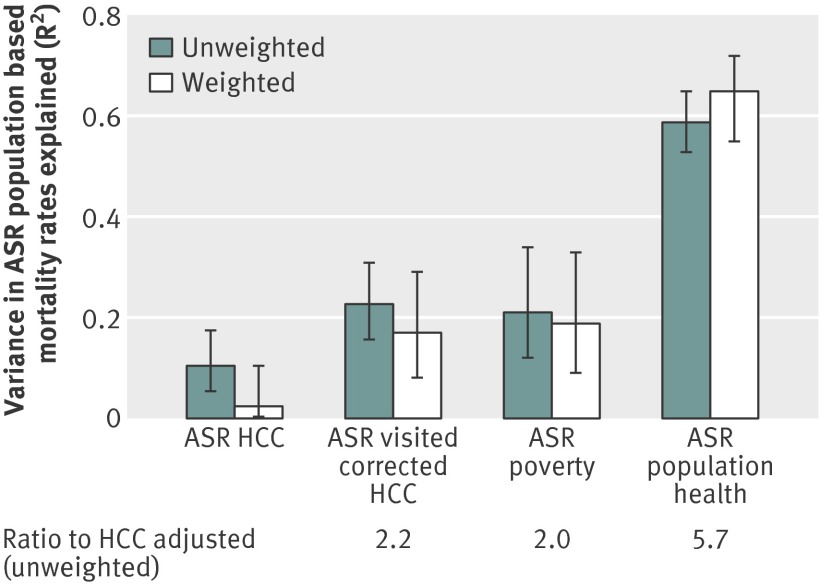
Figure 2 shows how well each index explained variation in age, sex, and race adjusted mortality, using unweighted and weighted regressions. Using regressions weighted by population, the standard HCC index explained less than 5% of the residual variation; the visit corrected HCC index and the poverty index explained more than three times as much (17% and 19%, respectively) and the population health index over 10 times as much (65%).

Fig 2 Ability to explain residual variation in age, sex, and race (ASR) adjusted hospital referral regions mortality using four methods of risk adjustment (R² statistics and 95% confidence interval; unweighted and weighted). HCC=Hierarchical Condition Categories

Ability to explain variation in spending

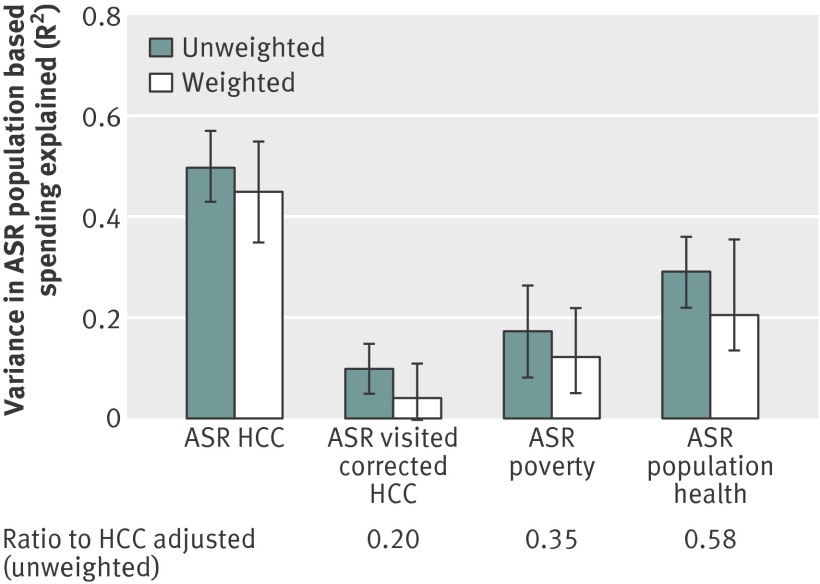
Age, sex, race, and price adjusted spending per capita in the 20% sample varied among regions from $5323 (£3225; €3851) to $15 706 (coefficient of variation=15.2, table 2). Adding the standard HCC index reduced this variation by 36% (coefficient of variation=9.8), but the visit corrected HCC index and the indices for poverty and population health had little impact (coefficient of variation=14.4, 14.8, and 13.9, respectively). Figure 3 shows the ability of the four indices to explain residual variation in age, sex, race, and price adjusted spending. In the weighted regressions, the standard HCC index explained the most: 45% of the residual variation in age, sex, race, and price adjusted spending; however, the visit corrected HCC explained the least (<5%). The poverty and population health indices explained 12% and 21% of the age, sex, and race adjusted variation, respectively.

Table 2.

 Descriptive statistics of the effect of four risk adjustment indices on variation in Medicare spending per beneficiary in 2007 across 306 hospital referral regions

Statistics	ASR price adjusted spending	ASR price HCC adjusted spending	ASR price HCC visit corrected spending	ASR price poverty spending	ASR price population health adjusted spending
Median (interquartile range)	8276 (7366-9053)	8409 (7915-8941)	8075 (7461-8999)	8208 (7268-8983)	8168 (7444-8930)
Mean	8305	8462	8249	8236	8267
Coefficient of variation	15.2	9.8	14.4	14.8	13.9
Extremal ratio	2.95	1.93	2.49	2.72	2.99
Coefficient of variation % change from ASR	—	−36.0	−5.7	−3.2	−8.9

ASR=age, sex, and race; HCC=Hierarchical Condition Categories.

Fig 3 Ability to explain residual variation in age, sex, race (ASR), and price adjusted hospital referral regions spending using four methods of risk adjustment (R² statistics and 95% confidence interval; unweighted and weighted). HCC=Hierarchical Condition Categories

Effects of adjustment in regions with low and high rates of visits

Table 3 illustrates the effect of risk adjustment on estimated age, sex, and race adjusted rates of mortality and spending per capita among hospital referral regions aggregated across fifths of visit rates (the visit rate in the highest fifth was 2.4 times that of the lowest fifth). For mortality, adding the standard HCC index to age, sex, and race risk adjustment increased the estimated relative mortality by 12.1% in the lowest visit fifth, and decreased it by 10.5% in the highest fifth. These shifts resulted in a difference of over 22% in estimated mortality rate between the highest and lowest fifths. By contrast, the visit corrected HCC index, poverty, and population health indices resulted in little change in estimated mortality compared with age, sex, and race adjustment alone. With the population health index, the difference in adjusted mortality rates between highest and lowest visit fifths was less than 1%.

Table 3.

 Effect on apparent mortality and Medicare spending of four methods of risk adjustment in regions ranked into fifths according to mean number of physician visits in last six months of life

Variables	Fifths of visits (95% CI), % change*					Ratio highest to lowest fifth
	1st (lowest)	2nd	3rd	4th	5th (highest)
Visits per decedent	18.0	23.6	26.8	31.2	43.9	2.43
Effect on mortality:
ASR adjustment only	51.0 (50.6 to 51.4)	54.0 (53.6 to 54.4)	53.1 (52.7 to53.6)	53.1 (52.7 to 53.5)	50.0 (49.5 to 50.4)	0.98
ASR HCC adjustment	57.2 (56.8 to 57.6), 12.1	55.3 (54.9 to 55.6), 2.4	53.1 (52.7 to 53.5), −0.1	51.2 (50.8 to 51.6), −3.6	44.7 (44.3 to 45.1), −10.5	0.78
ASR visit corrected HCC adjustment	51.8 (51.4 to 52.2), 1.5	52.6 (52.2 to 53.0), −2.5	52.1 (51.7 to 52.5), −2.0	52.4 (52.0 to 52.8), −1.4	52.2 (51.8 to 52.6), 4.5	1.01
ASR poverty adjustment	50.8 (50.4 to 51.3), −0.4	53.7 (53.3 to 54.2), −0.5	53.2 (52.8 to 53.7), 0.2	53.3 (52.8 to 53.7), 0.2	50.4 (49.9 to 50.8), 0.8	0.99
ASR population health adjustment	52.1 (51.6 to 52.5), 2.1	52.1 (51.6 to 52.5), −3.5	51.9 (51.5 to 52.4), −2.3	52.6 (52.2 to 53.0), −1.0	52.4 (51.9 to 52.8), 4.9	1.01
Effect on spending:
ASR price adjustment only	$7228 (7195 to 7262)	$8227 (8193 to 8260)	$8498 (8464 to 8531)	$8878 (8844 to 8912)	$9572 (9539 to 9605)	1.32
ASR price HCC adjustment	$8153 (8129 to 8177), 12.8	$8419 (8395 to 8443), 2.3	$8492 (8468 to 8516), -0.1	$8595 (8571 to 8619), -3.2	$8782 (8759 to 8805), -8.3	1.08
ASR price visit corrected HCC	$7342 (7318 to 7366), 1.6	$8027 (8003 to 8051), −2.4	$8337 (8314 to 8361), −1.9	$8767 (8743 to 87891), −1.3	9910 (9886 to 9933), 3.5	1.35
ASR price poverty	$7172 (7138 to 7206), −0.8	$8144 (8111 to 8178), −1.0	$8464 (8430 to 8498), −0.4	$8851 (8817 to 8885), −0.3	$9565 (9532 to 9598), −0.1	1.33
ASR price population health adjustment	$7372 (7337 to 7407), 2.0	$8019 (7985 to 8053), −2.5	$8341 (8307 to 8375), −1.8	$8819 (8785-8853), −0.7	$9837 (9802 to 9872), 2.8	1.33

$1.00 (£0.60; €0.72).

ASR=age, sex, and race; HCC=Hierarchical Condition Categories.

*Percent change from ASR adjusted mortality or spending.

For spending, adding the standard HCC method to age, sex, race, and price adjustment resulted in large swings in estimated spending by visit fifth: a relative increase of over 20% in the lowest fifth, and a relative decrease of 15% spending in the highest fifth. These large swings were not seen using the visit corrected HCC, poverty, or the population health indices; they resulted in only minor changes in estimated spending (−0.8% to 2.0% in the lowest fifth, and −0.1% to 3.5% in the highest fifth). Using the visit corrected HCC, poverty, and the population health indices for adjusting for illness resulted in estimated spending that was similar to adjustment by age, sex, race, and price adjustment alone: spending in the highest visit fifth was 33% to 35% greater than in the lowest fifth.

Discussion

Accurate health risk adjustment is critical to the equitable distribution of resources as more countries allow enrolees to have choice of insurer or provider. Our prior work showed that risk adjustment methods using International Classification of Diseases diagnosis codes recorded in administrative databases are biased by the strong influence observational intensity has on the frequency of diagnosis: the more encounters in the population, the sicker the population seems to be, independent of underlying burden of illness as measured by the age, sex, and race adjusted mortality. The current study evaluated two new approaches to health risk adjustment that do not depend on diagnoses recorded in administrative databases. One approach used a single measure of deprivation obtained from the US census; the second was a composite index of health based on five measures of population health. The deprivation and the population health indices performed better than the standard Hierarchical Condition Categories (HCC) index: they reduced and explained much more of the variation in age, sex, and race mortality and did not exhibit an observational intensity bias as measured by the frequency of physician visits. In contrast, the standard HCC index explained less than 5% of the variation in age, sex, and race adjusted mortality, increased rather than reduced variation, and resulted in implausible swings in mortality rates in regions with high and low levels of physician visits per capita.

The standard HCC index explained the most variation in age, sex, race, and price adjusted regional spending. However, the purpose of health risk adjustment for expenditures is not to maximize the explained R² in spending, but instead to capture the components of spending that are the consequence of poor health. The HCC index, created from administrative databases, may be correlated with spending (almost by construction), but the fact that it is so poorly associated at the regional level with mortality casts doubt on its effectiveness in adjustment for health risk. More importantly, when the standard HCC index was visit corrected, it accounted for only 5% of the variation in regional spending. Indeed, once the standard HCC index was corrected to control for observational intensity bias, both the deprivation and the population health indices performed better in terms of ability to explain variation in spending.

The population health index used data from two sources that were conveniently available for the entire US population. The Behavioral Risk Factor Surveillance System is an annual survey representative of the population. We selected only a few of the questions available on the survey. Our approach was to avoid those questions that could easily be influenced by the same observational intensity bias as present in the administrative databases (such as “Have you been told you have diabetes?”) and focus on unequivocal measures of population health, such as obesity, smoking status, and self perception of physical health. Still, these measures could be expanded to include additional dimensions of health. We also used two administrative database measures in our population health index: rates of admission to hospital for stroke and hip fracture. Prior work has shown that these “low variation” conditions are less subject to the influence of supply factors than other admissions to hospital as they are both “easy to diagnose” and universally lead to hospital stay.¹

Limitations of this study

Several limitations of this study should be considered. Firstly, because data are unavailable for Medicare Advantage populations (the managed care plan), our study only includes beneficiaries in traditional Medicare. However, the HCC models were developed, and continue to be calibrated, on the traditional Medicare population. Secondly, we used mortality as a proxy for overall population health rather than a more subtle measure. Given the inaccuracy of methods that rely on diagnoses from administrative databases for adjusting mortality, those interested in more subtle measures of health may need to find other approaches. Thirdly, we used county level measures of self reported illness, obesity, and smoking status rather than patient level measures. It is possible that patient level data will reveal different findings than those reported here. This is an empirical question that can and should be answered.

Implications for equitable distribution of funds in the United States

The Dartmouth Atlas of Health Care consistently shows more than a twofold variation in age, sex, and race adjusted spending among hospital referral regions across the United States. An important policy finding from our current study is that Medicare spending continues to show great regional variation when spending is further adjusted using the best predictors of illness as measured by mortality. A recent Institute of Medicine study on regional variations (mandated by the US Congress) found that adjustment with the standard HCC method seemed to reduce variation in spending.²⁹ Our study showed that the apparent reductions in regional variations in the Institute of Medicine’s study are the consequence of a flawed risk adjustment approach that conflates illness with observational intensity. Furthermore, since using HCC scores adjusts mortality downward in regions with high visit rates and upward in low visit regions, regression analysis using HCC adjustment will always show that higher intensity of care is associated with better health outcomes.^{30 31} These biases have become more than an interesting research finding as the Centers for Medicare and Medicaid Services move from volume based payments to payments related to risk adjusted outcomes.^{32 33}

Relevance to other countries

Belgium, the Czech Republic, Germany, Israel, the Netherlands, Slovakia, and Switzerland have implemented policies that enable consumers’ periodic choice between insurers. Van de Ven³⁴ pointed out that without effective regulation, competition between insurers creates incentives for them to attract people with low additional risk (“cream skimming”) and deter those with high risk (“adverse selection”). He argues that a system of risk equalization that reallocates resources between insurers according to the risk of their populations is critical to effective regulation. A system of risk equalization, in turn, requires adequate measures of additional risk at the level of the individual. As van de Ven pointed out, countries implementing choice between insurers typically had “poor to moderate” systems of risk equalization. The “most sophisticated risk adjustment formulas” van de Ven identified were the US Medicare program and the Netherlands statutory health insurance scheme. Both use methods that rely on data from administrative databases that can be noticeably improved by use of more accurate risk adjustment models that are not subject to observational intensity bias.

In England, patients in effect choose a local insurer, a clinical commissioning group (CCG), through choice of a general practitioner. To support allocation of funds across CCGs, the NHS has developed measures of health risk at the level of the individual, which include diagnoses from administrative data.^{17 18}Our study suggests that these will be inadequate to prevent “cream skimming” and “adverse selection,” and will ultimately jeopardize equitable distribution of healthcare resources. We recommend research to determine whether observational intensity bias applies in England and other countries, and whether health risk would be better estimated from data on poverty and morbidity.

Conclusion

Our studies point to the need for measures of health and morbidity independent of administrative database diagnoses. The new measures must be free of observational intensity, and they must efficiently and effectively assess population health when adjusting mortality and spending. Where might these measures come from? In the United States the Affordable Care Act contains provisions to pay for an annual survey to capture patient reported data. As envisioned in the Affordable Care Act, these data will primarily be used to assess patient experience, a critical outcomes measure for value based care. Our study suggests a “twofer” for this annual survey: it creates an opportunity for a national strategy to develop patient level population health measures for use in risk adjustment. Such measures would be useful to several federally sponsored interventions that require risk adjustment, such as payment under the Medicare Advantage program, shared savings under the Accountable Care Organization provision, payment withholds under programs to reduce readmissions, and premium adjustments under insurance exchanges. The data would also serve to support risk adjustment in observational studies of health outcomes, much of which is funded by federal agencies and the Patient-Centered Outcomes Research Institute established under the Affordable Care Act. Finally, in other countries where patients have a choice between providers or insurers, an adequate method of health risk adjustment is critical for equitable distribution of resources. Our findings suggest that these methods would be better estimated using data on health, and points to several candidate measures, including hip fracture and stroke rates, self reported health status, smoking, and obesity.

What is already known on this topic

• Illness adjustment methods using routinely recorded diagnoses are subject to bias associated with medical supply: populations with higher visit rates to physicians have more diagnoses and therefore seem to be sicker

• The bias is substantial; use of these methods results in the mortality in regions in the highest fifth of visit rates that were 12.5% lower than the regions in the lowest fifth

• When the US Medicare’s risk adjustment method was corrected to remove the effect of visit rates, mortality rates were similar in the highest and lowest fifths

What this study adds

• Two indices to health risk adjustment independent of physician diagnosis were evaluated: deprivation and five population health measures—smoking status, obesity, self reported illness, hip fracture, and admissions for stroke

• Both indices explained more of the variation in age, sex, and race adjusted mortality rates than Medicare’s diagnoses based method, with the population health index explaining 65% of the variation

• Once Medicare’s diagnoses based method was adjusted for visit rates it did a poor job of explaining variation in regional spending, the population health index explained the most

Cite this as: BMJ 2014;348:g2392