Leaf Shrinkage with Dehydration: Coordination with Hydraulic Vulnerability and Drought Tolerance^,,,

Leaf shrinkage is a potential driver of leaf hydraulic vulnerability, especially under mild stress, and carries strong ecological implications.

Abstract

Leaf shrinkage with dehydration has attracted attention for over 100 years, especially as it becomes visibly extreme during drought. However, little has been known of its correlation with physiology. Computer simulations of the leaf hydraulic system showed that a reduction of hydraulic conductance of the mesophyll pathways outside the xylem would cause a strong decline of leaf hydraulic conductance (K_leaf). For 14 diverse species, we tested the hypothesis that shrinkage during dehydration (i.e. in whole leaf, cell and airspace thickness, and leaf area) is associated with reduction in K_leaf at declining leaf water potential (Ψ_leaf). We tested hypotheses for the linkage of leaf shrinkage with structural and physiological water relations parameters, including modulus of elasticity, osmotic pressure at full turgor, turgor loss point (TLP), and cuticular conductance. Species originating from moist habitats showed substantial shrinkage during dehydration before reaching TLP, in contrast with species originating from dry habitats. Across species, the decline of K_leaf with mild dehydration (i.e. the initial slope of the K_leaf versus Ψ_leaf curve) correlated with the decline of leaf thickness (the slope of the leaf thickness versus Ψ_leaf curve), as expected based on predictions from computer simulations. Leaf thickness shrinkage before TLP correlated across species with lower modulus of elasticity and with less negative osmotic pressure at full turgor, as did leaf area shrinkage between full turgor and oven desiccation. These findings point to a role for leaf shrinkage in hydraulic decline during mild dehydration, with potential impacts on drought adaptation for cells and leaves, influencing plant ecological distributions.

As leaves open their stomata to capture CO₂ for photosynthesis, water is lost to transpiration, which needs to be replaced by flow through the hydraulic system. The leaf hydraulic system has two components, which act essentially in series: the pathways for water movement through the xylem from the petiole to leaf minor veins, and those through the living bundle sheath and mesophyll cells to the sites of evaporation (Tyree and Zimmermann, 2002; Sack et al., 2004; Sack and Holbrook, 2006). The decline in leaf hydraulic conductance (K_leaf) with dehydration may thus depend on both components. The importance of the xylem component is well established. Vein xylem embolism and cell collapse have been observed in dehydrating leaves (Salleo et al., 2001; Cochard et al., 2004a; Johnson et al., 2009), and computer modeling and experimental work showed that species with high major vein length per leaf area (VLA; i.e. for the first three vein-branching orders) were more resistant to hydraulic decline, providing more pathways around embolisms (Scoffoni et al., 2011). However, the physical impacts of dehydration on the extraxylem pathways have not been studied, even though in turgid leaves these pathways account for 26% to 88% of leaf hydraulic resistance (i.e. of 1/K_leaf), depending on species (Sack et al., 2003a; Cochard et al., 2004b). The aim of this study was to determine whether leaf shrinkage during dehydration relates to the decline of K_leaf as well as the structural determinants of leaf shrinkage.

The shrinkage of leaves with dehydration has drawn attention for over 100 years. Leaves shrink in their area (Bogue, 1892; Gardner and Ehlig, 1965; Jones, 1973; Tang and Boyer, 2007; Blonder et al., 2012) and, considered in relative terms, even more strongly in their thickness (Fig. 1; Meidner, 1952; Gardner and Ehlig, 1965; Downey and Miller, 1971; Syvertsen and Levy, 1982; Saini and Rathore, 1983; Burquez, 1987; McBurney, 1992; Sancho-Knapik et al., 2010, 2011). Leaves fluctuate in thickness daily and seasonally according to transpiration (Kadoya et al., 1975; Tyree and Cameron, 1977; Fensom and Donald, 1982; Rozema et al., 1987; Ogaya and Peñuelas, 2006; Seelig et al., 2012). Indeed, the relation of leaf thickness to water status is so tight that using leaf thickness to guide irrigation has led to water savings of up to 45% (Seelig et al., 2012).

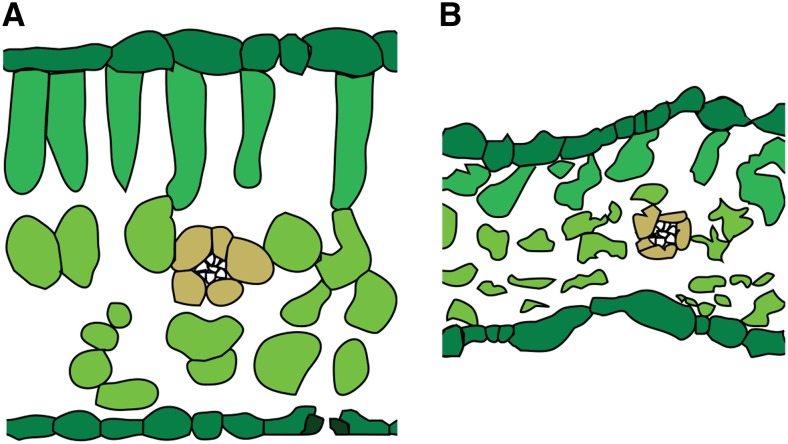
Figure 1.

Sketches of a fully turgid leaf (A) versus a strongly dehydrated leaf (B; drawings based on leaf cross sections of sunflower in Fellows and Boyer, 1978). Note the strong reduction in leaf thickness, cell thickness, and intercellular airspaces in the dehydrated leaf. Epidermal cells are shrunk in the dehydrated leaf, inducing whole-leaf area shrinkage. Note that this sketch represents shrinkage for a typical drought-sensitive species. Many species such as oaks (Quercus spp.) will experience less thickness shrinkage and an increase in intercellular airspace (see “Discussion”). [See online article for color version of this figure.]

Previous studies of leaf shrinkage with progressive dehydration have tended to focus on single or few species. These studies showed that thickness declines with water status in two phases. Before the bulk leaf turgor loss point (TLP; leaf water potential [Ψ_leaf] at TLP) is reached, the slope of leaf thickness versus Ψ_leaf or relative water content (RWC) is shallower than past TLP for most species (Meidner, 1955, Kennedy and Booth, 1958, Burquez, 1987, McBurney, 1992, Sancho-Knapik et al., 2010, 2011). This is because before TLP, declining Ψ_leaf is strongly driven by declines in turgor pressure, which have a relatively low impact on cell and airspace volume, whereas past the TLP, declining Ψ_leaf depends only on solute concentration, which increases in inverse proportion as cell water volume declines while airspaces may shrink or expand (Tyree and Hammel, 1972, Sancho-Knapik et al., 2011). However, the steepness of the slope of leaf thickness versus Ψ_leaf before TLP seems to vary strongly across species (Meidner, 1955; Kennedy and Booth, 1958; Fellows and Boyer, 1978; Burquez, 1987; Colpitts and Coleman, 1997; Sancho-Knapik et al., 2010).

A high leaf cell volume and turgor is crucial to physiological processes (Boyer, 1968; Lawlor and Cornic, 2002). Shrinkage may affect cell connectivity and water transport (Sancho-Knapik et al., 2011). However, no studies have tested for a possible relationship of leaf shrinkage with the decline of K_leaf during dehydration. Such an association would arise if, across species, shrinkage occurred simultaneously with vein xylem embolism or if tissue shrinkage led to declines in the extraxylem hydraulic conductance.

To refine our hypotheses, we modified a computer model of the leaf hydraulic system (Cochard et al., 2004b; McKown et al., 2010; Scoffoni et al., 2011) to predict the impact of losses of xylem and extraxylem conductance on the response of K_leaf to dehydration. We characterized the degree of leaf shrinkage in thickness, in the thickness of cells and airspaces within the leaf, and in leaf area for 14 species diverse in phylogeny, leaf traits, and drought tolerance. We hypothesized that loss of extraxylem hydraulic conductance should have a greater impact on K_leaf at less negative water potentials when xylem tensions are too weak to trigger embolism and induce dramatic declines in K_leaf. We hypothesized that species with greater degrees of shrinkage before TLP would experience greater loss of K_leaf. Furthermore, we hypothesized that species from moist habitats would have greater degrees of shrinkage.

For insight into the mechanisms and consequences of leaf shrinkage, we also investigated the relationships of 18 indices of leaf shrinkage with a wide range of aspects of leaf structure and composition, including gross morphology, leaf venation architecture, parameters of pressure-volume curves, and leaf water storage. We hypothesized that, across species, shrinkage in whole leaf, cell, and intercellular airspace thickness would be lower for species with greater allocation to structural rigidity and osmotic concentration, and thus shrinkage would be positively correlated with a lower modulus of elasticity (ε), less negative osmotic pressure at full turgor (π_o), lower leaf mass per area (LMA), and lower leaf density. Additionally, we tested the longstanding hypothesis that species with higher major VLA and/or minor VLA (i.e. the fourth and higher vein-branching orders) would shrink less in area and/or thickness with dehydration (Gardner and Ehlig, 1965). Finally, we tested the ability of dehydrated leaves to recover in size with rehydration. We hypothesized that recovery would be greater for mildly than for strongly dehydrated leaves and that species with greater leaf shrinkage would be better able to recover from shrinkage.

RESULTS

Computer Simulations Demonstrate the Potential Importance of Extraxylem Hydraulic Decline

We used computer simulation modeling with K_leaf version 6.1 (Cochard et al., 2004b; McKown et al., 2010; Scoffoni et al., 2011) to determine the impact of vulnerability of the outside-xylem mesophyll pathways in driving the decline of K_leaf with dehydration (Fig. 2; Table I; Supplemental Table S1). We generated eight leaf hydraulic vulnerability curves based on different assumptions about the distribution of hydraulic resistance and vulnerability characteristics of various components of the flow pathway. We considered two general cases: (1) most hydraulic resistance was within the outside-xylem component (i.e. the outside xylem hydraulic resistance [R_ox] > the xylem hydraulic resistance [R_x]); or, conversely, (2) R_x > R_ox. For each of these two general cases, we considered four vulnerability scenarios: (1) low vulnerability for xylem and outside-xylem components; (2) high vulnerability for only the outside-xylem component; (3) high vulnerability for only the xylem component; and (4) high vulnerability for the xylem and outside-xylem components (for additional details and parameterization of each scenario, see “Materials and Methods”). Although the vulnerability of the xylem in given vein orders and in the mesophyll was specified in the K_leaf model by a two-parameter sigmoidal function (Pammenter and Vander Willigen, 1998; see “Materials and Methods”), in all modeled scenarios a three-parameter logistic function was selected by maximum likelihood for the leaf vulnerability curve; the emergent whole-leaf response differed in structure from that specified for its components (Supplemental Table S1).

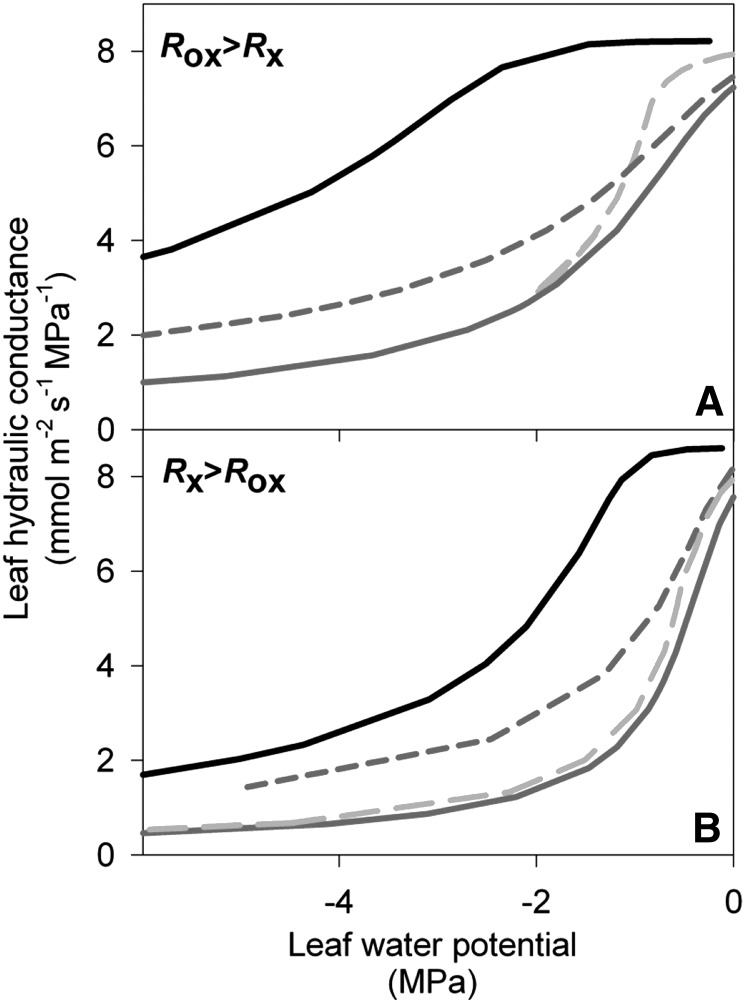
Figure 2.

Computer-simulated leaf hydraulic vulnerability curves indicating the theoretical impact of reducing hydraulic conductance in the within-xylem and outside-xylem components for leaves with high and low resistance outside the xylem (A and B, respectively). Simulations were run for leaves with: (1) low vulnerability for xylem and outside-xylem components (P₅₀ for the vulnerability of each component = −1 MPa; black line), (2) high vulnerability for only the outside-xylem component (P₅₀ = −1 and −0.25 MPa for the within-xylem and outside-xylem components, respectively; dark gray dashed line), (3) high vulnerability for only the xylem component (P₅₀ = −0.25 and −1 MPa for the within-xylem and outside-xylem components, respectively; light gray dashed line), and (4) high vulnerability for both the xylem and outside-xylem components (P₅₀ = −0.25 MPa; gray solid line).

Table I. Results from model simulations testing the impacts on leaf hydraulic vulnerability of declines in conductivity in the xylem and outside-xylem pathways.

For each set of simulations, we present R_ox, xylem P₅₀ and outside-xylem P₅₀, K_max, Ψ_leaf at leaf P₅₀ and leaf P₈₀, P_xylem at leaf P₅₀, and the initial slope of the leaf hydraulic vulnerability curve (at −0.1 MPa), obtained from the logistic function 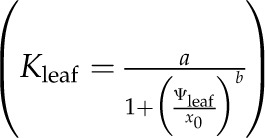, which was selected as the maximum likelihood model in all simulations (compare with Supplemental Table S1).

		Input Conditions				Output of Leaf-Level Responses
Scenario	Simulations	Rox	Xylem P50	Outside-Xylem P50	Kmax	Leaf P50	Leaf P80	Pxylem at P50	Initial Slope
		%	MPa		mmol m−2 s−1 MPa−1	MPa			mmol m−2 s−1 MPa−2
Rox > Rx	Low vulnerability for xylem and outside-xylem components	74	−1.00	−1.00	8.62	−5.50	−11.6	−0.74	−0.09
	High vulnerability for only the outside-xylem component	76	−1.00	−0.25	7.56	−2.37	−7.78	−0.28	−2.08
	High vulnerability for only the xylem component	71	−0.25	−1.00	8.18	−1.53	−2.72	−0.32	−0.28
	High vulnerability for xylem and outside-xylem components	74	−0.25	−0.25	7.26	−1.48	−3.83	−0.25	−1.97
Rx > Rox	Low vulnerability for xylem and outside-xylem components	39	−1.00	−1.00	9.03	−2.49	−5.03	−0.78	−0.32
	High vulnerability for only the outside-xylem component	42	−1.00	−0.25	8.32	−1.23	−3.92	−0.35	−4.50
	High vulnerability for only the xylem component	36	−0.25	−1.00	8.02	−0.83	−1.78	−0.39	−3.06
	High vulnerability for xylem and outside-xylem components	39	−0.25	−0.25	7.65	−0.68	−1.75	−0.30	−6.02

Consistent with expectations, the simulations showed that whole leaves were most vulnerable when both xylem and outside-xylem mesophyll components were vulnerable. The outside-xylem vulnerability had a substantial impact on K_leaf vulnerability. Simulating a greater vulnerability to dehydration in only the outside-xylem component or only the xylem led to substantially less negative water potential at 50% and 80% loss of K_leaf (P₅₀ and P₈₀) and steeper initial slopes than when simulating a low xylem and outside-xylem vulnerability (Fig. 2, A and B, compare light or dark gray dashed lines with black solid lines; Table I). Furthermore, because the outside-xylem mesophyll component is a terminal hydraulic bottleneck, it is critical for protection of the xylem component. Across simulations, P₅₀ was always considerably more negative than the pressure inside the xylem at P₅₀ (2- to 8-fold more negative; Table I). At given input values for the within-xylem and outside-xylem vulnerability, the leaf was less vulnerable when more hydraulic resistance was found outside the xylem (i.e. R_ox > R_x rather than R_x > R_ox), with more negative P₅₀ and P₈₀ values and vulnerability curves with shallower slopes (Table I; Fig. 2).

Furthermore, the outside-xylem vulnerability played the greatest role in driving the initial vulnerability at mild water deficits. The initial slope of the vulnerability curve (before the bulk of cavitation would occur) was steeper when the outside-xylem component was vulnerable than when only the xylem component was vulnerable (Fig. 2, A and B, compare gray dashed and light gray dashed lines; Table I) and similar to that found when both xylem and outside-xylem components were vulnerable (Fig. 2, compare gray dashed with gray solid lines; Table I). By contrast, the behavior of the leaf vulnerability curve at stronger water deficits was strongly influenced by the xylem component; thus, the P₈₀ values when both xylem and outside-xylem components were vulnerable were similar to that found in the simulation when only the xylem was vulnerable, substantially less negative than when only the outside-xylem was vulnerable (Fig. 2; Table I). There was less difference across simulations in the P₅₀ values (Table I).

These findings indicated a strong impact of reduction in mesophyll hydraulic conductance on K_leaf vulnerability, especially at high water potentials, with more pronounced effects of xylem embolism on K_leaf vulnerability under stronger dehydration (Fig. 2; Table I).

Leaf Shrinkage with Dehydration: Variation across Diverse Species

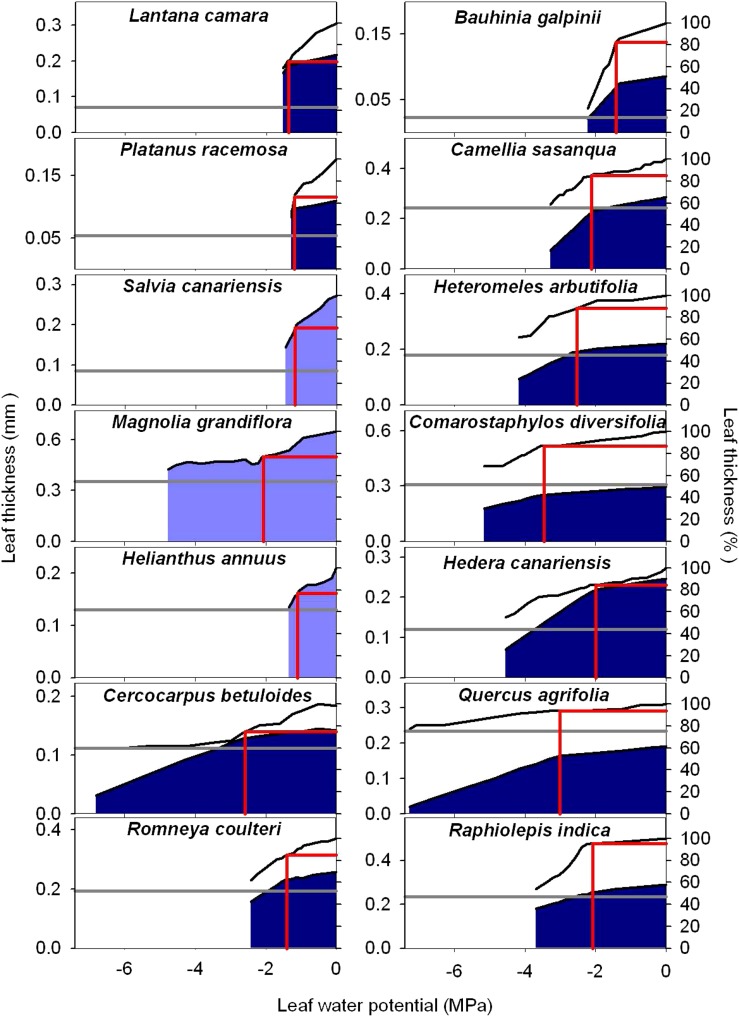
Species varied significantly in their leaf shrinkage with dehydration (Fig. 3) and in all nine key leaf shrinkage parameters (one-way ANOVA, P < 0.001; Tables II, III, IV, and V; Supplemental Table S2; for additional parameters that were correlated with the nine key parameters, see Supplemental Tables S2–S4 and Supplemental Results S1). Species varied 18-fold in the slope of thickness against Ψ_leaf before TLP (dT_leaf/dΨ), from −31% MPa⁻¹ for Platanus racemosa, which had slopes of cell and airspace thickness against Ψ_leaf before TLP (dT_C/dΨ and dT_A/dΨ, respectively) of −10% and −60% MPa⁻¹, respectively, to −1.7% MPa⁻¹ for Quercus agrifolia (dT_C/dΨ and dT_A/dΨ of −4.9 and −3.9, respectively). The dT_C/dΨ varied 3-fold across species, from −4.1% MPa⁻¹ for Cercocarpus betuloides to −13% MPa⁻¹ for Bauhinia galpinii, and dT_A/dΨ was even more variable, ranging from an increase in airspace of 3.9% MPa⁻¹ for Q. agrifolia to a reduction of airspace of 60% MPa⁻¹ for P. racemosa. The maximum shrinkage in thickness (PLT_dry; i.e. that observed in a dry leaf relative to a fully turgid leaf) varied 4-fold across species, from 23% for Q. agrifolia to 83% for B. galpinii (Table V). Notably, the proportion of the leaf thickness constituted of cell versus air did not shift significantly between full turgor and TLP. Across species, the mean ± se for the percentage of cell and air thickness at full turgor were 67% ± 4% and 33% ± 4%, respectively, very similar to those at TLP (PT_C,TLP and PT_A,TLP), 69% ± 5% and 31% ± 5%, respectively (paired Student’s t tests, P = 0.44–0.49; Supplemental Table S2).

Figure 3.

Plots of leaf thickness shrinkage versus Ψ_leaf for 14 species of diverse leaf form and texture and drought tolerance; a typical plot is presented for each species. The blue shaded areas represent the thickness of the cells, and the white areas represent the thickness of the intercellular airspace. The gray horizontal lines represent the maximum shrinkage in leaf thickness (i.e. for an oven-dried leaf). The red vertical lines represent TLP, and the red horizontal lines represent the thickness of the leaf at TLP. Species are ordered top left to bottom right from lowest to highest ε. Due to area wrinkling with dehydration of sunflower, M. grandiflora, and S. canariensis, the cell and airspace thickness could not be estimated, and only the whole-leaf shrinkage is shown in light blue (see “Materials and Methods”). [See online article for color version of this figure.]

Table II. Study species, family, and mean ± se for leaf thickness, area, mass per area, and pressure-volume parameters.

Species	Family	Plant Habit	Leaf Thickness at Full Turgor	Leaf Area	LMA	πo	πTLP	ε	RWC at TLP
Moist habitat			mm	cm2	g m−2	MPa			%
B. galpinii	Fabaceae	Shrub	0.17 ± 0.007	22.2 ± 1.44	45.0 ± 1.60	−1.15 ± 0.08	−1.41 ± 0.07	7.81 ± 1.61	81.4 ± 3.39
C. sasanquaa	Theaceae	Shrub	0.40 ± 0.01	12.8 ± 0.98	178 ± 9.08	−1.61 ± 0.13	−2.12 ± 0.18	7.98 ± 1.11	76.7 ± 3.35
Helianthus annuusa	Asteraceae	Herb	0.20 ± 0.01	101 ± 6.61	31.2 ± 1.06	−0.87 ± 0.12	−1.09 ± 0.12	5.49 ± 0.79	84.4 ± 1.50
L. camaraa	Verbenaceae	Shrub	0.29 ± 0.01	16.8 ± 1.22	61.4 ± 4.18	−1.10 ± 0.04	−1.37 ± 0.04	4.85 ± 0.33	78.0 ± 2.30
M. grandifloraa	Magnoliaceae	Tree	0.63 ± 0.04	77.2 ± 7.12	220 ± 11.0	−1.42 ± 0.02	−2.06 ± 0.05	13.3 ± 1.31	89.3 ± 1.20
P. racemosa	Platanaceae	Tree	0.17 ± 0.01	130 ± 14.4	56.3 ± 2.34	−0.93 ± 0.08	−1.19 ± 0.09	7.09 ± 0.25	87.0 ± 1.44
R. indicaa	Rosaceae	Shrub	0.52 ± 0.01	28.5 ± 2.55	211 ± 8.26	−1.37 ± 0.07	−2.07 ± 0.11	11.5 ± 0.81	88.3 ± 0.55
Dry habitat
C. betuloidesa	Rosaceae	Tree	0.22 ± 0.02	8.57 ± 1.58	121 ± 23.3	−1.64 ± 0.04	−2.59 ± 0.03	10.1 ± 0.70	85.1 ± 0.80
Comarostaphylis diversifoliaa	Ericaceae	Tree	0.49 ± 0.04	12.8 ± 0.61	253 ± 16.9	−2.51 ± 0.34	−3.45 ± 0.34	17.3 ± 2.23	85.5 ± 1.85
Hedera canariensisa	Araliaceae	Shrub	0.27 ± 0.02	67.2 ± 7.68	84.1 ± 11.0	−1.49 ± 0.07	−1.98 ± 0.09	12.8 ± 0.49	88.4 ± 1.40
H. arbutifoliaa	Rosaceae	Shrub	0.38 ± 0.01	21.5 ± 2.06	185 ± 12.4	−2.08 ± 0.09	−2.53 ± 0.10	16.4 ± 0.49	87.4 ± 0.53
Q. agrifoliaa	Fagaceae	Tree	0.30 ± 0.01	14.2 ± 0.70	188 ± 7.53	−2.31 ± 0.12	−3.00 ± 0.12	17.9 ± 1.28	87.5 ± 1.59
R. coulteri	Papaveraceae	Herb	0.36 ± 0.01	23.9 ± 0.67	78.1 ± 3.67	−1.01 ± 0.08	−1.40 ± 0.07	6.78 ± 0.33	87.2 ± 0.61
S. canariensis	Lamiaceae	Herb	0.26 ± 0.01	54.5 ± 8.28	41.4 ± 6.01	−0.92 ± 0.05	−1.18 ± 0.07	5.49 ± 0.21	83.1 ± 0.95

^aPressure-volume parameters are from Scoffoni et al. (2008, 2011).

Table III. Symbols, terms, units, derivation, and biological significance of the nine key leaf thickness and area shrinkage traits in this study.

An additional nine traits were quantified, and their calculation and correlations with these key traits are described in Supplemental Materials and Methods S1, Supplemental Results S1, and Supplemental Tables S2 to S4.

Symbols	Parameters	Units	Derivation	Significance
Thickness shrinkage
PLTleaf,TLP	Percentage loss of thickness at TLP	%	From plot of PLT versus Ψleafa	Estimate of leaf thickness shrinkage at TLP
PLTC,TLP	Percentage loss of cell thickness at TLP	%	From plot of PLTC,TLP versus Ψleafa	Estimate of the amount of cell thickness lost when cells become flaccid
PLTA,TLP	Proportion of intercellular airspace thickness lost at TLP	%	From plot of PLTA,TLP versus Ψleafa	Estimate of the amount of airspace thickness lost (or gained) when cells become flaccid
dTleaf/dΨ	Degree of shrinkage of leaf thickness	% MPa−1		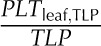Steepness of the decline of whole-leaf thickness with Ψleaf before cells become flaccid
dTC/dΨ	Degree of shrinkage of leaf cells	% MPa−1		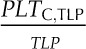Steepness of the decline of cell thickness with Ψleaf before cells become flaccid
dTA/dΨ	Degree of shrinkage of leaf intercellular airspace	% MPa−1		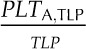Steepness of the decline of air thickness with Ψleaf before cells become flaccid
PLTdry	Percentage loss of thickness in a dry leaf	%		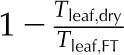Maximum amount of thickness shrinkage
Area shrinkage
PLAleaf,TLP	Percentage loss of area at TLP	%	From plot of PLA versus Ψleafa	Estimate of leaf area shrinkage at TLP
PLAdry	Percentage loss of area in a dry leaf	%		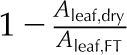Maximum amount of area shrinkage

^aBecause thickness of the leaf or tissues precisely at TLP could not be determined, we interpolated the value for TLP by assuming a linear decline of leaf dimensions with Ψ_leaf between the two surrounding measurements.

Table IV. Symbols, terms, units, derivation, and biological significance of the 28 leaf traits relating to composition, hydraulics, pressure-volume curves, water storage, and venation.

Δ, Change.

Symbols	Parameters	Units	Derivation	Significance
Leaf composition
PTcell,FT	Percentage cell thickness at full turgor	%		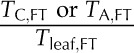Amount of cell thickness at full hydration
PTA,FT	Percentage air thickness at full turgor	%		Amount of air thickness at full hydration
PTcell,TLP	Percentage cell thickness at TLP	%		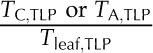Amount of cell thickness at TLP
PTA,TLP	Percentage air thickness at TLP	%		Amount of air thickness at TLP
LMA	Leaf mass per area	g m−2	Leaf dry mass per leaf area	–
Leaf density	–	g cm−3	Leaf dry mass per leaf volume	–
FA	Fraction air	–	(Leaf mass after water infiltration of the airspaces – leaf turgid mass) / leaf volume	Estimate of the amount of airspace in the leaf
FW	Fraction water	–	(Leaf turgid mass \x{2013} leaf dry mass) / leaf volume	Estimate of the amount of water in the leaf
FS	Fraction solid	–	1 – fraction air – fraction water	Estimate of the amount of solid in the leaf
Percentage air in a dry leaf	–	%	Leaf dry thickness × (1 – fraction solid in dry leaf)	Estimate of the amount of airspace in a dry leaf
Leaf hydraulics
Kmax	Maximum leaf hydraulic conductance	mmol m−2 s−1 MPa−1	y intercept of the maximum likelihood function of the vulnerability curve	Efficiency of water movement through a fully hydrated leaf
KTLP	Leaf hydraulic conductance at TLP	mmol m−2 s−1 MPa−1	Parameter of fitted vulnerability curve	Efficiency of water movement at πTLP
P50	Ψleaf at 50% loss of Kleaf	MPa	Parameter of fitted vulnerability curve	–
P80	Ψleaf at 80% loss of Kleaf	MPa	Parameter of fitted vulnerability curve	–
dKleaf/dΨ	Slope of the leaf hydraulic vulnerability curve at Ψleaf = −0.5 MPa	mmol m−2 s−1 MPa−1	Parameter of fitted vulnerability curve	Vulnerability of Kleaf to dehydration
gmin	Cuticular conductance	mmol m−2 s−1	Directly measured	Minimal epidermal conductance after stomatal closure
Pressure-volume curve parameters
πTLP = TLP	Osmotic pressure at TLP	MPa	Parameter of pressure-volume curve	Water potential at which cells become flaccid
πo	Osmotic pressure at full turgor	MPa	Parameter of pressure-volume curve	Concentration of solutes in cells
ε	Modulus of elasticity	MPa	Parameter of pressure-volume curve	Wall stiffness, i.e. Δ turgor pressure/ Δ RWC
RWCTLP	Relative water content at TLP	%	Parameter of pressure-volume curve	Leaf hydration when cells become flaccid
Water storage
CFT	Capacitance at full turgor	MPa−1	Δ(100− RWC)/Δ Ψleaf before πTLP	Amount of water storage before πTLP
CTLP	Capacitance at TLP	MPa−1	Δ(100− RWC)/Δ Ψleaf past πTLP	Amount of water storage after πTLP
SWC	Saturated water content	g g−1	Fresh mass – dry mass/leaf dry mass	Water storage index
C*FT	Leaf area-specific CFT	mol m−2 MPa−1	CFT × SWC × LMA	–
C*TLP	Leaf area-specific CTLP	mol m−2 MPa−1	CTLP × SWC × LMA × RWCTLP	–
Leaf venation
Major VLA	Major vein length per area	mm mm−2	Major vein length/leaf area	Sum of first, second, and third order vein lengths per leaf area
Minor VLA	Minor vein length per area	mm mm−2	Minor vein length/leaf area	Sum of fourth and higher order vein lengths per leaf area
VLA	Vein length per area	mm mm−2	Vein length/leaf area	Sum of major and minor vein lengths per leaf area
Ratio major to minor	Ratio of major to minor VLA	–	Major VLA/minor VLA	Leaf venation composition index
FEV	Free-ending veins per area	No. mm−2	No. of free-ending veins per area	–

Table V. Percentage loss of thicknesses and area at TLP and for oven-dried leaves.

nd, Not determined; ***, P < 0.001.

Species	PLTleaf,TLP	PLTdry	PLTC,TLP	PLTA,TLP	PLAleaf,TLP	PLAdry
B. galpinii	16 ± 2.3	83 ± 1.5	19 ± 0.31	14 ± 5.1	0.48 ± 0.16	21 ± 0.94
C. sasanqua	15 ± 1.2	43 ± 1.1	21 ± 0.30	3.3 ± 5.2	2.9 ± 0.38	5.0 ± 2.2
C. betuloides	18 ± 3.6	33 ± 5.0	11 ± 1.2	39 ± 16	4.8 ± 0.51	21 ± 2.3
C. diversifolia	12 ± 1.4	44 ± 1.9	16 ± 0.32	6.8 ± 3.4	1.2 ± 0.79	10 ± 0.88
H. canariensis	11 ± 1.3	62 ± 3.8	11 ± 0.18	−5.9 ± 8.7	0.96 ± 0.25	16 ± 0.93
Sunflower	22 ± 1.2	36 ± 1.6	nd	nd	14 ± 0.62	69 ± 1.4
H. arbutifolia	12 ± 2.1	53 ± 1.1	14 ± 0.51	7.8 ± 6.5	0.74 ± 0.27	4.9 ± 2.0
L. camara	38 ± 2.0	80 ± 1.9	16 ± 0.54	77 ± 5.3	9.4 ± 0.43	45 ± 2.1
M. grandiflora	22 ± 1.8	42 ± 3.3	11 ± 0.52	30 ± 1.9	nd	8.2 ± 1.1
P. racemosa	36 ± 4.0	70 ± 2.7	12 ± 0.48	72 ± 0.0	1.3 ± 0.47	26 ± 2.1
Q. agrifolia	5.1 ± 0.92	23 ± 1.7	15 ± 0.15	−12 ± 3.4	1.6 ± 0.13	7.0 ± 0.14
R. indica	4.6 ± 0.38	47 ± 2.2	12 ± 0.14	−1.8 ± 4.9	0.61 ± 0.31	14 ± 0.45
R. coulteri	16 ± 1.6	50 ± 1.5	12 ± 0.29	25 ± 5.3	3.9 ± 0.28	28 ± 1.4
S. canariensis	28 ± 7.2	66 ± 1.5	nd	nd	8.4 ± 1.1	57 ± 2.7
One-way ANOVA	***	***	***	***	***	***

The coordination of leaf thickness shrinkage with TLP also varied strongly across species. The percentage loss of leaf thickness at turgor loss point (PLT_leaf,TLP) varied 8-fold among species, from 4.6% for Raphiolepis indica to 38% for Lantana camara (Table V). The cell shrinkage at turgor loss point (PLT_C,TLP) varied 2-fold among species, from 11% for C. betuloides to 21% for Camellia sasanqua, and the intercellular airspace shrinkage at turgor loss point (PLT_A,TLP) ranged from a gain in airspace in the leaf of 12% for Q. agrifolia to a loss of airspace of up to 77% for L. camara (Table V). Species differences in PLT_leaf,TLP were driven by variation in PLT_A,TLP rather than PLT_C,TLP; there was a tight correlation of PLT_leaf,TLP with PLT_A,TLP (Spearman rank correlation [r_s] = 0.94, Pearson correlation [r_p] = 0.96, P < 0.001) but not with PLT_C,TLP (P > 0.05).

Percentage shrinkage in leaf area was much lower than that for thickness. Percentage loss of area at TLP (PLA_leaf,TLP) ranged from 0.5% for B. galpinii to 14% for sunflower (Helianthus annuus; Table V). The percentage loss of area in a dry leaf (PLA_dry; i.e. that for a dry leaf) ranged 14-fold across species, from 4.9% for Heteromeles arbutifolia to 69% for sunflower (Table V).

Species native to moist habitats experienced more shrinkage in thickness and area than species from dry habitats (for more details, see Supplemental Results S2).

Coordination of Leaf Shrinkage Responses and Leaf Hydraulic Vulnerability

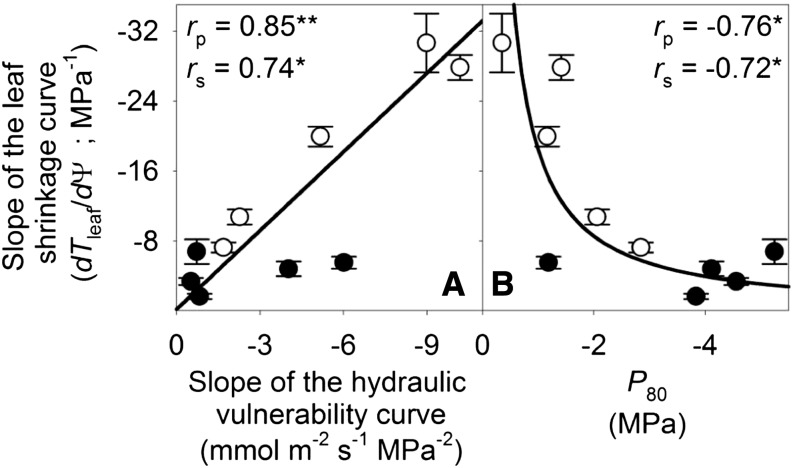
Across species, dT_leaf/dΨ and dT_C/dΨ correlated with the slope of the leaf hydraulic vulnerability curve at Ψ_leaf = −0.5 MPa (dK_leaf/dΨ) and with P₅₀ and P₈₀ (Fig. 4; Supplemental Table S3). No significant correlations were found between the slope of the shrinkage curve for the intercellular airspaces and dK_leaf/dΨ, P₅₀, or P₈₀ (Fig. 4; Supplemental Table S3). Species with greater PLT_dry tended to have higher maximum K_leaf (K_max; Pearson and Spearman coefficients r_p and r_s = 0.65 and 0.68, respectively, P < 0.05; Supplemental Table S3) and also experienced steeper dK_leaf/dΨ (r_p and r_s = 0.76–0.88, P < 0.05; Supplemental Table S3). No correlations were found between K_leaf at TLP and leaf shrinkage traits (|r_p| and |r_s| = 0.02–0.42, P > 0.05; Supplemental Table S3).

Figure 4.

Coordination of leaf shrinkage and leaf hydraulic vulnerability in 10 species of diverse leaf form and texture and drought tolerance. The slope of leaf hydraulic vulnerability at Ψ_leaf = −0.5 MPa (A) and Ψ_leaf at 80% loss of hydraulic conductance (B) were plotted against slope of total leaf thickness shrinkage before TLP. Species from moist habitats are represented in white, and woody species from dry habitats are represented in black. Fitted standardized major axes are as follows: 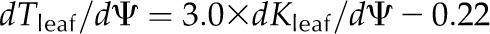for A and 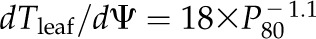for B. *P < 0.05, **P < 0.01.

Recovery from shrinkage in thickness for leaves dehydrated before TLP was high but not complete, ranging from 60% in Magnolia grandiflora to 99% in Romneya coulterii (Supplemental Table S5). For eight of 10 species tested, a similar recovery was found for leaves that had been dehydrated to before or past TLP (Supplemental Table S5; Supplemental Results S3).

Correlation of Leaf Shrinkage with Leaf Pressure-Volume Parameters, Water Storage, Structure, Venation Architecture, and Cuticular Conductance

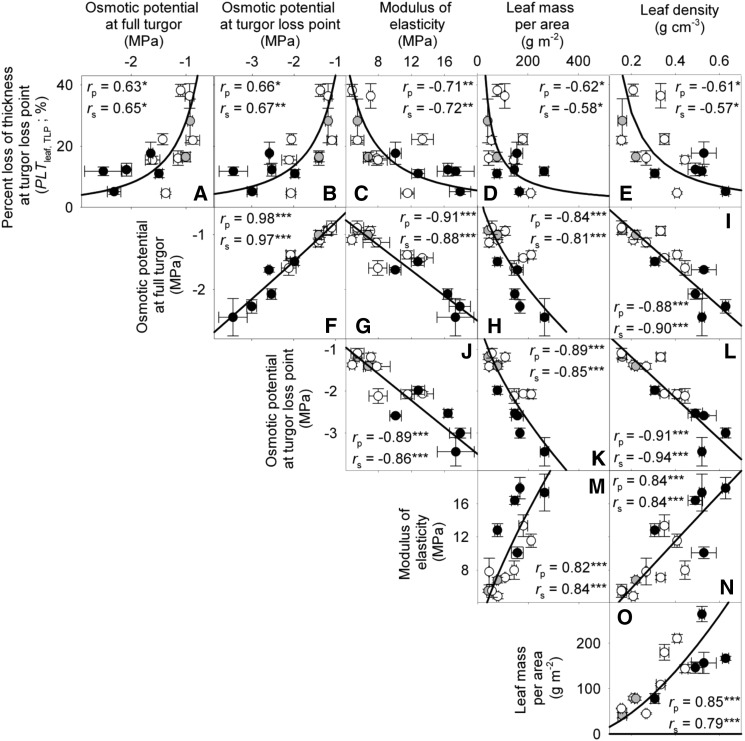
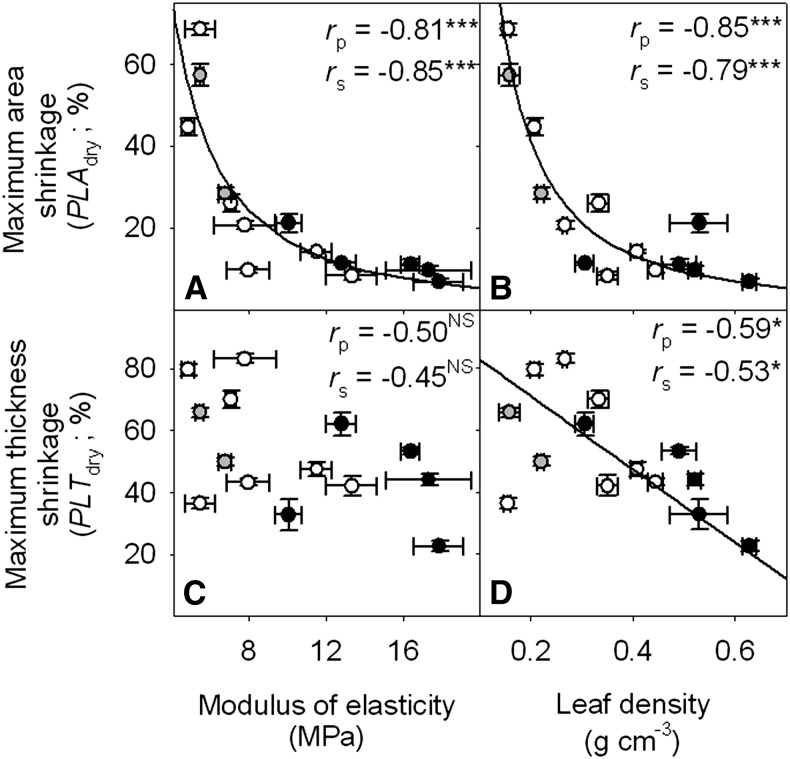
Across species, thickness shrinkage correlated with pressure-volume curve parameters (Fig. 5, A–C), which themselves were strongly intercorrelated (Fig. 5, F–O; Supplemental Table S3). Species with more negative π_o and osmotic pressure at TLP (π_TLP) and higher ε shrank less in thickness before TLP and tended to have shallower dT_leaf/dΨ, dT_C/dΨ, and dT_A/dΨ (r_p and r_s = 0.62–0.86, P < 0.05; Supplemental Table S3). Leaf area shrinkage also related to pressure-volume parameters. A high PLA_leaf,TLP correlated with low ε (r_p and r_s = −0.62 to −0.68, P < 0.05; Supplemental Table S3). PLA_dry correlated with high π_o and π_TLP and low ε (|r_p| and |r_s| = 0.80–0.83, P < 0.001; Fig. 6; Supplemental Table S3).

Figure 5.

Relationship of loss of leaf thickness at TLP with pressure-volume curve parameters and leaf structural traits for 14 species of diverse leaf form and texture and drought tolerance. A to E show traits plotted against the percentage loss of leaf thickness at TLP: leaf osmotic potential at full turgor (A), leaf osmotic potential at TLP (B), ε (C), LMA (D), and leaf density (E). F to O show the intercorrelation of those five traits. Species native to moist habitats are represented in white, woody species from dry habitats are represented in black, and herbs from dry habitats are represented in gray. Fitted standardized major axes are as follows: 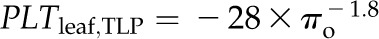for A, 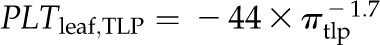for B, 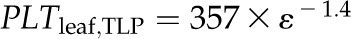for C, 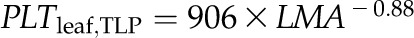for D, 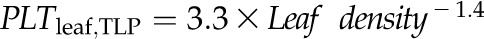for E, 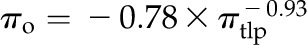for F, 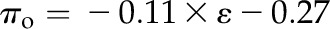for G, 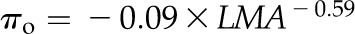for H, 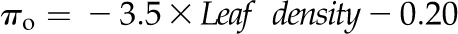for I, 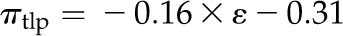for J, 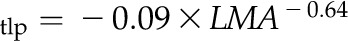for K, 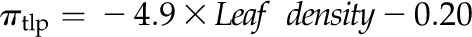for L, 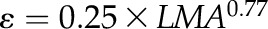for M, 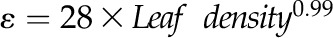for N, and 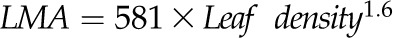for O. *P < 0.05, **P < 0.01, ***P < 0.001.

Figure 6.

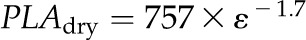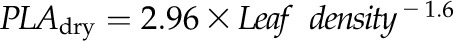Coordination of maximum leaf area and thickness shrinkage with ε and leaf density for 14 species of diverse leaf form and texture and drought tolerance. A, . B, . C, 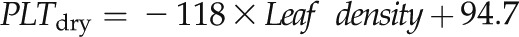. ^NSP > 0.05, *P < 0.05, ***P < 0.001. (Symbols as in Fig. 5.)

Notably, due to the strong relationship between ε (MPa) and PLA_dry (%), a fitted power law equation could be used to estimate ε from PLA_dry (r² = 0.66, P < 0.001):

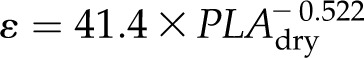(1)

Leaf shrinkage traits also correlated with water storage traits. With few exceptions, the magnitudes of dT_leaf/dΨ, dT_C/dΨ, and dT_A/dΨ correlated with leaf capacitances (amount of water storage) at full turgor and TLP and with saturated water content (capacitance at full turgor [C_FT], capacitance at π_TLP [C_TLP], and saturated water content [SWC]; r_p and r_s values up to 0.93, P < 0.05; Supplemental Table S3). The PLA_dry was positively correlated with C_FT, C_TLP, SWC, and leaf area-specific C_TLP (C*_TLP; r_p and r_s = 0.55–0.86, P < 0.05; Supplemental Table S3).

Across species, leaf shrinkage also related to leaf structure. The PLT_leaf,TLP correlated negatively with LMA and leaf density (Fig. 5, D and E), as did magnitudes of dT_leaf/dΨ, dT_C/dΨ, and PLA_dry (|r_p| and |r_s| = 0.70–0.87, P < 0.05; Supplemental Table S3). Species with thinner hydrated leaves tended to have higher PLA_dry (r_p and r_s = −0.57 to −0.62, P < 0.05; Supplemental Table S3). Leaf shrinkage tended to be independent of leaf area across species; only Ψ_leaf at 50% shrinkage in thickness showed a positive correlation with mean leaf area (r_p and r_s = 0.55–0.58, P < 0.05; Supplemental Table S3).

Leaf shrinkage was independent of most leaf vein traits. No correlation was found between dT_leaf/dΨ and major, minor, or total VLA (r_p and r_s = 0.25–0.57, P > 0.05; Supplemental Table S3). The few correlations observed between vein and shrinkage traits did not suggest causal dependency (Supplemental Table S3).

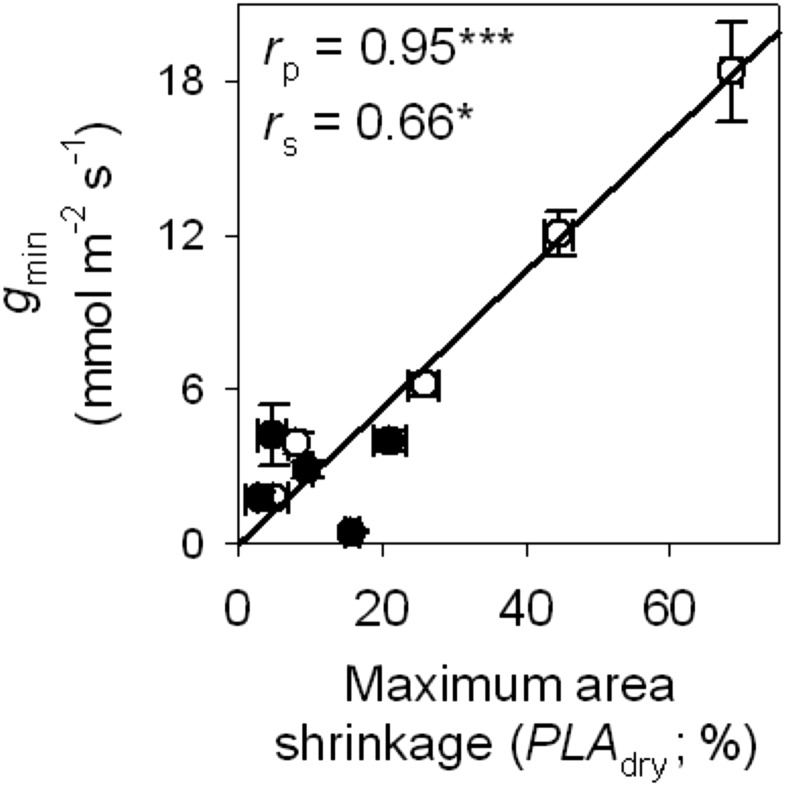
Cuticular conductance (g_min) was positively correlated with a number of leaf shrinkage parameters, such as PLT_leaf,TLP, and PLT_A,TLP, and the magnitudes of dT_leaf/dΨ, dT_A/dΨ, and PLA_dry (|r_p| and |r_s| = 0.65–0.91, P < 0.05; Fig. 7; Supplemental Table S3).

Figure 7.

Relationship between g_min and maximum leaf area shrinkage for 14 species of diverse leaf form and texture and drought tolerance. 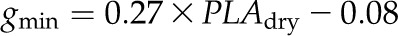. *P < 0.05, ***P < 0.001. (Symbols as in Fig. 4.)

Separating the Drivers of Leaf Shrinkage

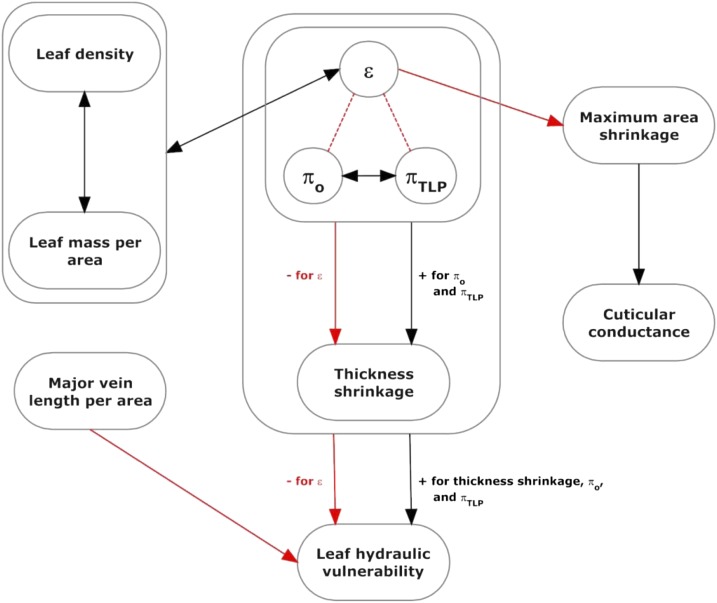
Most leaf pressure-volume parameters and structural features that correlated with leaf shrinkage were themselves intercorrelated (Fig. 5, F–O; Supplemental Table S3). To test for effects of single traits, holding others constant, partial correlation analysis was applied to: (1) PLT_leaf,TLP, ε, and π_o; (2) dT_leaf/dΨ, dK_leaf/dΨ, ε, and π_o; (3) PLT_leaf,TLP, ε, and g_min; (4) PLT_leaf,TLP, LMA, leaf density, ε, and π_o; and (5) PLA_dry, g_min, ε, and π_o (Supplemental Table S6). These analyses enabled us to develop a model of the influences of given traits on leaf shrinkage and the hydraulic vulnerability of the xylem and outside-xylem pathways (Fig. 8). Briefly, a high major VLA provides lower xylem hydraulic vulnerability independently of leaf shrinkage, which influences the outside-xylem vulnerability. A low degree of shrinkage in thickness is achieved at the cellular level through both high ε and more negative π_o and is linked to structural traits such as LMA and leaf density through ε. The ε also controls the maximum shrinkage in leaf area, which acts directly on g_min.

Figure 8.

Synthetic conceptual hypothesis for trait associations and impacts of leaf shrinkage and structural traits on leaf hydraulic vulnerability. Leaf hydraulic vulnerability is influenced independently by major VLA acting on the xylem pathways and leaf shrinkage in thickness acting on the outside-xylem pathways of water movement through the leaf. Thickness shrinkage is determined by cell properties (i.e. the pressure-volume curves parameter ε, π_o, and π_TLP). The dotted lines signify that the ε and osmotic pressures are not directly linked but strongly associated; saltier cells need a higher ε to maintain RWC at TLP above lethal levels (Bartlett et al., 2012b). The ε, being related to cell wall thickness, is correlated with leaf density and LMA, which are also related to cell wall thickness; thus, all these variables influence thickness shrinkage. The ε also influences PLA_dry. PLA_dry and not ε acts directly on g_min, possibly through enhanced leaky stomata (see Supplemental Discussion S2). Red arrows indicate significant negative correlations between traits, while black arrows indicate significant positive correlations between traits. Double-headed arrows indicate traits that are too intrinsically linked to tease apart. [See online article for color version of this figure.]

Consistent with this model for trait influences, we found that the effects of π_o and ε on leaf shrinkage were too intercorrelated to be distinguished. Thus, when accounting for the effect of either π_o or ε, the correlation between the other trait and the PLT_leaf,TLP disappeared (|r_partial| = 0.42–0.01, P > 0.05; Fig. 8; Supplemental Table S6). Similarly, LMA and leaf density were strongly related to pressure-volume parameters, and separate relationships with shrinkage could not be resolved (Figs. 5 and 8); when removing the effect of LMA or leaf density, the correlation between PLT_leaf,TLP and pressure-volume parameters disappeared, and when removing the effect of pressure-volume parameters, the correlation of leaf shrinkage with LMA or leaf density disappeared (|r_partial| = 0.06–0.47, P > 0.05). However, when removing the effect of PLT_leaf,TLP, the correlation between pressure-volume parameters and LMA or leaf density remained (r_partial = 0.70–0.82, P < 0.01).

Also consistent with our model for structural influences, we found that the linkages of leaf hydraulic vulnerability with the degree of leaf shrinkage were mediated by the pressure-volume parameters π_o and π_TLP (Fig. 8). Accounting for the effect of dT_leaf/dΨ, the correlation between dK_leaf/dΨ and π_o or π_TLP disappeared (|r_partial| = 0.04–0.16, P > 0.05). However, the correlation between dT_leaf/dΨ and dK_leaf/dΨ remained even when accounting for the effects of π_o, π_TLP, or ε, and the correlations between dT_leaf/dΨ and π_o, π_TLP, and ε remained even when accounting for dK_leaf/dΨ (|r_partial| = 0.61–0.74, P < 0.05; Supplemental Table S6), indicating that the linkage of shrinkage to pressure-volume parameters was more proximal than that of hydraulic vulnerability to pressure-volume parameters.

Leaf shrinkage in thickness was apparently indirectly correlated with g_min. The correlation of PLT_leaf,TLP and g_min seemed to be driven by their separate correlations with ε; when accounting for the effect of ε, the correlation between g_min and PLT_leaf,TLP disappeared (r_partial = 0.09, P > 0.05; Supplemental Table S6), but ε and PLT_leaf,TLP remained correlated after accounting for the effect of g_min (r_partial = −0.66, P < 0.05). By contrast, maximum shrinkage in area still remained tightly correlated with g_min after accounting for the effect of ε or π_o (r_partial = 0.90–0.91, P < 0.001; Fig. 8). The correlation between maximum shrinkage in area and ε or π_o was no longer significant after accounting for the strong linkage with g_min (|r_partial| = 0.42–0.43, P > 0.05; Supplemental Table S6).

Predicting Leaf Hydraulic Vulnerability from Thickness Shrinkage and Major Vein Density

Given the correlations of P₅₀ and P₈₀ with both major VLA and thickness shrinkage, and because according to our structural model these latter traits were related to the xylem and outside-xylem pathways, respectively, we tested whether they provided a strong prediction of P₅₀ and P₈₀. Indeed, multiple regression analysis showed a greatly improved r² when using both thickness shrinkage and major VLA for predicting P₅₀ or P₈₀ (r² = 0.87 for both P₅₀ and P₈₀ when using both shrinkage and major VLA, versus r² = 0.74–0.72 for P₅₀ or P₈₀ respectively, using only major VLA and r² = 0.52–0.55 for P₅₀ or P₈₀ respectively, using only dT_leaf/dΨ). The fitted models for predicting P₅₀ and P₈₀ were:

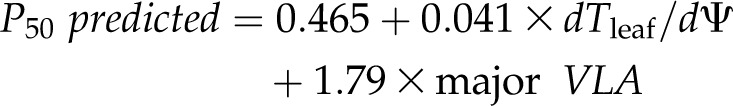(2)

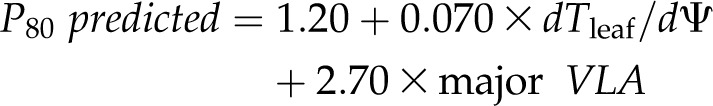(3)

The observed P₅₀ and P₈₀ were strongly correlated with values predicted from these models, with the slope close to 1 (0.96–0.97) and r² = 0.87 (Fig. 9).

Figure 9.

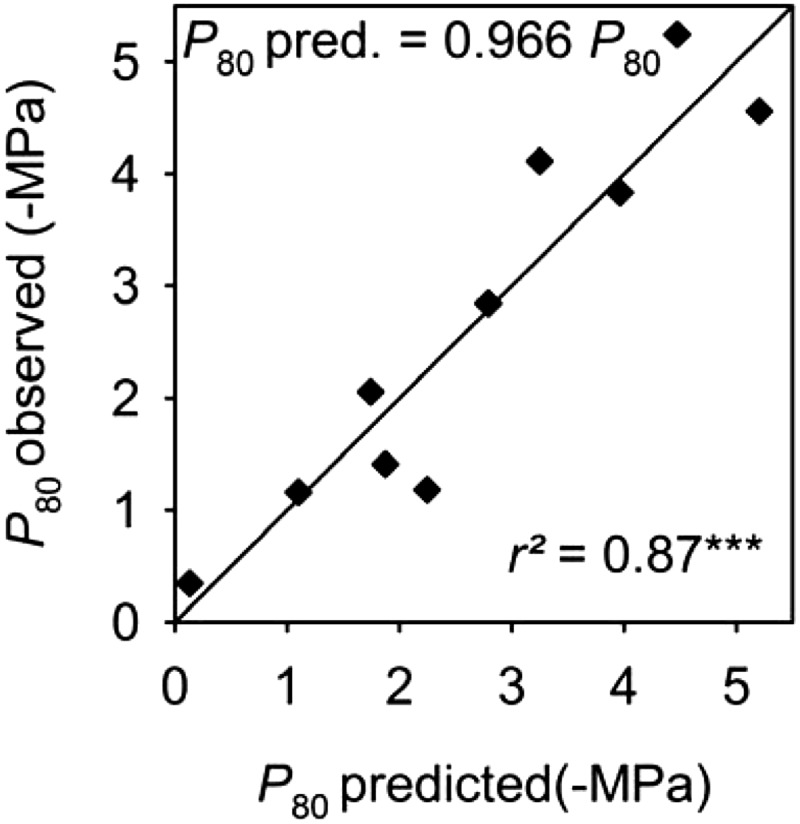
Ability of a model to predict P₈₀ from an equation based on leaf shrinkage and major VLA (Eq. 3). The plot of observed versus predicted values, with line fitted through the origin, showed low bias (slope close to 1.0) and very high r². Similar predictive power was found for P₅₀ (see “Results”). ***P < 0.001.

DISCUSSION

The results from computer modeling and experiments demonstrated that leaf shrinkage is a strong correlate and potential driver of leaf hydraulic vulnerability along with other drivers, such as xylem embolism and collapse, and aquaporin deactivation. Our detailed examination of leaf shrinkage provides new insight into its mechanisms and variation across species. Moreover, our results have strong ecological implications, given the great variation in shrinkage across species, with species native to dry habitat more resistant to shrinkage due to their more negative π_o or π_TLP (Ψ_leaf at TLP) and higher ε.

Impact of the Mesophyll on Leaf Hydraulic Vulnerability: Insights from the Computer Model

Results from model simulations confirmed the hypothesis that decline in extraxylem conductance should have strong impacts on K_leaf vulnerability, especially at high Ψ_leaf. The initial slope of K_leaf against Ψ_leaf was nearly as steep when only the extraxylem component was vulnerable to hydraulic decline as when both xylem and extraxylem components were vulnerable. Similarly, the impact of extraxylem vulnerability on the Ψ_leaf at P₅₀ and P₈₀ pointed to its particular influence on the early decline of K_leaf. The model simulations were consistent with a more vulnerable extraxylem component protecting the xylem from tensions that would cause embolisms and strong stomatal closure. Along the hydraulic pathway, the tension generated by transpiration is dissipated by frictional losses proportional to hydraulic resistance. As expected, simulations showed that in leaves where R_ox > R_x, and thus the extraxylem bottleneck was more pronounced, negative pressures would build up less strongly in the xylem for a given bulk Ψ_leaf than if R_x > R_ox. Substantial extraxylem resistance protects the xylem water pressure from declining to values that would trigger air seeding, thus leading to the S-shaped curve seen in the simulation where only the xylem is vulnerable (Fig. 2A, light gray dashed line). Additionally, an R_ox > R_x scenario allows cavitation to occur at more negative Ψ_leaf than if R_x > R_ox (Table I). Furthermore, regardless of the relative values of R_ox and R_x in the turgid leaf, extraxylem vulnerability always had a strong impact on the decline of K_leaf at high Ψ_leaf (Fig. 2, gray dashed lines). We note that this model assumed a steady-state transpiration rate. Short-term dynamics of mesophyll water potential could act directly on stomatal aperture and thus feedback on stomatal conductance and transpiration, but the principles shown here would act when steady state was established.

These model results are analogous to the hydraulic segmentation theory proposed for whole-tree architecture (Zimmermann, 1978). According to that theory, high resistances are found in the most distal parts of the trees (leaves, then lateral branches), so that tensions will be disproportionately large there, and reduced in proximal parts, thus delaying the onset of embolisms in the main trunk xylem, crucial for the tree’s survival. We found that resistance in the extraxylem component and its increase during leaf dehydration would prevent stronger tensions in the leaf vein xylem and delay the onset of xylem embolism or collapse. In essence, vulnerability in the xylem and extraxylem pathways partitions the low water potential caused by a given transpiration rate; greater vulnerability in extraxylem pathways preferentially partitions low potentials to the mesophyll, possibly delaying xylem embolism and strong stomatal closure.

Thus, in sum, decline in the extraxylem conductivity, which would likely occur during leaf shrinkage, leads to strong K_leaf reductions and protects the xylem from embolism during ongoing transpiration, which would lead to yet stronger K_leaf reductions and potentially necessitate energy for refilling xylem conduits (Nardini et al., 2011).

Impact of Leaf Shrinkage on Leaf Hydraulic Vulnerability

Previous studies showed that K_leaf decline in dehydrating leaves was correlated not only with xylem embolism but also with biochemical processes outside the xylem, such as aquaporin deactivation (Johansson et al., 1998; Kim and Steudle, 2007; Scoffoni et al., 2012). To our knowledge, our study is the first to implicate a physical influence of leaf shrinkage in the decline of K_leaf with dehydration, using the same correlational approach. These results support our model findings that extraxylem hydraulic decline would in principle impact on K_leaf for a given species. Furthermore, consistent with our hypotheses and the results of the model simulations, our experiments using diverse species confirmed the hypothesis that K_leaf declines were correlated across species with leaf thickness shrinkage, especially at high Ψ_leaf. Species that experienced the most severe shrinkage above TLP had steeper initial K_leaf declines and less negative P₈₀ values.

Is there an adaptive hydraulic function for a species' greater thickness shrinkage? As for our modeled results, a mechanism was suggested by the segmentation theory of Zimmermann (1978). Thickness shrinkage reduces K_leaf when the mesophyll, but not yet the xylem itself, experiences very negative water potential; this would amplify any water status signal that causes stomatal closure, thus preventing further decline in Ψ_leaf and sparing the xylem from embolism. Thus, species with xylem especially sensitive to air seeding would benefit from shrinkage that would reduce the conductance outside the xylem. Such “sacrifice” of mesophyll hydraulic conductance during dehydration would also be expected to delay intense cavitation during daily transpiration. This mechanism would be particularly useful given the partial reversibility of even strong leaf shrinkage shown by our rehydration experiments. After 1 h of rehydration, leaf discs had regained more than half their initial thickness, regardless of their level of dehydration (Supplemental Results S3; Supplemental Discussion S1).

Indeed, although shrinkage has not been previously investigated in this way, previous studies have pointed to a role of extraxylem pathways in K_leaf decline (for review, see Scoffoni et al., 2012). Recent studies of Arabidopsis suggested that bundle sheath cells acted as valves during drought by converting chemical signals from the vein xylem, such as abscisic acid, into a decrease in K_leaf by deactivating aquaporins (Shatil-Cohen et al., 2011; Pantin et al., 2012). Our modeling and experimental work were consistent in implicating reductions in the extraxylem pathways, whether caused by aquaporin deactivation, cell shrinkage, or both, in the decline of K_leaf with dehydration. Future work is needed to fully resolve the roles of xylem and extraxylem pathways and their interaction in determining the response of K_leaf to dehydration.

Drivers of Leaf Shrinkage and Its Relation to Leaf Vulnerability

Our experiments provided insight into processes occurring within specific leaf tissues during shrinkage (Supplemental Discussion S2). What are the structural factors that influence leaf shrinkage and thus hydraulic vulnerability? Previous studies have reported a correlation of hydraulic vulnerability with the pressure-volume parameters π_o and π_TLP (Crombie et al., 1985; Blackman et al., 2010; Scoffoni et al., 2012). This linkage could arise because a more negative π_TLP enables cells to maintain structural integrity (i.e. a higher RWC at lower Ψ_leaf; Blackman et al., 2010; Scoffoni et al., 2012). That hypothesis was supported in our study: the PLT_leaf,TLP was lower in species with more negative π_o and higher ε. Our findings for the linkage of shrinkage with pressure-volume parameters confirmed and expanded those of studies of fewer species. In one study of six species, leaves of woody plants shrank less than those of herbs, potentially due to their more negative π_o (Kennedy and Booth, 1958). In another study, species with low ε shrank more strongly in thickness (Syvertsen and Levy, 1982). In our study, partial correlation analysis could not tease apart the effects of π_o and ε on PLT_leaf,TLP, due to their strong association, and their combined impacts on determining cell shrinkage at TLP and thus RWC at TLP (Bartlett et al., 2012b). These results support the hypothesis that cell shrinkage depends on cell structural integrity (i.e. the pressure-volume parameters) and shrinkage influences leaf hydraulic vulnerability.

Tissue shrinkage may affect K_leaf decline by altering the pathways for water movement. The precise pathways of mesophyll water movement and, indeed, the identity of the cells that are the sites of water evaporation have remained puzzling questions for decades (Meidner, 1983). Three main pathways for water movement outside the xylem have been proposed: (1) water flows from the xylem to the bundle sheath cells and principally evaporates there (Boyer, 1985); (2) water flows mainly through or around epidermal cells, which have their walls better interconnected than mesophyll and palisade cells, and evaporates near stomata (Wylie, 1943; Sheriff and Meidner, 1974; Meidner, 1975); and (3) water evaporates from the mesophyll cells, but an appreciable part evaporates as well from the epidermal cells (Farquhar and Raschke, 1978). Cell shrinkage can reduce connections for water to flow (Sancho-Knapik et al., 2011) and additionally would reduce evaporative surface; both effects would reduce K_leaf. Tissue shrinkage during transpiration might in fact highlight where water principally evaporates within the leaf and how it varies among species (Canny et al., 2012). While Eucalyptus species showed equal shrinkage throughout the mesophyll, suggesting that transpirational water evaporates throughout the leaf, cotton (Gossypium hirsutum) showed the strongest shrinkage and potentially greater evaporation in the spongy mesophyll and in palisade cells surrounding the substomatal cavities (Canny et al., 2012). Whether the shrinkage of given leaf tissues or populations of cells has more effect than others on K_leaf (e.g. bundle sheath cells; Scoffoni et al., 2012) remains to be elucidated. Furthermore, it is unknown whether K_leaf decline is due to the direct effect of the physical impact of leaf shrinkage on hydraulic pathways, to an indirect effect of cell shrinkage on aquaporin activity (Johansson et al., 1998; Kim and Steudle, 2007), or to both. The shrinkage of airspaces may reflect structural changes (i.e. cell wall buckling) that would reduce extraxylem water flow by reducing cell contact and/or the conductance of cell walls.

The strength of the correlation of K_leaf vulnerability with leaf shrinkage, together with the model simulation results and the clear physical linkage of the pathways of water movement with cellular structure and tissue integrity, support a mechanistic linkage between vulnerability and shrinkage. An alternative argument, that the linkage of K_leaf vulnerability with leaf shrinkage is only circumstantial (i.e. that these responses are independently linked across species due to their association with moist habitat) remains possible. However, it is common to use physical principles to postulate a mechanistic basis for correlations. For example, this was used to establish connections between maximum K_leaf and leaf hydraulic vulnerability with xylem structure (i.e. with midrib conduit dimensions and VLA; Sack and Frole, 2006; Brodribb et al., 2007; Blackman et al., 2010; Scoffoni et al., 2011; Nardini et al., 2012), and here we have extended this approach to the extraxylem pathways. Further validation of this hypothesis will require tests using mutant phenotypes in model species and/or mechanistic manipulations to establish absolute causality.

Coupling the Effects of Leaf Shrinkage and Leaf Veins to Better Predict Hydraulic Vulnerability

Previous researchers hypothesized that leaf veins act as a “skeleton” that reduces leaf shrinkage during dehydration (Gardner and Ehlig, 1965). We found no relationship across species of the degree of shrinkage with major or total VLA. Instead, we found shrinkage to be closely related to leaf properties principally determined by mesophyll cells, π_o and ε. Notably, in some species, bundle sheath extensions (especially when fibrous) could play an important role in reducing shrinkage (Cutler, 2005; Pivovaroff et al., 2014).

Previous work showed that a greater major VLA reduces the leaf hydraulic vulnerability, providing more pathways for the water to flow around embolisms (Scoffoni et al., 2011). Thus, leaf shrinkage and the venation architecture are independent factors that both influence the vulnerability of K_leaf, factors representing the xylem and outside-xylem components, respectively. We found that including both major VLA and shrinkage led to a stronger ability to predict P₅₀ and P₈₀ than either factor alone, and Equations 2 and 3 provided a very strong prediction (Fig. 9), the strongest to our knowledge of leaf hydraulic vulnerability based on structural measurements. Previous work has also shown that P₅₀ and/or P₈₀ can be predicted across species by the dimensions of minor vein xylem conduits (Blackman et al., 2010) and that hydraulic decline of K_leaf and/or cell permeability can be related to properties of aquaporins and the effects of abscisic acid (Kim and Steudle, 2007; Shatil-Cohen et al., 2011). Our Equations 2 and 3 should be validated and extended with measurements for additional species, as they point to a great potential for estimating hydraulic vulnerability from easily measurable traits.

Applications of Leaf Shrinkage for Drought Monitoring and Drought Tolerance Assessment

Our findings support previous studies showing the uses of shrinkage for monitoring drought responses (i.e. for estimating RWC or Ψ_leaf from leaf thickness and area for given leaves; Meidner, 1952; Jones, 1973; Tyree and Cameron, 1977). Our study further points to the importance of resistance to shrinkage as a trait contributing to drought tolerance (Supplemental Discussion S3). Leaf shrinkage may have novel applications for the rapid estimation of drought tolerance parameters. In addition to the ability of shrinkage to predict K_leaf vulnerability described above, the very strong relationship between PLA_dry and ε highlights the potential for the estimation of ε using Equation 1 and easy, rapid measurements of PLA_dry. This equation should be validated and extended for additional species, for rapid estimation of ε, which typically is obtained from pressure-volume curves, and can take 1 to 2 d of measurements per species. Such rapid measurement of a key pressure-volume parameter complements the recently described osmometer measurement of π_o and π_TLP (Bartlett et al., 2012a).

Because species from drier habitats experienced less shrinkage in thickness, PLT_dry may be a good proxy trait for evaluating drought tolerance rapidly. By contrast, PLA_dry may be of limited value as a drought tolerance predictor, although a good proxy for ε. Notably, ε is not a general predictor of drought tolerance, although it may contribute to the tolerance of incipient drought by preventing early K_leaf decline and/or contribute indirectly to drought tolerance by preventing cell shrinkage to lethal levels. Indeed, a recent study quantified PLA_dry in 380 diverse species (Blonder et al., 2012) and found PLA_dry to be slightly higher for dry habitat species, although that trend may have arisen due to error in the measurements. In that study, PLA_dry was determined without first rehydrating the leaves to full turgidity, and erroneous negative PLA_dry data were included in that study. Such errors need to be avoided for accurate species comparisons, especially if values are to be used as proxies for more intensive physiological or ecological parameters.

CONCLUSION

Leaf shrinkage was tightly correlated with hydraulic responses, leaf and cell structure and composition, and drought adaptation. Consequently, leaf shrinkage parameters can be used as proxies for estimating hydraulic vulnerability, ε, and potentially drought adaptation. Future research on the anatomical basis of shrinkage, the precise mechanisms of leaf hydraulic decline, and the role of shrinkage-related traits in drought tolerance for a wide range of species can capitalize on these discoveries and improve the full range of their applications.

MATERIALS AND METHODS

Computer Modeling of the Theoretical Importance of the Xylem and Extraxylem Water Transport Pathways for Leaf Hydraulic Vulnerability

To refine our hypothesis that leaf shrinkage should influence leaf hydraulic vulnerability, we improved the K_leaf program (written by Hervé Cochard; Cochard et al., 2004b; McKown et al., 2010; Scoffoni et al., 2011; available on request from herve.cochard@clermont.inra.fr) to generate leaf hydraulic vulnerability curves. K_leaf creates a spatially explicit model of a leaf with up to six vein orders represented as a square grid of xylem resistors with outside-xylem resistors (“mesophyll” resistors) branching orthogonally from each junction of the vein grid. In modeled leaves, water exits through the mesophyll resistor located at each vein junction, with the bulk of the water exiting from the junctions of the minor veins. The model determines the hydraulic conductances of the xylem and outside-xylem pathways and of the whole leaf for leaves simulated with a given leaf size, length, and cross-sectional conductivity of each vein order and mesophyll hydraulic conductance. K_leaf 6.1 (developed for this study from the previous version 6.0) can simulate the loss of hydraulic conductance in each vein order and the mesophyll, corresponding to the effects of embolism and shrinkage, according to a typical vulnerability curve (Pammenter and Vander Willigen, 1998):

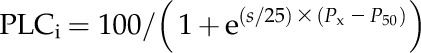(4)

where PLC_i is the percentage loss of hydraulic conductance in a given vein order or in the mesophyll, P_x is the pressure at that specific location, and s is the slope of the vulnerability curve. Having specified these component PLC responses, one can use K_leaf 6.1 to generate leaf hydraulic vulnerability curves (i.e. K_leaf versus Ψ_leaf) by imposing different transpiration rates, obtaining leaves with a range of different Ψ_leaf values corresponding to different tensions across vein orders and mesophyll. Simulations were run using a realistic elliptical leaf with an area of 9.1 cm², with 12 pairs of second-order veins and a total VLA of 6.9 mm mm⁻², and maximum vein cross-sectional conductivities based on estimations from measured xylem conduit dimensions in Juglans regia (as described by Scoffoni et al. [2011]). The findings would be applicable to other leaves with hierarchical reticulate venation (McKown et al., 2010).

We ran four types of simulations to test the relative impacts of differences in vulnerability between the vein xylem and extraxylem mesophyll. (1) All the vein orders and the mesophyll were assigned the same vulnerability, with P₅₀ of −1 MPa. (2) All the vein orders were assigned the same vulnerability, with P₅₀ of −1 MPa, while the mesophyll was assigned greater vulnerability, with P₅₀ of −0.25 MPa. (3) All the vein orders were assigned the same vulnerability, with P₅₀ of −0.25 MPa, while the mesophyll was assigned lower vulnerability, with P₅₀ of −1 MPa. (4) All the vein orders and the mesophyll were assigned the same vulnerability, with P₅₀ of −0.25 MPa. We used the slope parameter of 200 MPa⁻¹ in Equation 1 for all simulations, which is in the range of previously reported values (Pammenter and Vander Willigen, 1998). Because species also vary in the proportion of resistance distributed between xylem and outside-xylem pathways even when leaves are well hydrated (Sack et al., 2004, 2005), we ran each of the four simulations with two different parameterizations: (1) for well-hydrated leaves, most hydraulic resistance was outside the xylem (R_ox = 71%–76% of leaf resistance); or (2) for well-hydrated leaves, most resistance was inside the xylem (R_ox = 36%–42% of leaf resistance). To achieve these two types of leaves, we modified the conductivities of the first and second vein orders and the mesophyll (because of their high impacts on hydraulic conductances of the xylem and outside-xylem pathways, respectively), such that the K_leaf at full hydration had a similar value (7.54–8.95 mmol m⁻² s⁻¹ MPa⁻¹).

For each simulation, we constructed vulnerability curves by plotting K_leaf against Ψ_leaf, which was considered as equivalent to the modeled apoplastic mesophyll pressure. We fitted five types of functions to the curves, as used previously in the literature (Pammenter and Vander Willigen, 1998; Scoffoni et al., 2012), selecting the maximum likelihood model using the optim function in R 2.9.2 (http://www.r-project.org; Burnham and Anderson, 2002, 2004; Sack et al., 2006): linear (K_leaf = aΨ_leaf + y₀), two-parameter sigmoidal 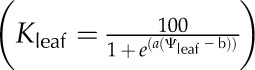(Pammenter and Vander Willigen, 1998), three-parameter sigmoidal 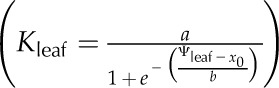, logistic 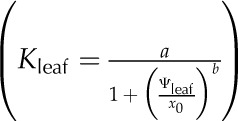, and exponential (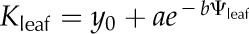). From the maximum likelihood function for each simulated whole-leaf vulnerability curve, we estimated the K_leaf at Ψ_leaf = 0 MPa (K_max), the Ψ_leaf at which K_leaf = 0.5 K_max and 0.20 K_max (P₅₀ and P₈₀, respectively), and the initial slope of the vulnerability curve at Ψ_leaf = −0.1 MPa.

Experimental Plant Material

Leaf shrinkage and its relationship to other physiological traits were determined for 14 species from 12 plant families selected for diversity in leaf size, shape, and drought tolerance. Species were sampled within and around the campus of the University of California, Los Angeles, and Will Rogers State Park, in Los Angeles, from November 2009 to May 2011 (Table II). Leaves from sunflower (Helianthus annuus var Sunspot; Botanical Interests) were collected from greenhouse plants grown from seeds in 3.6-L pots (average minimum, mean, and maximum values for temperature, 21.1°C, 23.2°C, and 26.0°C; for humidity, 44%, 51%, and 59%). Sunflowers were irrigated every 2 d, with 200 to 250 ppm solution of 20:20:20 nitrogen:phosphorus:potassium; the photosynthetically active radiation measured at midday on a sunny day was up to 550 μmol photons m⁻² s⁻¹ and, on average, 300 μmol photons m⁻² s⁻¹ (LI-250 light meter; LI-COR Biosciences).

Shoots with mature leaves were collected from the sun-exposed part of three individuals of each species (the entire stem for sunflowers) and then recut and rehydrated overnight in ultrapure water (0.22-mm Thornton 200 CR; Millipore).

Leaf Shrinkage Experiments: Testing Leaf Responses to Dehydration

Leaf shrinkage experiments were conducted on leaves detached from the rehydrated shoots of each species (n = 5 leaves per species) and placed in sealed bags (Whirl-Pak; Nasco) that had previously been exhaled in to prevent water loss. The parameters of shrinkage and hydraulics measured for excised leaves were assumed to be representative of those for leaves dehydrating on the plant (Supplemental Materials and Methods S1).

To quantify leaf shrinkage, each leaf was measured for area, thickness, mass, and volume at full hydration and during progressive dehydration (for additional details, see Supplemental Materials and Methods S1). Leaves were taped by their petioles to a metal bar in front of a fan to dehydrate and repeatedly removed for measurement. Leaf area was measured using a flatbed scanner (Canon Scan Lide 90; Canon) followed by image analysis (ImageJ software version 1.42q; National Institutes of Health). Leaf thickness was determined by averaging values taken in the centers of the bottom, middle, and top thirds of the leaf, using digital calipers (±0.01 mm; Fowler). Leaf mass was determined using an analytical balance (±0.01 mg; XS205; Mettler). Volume was determined as the product of leaf thickness and area. Once leaves had dehydrated beyond TLP or became too brittle to handle, they were placed in an oven for at least 3 d at 70°C before the dry leaf area, thickness, and mass were determined.

We partitioned the leaf thickness (i.e. the volume per area) into that of the cells and airspace (Roderick et al., 1999). The “thickness” of the cells (T_C,i) and of intercellular airspace (T_A,i) at each level i of dehydration were calculated:

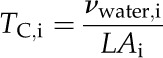(5)

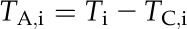(6)

where v_i is the volume of water at level i of dehydration (i.e. fresh leaf mass minus dry mass, divided by 1.0 g cm⁻³) and LA_i and T_i are the leaf area and thickness at dehydration level i. In this calculation, we assumed, based on observations of anatomical cross-sections (John et al., 2013), that the volume of the protoplasts and airspace would each be much greater than that of the solid component of the cell wall. In our calculation, the volume of cell walls would be counted with that of the airspace. However, our calculation of shrinkage parameters involved changes in the dimensions of each component with changes in leaf water status, and these parameters would not be affected by the volume of the cell wall, which would be effectively unchanged during leaf dehydration.

To plot leaf shrinkage responses for leaf area, the thickness of the leaf, cells, and airspace, and leaf volume, we calculated the absolute percentage loss at a given level of dehydration:

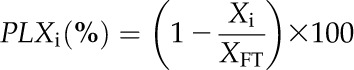(7)

where X_i, and X_FT represent the leaf area, leaf thickness, leaf cell thickness, leaf airspace thickness, and leaf volume at dehydration level i and for a fully turgid leaf, respectively.

The RWC (unitless) in the leaf at each dehydration level i was calculated as:

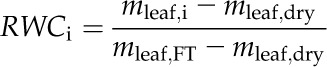(8)

where m_leaf,i is the mass of the leaf at dehydration level i, m_leaf,FT is the mass of the leaf at full hydration, and m_leaf,dry is the mass of the dry leaf (in g).

Leaf Shrinkage Experiments: Estimation of Ψ_leaf for Dehydrating Leaves

For high resolution of the shrinkage responses of leaf dimensions, we plotted leaf shrinkage against Ψ_leaf. We determined Ψ_leaf by summing the turgor pressure (Ψ_p) and solute potential (Ψ_s) estimated from the RWC using the fundamental leaf pressure-volume relationships (Bartlett et al., 2012b):

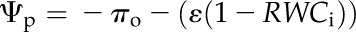(9)

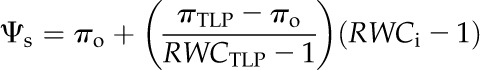(10)

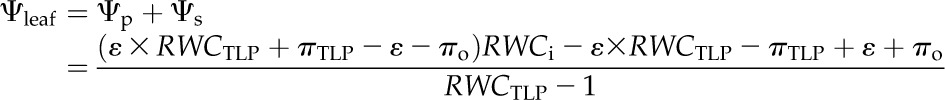(11)

where π_o, π_TLP, and ε are as defined and RWC_TLP is the RWC at TLP (%). Values for these parameters were species means obtained from pressure-volume curves (Table II), previously published for the same plants for nine species (Scoffoni et al., 2008, 2011), and using additional data collected in this study for Bauhinia galpinii, Platanus racemosa, Romneya coulteri, and Salvia canariensis by measuring Ψ_leaf and RWC during progressive dehydration of initially rehydrated leaves (n = 5 leaves per species; Sack, 2010). We assumed a constant ε in Equation 9 (i.e. a linear decline of Ψ_p with RWC), although a nonlinear decline has been reported in a number of species (Robichaux, 1984), indicating a variable ε according to leaf water status. However, a linear approximation of Ψ_p with RWC between full turgor and TLP often fits experimental data (including for our species) and is common in the literature (Koide et al., 2000; Bartlett et al., 2012b). Moreover, simulations showed that even declines of ε by severalfold between full turgor and TLP would in any case negligibly affect our calculations of Ψ_leaf using Equation 11 and the shrinkage traits calculated from it (data not shown).

Leaf Shrinkage Experiments: Determination of the Parameters of Leaf Shrinkage

To fully characterize leaf shrinkage with dehydration, we calculated 18 traits for each species (for derivations, see Table III; for data, see Supplemental Table S5), most of them relating to thickness shrinkage rather than area shrinkage, since we found area shrinkage to be much smaller before TLP than thickness shrinkage. The nine indices that we found to be most representative and useful were PLT_leaf,TLP, PLT_C,TLP, PLT_A,TLP, and PLA_leaf,TLP, PLT_dry and PLA_dry, and dT_C/dΨ, dT_A/dΨ, and dT_leaf/dΨ against Ψ_leaf between full turgor and TLP. These nine key indices were strongly correlated with nine additional parameters of leaf shrinkage that we determined for a comprehensive approach (Supplemental Table S4; Supplemental Materials and Methods S1).

Leaf Rehydration Experiments

We determined the recovery of leaf thickness for dehydrated leaves after rehydration using experiments on leaf discs (after Milburn, 1966). Shoots with healthy, mature sun-exposed leaves were collected from three individuals of 10 species, recut under pure water in the laboratory, and rehydrated overnight. The next day, leaves were placed underwater, and discs of 2 to 5 cm², depending on leaf size, were cut centrally between midrib and lamina (n = 5 per species), toweled dry, and measured for thickness and mass at full hydration. Next, shoot segments containing four leaves were recut under water and left to dehydrate on the bench or over a fan, such that leaves could be sampled either (1) between full turgor and TLP or (2) dehydrated past TLP. Then, each individual leaf on the shoot was sealed, still on the shoot, in a plastic sealable bag (Whirl-Pak; Nasco) that had been previously exhaled in. The shoot was then placed in a sealed plastic zipper bag with wet paper towels and left to equilibrate for at least 15 min and up to 2 h (as necessary for more dehydrated shoots), after which the Ψ_leaf was measured for the top and bottom leaves of the shoot using a pressure chamber (Plant Moisture Stress, model 1000), and if these differed by more than 0.2 MPa, the shoot was discarded. Leaf discs were cut from the two remaining leaves. As one treatment, leaf discs were cut under water to minimize the effect of embolism of the leaf xylem in dehydrated leaves in delaying or preventing rehydration and recovery of tissue dimensions. As a second treatment, using different shoots, leaf discs were cut in air to test whether the embolism of xylem and mesophyll cell walls would affect disc rehydration; these discs were then dipped in water to achieve a similar initial condition to those that were cut under water. Leaf discs were immediately placed in sealable plastic bags that had been previously exhaled in. Initial thickness and mass were measured for each disc using the digital calipers and balances described above. Discs were then submerged under ultrapure water with a height of 2 to 4 mm in a petri dish to rehydrate for 1 h, after which thickness and mass were measured. The percentage recovery in thickness was measured by dividing thickness after 1 h of rehydration by the average thickness at full hydration. If discs cut in air and under water did not differ significantly in their recovery, values were pooled.

Leaf Hydraulic Traits

We tested the correlation of leaf shrinkage parameters with leaf hydraulics traits and g_min. Values for leaf hydraulics traits were obtained from vulnerability curves determined using the evaporative flux method for 10 species (Scoffoni et al., 2011, 2012; Sack and Scoffoni, 2012): K_leaf at full turgor (K_max) and at TLP, the percentage decline of K_leaf at TLP, P₅₀ and P₈₀, and dK_leaf/dΨ. For g_min, we used values previously published for the same plants (Scoffoni et al., 2011).

Leaf Structural and Compositional Traits

We tested the correlation of shrinkage parameters with traits related to gross leaf morphology and composition averaged for five leaves per species (sampled from at least three individuals). For the leaves used in the shrinkage experiments, we measured fully hydrated leaf area (cm²) and thickness (mm), leaf dry mass per turgid leaf area (LMA; g m⁻²) and leaf density (g cm⁻³), calculated as LMA divided by leaf thickness. The fractions of leaf air, water, and solid were measured for four to 10 leaves per species by water infiltration into the airspaces (Roderick et al., 1999; Sack et al., 2003b). The airspace “thickness” in a dry leaf was obtained by multiplying the thickness of the dry leaf by (1 – solid fraction in the dry leaf), and the percentage airspace in a dry leaf was obtained by dividing its airspace thickness by the thickness of the dry leaf.

Leaf Water Storage Traits

SWC, C_FT, and C_TLP were obtained for each species from the pressure-volume curves described above (Sack et al., 2003b; Sack, 2010). Leaf area-specific capacitance at full turgor (C*_FT) and C*_TLP (in mol m⁻² MPa⁻¹) were then calculated:

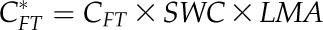(12)

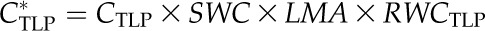(13)

Leaf Venation Traits

We tested the relationship of leaf shrinkage with published vein traits for the study plants (Scoffoni et al., 2011): major VLA (i.e. that of the first three branching orders of veins), minor VLA (i.e. that of higher vein-branching orders), total VLA (also known as “vein density”), and the ratio of major to minor VLA and free vein endings per area.

Statistics

We tested a priori hypotheses for the coordination of shrinkage parameters with pressure-volume parameters, hydraulic traits, and leaf structure and composition across species. As in previous studies using this approach (Brodribb et al., 2007; Waite and Sack, 2010; Scoffoni et al., 2011; Nardini et al., 2012), we did not correct individual correlations for multiple tests and present a correlation matrix of all traits only to illustrate the intercorrelative structure of all measured traits (Supplemental Table S3). We advise correction for multiple statistical tests before considering trait correlations that were not hypothesized a priori. Pearson coefficients were determined for both untransformed and log-transformed data, given that many relationships were nonlinear (Sokal and Rohlf, 1995). Spearman rank correlations were also determined, given that these are more robust in cases in which one or two outliers might drive a significant Pearson correlation (Sokal and Rohlf, 1995). For a conservative approach, we typically recognized relationships as significant only when P < 0.05 for both Spearman rank and Pearson correlations (r_s and r_p, respectively).

Partial correlation analyses (Sokal and Rohlf, 1995) were conducted when three variables of interest were intercorrelated across species. These analyses tested the relationship between two variables when the third is statistically held constant (implemented using the corpcor package in R; Schaefer et al., 2007).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Table S1. Parameters for simulated vulnerability.

• Supplemental Table S2. Mean ± SE of shrinkage, rehydration, pressure-volume, hydraulic, water storage, leaf structure, and leaf venation traits.

• Supplemental Table S3. Correlation matrix of 51 traits related to shrinkage, rehydration, pressure-volume curves, hydraulics, water storage, leaf structure, and venation across 14 species.

• Supplemental Table S4. Symbols, terms, unit, derivation, and biological significance of 9 additional leaf thickness, area, and volume shrinkage traits this study.

• Supplemental Table S5. Percent recovery in thickness after 1 h of rehydration for leaves of 10 species dehydrated before and past their turgor loss point.

• Supplemental Table S6. Partial correlation analysis results.

• Supplemental Results S1. Leaf shrinkage with dehydration: variation across diverse species of other shrinkage parameters and correlation with pressure volume parameters and cuticular conductance.

• Supplemental Results S2. Leaf shrinkage with dehydration: variation between species of wet and dry habitats.

• Supplemental Results S3. Recovery of leaf shrinkage in thickness.

• Supplemental Discussion S1. The impact of leaf shrinkage on leaf hydraulic vulnerability: studies based on rehydration kinetics.

• Supplemental Discussion S2. Mechanisms of leaf shrinkage: the role of the epidermis.

• Supplemental Discussion S3. Resistance to leaf shrinkage: an important trait contributing to drought tolerance?

• Supplemental Materials and Methods S1. Leaf shrinkage experiments: testing leaf responses to dehydration; determination of the other parameters of leaf shrinkage; and leaf structural and compositional traits.

Glossary

K_leaf

leaf hydraulic conductance

VLA

vein length per leaf area

TLP

turgor loss point

Ψ_leaf

leaf water potential

RWC

relative water content

R_ox

outside xylem hydraulic resistance

R_x

xylem hydraulic resistance

P₅₀

50% loss of K_leaf

P₈₀

80% loss of K_leaf

PLA_leaf,TLP

percentage loss of area at TLP

PLA_dry

percentage loss of area in a dry leaf

PLT_leaf,TLP

percentage loss of leaf thickness at turgor loss point

PLT_C,TLP

cell shrinkage at turgor loss point

PLT_A,TLP

intercellular airspace shrinkage at turgor loss point

dT_leaf/dΨ

slope of thickness against Ψ_leaf before TLP

dT_C/dΨ

slope of cell thickness against Ψ_leaf before TLP

dT_A/dΨ

slope of airspace thickness against Ψ_leaf before TLP

PLT_dry

maximum shrinkage in thickness

dK_leaf/dΨ

slope of the leaf hydraulic vulnerability curve at Ψ_leaf = −0.5 MPa

K_max

maximum leaf hydraulic conductance

ε

modulus of elasticity

π_o

osmotic pressure at full turgor

π_TLP

osmotic pressure at TLP

C_FT

capacitance at full turgor

C_TLP

capacitance at π_TLP

SWC

saturated water content

C*_TLP

leaf area-specific C_TLP

g_min

cuticular conductance

LMA

leaf mass per area

r_s

Spearman rank correlation

r_p

Pearson correlation