Polarity of Water Transport across Epidermal Cell Membranes in Tradescantia virginiana^,,

An outward bias polarizing of water transport, which appears to be a property of the intact membrane/protein complex of epidermal cells in situ.

Abstract

Using the automated cell pressure probe, small and highly reproducible hydrostatic pressure clamp (PC) and pressure relaxation (PR) tests (typically, applied step change in pressure = 0.02 MPa and overall change in volume = 30 pL, respectively) were applied to individual Tradescantia virginiana epidermal cells to determine both exosmotic and endosmotic hydraulic conductivity (L_p^OUT and L_p^IN, respectively). Within-cell reproducibility of measured hydraulic parameters depended on the method used, with the PR method giving a lower average coefficient of variation (15.2%, 5.8%, and 19.0% for half-time, cell volume [V_o], and hydraulic conductivity [L_p], respectively) than the PC method (25.4%, 22.0%, and 24.2%, respectively). V_o as determined from PC and PR tests was 1.1 to 2.7 nL and in the range of optically estimated V_o values of 1.5 to 4.9 nL. For the same cell, V_o and L_p estimates were significantly lower (about 15% and 30%, respectively) when determined by PC compared with PR. Both methods, however, showed significantly higher L_p^OUT than L_p^IN (L_p^OUT/L_p^IN ≅ 1.20). Because these results were obtained using small and reversible hydrostatically driven flows in the same cell, the 20% outward biased polarity of water transport is most likely not due to artifacts associated with unstirred layers or to direct effects of externally applied osmotica on the membrane, as has been suggested in previous studies. The rapid reversibility of applied flow direction, particularly for the PR method, and the lack of a clear increase in L_p^OUT/L_p^IN over a wide range of L_p values suggest that the observed polarity is an intrinsic biophysical property of the intact membrane/protein complex.

The conductivity of membranes to water (hydraulic conductivity [L_p]) is an important property of the cells of all organisms, and whether plant cell membranes exhibit a polarity in this property has been debated for a number of decades (Dainty and Hope, 1959; Steudle, 1993). Most early evidence for polarity was based on transcellular osmotic experiments using giant algal cells in the Characeae, in which the relative areas of cell membrane exposed to conditions of osmotic inflow (endosmosis) or outflow (exosmosis) could be varied and, hence, L_p for both directions determined (Tazawa and Shimmen, 2001). Interpretation of these experiments is complicated by unstirred layer (USL) effects (Dainty, 1963), but even after accounting for these, it was concluded that inflow L_p (L_p^IN) was higher than outflow L_p (L_p^OUT) in these cells, with L_p^OUT/L_p^IN of about 0.65 (Dainty, 1963). When using osmotic driving forces in algal cells, L_p^OUT/L_p^IN values of between 0.5 and 0.91 have been reported in many studies (Steudle and Zimmermann, 1974; Steudle and Tyerman, 1983; Tazawa et al., 1996), and the same direction of polarity was also reported using osmotic driving forces in whole roots of maize (Zea mays; Steudle et al., 1987). When applying hydrostatic driving forces in algal cells using the pressure probe (Steudle, 1993), which is less influenced by USL effects (Steudle et al., 1980), L_p^OUT/L_p^IN has been closer to 1 (0.83–1; Steudle and Zimmermann, 1974; Steudle and Tyerman, 1983). However, in higher plant cells, an analysis of the data presented by Steudle et al. (1980, 1982) and Tomos et al. (1981) indicates the opposite polarity, with L_p^OUT/L_p^IN averaging from 1.2 to 1.4. Moore and Cosgrove (1991) used two contrasting hydrostatic methods to measure L_p in sugarcane (Saccharum spp.) stem cells: (1) the most commonly used pressure relaxation (PR) method, in which cell turgor pressure (P_cell) changes during the measurement, and (2) the more technically demanding pressure clamp (PC) method, in which P_cell is maintained constant. Consistent with other studies in higher plant cells, Moore and Cosgrove (1991) reported average L_p^OUT/L_p^IN from 1.15 (PC) to 1.65 (PR). Using the PR method in epidermal cells of barley (Hordeum vulgare), Fricke (2000) reported only a modest L_p^OUT/L_p^IN (based on reported half-time [T_1/2]) of 1.08. In view of the contribution of proteins (e.g. aquaporins) to overall membrane L_p, Tyerman et al. (2002) suggested that polarity may result either from asymmetry in the pores themselves or from an active regulation of the conductive state of the pores in response to the experimental conditions that cause inflow or outflow. Either of these mechanisms may explain the wide range of values reported in the literature for L_p^OUT/L_p^IN. Cosgrove and Steudle (1981) reported that a substantial (6-fold) and rapid (within 20 s) reduction in L_p could occur in the same cell, and in hindsight, this presumably reflected the influence of aquaporins. Cosgrove and Steudle (1981) did not consider the lower L_p as indicative of the L_p in situ, and Wan et al. (2004) reported that a reduction in L_p was associated with perturbations to P_cell on the order of 0.1 MPa. Hence, if measured membrane L_p itself can exhibit substantial changes over relatively short periods of time in the same cell, then further study of systematic differences between L_p^OUT and L_p^IN will require a robust hydrostatic methodology (PC or PR) that can reversibly and reproducibly apply small perturbations in pressure (P) to individual cells over short periods of time.

For the PR method, a T_1/2 of water exchange is measured by fitting an exponential curve to the observed decay in P_cell over time following a step change in volume, and membrane L_p can be calculated if cell surface area (A), cell volume (V_o), and volumetric elastic modulus (ε) are known (Steudle, 1993). In practice, A and V_o are typically calculated from optical measurements of individual cell dimensions or estimates using average values, and ε is calculated based on V_o and an empirical change in pressure (dP) to change in volume (dV) relation for each cell (Steudle, 1993; Tomos and Leigh, 1999). In the PC method, first developed by Wendler and Zimmermann (1982), V_o (and, given reasonable assumptions about cell geometry, A) is estimated without the need for optical measurements, and L_p can be measured without the need to determine dP/dV or ε. However, this method is technically more demanding because it requires precise P control as well as a continuous record of the volume flow of water across the cell membrane (as measured by changes in the position of the cell solution/oil meniscus within the glass capillary over time) and has rarely been used (Wendler and Zimmermann, 1982, 1985; Cosgrove et al., 1987; Moore and Cosgrove, 1991; Zhang and Tyerman, 1991; Murphy and Smith, 1998). Since volume (V) is continuously changing over time, this approach may also be influenced by the hydraulic conductance of the capillary tip (K_h) used to make the measurements as well as surface tension effects due to the progressive changes in capillary diameter with meniscus position, and these influences have not been quantitatively addressed.

Automation of the pressure probe operation, particularly automatic tracking of the meniscus location in the glass microcapillary tip, would address many of the above-mentioned issues, and to date, several attempts have been made to monitor the meniscus location using electrical resistance (Hüsken et al., 1978) or hardware-based image analysis (Cosgrove and Durachko, 1986; Murphy and Smith, 1998). Recently, Wong et al. (2009) redesigned the automated cell pressure probe (ACPP), originally proposed by Cosgrove and Durachko (1986), using a software-based meniscus detection system and a precise pressure control system. In the new ACPP system, both the position of the meniscus and oil pressure (P_oil) are recorded frequently (typically at 10 Hz), and P_oil is controlled with a resolution of ±0.002 MPa. We have combined the ACPP with a new technique to reproducibly fabricate microcapillary tips of known hydraulic properties (Wada et al., 2011) in order to correct for K_h and surface tension effects in both PC and PR estimates of the water relations parameters of Tradescantia virginiana epidermal cells and have determined the relation of L_p^OUT to L_p^IN in these cells.

RESULTS AND DISCUSSION

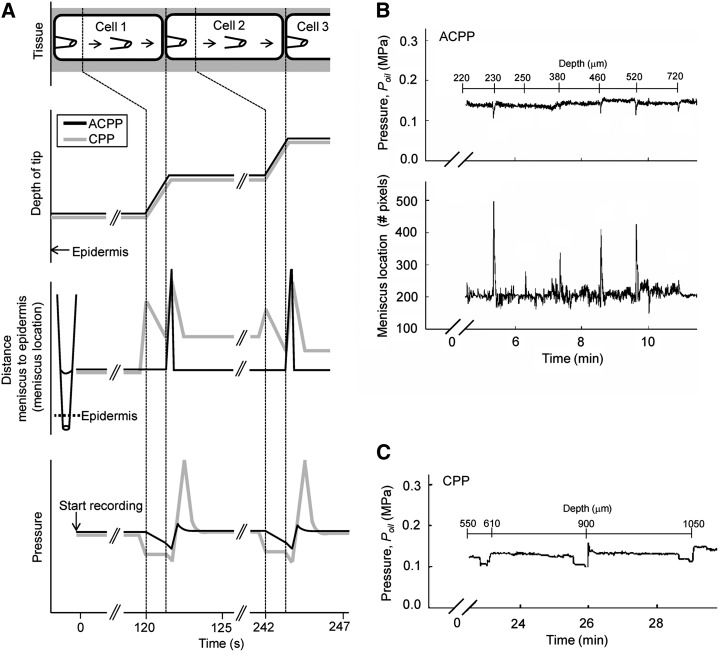
Comparison of ACPP and Cell Pressure Probe

While the overall processes involved in ACPP and cell pressure probe (CPP) operation are very similar (Fig. 1A) and repeatable values of P_cell can be obtained for sequential measurements of cells in a tissue using either system (Fig. 1B), the operator skill required to accomplish these measurements is much less for the ACPP. Because P_oil in the ACPP is automatically controlled by a proportional integral derivative algorithm to maintain either the meniscus position or the pressure at a set value, there is a tradeoff among the speed of response, overshoot or undershoot, and noise in the controlled or controlling parameters (Wong et al., 2009). However, the initial disturbance to P_cell when moving through a series of cells in a tissue is generally less with the ACPP (Fig. 1B) than with the CPP (Fig. 1C). An example of a P_cell disturbance can be seen in the CPP for the cell located at 900 μm in Figure 1C, as there is a clear relaxation in P_cell immediately following penetration. Such relaxations are not typically observed during ACPP operation (Fig. 1B).

Figure 1.

Sequential measurements with depth of P_cell in grape mesocarp tissue as conducted with a fully ACPP compared with a manually operated CPP. A, Schematic of the experimental protocol. Dashed lines indicate stationary and forward movement phases of the capillary into the tissue. In both cases, the forward movement is controlled manually using a motorized micromanipulator. For the ACPP, the oil/sap meniscus is maintained automatically at a single location by changes in P_oil. During forward movement, feedback control automatically reduces P_oil, but upon penetration into the next cell, the meniscus quickly moves away from the control point and causes a compensating response in P_oil as well as signals the operator that forward movement should be stopped. For the same experiment using a CPP, the meniscus location is monitored through the microscope by eye and P_oil is adjusted manually either with switches for increasing or decreasing P_oil directly or by manual adjustments to a P_oil controller. Prior to forward movement, the operator reduces P_oil, initiates forward movement, stops forward movement when a rapid meniscus movement is seen, and adjusts P_oil to return the meniscus to the perceived initial point of movement, which may be closer to or farther from the epidermis than the original meniscus location. B, Typical ACPP recording of P_oil and meniscus location and manually recorded depth of tip in the tissue for seven cells with a P_cell of around 0.15 MPa. Peaks in meniscus location indicate the puncturing of a new cell. C, Typical CPP recording for four cells having a P_cell of around 0.13 MPa, as in B.

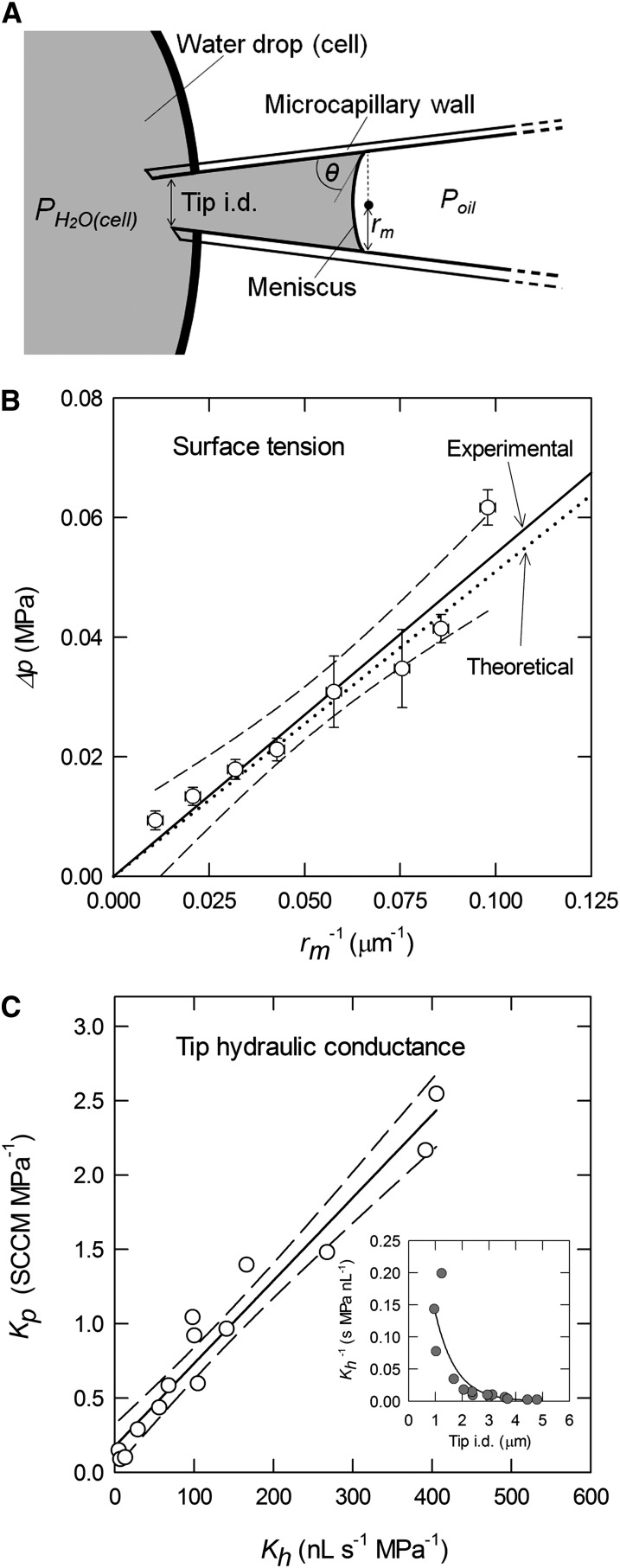
One advantage of the ACPP is that synchronous data on the location of the meniscus within the capillary, the capillary diameter at that location, and P_oil are routinely collected (Wong et al., 2009; Wada et al., 2011), and short-duration video recording is also possible. Video recordings have been useful in documenting the relatively small volume errors (less than 1%) resulting from changes either in the meniscus size or shape (Wong et al., 2009), and for this study, video recordings were used to determine features such as the wetting angle within the capillary (Fig. 2). Data on the location and size of the meniscus allowed the routine correction for differences between P_oil and P_cell due to both static (surface tension) and dynamic (tip conductance) effects, and while the corrections were typically not large for the microcapillaries used to measure T. virginiana cells, both corrections increase with decreasing capillary size and, hence, may be important when using smaller microcapillaries for smaller cells. For static (surface tension) effects, the estimated theoretical relation was well within the 95% confidence intervals of the empirically determined relation (Fig. 2B); hence, the empirically determined relation was used to routinely correct for surface tension effects in all subsequent data. For the tips and conditions used in this study, the correction for surface tension effects was generally less than 0.01 MPa. Routine correction for dynamic (K_h) effects required measurement of either tip pneumatic conductance (K_p) or tip size (Fig. 2C), but because the data for K_p was routinely available as part of microcapillary manufacturing (Wada et al., 2011), this was the method used. The measured K_p values for the tips used in this study were 0.66 to 1.07 standard cubic centimeters per minute (SCCM) MPa⁻¹, giving a calculated K_h of 75 to 160 nL s⁻¹ MPa⁻¹, very similar to the hydraulic resistance of tips of a similar size reported by Zhang and Tyerman (1991). From Equation 2 (P_cell − P_oil = a/r_m + dV/dt × 1/K_h), the differences between measured P_oil and P_cell due to K_h were generally less than 0.0001 MPa; hence, for the tips and cells used in this study, the effects of K_h and surface tension were very small, but the magnitude of both of these effects will increase if smaller tips are used.

Figure 2.

A, Schematic presentation of a microcapillary tip at equilibrium in a water drop or cell (for abbreviations, see “Materials and Methods”). B, Δp (= P_oil – P_H2O) as a function of r_m⁻¹ for a tip in a water drop (P_H2O = 0) at equilibrium. The linear regression line obtained from measured values of r_m⁻¹ (x) and Δp (y) was y = 0.0524x + 0.0001 (r² = 0.92), resulting in an experimentally determined value of slope (a) of 52.4 mN m⁻¹. Dashed lines indicate the 95% confidence intervals as calculated from Student’s percentage t distribution as obtained from 36 to 115 frames. The dotted line indicates a theoretical value based on θ = 50.4° (observed) and t = 40.0 mN m⁻¹ for dimethyl silicone oil, similar in composition to the silicone oil used. C, Linear relation between K_p and K_h. SCCM refers to standard cubic centimeters per minute indicating cm³ min⁻¹ at 0°C at 1 atmosphere. The linear regression line between K_h (x) and K_p (y) was y = 0.0056x + 0.1753 (r² = 0.95). The inset shows the relationship between tip resistance (y; K_h⁻¹) and tip i.d. (x) of y = 0.507exp^−1.308*x (r² = 0.72).

Synchronous data of meniscus position and P_oil also allow the quantification of irregular meniscus movement by classifying meniscus data into occurrences of movement (the rate of the volume change [dV/dt] ≠ 0) or temporary nonmovement (dV/dt = 0) under conditions when P was changing (the rate of the pressure change [dP/dt] ≠ 0) and meniscus movement would be expected. Storage of tips at high relative humidity substantially reduced the fraction of time this phenomenon was observed (from 0.44 to 0.05; Table I) when tips were tested in a water drop, although the basis for the nonmovement itself is not clear. In the literature, similar meniscus behavior has often been attributed to tip plugging by cell debris (Zimmermann et al., 1980), but for these tests there was no cell. Since the apparent plugging was reversible, and we observed small pockets of oil adhering to the inner surface of water-filled glass capillaries, we hypothesize that temporary plugging may be due to small quantities of oil temporarily bridging across the interior of the capillary tip, establishing an inner and outer oil/water meniscus of sufficiently small radius that comparatively large pressure differentials are required to break the bridge. The influence of humidity may be to condition the glass surface (possibly an electrostatic effect) and reduce the chance of oil bridges forming.

Table I. Effects of microcapillary storage at low and high humidity on irregular meniscus movement during ACPP experiments.

Microcapillaries used had a tip i.d. of 2 μm, and meniscus movement under changing pressure conditions (dP_oil/dt ≠ 0) were evaluated at regions of 30 and 100 μm of inner capillary diameter. When the meniscus stopped moving, the recorded value of dV/dt was 0. Because there was no significant difference (Student’s t test, P > 0.05) between regions, values for both regions were pooled. ***Significant difference at P < 0.001. Data are means ± sd of n = 6 microcapillaries tested.

Treatment	Total No. of Frames per Tip Analyzed for Which dPoil/dt ≠ 0	No. of Frames for Which dV/dt = 0	Fraction of dV/dt = 0 Frames
Low RH (45%–55%)	141.2 ± 26.7	63.5 ± 30.7	0.44 ± 0.19
High RH (100%)	120.5 ± 23.3	5.2 ± 5.2***	0.05 ± 0.05***

Cell Water Relations Parameters of T. virginiana Leaf Epidermal Cells

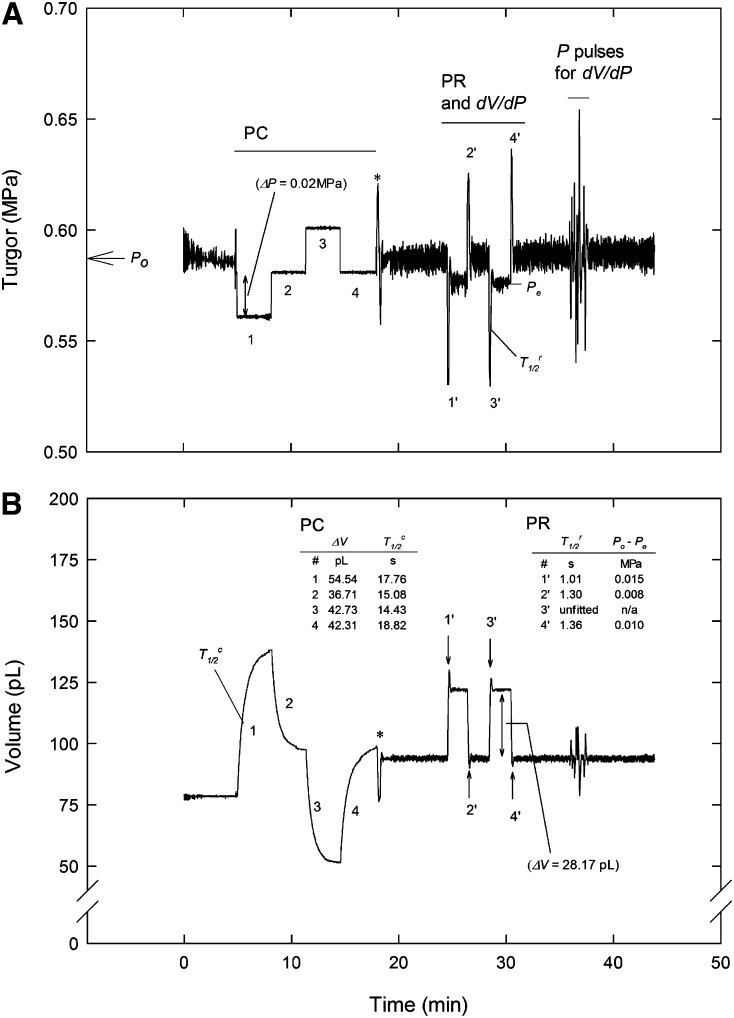
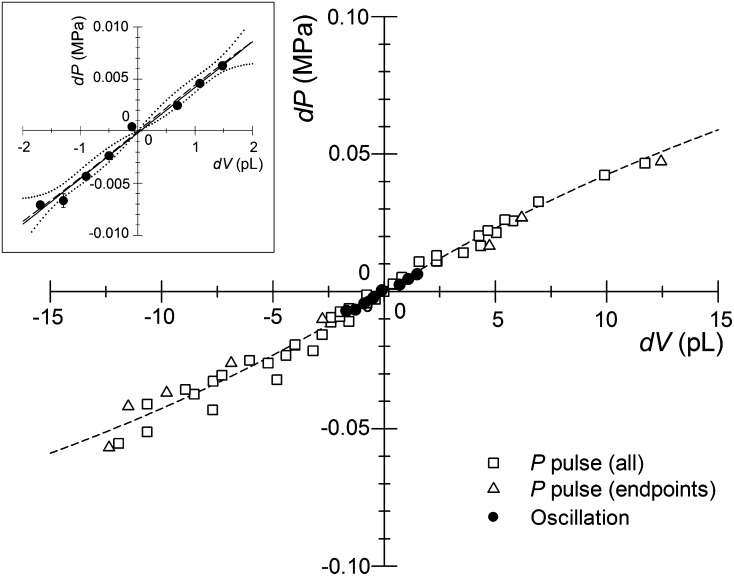
The ACPP was used to make a series of relatively small PCs (±0.02 MPa), PRs (±28 pL), and P pulses (maximum ±0.07 MPa) in the same cell over a period of about 30 min (Fig. 3). These changes are well below the levels of the P difference at which plasmodesmata closure was observed (e.g. 0.2 MPa in Nicotiana clevelandii; Oparka and Prior, 1992) or P disturbance (0.1–0.2 MPa) reported to give a significant decline in L_p in maize cortical cells after 1 min (Wan et al., 2004). For the latter hydraulic disturbance, we have similarly noted increased T_1/2 in T. virginiana epidermal cells when applying P steps of greater than 0.15 MPa (data not shown). Thus, it appears important to limit the size of P and V steps using the pressure probe in order to obtain an accurate estimate of membrane hydraulic properties in situ. P pulses are only used to establish an empirical relation of the applied step change in pressure (ΔP) to the corresponding change in volume (ΔV; dV/dP) for each measured cell at its current P, and the most common approach to establishing this relationship is to measure the maximum (end-point) ΔV that occurs for each of a series of imposed ΔP pulses. For a cell at constant P, however, all instantaneous values of P and V for any short-term changes in either value should express the same dV/dP, and this was the case whether only end-point values or all values collected during the P pulse were used (Fig. 4). As reported by Cosgrove and Durachko (1986) and expected from theory, as the size of the ΔP pulses increase and more time is required to complete the pulse, the opportunity for water flow across the cell membrane increases and the observed relation between ΔP and ΔV becomes nonlinear. For large ΔP pulses, Equation 3a of Tomos et al. (1981) can be used to estimate dV/dP near the origin, but for the small control oscillations (outside of PC, PR, and P pulse tests in Fig. 3), a simple linear regression through the oscillation data was equivalent to the sigmoidal fit (Fig. 4, inset). Also, in many cases, a sigmoidal fit could not be obtained due to the limited range of P and V values during the oscillation (data not shown). The best estimate for dV/dP will be from the smallest ΔP values available, and in our case, the control oscillations (ΔP of ±0.01 MPa), which presumably cause a minimal disturbance to the cell water relations, were sufficient to obtain this relation (Fig. 4). All reported estimates of dV/dP for each cell were obtained using the control oscillations.

Figure 3.

Example ACPP recording showing turgor (P_cell; A) and V (B) of cell fluid in the capillary for repeated PC and PR experiments on the same T. virginiana epidermal cell. Also shown are the water relations parameters calculated from each experiment. Following the PR experiments, a series of P pulses were manually applied in order to expand the range for measurement of dV/dP for this cell. Asterisks indicate the manual switch between PC and PR modes.

Figure 4.

Relationship between dV and dP for the cell shown in Figure 3, either during the period of P pulses (white symbols) or during periods when P and V were stable but oscillating due to feedback control (black circles). The dV and dP relationship is typically obtained from conventional P pulses using only the end-point values for each pulse (white triangles), but this relation is consistent with all the P pulse data (all white symbols) and consistent with the sigmoidal relation (dashed line) expected from theory (see text). The inset shows the dV/dP relation from control oscillations around the meniscus set point at each equilibrium P_cell (Fig. 3). Each data point is the mean ± 95% confidence interval of n = 6 to 504 frames collected at each meniscus location as calculated from Student’s percentage t distribution (most error bars are hidden by the symbol). In the inset, the long dash line is the sigmoidal relation fit to the mean oscillation points, with the short dash lines indicating the 95% confidence interval for this relation. The solid line within this confidence interval is a simple linear regression (y = 0.0044x − 0.0002 [r² = 0.99]) fit to all oscillation data points.

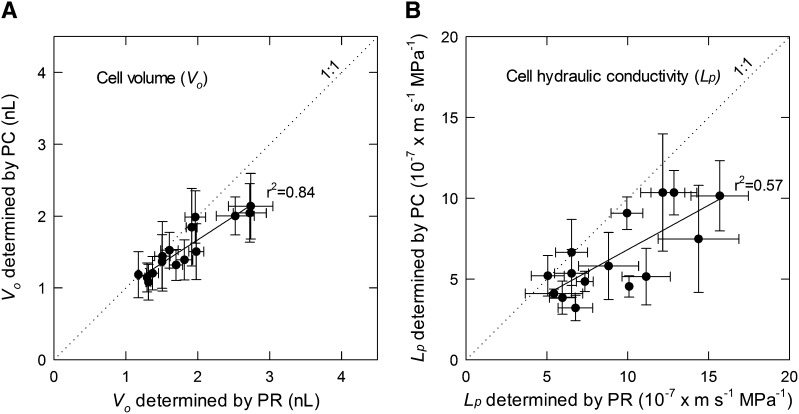
For PCs, the size of the step in P is set and the measured response is the change in the V of fluid in the capillary over time, whereas for PRs, the change in V is set and the change in P is measured. In both cases, the measured response is statistically fit to an exponential decay (Eq. 3 or 8) to obtain the parameters needed to calculate L_p and V_o, as described previously (Steudle, 1993). In some cases (e.g. PR replicate 3 in Fig. 3), the variation (noise) in the response made it impossible to obtain a reliable fit (nonconvergence condition in SAS PROC NLIN), but for most cases, the fits were very good, with narrow confidence limits on the fit line (Supplemental Figs. S1 and S2) as well as relatively small se for 1/b (Supplemental Table S1), which is directly proportional to T_1/2 (Eq. 4). The average and se estimates, respectively, for 1/b for all cells were 46.0 and 0.22 s for PC and 1.95 and 0.07 s for PR. The estimates obtained for T_1/2, ΔV, and P_o – P_e (see Eq. 5) using the same method repeatedly on the same cell were reasonably reproducible (Fig. 3). For the 15 cells of this study, within-cell repeatability was generally better for PR tests than for PC tests, with the PR method giving average coefficients of variation of 15.2%, 5.8%, and 19% for T_1/2, V_o, and L_p, respectively, and the PC method giving average coefficients of variation of 25.4%, 22%, and 24.2% for the same parameters (Table II). Cell volumes as determined from either method were between 1 and 2.7 nL, which was in the range of the optically estimated V_o values of 1.5 to 4.9 nL for these cells (data not shown), and L_p ranged from about 3 to 13 × 10⁻⁷ m s⁻¹ MPa⁻¹, which extends to the upper range of values reported for T. virginiana (Tomos et al., 1981) and pea (Pisum sativum) epicotyl (Cosgrove and Steudle, 1981). There was a clear correlation between the two methods for V_o and L_p (Fig. 5), but in both cases, the differences increased with increasing magnitude, particularly for V_o (Fig. 5). In both cases, the slope of the linear regression was significantly less than 1:1, and for V_o, the intercept was significantly greater than 0 (P = 0.03), but for L_p, the intercept was not different from 0 (data not shown). The only critical assumptions for the calculation of V_o using either the PC or PR are that cell total water potential does not change from the initial to the final state and that all solutes are retained by the cell (i.e. that the cell can be regarded as an ideal osmometer; Wendler and Zimmermann, 1982). For the same cell, we assumed the same value of osmotic potential for both methods, so the systematic difference between methods in calculated V_o indicates that there was a systematic difference in the overall P change for a given change in v (see Eq. 5) or ΔV (Eq. 9). The reason for this discrepancy is not known but currently under investigation. Compared with the PC method, the PR method is completed in a shorter time and does not require an extrapolation over time to obtain v, but V_o from the PR method also includes elastic effects (dV/dP; Eq. 5) that are not included in the PC method because P is maintained constant (Wendler and Zimmermann, 1982). Hence, it is difficult to suggest which method should be regarded as the most accurate.

Table II. Water relations parameters of individual leaf epidermal cells of T. virginiana measured using the ACPP to make repeated PC and PR experiments in the same intact cell.

Data for each cell are means (coefficient of variation [CV]) of n = 3 to 4 PCs or PRs as in Figure 3, pooling both inflow and outflow results. The range for P_cell for these cells was 0.41 to 0.83 MPa, and that for osmotic potential, determined on nearby cells, was from −1.08 to −0.70 MPa. s_v is the initial volume flow rate observed during a PC.

Cell	T1/2		Voa		εb	Lp
	PC	PR	PC	PR		PC		PR
	s		nL		MPa	× 10−7 m s−1 MPa−1	sv (10−16 × m−3 s−1)	× 10−7 m s−1 MPa−1
1	16.4 (13.4)	1.3 (6.3)	2.0 (18.3)	2.0 (7.3)	8.5 (7.3)	10.4 (13.3)	18.9	12.9 (11.0)
2	40.9 (13.0)	2.7 (36.1)	1.5 (16.4)	1.6 (7.6)	9.8 (7.6)	4.10 (6.9)	6.2	5.44 (32.6)
3	43.2 (10.7)	1.2 (42.5)	2.0 (13.2)	2.5 (10.5)	17.0 (10.5)	4.54 (14.5)	8.3	10.1 (69.2)
4	37.1 (32.2)	1.7 (13.9)	1.8 (29.3)	1.9 (4.0)	12.8 (4.0)	5.34 (27.6)	8.9	6.53 (16.1)
5	17.5 (29.3)	1.1 (8.8)	1.5 (25.8)	2.0 (5.3)	11.1 (5.3)	10.4 (35.1)	15.3	12.2 (11.2)
6	29.6 (37.1)	1.3 (19.2)	1.2 (27.1)	1.2 (1.3)	11.0 (1.3)	5.80 (35.9)	7.1	8.81 (21.1)
7	42.8 (29.6)	1.5 (13.3)	1.1 (23.0)	1.3 (2.7)	13.7 (2.7)	3.85 (26.6)	4.6	5.96 (13.4)
8	32.4 (32.6)	1.5 (4.2)	2.1 (21.3)	2.7 (11.3)	17.3 (11.3)	6.65 (30.8)	12.4	6.53 (15.1)
9	33.8 (28.3)	2.3 (17.3)	1.4 (33.6)	1.5 (7.1)	11.2 (7.1)	5.20 (24.1)	7.5	5.05 (20.1)
10	17.9 (13.5)	1.0 (11.3)	1.1 (17.7)	1.3 (2.3)	12.7 (2.3)	9.08 (11.1)	11.4	9.95 (9.8)
11	56.2 (26.4)	2.0 (22.1)	1.2 (19.4)	1.4 (6.1)	9.3 (6.1)	3.21 (24.5)	4.1	6.77 (15.8)
12	16.3 (23.0)	1.3 (6.6)	1.3 (16.3)	1.7 (5.4)	6.6 (5.4)	10.2 (21.4)	3.5	15.7 (11.3)
13	39.5 (27.3)	1.9 (3.3)	2.0 (20.0)	2.7 (8.4)	7.2 (8.4)	5.51 (33.9)	2.4	11.1 (13.4)
14	31.7 (5.8)	1.7 (5.1)	1.4 (20.1)	1.8 (6.4)	10.9 (6.4)	4.85 (12.9)	5.3	7.35 (7.1)
15	25.4 (58.9)	1.1 (18.3)	1.4 (27.4)	1.5 (1.6)	7.9 (1.6)	7.48 (44.3)	4.2	14.4 (17.4)
Mean ± sd (CV)c	32.1 ± 11.8 (25.4)	1.6 ± 0.5 (15.2)	1.5 ± 0.2 (21.9)	1.8 ± 0.5 (5.8)	11.1 ± 3.2 (5.8)	6.41 ± 2.48 (24.2)	8.0 ± 4.7	9.25 ± 3.40 (19.0)

^aOptically determined V_o was on average 2.56 nL, ranging from 1.50 to 4.93 nL.  ^bε average for each cell was determined from dP/dV during pressure oscillations and V_o as determined from PR.  ^cAverage of the CV values for each cell.

Figure 5.

Relation of V_o (A) and L_p (B) as determined by PR (x axis) or PC (y axis) experiments for the cells of Table II. Each data point is the mean ± sd of n = 3 to 4 PCs or PRs performed in the same cell as in Figure 3, pooling both inflow and outflow results. The solid line is the linear regression of PC and PR data. The linear regression statistics shown are for mean PR (x) and PC (y) points and for V_o is y = 0.65x + 0.36 and for L_p is y = 0.55x + 1.32 × 10⁻⁷. The dotted line indicates a 1:1 relation.

In this study, both PC and PR methods were used on the same cell, and both methods used inflow and outflow conditions (Fig. 3). Hence, a very powerful statistical test, equivalent to pooling many paired comparisons, for the effect of method and flow direction on cell water relations parameters was possible. For all parameters, these tests showed significant to very highly significant effects, with the PC method giving generally lower estimates of V_o and L_p and higher estimates for T_1/2 than the PR method and inflow conditions giving generally longer T_1/2 and lower L_p than outflow conditions (Table III). For the same cell, L_p and T_1/2 are closely related (Eq. 7), but they are calculated differently for the PC and PR methods, and in addition, the values of T_1/2 do not depend on an assumed cell membrane area. Hence, the fact that there was a 12% to 27% reduction in L_p and a corresponding increase in T_1/2 for inflow compared with outflow, regardless of method (Table III), is strong evidence that these cell membranes and/or the membrane complex exhibit polarity in water transport. T_1/2 for PC will always be longer than T_1/2 for PR in the same cell because cell wall elastic effects are not present in PC (Wendler and Zimmermann, 1982), and the significant interaction term between method and direction for T_1/2 in Table III simply reflects the larger difference for the larger value.

Table III. Statistical summary of cell water relations parameters for the cells shown in Table II.

The means ± sd (n = 15) for different methods and different directions of induced water flow are shown, together with the P values for the main effects of method and flow direction. The method × flow direction interaction term was only significant (P = 0.008) for T_1/2. For all parameters, the main effect of cells was very highly significant (data not shown).

Parameter	Method	Inflow	Outflow	Method P	Direction P
Vo (nL)	PC	1.78 ± 0.49	1.55 ± 0.60	0.0014	0.0358
	PR	1.96 ± 0.72	1.97 ± 0.65
Lp (×10−7 m s−1 MPa−1)	PC	5.28 ± 2.39	6.71 ± 2.83	0.0001	0.0143
	PR	8.18 ± 3.62	9.14 ± 3.10
T1/2 (s)	PC	36.7 ± 14.5	28.6 ± 12.7	0.0001	0.0052
	PR	1.73 ± 0.71	1.45 ± 0.37

As reported by Dainty (1963), the effects of USLs in our experiments were found to be negligibly small. For inflow and outflow during PRs, which have the highest potential for USL effects, the maximum USL thickness was only 0.2 to 1.39 μm (Ye et al., 2006; Eq. 3), compared with cell diameters of 70 to 140 μm. Using our measured cell osmotic pressure (π_o) values as the bulk solute concentration, maximum fluxes of water across the cell membrane of 4.5 × 10⁻⁷ m s⁻¹ (from our L_p times the maximum applied P pulse, dP/dV × ΔV), and a conservative diffusion coefficient for solutes in aqueous solution of 5 × 10⁻¹⁰ m² s⁻¹ (Dainty, 1963), the difference in solute concentration between the bulk solution and the membrane was 0.11% (Ye et al., 2006; Eq.1). Even assuming a much lower diffusion coefficient for the cell wall space of 3 × 10⁻¹¹ m² s⁻¹ (Kramer et al., 2007), this difference is only 1.9%. Hence, the potential effect of USLs on our estimates of L_p is negligible.

A similar degree of L_p polarity, in the same direction, has been reported for stem parenchyma in Saccharum species (Moore and Cosgrove, 1991), although in their case L_p^OUT/L_p^IN was greater for PR (1.65) than for PC (1.16) methods, and we found the opposite (1.11 for PR and 1.27 for PC methods). Moore and Cosgrove (1991) suggested that the greater polarity found for the PR method may have been due to the fact that this method imposed larger changes in P_cell than the PC method, but in our case, the P_cell changes for both methods were small and similar (Fig. 3). Based on the loss of polarity that occurred when cells were treated with mercury (Tazawa et al., 1996), it is reasonable to propose that aquaporins are responsible for polarity, either intrinsically, by pore asymmetry, or by active regulation, as suggested by Tyerman et al. (2002). If active regulation is responsible for the asymmetry that we observed, then, particularly for the PR method (T_1/2 of about 1.5 s), this regulation must be relatively rapid and highly reversible. The PR steps in this study were made at a time interval of about 90 s, but the ACPP (Wong et al., 2009) can make more frequent steps and, hence, will be instrumental in testing this hypothesis. Tazawa et al. (1996) have suggested that aquaporins increase both L_p as well as polarity, but if this were the case, then for the relatively wide range of L_p values that we observed in the 15 cells of this study (Table II; Fig. 5B), it would be anticipated that cells with higher L_p might be expected to exhibit higher values of L_p^OUT/L_p^IN, but no such correlation was observed (Supplemental Fig. S3). Hence, these data are suggestive that the observed polarity may be an intrinsic biophysical property of the intact membrane/protein complex. Polarity may play an important role in directed solute/water transport processes, such as localized refilling of embolized xylem (Brodersen et al., 2010). A higher L_p^OUT than L_p^IN would mean that, at steady state, a smaller area of membrane would be required to support water outflow into the xylem than the area of membrane supporting inflow to the cell, possibly allowing the refilling process to be restricted to pit areas, as suggested by Brodersen et al. (2010). The same geometric principle and advantage of a higher L_p^OUT than L_p^IN may also apply generally to water uptake by roots, since the transport path is radial, and hence, the membrane area for transport decreases along the path, particularly for the cells close to the xylem.

MATERIALS AND METHODS

Plant Material and Cell Turgor Measurements

Experiments were conducted with greenhouse-grown Tradescantia virginiana plants. Plants were grown under greenhouse conditions in 2-L pots filled with a mixture of GrowCoir (Greenfire), clay pellets, and perlite (4:1:1 by volume) in a temperature-controlled greenhouse (day/night cycle of 30°C/20°C ± 3°C; 40%/70% ± 10% relative humidity [RH]; and natural light with a daily maximum of 1,200 μmol photons m⁻² s⁻¹ photosynthetically active radiation). Plants were fully watered daily with a modified Hoagland nutrient solution (in mm: NO₃⁻, 6.85; NH₄⁺, 0.43; PO₄³⁻, 0.84; K⁺, 3.171; Ca²⁺, 2.25; Mg²⁺, 0.99; SO₄²⁻, 0.50; and in μm: Fe²⁺, 28.65; Mn²⁺, 4.91; BO₃³⁻, 24.05; Zn²⁺, 1.83; MoO₄²⁻, 0.17; Cu²⁺, 2.52) with electrical conductivity of 1.00 dS m⁻¹ at pH 5.75 and an osmotic potential of −0.04 ± 0.01 MPa. Plants were typically kept for several days under laboratory conditions (diffuse fluorescent light and 25°C air temperature) for measurement. P_cell was measured using the ACPP described by Wong et al. (2009), typically collecting P and V data at 7.5 Hz for epidermal cells in fully expanded leaves of 361 ± 85 mm in length and 20 ± 4 mm in width (mean ± sd of n = 9 leaves). In most cases, the plants were exposed to laboratory environmental conditions, but in some cases, all but the test leaf was enclosed in a clear plastic bag to minimize plant transpiration and any changes in overall plant water status over time.

The performance and sensitivity of the ACPP system were also compared with a manually operated CPP using greenhouse-grown grape berries (Vitis vinifera ‘Chardonnay’; Wada et al., 2008). Preveraison berries (stage II of development) were harvested randomly from different parts of the berry cluster (Wada et al., 2008) and immediately placed into aluminized mylar bags that excluded light and prevented transpiration before they were transported and analyzed in the laboratory (Thomas et al., 2006; Wada et al., 2008). With berries, it was possible to puncture multiple cells with increasing depth, beginning at the epidermis.

Microcapillary Manufacturing

Microcapillary tips were prepared from borosilicate micropipette glass (o.d./i.d. of 1.00/0.75 mm; Stoelting) using a micropipette puller (Kopf 750; David Kopf Instruments). Tips were beveled in a jet stream of beveling solution (Ogden et al., 1978) at an angle of approximately 40° using a microscope (100×). Tip size was controlled by adjusting beveling time (30–120 s), speed of the jet stream (2.0–2.3 m s⁻¹), and depth of the tip within the stream (25–50 μm). During beveling, pressurized air (approximately 0.37 MPa) was applied to the basal capillary end to prevent the entry of grinding compound through the open tip, and K_p of each capillary was calculated as described by Wada et al. (2011). After beveling, microcapillary tips, still under pressure, were dipped in glass cleaner (S.C. Johnson and Son) and rinsed with a jet of distilled water. Tips used in ACPP experiments had an i.d. of 2 to 3.5 μm and were typically stored for 2 d at 100% RH before usage (see below).

Microcapillary Storage

In preliminary experiments, microcapillaries were typically stored under laboratory conditions (45%–55% RH) before being filled with oil (dimethyl silicone fluid; Thomas Scientific) and assembled onto the ACPP. These microcapillaries could be inserted into a droplet of water and a stable oil/water meniscus established at any chosen point within the capillary by adjusting P_oil. However, it was observed that when P_oil was changing (when dP_oil/dt was not 0), the meniscus did not move smoothly from one location to another but rather moved in jumps, appearing to be periodically “stuck” at different locations. This was not commonly observed for freshly pulled tips. The effect of tip storage at low (45%–55%) and high (100%) humidity for 14 d on this phenomenon was quantified by adjusting the feedback control parameters of the ACPP (Wong et al.., 2009) to achieve approximately sinusoidal oscillations in P_oil with a frequency of about 0.5 Hz and a variable amplitude (0.001–0.008 MPa) and observing the rate of change (μm s⁻¹) in meniscus location when dP_oil/dt was not 0. This test was performed while collecting P_oil and meniscus location data at 30 Hz and at locations corresponding to approximately 30 and 100 μm of inner capillary diameter for each tip tested (n = 6).

Correcting for Surface Tension and K_h

The surface tension (t in mN m⁻¹) at a silicon oil/water interface (meniscus) will cause a pressure difference (Δp) across the meniscus according to the Young-Laplace equation (Ghosh, 2009):

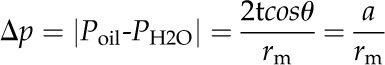(1)

where r_m is the meniscus radius (assumed equal to half the capillary i.d.) and θ is the contact angle between the water and the capillary wall. This equation predicts a reciprocal relation between Δp and r_m with a slope, a (=2tcosθ). To empirically determine a, the meniscus was moved to a series of positions of different r (10–100 μm, corresponding to a distance of 65–5,950 μm from the tip) by changing P_oil. At each stationary meniscus location, P_oil was measured together with r_m. At r_m values of 10 to 100 μm, θ was relatively constant at 50.4° ± 2.9° (mean ± sd, as obtained from n = 8 images of the static meniscus). A value of t = 40 mN m⁻¹ for dimethyl silicone (Xue et al., 2006) was used together with the observed value of θ to calculate an expected value for a.

K_h was determined as the slope of the linear relationship between the rate of the volume change of water (dV/dt) in the capillary and the pressure difference between the water in the capillary (P_H2O from Eq. 1) and the water in a water drop with r ≅ 1 mm (0.00015 MPa, assumed equivalent to atmospheric pressure). Water volume in the capillary was calculated as described by Wong et al. (2009) and measured at 7.5 Hz. All data reported for P_cell in this work include corrections to P_oil for the static effects of surface tension (a/r_m; Eq. 1) as well as dynamic effects (K_h), according to Equation 2:

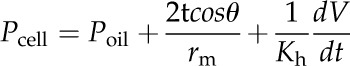(2)

Values of dV/dt were defined as negative for movement of the meniscus toward the tip and positive for movement away from the tip.

PR Experiments

PR experiments were conducted using the “meniscus-position step” function described by Wong et al. (2009), recording the change in P_cell over time [P_cell(t)] after the meniscus had reached its new set point and the volume step was complete. The change (relaxation) in P_cell over time is described by a monophasic-exponential function (Zhu and Steudle, 1991; Steudle, 1993):

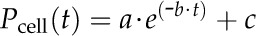(3)

where a = P_max − P_e, b = the rate constant of cell water exchange, and c = P_e. P_e is the final equilibrium P_cell at the end of the relaxation. The T_1/2 of cell water exchange during a PR (T_1/2^r) can be calculated as follows:

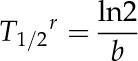(4)

In this study, data for P_cell(t) were only analyzed after the meniscus had reached the set point in order to exclude the elastic effects that occur during the step. An alternative approach to correct P_cell(t) for transient elastic effects during a PR is presented by Steudle et al. (1980).

Cell volume was also determined from PRs (V_o^r) according to the theory of Malone and Tomos (1990; see their Eq. 5):

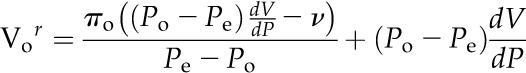(5)

where π_o and dV/dP are as already defined, P_o is the original equilibrium cell pressure, and v is the volume of liquid removed from or introduced to the cell. Because the ACPP records V and P at a relatively high frequency (10–30 Hz), a number of alternative approaches were used to measure dV/dP (see “Results and Discussion”).

The ε was calculated as follows:

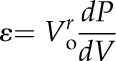(6)

The cell hydraulic conductivity (L_p^r) was determined based on values of T_1/2^r, V_o^r, ε, and π_o according to:

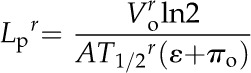(7)

where A was determined from V_o^r by assuming that cells were column shaped with radius (r) and length (l; Tomos et al., 1981). Cell dimensions were measured microscopically on 88 cells using an image-analysis software (NIH Image version 1.61; National Institutes of Health). Since the ratio of l to r was 3.8 ± 1.65 (mean ± sd, n = 88), the mean l/r value was regarded as the representative ratio to calculate A from V_o with the conversion A = 5.77V_o^2/3.

PC Experiments

PC experiments were conducted using the “pressure-step” function described by Wong et al. (2009), recording the change in volume over time [ΔV^c(t)] after the final clamped pressure had been reached (i.e. the pressure step was complete). The change (relaxation) in V over time is described by a monophasic-exponential function (Wendler and Zimmermann, 1982):

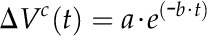(8)

where a = total volume change in the microcapillary and b = the rate constant for cell water exchange. As for the PR, ΔV^c(t) data were only used after the pressure had reached the set point in order to exclude transient elastic effects. The corresponding T_1/2 of the volume relaxation (T_1/2^c) can be calculated according to Equation 4, substituting T_1/2^c for T_1/2^r. Cell volume from a PC (V_o^c) was determined based on the theory of Wendler and Zimmermann (1982; their Eq. 5):

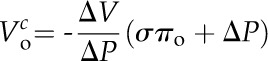(9)

where ΔV is the overall change in liquid volume in the microcapillary, from the initial equilibrium state to the final equilibrium state (i.e. ΔV at infinite time from Eq. 8). Note that Wendler and Zimmermann (1982) refer to ΔV as “the change in cell volume,” but once P is clamped, there should be no change in cell volume. ΔP is the applied step change in pressure. The reflection coefficient (σ) was assumed to be unity, which is considered a reasonable approximation when the capillary tip is located in the vacuole (Steudle, 1993; Murphy and Smith, 1998).

The cell hydraulic conductivity from PC experiments (L_p^c) was calculated according to Equation 10 (Wendler and Zimmermann, 1982). Equation 10 is independent of ε but relies on A as derived from the measured V_o^c:

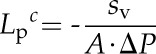(10)

where s_v is the initial slope of the volume relaxation (=ΔV/Δt for t→0), which was determined from the fitted curve of Equation 8. As for the PR experiments, only the data after the pressure had reached its new set point were used to determine the fitted curve. A was determined from V_o^c as described for PR experiments (see above).

π_o

The cell π_o in the vicinity of the cells used for P measurements was measured directly in some cases using a nanoliter osmometer (Clifton Technical Physics) as described by Shackel (1987). The same relation between epidermal cell π_o and bulk tissue π_o was found as that reported by Nonami and Schulze (1989), so for the remaining cells, π_o was either estimated from a measurement of bulk tissue π_o or simply taken as a mean value (−0.73 MPa), since all measured values exhibited a relatively narrow range (−0.67 to −0.83 MPa) and since this estimate would not affect any comparisons conducted within the same cell.

Microscope

Epidermal cells of T. virginiana leaves were viewed at 600× through a microscope equipped with a vertical illuminator (BHMJ system; Olympus) and a ×20 objective (I-LM546; Olympus) linked to a monochrome digital camera (model CV-50, JAI Technologies), as described by Wong et al. (2009). The length, width, and thickness of the cells were measured using image-analysis software (NIH Image version 1.61).

Data Analysis

All statistical data analyses were performed using SAS (version 9.2; SAS Institute). Nonlinear regression (PROC NLIN) was used to fit the measured changes of P or V to the expected exponential decay over time following a step change in V or P, respectively (Eq. 3 or 8), using only data collected after the targeted step change had been reached. Typically, data for two replicate PCs and PRs for both inflow and outflow directions were collected from each cell, as shown in Figure 3. Traditional measures of goodness of fit (r²) are not available in PROC NLIN, but approximate se values for the fit parameters are given. Cell parameters (e.g. V_o, L_p, and T_1/2) were determined separately for each replicate PC or PR, and these estimates were considered as subsamples within a cell. Statistical tests (SAS PROC GLM) for the significance of flow direction, clamping method, or their interaction on cell parameters were based on considering individual cells as a factor, and hence, these tests are equivalent in power to that of a pooled pairwise comparison within the same cell.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. An example of PC data showing an exponential fit to the raw data of the observed change in volume within the capillary over time.

• Supplemental Figure S2. An example of PR data showing an exponential fit to the raw data of the observed change in pressure over time.

• Supplemental Figure S3. Lack of relation between the L_P^OUT/L_P^IN ratio and the average L_P.

• Supplemental Table S1. Statistical results for the parameters of the individual fit curves shown in the supplemental Figures S1 and S2.

Glossary

L_p

hydraulic conductivity

USL

unstirred layer

L_p^IN

inflow hydraulic conductivity

L_p^OUT

outflow hydraulic conductivity

PR

pressure relaxation

PC

pressure clamp

P_cell

cell turgor pressure

P

pressure

T_1/2

half-time

A

cell surface area

V_o

cell volume

ε

volumetric elastic modulus

V

volume

K_h

hydraulic conductance of the capillary tip

ACPP

automated cell pressure probe

P_oil

oil pressure

CPP

cell pressure probe

K_p

tip pneumatic conductance

ΔP

change in pressure

ΔV

change in volume

RH

relative humidity

dV/dP

slope of the relation of pressure to volume for the cell

π_o

osmotic pressure