Principal components analysis of protein sequence clusters

Abstract

Sequence analysis of large protein families can produce sub-clusters even within the same family. In some cases, it is of interest to know precisely which amino acid position variations are most responsible for driving separation into sub-clusters. In large protein families composed of large proteins, it can be quite challenging to assign the relative importance to specific amino acid positions. Principal components analysis (PCA) is ideal for such a task, since the problem is posed in a large variable space, i.e. the number of amino acids that make up the protein sequence, and PCA is powerful at reducing the dimensionality of complex problems by projecting the data into an eigen-space that represents the directions of greatest variation. However, PCA of aligned protein sequence families is complicated by the fact that protein sequences are traditionally represented by single letter alphabetic codes, whereas PCA of protein sequence families requires conversion of sequence information into a numerical representation. Here, we introduce a new amino acid sequence conversion algorithm optimized for PCA data input. The method is demonstrated using a small artificial dataset to illustrate the characteristics and performance of the algorithm, as well as a small protein sequence family consisting of nine members, COG2263, and finally with a large protein sequence family, Pfam04237, which contains more than 1,800 sequences that group into two sub-clusters.

Introduction

Protein sequence analysis is useful in many applications including identification of functional domains [1] and prediction of protein–protein interactions [2]. However, quantitative statistical analysis of protein sequence variations is complicated by the fact that protein amino acid sequences are conventionally represented by an alphabetic one-letter code whereas quantitative statistical analyses of protein sequence variations requires some form of numerical representation of the amino acid sequence information. Many methods have been explored to solve this problem but basically two techniques are commonly used: (1) assigning a number to each amino acid calculated based on their biochemical properties, and (2) using binary vectors to represent distinct amino acid types.

Statistical analyses of protein sequence patterns have been used for many purposes. Genetic code organization has been explored using indices for amino acids based on their physicochemical characteristics [3–5]. Amino acid substitution matrices based on solvent accessibility, charge and volume have been used to define protein families [6]. Assignment of numerical values for each amino acid type using the electron–ion interaction potential (EIIP) method has been used to detect conserved regions in proteins [7, 8]. Sequence weighting has been introduced to decrease sequence redundancy in protein families and to emphasize diversities in multiple sequence alignments (MSA) [9]. Though biased in some conditions [10], sequence weighting has been shown to be useful in combination with other methods [11].

Binary vector profiling of protein sequence patterns is also a popular method for predicting functional residues in protein families. In this algorithm, a binary vector with a length of 20 bits is used to represent each amino acid type [12], essentially as a letter is represented by a byte in computer binary storage. An amino acid type is converted to a binary vector by assigning a unique register in the 20-element vector a value of 1, with all other positions equal to 0, for each amino acid type. This binary profiling technique demonstrated good performance for predicting binding sites in proteins [13].

Another vector-based encoding scheme was provided by Atchley et al. [14], which is a combination of the two methods just described. Instead of a binary vector of 20 elements, a vector of five non-zero variables was used to explain each residue based on amino acid properties. This method is called Amino Acid Property (AAP) Encoding [11]. The AAP method generates vectors with fewer elements and continuous variables, which make this method easier for statistical analysis [11].

Specifically conserved amino acid positions considered to be related to functional specificity have been referred to as specificity-determining positions (SDPs) [15]. Various tools have been developed to detect SDPs [16] including phylogenetic trees methods [17–19], methods based on global variability representative positions detection [20–22] and multivariate analyses [12]. Phylogenetic trees use MSA data to build a tree to show subfamilies and the branching points are the conserved positions for the subfamilies. On the other hand, methods based on global variability representative positions were designed to detect variation positions which could represent the variations of the whole alignment. Multivariate analyses like principal components analysis (PCA) have also been applied to analyze subfamilies because of its power for multidimensional data simplification. Binary vector [12] profiling has been used for PCA and a recently developed PCA-like method called multiple correspondence analysis has also been applied to reduce data dimensionality using a similar binary vectors theory [15].

PCA is a powerful mathematical technique used to reduce the dimensionality of the parameter space, and it is widely used in physics [23], ecology [24], and metabonomics [25]. The idea of using PCA for protein sequence analysis was suggested by Casari et al. after converting the amino acid sequence information using the binary method [12]. Gogos et al. [26] showed that PCA can be very useful in assigning function to protein sequences using the binary method. However, the binary vector method introduces more variables because a single amino acid type is represented by many vector elements, which makes the analysis complex. PCA has also been used to detect conserved regions in proteins using the EIIP letter to number conversion [8] but the results were not satisfactory and wavelet transformation had to be used to increase detection efficiency.

In our application, we wish to use PCA to quantitatively, systematically, and rapidly to identify sequence positions whose variability drives sequence cluster separations in algorithms such as CLuster ANalysis of sequences (CLANs) [27]. In order to apply PCA to address this problem, protein sequence information encoded by the alphanumeric one-letter system must be converted to a numerical representation scheme that faithfully preserves variability that occurs at a given position in a sequence family. Existing methods for converting protein sequence alignments into numerical representation are not optimal for PCA data input. In this paper, we introduce a letter-to-number conversion method designed to be more optimal for PCA data input. This new method does not assign a fixed number to each amino acid but rather assigns a number that directly reflects the magnitude of the variance in each sequence position. We demonstrate our method by applying PCA to converted data from a small pair of artificial protein sequence families, a small protein family comprised of nine sequences corresponding to Cluster of Orthologous Groups (COG) COG2263 and large protein family comprised of over 1,800 sequences, Pfam04237, that naturally divides into two sub-clusters when the CLANs algorithm is applied [28]. The latter example illustrates the power of the conversion algorithm, enabling PCA to quantitatively identify which amino acid sequence positions are most responsible for separation of two sequence sub-clusters by CLANs in a very large sequence family.

Materials and methods

Conversion method

In this method, we start with a multiple sequence alignment. We then calculate how many times each amino acid occurs in a given column in an aligned sequence. We refer to this number as the occurrence frequency. The occurrence frequencies are then sorted from low to high, resulting in a rank order for each amino acid type in each column, i.e. those amino acids with the lowest occurrence frequency are assigned the smallest rank order number and those with the highest occurrence frequency are assigned the largest rank order number. When two amino acids have the same occurrence frequency, the amino acid that comes last in alphabetical order is given the lowest rank order number. The rank order for each amino acid type is then used to replace the letter for each amino acid in each column in the aligned sequences. The resulting distribution of numbers reflects the degree of amino acid variation that occurs at that location in the sequence. For example, only a single number will occur in a column for positions that are strictly conserved, resulting in minimum possible variance. At the opposite extreme, for positions that are not conserved at all, 20 different numbers would randomly occur in the column resulting in a maximum possible variance. Any gaps in the sequence, marked by a ‘-’ in the sequence alignment, are converted to ‘0’, meaning that these positions make no contribution to variance. This matrix is then used to compute a mean-centered variance/covariance matrix used for PCA. Data conversion was done in Matlab (R2009a, MathWorks) using a home written program.

Generation of the artificial test dataset

An artificial dataset was generated to simulate 20 protein sequences containing nine amino acids in each sequence. The test dataset was divided into two groups of ten to simulate two different sequence families. The artificial sequence families contained positions that were strictly conserved across both groups (Table 1, Column 6), positions that were strictly conserved in each group but different between the groups (Table 1, Column 1), positions that were strictly conserved in group #1 and completely variable in group #2 (Table 1, Column 9), and several positions with differing degrees of sequence variation between the two groups (Table 1, Columns 2, 3, 4, 7, and 8).

Table 1.

Artificial test dataset divided into two groups (Group #1: 1–10 & Group#2: 11–20)

	Position #1	Position #2	Position #3	Position #4	Position #5	Position #6	Position #7	Position #8	Position #9
Sequence #1	A	A	A	C	F	C	C	D	A
Sequence #2	A	C	C	D	G	C	D	E	A
Sequence #3	A	A	A	E	H	C	C	F	A
Sequence #4	A	C	C	F	I	C	D	D	A
Sequence #5	A	A	A	C	F	C	C	E	A
Sequence #6	A	C	C	D	G	C	D	F	A
Sequence #7	A	A	A	E	H	C	C	D	A
Sequence #8	A	C	C	F	I	C	D	E	A
Sequence #9	A	A	A	C	F	C	C	F	A
Sequence #10	A	C	C	D	G	C	D	D	A
Sequence #11	C	D	A	F	C	C	D	A	H
Sequence #12	C	E	C	G	D	C	F	G	I
Sequence #13	C	D	A	H	F	C	D	A	K
Sequence #14	C	E	C	F	G	C	F	G	L
Sequence #15	C	D	A	G	C	C	D	A	M
Sequence #16	C	E	C	H	D	C	F	G	N
Sequence #17	C	D	A	F	F	C	D	A	P
Sequence #18	C	E	C	G	G	C	F	G	Q
Sequence #19	C	D	A	H	C	C	D	A	R
Sequence #20	C	E	C	F	D	C	F	G	S

Selection of protein sequence families for testing

One small protein sequence family composed of nine sequences and nominally 240 amino acids in the protein sequence was examined, namely Cluster of Orthologous Groups (COG) COG2263, whose sequence data was obtained from the National Center for Biotechnology Information (NCBI) (http://www.ncbi.nlm.nih.gov/). An advantage of using a small sequence family of relatively large proteins is that it provides a way to explore the performance of the algorithm for cases of high dimensionality and it makes it straight-forward to analyze the resulting PCA scores plot. We also considered a large protein sequence family, Pfam04237, which contains more than 1,800 protein sequences with a nominal protein length of 196 amino acids. We previously showed that a CLANs analysis of Pfam04237 resolves into two sub-clusters containing more than 1,400 protein sequences [28] with the remaining ~400 sequences were scattered in the CLANS plot and did not obviously belong to either sub-cluster. Therefore we selected the 1,414 protein sequences that clearly belonged to one of the two sub-clusters as a third test case.

Statistical analysis and data representation

PCA was conducted using SIMCA-P+ 11 (Umetrics). Protein structures were drawn in PyMOL (Version 1.5.0.1 Schrödinger, LLC).

Results and discussion

Analysis of the artificial dataset

The artificial test dataset was constructed to examine how the conversion algorithm performed for several different types of amino acid variation that might occur within a sequence family or between sequence families. We defined two groups to represent two distinct protein sequence families where rows 1–10 defined Group 1 and rows 11–20 defined Group 2 (Table 1). Column 6 was strictly conserved across both groups, column 3 was conserved across the two groups with two allowed amino acid types, and column 9 was designed to have the most variance between the two groups, where the position was strictly conserved in Group 1 and completely random in Group 2. Column 1 is interesting in that it represents a position that is strictly conserved in each group, but the amino acid type is different between the two groups. All other columns were intended to have intermediate amounts of variance. The conversion algorithm was applied to the artificial dataset resulting in the matrix shown in Table 2. The mean centered variance/covariance matrix, calculated from the converted data is shown in Table 3. Analysis of the diagonal elements of the variance/covariance matrix, which correspond to the variance of the individual amino acid positions, revealed decreasing variance by amino acid position in the order (9 > 4 > 5 > 8 > 2 > 7 > 1/3 > 6), for the most part consistent with the intended variance designed into the artificial sequence alignment. An interesting exception is position #1, which should cause distinction between the two groups, but the position exhibits small variance, it is less strongly weighted by the algorithm.

Table 2.

Converted artificial test dataset divided into two groups (1–10 and 11–20)

	Position #1	Position #2	Position #3	Position #4	Position #5	Position #6	Position #7	Position #8	Position #9
Sequence #1	2	4	2	5	6	1	2	3	11
Sequence #2	2	3	1	4	5	1	3	2	11
Sequence #3	2	4	2	1	2	1	2	1	11
Sequence #4	2	3	1	6	1	1	3	3	11
Sequence #5	2	4	2	5	6	1	2	2	11
Sequence #6	2	3	1	4	5	1	3	1	11
Sequence #7	2	4	2	1	2	1	2	3	11
Sequence #8	2	3	1	6	1	1	3	2	11
Sequence #9	2	4	2	5	6	1	2	1	11
Sequence #10	2	3	1	4	5	1	3	3	11
Sequence #11	1	2	2	6	4	1	3	5	10
Sequence #12	1	1	1	3	3	1	1	4	9
Sequence #13	1	2	2	2	6	1	3	5	8
Sequence #14	1	1	1	6	5	1	1	4	7
Sequence #15	1	2	2	3	4	1	3	5	6
Sequence #16	1	1	1	2	3	1	1	4	5
Sequence #17	1	2	2	6	6	1	3	5	4
Sequence #18	1	1	1	3	5	1	1	4	3
Sequence #19	1	2	2	2	4	1	3	5	2
Sequence #20	1	1	1	6	3	1	1	4	1

Table 3.

Variance/covariance matrix for the converted data shown in Table 2

	#1	#2	#3	#4	#5	#6	#7	#8	#9
#1	0.26	0.53	0	0.053	−0.11	0	0.13	−0.63	1.45
#2	0.53	1.32	0.26	−0.11	0.053	0	0.39	−1.16	3.02
#3	0	0.26	0.26	−0.21	0.26	0	0.13	0.1	0.13
#4	0.053	−0.11	−0.21	3.16	0.42	0	0.16	−0.053	0.37
#5	−0.11	0.053	0.26	0.42	2.83	0	0.079	0.23	−0.45
#6	0	0	0	0	0	0	0	0	0
#7	0.13	0.39	0.13	0.16	0.079	0	0.72	−0.026	0.99
#8	−0.63	−1.16	0.1	−0.053	0.23	0	−0.026	2.01	−3.34
#9	1.45	3.03	0.13	0.37	−0.45	0	0.99	−3.34	12.3

PCA was conducted on the variance/covariance matrix. The resulting eigenvectors and eigenvalues are shown in Table 4. In the PCA scores plot (Fig. 1a), the two groups separated along the first principal component direction (PC1). The absolute values of the four largest PC1 loadings decreased in the order 9 > 8 > 2 > 1 (Fig. 1b). Inspection of the raw sequences in Table 1 illustrates that the variance increases as the number of amino acids occurring in the position increases (Table 1, column 9). The fact that column eight has greater weighting than column two in the PC1 loading reflects that five total amino acids vary in column eight (three amino acids vary in Group 1 and two different amino acids vary in Group 2), whereas only four amino acids vary in column two (two amino acids vary in each Group 1 and Group 2). In contrast with the PC1 loadings, the variance/covariance matrix reveals that column four has greater variance than column eight (Table 3). This occurs because, while there are seven total amino acids varying across the two groups, one amino acid occurs and varies in both groups. Likewise, in column five, there are also seven amino acids that vary, but two vary in both groups, so the variance for this position is smaller than for position four. Examination of the second principal component (PC2) explains variance not segregated by group (Fig. 1a). For example, the strong group-independent variations in positions #4 and #5 result in large loadings in PCs (Fig. 1a; Table 4). This simple example using an artificial data set illustrated that the algorithm produced the expected features in the PCA scores and loadings plots.

Table 4.

Eigenvectors and eigenvalues from diagonalization of the variance/covariance matrix in Table 3

PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	EV
.11	−.010	−.01	−.16	.15	.021	−.52	−.010	−.82	14.4
.24	−.023	.14	−.22	.59	−.47	−.37	.00	.41	3.46
.01	−.01	.16	.11	.30	−.51	.67	−.00	−.41	2.61
.029	.82	−.55	−.044	.067	−.11	.032	.00	.00	1.22
−.039	.56	.81	−.064	−.14	.088	−.049	−.00	.00	.78
.00	.00	.00	.00	.00	.00	.00	1.00	−.01	.31
.075	.064	.037	.34	.67	.64	.12	.00	.00	.062
−.28	.047	.024	.84	−.044	−.30	−.35	−.00	−.00	.00
.92	.014	.019	.30	−.25	−.010	.037	.00	.00	.00

The first nine columns represent the loadings of the nine eigenvectors ordered from left to right. The last column is the vector of eigenvalues

Fig. 1.

PCA of the artificial test dataset. The PCA scores plot (PC1 vs PC2) is shown in a and the corresponding PCA loadings plot is shown in b. The first two PCs explained 78.1 % of total variance including 63 % contribution of PC1

Analysis of protein sequences in COG2263

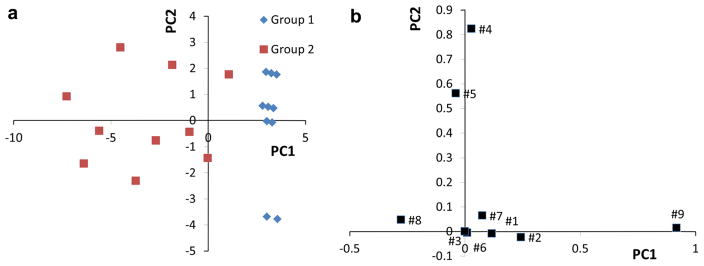
COG2263 represents a small protein sequence family having nine members with 240 aligned amino acid positions within the family. The sequence relationships among the different proteins were obtained from the PCA scores plot (Fig. 2a). The general positional relationships of the individual protein sequences in the PCA scores plot were similar to the positional relationships found in the dendrogram (Fig. 2b). For example, Ta1320 and TVN0270 are very close in the scores plot and they are adjacent in a common branch in the dendrogram. PH1948, PAB1205 and AF0205 also had similar positional relationships between the PCA scores plot and dendogram. Investigation of the sequence alignment for COG2263 indicates that MJ0284 contains an 11-residue insertion not present in MTH1918. Whereas the dendogram algorithm groups these two sequences together, our PCA indicates separation along the PC2 dimension, albeit, the two sequences have PC1 weightings, which is consistent with sequence clustering in the dendogram. The information contained in the corresponding loadings plot makes it possible to identify sequence relationships that dominate the overall protein positional relationships with single amino acid position resolution. This result follows from PCA theory, where loadings with the large absolute values contribute the most to determining the direction and distance of separation in the scores plot. In other words, the sequence position variables with large absolute values of the loadings are most important in determining those sequence variations that distinguish protein sequence families.

Fig. 2.

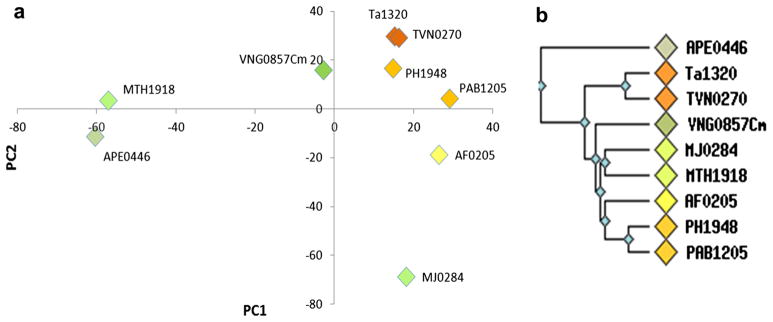
PCA scores plot and dendogram of COG2263. The PCA scores plot (PCA1 vs PCA2) of COG2263 is shown in a and the dendrogram of COG2263 from the NCBI (http://www.ncbi.nlm.nih.gov/) is shown in b. The first two PCs explained 57.1 % of total variance including 32 % contribution of PC1

In order to connect the information contained in the PCA loadings plot with the structure of the proteins in the sequence family, we used a cutoff equal to 40 % of the Euler distance from the origin to the most distant loading to identify those amino acid positions that accounted for the most variance across the family. We then defined four categories of Euler distances ranging from >90 %, 80–90 %, 60–80 % and 40–60 % of the maximum Euler distance and these were given distinct color assignments (Fig. 3a). The loadings along with their colors were mapped onto a representative protein structure, PH1948 (PDB-ID: 1WY7), as an example, in Fig. 3b, c.

Fig. 3.

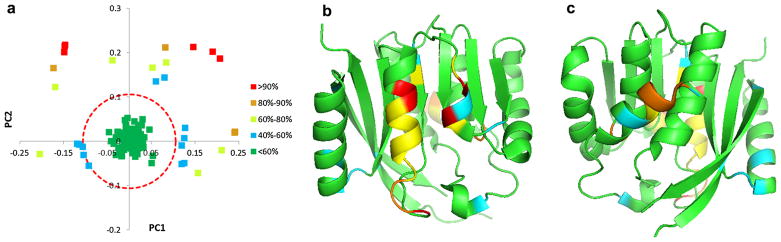
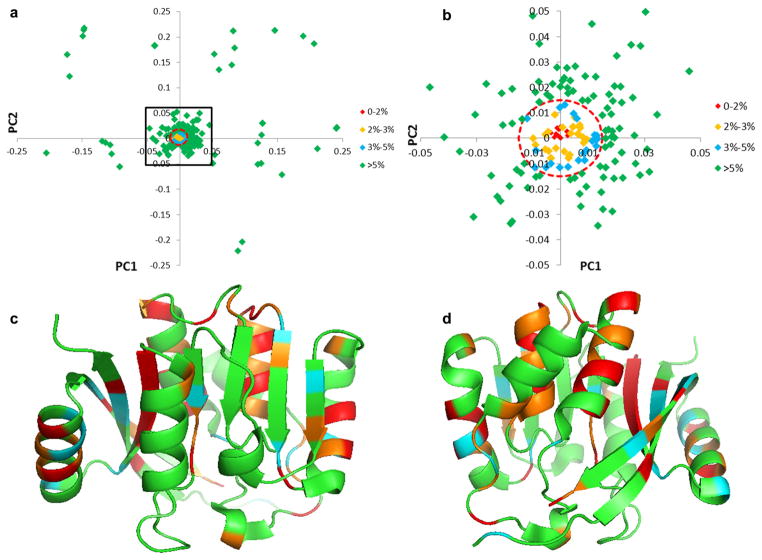
Identification of the most variable amino acid positions within COG2263. The PCA loadings plot (PC1 vs PC2) is shown in a. The Euler distance to the centroid was calculated and a cutoff corresponding to 40 % of the largest Euler distance was used to filter the data (Red dashed-line circle). There were 51 out of 240 amino acid positions that exceeded the cutoff. These were color-coded according to decreasing percentage of the maximum Euler distance as follows: Red (>90 %) >Orange (80–90 %) > Yellow (60–80 %) > Cyan (40–60 %) > Green (< 40 %). The ribbon-rendering of protein (PDB-ID: 1WY7) was color-coded according to the loadings and two different views are shown in b and c

The PCA loadings were also used to identify the most conserved amino acid positions within the sequence family. For this application, we needed to identify loadings with the smallest Euler distances. We selected a cutoff threshold with an upper limit corresponding to 5 % of the Euler distance from the origin to the most distant loading (Fig. 4a, b). Again, the identified loadings were assigned a color according to their corresponding Euler lengths (Fig. 4a, b) and those loadings having Euler distances <2 % of the maximum were identified as the most conserved positions within the sequence. Using this threshold, all residue positions with Euler distances <5 % of the maximum Euler distance were colored on the ribbon diagram of a representative structure from the sequence family to allow visual inspection of the locations of conserved positions within the sequence (Fig. 4c, d).

Fig. 4.

Identification of most strongly conserved residues from the PCA loadings. The PCA loadings plot (PC1 vs PC2) is shown in a, and the region enclosed in the black frame is shown in b. The Euler distance to the centroid was calculated, and a circle with an Euler radius corresponding to 5 % of the largest loading was used as an upper limit to filter the data (Red broken-line cycle). In the figure 89 out of 240 amino positions had Euler distances<5 % cutoff and these were color-coded according to Red <Orange < Cyan < Green. In c and d (rotated by 180°), the most conserved amino acid positions were colored in the ribbon representations of the protein (PDB-ID: 1WY7) using the same color assigned to the loadings plot data

Analysis of protein sequences in Pfam04237

Pfam04237 is composed of more than 1,800 protein sequences with a nominal length of 196 amino acids. We previously conducted a CLANs analysis of this family [28], which revealed that the family largely divided into two sub-clusters consisting of about 1,400 of the sequences. Here we focus on just the 1,414 sequences in the two sub-clusters. The CLANs analysis of this subset of Pfam04237 is shown in Figure S1.

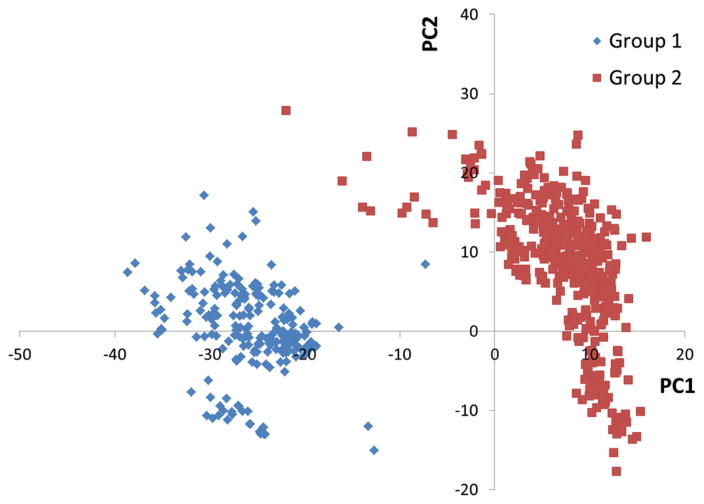
A natural question, then, is what are the sequence variations that are most responsible for division of this sequence family into two sub-clusters? Clearly, when the number of protein sequences becomes large, in this case exceeding 1,400, and/or the number of amino acids in the protein sequence becomes large, about 196 amino acids per protein, answering this question becomes increasingly challenging, and well suited for PCA. In our application, each amino acid position defines a variable for PCA. The weightings or loadings in the PCA eigenvectors, then, report on the degree to which the variable positions are responsible for cluster separation. We demonstrate the power of our approach by applying our conversion method to enable PCA of the >1,400 proteins sequences in the Pfam04327 subset used for the CLANs analysis above. PCA of this subset produced a scores plot in which the proteins separate into two statistically significant distinct clusters (Fig. 5), mainly along the PC1 direction.

Fig. 5.

Scores plot from the PCA of the 1,414 protein sequence subset of Pfam04327. The larger sub-cluster is composed of 1,040 sequences and the blue cluster is composed of 374 sequences. About 41 % of the variance explained by the first two PCs including 30 % contribution of PC1

Analysis of the PCA loadings for this data enabled identification of those amino acid positions in the sequence family most responsible for sub-cluster separation (Fig. 6a). There were 44 out of 196 loading points that exceeded a cutoff of 30 % of the maximum loading Euler distance. Mapping these loadings onto a representative structure from Pfam04327 (PDB-ID: 3H9X) made it possible to visualize where these sequence positions lie on the structure (Fig. 6b, c).

Fig. 6.

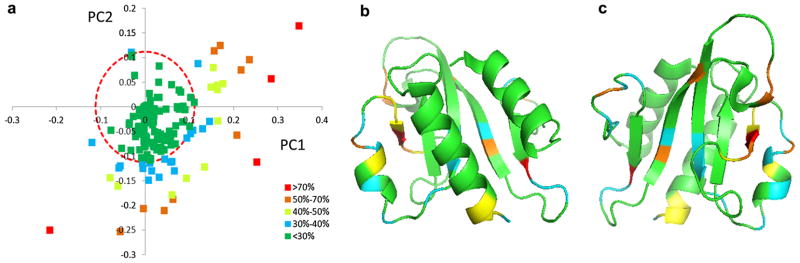
PCA loadings data mapped onto a representative structure from Pfam04327. The PCA loadings plot (PC1 vs PC2) is shown in a. The longest Euler distance from the centroid to a loadings point was determined and a distance equal to 30 % of the largest Euler distance was used as an upper limit cutoff. Loading points beyond a circle centered at the origin with a radius equal to the upper limit cutoff (red dashed-line circle) were considered important for driving cluster separation. Loading points were color-coded according to their distance relative to the longest Euler distance as indicated in the plot with red >orange > yellow > cyan > green. The ribbon diagrams of a representative structure from Pfam04327 (PDB-ID: 3H9X) are shown in two different orientations b and c (rotated by 180°) with important amino acid positions colored according to the same scheme used in the loading plot

Alternatively, we can define a cutoff just based on the PC1 weighting for identifying residue positions responsible for cluster separation, which may be more meaningful in cases where the cluster separation is mainly along PC1 which is observed in most cases. Accordingly, we chose 30 % of the maximum PC1 eigenvector weighting as the cutoff (Figure S2a). These loadings were then mapped onto the representative structure in Figures S2b and S2c. The 30 % cutoff is entirely arbitrary, and can be adjusted to produce any desired number of sequence positions for consideration. In the extreme case, one could ask what is the single amino acid position whose variance contributes most to cluster separation, which would be identified as the largest weighting in the PC1 eigenvector. Alternatively, one could select the top ten contributors, or the number of contributors that account for a certain extent of variance in the dataset.

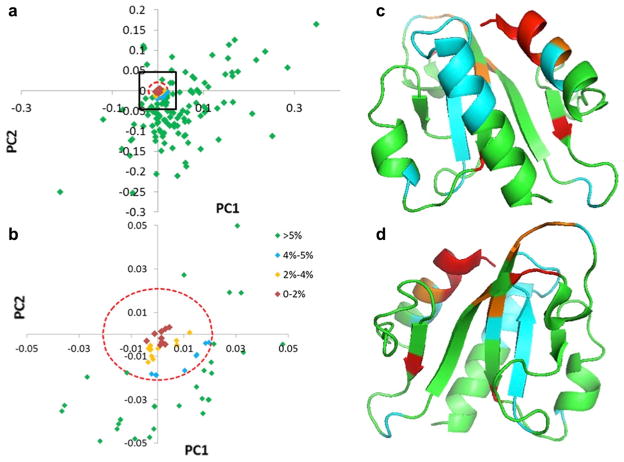
Having used the PCA to identify those amino acid positions most responsible for cluster separation, we then interrogated the loadings data to identify those amino acid positions that were most conserved across the family. To do this, we selected a maximum threshold cutoff of 5 % and all loadings below this threshold were considered the most conserved amino acid positions. This approach is illustrated in Fig. 7 where 62 out of 196 loadings were identified as the most conserved residues, and these residues were grouped into four color-coded categories (0–2 %-red, 2–4 %-orange, 4–5 %-cyan, >5 %-green). The conserved amino acid positions were mapped onto a representative structure and colored according to their Euler distances Fig. 7b, c. Euler distances shorter than 2 % of the maximum (colored red) indicated the most conserved positions across the family.

Fig. 7.

Analysis of the PCA loadings data for Pfam04327 to identify conserved residue positions. The PCA loadings plot (PC1 vs PC2) is shown in a and a zoomed-in view contained in the black box in a is shown in b. Euler distances to the centroid were calculated, and a distance equal to 5 % of the largest was used to filter the data (red broken-line circle). The ribbon rendering of a representative from Pfam04327 (PDB-ID: 3H9X) is shown in two different views in c and d (rotated by 180°) with the amino acid positions colored as indicated in the figure

Finally, repeating this analysis using a maximum threshold of 5 % just along the PC1 direction to identify the most conserved residues across the family (Figure S3a) identified 103 out of 196 loadings and these were assigned a color based on the following categories (0–2 %-red, 2–4 %-orange, 4–5 %-cyan, >5 %-green). The most conserved loadings were mapped onto the ribbon diagram of protein 3H9X in Figure S3b and S3c.

Conclusions

In this paper, we introduce a novel method for converting alphabetic designation of amino acids in aligned protein sequence families into numerical representation intended to be useful for PCA. Unlike existing conversion methods, this method does not assign each amino acid to a fixed number, or represent each amino acid type with a binary vector, but assigns a number that directly reflects the amino acid variance based on the occurrence frequencies for each aligned position. The method was tested on a small artificial dataset to provide insight into the performance of the conversion method, yielding expected results based on intuition and design of the artificial dataset. The method was then tested on a real protein sequence family, COG2263, which contained nine protein sequences and 240 aligned amino acid sequence positions. In this example, the PCA was shown to reproduce the positional sequence relationships for most members identified using a conventional dendogram analysis. We also illustrated how the Euler distance from the origin to the loading points, along with consideration of the direction of the Euler vector relative to the direction of separation of the clusters, could be used to identify sequence positions that experienced the strongest amino acid variation and these positions were mapped onto a representative protein structure to elucidate how the most variable amino acid positions varied in the context of the protein structure. Finally, we applied our method to a large protein sequence family containing more than 1,800 sequence, for which a subset of >1,400 members grouped into two distinct sub-clusters using the CLANs analysis. Clearly, in this example, the power of the PCA-based approach was highlighted, given its characteristics for projecting directions of greatest variance in extremely hyperdimensional spaces onto eigenspaces composed of a relatively small number of principal components, and by doing so, making it quite straight-forward to identify those residue positions that were most strongly responsible for sub-clustering in this large sequence family. We also demonstrated that we could use an upper limit threshold to identify those residues that were most conserved across a large dataset.

Overall, we have shown that PCA of protein sequence family using data converted into a numerical representation that is designed to be appropriate for PCA generates intuitively reasonable results and enables the power of the PCA approach to be applied to enable quantitative analysis of protein sequence family relationships. It is also important to note that our technique does not address the fundamental problem of protein sequence alignment. Rather, our technique provides a tool to quantitatively analyze variance in amino acid positions given a multiple sequence alignment. Besides its emphasis on identification of specific amino acid positions that experience maximum variance in aligned protein sequences, our PCA-based technique can potentially be used to explore amino acid covariance relationships in sequence families that might play an important roles in protein function, structure, and biophysical properties such as solubility and stability.