Examining the acquisition of phonological word-forms with computational experiments

Abstract

It has been hypothesized that known words in the lexicon strengthen newly formed representations of novel words, resulting in words with dense neighborhoods being learned more quickly than words with sparse neighborhoods. Tests of this hypothesis in a connectionist network showed that words with dense neighborhoods were learned better than words with sparse neighborhoods when the network was exposed to the words all at once (Experiment 1), or gradually over time, like human word-learners (Experiment 2). This pattern was also observed despite variation in the availability of processing resources in the networks (Experiment 3). A learning advantage for words with sparse neighborhoods was observed only when the network was initially exposed to words with sparse neighborhoods and exposed to dense neighborhoods later in training (Experiment 4). The benefits of computational experiments for increasing our understanding of language processes and for the treatment of language processing disorders are discussed.

INTRODUCTION

It is generally accepted that representations of phonological segments, lexical word-forms, and semantic information (among other types of representations) are involved in the production and recognition of spoken words (e.g., Dell, Schwartz, Martin, Saffran & Gagnon, 1997; Vitevitch & Luce, 2005). These representations also play a role in, and indeed must be formed in the acquisition of new words (Storkel & Morrisette, 2002). When one encounters a novel word, one must activate the existing representations of phonological segments until a new lexical representation can be created and associated with the appropriate meaning. Much research has examined the biases that influence how children learn the meanings of new words (e.g., Gershkoff-Stowe & Smith, 2004). The present investigation, however, focused on another part of the word-learning process, namely the formation of lexical representations, or phonological word-forms, and examined how existing lexical representations influence the acquisition of novel word-forms.

Infants (Hollich, Jusczyk & Luce, 2002), toddlers (Storkel, 2009), preschool children (Storkel, 2001; 2003) and college-age adults (Storkel, Armbruster, & Hogan, 2006; see also Stamer & Vitevitch, 2012) learn novel words that sound similar to many known words (i.e., the novel word has a dense neighborhood) more readily than novel words that sound similar to few known words (i.e., the novel word has a sparse neighborhood).¹ This influence of existing words on the acquisition of novel words has been found when the novel words are nouns (Storkel, 2001), verbs (Storkel, 2003), or homonyms (Storkel & Maekawa, 2005), and has also been found in naturalistic contexts, in addition to laboratory-based experiments (Storkel, 2004; 2009).

To account for the influence of existing lexical representations on the acquisition of a novel word-form, Storkel et al. (2006) suggested that the partial phonological overlap that exists between the novel word and the representations of known words in the lexicon strengthen the newly formed lexical representation of a novel word (see also Jusczyk, Luce, & Charles–Luce, 1994). A newly formed representation that resembles many known words in the lexicon will be strengthened to a greater extent then a newly formed representation that resembles few known words in the lexicon, hence the advantage for learning novel words with dense compared to sparse neighborhoods.

This account of how existing lexical knowledge affects the process of word-learning is appealing for several reasons including that it is intuitive and simple to understand. However, it lacks the necessary detail to make precise predictions about how the process of word learning might be affected by differences among word-learners or by differences in the word-learning environment. To better explore these questions, we developed a simple computer model (using connectionist principles) that captured the essence of the account proffered by Storkel et al. (2006).

Although a number of computational models of the process of “word-learning” in children have been previously developed, many have focused on the acquisition of conceptual information, or the acquisition of the association between conceptual information and the lexical word-form rather than focus solely on how lexical knowledge influences the acquisition of word-forms, as in the present case (e.g., Cottrell & Plunkett, 1994; Gasser & Smith, 1998; Howell, Jankowicz & Becker, 2005; Plunkett, Sinha, Moller, & Strandsby, 1992; Yu, 2005). Models that have investigated the acquisition of word-forms have not accounted for the influence of neighborhood density on word-learning (e.g., Plunkett & Marchman, 1996; Li, Zhao & MacWhinney, 2007; Regier, 2005; Sibley, Kello, Plaut & Elman, 2008). Rather then modify an existing model, we found it more advantageous to build our own computational model, allowing us to focus solely on the influence of neighborhood density on word-learning (N.B., we do not deny that syntactic, semantic, and other factors influence word-learning, we simply wished to focus on this one aspect of word-learning, specifically, how the number of existing, similar sounding word-forms influences the acquisition of novel word-forms).

In the present studies we used a multi-layered, auto-associative network with distributed representations, trained with the back-propagation learning algorithm to test how existing words in the lexicon influence the acquisition of novel words. A multi-layered network has several layers of processing units—input, hidden, and output units—whereas a single-layered network lacks hidden units. An associative network must learn that two patterns are related to each other. When the network is presented with one pattern, the network must compute the other associated pattern. In the case of an auto-associative network, the pattern that is computed is identical to the one that is initially presented to the model (e.g., produce X when given X). In contrast, a hetero-associative network must learn to associate two different patterns (e.g., produce Y when given X). Both types of associative networks are ideally suited for the efficient storage of patterns that must be produced at some later point in time (Rumelhart, McClelland, et al., 1986).

Although it might be tempting to view the auto-associative network as an analogue of various tasks commonly used in psycholinguistic experiments of word-learning—such as the nonword repetition task in which a child hears a novel word-form and must repeat it aloud as quickly and as accurately as possible (e.g., Gathercole, 2006)—it is important to note that we did not create a computer simulation of human performance in the nonword repetition (or any other) task. Rather, we are using a simple, computational model to examine how knowledge is structured in the mental lexicon, and how current knowledge might affect the acquisition of new word-forms. In order to assess the knowledge that the network has, we examined how well it learned to associate input and output patterns that were identical. Presenting the network with a pattern and examining the output that it produces is simply one way to evaluate the knowledge of the network; see the Results and Discussion section of the present studies for another method we used to evaluate the knowledge that the network acquired (i.e., generalization—accuracy in producing patterns that the network was not trained on).

One account for the acquisition of novel word-forms (Storkel et al., 2006; among others) suggests that the partial phonological overlap between a novel word and known words in the lexicon serves to strengthen the newly formed lexical representation of the novel word. However, in the case of spoken word recognition (e.g., Luce & Pisoni, 1998), phonological overlap results in increased confusability among word-forms, making it more difficult to quickly and accurately retrieve a known word-form from the lexicon. Similarly, Swingley and Aslin (2007) suggested that the partial phonological overlap among words leads to competition during word-learning. In Experiment 1 we examined whether similar sounding words would indeed facilitate (or interfere with) the acquisition of lexical word-forms.

In Experiment 2 we examined whether the network could extract relevant information from the patterns that it was presented with if the words containing those patterns were presented over time, much like a human language-learner is presented with the words it must acquire, instead of all at once as in Experiment 1. Finally, in Experiments 3 and 4 we made various manipulations—such as reducing cognitive resources, or exposing the model to learning environments that might retard typical development—that are difficult or unethical to implement in experiments with human language-learners to explore how word-learning might be affected by these conditions.

Although the computational model used in the present study is admittedly simple, such models can nevertheless provide us with several important insights, as discussed by Lewandowsky (1993; see also Norris, 2005) and others. Namely, the computational model made explicit the mechanisms of word learning that were previously described only in verbal form (Jusczyk, Luce, & Charles-Luce, 1994; Storkel et al., 2006). Making the hypothesized mechanisms of word learning explicit in a computational model prevents one from making predictions that are contradictory or logically incompatible—which might occur unintentionally when making predictions from a model that exists only in verbal form. Furthermore, the model that we developed in the present study enabled us to explore the influence of variables and conditions that—for ethical and practical reasons—would be impossible to examine in real word-learners.

EXPERIMENT 1

A connectionist network of the type employed in the present study (multi-layered, auto-associative network with distributed representations) appears ideally suited for capturing the essence of the verbal theory of word-learning proposed by Storkel et al. (2006; see also Jusczyk, Luce, & Charles-Luce, 1994). Recall that Storkel et al. (2006) suggested the partial phonological overlap between a novel word and known words in the lexicon serves to strengthen the newly formed lexical representation of the novel word. That is, the novel word and the known words share certain sub-patterns, or regularities. The newly formed representation of a novel word with a sub-pattern or regularity that is more prevalent in the lexicon (i.e., the phonological sub-pattern is found in many words) will be strengthened to a greater extent then a newly formed representation of a novel word with a sub-pattern that is less prevalent in the lexicon, accounting for the advantage in learning novel words with dense neighborhoods observed in a number of word-learning studies.

The effect of shared sub-patterns or regularities on learning has also been examined in previous research with connectionist networks used to model various cognitive processes. The influence of these regularities and sub-patterns on learning has been referred to as a conspiracy effect, and comes about in connectionist models in the following way (Rumelhart, McClelland et al., 1986; pg. 81):

When a new item is stored, the modifications in the connection strengths must not wipe out existing items. This can be achieved by modifying a very large number of weights very slightly. If the modifications are all in the direction that helps the pattern that is being stored, there will be a conspiracy effect: The total help for the intended pattern will be the sum of all the small separate modifications…

In a connectionist model of the lexicon, a novel word-form that is similar to—by the virtue of sharing sub-patterns with—many existing words in the lexicon will produce many small changes in the connection weights. Adding up many small changes in the connection weights will facilitate the storage of that novel item. In this way, the representation of a novel word may be “strengthened” by the representations of known words that sound similar to it. In contrast, a novel word-form that is similar to few existing words in the lexicon will produce fewer small changes in the connection weights. Adding up fewer small changes in the connection weights results in less benefit for the storage of that novel item.

Although it seems straightforward that known patterns will facilitate the acquisition of similar novel patterns in both humans (learning words) and connectionist networks, other studies of connectionist networks have found that similarity among items may lead to interference or confusability among the similar items, and be detrimental to learning (Rumelhart, McClelland et al., 1986). A similar detriment to learning (perhaps) resulting from similarity between known and novel items has also been observed in studies of word-learning in humans (e.g., in typically developing children, Swingley & Aslin, 2007; in children with speech sound delays, Storkel, 2004). We, therefore, thought it prudent to verify that a multi-layered, auto-associative network with distributed representations would indeed capture the essence of the verbal theory of word-learning proposed by Storkel et al. (2006; see also Jusczyk, Luce, & Charles-Luce, 1994). If this type of connectionist network does indeed show a “conspiracy effect,” then such a model will be suitable for further exploring questions related to the influence of neighborhood density on word-learning.

METHODS

Network architecture

A multi-layer network consisting of 18 input units, 6 hidden units, and 18 output units was created with tLearn (Plunkett & Elman, 1997). Each of the input units was connected to each of the hidden units. Similarly, each of the hidden units was connected to each of the output units. All connections were feed-forward only; there were no feedback connections. That is, the input units fed information to the hidden units, and the hidden unit fed information to the output units; information did not flow “backwards” from the output units to the hidden units, nor from the hidden units to the input units.

Five “seeds” were used to initialize the random settings on the connection weights. The same five seeds were used to test both sets of stimuli (described below). One can think of each network “seed” as an individual participant in a conventional in vivo experiment, thereby allowing us to more broadly generalize the results of our experiments. Initial bias offset, used to introduce non-linearity into the network, was set to zero. The initial weights were randomly distributed in the range ± .5. The learning rate, which determines how fast the weights are changed, was set to .1000. Momentum, which determines the proportion of the weight changes from the previous learning trial that will be used on the current learning trail, was set to .0003 (Plunkett & Elman, 1997). These values were the same for, and held constant throughout all of the Experiments that are reported.

The input activation function to the nodes is given in Equation 1:

$${\mathit{net}}_i={\sum }_j{w}_{ij}{a}_j$$ (Eq. 1)

where the net input to node i is the sum of the activation a_j of the nodes that send to node i, and wij refers to the weights on the connections from nodes j to node i. The output activation function of each node is given in Equation 2:

$$a_i=\frac{1}{1+e^{-{\mathit{net}}_i}}$$ (Eq. 2)

where a_i refers to the output of node_i, net_i is the net activation flowing into the node, and e is the exponential.

The 18 input units received 18-bit vectors containing 1’s and 0’s as input. The first 6 bits in the vector represented the initial segment of a word, bits 7–12 in the vector represented the medial segment of a word, and bits 13–18 in the vector represented the final segment of a word. Because the same 18 input units were used to represent each word that the network had to learn, distributed representations were used in this network to represent phonetic-like “micro-features,” described in more detail below (Rumelhart, McClelland et al., 1986). Distributed representations contrast with localist representations in which a single processing unit responds to a concept or entity. If localist representations were used to represent words in the present network, the model would be limited to acquiring only 18 words.

Stimuli

The network was presented with short “words” comprised of 3 phonological segments in a consonant-vowel-consonant syllable structure. (We use the term “word” with some liberty. All of these sequences were equally novel to the networks even though some of the sequences we created correspond to real words in English. The frequency with which the words were presented to the network was the same for each word. That is, “word frequency” was controlled.) Words were created using 10 consonants that were acquired relatively early in English (/p/, /b/, /k/, /g/, /t/, /d/, /f/, /v/, /m/, /n/), and 10 vowels, primarily monophthongs and nonphonemic dipthongs (/i/, /ɪ/, /e/, /ε/, /æ/, /u/, /ʊ/, /o/, /ɔ/, /ɑ/).

Six bits were used to code phonetic-like features for each segment in the words. The first bit coded the consonantal nature of the segment (1 = consonant, 0 = vowel). The second bit coded voicing (1 = voiced, 0 = voiceless). The third and fourth bits coded information that roughly corresponded to manner of articulation with the third bit coding for sonority in the consonants and for tenseness in the vowels, and the fourth bit coding for continuance in the consonants and for roundedness in the vowels. The fifth and sixth bits coded information that roughly corresponded to place of articulation with the fifth bit coding an anterior place of articulation, and the sixth bit coding for coronal articulation in consonants, or middle tongue height in vowels. Thus the word /vot/ would be presented to the network as 110110011101100011. Because of the limited number of features used to represent the phonemes, no central vowels were used.

The use of phonetic-like “micro-features” (Rumelhart, McClelland et al., 1986) contrasts with the approach that has been used in some simulations looking at other aspects of language in which a whole word is represented with random bit vectors (e.g., Ellis & Lambon Ralph, 2000). Our decision to use micro-features should not be construed as a commitment to a particular linguistic, phonological, phonetic, or other type of theory. Rather, we simply wished to mimic (in an admittedly simplified way) the manner in which larger elements (i.e., words) are formed by combining smaller elements (i.e., phonemes) in real, human language (see Brousse & Smolensky (1989) for a discussion of this type of combinatorial representational scheme). Furthermore, we used vectors to represent phonetic-like features rather than an arbitrary vector to represent the phonemes to give the network input that resembled, at least in a rudimentary way, the input a human word-learner receives.

Trained Items

Using this set of phonetic-like features, we created 60 CVC sequences (listed in the appendix) to train and assess the performance of the connectionist network. Eighteen of those items were designated “target” items, with the remaining 42 being “neighbors” of the targets. Of the 18 targets, 3 were designated to have a dense neighborhood, and 15 were designated to have a sparse neighborhood. Each dense target had 9 neighbors, with three neighbors being formed by a substitution in each of the three phoneme positions. Each of the sparse targets had a single neighbor, with 5 sparse targets having a neighbor being formed by a substitution in the initial phoneme position, 5 sparse targets having a neighbor being formed by a substitution in the medial phoneme position, and 5 sparse targets having a neighbor being formed by a substitution in the final phoneme position.

Appendix.

List A	Targets	Neighbors			Generalization Items
		Conset	Vowel	Cfinal	Conset	Vowel	Cfinal
Dense	vot	bot	væt	vop	not	vut	vov
		dot	vʊt	vog
		got	vct	vof
	kɪp	bɪp	kip	kɪm	dɪp	kep	kɪd
		fɪp	kɑp	kɪv
		nɪp	kEp	kIb
	mek	vek	muk	met	pek	mɑk	mef
		tek	mok	meb
		dek	mæk	men
Sparse	vim	dim			pim
	dεn	vεn			fεn
	kon	ton			pon
	nɑb	vɑb				nib
	biv	miv					bif
	fed		fod			fɑd
	mʊg		mɪg			mɔg
	tɔp		tæp			tʊp
	gɔk		gʊk		kɔk
	pɪt		pεt				pɪf
	næv			næm			næf
	tum			tuv			tug
	pʊb			pʊd			pʊv
	guf			gud	kuf
	bæg			bæd		beg

List B	Targets	Neighbors			Generalization Items
		Conset	Vowel	Cfinal	Conset	Vowel	Cfinal
Dense	vim	pim	vɑm	vip	gim	vem	vid
		fim	vem	vig
		kim	vIm	vib
	pɪt	bɪt	pεt	pɪk	tɪt	pɑt	pɪv
		gɪt	put	pɪf
		dɪt	pct	pɪn
	næv	mæv	nʊv	næd	tæv	nεv	næt
		fæv	nov	næk
		dæv	nev	næm
Sparse	mʊg	dʊg			kUg
	fed	ped			ted
	guf	nuf			kuf
	vot	fot				vʊt
	gck	vɔk					gɔg
	tum		tom			tʊm
	dεn		din			dɑn
	bæg		bεg			beg
	pʊb		pæb		fʊb
	kɪp		kεp				kɪb
	mek			meb			mep
	tcp			tɔn			tɔf
	biv			bif			bik
	kon			kod	mon
	nɑb			nap		nɔb

The construction of phonological neighbors using only the substitution of phonemes enabled us to use words of all the same length, which greatly simplified the architecture of the network. This decision should not be construed as a commitment to any theoretical or operational definition of neighbors, phonological similarity, etc. Further note that “neighbors” have also been defined in psycholinguistic experiments using only substitutions of phonemes as well as the substitution, addition, and deletion of phonemes (see Vitevitch, 2002; Davis, Perea & Acha, 2009).

No word was a neighbor of more than one target. In total there were 30 items distributed across 3 neighborhoods that were designated as being part of a dense neighborhood, and 30 items distributed across 15 neighborhoods designated as being part of a sparse neighborhood.²

Generalization Items

Using the same phonetic-like features, an additional 24 CVC sequences were created. Importantly, the network was not trained on any of these items. Rather, these untrained items were used to test how well the model generalized the knowledge it may have acquired from the items in the training set. If the network shows comparable performance on the “generalization items” as it does on the items it was trained on, this would suggest that the network extracted important information about the regularities found in the input, and could use that information to process the novel items. However, if the network fails to perform on the “generalization items” as it did on the trained items, this would suggest that the network learned only about the peculiarities of the trained items rather than more general information about the words it was trained on.

The 24 generalization items consisted of the following items: for each dense target, 3 new neighbors were created (one formed by a substitution in each phoneme position), and for each sparse target 1 new neighbor was created. For the sparse targets, 5 targets had generalization items formed by a substitution to the phoneme in the initial position, 5 targets had generalization items formed by a substitution to the phoneme in the medial position, and 5 had generalization items formed by a substitution to the phoneme in the final position. In each case, 3 of the 5 generalization items for the sparse targets were formed by a substitution in the same position as the trained neighbor, and one of the 5 generalization items was formed by a substitution in each of the other positions than the trained neighbor.

To ensure that the results we obtained from the experiments were not due to unique characteristics of the targets, neighbors, or generalization items, we rearranged the targets such that some of the items that had previously been designated “sparse” targets were now “dense” targets, and vice versa. Compare, for example, the word /vot/ and its neighbors in List A and in List B. In List A, /vot/ was designated as a target word with a dense neighborhood, whereas in List B, the same word was designated as a target word with a sparse neighborhood. A new set of neighbors and generalization items were created following the same guidelines described above. One can think of the use of two “vocabularies” in the present experiment as being analogous to the counterbalancing of stimuli in a conventional in vivo experiment, thereby allowing us to more broadly generalize the results of our experiments. Each network “seed” was trained and tested on both vocabularies.

Procedure

The connectionist network was trained with all of the 18 targets, and all of the 42 neighbors for 1000 epochs using 5 different initial randomizations of connection weights. That is, all of the words were presented to the network for training regardless of whether they were targets or neighbors, and whether they were dense or sparse (with the exception of the generalization items, which the network was never trained on). The words were presented randomly without replacement. The same randomized start-states were used to train the network on the other set of 18 targets, and 42 neighbors for 1000 epochs; again presentation and training of the words occurred all at once. Training (i.e., adjustment of the connection weights) was accomplished using the back-propagation learning algorithm (Elman et al., 1996). Weights were updated after the presentation of each pattern. Because our targets were 1s and 0s, cross-entropy error was used during training (to allow errors to continue to modify the connection weights even though the nodes may have saturated), but root-mean-square error (RMSE) was analyzed in what follows.

RESULTS AND DISCUSSION

The data in the following computational experiments were analyzed in a manner analogous to the group studies employing human participants (cf., Spieler & Balota, 1997). That is, overall performance for each network (i.e., participant) was assessed by computing the mean root-mean-square error (RMSE; or simply referred to as error in the text that follows) between the vector representing the output produced by the network and the desired output vector (i.e., a vector identical to the input vector) for the dense and sparse items of interest. Smaller error values indicate that the output of the model was closer to the desired output, suggesting better learning by the network. By contrast, larger error values indicate that the output of the model was further from the desired output, suggesting poorer learning by the network.

Analysis of variance (ANOVA) was used to compare the performance of the networks on the two groups of words. This method of analysis allowed us to determine if the (group of) networks produced a pattern of word-learning that was qualitatively similar to the pattern of word-learning observed in (groups of) human participants: dense words are strengthened more than and therefore learned more readily than sparse words.

Trained Items

For the targets, the dense targets had less error (mean = .632, sd = .121) than the sparse targets (mean = 1.073, sd = .075), suggesting that the network more readily learned the dense targets than the sparse targets, F (1, 9) = 56.23, p < .0001. Similarly, for the neighbors, the words in the dense neighborhood had less error (mean = .945, sd = .038) than the words in the sparse neighborhood (mean = 1.013, sd = .052), suggesting that the network more readily learned the dense neighbors than the sparse neighbors, F (1, 9) = 17.07, p < .01.

Notice that the size of the effect for the targets is larger than the size of the effect for the neighbors, even though all of the targets and neighbors were trained at the same time. To better understand this difference it might be helpful to refer to the stimuli listed in the appendix. First consider the sparse items. Each sparse target had only 1 word that was phonologically similar to it, namely the neighbor. Each neighbor in the sparse category also had only 1 word that was phonologically similar to it, namely the target word. Therefore, each sparse word (whether it was a target or a neighbor) was strengthened by the sub-patterns that occurred in only one other word.

Now consider, for example, the dense target word /vot/, which has 9 words that are phonologically similar to it: /bot, dot, got, væt, vʊt, vct, vop, vog, vof/. The representation of the target word /vot/ was strengthened by the sub-patterns (e.g., _ot, v_t, vo_) that occur in those 9 neighbors. Now consider one of the neighbors of the target word /vot/, like /bot/. The word /bot/ has only 3 words that are phonologically similar to it: the target word /vot/, and the neighbors of the target word, /dot/ and /got/, which are also neighbors of the target /vot/. The difference in the number of words that are phonologically similar to each target and to each neighbor in the dense category—and therefore the number of sub-patterns that serve to strengthen each target and each neighbor—may account for the difference in the size of the effect for the targets and the neighbors.

Generalization Items

To further test how known word forms influence the acquisition of novel words we examined how the networks would respond to word-forms that they had not been trained on (i.e., the “generalization items”). If the networks simply learned the peculiarities of the items they were trained on, then the networks should perform quite poorly on the generalization items, and should not show a processing advantage for untrained words that are part of a dense neighborhood. Alternatively, if the networks extracted relevant sub-patterns from the input, and were able to exploit that information, then the networks should show an advantage in processing the novel words that are part of a dense neighborhood by producing smaller RMSE values for those generalization items. The results show that novel items that belonged to the dense neighborhoods had less error (mean = 1.13, sd = .032) than the novel items that belonged to the sparse neighborhoods (mean = 1.23, sd = .062), F (1, 9) = 19.41, p < .01, suggesting that the networks did indeed extract relevant sub-patterns from the input, and were able to exploit those sub-patterns to “strengthen” the representations of the novel words in the generalization set.

The results of the present experiment show that a “conspiracy” among sub-patterns found in many words serves to strengthen the representations of the words that contain those sub-patterns. Evidence of such “strengthening” was observed in the words that the network was initially trained on—compare the size of the effect for the targets and for the neighbors—and was also observed in a set of novel words that contained those sub-patterns (i.e., the generalization items).

The results of the present experiment also suggest that the sub-patterns that are extracted from the words are larger than individual segments. As discussed in Footnote 2, the frequency with which the phonological segments occurred in the words varied in such a way that there tended to be more occurrences in the sparse words than in the dense words. This disparity might lead one to predict that the “additional practice” received by the segments in words with sparse neighborhoods should give sparse words a benefit in acquisition. The results of the present experiment, however, showed the opposite result: words with dense neighborhoods were learned better than words with sparse neighborhoods. This does not mean that the frequency with which segments occur in words (i.e., phonotactic probability) does not affect processing, or more specifically word-learning; indeed work by Storkel and Lee (2011) suggests that it does. Rather we believe that the influence of phonotactic probability may be due to another level of representation (i.e., something smaller than words, like biphones or phones, which are representations that were not included in the present model), or a different process related to word-learning (i.e., a process that signals the cognitive system that the input is not known and should be learned as described in Storkel (2011); the word-learning problems exhibited by children with functional phonological delays as reported in Storkel (2004) is also consistent with the hypothesis that lexical and sub-lexical representations are involved in word-learning).

The conspiracy effect observed in our connectionist network provides us with a computational model that is more detailed than the verbal theory of word learning proposed by Storkel et al. (2006), which suggested that known words with dense neighborhoods strengthened representations of novel words to a greater degree than known words with sparse neighborhoods. Although this model does not account for all aspects of word-learning, the model does capture an important part of word-learning, and enables us to explore other questions about word-learning that could not readily be examined with human participants.

Before exploring those questions with our model, it is necessary to address an important matter related to the manner in which training occurred in the present experiment. Recall that the network was trained on all of the targets and neighbors at once. The presentation of all of the items at once may have enabled the network to extract the relevant sub-patterns from the input, and use them to strengthen the representations of the word-forms. Rarely (if ever!) is one exposed to all of the words of a language at once. Rather, exposure to the words of a language occurs over time. The manner in which children are naturally exposed to the words in one’s language raises the important question of whether our connectionist network would be able to successfully extract relevant sub-patterns from the input, and use them to strengthen the representations of word-forms if that input were distributed over time. That is, the sub-patterns in the input are not present at the outset of training, simply waiting to be extracted; rather the relevant sub-patterns appear in the input over time. To examine this important question, we conducted the following experiment, in which the network was incrementally trained on the word-forms.

EXPERIMENT 2

Although our connectionist network captures certain important aspects of the process of acquiring phonological word-forms—namely, phonological similarity serves to strengthen lexical representations during acquisition—this effect may simply be an epiphenomenon of the manner in which the network was trained: all of the targets and neighbors were presented to the network at once. To verify that our connectionist network can extract relevant sub-patterns from input that is distributed through time, the present experiment trained the network incrementally on the targets and neighbors. For example, the network was first trained for 100 epochs on 3 words that would come to have a dense neighborhood, and 3 words that would come to have a sparse neighborhood. In the next 100 epochs of training, the network continued to be trained on the initial set of items, but now received 3 more words with a dense neighborhood (i.e., 1 neighbor of each dense target) and 3 more words with sparse neighborhoods (i.e., new sparse targets). The network continued to receive an increasing number of words in the training set in this way, until the network had received all of the dense and sparse items (which occurred after 1000 epochs of training, facilitating comparison to Experiment 1).

This method of exposing the network to the words in the training set more closely approximated in several ways the manner in which word-learners are exposed to the words that they acquire. First, as noted above, word-learners are not exposed to all of the words in their vocabulary all at once. Rather, a word-learner acquires the words that comprise his vocabulary gradually over time. In addition, words in the language with dense neighborhoods gradually come to have dense neighborhoods in the vocabulary of a language-learner, with the asymmetry between dense and sparse neighborhoods increasing with development (Charles-Luce & Luce, 1990; 1995). Will the same learning benefits observed for words with dense neighborhoods in Experiment 1 be observed in the present experiment when the vocabulary is acquired in a manner more akin to how a child acquires his vocabulary?

With this more naturalistic way of exposing the network to words in the language, we were also able to examine two different aspects of word learning, namely, lexical configuration and lexical engagement. Leach and Samuel (2007) defined lexical configuration as the factual knowledge associated with a word, such as its phonological form, meaning, etc. This type of information is incremental in nature, with more knowledge of this type being added to the representation with each exposure. If our network does indeed acquire information regarding the lexical configuration of the first set of words it was trained on from the very beginning (i.e., the 3 “dense” and the 3 “sparse” targets), then the error rate for this initial set of words should decrease with each exposure.

In contrast, Leach and Samuel (2007) define lexical engagement as the way in which a lexical entry interacts with other lexical (and sub-lexical) representations (e.g., lexical word forms compete during word recognition; Luce & Pisoni, 1998). If the items that our network is trained on truly become integrated into the lexicon, then relevant sub-patterns should emerge from the lexicon, despite the network being exposed to the input gradually over time (rather than all at once as in Experiment 1), and be increasingly exploited by the network when presented with novel items. The generalization items provide us with a unique way to evaluate the lexical engagement of the trained items. If newly trained words become integrated into the lexicon, then the network should better “see” the important sub-patterns that are gradually emerging, and can better exploit that information to process the novel generalization items, resulting in the error rate for the generalization items (which the network is never trained with) decreasing over time. However, if information about the newly trained words is not integrated into the lexicon, then important sub-patterns will not be detected or exploited in the processing of the generalization items, resulting in the error rate for the generalization items remaining unchanged over time. To evaluate the ability of the network to extract relevant sub-patterns from incrementally presented input, and to assess lexical configuration and lexical engagement, the present experiment was performed.

METHODS

Network architecture

The same network architecture, software package, and parameter settings used in Experiment 1 were used in the present experiment. However, different “seeds” were used to provide randomized initial connection weights to the networks.

Stimuli

The same targets, neighbors, and generalization items used in Experiment 1 were used in the present experiment. As in the previous experiment, some of the targets were re-assigned to different neighborhood density conditions to better generalize our results.

Procedure

The network was trained for 100 epochs on 3 dense and 3 sparse words. For training epochs 101–200, the network continued to be trained on the initial set of items, but now received 3 more words with a dense neighborhood (i.e., 1 neighbor of each dense target) and 3 more words with sparse neighborhoods (i.e., new sparse targets). For training epochs 201–300, the network continued to be trained on the previous 12 items, but now received 3 more words with a dense neighborhood (i.e., 1 neighbor of each dense target) and 3 more words with a sparse neighborhood (i.e., neighbors of the sparse items from the initial training set). Training continued in this way with the dense words continuing to receive a new neighbor, and the sparse words alternating between learning a new sparse target and the neighbor of a previously learned sparse target.

RESULTS AND DISCUSSION

To demonstrate that the finding obtained in Experiment 1—novel words with dense neighborhoods are acquired more readily than novel words with sparse neighborhoods—was not due to the particular way in which the network was trained on the words in the vocabulary, we trained the network in the present experiment on a vocabulary that gradually increased in size. As in Experiment 1, network performance was assessed with the mean root mean square error. Smaller error values indicate that the output of the model was closer to the desired output, suggesting better learning by the network, whereas, larger error values indicate that the output of the model was further from the desired output, suggesting poorer learning by the network. ANOVA was again used to compare the performance of the networks on the two groups of words varying in neighborhood density.

Trained Items

For the targets, the dense targets had less error (mean = .548, sd = .064) than the sparse targets (mean = 1.047, sd = .054) after 1000 epochs of incremental training, suggesting that the network more readily learned the dense targets than the sparse targets, F (1, 9) = 233.346, p < .0001. Similarly, for the neighbors, the words in the dense neighborhood had less error (mean = .939, sd = .044) than the words in the sparse neighborhood (mean = 1.012, sd = .056) after 1000 epochs of incremental training, suggesting that the network more readily learned the dense neighbors than the sparse neighbors, F (1, 9) = 11.45, p < .01. Despite being exposed to the input in an incremental fashion, the network was still able to extract relevant sub-patterns from the input and exploit those regularities to learn the dense items better than the sparse items.

Generalization Items

As in Experiment 1, we examined the performance of the networks on a set of novel words that they had not been trained on (i.e., the “generalization items”). If the networks simply learned the peculiarities of the items they were trained on in this incremental training regime, then the networks should perform quite poorly on the generalization items, and should not show a processing advantage for untrained words that are part of a dense neighborhood. Alternatively, if the networks extracted relevant sub-patterns from the input they received over time, and were able to exploit that gradually unfolding information, then the networks should show an advantage in processing the novel words that are part of a dense neighborhood by producing smaller RMS values for those generalization items.

The results showed that novel items that belonged to the dense neighborhoods had less error (mean = 1.08, sd = .061) than the novel items that belonged to the sparse neighborhoods (mean = 1.16, sd = .068), F (1, 9) = 5.89, p < .05, after 1000 epochs of incremental training, suggesting that the networks did indeed extract relevant sub-patterns from the input, and were able to exploit those gradually unfolding sub-patterns to “strengthen” the representations of the novel words in the generalization set. The present results suggest that the ability of the network to exhibit a conspiracy among relevant sub-patterns that strengthen similar lexical representations is not due solely to the network being trained on all of the targets and neighbors at the same time; relevant sub-patterns can indeed be extracted from input that is distributed through time.

Lexical Configuration and Lexical Engagement

To assess the ability of the network to acquire information related to lexical configuration and lexical engagement additional analyses were performed on the data from the present experiment. If our network continued to acquire information regarding the lexical configuration of the first set of words it was trained on (i.e., “factual” information about those word-forms), then the error rate for this initial set of words should decrease with additional exposures. Network performance on the 6 items that the network was initially trained on (3 that would come to have a dense neighborhood and 3 that would come to have a sparse neighborhood) was evaluated after every 100 epochs (for a total of 1000 epochs). In assessing network performance, the amount of error for each pattern was calculated using the root mean square. A 2 (Density) X 10 (Epochs) ANOVA was used to assess the amount of RMSE in these items over time. Larger error values indicate that the model did not learn those patterns very well, whereas smaller error values indicate that the model learned those patterns more readily.

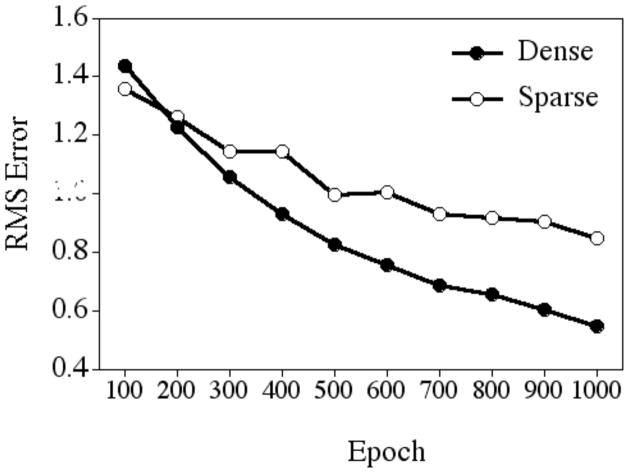
The mean RMSE for the targets at every 100 epochs is shown in Figure 1. Consistent with the prediction that the network would continue to acquire information regarding the lexical configuration of the first set of words it was trained on (i.e., “factual” information about those word-forms), the error rate for this initial set of words decreased with additional exposures. That is, RMSE was significantly less after 1000 epochs of training (mean = .697, sd = .181) than the RMSE after only 100 epochs of training (mean = 1.397, sd = .083), F (9, 81) = 382.674, p < .0001. As in the previous analyses, an influence of neighborhood density was also observed. The initially trained items that would come to have dense neighborhoods had overall less error (mean = .873, sd = .291) than the initially trained items that would come to have sparse neighborhoods (mean = 1.040, sd = .194), further suggesting that the network more readily learned the dense items than the sparse items, F (1, 9) = 10.116, p < .05.

Figure 1.

Root-mean-square error over 1000 epochs of incremental training for the 6 items the network was initially trained on (3 dense and 3 sparse).

Perhaps more interesting, there was a significant interaction between density and training, F (9, 81) = 16.150, p < .0001, such that the dense targets improved more with training (a decrease in RMSE of .890 from 100 to 1000 epochs) than the sparse targets (a decrease in RMSE of .511 from 100 to 1000 epochs). Notice that at 100 epochs the difference in performance between the dense (mean = 1.438, sd = .052) and sparse target words (mean = 1.357, sd = .091) is not statistically significant, F (1, 9) = 4.710, p > .05. This is not surprising, as none of the target words had any neighbors at this point in training, meaning there was no difference in neighborhood density yet. This condition provides us with an important “baseline” from which to track the influence of adding neighbors to the training set. As training progressed, one neighbor was added to the neighborhood of the sparse targets, whereas nine neighbors eventually populated the neighborhood of the dense targets. As the asymmetry in the number of neighbors in the dense and sparse neighborhoods increased over time, the processing benefit for the target word in the dense neighborhoods also increased. This provides additional support for the hypothesis that similar sounding words act to strengthen lexical representations, with more neighbors conferring greater benefit. This finding also highlights how the processing benefits of a dense neighborhood can accrue over time.

To examine lexical engagement in our network, we examined performance on the generalization items as the network was being incrementally trained. If newly trained words are integrated into the lexicon, then the network should continually extract the gradually emerging but relevant sub-patterns to better process the novel generalization items. This should result in the error rate for the generalization items (which the network was never trained with) decreasing over time. However, if information about the newly trained words is not integrated into the lexicon, then important sub-patterns will not be detected or exploited in the processing of the generalization items, resulting in the error rate for the generalization items remaining unchanged over time.

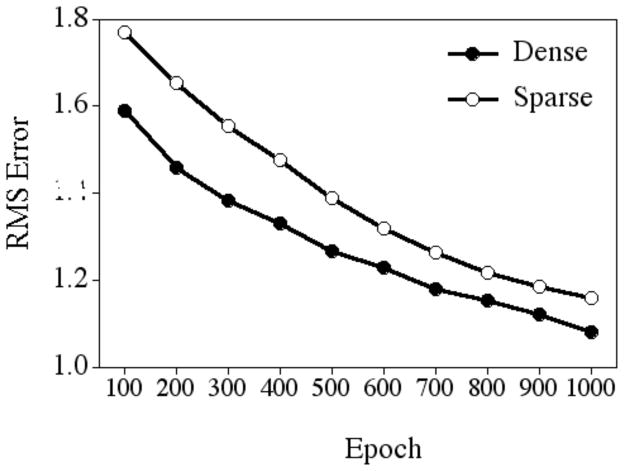
The mean RMSE for the generalization items at every 100 epochs is shown in Figure 2. As the network was trained on an increasing number of targets and neighbors, network performance on the (untrained) generalization items improved over time. That is, RMSE was significantly less after being trained on all of the targets and neighbors at 1000 epochs of training (mean = 1.120, sd = .075) than the RMSE after only being trained on 3 dense targets and 3 sparse targets at 100 epochs of training (mean = 1.338, sd = .196), F (9, 81) = 504.805, p < .0001. These results suggest that lexical engagement was indeed occurring. That is, information about the new items the network was trained on was indeed being integrated into the lexicon, enabling the network to extract relevant sub-patterns and exploit those sub-patterns to continually improve upon its processing of the (untrained) generalization items. If the network was only learning more “factual” information about each trained word to simply improve the representation of those items (i.e., lexical configuration) rather than dynamically integrating those newly acquired word-forms into the lexicon, then performance on the generalization items would have remained the same regardless of how many or what kind of words were acquired.

Figure 2.

Root mean square error for the generalization items over 1000 epochs of incremental training.

Furthermore, the novel generalization items that were part of the dense neighborhoods had less error (mean = 1.279, sd = .166) than the novel generalization items in the sparse neighborhoods (mean = 1.398, sd = .206), F (1, 9) = 18.274, p < .01. This result provides additional evidence in support of a lexical conspiracy: words that resemble many known words in the lexicon are “strengthened” to a greater extent than words that resemble few known words in the lexicon.

Finally, there was an interaction between density and epochs for the generalization items, F (9, 81) = 15.487, p < .0001, such that RMSE decreased less over time for the novel generalization items that were part of a dense neighborhood (a decrease in RMSE of .509 from 100 to 1000 epochs) than the novel generalization items that were part of a sparse neighborhood (a decrease in RMSE of .609 from 100 to 1000 epochs). Although it might seem counterintuitive that a smaller decrease in error is indicative of better performance, consider the following explanation to see how this result is still consistent with the hypothesis that a novel word is strengthened to a greater degree by being similar to many rather than few known words.

In a connectionist model with distributed representations, the same processing units are used to produce various patterns of activation to represent each of the words in the lexicon. In the case of a dense neighborhood, the connection weights on those processing units assume values that lie somewhere in the middle of all of the values of the connection weights associated with the words in the neighborhood, thereby minimizing overall error in the representation of any of those words. As more words continue to be added to a dense neighborhood, smaller and smaller changes are required to maintain optimal values for the connection weights. When the network is tested on a novel word from a dense neighborhood, the novel word is never very far from the other words in the neighborhood and therefore never very far from the optimized values of the connection weights. As the connection weights are “tuned” more and more finely to better represent the words in the dense neighborhood, the amount of error produced by the network in processing the novel word (i.e., the generalization item) will also continue to decrease.

However, in the case of a sparse neighborhood, the connection weights have been configured to represent the known target word with as little error as possible. The subsequent addition of a word to such a neighborhood may require a large change in some of the connection weights in order to maintain the representation of the known word (i.e., the target), and to represent the newly added neighbor. When the network is tested on a novel word from a sparse neighborhood, the novel word may be very far from the other words in the neighborhood, and will therefore be very far from the optimized values of the connection weights, resulting in a large amount of error in processing the generalization item. As the connection weights are not tuned as often as they are when new words are added to a dense neighborhood, the network will continue to produce a relatively large amount of error in processing the generalization item with a sparse neighborhood.

Overall, the results of Experiment 2 resemble those of Experiment 1 in that similar lexical representations conspire to facilitate the processing of novel representations. Specifically, processing of novel items that are similar to many known words will benefit to a greater degree than novel items that are similar to few known words. The important contribution of Experiment 2 is that this facilitative effect among lexical representations was shown to emerge even when the lexicon grew over time. Recall that in Experiment 1, the network was trained on the entire vocabulary all at once, not in an incremental fashion as in the present experiment. The facilitative effect among lexical representations can, therefore, emerge as the relevant sub-patterns in the input unfold over time. Given that the network can still extract relevant sub-patterns with incremental exposure to the input—a manner of exposure that is more similar to the way humans are exposed to the words in the ambient language—we now have a simple, computational model of word-learning that can be used to explore the questions we initially posed: how is the process of word learning affected by differences (in cognitive resources) among word-learners and by differences in the word-learning environment.

EXPERIMENT 3

The results obtained from Experiments 1 and 2 suggest that (at least one aspect of) learning novel word-forms may rely on a general processing principle that is captured by our simple connectionist model: known words that are similar to each other conspire to strengthen the representations or facilitate processing of phonologically similar novel words. With this simple model, we can now explore a number of questions about word-learning that we might not be able to examine easily with human word-learners. For example, a number of researchers have suggested that various cognitive resources—short-term memory (Gathercole & Baddeley, 1989) or attention (Dixon & Salley, 2006)—influence the process of word learning, such that learning becomes more difficult (i.e., more errors are made) when fewer processing resources are allocated to the word-learning process. More specifically, how might differences in cognitive resources influence the processing advantage for words from dense neighborhoods in word learning (observed in numerous studies and in Experiments 1 and 2)? One might predict that a reduction in cognitive resources will affect the learning of dense and sparse words equivalently, resulting in an overall decrement in word-learning performance. A larger reduction in cognitive resources would result in a larger performance decrement in word-learning.

Alternatively, one might predict that a reduction in cognitive resources will result in the development of an alternative (and overall less efficient) processing strategy to learn new words. In the context of learning novel words from dense and sparse neighborhoods, one might expect to observe the processing advantage for words from dense neighborhoods, but only in a limited range of available processing resources. Once cognitive resources have been reduced below a certain point, however, one might expect an alternative processing strategy to emerge: because of their uniqueness, novel words from sparse neighborhoods may now be more readily learned than words from dense neighborhoods. As there are fewer words in sparse neighborhoods (by definition), fewer words overall will, of course, be learned, resulting in what appears to be a decrement in word-learning performance when cognitive resources are reduced.

To further explore how differences in the internal processing resources available to the network influence the advantage in word-learning for words from dense neighborhoods, the present experiment was performed. The amount of internal processing resources available to the network was manipulated by varying the number of “hidden” units in the model from one to six. (Recall that the networks used in Experiments 1 and 2 had 6 hidden units.) Manipulating the number of hidden units in a network is a well-established approach for approximating differences in computational resources in humans (Brown, 1997; Seidenberg & McClelland, 1989; Thomas & Karmiloff-Smith, 2003). The results of this experiment may offer unique insight into the debate about the cause of various language disorders. The two outcomes described above roughly correspond to the classic distinction made in the literature, and described by Rice (2003), between language delay and language deviance as the underlying cause of various language disorders. Said another way, language disorders may simply be extreme cases of normal variation in processing rather than the result of a qualitatively different processing mechanism (Tomblin, Zhang, Weiss, Catts & Ellis Weismer, 2004).

In the case of the present simulation, an outcome consistent with the idea that language disorders are caused by language delay would be a continuous change in the number of hidden units being associated with a continuous change in performance in the word-learning task (i.e., dense is always better than sparse, but overall performance decreases as the number of hidden units decreases). An outcome consistent with the idea that language disorders are caused by language deviance we would observe a discontinuous shift, for example, an advantage for dense over sparse words when the networks had 4–6 hidden units, but an advantage for sparse over dense words when the networks had 1–3 hidden units.

METHODS

Network architecture

The same network software package used in Experiments 1 and 2 was used in the present experiment. The network architecture was also similar to that used in Experiments 1 and 2, except the number of hidden units varied from one hidden unit to six hidden units (the number of hidden units used in Experiments 1 and 2). A new set of random “seeds” was used in the present experiment to provide randomized initial connection weights to the networks, but the same set of seeds were used in each of the networks in this experiment.

Stimuli

The same targets, neighbors, and generalization items used in Experiment 1 were used in the present experiment.

Procedure

The network was trained on all of the targets and neighbors at the same time (as in Experiment 1) for 1000 epochs.

RESULTS AND DISCUSSION

A 2 (Density) X 6 (Number of Hidden Units) ANOVA was used to assess the performance of the networks (via RMSE) when tested on the targets and neighbors (which the networks were trained on for 1000 epochs), and on the (untrained) generalization items. Smaller error values indicate that the output of the model was closer to the desired output, suggesting better learning by the network, whereas, larger error values indicate that the output of the model was further from the desired output, suggesting poorer learning by the network.

Trained Items

For the targets (see Figure 3), a main effect of neighborhood density was observed such that dense targets had less error (mean = 1.243, sd = .315) than the sparse targets (mean = 1.485, sd = .208) after 1000 epochs of training, suggesting that all of the networks more readily learned the dense targets than the sparse targets, F (1, 54) = 805.758, p < .0001. A main effect of number of hidden units was observed, such that the networks with more hidden units (i.e., internal processing resources) learned the target words better (6 hidden units: mean = 1.175, sd = .346) than networks with fewer hidden units (1 hidden unit: mean = 1.583, sd = .122), F (5, 54) = 108.560, p < .0001.

Figure 3.

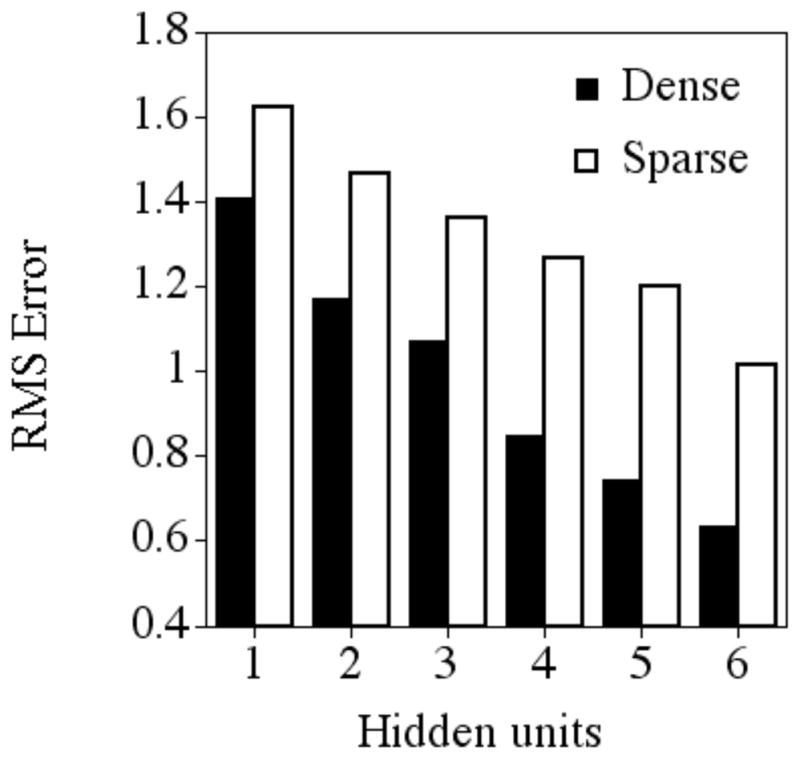
Mean root mean square error after 1000 epochs of training for the dense and sparse target words in networks with varying numbers of hidden units.

Finally, an interaction between neighborhood density and number of hidden units was observed, such that the networks with greater processing resources discriminated between the dense and sparse targets more than the networks with fewer processing resources: the network with 6 hidden units had a mean difference of .276 between dense and sparse targets, whereas the network with 1 hidden unit had a difference of .166 between dense and sparse targets, F (5,54) = 6.706, p < .001. The nature of this interaction (ordinal rather than disordinal) suggests that networks with a smaller amount of processing resources do not adopt a completely different processing strategy than networks with greater amounts of processing resources in order to perform the task of learning words. Rather, all of the networks—regardless of the amount of internal processing resources available to them—employed a similar processing strategy to learn the words. The difference in the amount of internal processing resources available to the networks seemed only to influence the degree of success that the networks had in learning the words. These results suggest that problems in word learning related to processing resources may be better described as language delays rather than language deviances (Rice, 2003).

To further illustrate that the networks employed similar mechanisms to learn the target words, but that the networks with fewer processing resources were simply delayed in their learning, we equated the performance of the network with 6 hidden units to the performance of the network with 1 hidden unit (an approach that is commonly employed in studies examining language disorders to distinguish language delay from language disorder). Equivalent performance on dense and sparse targets was observed after 500 epochs of training in the network with 1 hidden unit (dense = 1.467; sparse = 1.663) and only 100 epochs of training in the network with 6 hidden units (dense = 1.498; sparse = 1.643), F (1, 18) = 3. 405, p = .08, not significant. Clearly the network with fewer processing resources could learn the dense and sparse targets, and learn them as well as the network with more processing resources. The network with fewer processing resources, however, required additional training to do so. This result further suggests that problems in word learning related to processing resources may be better described as language delays rather than language deviances (Rice, 2003).

Analysis of the neighbors showed a fairly similar pattern of results. A main effect of neighborhood density was observed such that dense neighbors had less error (mean = 1.371, sd = .221) than the sparse neighbors (mean = 1.444, sd = .224) after 1000 epochs of training, suggesting that all of the networks more readily learned the dense neighbors than the sparse neighbors, F (1, 54) = 205.851, p < .0001. A main effect of number of hidden units was observed such that the networks with more hidden units (i.e., internal processing resources) learned the target words better (6 hidden units: mean = 1.238, sd = .276) than networks with fewer hidden units (1 hidden unit: mean = 1.596, sd = .087), F (5, 54) = 196.313, p < .0001. In this case, however, there was no interaction between neighborhood density and number of hidden units, F (5, 54) = .339, p = .88, not significant.

As with the targets, equivalent performance on the dense and sparse neighbors was observed after 500 epochs of training in the network with 1 hidden unit (dense = 1.535; sparse = 1.636) and only 100 epochs of training in the network with 6 hidden units (dense = 1.547; sparse = 1.630), F (1, 18) = 1.391, p = .25, not significant. Like the targets, the network with fewer processing resources required more training epochs to reach the same level of performance on the dense and sparse neighbors as the network with more processing resources, further suggesting that problems in word learning related to processing resources may be better described as language delays rather than language deviances.

Generalization Items

To further demonstrate that the networks with only one hidden unit were learning to extract relevant sub-patterns from the input, but were only doing it more slowly than the networks with 6 hidden units, we examined the performance of networks on the (untrained) generalization items. If the reduction in processing resources limited the network with just one hidden unit to learn only about the items it was trained on rather than to extract relevant sub-patterns from the input and exploit those patterns when processing other items, then performance on the generalization items should be quite poor. Such a result might then suggest that the networks with fewer processing resources were employing a qualitatively different processing mechanism to learn words. Alternatively, if all of the networks were able to generalize performance to a novel set of words, but at different rates, that might further suggest that problems in word learning related to processing resources may be better described as language delays rather than language deviances.

For the generalization items, a main effect of neighborhood density was observed such that there was less error on the generalization items from the dense neighborhoods (mean = 1.449, sd = .171) than on the generalization items from the sparse neighborhoods (mean 1.549, sd = .166) after 1000 epochs of training, suggesting that all of the networks extracted relevant sub-patterns from the input and exploited that information in the processing of the novel items, F (1, 54) = 241.101, p < .0001. A main effect of number of hidden units was also observed such that the networks with more hidden units (i.e., internal processing resources) performed better on the generalization items (6 hidden units: mean = 1.382, sd = .224) than networks with fewer hidden units (1 hidden unit: mean = 1.638, sd = .078), F (5, 54) = 72.088, p < .0001. Again, there was no interaction between neighborhood density and number of hidden units, F (5, 54) = .793, p = .56, not significant.

Equivalent performance on the novel dense and sparse generalization items was also observed after 500 epochs of training in the network with 1 hidden unit (dense = 1.564; sparse = 1.687) and only 100 epochs of training in the network with 6 hidden units (dense = 1.581; sparse = 1.6870, F (1, 18) = .522, p = .48, not significant. This result suggests that fewer processing resources not only impair the acquisition of the targets and neighbors, but also reduces the ability of the network to extract relevant sub-patterns from the input and exploit them in the processing of novel items. This result is also consistent with the results obtained in the analyses of the targets and neighbors in suggesting that problems in word learning related to processing resources may be better described as language delays rather than language deviances.

The results of the present experiment further suggest that known words are used to “strengthen” the representations of phonologically similar novel words, such that a novel word that is similar to many known words will be learned more readily than a novel word that is similar to few known words. More interestingly, the results of the present experiment suggest that this influence of known words on the learning of novel words is robust to differences in the availability of processing resources. That is, regardless of how many hidden units the networks possessed, a word learning advantage for dense words was still observed. Granted, in the networks with fewer processing resources (i.e., fewer hidden units), learning proceeded at a slower rate than the networks with more processing resources (i.e., many hidden units), but radically different learning strategies were not employed to circumvent the restriction of resources in order to learn the words.

Interestingly, a similar pattern of delayed rather than deviant learning has been observed in real word-learners. Evans, Saffran, and Robe-Torres (2009) found that children with specific language impairment (SLI) were able to implicitly compute the probabilities of adjacent sound sequences and thereby learn novel words embedded in a continuous stream of artificial speech. However, the children with SLI required approximately double the exposure to the artificial language as their typically developing peers to reach the same level of above-chance performance. Although on the surface the patterns of behavior are similar, it is important to acknowledge the differences between the present simulation and the experiments reported by Evans et al. with regard to the task employed, the cognitive demands of the task, the type of learning examined, etc.

EXPERIMENT 4

The experiments in the present study examined how the number of similar sounding words affects the acquisition of those words. Being similar to many words resulted in a larger lexical conspiracy that facilitated acquisition of those words to a greater extent than being similar to fewer words. This benefit to processing was observed when the words to be acquired were presented all at once (Experiment 1), as well as when the words to be acquired were distributed over time (Experiment 2). In Experiment 3, we were able to examine how differences in the availability of processing resources further affected the influence of neighborhood density on word learning. In each case, a robust advantage in learning novel words that were similar to many rather than few known words was observed.

In the present experiment we sought to examine how varying the input might influence the processing advantage typically observed in word learning. A classic approach to studying word learning is to examine the input that a child receives (e.g., the work of Roger Brown, 1973). Furthermore, current verbal models of word learning suggest that children extract relevant patterns from the input and then use these patterns to facilitate learning (e.g., Hirsch-Pasek, Golinkoff, & Hollich, 2000; Smith, 2000). Moreover, the main approach in conventional speech and language therapy is to alter the input in some way. Taken together, the structure of the input is viewed as crucial for learning from a variety of perspectives. In Experiments 1–3, the input to the model was balanced with regards to the number of dense and sparse words the networks received. How would the facilitative influence of neighborhood density on word-learning be affected if the input was not balanced?

The strict control of lexical exposure required to examine this question in the real world is, of course, not something that could be accomplished with ease. Furthermore, the possibility that manipulating the input might actually retard language development in some way also makes exploration of this question in the real world problematic on ethical grounds. However, in addition to using computational models to better specify the mechanisms described by verbal models (Elman et al., 1996; Lewandowsky, 1993), “computational experiments” can be used to explore questions, such as the present one, that are difficult—for ethical or practical reasons—to examine in the real world (Plunkett & Elman, 1997). Therefore, we examined this question with our computational model using the experimental approach of testing extremes. That is, the networks in the present experiment either received incremental training on all of the dense words first, followed by all of the sparse words (Dense-Sparse Training Regime), or received incremental training on all of the sparse words first, followed by all of the dense words (Sparse-Dense Training Regime). To examine longer-term effects of this unbalanced exposure regime, we continued to train the networks for an additional 1000 epochs on the full set of targets and neighbors.

METHODS

The same network software package used in the previous experiments was used in the present experiment. The network architecture, stimuli, and training procedure were also similar to those used in Experiment 2, with the following exception. Five networks were first exposed to the items from dense neighborhoods (six words at a time, for 100 epochs, with six more words added to the training set, etc.). Once the network had been exposed to all 30 items (targets and neighbors) from the dense neighborhoods, the items from the sparse neighborhoods were added to the training sets (with six sparse items added to the training set, trained for 100 epochs, then six more sparse items added to the training set, etc.). This training regime will be referred to as the dense-sparse training regime.

Another set of five networks (that were identical in every way except in the training regime) was first exposed to the items from sparse neighborhoods (six words at a time, for 100 epochs, with six more words added to the training set, etc.). Once the network had been exposed to all 30 items (targets and neighbors) from the sparse neighborhoods, the items from the dense neighborhoods were added to the training sets (with six dense items added to the training set, trained for 100 epochs, and six more dense items added to the training set, etc.). This training regime will be referred to as the sparse-dense training regime.

Training to 1000 epochs of incremental learning facilitated comparison to Experiment 2. However, to further examine the long-term consequences of these different training regimes, we continued to train the network on all of the targets and neighbors (now presented all together) for an additional 1000 epochs.

RESULTS AND DISCUSSION

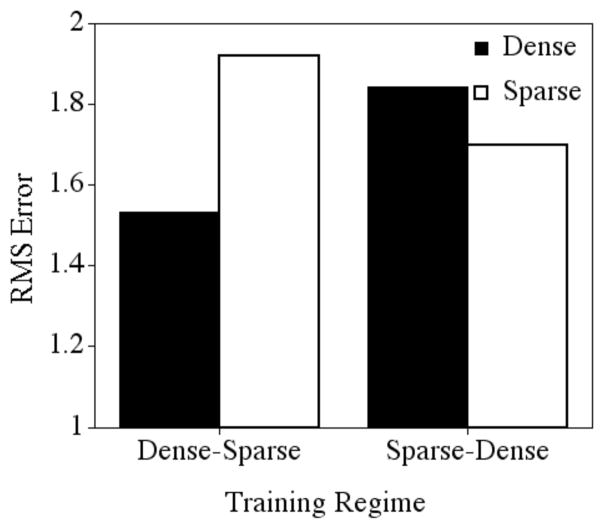
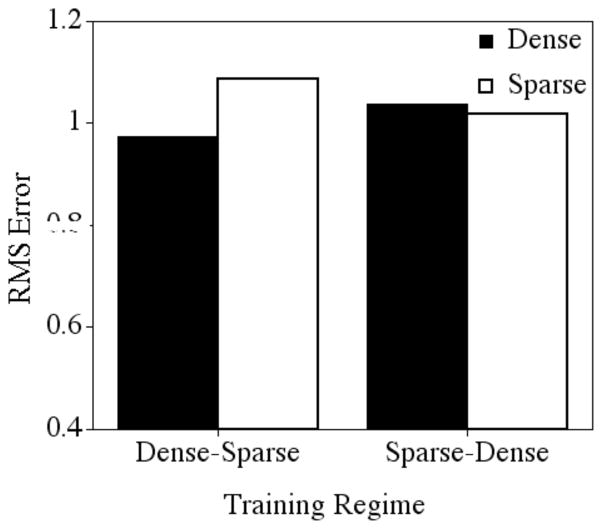
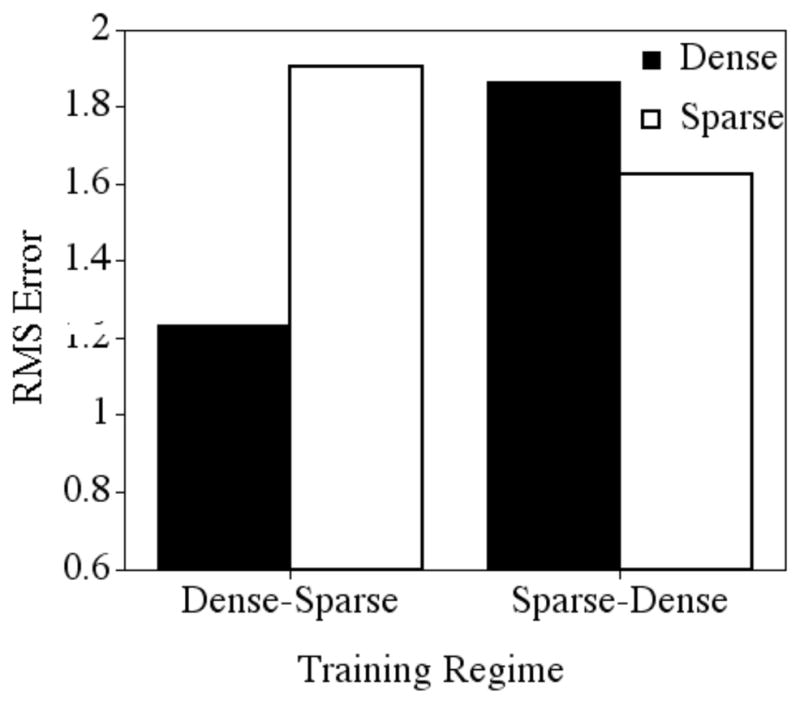
Network performance was again assessed using root mean square error. Rather than just evaluate the networks after receiving 1000 epochs of training, we wanted to better capture how the performance of the networks might change as a function of the different training regimes. Consequently, a 2 (training regime: Dense-Sparse versus Sparse-Dense) X 2 (Density: Dense versus Sparse) X 2 (Epochs: 100, 1000) ANOVA was used to assess the amount of RMSE (separately) in the targets, neighbors, and generalization items so that we could present a better picture of how performance changed over time as a function of the different training regimes.

Separate analyses were also performed after the additional 1,000 epochs of training that the networks received on all of the targets and neighbors (i.e., network performance assessed at epoch 2000). Smaller error values indicate that the output of the model was closer to the desired output, suggesting better learning by the network, whereas, larger error values indicate that the output of the model was further from the desired output, suggesting poorer learning by the network.

Target Word-Forms

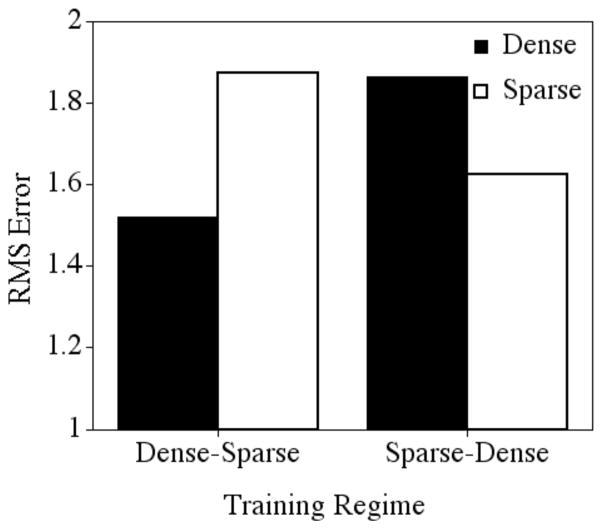
A significant three-way interaction was found among the variables: training regime, density, and epochs, F (1, 18) = 16.992, p < .001. All of the two-way interactions and main effects were also significant. Not surprisingly, there was a main effect of epoch, indicating that performance on the targets improved with training (mean after 1000 epochs = .883, sd = .246, mean after 100 epochs = 1.657, sd = .281), F (1, 18) = 1514.237, p < .0001. To facilitate discussion of the three-way interaction, we will consider the networks early in training (after being exposed to 100 training epochs, and only a portion of the input) and later in training (after being exposed to 1000 training epochs, and all of the input).

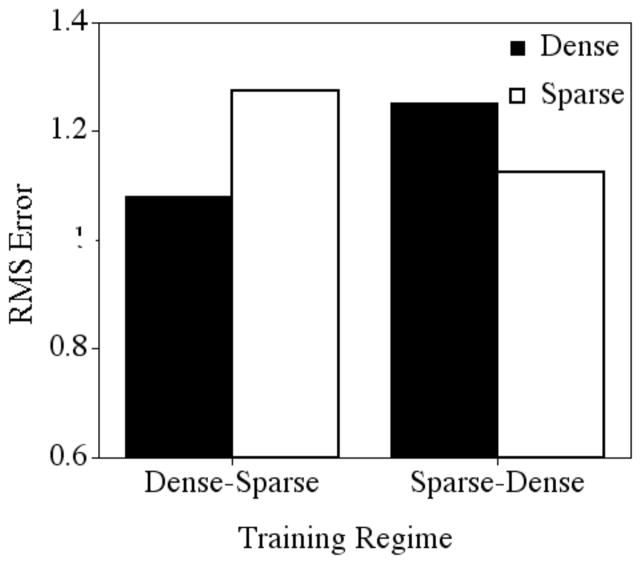
After 100 epochs of training (see Figure 4), a significant two-way interaction was observed between density and training regime, F (1, 18) = 498.276, p < .0001. In the Dense-Sparse training regime, performance on the sparse targets (which the network had not been exposed to yet, mean = 1.905, sd = .036) was poorer than performance on the dense targets (which the network had been trained on for 100 epochs, mean = 1.235, sd = .100). However, in the Sparse-Dense training regime, performance on the sparse targets (which the network had been trained on for 100 epochs, mean = 1.624, sd = .066) was better than performance on the dense targets (which the network had not been exposed to yet, mean = 1.863, sd = .110). It is perhaps not surprising that the networks performed well on the items they had been trained on, and more poorly on items they had not been trained on, even if that exposure was brief (i.e., 100 epochs).

Figure 4.

Mean root mean square error after 100 epochs of training for the dense and sparse targets in the two training regimes.

After 1000 epochs of training (see Figure 5), when the networks had been exposed to all of the items, performance of the networks again showed an interaction between training regime and density, F (1, 18) = 534.519, p < .0001. In the Dense-Sparse training regime, performance on the dense targets remained better (mean = .520, sd = .050) than performance on the sparse targets (mean = 1.190, sd = .045). However, in the Sparse-Dense training regime, performance on the dense targets (mean = .924, sd = .064) was equivalent to performance on the sparse targets (mean = .900, sd = .036). Despite a late entry into the training set, the relevant sub-patterns in the dense words were extracted and exploited, allowing the network to improve the representation of these items at a faster rate than the sparse words. That is, the representations of the dense targets were strengthened to such an extent, that performance on the dense targets “caught up” to the performance on the sparse targets, even though the network had received more training overall on the sparse targets.

Figure 5.

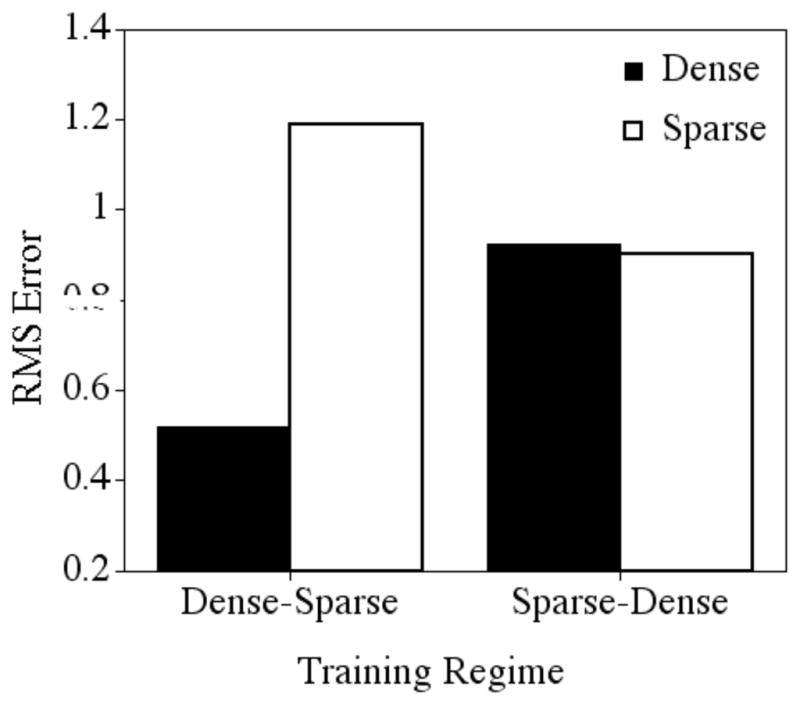
Mean root mean square error after 1000 epochs of training for the dense and sparse targets in the two training regimes.

The networks received 1000 additional exposures to all of the dense and sparse words. During these exposures no new words were added to the training set. Thus, the network simply received additional exposure to all of the targets (and neighbors), and performance was assessed after a total of 2000 epochs. At epoch 2000 (see Figure 6), performance of the networks showed an interaction between training regime and density, F (1, 18) = 31.892, p < .0001. In the Dense-Sparse training regime, performance on the dense targets remained better (mean = .380, sd = .069) than performance on the sparse targets (mean = .916, sd = .050). However, in the Sparse-Dense training regime, performance on the dense targets (mean = .498, sd = .100) was now better than performance on the sparse targets (mean = .743, sd = .072), despite the initial advantage observed for sparse targets in this training regime.

Figure 6.

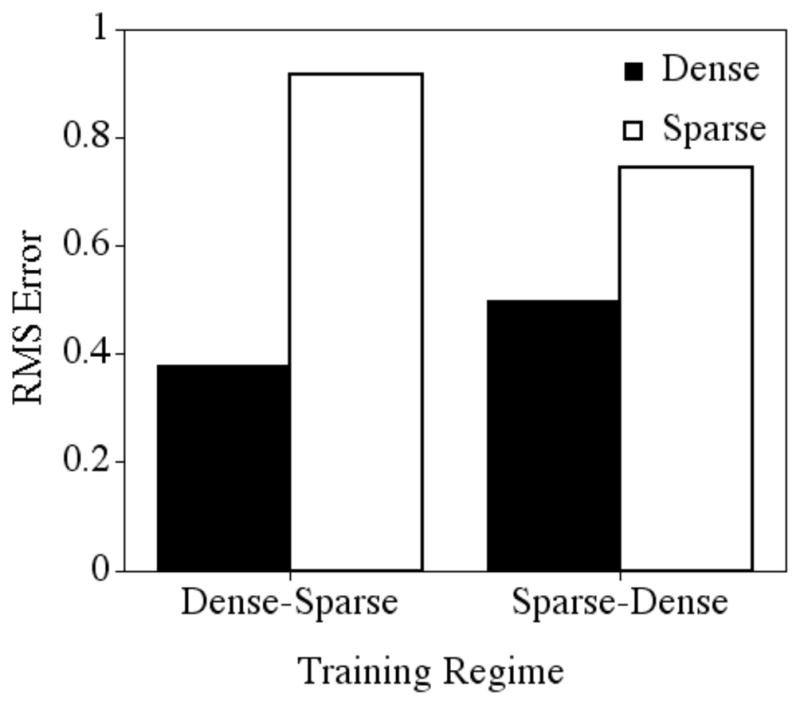
Mean root mean square error after a total of 2000 epochs of training for the dense and sparse targets in the two training regimes. Performance was assessed after the networks had been exposed to all of the targets (by epoch 1000), and after an additional 1000 exposures.

A well-known characteristic of connectionist networks is that smaller changes tend to be made to connection weights as training progresses. It is therefore somewhat surprising that the dense words in the Sparse-Dense training regime—which were added to the training set relatively late in the training process—were learned as well as they were. The common sub-patterns found among the neighbors of words in dense neighborhoods may suggest a method for overcoming the decrease in plasticity of the connection weights that occurs as training progresses often observed in networks of this type. Additional computational experiments are required to determine the relevant parameters by which this approach affects the plasticity of the network—such as the number and diversity of sub-patterns in the training set, and when those items enter the training set—as well as their limits.

Neighboring Word-Forms

For the neighbors, a significant three-way interaction was also found among the variables: training regime, density, and epochs, F (1, 18) = 7.804, p < .05. As with the targets, there was a main effect of epoch, indicating that performance on the targets improved with training (mean after 1000 epochs = 1.009, sd = .119; mean after 100 epochs = 1.705, sd = .151), F (1, 18) = 1414.760, p < .0001. As above, to facilitate discussion, we will consider the networks early in training (after being exposed to 100 training epochs, and only a portion of the input) and later in training (after being exposed to 1000 training epochs, and all of the input).

After 100 epochs of training (see Figure 7), a significant two-way interaction was observed between density and training regime, F (1, 18) = 447.581, p < .0001. In the Dense-Sparse training regime, performance on the sparse neighbors (which the network had not been exposed to yet, mean = 1.874, sd = .036) was poorer than performance on the dense neighbors (mean = 1.521, sd = .046). Note, that the network had only been exposed to the dense target words and one neighbor of each of the target words at this point in training; they had not actually been trained on all of the dense neighbors yet. Despite this limited exposure, the network was able to extract and exploit relevant sub-patterns to more efficiently process the (mostly untrained) dense neighbors.

Figure 7.

Mean root mean square error after 100 epochs of training for the dense and sparse neighbors in the two training regimes.

In the Sparse-Dense training regime, performance on the sparse neighbors (for 100 epochs, mean = 1.624, sd = .066) was better than performance on the dense neighbors (mean = 1.863, sd = .110). Recall that at this point, the network had been trained on just 6 sparse target words, and had not been exposed to any dense words (targets or neighbors), so it is not surprising that the networks performed better on the items they had been trained on, and more poorly on items they had not been exposed to at all.

After 1000 epochs of training (see Figure 8), when the networks had been exposed to all of the items, performance of the networks again showed an interaction between training regime and density, F (1, 18) = 423.953, p < .0001. In the Dense-Sparse training regime, performance on the dense neighbors remained better (mean = .899, sd = .046) than performance on the sparse neighbors (mean = 1.147, sd = .070). In contrast to the performance of the network on the targets after 1000 epochs, the network in the Sparse-Dense training regime continued to show better performance on the sparse neighbors (mean = .911, sd = .049) than the dense neighbors (mean = 1.079, sd = .032), F (1, 9) = 118.796, p < .0001. We believe this difference in performance between the targets and neighbors is again due to the difference in the number of words that sound similar to the targets and the number of words that sound similar to the neighbors (as discussed in Experiment 1).

Figure 8.

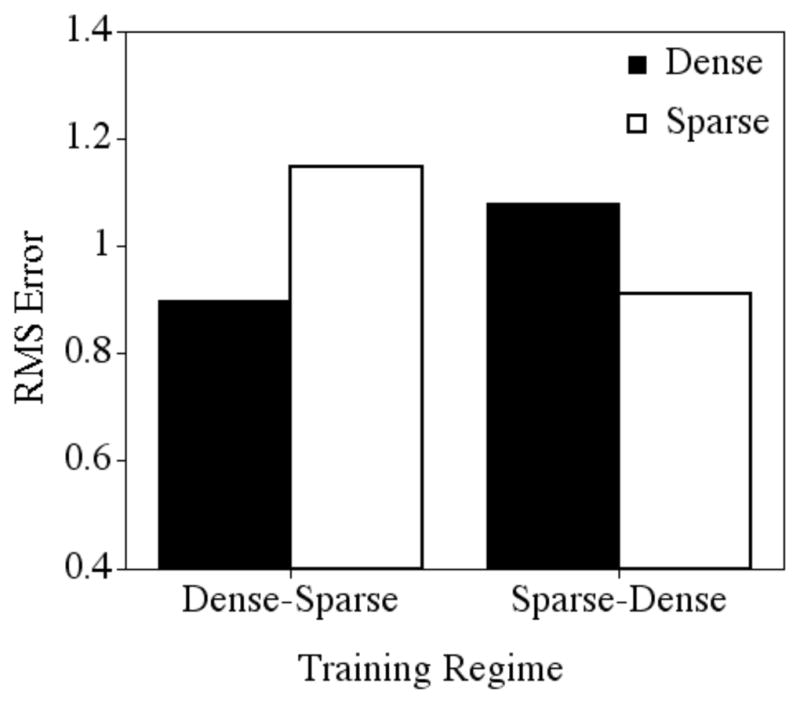
Mean root mean square error after 1000 epochs of training for the dense and sparse neighbors in the two training regimes.

Indeed, the continued advantage for sparse over dense neighbors in the Sparse-Dense training regime decreases with continued exposure to the word-forms. At epoch 2000 (see Figure 9), performance of the networks shows an interaction between training regime and density, F (1, 18) = 83.911, p < .0001. In the Dense-Sparse training regime, performance on the dense neighbors remained better (mean = .735, sd = .071) than performance on the sparse neighbors (mean = .849, sd = .044), F (1, 9) = 61.787, p < .0001. In the Sparse-Dense training regime, performance on the sparse neighbors (mean = .746, sd = .058) also remained better than performance on the dense neighbors (mean = .806, sd = .034), F (1, 9) = 23.886, p < .001, in contrast to the pattern observed for the targets.

Figure 9.

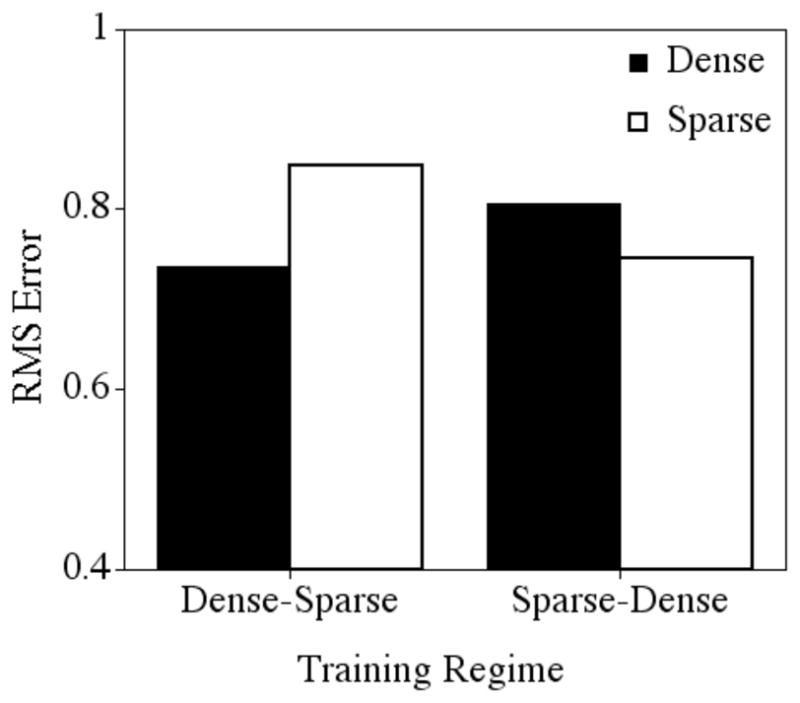
Mean root mean square error after a total of 2000 epochs of training for the dense and sparse neighbors in the two training regimes. Performance was assessed after the networks had been exposed to all of the words (by epoch 1000), and after an additional 1000 exposures.

Generalization Items

As with the targets and neighbors, a significant three-way interaction was found in the performance on the generalization items among the variables: training regime, density, and epochs, F (1, 18) = 25.717, p < .0001. As above, to facilitate discussion, we will consider the networks early in training (after being exposed to 100 training epochs, and only a portion of the input) and later in training (after being exposed to 1000 training epochs, and all of the input).

After 100 epochs of training (see Figure 10), a significant two-way interaction was observed between density and training regime, F (1, 18) = 286.598, p < .0001. In the Dense-Sparse training regime, performance on the sparse generalization items was poorer (mean = 1.919, sd = .049) than performance on the dense generalization items (mean = 1.532, sd = .066); recall that the network had not been exposed to any sparse targets or neighbors yet, however. In the Sparse-Dense training regime, performance on the sparse generalization items (for 100 epochs, mean = 1.699, sd = .051) was better than performance on the dense neighbors (mean = 1.842, sd = .080). Despite the limited exposure to targets and neighbors in each training regime, the network was able to extract and exploit relevant sub-patterns to more efficiently process the generalization items.

Figure 10.

Mean root mean square error after 100 epochs of training for the (untrained) dense and sparse generalization items in the two training regimes.

After 1000 epochs of training (see Figure 11), when the networks had been exposed to all of the items, performance of the networks again showed an interaction between training regime and density, F (1, 18) = 65.894, p < .0001. In the Dense-Sparse training regime, performance on the dense generalization items remained better (mean = 1.080, sd = .045) than performance on the sparse generalization items (mean = 1.274, sd = .079). In the Sparse-Dense training regime, performance on the sparse generalization items remained better (mean = 1.125, sd = .064) than the performance on the dense generalization items (mean = 1.252, sd = .059).

Figure 11.

Mean root mean square error after 1000 epochs of training for the (untrained) dense and sparse generalization items in the two training regimes.

Performance on the generalization items after 2000 epochs of training (i.e., an additional 1000 exposures to all of the targets and neighbors) yielded a pattern of results that was a little different than the pattern of results obtained at 1000 epochs, F (1, 18) = 14.493, p < .01, as shown in Figure 12. In the Dense-Sparse training regime, performance on the dense generalization items remained better (mean = .972, sd = .043) than performance on the sparse generalization items (mean = 1.087, sd = .049). However, in the Sparse-Dense training regime, performance on the dense generalization items (mean = 1.038, sd = .062) was now statistically equivalent to the performance on the sparse generalization items (mean = 1.016, sd = .058), F (1, 9) = .449, p = .52, not significant.

Figure 12.

Mean root mean square error after a total of 2000 epochs of training for the (untrained) dense and sparse generalization items in the two training regimes. Performance was assessed after the networks had been exposed to all of the words (by epoch 1000), and after an additional 1000 exposures.

Although performance on the target words in the Sparse-Dense training regime had completely reversed from a performance advantage for the sparse targets to a performance advantage for the dense targets by this point in training, we did not observe such a dramatic change in the performance for the neighbors and the (untrained) generalization items. Note, however, that performance on the dense and sparse neighbors, and the dense and sparse generalization items did become more similar with additional exposure to the targets and neighbors. We predict that additional exposure in the Sparse-Dense training regime to the dense and sparse targets and neighbors would ultimately result in the predicted performance advantage for dense items over sparse.

Overall, the results of this experiment show a number of interesting points. Most obvious is the significant and long-lasting impact that initial input conditions have on the development of the lexicon and on subsequent lexical performance. Networks that were initially exposed to sparse followed by dense words (the Sparse-Dense Training Regime) developed a lexicon that was less sensitive to relevant sub-patterns in the input. Networks in this training regime were ultimately able to show a processing advantage for dense targets, but such an advantage was not observed for the dense neighbors. Furthermore, as evidenced in the performance on the generalization items, networks in the Sparse-Dense training regime did not exploit the knowledge of relevant sub-patterns that had been extracted from the input to the same extent as networks that had been exposed to the same words in the Dense-Sparse training regime. The failure of networks in the Sparse-Dense training regime to learn and generalize lexical knowledge was still evident even after additional training exposures (i.e., 1000 additional epochs of training on all of the targets and neighbors), suggesting that the (detrimental) influences of the initial input conditions on processing are also long-lasting.

Although the results of the present experiment suggest that the initial input conditions have large and long-lasting effects on lexical processing, the present results also hint towards a method to alleviate some of the detrimental impacts that initial input conditions may have on subsequent processing. Consider the results for the dense targets in the Sparse-Dense training regime. Despite disadvantageous processing of the dense targets early on in this training regime, additional training (1000 more epochs) of the targets and neighbors ultimately showed the advantage for dense words that had been previously observed in human word-learners (e.g., Storkel et al., 2006) and in Experiments 1–3. Granted, this processing advantage was not as large as the performance advantage observed in the targets in the Dense-Sparse training regime, but it nevertheless did emerge after additional training.

For the neighbors and generalization items, we did not observe a change in processing that was as dramatic as the change in processing observed in the target words. However, in the case of the generalization items in the Sparse-Dense training regime, delayed exposure to words with dense neighborhoods did result in the performance of the networks equaling that of the initially trained sparse items. Perhaps even more training would have produced the processing advantage for the dense generalization items (and the neighbors as well).

We suspect that the failure of the neighbors and generalization items to produce the dramatic reversal in processing may have again been due (in part) to the difference in the number of words that are actually similar to the targets, neighbors, and generalization items (see the explanation in the discussion of Experiment 1). Recall that each sparse target is phonologically similar to only one word (i.e., the neighbor), whereas each dense target is phonologically similar to 9 neighbors. For the neighbors, each sparse neighbor has only one word that is a phonologically similar neighbor to it (the sparse target), whereas each dense neighbor is similar to three words (two other neighbors and the target word). For the generalization items, each sparse generalization item is similar to only one item (the target), and each dense generalization item is similar to four words (the target word and only three of its neighbors). The difference in performance to the targets, neighbors, and generalization items suggests that therapeutic interventions in humans that rely solely on increased exposure might lead to learning of the words targeted in treatment, but may not lead to the extraction of relevant sub-patterns that are important for learning novel words. Given that most treatment approaches strive to affect change that extends beyond the specific items used in treatment, teaching items from dense neighborhoods to increase the asymmetry between dense and sparse neighborhoods could lead to the dense sub-patterns becoming more salient, thereby facilitating their extraction and use in learning novel word-forms. Additional computational experiments and studies with human word-learners are required to test these predictions derived from the present study.

The detrimental and long-lasting impact of the initial input conditions observed in the present experiment also speaks to the utility of computational experiments. The stringent control over the input and the influence on lexical processing of one of the input conditions would have made it practically and ethically impossible to conduct a similar experiment with human language learners. Our use of a computational model in this experiment enabled us to observe the effects of various initial input conditions on subsequent performance in silica, and to consider the implications for treatment should similar conditions of impoverished input be encountered in the clinical setting.

Finally, the results of the present experiment further suggest that the underlying mechanism employed in word learning is a “strengthening” of lexical representations by similar word-forms. Despite what may have appeared initially in one case—the Sparse-Dense training regime—as an advantage for sparse items over dense items, and therefore as evidence for varying amounts of competition among lexical representations, the performance of the network on the generalization items raises some questions about such an account. Performance on all of the untrained generalization items improved over time, even though the network had not been exposed to and trained on a specific neighbor of that item. This result suggests that a novel word-form does not actually have to be a “member” of a specific phonological neighborhood to obtain some benefit from the known words in the lexicon. Rather, more general word knowledge can be extracted and exploited to facilitate the processing of novel word-forms. It is not clear how performance on all of the untrained generalization items (even those without neighbors in the lexicon) would have improved over time if competition were the underlying mechanism in word learning, as has been proposed by others (e.g., Swingley & Aslin, 2007).

GENERAL DISCUSSION

Four computational experiments were reported in the present study. In Experiment 1 we exposed a multi-layered network to target words that differed in the number of phonological neighbors to examine whether the similar sounding words would facilitate the acquisition of the target words, leading to target words with more neighbors being learned better than target words with fewer neighbors, or whether the similar sounding words would interfere with the acquisition of the target words, leading to target words with few neighbors being learned better than target words with more neighbors. The results of that experiment as well as the experiments that followed provided several pieces of evidence that suggest that similar sounding words facilitate the acquisition of target words, thereby giving us a computational mechanism for the verbal model proposed by Storkel et al. (2006; see also Jusczyk, Luce, & Charles-Luce, 1994) for the acquisition of novel word forms. Experiment 2 demonstrated that similar sounding words strengthen the representations of target words, even when the network is gradually exposed to the words in the lexicon (rather than being trained on the words all at once, as in Experiment 1).

Satisfied that the computational model reasonably captured the important characteristics of the typical word-learner, we proceeded in Experiments 3 and 4 to explore the influence of two variables on word-learning that could not be examined in real word-learners due to ethical and practical considerations. For example, in Experiment 3 we manipulated the number of hidden units in the model to examine how (perhaps innate) differences in processing resources might affect word-learning. Finding a large enough sample of real word-learners that significantly differ in the amount of processing resources to examine this question is likely to be challenging, at best. When all other conditions are the same, networks with fewer processing resources required more training to reach comparable performance levels of networks with more processing resources. Interestingly, the networks with fewer processing resources did not adopt a different processing strategy to acquire the novel words. That is, all of the networks, regardless of the amount of available processing resources, showed an advantage in the acquisition of dense words over sparse words.

In Experiment 4, the networks were exposed to the same words in two different environments. In one condition, the networks were first exposed to sparse words until all of the sparse words had been added to the lexicon. The networks were then exposed to the dense words, until all of the words had been added to the lexicon. This condition was referred to as the Sparse-Dense training regime. In the other condition, the Dense-Sparse training regime, the networks were first exposed to all of the dense words, with the sparse words being added to the lexicon later on in the training set. Given the concern that the Sparse-Dense training regime might, in some way, adversely affect lexical development, carrying out such an experiment with real word-learners is, of course, ethically not possible. (The logistics of creating such highly controlled conditions in the environment also make this experiment impossible to carry out with real word-learners.) The results of this experiment did indeed indicate that word learning performance in the Sparse-Dense training regime lagged behind that in the Dense-Sparse training regime.

We do not believe that the results of Experiments 1–4 are unique to the architecture of or the learning algorithm employed in the networks used in the present study. Recall that the networks used in the present study had distributed representations, and that connection weights were adjusted with the back-propagation of error algorithm. Rather, we believe that the “strengthening” of lexical representations during word-learning can be accomplished in a variety of connectionist networks as well as in many other types of computational models.

Indeed, Page (2000) discussed how a localist neural network—where a single node is used to represent an entity (i.e., one node represent dog, another node represents shoe, etc.)—with a competitive learning algorithm could also produce a learning advantage for novel words that are similar to many known words compared to novel words that are similar to few known words (see also Grossberg, 1972). When a novel word-form is presented to the localist network, several uncommitted nodes become partially activated by the input, and compete with each other to become the node that will be committed to representing that input pattern (i.e., that word) in the future; this is known as a competitive learning algorithm. Each of these competing nodes will adapt the weights on the connections it receives from the input nodes in an attempt to better match the input pattern. Eventually, one node will match the input pattern better than the other competing nodes, and will become committed to representing that word.

The “losing” nodes remain uncommitted (i.e., they don’t represent a known word), but because of the previous competition, their weights are in an excellent position to represent a new input pattern that is similar to the previously learned input pattern. Thus, another novel input that is similar to many known words will benefit more from the connection weights that are predisposed (as a result of previous competitions among uncommitted nodes) to represent that new word than a novel input that is similar to few known words. Although the connectionist architecture and learning algorithm described by Page (2000) are different from those employed in the present experiment, both models provide a more precise, mechanistic account of how the representation of a novel word might be “strengthened” by sounding similar to many (rather than few) known words.

As described by Lewandowsky (1993; see also Norris, 2005), computational models benefit researchers in several ways. For example, the computational model developed in the present study made explicit the mechanisms of word learning that were previously described only in verbal form (Jusczyk, Luce, & Charles-Luce, 1994; Storkel et al., 2006). Other verbal descriptions of the mechanisms that underlie various word-learning phenomena might also benefit from the process of developing a computational model. Furthermore, the model that we developed in the present study enabled us to explore the influence of variables and conditions that—for ethical and practical reasons—would be impossible to examine in real word-learners. The computational experiments employed in the present study offer us a technique that can be used to further explore word learning that—in conjunction with psycholinguistic experiments—can greatly increase our understanding of this process.

These as well as other reasons speak to the important role that computational modeling and experimentation plays in increasing our understanding of language processing and language processing disorders. Despite the simplicity of the model employed in the present computational experiments it is important to keep in mind that “[m]odels are not intended to capture fully the processes they attempt to elucidate. Rather, they are explorations of ideas about the nature of cognitive processes. In these explorations, simplification is essential—through simplification, the implications of the central ideas become more transparent” (McClelland, 2009; pg. 11). We believe the present simulations have greatly elucidated the manner in which neighborhood density influences the process of word-learning.

Despite the simplicity of the network used in the present simulations, the results of these computational experiments point to (at least) two topics worthy of further investigation either through computational or psycholinguistic experiments. The results of all of the present experiments suggest that another level of representation may be necessary to account for the influence of segment frequency (as described in Footnote 2) on word learning. In addition, the results of Experiment 4 hint towards a method that might overcome the loss of plasticity in connection weights that occurs with increased training often observed in the type of network used in the present study. The improved performance of dense targets in the Sparse-Dense Training Regime suggests that items added later to the training set can still be acquired if those new items are similar to each other. Additional work is required to fully understand the novel observations derived from the simple model used in the present study, and to explore the deeper implications of these observations for connectionist networks more generally.