Extension of UNRES force field to treat polypeptide chains with D-amino-acid residues

Abstract

Coarse-grained force fields for protein simulations are usually designed and parameterized to treat proteins composed of natural L-amino-acid residues. However, D-amino-acid residues occur in bacterial, fungal (e.g., gramicidins), as well as human-designed proteins. For this reason, we have extended the UNRES coarse-grained force field developed in our laboratory to treat systems with D-amino-acid residues. We developed the respective virtual-bond-torsional and double-torsional potentials for rotation about the C^α · · · C^α virtual-bond axis and two consecutive C^α · · · C^α virtual-bond axes, respectively, as functions of virtual-bond-dihedral angles γ. In turn, these were calculated as potentials of mean force (PMFs) from the diabatic energy surfaces of terminally-blocked model compounds for glycine, alanine, and proline. The potential-energy surfaces were calculated by using the ab initio method of molecular quantum mechanics at the Møller-Plesset (MP2) level of theory and the 6-31G(d,p) basis set, with the rotation angles of the peptide groups about ${\text{C}}_{i-1}^{\alpha }\cdots {\text{C}}_i^{\alpha }({\lambda }^{(1)})$ and ${\text{C}}_i^{\alpha }\cdots {\text{C}}_{i+1}^{\alpha }({\lambda }^{(2)})$ used as variables, and the energy was minimized with respect to the remaining degrees of freedom. The PMFs were calculated by numerical integration for all pairs and triplets with all possible combinations of types (glycine, alanine, and proline) and chirality (D or L); however, symmetry relations reduce the number of non-equivalent torsional potentials to 13 and the number of double-torsional potentials to 63 for a given C-terminal blocking group. Subsequently, one- (for torsional) and two-dimensional (for double-torsional potentials) Fourier series were fitted to the PMFs to obtain analytical expressions. It was found that the torsional potentials of the x-Y and X-y types, where X and Y are Ala or Pro, respectively, and a lowercase letter denotes D-chirality, have global minima for small absolute values of γ, accounting for the double-helical structure of gramicidin A, which is a dimer of two chains, each possessing an alternating D-Tyr-L-Tyr sequence, and similar peptides. The side-chain and correlation potentials for D-amino-acid residues were obtained by applying the reflection about the ${\text{C}}_{i-1}^{\alpha }\cdots {\text{C}}_i^{\alpha }\cdots {\text{C}}_{i+1}^{\alpha }$ plane to the respective potentials for the L-amino-acid residues.

1 Introduction

Less than 1 % of all known protein and peptide structures contain D-amino acids.¹ However, D-amino acids are abundant in natural proteins and peptides,² such as cone snail venoms,³ the murein of bacteria,⁴ fungus-produced antibiotics,^5,6 etc., and it is estimated that the D-amino acid market will reach $ 3.7 billion by the year 2017.⁷ Therefore, molecular simulations must be able to treat polypeptides and proteins containing D-amino-acid residues. For all-atom force fields, except those which contain sine torsional terms, there is no problem to handle the D-configuration; however, coarse-grained force fields require additional parameterization for this purpose. Because the coarse-grained force fields offer an enormous advantage for reducing the cost and broadening of the time step of simulations,^8,9 it is worth investing this effort in extending the range of application of such approaches. However, most of the known coarse-grained force fields developed for proteins can treat only the natural L-amino acids.

In the last several years, we have been developing the coarse-grained UNited RESidue (UNRES) force field for simulation of protein structure and dynamics.^10–22 Unlike most of the other force fields, UNRES has been derived^13,23 and parameterized^{13–15,17,19–22,24} as a potential of mean force of polypeptide chains immersed in water. UNRES proved to be a powerful tool in predicting protein structure, as assessed in the Critical Assessment of Techniques for Protein Structure Prediction (CASP) experiments.^25–29 In CASP4, we predicted, for the first time, the complete structure of a 70-residue protein, bacteriocin S (target T0102); with the introduction of correlation terms, we also were able to treat proteins with β-structure.²⁷ During the CASP5 exercise in 2004, we predicted nearly the complete structure (203 out of 235-residues) of a six-a-helix bundle protein (target T0198), complete or nearly complete structures of three other smaller a- and a + b-proteins, and significant portions of structures of other proteins.²⁸ It has also been extended to run coarse-grained molecular dynamics^8,9,30,31 and to study oligomeric proteins.^32,33 Recently, trans-cis isomerization of peptide groups has been introduced into UNRES.²² UNRES has also been applied to study biological problems such as amyloid formation,^34,35 signaling³⁶ and chaperone dynamics.³⁷

In this work, we extend the UNRES force field to treat systems with D-amino-acid residues. For this purpose, we revise the local potentials that depend on amino-acid chirality, namely the virtual-bond torsional and double torsional potentials, the side-chain local potentials, and the correlation potentials. Of those, introduction of the torsional, double-torsional, and virtual-bond-angle potentials (which also depend on the adjacent virtual-bond-dihedral angles) requires reparameterization of the force field, while the other potentials for D-amino-acid residues are obtained in a trivial manner by applying symmetry operations to the respective potentials for the natural L-amino acid residues, as shown in section 2.2. In this work, we have determined the torsional and double-torsional potentials for D-amino-acid residues. The virtual-bond-angle potentials for D-amino-acid residues will be introduced later.

2 Methods

2.1 UNRES representation of polypeptide chain

In the UNRES model,^{10–13,15–23} a polypeptide chain is represented as a sequence of α-carbon (C^α) atoms with attached united side chains (SC’s) and united peptide groups (p’s) positioned halfway between two consecutive C^α’s. Only the united side chains and united peptide groups act as interaction sites, while the C^α atoms assist only in the definition of geometry (Figure 1). The effective energy function is defined as the restricted free energy (RFE) or the potential of mean force (PMF) of the chain constrained to a given coarse-grained conformation along with the surrounding solvent.^13,18,23 This effective energy function is expressed by eq 1.

Fig. 1.

The UNRES model of polypeptide chains. The interaction sites are peptide-group centers (p), and side-chain centers (SC) attached to the corresponding α-carbons with different C^α · · · SC bond lengths, d_SC. The peptide groups are represented as dark gray circles and the side chains are represented as light gray ellipsoids of different size. The α-carbon atoms are represented by small open circles. The geometry of the chain can be described either by the virtual-bond vectors dC_i (from ${\text{C}}_i^{\alpha }$ to ${\text{C}}_{i+1}^{\alpha }$), i = 1, 2, …, n − 1, and dX_i (from ${\text{C}}_i^{\alpha }$ to SC_i), i = 2, …, n − 1, represented by thick lines, where n is the number of residues, or in terms of virtual-bond lengths, backbone virtual-bond angles θ_i, i = 1, 2, …, n − 2, backbone virtual-bond-dihedral angles γ_i, i = 1, 2, …, n − 3, and the angles α_i and β_i, i = 2, 3, …, n − 1 that describe the location of a side chain with respect to the coordinate frame defined by ${\text{C}}_{i-1}^{\alpha },{\text{C}}_i^{\alpha }$, and ${\text{C}}_i^{\alpha }{\text{C}}_{i+1}^{\alpha }$.

$$\begin{array}{l}U=w_{SC}\sum _{i<j}{U}_{{SC}_i{SC}_j}+w_{\mathit{SCp}}\sum _{i\ne j}{U}_{{SC}_i{p}_j}+w_{pp}^{\mathit{VDW}}\sum _{i<j-1}{U}_{p_i{p}_j}^{\mathit{VDW}}+w_{pp}^{el}{f}_2(T)\sum _{i<j-1}{U}_{p_i{p}_j}^{el}\\ +w_{\mathit{tor}}{f}_2(T)\sum _i{U}_{\mathit{tor}}({\gamma }_i)+w_{\mathit{tord}}{f}_3(T)\sum _i{U}_{\mathit{tord}}({\gamma }_i,{\gamma }_{i+1})\\ +w_b\sum _i{U}_b({\theta }_i)+w_{\mathit{rot}}\sum _i{U}_{\mathit{rot}}({\alpha }_{{SC}_i},{\beta }_{{SC}_i})+w_{\mathit{bond}}\sum _i{U}_{\mathit{bond}}(d_i)\\ +w_{\mathit{corr}}^{(3)}{f}_3(T)U_{\mathit{corr}}^{(3)}+w_{\mathit{corr}}^{(4)}{f}_4(T)U_{\mathit{corr}}^{(4)}+w_{\mathit{corr}}^{(5)}{f}_5(T)U_{\mathit{corr}}^{(5)}+w_{\mathit{corr}}^{(6)}{f}_6(T)U_{\mathit{corr}}^{(6)}\\ +w_{\mathit{turn}}^{(3)}{f}_3(T)U_{\mathit{turn}}^{(3)}+w_{\mathit{turn}}^{(4)}{f}_4(T)U_{\mathit{turn}}^{(4)}+w_{\mathit{turn}}^{(6)}{f}_6(T)U_{\mathit{turn}}^{(6)}\end{array}$$ (1)

where the U’s are energy terms, θ_i is the backbone virtual-bond angle, γ_i is the backbone virtual-bond-dihedral angle, α_i and β_i are the angles defining the location of the center of the united side chain of residue i (Figure 1), and d_i is the length of the ith virtual bond, which is either a C^α · · · C^α virtual bond or C^α · · · SC virtual bond. Each energy term is multiplied by an appropriate weight, w_x, and the terms corresponding to factors of order higher than 1 are additionally multiplied by the respective temperature factors which were introduced in our recent work¹⁶ and which reflect the dependence of the first generalized-cumulant term in those factors on temperature, as discussed in refs 16 and 38. The factors f_n are defined by eq 2.

$$f_n(T)=\frac{ln[exp(1)+exp(-1)]}{ln\{exp[{(T/T_{\circ })}^{n-1}]+exp[-{(T/T_{\circ })}^{n-1}]\}}$$ (2)

where T_° = 300 K.

The term U_SCiSCj represents the mean free energy of the hydrophobic (hydrophilic) interactions between the side chains, which implicitly contains the contributions from the interactions of the side chain with the solvent. The term U_SCipj denotes the excluded-volume potential of the side-chain – peptide-group interactions. The peptide-group interaction potential is split into two parts: the Lennard-Jones interaction energy between peptide-group centers ( $U_{p_i{p}_j}^{\mathit{VDW}}$) and the average electrostatic energy between peptide-group dipoles ( $U_{p_i{p}_j}^{el}$); the second of these terms accounts for the tendency to form backbone hydrogen bonds between peptide groups p_i and p_j. The terms U_tor, U_tord, U_b, U_rot, and U_bond are the virtual-bond-dihedral angle torsional terms, virtual-bond dihedral angle double-torsional terms, virtual-bond angle bending terms, side-chain rotamer, and virtual-bond-deformation terms; these terms account for the local properties of the polypeptide chain. The terms $U_{\mathit{corr}}^{(m)}$ represent correlation or multibody contributions from the coupling between backbone-local and backbone-electrostatic interactions, and the terms $U_{\mathit{turn}}^{(m)}$ are correlation contributions involving m consecutive peptide groups; they are, therefore, termed turn contributions. The multibody terms are indispensable for reproduction of regular α-helical and β-sheet structures.^13,23,39

The energy-term weights are determined by force-field calibration to reproduce the structure and folding thermodynamics of selected training proteins.^16,40 As a training proteins LysM domain from E. coli (and R + protein; PDB code: 1E0G),⁴¹ the Fbp28Ww domain from Mus musculus (a protein; PDB code: 1E0L),⁴² the albumin-binding GA module (an R protein; PDB code: 1GAB),⁴³ and the IgG-bindingdomain from streptococcal protein G (an R + protein; PDB code: 1IGD)⁴⁴ and namely the tryptophan cage (PDB code: 1L2Y)⁴⁵ and the tryptophan zipper 2 (PDB code: 1LE1)⁴⁶ were used.

The present UNRES is parameterized for L-amino acid residues. To extend it to D-amino-acid residues, the terms that depend on chirality must be changed. These are the torsional (U_tor), double-torsional (U_tord), side-chain-rotamer (U_rot), correlation (U_corr) and virtual-bond-angle (U_b) potentials. In the subsequent sections we will describe the modification of these potentials for D-amino acid residues. Because the torsional and double-torsional potentials require the greatest effort, we will devote most of the description to these potentials.

2.2 Effect of amino-acid chirality on the side-chain-rotamer and correlation potentials

As mentioned in section 2.1, amino-acid chirality affects the torsional, double-torsional, side-chain rotamer, virtual-bond-bending, and correlation potentials. We begin the discussion with the side-chain rotamer potentials, U_rot, because their dependence on chirality is straightforward. The latest potentials derived in ref. 19 have the form of polynomials in the local coordinates of a side chain, in which, for the ith residue, the x axis is the bisector of the ${\text{C}}_{i-1}^{\alpha }\cdots {\text{C}}_i^{\alpha }\cdots {\text{C}}_{i+1}^{\alpha }$, virtual-bond angle, the y axis is perpendicular to the x axis, lies in the plane of the three C^α atoms, and runs in the direction from ${\text{C}}_{i-1}^{\alpha }$ to ${\text{C}}_{i+1}^{\alpha }$, and the z axis forms a right-handed orthogonal coordinate system with the x and y axes (see Figure 1 in ref. 19 for the illustration of the definition of the local-coordinate system). The change of chirality is achieved just by reflection of a side-chain center in the xy plane; consequently, the sign at all coefficients that pertain to the local z coordinate in eq 3 of ref 19 must be changed. Similarly, the D-chirality can be introduced in the older (statistical) side-chain-rotamer potentials¹² by changing the sign of the coefficients in eq 8 of ref 12 corresponding to odd powers of the polar angle β, which changes sign when the chirality is changed.

Changing chirality is also straightforward for the correlation potential, $U_{\mathit{corr}}^{(m)}$. These potentials contain the coefficients of the second-order Fourier expansion of the local-interaction-energy surfaces, e_X, where X denotes a basic type of amino-acid residue (glycine, alanine, and proline, where alanine represents all non-glycine and non-proline residues) in terms of the angles λ⁽¹⁾ and λ ⁽²⁾ for rotation of the peptide groups about the C^α · · · C^α virtual bonds of terminally-blocked amino-acid residues,¹³ as given by eq 3.

$$e_X({\lambda }^{(1)},{\lambda }^{(2)})={\mathbf{b}}_{\mathbf{1}\mathbf{X}}^{\mathbf{T}}\mathbf{u}+{\mathbf{b}}_{\mathbf{2}\mathbf{X}}^{\mathbf{T}}\mathbf{v}+{\mathbf{u}}^{\mathbf{T}}{\mathbf{C}}_{\mathbf{X}}\mathbf{u}+{\mathbf{v}}^{\mathbf{T}}{\mathbf{D}}_{\mathbf{X}}\mathbf{v}+{\mathbf{u}}^{\mathbf{T}}{\mathbf{E}}_{\mathbf{X}}\mathbf{v}+\dots$$ (3)

with

$$\mathbf{u}\equiv \mathbf{u}({\lambda }^{(1)})=\left(\begin{array}{l}cos{\lambda }^{(1)}\hfill \\ sin{\lambda }^{(1)}\hfill \end{array}\right),\mathbf{v}\equiv \mathbf{v}({\lambda }^{(2)})=\left(\begin{array}{l}cos{\lambda }^{(2)}\hfill \\ sin{\lambda }^{(2)}\hfill \end{array}\right)$$ (4)

where b_1X and b_2X are the 2-dimensional vectors of first-order Fourier coefficients and the matrices C_X, D_X, and E_X are the 2 × 2 matrices of second-order Fourier coefficients of the second-order expansion of the energy surface in the angles λ⁽¹⁾ and λ⁽²⁾ for residue X. Additionally, C_X represents symmetric traceless matrices; therefore, c_X,22 = −c_X,11 and d_X,22 = −d_X,11.

The energy surface of a D-amino-acid-residue, e_x, where the lowercase letter denotes the D-chirality; x = Ala_D or Pro_D (because glycine does not have a side chain and, consequently, is not chiral) is obtained from that of the corresponding L-amino-acid residue by applying the inversion operation to the angular variables, as given by eq 5.

$$e_x({\lambda }^{(1)},{\lambda }^{(2)})=e_X(-{\lambda }^{(1)},-{\lambda }^{(2)})={\mathbf{b}}_{\mathbf{1}\mathbf{x}}^{\mathbf{T}}\mathbf{u}+{\mathbf{b}}_{\mathbf{2}\mathbf{x}}^{\mathbf{T}}\mathbf{v}+{\mathbf{u}}^{\mathbf{T}}{\mathbf{C}}_{\mathbf{x}}\mathbf{u}+{\mathbf{v}}^{\mathbf{T}}{\mathbf{D}}_{\mathbf{x}}\mathbf{v}+{\mathbf{u}}^{\mathbf{T}}{\mathbf{E}}_{\mathbf{x}}\mathbf{v}+\dots$$ (5)

with

$$\begin{array}{c}{\mathbf{b}}_{\mathbf{1}\mathbf{x}}={\mathbf{Ub}}_{\mathbf{1}\mathbf{X}}=\left(\begin{array}{c}{b}_{11X}\\ -b_{21X}\end{array}\right),{\mathbf{b}}_{\mathbf{2}\mathbf{x}}={\mathbf{Ub}}_{\mathbf{2}\mathbf{X}}=\left(\begin{array}{c}{b}_{12X}\\ -b_{22X}\end{array}\right)\\ {\mathbf{C}}_{\mathbf{x}}={\mathbf{UC}}_{\mathbf{X}}{\mathbf{U}}^{\mathbf{T}}=\left(\begin{array}{cc}{c}_{X11}& -c_{X12}\\ -c_{X12}& c_{X22}\end{array}\right),\\ {\mathbf{D}}_{\mathbf{x}}={\mathbf{UD}}_{\mathbf{X}}{\mathbf{U}}^{\mathbf{T}}=\left(\begin{array}{cc}{d}_{X11}& -d_{X12}\\ -d_{X12}& d_{X22}\end{array}\right),\\ {\mathbf{E}}_{\mathbf{x}}={\mathbf{UE}}_{\mathbf{X}}{\mathbf{U}}^{\mathbf{T}}=\left(\begin{array}{cc}{e}_{X11}& -e_{X12}\\ -e_{X21}& e_{X22}\end{array}\right)\end{array}$$ (6)

where U is the matrix for reflection in the ${\text{C}}_{i-1}^{\alpha }\cdots {\text{C}}_i^{\alpha }\cdots {\text{C}}_{i+1}^{\alpha }$ plane.

$$\mathbf{U}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$ (7)

Thus, introducing the D-chirality in the correlation terms is achieved by changing the signs of the coefficients of the second-order expansion of e_X at the terms with odd sine powers.

2.3 Determination of torsional and double-torsional potentials

As opposed to U_rot, the virtual-bond-torsional, U_tor, and double-torsional potentials, U_tord that contain residues with mixed chirality, must be redetermined. The procedure developed in our earlier work¹⁴ was used, in which the respective potentials of mean force are calculated first from the energy maps of terminally-blocked amino-acid residues and then a one- (for U_tor) or two-dimensional (for U_tord) Fourier series is fitted to them. The harmonic-entropy contribution is also considered. The potentials of mean force corresponding to U_tor and U_tord are thus defined by eqs 8 and 9, respectively. The terminally-blocked di- and tripeptide systems used for the derivation of the torsional and double-torsional potentials are illustrated in Figure 2A and B, respectively.

Fig. 2.

Illustration of the model terminally blocked dipeptides (a) and tripeptides (b) constructed to compute the integrals of eqs 8 and 9. Each X,Y and Z denotes sidechains of Ala_L, Ala_D, Gly, Pro_L or Pro_D.

$$\begin{array}{l}{U}_{XY}(\gamma )=-{\beta }^{-1}ln\{\frac{1}{{(2\pi )}^3}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }\\ {[det{\mathbf{H}}^{\ast }({\lambda }_1,\gamma -\pi -{\lambda }_2)\times det{\mathbf{H}}^{\ast }({\lambda }_2,{\lambda }_3)]}^{-\frac{1}{2}}\\ exp\left[-\beta [e_X({\lambda }_1,\gamma -\pi -{\lambda }_2)+e_Y({\lambda }_2,{\lambda }_3)]\right]d{\lambda }_{1}d{\lambda }_{2}d{\lambda }_3\}\\ +{\beta }^{-1}ln\left\{\frac{1}{{(2\pi )}^3}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{[det{\mathbf{H}}^{\ast }({\lambda }_1,{\lambda }_2)]}^{-\frac{1}{2}}exp[-\beta e_X({\lambda }_1,{\lambda }_2)]d{\lambda }_{1}d{\lambda }_2\right\}\\ +{\beta }^{-1}ln\left\{\frac{1}{{(2\pi )}^3}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{[det{\mathbf{H}}^{\ast }({\lambda }_2,{\lambda }_3)]}^{-\frac{1}{2}}exp[-\beta e_Y({\lambda }_2,{\lambda }_3)]d{\lambda }_{1}d{\lambda }_2\right\}\end{array}$$ (8)

where e_X and e_Y are the energy surfaces for the terminally-blocked residues of type X and Y respectively, H^* is the energy Hessian computed over all variables except for the angles λ_i and λ_j (the terms with det H^* account for the harmonic-entropy contribution to the PMF), β = 1/RT where R is the universal gas constant and T is the absolute temperature. For Y = Pro, the C-terminal blocking group of the X residue is pyrrolidine; otherwise it is the methyl group.

$$\begin{array}{l}{U}_{\mathit{XYZ}}({\gamma }_1,{\gamma }_2)=-{\beta }^{-1}ln\{\frac{1}{{(2\pi )}^4}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }\\ {[det{\mathbf{H}}^{\ast }({\lambda }_1,{\gamma }_1-\pi -{\lambda }_2)\times det{\mathbf{H}}^{\ast }({\lambda }_2,{\gamma }_2-\pi -{\lambda }_3)\times det{\mathbf{H}}^{\ast }({\lambda }_3,{\lambda }_4)]}^{-\frac{1}{2}}\\ exp[-\beta [e_X({\lambda }_1,{\gamma }_1-\pi -{\lambda }_2)+e_Y({\lambda }_2,{\gamma }_2-\pi -{\lambda }_3)\\ +e_Z({\lambda }_3,{\lambda }_4)]]d{\lambda }_{1}d{\lambda }_{2}d{\lambda }_{3}d{\lambda }_4\}-[U_{XY}({\gamma }_1)+U_{YZ}({\gamma }_2)]\\ +{\beta }^{-1}ln\left\{\frac{1}{{(2\pi )}^2}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{[det{\mathbf{H}}^{\ast }({\lambda }_1,{\lambda }_2)]}^{-\frac{1}{2}}exp[-\beta e_X({\lambda }_1,{\lambda }_2)]d{\lambda }_{1}d{\lambda }_2\right\}\\ +{\beta }^{-1}ln\left\{\frac{1}{{(2\pi )}^2}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{[det{\mathbf{H}}^{\ast }({\lambda }_2,{\lambda }_3)]}^{-\frac{1}{2}}exp[-\beta e_X({\lambda }_2,{\lambda }_3)]d{\lambda }_{2}d{\lambda }_3\right\}\\ +{\beta }^{-1}ln\left\{\frac{1}{{(2\pi )}^2}{\int }_{-\pi }^{\pi }{\int }_{-\pi }^{\pi }{[det{\mathbf{H}}^{\ast }({\lambda }_3,{\lambda }_4)]}^{-\frac{1}{2}}exp[-\beta e_X({\lambda }_3,{\lambda }_4)]d{\lambda }_{3}d{\lambda }_4\right\}\end{array}$$ (9)

It should be noted that, because the single-torsional potentials U_XY and U_YZ are subtracted from the RFE of the terminally-blocked tripeptide, U_XYZ contains only that part of the free energy of the rotation about the C^α · · · C^α virtual-bond angles that cannot be accounted for by the single-torsional contributions.

The presence of γ₁ − π − λ₂ in eqs 8 and 9 and γ₂ − π − λ₃ in eq 9 arises from the fact that λ₂ is shared between residues X and Y in the dipeptide and in the tripeptide systems, and λ₃ is shared between residues Y and Z in the tripeptide system. The diabatic energy surface, e_X, of a terminally-blocked amino-acid residue X can be expressed as a function of two local angles λ⁽¹⁾ and λ⁽²⁾ for rotation about the consecutive virtual C^α · · · C^α bonds, defined by Nishikawa et al.⁴⁷ and also shown in Figure 3. The local angles of consecutive residues are, in turn, related to the chain-wide angles λ₁, λ₂, …, λ_n shown in Figure 2 by eq 10.

Fig. 3.

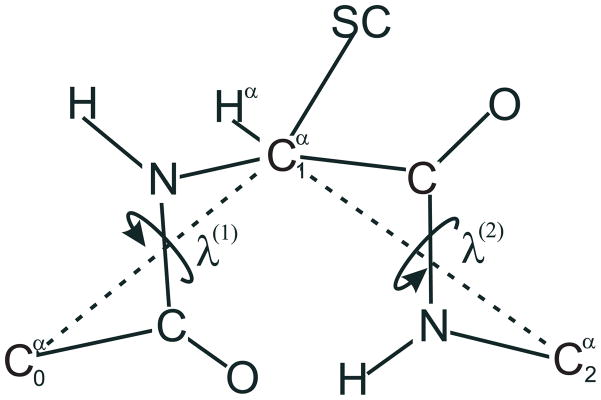
Definition of the dihedral angles λ⁽¹⁾ and λ⁽²⁾ for rotation of a peptide unit about the C^α · · · C^α virtual bonds of a peptide unit.⁴⁷

$$\begin{array}{l}{\lambda }_i^{(1)}={\lambda }_i,i=1,2,\dots ,n\\ {\lambda }_i^{(2)}={\lambda }_{i+1},i=1,2,\dots ,n-1\\ {\lambda }_n^{(2)}={\lambda }_n\end{array}$$ (10)

The integrals in eqs 8 and 9 were calculated by numerical quadrature by summing the values of the integrand over the nodes of a multidimensional grid in the angles λ. The grid size was the same as that with which the corresponding potential-energy surfaces were obtained. The presence of a proline residue reduced the dimensions of a grid by one, because the λ⁽¹⁾ angle of the proline residue is determined by the requirement to obey the constraints accruing from the presence of the pyrrolidine ring. The presence of proline residues also made it necessary to interpolate linearly between the closest points of the original grid to estimate the energy and the logarithm of the determinant of Hessian values for residues preceding proline; otherwise, all energies were taken directly from the ab initio values computed at grid points. This was caused by the fact that λ⁽¹⁾ of a proline residue is a function of λ^(2).48 Thus, even if λ⁽²⁾ is on the grid, λ⁽¹⁾ need not be, if the residue is proline. The angle λ⁽¹⁾ is, in turn, related by eq 10 to λ⁽²⁾ of the preceding residue; therefore, the last angle also, generally, takes values outside the grid points. For non-proline residues, λ⁽¹⁾ is unrestricted. Consequently, the virtual-bond dihedral angles γ are from a grid of the same spacing as the angles λ and, by eq 10, all points taken to evaluate the integrals that occur in eq 8 and eq 9 are on the grid.

In the UNRES force field, the torsional potentials are expressed as a one- and two-dimensional Fourier series, respectively (eqs 11 and 12)

$$U_{XY}(\gamma )=a_0+\sum _{i=1}^{n1}{a}_{i}cos(i\gamma )+b_{i}sin(i\gamma )$$ (11)

$$\begin{array}{l}{U}_{\mathit{XYZ}}({\gamma }_1,{\gamma }_2)=c_0+\sum _{i=1}^{n2}{c}_i^{(1)}cos(i{\gamma }_1)+d_i^{(1)}sin(i{\gamma }_1)+\\ \sum _{i=1}^{n2}{c}_i^{(2)}cos(i{\gamma }_1)+d_i^{(2)}sin(i{\gamma }_1)+\\ \sum _{i=1}^{n2}\sum _{j=1}^{i-1}{e}_{ij}cos[j{\gamma }_1+(i-j){\gamma }_2]+f_{ij}cos[j{\gamma }_1-(i-j){\gamma }_2]\\ g_{ij}sin[j{\gamma }_1+(i-j){\gamma }_2]+h_{ij}sin[j{\gamma }_1-(i-j){\gamma }_2]\end{array}$$ (12)

where a_i, b_i, …, h_ij are coefficients and n1 and n2 are the orders of the expression; we used n1 = 6 and n2 = 8. The coefficients in eqs 11 and 12 were calculated by fitting the U_XY and U_{XY Z} surfaces (obtained by numerical integration) to eqs 11 and 12, respectively. As in previous work,¹⁴ the target function F consisted of the sum of the squares of the errors over the grid points in γ₁ and γ₂ and an entropy-like or smoothing term preventing too large a variation of the fitted functional expression between the points of the grid (eq 13).

$$F=\sum _{i=1}^N{[U_i^{\mathit{num}}-U_i(X)]}^2+\alpha {\int }_{\gamma }\mathrm{\Delta }U(\gamma )exp[\mathrm{\Delta }U(\gamma )]d\gamma$$ (13)

where $U_i^{\mathit{num}}$ denotes the value of a torsional or a double-torsional potential at grid point i, obtained by numerical integration of the energy surfaces of terminally-blocked amino-acid residues (eq 8 or 9), U_i(X) denotes the value of U calculated by using the Fourier series (eqs 11 or 12), ΔU (γ) is the difference between the U expressed by eqs 11 or 12 and the value at that point obtained by linear interpolation between the grid points, and α is the weight of the Shannon-entropy term; we used α = 0.2. The value of α was set after several trial calculations to provide both smooth potentials and good fit to numerically calculated PMF values. The target function of eq 13 was minimized with respect to the coefficients a₀, a₁ …, b₆ (for single-torsional potentials; eq 11) or c₀, c₁, …, h_8,8 (for double-torsional potentials; eq 12) by using the Secant Unconstrained Minimization SoLver (SUMSL) procedure.⁴⁹ The Shannon-entropy term (the last term in eq 13) prevents the fitted functions from oscillating between grid points, and therefore, enables one to obtain quite smooth functions despite using a large number of Fourier terms. It takes a zero value when the function is linear between the grid points and increases considerably if the function oscillates between the grid points.

It can easily be demonstrated that the symmetry relations expressed by eqs 14 and 15 hold; there are only 2 × 13 independent torsional potentials and 2 × 63 independent double-torsional potentials, respectively. The two sets of torsional and double-torsional potentials appear because a regular or proline residue, respectively, can follow a di- or tripeptide fragment in a polypeptide chain; if the following residue is proline, the model system implemented to derive the respective potential is blocked by the N-pyrrolidine group.

$$U_{\mathit{tor};\overline{XY}}(\gamma )=U_{\mathit{tor};XY}(-\gamma )$$ (14)

$$U_{\mathit{tord};\overline{\mathit{XYZ}}}({\gamma }_1,{\gamma }_2)=U_{\mathit{tord};\mathit{XYZ}}(-{\gamma }_1,-{\gamma }_2)$$ (15)

where X, Y, and Z denote amino-acid-residue types of a given chirality (L or D), and a bar over a symbol denotes the change of enantiomer chirality; this operation does not affect glycine.

2.4 Calculations of the energy surfaces for terminally-blocked amino-acid residues

In our previous work,¹⁴ we computed the energy maps of terminally-blocked amino-acid residues by using ab initio molecular quantum mechanics with the 6-31G(d,p) basis set. Because less powerful resources were available at that time, the energy was minimized in the Restricted Hartree-Fock (RHF) scheme and, subsequently, the single-point MP2 energy correction was computed for the energy-minimized conformation. Moreover, interfacing a residue to the following proline residue was modeled by blocking it with an N′,N′-dimethyl group. In this work, all energy maps were recalculated by minimizing the energy in the MP2/6-31G(d,p) scheme; additionally, as mentioned in section 2.3, we used the C-terminal pyrrolidine group and not the N,N-dimethylamine blocking group for residues preceding proline. Consequently, all diabatic energy maps of trans-N-acetyl-alanyl-N′-methyl amide, trans-N-acetyl-alanyl-N′-pyrrolidylamide, trans-N-acetyl-glycyl-N′-methyl amide, trans-N-acetyl-glycyl-N′-pyrrolidylamide trans-N-acetyl-prolyl-N′-methyl amide, and trans-N-acetyl-prolyl-N′-pyrrolidylamide were computed. The angles λ⁽¹⁾ and λ⁽²⁾ were used as grid variables; both varied from −180° to 180° with a 15° step. The energy was minimized with respect to all other degrees of freedom. Energy Hessians (second-derivative matrices or force-constant matrices) were calculated at every grid point to determine the harmonic-entropy contribution to the PMF (eqs 8 and 9).

3 Results and discussion

3.1 Energy maps of terminally-blocked amino-acid residues

The potential-energy surfaces of trans-N-acetyl-L-alanyl-N′-methyl amide, trans-N-acetylL-alanyl-N′-pyrrolidylamide, trans-N-acetyl-glycyl-N′-methyl amide, trans-N-acetyl-glycyl-N′-pyrrolidylamide, trans-N-acetyl-L-prolyl-N′-methyl amide, trans-N-acetyl-L-prolyl-N′-pyrrolidylamide are shown in the Fig. 4 and 5, respectively. The potential-energy surfaces of terminally-blocked D-amino acid residues can be obtained from those shown in Figures 4 and 5 by applying the inversion-symmetry operation (eq 5). The potential-energy maps for the Ac-Ala_L-NHMe and Ac-Gly-NHMe systems (Figure 4A and 4C) resemble those obtained in our earlier study (Figure 4a and 4c in ref 14). It should be noted that, in that study,¹⁴ we included the second-order electron-correlation contribution to the energy only as a correction calculated for RHF-energy-minimized conformations. However, the Ac-Gly-NMe₂ and Ac-Ala_L-NMe₂ potential-energy surfaces used in our previous study¹⁴ to represent the residues preceding proline (Figure 5 in ref 14), exhibit some differences with respect to the Ac-Gly-Pyr and Ac-Ala_L-Pyr potential-energy surfaces (Figure 4B and 4D). The most significant difference is that the high-energy regions λ⁽¹⁾ = 0° and λ⁽²⁾ = 0°, and λ⁽¹⁾ = 0° and λ⁽²⁾ = 180°, are noticeably smaller for both Ac-Gly-Pyr and Ac-Ala_L-Pyr compared to those for Ac-Gly-NMe₂ and Ac-Ala_L-NMe₂, respectively. This feature results from the lack of specific hydrogen-bonding interactions, especially those in the ${\text{C}}_{eq}^7$ conformation, which create narrow and deep energy minima. With the bulky pyrrolidine group in place of a C-terminal amide-hydrogen atom, a broader but shallower minimum is present. Moreover, the high-energy regions of Ac-Gly-Pyr and Ac-Ala_L-Pyr have more complex shape than those of Ac-Gly-NMe₂ and Ac-Ala_L-NMe₂, which is understandable in view of the more complex shape of the Pyr blocking group compared to that of the NMe₂ group.

Fig. 4.

Contour plots of the diabatic potential-energy surfaces of Ac-Ala_L-NHMe (A), Ac-L-Ala_L-Pyr (B), Ac-Gly-NHMe (C), and Ac-Gly-Pyr (D) obtained with the MP2/6-31G(d,p) ab initio method. Energies (kcal/mol) are expressed as relative values with respect to the global-minimum value for a given system, which occurs at (λ⁽¹⁾ = −60°, λ⁽²⁾ = 60°) for Ac-Ala_L-NHMe, (λ⁽¹⁾ = −60°, λ⁽²⁾ = 60°) or (λ⁽¹⁾ = 60°, λ⁽²⁾ = −60°) for Ac-Gly-NHMe, (λ⁽¹⁾ = −135°, λ⁽²⁾ = 135°) for Ac-Ala_L-Pyr and (λ⁽¹⁾ = 180°, λ⁽²⁾ = 180°) for Ac-Gly-Pyr (d). The energy color scale (kcal/mol) is on the top of the figure.

Fig. 5.

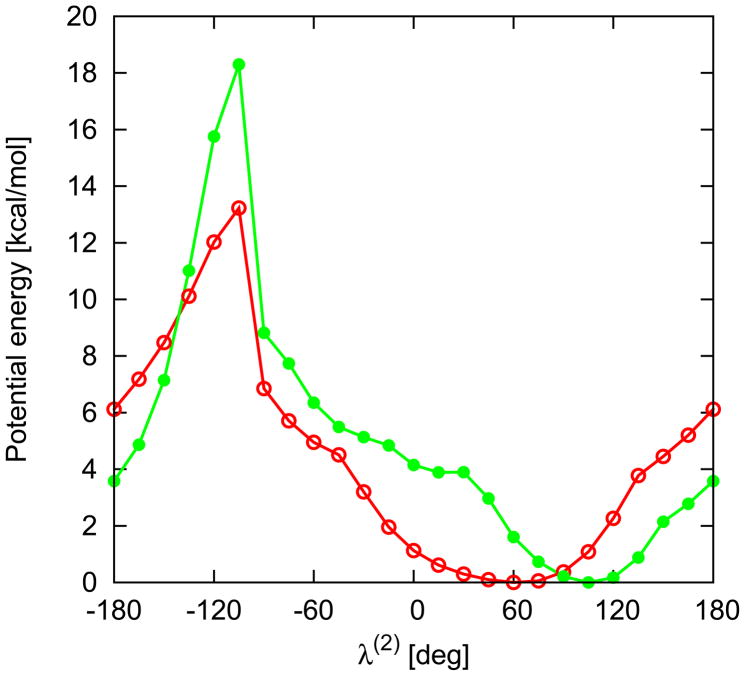
Relative energy profiles (kcal/mol) of Ac-Pro_L-NHMe (red line) and Ac-Pro_L-Pyr (green line) in λ⁽²⁾ angle calculated with MP2/6-31G(d,p) ab initio method.

Another difference between the potential-energy maps of NMe₂- and Pyr-blocked residues is the shape and topology of the energy minima. In Ac-Ala_L-NMe₂, two clearly-separated minima at (λ⁽¹⁾ = −60°, λ⁽²⁾ = 90°) and and (λ⁽¹⁾ = −150°, λ⁽²⁾ = 150°), respectively can be observed, which correspond to the ${\text{C}}_{eq}^7$ and extended conformation, respectively (it should be noted, though, that the hydrogen bond characteristic of the ${\text{C}}_{eq}^7$ conformation is absent because of replacement of the amide-hydrogen atom with a methyl group). For Ac-Ala_L-Pyr, these two minima are shifted to (λ⁽¹⁾ = −75°, λ⁽²⁾ = 90° and λ⁽¹⁾ = −135°, λ⁽²⁾ = 135°) and nearly merged to create a broad low-energy region comprising the ${\text{C}}_{eq}^7$ and extended conformations. This feature is also likely to result from use of the full MP2/6-31G(d,p) energy function in the present study.

Yet bigger differences, resulting from use of a different C-terminal blocking group and minimization of a different energy function, can be observed between Ac-Pro-NMe₂ (Figure 6 in ref 14) and Ac-Pro_L-Pyr (Figure 5). The Ac-Pro_L-Pyr potential-energy plot exhibits only one minimum, while that of Ac-Pro_L-NMe₂ has two maxima. The maximum that appeared at λ⁽²⁾ = 30° for Ac-Pro_L-NMe₂ has coalesced with the minimum at λ ²⁾ ≈ 60° into an inflexion point at λ⁽²⁾ ≈ 20°. These differences and inclusion of the harmonic-entropy contribution result in different torsional and double torsional potentials involving a proline residue.

3.2 Torsional potentials

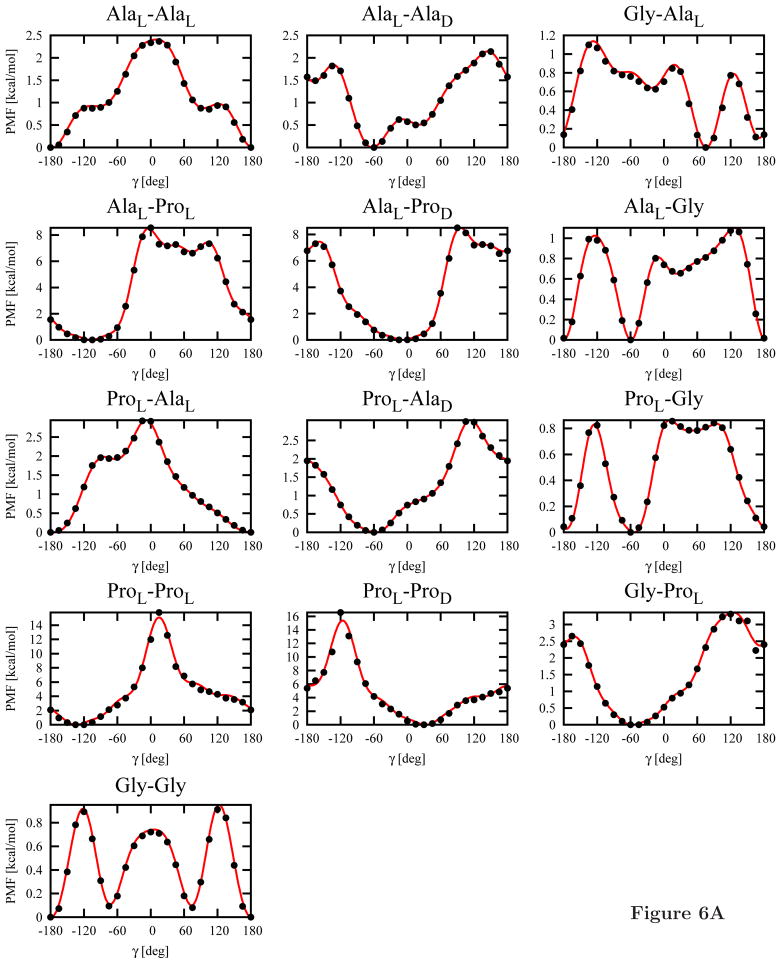
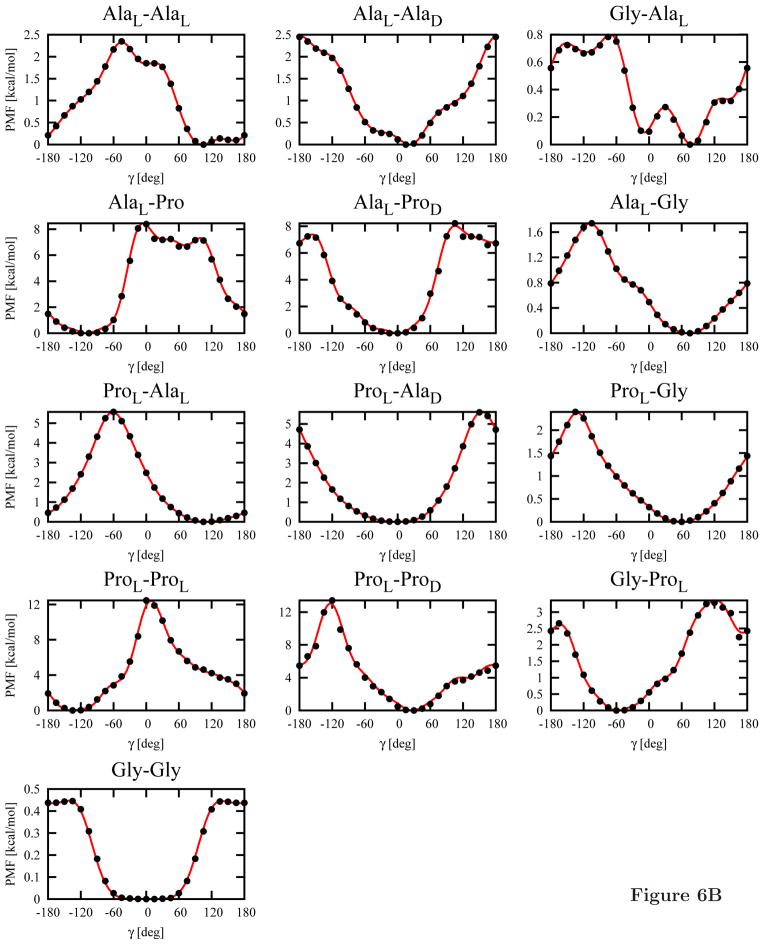
The 13 independent torsional potentials (see section 2.3) for each of the C-terminal blocking groups (NHMe or Pyr; a total of 26 potentials) calculated from the MP2/6-31G(d,p) potential-energy maps by using eq 8 are shown in Figure 6. Subsequently, Fourier series (eq 11) were fitted to them. The Fourier coefficients are collected in Table S1 of Supplementary Material.

Fig. 6.

Plots of the torsional potentials U_XY (γ), where X and Y denote Gly, Ala_L, Pro_L, Ala_D or Pro_D, calculated from the MP2/6-31G(d,p) potential-energy surfaces of terminally-blocked amino-acid residues by using eq 8 (circles) and Fourier fit to these points (eq 11; lines). Panel A: Ac-X-Y-NHMe systems, panel B: Ac-X-Y-Pyr systems.

Despite the more elaborate methodology for calculating the energy surfaces of terminally-blocked amino-acid residues, the torsional potentials of the L-amino-acid-residue sequences blocked with the NHMe group at the C-terminus (Figure 6A) resemble the previously determined potentials (Figure 8a in ref 14). As previously observed,¹⁴ three minima are present in the Gly-Gly potentials at γ = 180° and γ = ±60°, respectively. These minima correspond to extended, type I′ or type II′ (for γ = −60°) and type I or type II (for γ = 60°) β-turns, respectively. As in our previous work,¹⁴ the only minimum of the Ala_L-Ala_L torsional potential corresponds to the extended structure (Figure 7A). This feature results from the fact that, for the extended structure, both residues can form the energetically-favorable ${\text{C}}_{eq}^7$ conformation with a C=O· · · H-N hydrogen bond, as illustrated in Figure 7A. On the other hand, both residues can also be in the extended conformation, which forms a broad low-energy region (Figure 4A and 4C) and, consequently, has high entropy. No minimum corresponding to an α-helical structure is present (γ ≈ 60°), which is understandable because that structure is stabilized only by interactions between the second- and third-neighbor residues, which are not included in the torsional potentials.

Fig. 7.

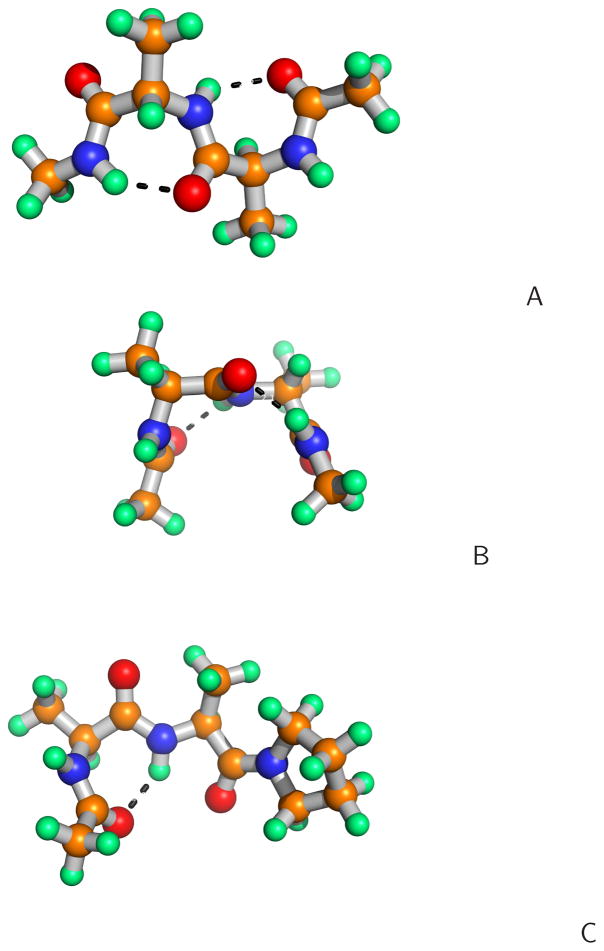
The structures of the dipeptides with the most significant statistical weight in the partition function at the global minimum of the torsional PMF for the (A) Ac-Ala_L-Ala_L-NHMe (λ⁽¹⁾ = −60°, λ⁽²⁾ = 60°, λ⁽³⁾ = −60°, λ⁽⁴⁾ = 60°), (B) Ac-Ala_L-Ala_D-NHMe (λ⁽¹⁾ = −60°, λ⁽²⁾ = 60°, λ⁽³⁾ = 60°, λ⁽⁴⁾ = −60°), (C) Ac-Ala_L-Ala_L-Pyr (λ⁽¹⁾ = −60°, λ⁽²⁾ = 60°, λ⁽³⁾ = −135°, λ⁽⁴⁾ = 135°) systems.

As mentioned in section 2.3, the torsional potentials for the system in which both amino-acid residues are in the D-configuration can be obtained by inverting the potentials for L-aminoacid-residue sequences about γ = 0° (eq 14); the same holds for the torsional potentials of the Gly-X and X-Gly sequences, where X denotes alanine or proline. Conversely, the potentials for the sequences of mixed-chirality dipeptides exhibit a different pattern, as shown in Figure 6. The energy minima occur for small absolute values of γ regardless of whether Ala or Pro is involved and regardless of the type of the C-terminal blocking group. This feature arises from the fact that, for small values of γ, both residues can occur in the energetically-favorable ${\text{C}}_{eq}^7$ conformation (for the L-configuration) or ${\text{C}}_{ax}^7$ conformation (for the D-configuration) or in the portion of the extended-structure region adjacent to the ${\text{C}}_{eq}^7({\text{C}}_{ax}^7)$ region. This situation is illustrated in Figure 7B) for the Ala_L-Ala_D dipeptide. Moreover, the presence of three minima for the Ac-Gly-Gly-NHMe system (Figure 6A) can also now be explained because glycine is an achiral amino acid and any sequence of ${\text{C}}_{eq}^7$ and ${\text{C}}_{ax}^7$ conformations corresponds to low energy of intra-residue interaction. It should be noted that four minima are also present for the Ala_L-Ala_D-NHMe systems; the global minimum occurs at γ ≈ −60° and the second one occurs at γ ≈ 30°. Of course, for the Ac-Ala_D-Ala_L-NHMe sequence, these minima occur at γ ≈ 60° and γ ≈ −30°, respectively, by eq 14.

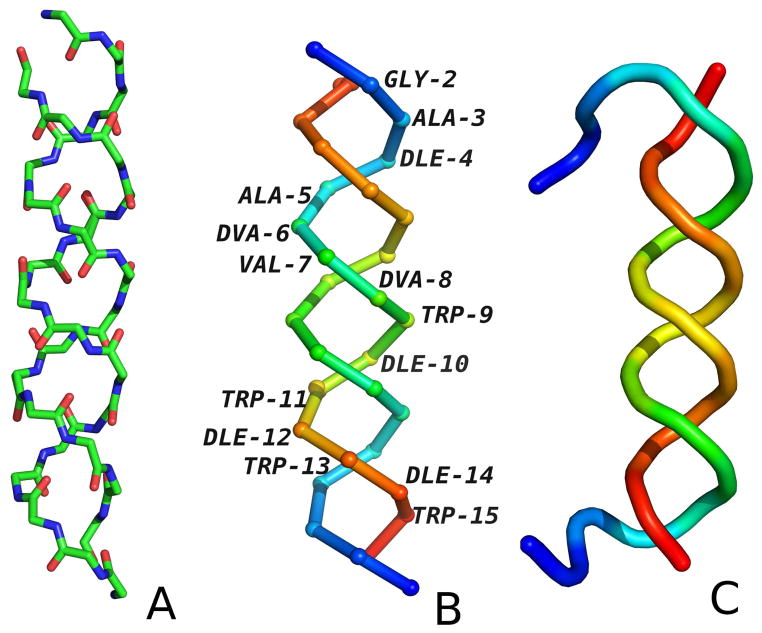
The location of the minima for the alternating sequences of L- and D-amino-acid residues has very interesting structural implications, namely twisting of a pair of a two-strand β-sheet into a double helix. This feature arises because not only C⁷ (axial or equatorial) but also extended conformations, which are capable of forming inter-strand hydrogen bonds, contribute to the partition function at the minima of the torsional potentials for the DL- or LD-chirality sequences. The doubly-helical structure of gramicidin D (PDB code: 1AL4; Figure 8), which is a heterodimer of two chains, each with alternating D- and L-residue sequences, confirms this observation. Our observations of torsional poteitials behaviour were confirmed by conducting MREMD (multiple replica exchange molecular dynamics) of gramicin D (Fig 8C). The structure with the lowest potential energy obtained in 250K is in left-handed double-helix. The RMSD is 3.70Å and is a result of shift by one residue of turn and flexibile N-terminal fragments.

Fig. 8.

The experimental structure of gramicidin D (PDB code: 1AL4). (A) The backbone with all atoms shown to indicate the hydrogen-bonding contacts, (B) The C^α trace with residues colored from blue to red from the N-terminus to the C-terminus for each chain. (C) The cartoon representation of structure obtained from MREMD simulation at 250K colored from blue to red from the N-terminus to the C-terminus for each chain.

As can be seen from Figure 6B, the torsional potentials for the Pyr-blocked dipeptides are different from those for NHMe-blocked ones. The most significant difference occurs for the Gly-Gly dipeptide, for which the two minima at γ ≈ ±60° coalesce into a broad minimum region centered at γ = 0° and the extended-chain minimum at γ = 180° becomes very shallow. Similar differences occur for all glycine-containing systems. For the other systems, the torsional potentials for Pyr-blocked dipeptides have less pronounced fine structure compared to those for the NHMe-blocked systems. This is understandable because the large blocking group, which does not have a proton donor, prevents the formation of local hydrogen bonds and, thus, their formation cannot be reflected in the minima of the torsional potentials.

An analysis of the plots (Figure 6) also reveals that L-proline is an efficient helix breaker. For the Ala_L-Pro_L-NHMe dipeptide, the torsional-potential values are about 9 kcal/mol in the entire region from γ = 0° to γ = 90°, i.e., for all possible values of γ corresponding to α-helical conformations (Figure 6A). If D-proline is inserted in the sequence, such high values of the torsional potential do not occur. This result contradicts the experimental observation that D-proline is a strong α-helix breaker.^50,51 Thus, longer-range than intraresidue interactions must determine helix destabilization by D-proline.

3.3 Double-torsional potentials

All 126 independent potentials (63 for each type of the C-terminal blocking group) were calculated from the MP2/6-31G(d,p) potential-energy surfaces of terminally-blocked glycine, alanine, and proline, by using eq 9. To provide an example, the 4 U_{AlaL–Ala(D,L)–Ala(D,L)–NHMe}(γ₁, γ₂) and the 4 U_{AlaL–Ala(D,L)–Ala(D,L)–P yr} (γ₁, γ₂) PMF surfaces are shown in Figure 9; the surfaces for the system in which the first residue is Ala_D are related to those by eq 15. The other PMF surfaces are shown in Figure S1 of Supplementary Material. Two-dimensional Fourier series (eq 12) were subsequently fitted to the PMFs; the coefficients are collected in Table S2 of Supplementary Material.

Fig. 9.

Sample contour plots of the double-torsional potentials for alanine-type tripeptides, U_{L–Ala–(D,L)–Ala–(D,L)–Ala–NHMe}(γ ⁽¹⁾, γ ⁽²⁾) (A, C, E, G) and U_{L–Ala–(D,L)–Ala–(D,L)–Ala–Pyr}(γ ⁽¹⁾, γ ⁽²⁾) (B, D, F, H). The energy scale (kcal/mol) is on the top of the figure.

As observed for the torsional potentials (section 3.2, the double-torsional potentials are similar to those derived in our previous work,¹⁴ some differences arising for proline-containing tripeptides and the tripeptides blocked with the pyrrolidine C-terminal group. As for the torsional potentials discussed in the previous section, the difference between PMF minima and maxima is usually larger when the tripeptide is blocked with the pyrrolidine group. Even though the double-torsional potentials account for the third-order correlations, the range of their variation is comparable to that of the torsional potential and they, therefore, cannot be ignored in the UNRES effective energy function.

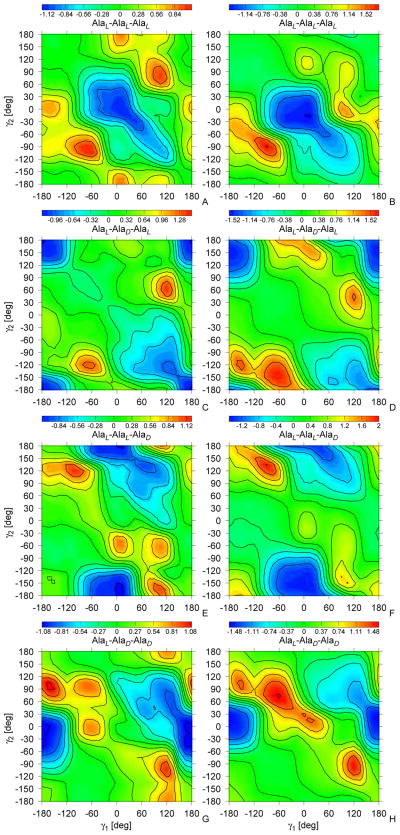
The global minimum for the Ac-Ala_L-Ala_L-Ala_L-NHMe double-torsional potential (Figure 9A) occurs at (λ⁽¹⁾ = 15°, λ⁽²⁾ = −15°) and the minimum region extends along the γ₂ = γ₁ axis towards positive values of γ₁. Thus, the double-torsional potentials for all-L-residue polypeptide chains diminish the propensity towards extended chain conformations and drive the chain at right-handed α-helical conformations. When the L-alanine residue in the middle of the sequence is replaced by D-alanine (Figure 9C), the global minimum is shifted towards γ₁ = γ₂ = 180° and also a shallower minimum appears at γ₁ = 120° and γ₂ = 120°. Thus, for sequences with alternating chirality, the double-torsional potentials have the opposite effect as that of the torsional potentials which favor small values of γ (Figure 6). For the Ac-Ala_L-Ala_L-Ala_D-NHMe system sequence (Figure 9E), the global minimum is located at γ₁ = 15°, γ₂ = −165° and for the Ac-Ala_L-Ala_D-Ala_D-NHMe system (Figure 9G) the global minimum occurs at γ₁ = −15°, γ₂ = 180°, as in β-bulge structures.⁵² The double-torsional potentials for the Pyr-blocked systems (Figure 9B, D, and F) are close to those of the NHMe-blocked system except that the minimum regions are less structured. It should be stressed that both torsional and double torsional potentials contribute to final structure of protein and cannot be separated in easy manner. Structure of gramicidin D obtained from simulation (Fig. 8) cannot be solely contributed to torsional interactions but is a sum of all interactions.

4 Summary

In this work, the potential-energy surfaces of terminally-blocked glycine, L-alanine, and L-proline were calculated at the MP2/6-31G(d,p) ab initio level. The C-terminal blocking group was either the N-methylamino group to account for the situation in which the next residue in the chain is not a proline residue, or pyrrolidine to account for the connection of the residue to a proline residue next in the amino-acid sequence. For Gly and Ala_L, the energy maps were constructed on the grid of the angles λ⁽¹⁾ and λ⁽²⁾ for rotation about the C^α · · · C^α virtual bonds (Figure 3); for L-proline one-dimensional potential-energy surfaces in λ⁽²⁾ were constructed because, for L-proline, λ⁽¹⁾ is a function of λ⁽²⁾ due to the constraint imposed by the presence of the rigid pyrrolidine ring. For each grid point, the energy was minimized with respect to all other degrees of freedom. Energy Hessians were calculated at each grid point to account for harmonic-entropy contributions. Based on the calculated potential-energy surfaces, the energy surfaces of D-alanine and D-proline were constructed by applying the inversion operation.

On the basis of the calculated energy surfaces, the torsional and double torsional potentials for rotation about one or two consecutive C^α · · · C^α virtual-bond axes (defined by the virtual-bond-dihedral angle γ or two consecutive virtual-bond-dihedral angles γ₁ and γ₂), respectively, were calculated and one- or two-dimensional Fourier series, respectively, were fitted to them to obtain the potentials for use in the UNRES force field. The potentials were calculated for all possible combinations of D- and L-amino-acid residues and for both the N-methylamide and pyrrolidine blocking groups. Because the change of the chirality of all residues is equivalent to inversion of the sign of the angle γ or of the angles γ₁ and γ₂, respectively, there are only 13 and 63 independent torsional and double-torsional potentials for each type of C-terminal blocking group, respectively. For L-amino-acid residues and the NHMe C-terminal blocking group, the potentials are very similar to those determined in our previous work;¹⁴ they are, however, more accurate than the earlier¹⁴ ones because of full minimization of the MP2/6-31G(d,p) energy function instead of energy minimization in the RHF/6-31G(d,p) approximation and adding the second-order correction to energy and because of use of the pyrrolidine blocking group to account for a succeeding proline residue instead of using the N′,N′-dimethylamine group.

For sequences with alternating chirality, the torsional and double-torsional potentials exhibit shifted low-energy regions with respect to those for all-L or all-D-amino-acid residue sequences. The torsional potentials for the Ala-Ala sequence exhibit the global energy minimum at the extended conformation, which corresponds to the sequence of two ${\text{C}}_{eq}^7$ or extended conformations of consecutive residues. When the chirality of one of the residues is changed, the preferred absolute value of the γ angle is small; this corresponds to a sequence of ${\text{C}}_{eq}^7$ and ${\text{C}}_{ax}^7$ conformations or vice versa, depending on the chirality of the first residue or of two extended conformations adjacent to the respective C⁷ region. This feature is reflected in the experimental conformation of gramicidin D, which forms a dimer which has a conformation of a left-handed double helix; this double helix can be considered as a distorted two-stranded intermolecular β-sheet and has the hydrogen-bond pattern characteristic of a β-sheet (Figure 8).

We have also demonstrated that the correlation and the side-chain-rotamer potentials of D-amino-acid residues can be obtained from those of L-amino-acid residues by reflection of the respective coefficients in the xy plane of a local coordinate system associated with the C^α · · · C^α · · · C^α unit of a given residue. To complete the extension of UNRES to systems containing D-amino-acid residues, the virtual-bond-angle potentials must be determined; these potentials also depend on the virtual-bond-angles γ₁ and γ₂ adjacent to a given virtual-bond-angle θ. This work in currently underway in our laboratory. We also plan to run series of simulation of proteins eg. gramicidin D containing D-aminoacid residues to check their folding pathways and properties.

The UNRES software is an open source software and can be obtained from webpage: www.unres.pl