Net Risk Reclassification P Values: Valid or Misleading?

Abstract

Background

The Net Reclassification Index (NRI) and its P value are used to make conclusions about improvements in prediction performance gained by adding a set of biomarkers to an existing risk prediction model. Although proposed only 5 years ago, the NRI has gained enormous traction in the risk prediction literature. Concerns have recently been raised about the statistical validity of the NRI.

Methods

Using a population dataset of 10000 individuals with an event rate of 10.2%, in which four biomarkers have no predictive ability, we repeatedly simulated studies and calculated the chance that the NRI statistic provides a positive statistically significant result. Subjects for training data (n = 420) and test data (n = 420 or 840) were randomly selected from the population, and corresponding NRI statistics and P values were calculated. For comparison, the change in the area under the receiver operating characteristic curve and likelihood ratio statistics were calculated.

Results

We found that rates of false-positive conclusions based on the NRI statistic were unacceptably high, being 63.0% in the training datasets and 18.8% to 34.4% in the test datasets. False-positive conclusions were rare when using the change in the area under the curve and occurred at the expected rate of approximately 5.0% with the likelihood ratio statistic.

Conclusions

Conclusions about biomarker performance that are based primarily on a statistically significant NRI statistic should be treated with skepticism. Use of NRI P values in scientific reporting should be halted.

The evaluation of biomarkers to improve risk prediction is a common theme in modern research. New statistical methods for reporting the improvement in prediction performance gained by adding a biomarker to standard risk factors have become common place in publications. In particular, the Net Reclassification Index (NRI) has gained huge popularity since its introduction in 2008 (1,2). A search with Google Scholar on December 16, 2013, yielded 1810 citations of the seminal NRI paper (1) published in 2008. Of those, approximately half (n = 964) occurred in 2012 or 2013. The NRI has gained a reputation as being sensitive to clinically important changes in risk (3,4). It has gained most traction in cardiovascular research, but its use in cancer research publications is accelerating (5–9).

Recent statistical research has raised questions about the validity of conclusions based on the NRI (10,11). Moreover, there has been surprisingly little theoretical or empirical work done examining the validity of the NRI statistic and its associated P value. Therefore we set about evaluating whether the rate of false-positive conclusions using the NRI statistic is acceptable by simulating realistic studies involving biomarkers with no predictive information.

Methods

We considered a scenario where a panel of 4 biomarkers is to be evaluated for its capacity to improve prediction of an outcome beyond an existing risk prediction score. For example, these may represent four candidate biomarkers to improve prediction of 5-year breast cancer risk calculated with the Gail model (12). We generated data for a hypothetical population and simulated studies conducted in that population to determine the proportion of studies that yielded positive statistically significant results for the biomarker panel. Detailed descriptions and data are provided in the Supplementary Materials (available online).

Population Data Description

The method for generating data has been used previously by us (13,14) and by others (15), and the dataset is provided in the Supplementary Materials (available online). The population was comprised of 10000 subjects, of whom 1017 (10.2%) experienced the outcome event and 8983 did not. The baseline clinical risk score was normally distributed in case patients (those with events) and in control subjects (those without events), with a mean difference of 1.73 and standard deviation of approximately 1. Consequently the area under the receiver operating charateristic curve (AUC) for the baseline risk score was 0.88. The four biomarkers that were investigated for their prediction improvement were generated to have no relationship with the outcome. Specifically, in both case patients and in control subjects, the biomarkers had approximately standard normal distributions (Table 1). In a logistic regression model applied to the population of 10000 subjects, including the clinical score and the four markers as predictors, none of the markers were associated with the outcome (Table 1).

Table 1.

Distributions of biomarkers and of the clinical risk score in case patients and in control subjects in the population (n = 10000)

Predictor	Case patients, mean (SD) (n = 1017)	Control subjects, mean (SD) (n = 8983)	Odds ratio	P*
Clinical risk score	1.73 (1.03)	0.01 (0.99)	5.59	<.01
Marker 1	–0.06 (1.01)	0.01 (1.01)	0.94	.10
Marker 2	–0.02 (1.02)	–0.02 (0.99)	1.00	.97
Marker 3	0.01 (0.97)	–0.01 (1.00)	1.03	.49
Marker 4	0.05 (0.98)	0.00 (1.00)	1.01	.72

* Two-sided Wald P values are shown for coefficients in a logistic regression model fit to the population that includes the clinical score and the four candidate markers. SD = standard deviation.

Sampling of Training and Test Datasets and Risk Estimation

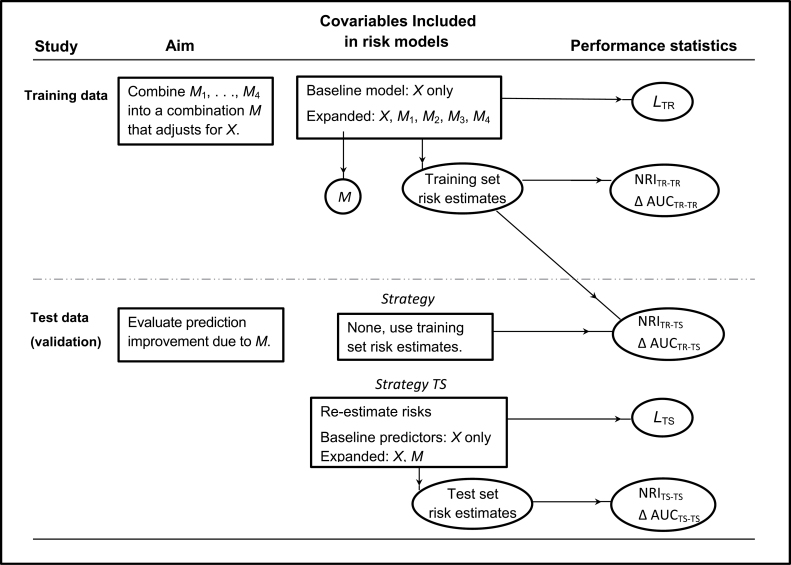
We selected 420 subjects at random from the population for a training dataset. We fit two logistic regression models: the baseline model that included only the clinical risk score (labeled X in Figure 1) and an expanded model that, in addition to X, also included the four markers (labeled as M ₁, M ₂, M ₃, and M ₄). The fitted models were used to calculate risk estimates for each subject in the training dataset. In addition, the linear combination of the markers M ₁–M ₄, derived from the expanded model, was used to define a combination marker M for subsequent validation in an independent test dataset.

Figure 1.

Schema for study design and analysis. The goal was to evaluate if a panel of four biomarkers (M ₁,M ₂,M ₃,M ₄) could improve prediction of a binary outcome (event or case–control status) over a standard clinical score, X. The combined marker M is derived from the expanded model including M ₁–M ₄ fit in the training dataset. Δ AUC = change in the area under the receiver operating characteristic curve; L = likelihood ratio statistic; NRI = net reclassification index; TR = training dataset; TS = test dataset.

It is well known that models fit to training data will appear to perform better than in reality when evaluated in the same training data. An ideal approach to avoiding this overoptimism is to evaluate performance in an independent test dataset. We randomly selected another set of subjects from the population for the test dataset. Test set sample sizes of 420 and 840 were used. We fit two logistic regression models: the baseline model that included only the risk score X and an expanded model that included the combination marker M in addition to X. These latter models are likely to fit the data in the test dataset better than those derived from the training dataset.

For each subject in the test dataset, we calculated risk estimates using two strategies. In the training set (TR) strategy we applied the training set–derived models to each subject’s baseline and marker data. In the test set (TS) strategy we applied the test set–derived models to each subject’s data.

Prediction Performance Improvement Statistics and P Values

The improvement in performance attributable to the four-marker panel was assessed using the NRI statistic. We focus here on the category-free NRI statistic because, unlike earlier versions of the NRI, the category-free NRI does not require making choices for categories of risk. In most cancer settings, clinically meaningful risk categories do not exist. The category-free NRI statistic is calculated as the net proportion of case patients for whom the risk with the expanded model is higher than the risk with the baseline model plus the net proportion of control subjects for whom the risk with the expanded model is lower than the risk with the baseline model:

$$\begin{array}{l}\text{NRI }= \left\{\begin{array}{l}\mathrm{Pr}\text{oportion}\left({\text{risk}}^{\exp }>{\text{risk}}^{\text{base}}| \text{case patients}\right) \\ - \text{Proportion}\left({\text{risk}}^{\exp }<{\text{risk}}^{\text{base}}| \text{case patients}\right)\end{array}\right\}\\ + \left\{\begin{array}{l}\text{Proportion}\left({\text{risk}}^{\exp }<{\text{risk}}^{\text{base}}| \text{control subjects}\right) \\ - \text{Proportion}\left({\text{risk}}^{\exp }>{\text{risk}}^{\text{base}}| \text{control subjects}\right)\end{array}\right\}\end{array}$$

where risk^base is the risk estimate for the baseline model and risk^exp is the risk estimate for the expanded model that includes the markers as well as the baseline risk score. We divide the estimated NRI by its standard error estimate under the null hypothesis (1) and compare with the standard normal distribution to obtain a one-sided P value.

Another statistic that is often used to compare two risk models is the change in the AUC statistic, written ΔAUC. For ΔAUC, we calculated the empirical AUC statistics associated with the estimated risks from the baseline and expanded models and took the difference. The standard Delong method (16,17) was used to calculate a one-sided P value.

Both the NRI and ΔAUC statistics were calculated with training set data using risks estimated from models fit to the training data. The corresponding indexing is TR-TR in Figure 1 and Table 2. The NRI and ΔAUC statistics were also calculated with test set data using risks derived from models fit to training data (TR-TS indexing) and finally with test set data using risks derived from models fit to test set data (TS-TS indexing).

Table 2.

Rates at which the null hypothesis of no performance improvement is rejected in favor of the one-sided alternative hypothesis that prediction is improved by adding the four biomarker panel to the baseline clinical score*

Dataset for calculating performance improvement†	NRI‡	LR‡	ΔAUC‡
Training set (n = 420)
Using training set risks, TR-TR	63.0%	5.3%	9.8%
Test set (n = 420)
Using training set risks, TR-TS	23.2%	—	1.1%
Using re-estimated risks, TS-TS	19.4%	4.7%	1.5%
Test set (n = 840)
Using training set risks, TR-TS	34.4%	—	0.6%
Using re-estimated risks, TS-TS	18.8%	5.1%	1.8%

* Because the biomarkers have no association with the outcome in the population, all rejections are false-positive results. ΔAUC = change in the area under the receiver operating characteristic curve; LR = likelihood ratio; NRI = Net Reclassification Index; TR = training dataset; TS = test dataset.

† Five thousand simulated studies in which the biomarkers have no association with outcome.

‡ Nominal rejection rates are 5.0%.

Traditional likelihood ratio statistics and P values for the expanded vs baseline models in the training data were used to determine whether the markers (M ₁, M ₂, M ₃, M ₄) were associated with the outcome after controlling for the baseline risk score X. The likelihood ratio statistic is denoted by LR_TR and has four degrees of freedom. In the test dataset we also calculated a likelihood ratio statistic (LR_TS) to determine if the marker combination M was associated with risk after controlling for the baseline risk score. This statistic has one degree of freedom.

Simulation Studies

We repeated the exercise of selecting training and test datasets from the population data 5000 times. We summarized the number of simulations in which each of the performance improvement statistics was greater than zero and statistically significant at the nominal .05 significance level.

Results

NRI Statistics

Remarkably, in 3149 (63.0%) of the 5000 simulations, the training dataset NRI statistic, NRI_TR-TR and its P value indicated that the four markers in combination improved prediction over the baseline risk score alone (Table 1).

Even with the independent test data, in 1160 (23.2%) of the 5000 simulations, the smaller (n = 420) test dataset NRI indicated that the markers improved prediction when the risks were derived from the training data (NRI_TR-TS). Because practitioners may only evaluate performance in test data if the training data provide a statistically significant result, we also considered the 3149 validation studies (ie, test datasets) that were preceded by training studies where the NRI was positive and statistically significant. Among these 3149 studies, we found that the test dataset NRI _TR-TS was positive and statistically significant 28.1% of the time. Larger test datasets (n = 840) led to even higher rates of false-positive conclusions with the NRI_TR-TS statistic. Overall, 34.4% of test set NRI_TR-TS statistics were positive and statistically significant, whereas the fraction was 41.3% when considering only those preceded by a statistically significant training set NRI.

Re-estimating the risks in the test dataset led to somewhat lower rates of false-positive conclusions with the NRI statistic (NRI_TS-TS), but the rates were nevertheless unacceptably high. With the smaller sample size, false-positive conclusions occurred in 19.4% of the 5000 simulated studies and in 20.5% of the 3149 that were preceded by a positive training study. With the larger sample size, the corresponding rates were 18.8% and 18.5%, respectively.

ΔAUC statistics

In the training data, the ΔAUC statistic also yielded overoptimistic results but at a lower rate than the NRI. ΔAUC was positive and statistically significant in 9.8% of studies.

In the test datasets the ΔAUC statistic was rarely positive and statistically significant. The rates at which it erroneously indicated that the markers improved prediction were no greater than 2.0% regardless of which risk estimates were used or the sample size of the test dataset.

Likelihood Ratio Statistics

The likelihood ratio statistics calculated in the training and test datasets rejected the null hypothesis at a rate of approximately 5.0%, which was the nominal significance level.

Discussion

In our population data, the markers had no predictive capacity. Yet in simulated studies, the NRI statistic and its P value yielded positive conclusions about them with alarmingly high frequency. This occurred not only in training data where the frequency of false-positive conclusions was 63.0% but also in independent test datasets where the frequencies were 18.8% to 34.4% overall and 18.5% to 41.3% when preceded by a positive training set study.

It is considered poor statistical practice to use the same data to train models and to evaluate their performances because of the inherent overoptimistic bias produced. Nevertheless it is most common to do this in practice, at least when the number of markers is small because test data is usually unavailable and because over fitting is not considered to be a major issue with a small number of markers. However our simulations show that the rate of false-positive conclusions with the NRI statistic is very high in training data, even with one to four markers. In particular, with 420 subjects and an event rate of 10.2%, this approach lead to false-positive results in 63.0% of studies when four markers were considered and in 19.4% of studies when one marker was considered. Evidence for the latter statement can be seen from the results in Table 1 for NRI_TS-TS where risks with and without the single marker M were estimated in the test dataset and the corresponding NRI was calculated in the test dataset.

Use of an independent validation study is considered ideal for evaluating the prediction performance of markers because it avoids the aforementioned overoptimistic bias of fitting and evaluating models on a single dataset. We found, however, that false-positive conclusions based on the NRI statistic occurred with high frequency even in validation test data using risks derived from training data (NRI_TR-TS). This corroborates recent work in the statistical literature (10,11) that shows the NRI statistic can be made positive simply by use of poorly fitting risk models. Unfortunately, we found that refitting the models in the test dataset did not offer a solution, as evidenced by the high false-positive rate associated with NRI_TS-TS.

We included the ΔAUC statistic in our evaluations because it is commonly used in practice and because historically the NRI was introduced to improve upon the ΔAUC. However we do not promote its use, primarily because it lacks clinical relevance to the risk prediction problem. Nevertheless it was interesting to see that it did not share the NRI’s tendency to provide false-positive conclusions in validation data and that in training data the rate of false-positive conclusions was much reduced relative to the NRI.

Our simulations focused on the category-free NRI statistic. In circumstances where risk categories exist, a corresponding category-based NRI statistic can be calculated (1). Although one simulation study that considered the setting where a single biomarker is evaluated in a large training dataset (n = 5000 with 10.0% event rate) found that a three- or four-category NRI yielded false-positive conclusions in approximately 5% of studies (18), we have documented in another setting that very high rates of false-positive conclusions can also occur with category-based NRI statistics (19). The problem we have documented here is therefore not unique to the category-free NRI. We surmise that in practice the problem of high rates of false-positive conclusions may be more severe with the category-free NRI than with the category-based NRI. Unfortunately, it is unclear under what circumstances the category-based NRI is well behaved. Moreover, there is no theory to provide insight or to support its use. Therefore, conclusions about improved risk prediction that are supported primarily by the P value of the category-based NRI statistic are also tenuous.

To exemplify the practical importance of our results, we consider how they affect the interpretation of the results of a recent study published in the New England Journal of Medicine (9). The study reported the category-free NRI for a panel of six biomarkers. A test dataset was not available, so the study used a single training dataset to fit risk models and evaluate the performance of the six-marker panel. The predictive capacity of the six-marker panel did not yield a statistically significant change in the AUC statistic, but it did yield a statistically significant category-free NRI statistic. According to our findings, these results would not be unexpected, even if the biomarkers were completely uninformative. Positive conclusions about the capacity of the markers to improve risk prediction based on statistical significance of the NRI statistic alone cannot be trusted. Fortunately the investigators included additional analyses that provided more trustworthy evidence in favor of their biomarkers.

The simulation scenarios we considered are similar to those used by others evaluating prediction performance metrics (15). We used normal distributions in case patients and control subjects for markers and other covariables. We only considered markers that were uninformative of outcome because our interest was in the rates of false-positive conclusions made about them. The sample sizes and event rates were reasonable relative to the numbers of predictors in the risk models. In the training dataset, the expected number of events was 42, whereas the number of predictors was at most five, yielding an events-to-predictor ratio of 8.2. This events-to-predictor ratio is in line with standard rules of thumb (20). In the test data, the events-to-predictor ratio exceeded 21 (42 / 2 = 21).

Although we used standard methods to calculate P values for the NRI and ΔAUC statistics, we note that these methods are not valid for the TR-TR and TS-TS versions of these statistics where the same data is used to fit models and to calculate the performance measures (14,21–23). As explained in the Supplementary Material (available online), the problem is not simply overoptimism, but there are also concerns about nonnormal distributions for the statistics. Currently there are no valid statistical methods for testing NRI = 0 and ΔAUC = 0 based estimates derived from the same data used to fit risk models. Testing can be better accomplished by using likelihood ratio statistics (14).

Why are rates of false-positive conclusions not close to the nominal 5.0% level for the TR-TS statistics where separate datasets are used to fit risk models and to estimate performance? This is discussed in the Supplementary Materials (available online), where we note that the performance of the expanded training set–derived model is actually worse than that of the baseline training set–derived model because the former simply adds statistical noise (ie, uninformative markers) to the baseline score. For this reason the ΔAUC tends to be negative, not zero, and consequently the rate of false-positive conclusions is 0.6% to 1.8%, less than the nominal 5.0% rate that is expected when ΔAUC is truly zero. It is particularly concerning that the NRI statistic provides 23.2% to 34.4% rates of positive conclusions when the expanded model tends to be worse than the baseline model.

The key implication of our findings is that one should not rely on statistical significance of the NRI statistic as evidence for improved prediction performance in biomarker evaluation studies. Statistical significance can easily occur even when the biomarker is not predictive. The recent tendency toward reporting the NRI and its P value in publications should be halted.

Instead, we make two recommendations. First, we recommend that a standard test of the statistical significance of the regression coefficients for the markers in the expanded risk model be reported. For example, the likelihood ratio statistic can be used for this purpose. Not only does it have reliable statistical properties, but it also has been shown mathematically that if the markers contribute to risk while controlling for X, the corresponding population values of the category-free NRI and the ΔAUC cannot be zero (14). There is no need for additional testing. In the six-biomarker analysis presented in Table 1 of the aforementioned New England Journal of Medicine article (9), the statistically significant regression coefficient associated with the high vs low “panel value” is ample evidence that the population values of ΔAUC and NRI are not zero.

Second, we recommend that clinically relevant ways to describe improvement in prediction be reported. We and others (24,25) have argued that the ΔAUC is not clinically relevant, but the NRI statistic is also not a clinically relevant measure of prediction performance. A recent critical review of the NRI statistic (26) notes an array of issues with interpreting the NRI. For example, the NRI is commonly misinterpreted as “the proportion of patients reclassified to a more appropriate risk category” (27) or as the proportion of patients “more appropriately classified” (9). The fact that the NRI considers all changes in risk or risk category equal is another fundamental flaw. Gail (28) notes further problems with the NRI. More straightforward approaches to describing improvement in prediction should be encouraged. Descriptive information in risk reclassification tables, changes in proportions of case patients and control subjects above (or below) relevant risk thresholds (13), and the corresponding summaries of net benefit (29) or relative utility (30), which are also used in practice (31–34) seem particularly appealing.

Funding

This work was supported by the National Institutes of Health (RO1 GM054438 and U24 CA086368 to MSP; U01 CA152637 to CIL; R01 CA152089 to HJ).

The study sponsor had no role in the the design of the study; the collection, analysis, and interpretation of the data; the writing of the manuscript; and the decision to submit the manuscript for publication.