Functional Generalized Additive Models

Abstract

We introduce the functional generalized additive model (FGAM), a novel regression model for association studies between a scalar response and a functional predictor. We model the link-transformed mean response as the integral with respect to t of F{X(t), t} where F(·,·) is an unknown regression function and X(t) is a functional covariate. Rather than having an additive model in a finite number of principal components as in Müller and Yao (2008), our model incorporates the functional predictor directly and thus our model can be viewed as the natural functional extension of generalized additive models. We estimate F(·,·) using tensor-product B-splines with roughness penalties. A pointwise quantile transformation of the functional predictor is also considered to ensure each tensor-product B-spline has observed data on its support. The methods are evaluated using simulated data and their predictive performance is compared with other competing scalar-on-function regression alternatives. We illustrate the usefulness of our approach through an application to brain tractography, where X(t) is a signal from diffusion tensor imaging at position, t, along a tract in the brain. In one example, the response is disease-status (case or control) and in a second example, it is the score on a cognitive test. R code for performing the simulations and fitting the FGAM can be found in supplemental materials available online.

1 Introduction

This paper studies regression with a functional predictor and a scalar response. Suppose one observes data {(X_i(t), Y_i) : t ∈ τ} for i = 1, …, N, where X_i is a real-valued, continuous, square-integrable, random curve on the compact interval τ and Y_i is a scalar. We assume that the predictor, X(·), is observed at a dense grid of points. The problem addressed here is estimation of E(Y_i∣X_i), which is assumed independent of i. We introduce the model

$$g\left\{E(Y_i\mid X_i)\right\}={\theta }_0+{\mathit{\int }}_{\tau }F\{X_i(t),t\}\mathit{dt},$$ (1)

where θ₀ is the intercept, g is a known link function, and F is an unspecified smooth function to be estimated. As a special case, when g(x) = x and F(x, t) = β(t)X_i(t), we obtain the most commonly used regression model in functional data analysis, the functional linear model (Ramsay and Dalzell 1991), henceforth the FLM,

$$E(Y_i\mid X_i)={\theta }_0+{\mathit{\int }}_{\tau }\beta (t)X_i(t)\mathit{dt},$$ (2)

where β(·) is the functional coefficient with β(t) describing the effect on the response of the functional predictor at time t. The FLM can be thought of as multiple linear regression with an infinite number of predictors, as we now explain. Let t_ij = t_j for 1, …, J denote the observation times for the curves X_i(·); then the usual multiple linear regression model $E(Y_i\mid X_i(t_1),\dots ,X_i(t_J))={\beta }_0+{\sum }_{i=1}^J{\beta }_j{X}_i(t_j)={\beta }_0+J^{-1}{\sum }_{i=1}^J{\beta }_j^{\prime }{X}_i(t_j)$ can be viewed as a Riemann sum approximation that converges to (2) as J → ∞. This model has been extended to a functional generalized linear model, i.e. a model of the form g{E(Y_i∣X_i)} = θ₀ + ∫_τ X_i(t)β(t)dt (e.g., James 2002; Müller and Stadtmüller 2005).

Now consider an additive model of the form $E\{Y_i\mid X_i(t_1),\dots ,X_i(t_J)\}={\theta }_0+{\sum }_{j=1}^J{f}_j\{X_i(t_j)\}$, where the f_j’s are unspecified smooth functions. The basic idea is to rewrite the model as $E\{Y_i\mid X_i(t_1),\dots ,X_i(t_J)\}={\theta }_0+J^{-1}{\sum }_{j=1}^{J}F\{X_i(t_j),t_j\}$, and then let J → ∞ and add a link function. The model obtained is our model (1). We call model (1) the functional generalized additive model (FGAM). Our modelling approach provides greater flexibility, as it does not make the strong assumption of linearity between the functional predictor and the functional parameter. To overcome the so called curse of dimensionality, we will perform smoothing in both the x and t components of F(·, ·). Just as the FLM is the natural extension of linear models to functional data, our model is the natural extension of generalized additive models (GAMs) to functional data.

There are few instances in the literature of nonparametric, additive structures being used for scalar on function regression models. Müller and Yao (2008) and James and Silverman (2005) both consider GAMs that use linear functionals of the predictor curves as covariates. The former approach regresses on a finite number of functional principal components scores and the latter approach searches for linear functionals using projection pursuit. Both models rely strongly on the linear directions they estimate; in contrast, our modelling approach regresses on the functional predictors directly. A model that is additive in the principal component scores is not additive in X(t) itself, and vice versa. Therefore, our FGAM and the additive model of Müller and Yao (2008) are different and should be considered complementary, rather than competitors.

Additive models are attractive for a number of reasons; see for example Buja et al. (1989) and Hastie and Tibshirani (1990), which are standard, early references. Initial work in the area advocated smoothing splines and backfitting for fitting these models. Additional theory for backfitting was developed in a series of papers by Opsomer and Ruppert (1997, 1998, 1999). An alternative to classical backfitting is the smooth backfitting of Mammen et al. (1999). Though not as widely used, it has been shown to offer a number of advantages; see Nielsen and Sperlich (2005) for a discussion of its implementation and practical performance. Recently, penalized regression splines have proven successful in a number of applications. Estimation in this case is most often done with penalized, iteratively reweighted least squares (P-IRLS) with smoothing parameters chosen using generalized cross validation (GCV); for example, see Marx and Eilers (1998), Ruppert et al. (2003), and Wood (2006b). This is the approach we adopt to estimate the FGAM. In general, additive models offer increased flexibility and potentially lower estimation bias than linear models while having less variance in estimation and being less susceptible to the curse of dimensionality than models that make no additivity assumptions. The proposed model (1) provides greater flexibility than the FLM, while still facilitating interpretation and estimation.

One area where this increased flexibility is useful is diffusion tensor imaging (DTI), which we consider in Section 5. The dataset contains closely spaced evaluations of measures of neural functioning on multiple tracts in the brain for patients with multiple sclerosis and healthy controls. We will use these measurements as regressors and predict multiple health outcomes to gain a better understanding of how the disease is related to DTI signals. Our model is able to quantify the effect that the functional predictor has on the response at each position along the tract, something that a model such as the GAM of Müller and Yao (2008) is unable to do, since it uses principal component scores and hence loses information about tract location. Another potential application of FGAM is to study how a risk factor trajectory such as body mass index or systolic blood pressure is related to a health outcome such as developing hypertension (e.g. see the study in Li et al. 2007). Our FGAM can locate times of life when the risk factor has its greatest effect; this is not possible if principal component scores are used in a GAM.

For estimation of the model (1), we will use P-splines (Eilers and Marx 1996). However, there will be some differences from standard fitting of tensor product P-splines. Namely, our design matrix is obtained from integrating products of B-splines over functional covariates. P-splines offer many computational advantages. Additional scalar or functional predictors can be incorporated in a simple way and will not require backfitting. Both types of predictors can be included in either a linear or an additive fashion. Though we use P-splines, our estimation procedure can incorporate other bases and penalties for some or all of the covariates. We use well-developed, efficient techniques for the computations (Wood 2006b; Ramsay et al. 2009).

We also propose transforming the functional predictors using the empirical cumulative distribution function (empirical cdf) at fixed values of t. This transformation is convenient for estimation purposes and retains the interpretation advantages provided by the FGAM when the raw curves are used. Considering again the DTI data example, when this transformation is used, we can now infer the effect on the response of a subject being in the pth-quantile for the functional predictor at a particular location along the tract.

To see how our model can aid in uncovering the underlying structure of a functional regression problem, consider Figure 1. The figure shows the estimated surface, F̂(·, ·), for one of the functional predictors in the DTI dataset when the response is disease status (= 1 if the subject has the disease). Overlaid on the surface are the observed functional predictor values for two subjects. The surface is non-linear in x, so an FLM based on the predictors may be inadequate for this problem. We see that for the most part, the solid curve, belonging to a control subject, takes smaller values on the surface than the dashed curve, which belongs to a MS patient, does; thus, the subject with MS will have a higher fitted value and is more likely to be classified as having the disease. It will be shown for this dataset that the added generality of our approach leads to improved predictive accuracy over the FLM.

Figure 1.

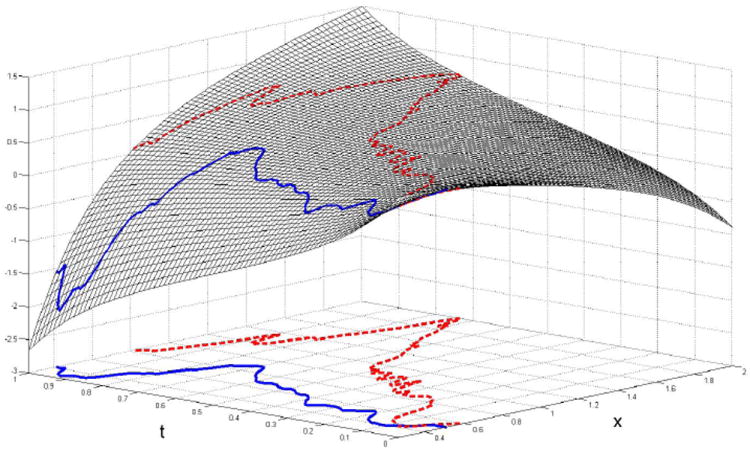
Estimated surface F̂(x, t) and two predictor curves for the DTI dataset. The solid curve belongs to a control and the dashed curve belongs to an MS patient.

We also show how standard error estimates for the parameters of the FGAM are obtained and examine the performance of confidence bands constructed from these standard errors through a simulation study. These are used to make approximate inferences about the estimated surface and the estimated second derivative surface ∂²/∂x² F̂(x, t) which can be used to detect nonlinearity in x. Several diagnostic plots such as the one in Figure 1 are available for exploring the relationship between the predictors and the response.

The article is organized as follows. Section 2 introduces the FGAM in more detail. Our estimation procedure using P-splines is discussed in Section 3. Section 4 applies our model to simulated datasets and compares it with some standard regression models used in functional data analysis. Section 5 discusses the results of applying our model to the DTI dataset. Section 6 concludes with a brief discussion and mentions some possible extensions.

2 Functional Generalized Additive Model

In this section, we introduce our representation for F(·, ·), describe the identifiability constraints, and discuss a transformation of the functional predictor. It is assumed that τ = [0, 1] and that X(·) takes values in a bounded interval which, without loss of generality, can be taken as [0, 1]. The latter assumption is guaranteed by the proposed transformation of the functional predictors discussed in Section 2.2.

We will model F(·, ·) using tensor products of B-splines. Splines are commonly used for estimation of functional linear models. For example, smoothing splines are used by Crambes et al. (2009) and Yuan and Cai (2010) and penalized splines are considered by Cardot et al. (2003) and Goldsmith et al. (2010b). These papers impose smoothness using a penalty on the integrated, squared second derivative of the coefficient function. Instead, we use the popular Psplines of Eilers and Marx (1996). P-splines use low rank B-splines bases with equally-spaced knots and a simple difference penalty on adjacent coefficients to control smoothness.

The many advantages of using P-spline estimators in additive modelling are discussed in detail in Marx and Eilers (1998). The implementation with P-splines will make it possible to estimate all the components of the model at once. While backfitting could be implemented for the case of multiple predictors, it is not feasible for estimating (1). It will be shown that the fitted values for the FGAM are linear in the tensor product B-spline coefficients so we actually have a penalized generalized linear model (GLM). By using fewer knots than there are observations, the size of the system of equations for the estimation is reduced. Penalized splines are fairly insensitive to the position and the number of knots compared to unpenalized splines. Also, unlike smoothing splines, P-splines allow any degree of B-spline to be used with any order of differencing for the penalty.

2.1 Notation and Identifiability Constraints

A bivariate spline model is used for F(·, ·) so that

$$F(x,t)=\sum _{j=1}^{K_x}\sum _{k=1}^{K_t}{\theta }_{j,k}{B}_j^X(x)B_k^T(t)$$ (3)

where $\{B_j^X(x):j=1,\dots ,K_x\}$ and $\{B_k^T(x):k=1,\dots ,K_t\}$ are spline bases on [0, 1]. We will use B-spline bases. It follows from combining (1) and (3), that we obtain the GLM

$$g\{E(Y_i\mid X_i)\}={\theta }_0+{\mathit{\int }}_{\tau }F\{X_i(t),t\}\mathit{dt}={\theta }_0+\sum _{j=1}^{K_x}\sum _{k=1}^{K_t}{\theta }_{j,k}{Z}_{j,k}(i),$$ (4)

where $Z_{j,k}(i)={\mathit{\int }}_{\tau }{B}_j^X\{X_i(t)\}{B}_k^T(t)\mathit{dt}$. Each Z_j,k(i) can be approximated by, say, Simpson’s rule.

For identifiability, we require ${\sum }_{i=1}^N{\mathit{\int }}_{\tau }F(X_i(t),t)\mathit{dt}=0$ (Wood 2006b, Section 4.2). This constraint may not be enough to ensure identifiability on its own, however, so we must perform a further check for numerical rank deficiency during fitting. The details are explained in the next section. Additional discussion of identifiability for the FGAM is also provided in Appendix A available in the online supplemental materials.

2.2 Transformation of the Predictors

Depending on the number of B-splines used for each axis, there could be a particular tensor product of B-splines that has no observed data on its support. This would lead to Z_j,k(i) = 0 for all i for some j, k pair; resulting in the design matrix containing a column of zeros. One remedy for this is to transform X(t) by G_t(x) := P{X(t) < x} for each value of t. Our model becomes

$$g\{E(Y_i\mid X_i)\}={\theta }_0+{\mathit{\int }}_{\tau }F[G_t\{X_i(t)\},t]\mathit{dt}={\theta }_0+\sum _{j=1}^{K_x}\sum _{k=1}^{K_t}{\theta }_{j,k}{\mathit{\int }}_{\tau }{B}_j^G[G_t\{X_i(t)\}]B_k^T(t)\mathit{dt},$$ (5)

where B^G(·) is a new B-spline basis with support on [0, 1]. Loosely, the data are being “stretched out” to fill the entire space that the grid of B-splines will cover. For any t, the transformed points will lie uniformly between [0, 1]. Though the estimation procedure is the same in both cases, clearly, F(·, ·) in (5) will have a different estimate from F(·, ·) in (1). We estimate G_t(·) using the empirical cdf ${\widehat{G}}_t(x)=n^{-1}\sum _{i=1}^{n}I\{X_i(t)<x\}$, where I{A} = 1 if condition A is true and I{A} = 0 otherwise. Once the Z_j,k(i)’s have been estimated, the fitting procedure is analogous to the case when the cdf transformation is not used. Another advantage of using this approach is that it does not require any assumptions about the range of the predictors. Besides the computational advantages, this transformation retains the benefit of ease of interpretation. In fact, F(p, t) is the effect of X(t) being at its pth quantile.

Another potentially useful transformation we do not pursue in this paper is ${\widehat{H}}_t(x)=n^{-1}{\sum }_{i=1}^n\mathrm{\Phi }\left[\frac{x-X_i(t)}{h_t}\right]$, where Φ(·) denotes the standard normal cdf and h_t is a user chosen bandwith that can depend on t. The advantage of this transformation over the empirical cdf transformation is that future observations falling below[above] the minimum[maximum] value of the training data at a particular t are not all assigned the value zero[one].

Due to the penalization used later when fitting the FGAM, parameter estimates can still be obtained when the design matrix has a column of zeros. However, we expect our transformation will improve both the numerical and statistical stability of our estimates. Note also that if there exists any pointwise transformation, H_t(·), such that $g\{E(Y_i\mid X_i)\}={\mathit{\int }}_{\tau }\beta (t)H_t\{X_i(t)\}\mathit{dt}$, then the FGAM will still hold; and similarly, for any model of the form (5) for a general transformation G_t(·). Thus, the FGAM is invariant to transformations of the predictor, unlike the FLM.

3 Estimation

In this section, we present the estimation procedure for F(·, ·). First, we review P-spline type penalties and discuss penalized GLMs and the selection of smoothing parameters. We then describe the estimated surface and discuss construction of pointwise confidence bands for these estimates. We conclude the section by showing how to include additional functional and nonfunctional predictors in the model.

3.1 Roughness Penalties

Smoothing can be achieved by using row and column penalties as in Marx and Eilers (1998). The row penalty is ${\lambda }_1{{\sum }_{j=d+1}^{K_x}({\mathrm{\Delta }}_j^d{\theta }_{j,k})}^2$, where ${\mathrm{\Delta }}_j^d{\theta }_{j,k}$ is the dth difference of the sequence θ_j−d,k, …, θ_j,k (k held fixed). The column penalty is ${\lambda }_2{{\sum }_{k=d+1}^{K_t}({\mathrm{\Delta }}_k^d{\theta }_{j,k})}^2$, where ${\mathrm{\Delta }}_k^d{\theta }_{j,k}$ is the dth difference of the sequence θ_j,k−d, …, θ_j,k (j held fixed). Selection of the penalty parameters λ₁ and λ₂ is discussed in Section 3.2.

Proceeding similarly to Marx and Eilers (2005), we first place the Z_j,k(i)’s in a matrix as follows. Let Z_i = vec {ℤ(i)} be the K_xK_t-vector obtained by stacking the columns of $\mathbb{Z}(i)={[Z_{j,k}(i)]}_{j=1,\dots ,K_x}^{k=1,\dots ,K_t}$, and let ℤ = [Z₁ Z₂ ⋯ Z_N]^T. The penalty matrix is given by

$$\mathbb{P}={\lambda }_1{\mathbb{P}}_1^T{\mathbb{P}}_1+{\lambda }_2{\mathbb{P}}_2^T{\mathbb{P}}_2,$$ (6)

with ℙ₁ = D_x ⊗ I_Kt, ℙ₂ = I_Kx ⊗ D_t where I_p is the p × p identity matrix, ⊗ is the Kronecker product, and D_x and D_t are matrix representations of the row and column difference penalties with dimension (K_x − d_x) × K_x and (K_t − d_t) × K_t, respectively. The parameter, d, denotes the prespecified degree of differencing. Note that additional penalties such as an overall ridge penalty could also be incorporated.

To incorporate the intercept, a leading column of ones must be added to ℤ and a leading column of zeros must be added to ℙ₁ and ℙ₂. Throughout the rest of the paper, this has been done unless otherwise indicated. When we don’t wish to consider the intercept, M_[−i,−j] will denote the matrix M with its ith row and jth column removed and ν_[−i] will denote the vector ν excluding its ith entry.

3.2 Penalized GLMs and Smoothing Parameter Selection

Let the response vector, Y, be from an exponential family with density having the form $f_Y(\mathbf{y};\mathit{\zeta },\varphi )={\prod }_{i=1}^N\exp [\{y_i{\zeta }_i-b({\zeta }_i)\}/a(\varphi )+c(y_i,\varphi )]$, where ζ is the canonical parameter vector with components satisfying ζ_i = (b′)⁻¹(μ_i) and ϕ is the dispersion parameter. Parameterizing E(Y∣X) as a standard GLM with known link function, g(·), let η := ℤθ and μ := E(Y∣X), so that η = g(μ). The constraint discussed in Section 2.1 is enforced by requiring 1^Tℤ_[,−1]θ = 0. Formally, this is done by obtaining the QR decomposition of ${({\mathbf{1}}^T{\mathbb{Z}}_{[,-1]})}^T=[\begin{array}{cc}{\mathbf{Q}}_1& {\mathbb{Q}}_2\end{array}]\left[\begin{array}{l}{ℝ}_1\\ {ℝ}_2\end{array}\right]$, where ℚ₂ has dimension (1 +K_xK_t) × K_xK_t. The constrained optimization problem is then replaced by an unconstrained optimization (outlined below) over θ_q, where θ_q is such that θ = ℚ₂θ_q. For notational simplicity, for any matrix M, define M̃ = Mℚ₂.

The penalized log-likelihood to be maximized is

$$l({\mathit{\theta }}_q;{\lambda }_1,{\lambda }_2)={\sum _{i=1}^N\log \{f_Y(y_i;{\zeta }_i,\varphi )\}-{\lambda }_i\Vert {\stackrel{\sim }{\mathbb{P}}}_1{\mathit{\theta }}_q\Vert }^2-{\lambda }_2{\Vert {\stackrel{\sim }{\mathbb{P}}}_2{\mathit{\theta }}_q\Vert }^2.$$

The coefficients are estimated using penalized iteratively re-weighted least squares (P-IRLS). Specifically, at the (m + 1)th iteration we take

$${\widehat{\mathit{\theta }}}_{q,m+1}={\left({\stackrel{\sim }{\mathbb{Z}}}^T{\widehat{\mathrm{W}}}_m\stackrel{\sim }{\mathbb{Z}}+{\lambda }_1{\stackrel{\sim }{\mathbb{P}}}_1^T{\stackrel{\sim }{\mathbb{P}}}_1+{\lambda }_2{\stackrel{\sim }{\mathbb{P}}}_2^T{\stackrel{\sim }{\mathbb{P}}}_2\right)}^{-1}{\stackrel{\sim }{\mathbb{Z}}}^T{\widehat{\mathrm{W}}}_m{\widehat{\mathbf{u}}}_m,$$ (7)

where û_m is the current estimate of the adjusted dependent variable vector, u, and Ŵ_m is the current estimate of the diagonal weight matrix, W. The components of u are given by u_i = η_i + (y_i − μ_i)g′ (μ_i). The ith diagonal element of W is w_ii = 1/{V (μ_i)[g′ (μ_i)]²}, with V (μ_i) = b″(ζ_i). To initialize the algorithm, use μ₀ = Y and η₀ = g(Y), adjusting y_i if necessary to avoid η_i = ∞.

To efficiently construct (7) and to detect rank deficiency, the following procedure is used. First,use the QR-decomposition to form W^1/2ℤ̃ = ℚℝ where ℚ is orthogonal, ℝ is upper triangular, and ${\mathrm{W}}^{1/2}=\mathrm{diag}(w_{11}^{1/2},\dots ,w_{\mathit{NN}}^{1/2})$. Next, use the Choleski decomposition to obtain ${\mathbb{Q}}_2^T\mathbb{P}{\mathbb{Q}}_2={\mathrm{L}}^T\mathrm{L}$. Pivoting should be used here because ℙ is positive semi-definite instead of positive definite. Now, from a singular value decomposition form [ℝ^T L^T ]^T = UDV^T, where U and V are orthogonal and D is a diagonal matrix containing the singular values. At this point, we ensure identifiability by removing the columns and rows of D and the columns of U and V corresponding to singular values that are less than the square root of the machine precision times the largest singular value (Wood 2006b, p. 183). It then follows that (7) can be obtained from ${\widehat{\mathit{\theta }}}_{q,m+1}=\mathrm{V}{\mathrm{D}}^{-1}{\mathrm{U}}_1^T{\mathbb{Q}}^T{\mathrm{W}}^{1/2}{\widehat{\mathbf{u}}}_m$, where U₁ is the sub-matrix of U satisfying ℝ = U₁ DV^T. At the final iteration, say M, our solution for θ is given by θ̂ = ℚ₂ θ̂_q,M, and it can be shown that this satisfies 1^T ℤ_[,−1]θ̂ = 0 as required (Wood 2006b, Section 1.8.1).

Generalized cross validation (GCV) can be used to choose the smoothing parameters; see Wood (2004, Section 4.5.4) for justification of its use for non-identity link GAMs. The GCV score for λ₁ and λ₂ is given by

$$\mathit{GCV}({\lambda }_1,{\lambda }_2)=\frac{\mathit{nD}(\mathbf{Y};\widehat{\mathit{\mu }}:{\lambda }_1,{\lambda }_2)}{{\{n-\gamma \mathrm{tr}(\mathrm{H})\}}^2},$$ (8)

where H is known as the influence matrix and is related to the fitted values by μ̂ : = g⁻¹(ℤθ̂_M) = g⁻¹ (Hu_M) and D(Y; μ̂ : λ₁, λ₂) denotes the model deviance. The model deviance is defined to be twice the difference between the log-likelihoods of the saturated model, which has one parameter for each observation, and the given model. Formulas for the deviance for some common GLMs are given in McCullagh and Nelder (1989, Section 2.3); for example, for an identity link GLM, D(Y; μ̂ : λ₁, λ₂) = ∥Y − HY∥². The constant γ ≥ 1 is usually chosen to take values between 1.2 and 1.4 to combat the tendency of GCV to undersmooth. For additional safeguards against undersmoothing, lower bounds could also be placed on the smoothing parameters.

A choice must be made on the order in which the P-IRLS and the smoothing parameter selection iterations are performed. For what is termed outer iteration, for each pair of smoothing parameters considered, a GAM is estimated using P-IRLS until convergence. The other possibility, known as performance iteration, is to optimize the smoothing parameters at each iteration of the P-IRLS algorithm. The latter approach can be faster than outer iteration; however, it is more susceptible to convergence problems in the presence of multicollinearity (Wood 2006b, Chapter 4).

Our model can conveniently be fit in R using the mgcv package (Wood 2011, 2004). The details of how this is done are available in Appendix B of the supplemental materials. We use outer iteration and Newton’s method for minimizing the GCV score, the package defaults. Using this package also allows for many possible extensions (e.g. mixed effects terms, formal model selection, alternative estimation procedures, etc.) beyond the scope of the current paper. Our code is available in an online supplement as well as in the R package refund.

3.3 Estimated Surface

For a given θ̂, we can evaluate the estimated surface at any grid of points in its domain. Let X be an arbitrary column vector of length n₁ taking values in the range of X(·) and T be the observation times or any vector of length n₂ taking values in [0, 1]. We let F̂ denote the estimated surface evaluated on the mesh defined by X and T. To obtain F̂, let B_x be the n₁n₂ × K_x matrix of x-axis B-splines evaluated at X ⊗ 1_n2, i.e., ${\mathrm{B}}_x=\left[{\mathbf{B}}_1^X(\mathbf{X}\otimes {\mathbf{1}}_{n_2})\cdots {\mathbf{B}}_{{\mathit{K}}_x}^{\mathit{X}}(\mathbf{X}\otimes {\mathbf{1}}_{n_2})\right]$, where 1_n denotes a column vector of length n. Similarly, define B_t as the n₁n₂ × K_t matrix of B-splines evaluated at 1_n1 ⊗ T. Next, define the n₁n₂ × K_x K_t matrix

$$\mathrm{B}=({\mathrm{B}}_x\otimes {\mathbf{1}}_{K_t}^T)\odot ({\mathbf{1}}_{K_x}^T\otimes {\mathrm{B}}_x),$$ (9)

where ⊙ denotes element-wise matrix multiplication. The estimated surface is then given by F̂ = Bθ̂_[−1].

3.4 Standard-error bands

For a response from any exponential family distribution, one simple way to construct approximate, pointwise confidence bands for F̂(x, t) conditional on the estimated smoothing parameters is to use a sandwich estimator in the same manner as Hastie and Tibshirani (1990, Section 6.8.2) and Marx and Eilers (1998). However, we found through our simulation studies that these intervals do not have adequate coverage for our model, a result also noticed for univariate GAMs in Wood (2006a). This is because these intervals assume θ̂ is unbiased, which will not be the case when θ ≠ 0, due to the penalization involved in the estimation.

To overcome the bias in the parameter estimation, we use the Bayesian approach of Wahba (1983). Using the improper prior π(θ) ∝ exp (−θ^T ℙθ/2), it can be shown that

$$\mathit{\theta }\mid {\mathbb{Z}}^T\mathrm{W}\mathbf{u},{\lambda }_1,{\lambda }_2\sim N{(({\mathbb{Z}}^T\mathrm{W}\mathbb{Z}+\mathbb{P})}^{-1}{\mathbb{Z}}^T\mathrm{W}\mathbf{u},{({\mathbb{Z}}^T\mathrm{W}\mathbb{Z}+\mathbb{P})}^{-1}\varphi ),$$

see e.g. Wood (2006b, Section 4.8). To estimate W, we use the estimated weight matrix at the final P-IRLS iteration, Ŵ_M. If it is necessary to estimate the dispersion parameter, ϕ, we use $\widehat{\varphi }={\sum }_{i=1}^{n}V{({\widehat{\mu }}_i)}^{-1}{(y_i-{\widehat{\mu }}_i)}^2/\left[N-\mathrm{tr}(\mathrm{H})\right]$. Letting V_θ̂ = (ℤ^T Ŵ_M ℤ + ℙ)⁻¹ ϕ̂ and recalling that the estimated surface is given by F̂ = Bθ̂_[−1], where B is defined in (9), the variance of F̂ is given by var{F̂} = BV_{θ̂[−1,−1]} B^T. Taking F̂ ± 2{diag(var{F̂})}^1/2 gives approximate 95% empirical Bayesian confidence bands for F.

These Bayesian intervals have a nice frequentist property “across the function”: in repeated random experiments with the same F, the observed coverage probabilities averaged over the observation points will tend to be close to the nominal coverage level. This property was borne out in the simulation experiments of several papers including Wahba (1983) and Nychka (1988) for the case of smoothing splines and Wood (2006a) for thin-plate regression splines. It will be examined for the FGAM through a simulation study in Section 4.2.

Depending on the application, a particular linear combination of the elements of F̂ may be of interest. If we let c be a vector of the same length as F̂, then we can also construct confidence bands of the form c^T F̂ ± 2{c^T (var{F̂})c}^1/2. For example, this could be used to determine approximately whether two observed curves have significantly different effects on the response at a particular value of t. Under a null hypothesis of H₀ : θ = 0, θ̂ is unbiased and we can use the sandwich estimator for the variance, V_f = V_θ̂ℤ^TŴ_M ℤV_θ̂/ϕ̂, to conduct approximate hypothesis tests for subsets of θ For example, we can construct surfaces of approximate t-statistics by scaling the estimated surface values by the reciprocal of their standard error (the diagonal elements of V_f).

For any pointwise transformation, H_t(·), of the predictor used (including H_t(x) = x), it is of interest to test whether ∂²/∂h² F(h, t) = 0 for all h and t, since this implies F{H_t(x), t} = β(t) H_t(x) for some function β(·). Since derivatives of B-splines are simple to compute, an estimate of the second derivative of the surface and the Bayesian confidence intervals for the second derivative are easily obtained by replacing B_x in (9) with evaluations of the second derivatives of the x-axis B-splines evaluated at the same points used for B_x. While we cannot use our confidence bands for global inferences of this type, they do provide a rough heuristic for the desired test.

3.5 Multiple Predictors

Because of the modularity of penalized splines (Ruppert et al. 2003), including multiple functional predictors as well as scalar predictors in the model is straightforward. Each additional functional predictor requires that two more smoothing parameters be selected. We will outline the procedure for the case of two functional covariates [say X₁(·), X₂(·)] and one scalar covariate (say W). The model is g{E(Y_i∣X_i,1, X_i,2, W_i)} = θ₀ + ∫_τ1 F₁{X_i,1(t), t}dt + ∫_τ2 F₂{X_i,2(t), t}dt + F₃(W_i), and both X₁(·) and X₂(·) can be transformed by their empirical cdfs. Further extensions are similar. As before, we use B-spline bases for both axes for both functional predictors and now also for W. One must also choose degrees of differencing to be used for each penalty. Let ℤ⁽¹⁾ and ℤ⁽²⁾ denoted the matrices of integrated tensor product B-splines for X₁ and X₂, respectively. Similarly, define ℙ⁽¹⁾ and ℙ⁽²⁾ [see (6)]. Let B^(W) be the matrix of W B-splines evaluated at the observed values of W and let θ^(W) be the corresponding vector of B-spline coefficients for W. The penalty matrix for the smooth of W is given by ${\mathbb{P}}^{(W)}={\lambda }_w{\mathrm{D}}_w^T{\mathrm{D}}_w$, where D_w is the differencing matrix for W and λ_w is its smoothing parameter. For identifiability, add the constraint 1^TB^(W) θ^(W) = 0 (the usual constraint for each functional component in a standard additive model). We place the same constraint on both functional predictors as in the previous section. Thus, we have three total constraints. Construct

$$\mathbb{Z}=\left[\mathbf{1}{\mathrm{B}}^{(W)}{\mathbb{Z}}^{(1)}{\mathbb{Z}}^{(2)}\right],\mathbb{P}=\mathrm{diag}(0,{\mathbb{P}}^{(W)},{\mathbb{P}}^{(1)},{\mathbb{P}}^{(2)},\mathrm{and}\mathit{\theta }={(1,{\mathit{\theta }}^{(W)},{\mathit{\theta }}^{(1)},{\mathit{\theta }}^{(2)})}^T.$$

To accommodate a linear effect of the covariate W, replace B^(W) in ℤ with the observed values of W and replace ℙ^(W) with zero in the above formula for ℙ.

Note that it is also possible to have a linear effect for some functional predictors and additive effects for others; e.g. a model of the form g{E(Y_i∣X_i)} = θ₀ + f(W_i) + ∫_τ1 β(t)X_1i(t)dt + ∫_τ2 F{X_2i(t), t}dt. Using the roughness penalty approach for estimating FLMs mentioned in Section 4.1, this can be implemented by making straightforward changes to ℤ⁽¹⁾ and ℙ⁽¹⁾ (see Ramsay and Silverman 2005, Chapter 15 for details).

4 Simulation Experiment

In this section, we perform simulations to assess the empirical performance of our FGAM. We first assess the ability of our FGAM to predict out-of-sample data in the Gaussian response case and compare its performance with several other functional regression models. Next, we examine the coverage properties of the empirical Bayesian confidence bands proposed in Section 3.4.

To generate the data, we created 1000 replicate data sets each consisting of N curves sampled at 200 equally-spaced points in [0, 1] as follows: Let $X_i(t)={\sum }_{j=1}^J{\gamma }_j\left[Z_{1ij}{\varphi }_{1j}(t)+Z_{2ij}{\varphi }_{2j}(t)\right]$ where Z_hij ~ N(0, 1), ${\varphi }_{1j}(t)=\sqrt{2}\cos (\mathit{\pi jt})$, ${\varphi }_{1j}(t)=\sqrt{2}\sin (\mathit{\pi jt})$, and ${\gamma }_j=\frac{2}{j}$; h = 1, 2; i = 1,…, N; j = 1,…, J. We consider two values for J, J = 5 and J = 500, the former resulting in much smoother predictor trajectories. We examine two cases for the true surface, F(x, t), one where the FLM holds, F(X(t), t) = β(t)X(t) and the other where it does not. For the linear true model, F(x, t) = xt. For the nonlinear true model, we use $F(x,t)=-.5+\exp \left[-{(\frac{x}{5})}^2-{(\frac{t-.5}{.3})}^2\right]$, which looks like a hill or bivariate normal density.

The error variance changes with each sample so that the empirical signal to noise ratio (SNR) defined by $\mathrm{SNR}=\frac{s_{\widehat{y}}^2}{{\sigma }^2}$, where $s_{\widehat{y}}^2=\frac{1}{N-1}\sum _{i=1}^N{\left[{\mathit{\int }}_{\tau }F(X_i(t),t)\mathit{dt}-N^{-1}{\sum }_{i=1}^N{\mathit{\int }}_{\tau }F(X_i(t),t)\mathit{dt}\right]}^2$ remains consider the values SNR= 1, 2, 4, 8 in our simulations.

4.1 Out-Of-Sample Predictive Performance

We fit FGAM and compare its out-of-sample predictive accuracy with three other popular functional regression models, the FLM, the kernel estimator of Ferraty and Vieu (2006), and the functional additive model (FAM) of Müller and Yao (2008). The coding used in our analyses was done in R (R Development Core Team 2011). The fda package (Ramsay et al. 2011) implements the standard tools of functional data analysis in R. As an initial step in fitting our model, the FLMs and the FAM, we use this package to smooth the data using B-spline basis functions and a roughness penalty with smoothing parameter chosen by GCV.

There are two main approaches for estimating the coefficient function β(·) for a FLM. The first uses smoothing or penalized splines and the second uses a functional principal component analysis (fPCA). We refer to these as FLM1 and FLM2, respectively. These models can be fit in R using the fda package, more specifically, the functions fRegress for FLM1 and pca.fd for FLM2. See Ramsay et al. (2009, Chapter 9) for computational details. For FLM1, we choose the smoothing parameter by minimizing GCV. For FLM2, we conduct a functional principal component analysis with a constant, light amount of smoothing and retain enough components for each simulation scenario to explain 90% of the total variability of the functional predictor. Once the scores are estimated, the final step to estimating FLM2 is fitting an unpenalized linear model in the scores.

To fit the FAM, we use the same number of principal component scores and the same estimation procedure as for FLM2. The difference comes in the next step, where a generalized additive model is fit using the scores as predictors. To estimate the GAM, we use the default settings in the mgcv package and 11 basis functions for each additive term.

The final model we fit is described in detail in Ferraty and Vieu (2006, Chapter 5). The response is predicted by the nonlinear operator r(X) := E(Y∣X). This operator is estimated by a functional extension of the Nadaraya-Watson kernel estimator:

$$\widehat{r}(X)=\frac{{\sum }_{i=1}^N{Y}_{i}K\{h^{-1}d(X,X_i)\}}{{\sum }_{i=1}^{N}K\{h^{-1}d(X,X_i)\}},$$ (10)

where K is an asymmetrical kernel with bandwidth h and d is a semimetric. Continuity or Lipschitz continuity of the regression operator in the semimetric is assumed. We used the quadratic kernel, $K(u)=\frac{3}{4}(1-u^2)1_{[-1,1]}(u)$, and the semimetric d(X_i, X_i′) = [∫_τ {X_i(t) − X_i′(t)}²dt]^1/2. Code for fitting this model with automatic bandwidth selection can be obtained from: http://www.math.univ-toulouse.fr/staph/npfda. Note the differences in the assumptions and complexities of these three models: the simplest model assumes the response is linear in the functional predictor, the FGAM lessens the restrictions to additivity in the functional predictor, and the kernel estimator makes no restrictions on the form of the regression function other than continuity.

Each training set contained 67 curves and 33 curves were used for the test set. The performance of the models was measured by the out-of-sample $\mathrm{RMSE}={\left[{33}^{-1}\sum _{i\in \left\{\mathrm{test\; set}\right\}}{(y_i-{\widehat{y}}_i)}^2\right]}^{1/2}$. We report results for both the FGAM fit to the original data and the FGAM fit after X has been transformed using the empirical cdf transformation given in (5). In both cases, six cubic B-splines were used for the x-axis and seven cubic B-splines were used for the t-axis with second degree difference penalties for both axes. The tuning parameter, γ, for the GCV criterion (8) was taken to be 1.0 in all cases. The mgcv package requires that the number of coefficients to estimate be less than the sample size, so we must have the product of the dimensions of the bases be less than the sample size minus one (for the intercept). The results of the simulations are summarized in Figure 2.

Figure 2.

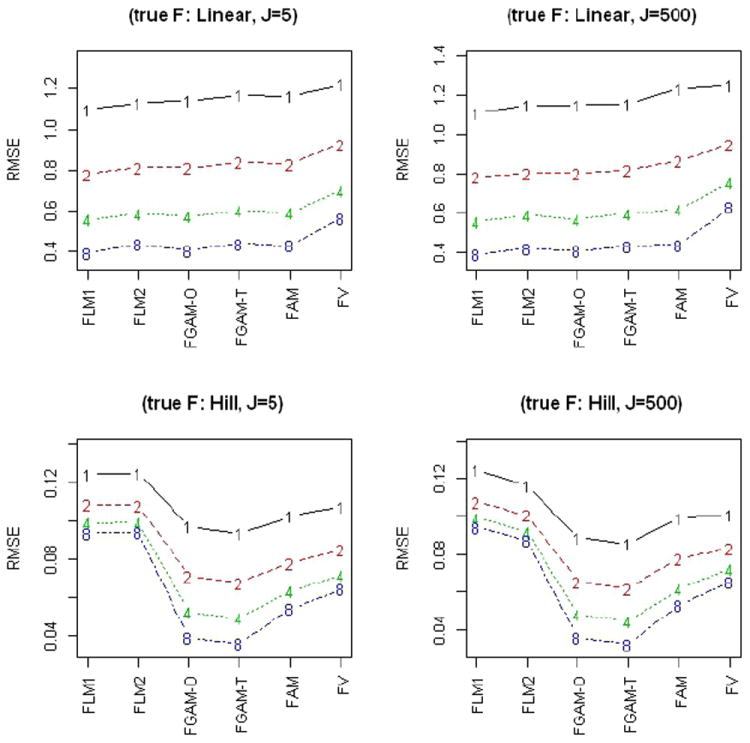
Median RMSE across 1000 simulations for six different functional regression models, four different empirical signal to noise ratios and rough (J=500) and smooth (J=5) predictor functions. a) Linear true model, b) Nonlinear (“Hill”) true surface.

The figure reports the median RMSE’s across the 1000 simulations for each scenario and model. We see that the FGAM loses little to the FLM in terms of predictive accuracy when the FLM is the true model and provides substantial improvements in the case when the FLM is not the true model. In fact, all the models perform quite similarly in the linear true model case with the exception of the Ferraty and Vieu model (10) which performs considerably worse. In the nonlinear true model case, we see that fitting an FGAM to the transformed data performs slightly better than fitting an FGAM to the original curves and that in general the FGAM offers significant advantages over all the other models. As expected, the differences in performance between the different models become more pronounced as the fixed empirical signal to noise ratio increases.

4.2 Bayesian Confidence Band Performance

We now assess the average coverage probabilities (ACP) of the confidence bands from Section 3.4. The observed ACP for the ith simulation is given by

$$\mathit{ACP}=\frac{1}{625}\sum _{j=1}^{25}\sum _{k=1}^{25}I\{F(x_j^{(i)},t_k^{(i)})\in C_{.95}(x_j^{(i)},t_k^{(i)})\},$$

where { $(x_j^{(i)},t_k^{(i)})$; j, k = 1,…, 25} are a subset of the N × 200 observed X(t) and t values for the ith simulation and $C_{.95}(x_j^{(i)},t_k^{(i)})$} is the entry of F̂⁽ⁱ⁾ ±2{diag(var{F̂⁽ⁱ⁾})}^1/2 corresponding to $(x_j^{(i)},t_k^{(i)})$. We consider two values for the sample size, N = 100 (combining the training and test sets from the previous section) and N = 500, the same true surfaces from the previous section, and two values for the empirical signal to noise ratio, two and four. For both the x and t axes, we use nine basis functions, cubic B-splines, and a second order difference penalty. We report results for the FGAM fit without an intercept to the untransformed predictor curves with J = 500. The results for J = 5 were nearly identical.

To reduce the number of times that the confidence bands are evaluated at points outside the region jointly defined by the observed (X_i(t_j), t_j) values, only grid points that are inside the convex hull defined by the observed values for each simulation are used in the calculation of mean ACP. A final modification is necessary to account for the identifiability constraint imposed on the FGAM. To do this, we fit the FGAM (including the constraint) with negligible amounts of smoothing to the true E(Y_i∣X_i) values (without noise) and take the fitted values to be the true responses. The mean ACP across the 500 simulations is displayed in Table 1 for each simulation scenario.

Table 1.

Mean ACP across 500 simulations for nominal coverage probability 0.95.

	N=100		N=500
True Surface	SNR=2	SNR=4	SNR=2	SNR=4
Linear	0.9746	0.9684	0.9704	0.9702
Nonlinear	0.9597	0.9665	0.9613	0.9592

We see from the table that the coverage is fairly close to the nominal level of 0.95, though there is a slight problem with over-coverage in all the scenarios. Further analysis shows that the average estimated Bayesian standard errors for the surface are larger than the Monte Carlo standard deviation of the estimated surface, which is causing in the over-coverage. This is a biproduct of the Bayesian intervals trying to correct for the smoothing bias inherent in nonparametric regression. Recall that these intervals do not account for uncertainty in the estimation of λ₁ and λ₂. If more precise confidence bands are required, alternatives such as bootstrapping could be employed; see Wood (2006a, Section 4). These results indicate that it is safe to use the Bayesian confidence bands to make inferences about the true surface F(x, t). We additionally ran a subset of these simulation scenarios while computing the confidence bands using the sandwich estimator of the variance of the estimated surface(results not included) and found there could be substantial under-coverage in the nonlinear true model case as a result of bias due to smoothing.

5 Application to Diffusion Tensor Imaging Dataset

We now assess the performance of our model on a DTI tractography study. DTI is a technique for measuring the diffusion of water in tissue. Water diffuses differently in different types of tissue, and measuring these differences allows for detailed images to be obtained. Our dataset comes from a study comparing certain white matter tracts of multiple sclerosis (MS) patients with control subjects. MS is a central nervous system disorder that leads to lesions in the white matter of the brain which disrupts the ability of cells in the brain to communicate with each other. This dataset was previously analyzed in Goldsmith et al. (2010b) and Greven et al. (2010).

The result of the DTI tractography, is a 3×3 symmetric, positive definite matrix (equivalently, a three dimensional ellipsoid) that describes diffusion at each desired location in the tract. We consider three functions of the estimated eigenvalues from these matrices: fractional anisotropy, parallel diffusivity, and perpendicular diffusivity. Fractional anisotropy measures the degree to which the diffusion is different in directions parallel and perpendicular to the tract, with zero indicating an isotrophic diffusion. More precisely, if the eigenvalues of the ellipsoid are given by λ₁, λ₂, λ₃, fractional anisotropy is equal to ${\left[3\{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2\}/\{2({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)\}\right]}^{1/2}$, where λ̄ = (λ₁ + λ₂ + λ₃)/3. Parallel (or axial or longitudinal) diffusivity is the largest eigenvalue of the ellipsoid. Perpendicular diffusivity is an average of the two smaller eigenvalues. See Mori (2007) for an overview of DTI.

Standard magnetic resonance imagining is used for diagnosing MS, but it is believed that the extra information provided by the tract profiles produced from DTI can be used to understand the disease process better. As an example of the types of effects we could investigate with our model, it has been found (Reich et al. 2007) that parallel diffusivity is increased along the corticospinal tracts of people with MS. We would hope to see this effect if we were using parallel diffusivity measurements along that tract to predict MS status. We consider the corpus callosum tract in our analysis because it is related to cognition.

As an illustration of the FGAM, we fit our model using each of the three diffusion measures separately and compare the results with the same models introduced in the previous section. We also compare using the original curves as the predictor (1) with using the empirical cdf of the curves (5). Figure 3 contains plots of the parallel diffusivity measurements along the corpus callosum tract and the corresponding empirical cdf-transformed values for each subject in the training set.

Figure 3.

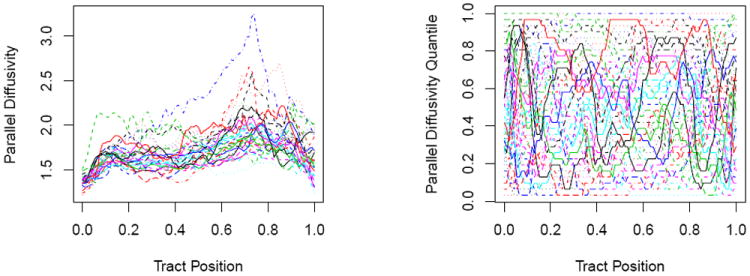
a) Observed parallel diffusivity along the corpus callosum tract for a sample of MS patients. b) Parallel diffusivity along the corpus callosum tract transformed by its empirical cdf for the same patients.

Throughout the analysis, when fitting the FGAM, we use cubic B-splines with second-order difference penalties, six B-splines for the x (p)-axis, and seven B-splines for the t-axis. We found our results to be insensitive to these choices, and for brevity we do not include results for other values considered. Throughout this section, γ in (8) is taken to equal 1.4. To evaluate the performance of the models, we examine their leave-one-curve-out prediction error. We repeatedly fit each model using all the samples except one and then use the fit to predict the left-out sample. This process is repeated until every sample has been left-out once. Our performance measure is the root mean squared error, defined as $\mathrm{RMSE}={\left[N^{-1}\sum _{i=1}^N{(y_i-{\widehat{y}}_{(i)})}^2\right]}^{1/2}$, where ŷ_(i) is the predicted value of the ith response value when this sample is left out of the estimation.

5.1 Predicting PASAT Score

The first variable we predict is the result of a Paced Auditory Serial Addition Test (PASAT), a cognitive measure taking integer values between 0 and 60. The subject is given numbers at three second intervals and asked to add the current number to the previous one. The final score is the total number of correct answers out of 60. MS patients often perform significantly worse than controls on this test. Since the corpus callosum is known to play a role in cognitive function, we might expect to see that the functional measurements along this tract have a significant impact in forecasting PASAT score. The PASAT was only administered to subjects with MS. One subject with peculiar tract profiles was removed for simplicity and to avoid dealing with missing values.

The estimated surface F̂(p, t) [see (3)] is shown in Figure 4(a) for transformed parallel diffusivity. Figure 4(b) shows a contour plot of the observed pseudo-t statistics discussed in Section 3.4. We can see from this figure that parallel diffusivity for tract positions around 0.4 – 0.6 appears to be influential on the predicted response; subjects in the middle quantiles for this measurement at these positions are more likely to score higher on the PASAT, while the opposite is true for subjects in the upper quantiles at this location.

Figure 4.

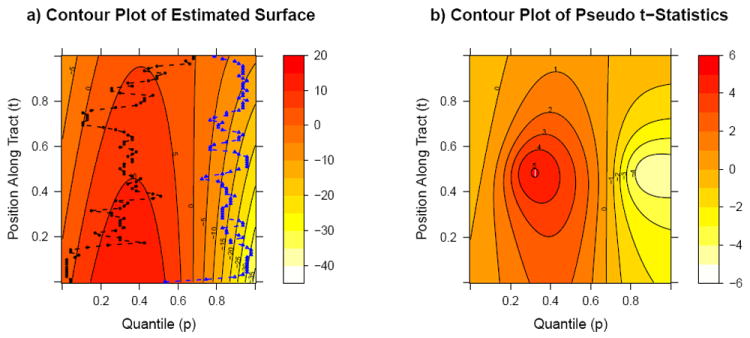
a) Contour plot of the estimated surface, F̂(p, t) [see (3)], for transformed parallel diffusivity along the corpus callosum tract. Also included are the transformed parallel diffusivity measurements for two subjects. b) Contour plot of pseudo t-statistics (estimated surface value divided by its standard error). The response is PASAT score.

Figure 5 shows an example of a slice of the estimated surface when the untransformed curves are used for a fixed x value (left) and for a fixed position along the tract, t, (right). Parallel diffusivity along the corpus callosum is used as the predictor in these plots which also include twice standard error bands based on the sandwich estimator described earlier. Figure 5 also shows the same slices for the estimated second derivative of the surface with respect to t. This can give us a rough idea of whether the linear model is sufficient. In practice, we look at these plots for a representative sample of values with both the predictor value fixed and with the position fixed. We see that the second derivative is significantly non-zero in some regions, which suggests inadequacy of using an FLM in the untransformed predictors.

Figure 5.

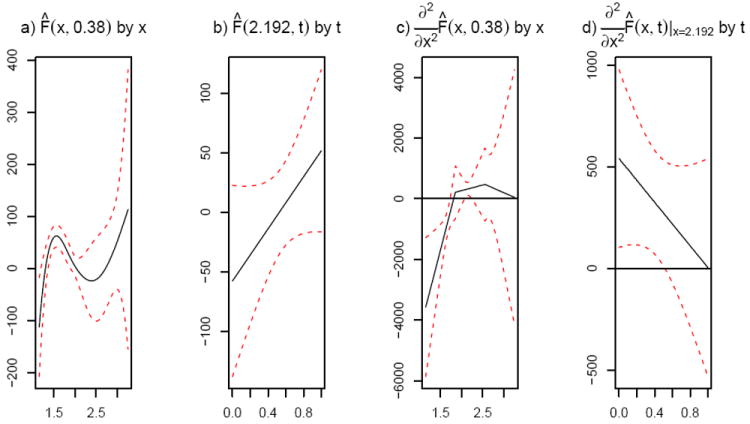
A sample of slices of the estimated surface [plots a) and b)] and estimated second derivative surface [c) and d)] for fixed tract positions [a) and c)] and fixed untransformed actual predictor [b) and d)] along with the corresponding Bayesian confidence bands for parallel diffusivity with PASAT score as the response variable.

Table 2 reports out-of-sample RMSE from separately using each of the three different diffusivity measurements along the corpus callosum tract as predictors in the five models under consideration. Here, using FGAM with the empirical cdf transformation (FGAM-T) led to improved forecasting accuracy compared to using the raw measurements as predictors (FGAM-O). In fact, FGAM-T (5) has lower out-of-sample RMSE than both FLMs for all the functional predictors considered, indicating that a linear model may be too restrictive in this application. Our FGAM-T compares favourably with the functional kernel regression model (10) and the FAM, showing better performance when either perpendicular diffusivity or fractional anisotropy are used as predictors. Though the kernel estimator provided slightly improved predictions in the parallel diffusivity case, the complex nature of its fit makes visualization difficult, so it is less useful than the FGAM for helping us understand the relationship between the DTI measurements and the PASAT scores.

Table 2.

Leave-one-curve-out RMSEs for the three different functional predictors of PASAT score using the following models: FGAM using the original curves (FGAM-O), FGAM using the empirical cdf transformation [FGAM-T, (5)], FLM1, FLM2, FV (10), and FAM.

Measurement	FGAM-O	FGAM-T	FLM1	FLM2	FV	FAM
Perpendicular Diffusivity	12.22	10.46	10.98	11.27	11.16	11.71
Fractional Anisotropy	12.55	11.60	11.87	11.91	12.11	12.70
Parallel Diffusivity	11.94	12.09	12.32	12.24	11.97	11.86

5.2 Predicting MS status: Logistic Link

We now consider classifying the disease status of subjects. Since the PASAT was only given to the subjects with MS, our sample size is now 88 and includes controls. We include results using the untransformed curves only. The results using the quantile transformation were similar. We again use the leave-one-curve-out procedure described earlier. Fitting the FGAM resulted in the estimated surface displayed in Figure 1 when perpendicular diffusivity is used as the predictor. The observed perpendicular diffusivity for two subjects is overlaid on the plot; recall the interpretation given in the introduction. It appears that the predictor values at the end of the tract corresponding to t = 1 have a strong influence in predicting disease status. Subjects in the lower range for perpendicular diffusivity at this end of the tract seem to be less likely to be classified as having MS, whereas subjects in the upper range at this position are more likely to have MS. Models were also fit using fractional anisotropy and parallel diffusivity as predictors. A fourth model was considered that included a nonparametric component for the subject’s age in addition to using perpendicular diffusivity. Figure 6 contains a plot of the ROC curves for these fitted models. The model using fractional anisotropy performs almost universally worse than the other three models. None of the other three models considered perform universally better than the others. Including age as a covariate in the model with perpendicular diffusivity did not improve performance.

Figure 6.

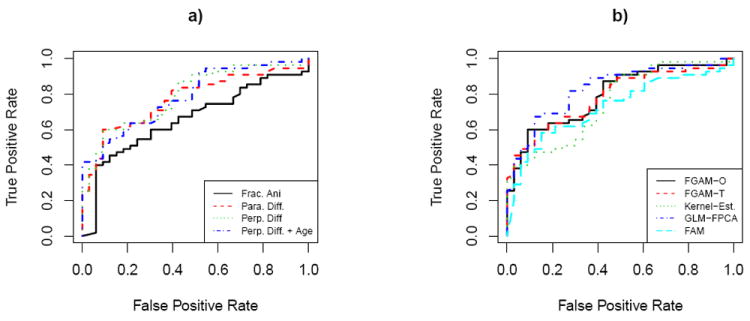
a) Leave-one-curve-out ROC curves for different FGAMs fit each using a different functional predictor and an FGAM including perpendicular diffusivity and a functional component for age. The response is MS status. b) Leave-one-curve-out ROC curves for both FGAM fits, and three other functional regression models when perpendicular diffusivity is the functional predictor.

We also compared the FGAM fits to three other generalized functional regression models. The first is the Ferraty+Vieu estimator (10) from the previous section. The use of this estimator for classification is discussed in detail in Ferraty and Vieu (2006, Chapter 8). The second alternative model considered is a GLM in the functional principal component scores (GLM-FPCA) and the third model is a GAM in the functional principal component scores (FAM). The leave-one-curve-out ROC curves are displayed in the right plot of Figure 6 when perpendicular diffusivity is the covariate. There is little difference in performance between the models used.

6 Discussion

A new model for functional regression with a scalar response has been developed. The functional linear model has been extended to an additive structure allowing for more complicated relationships to be modelled while still being highly interpretable. Our approach can handle responses from any exponential family distribution as well as multiple functional or scalar predictors.

In our simulation results, we showed that our FGAM can provide nearly identical results to the FLM when the FLM is the true model, and offered substantial improvements when the FLM was not the true model. We also showed that our proposed confidence bands can achieve average coverage probabilities close to the nominal confidence level. For the analysis of the DTI dataset, FGAM performed favourably when compared with some standard functional regression models.

Our methodology opens up many research problems. One goal for future work is to add several more functional predictors (e.g. for the DTI dataset, multiple tracts and more summaries of the diffusion for each tract). This would require faster techniques for smoothing parameter selection than our current methods. A Bayesian model and MCMC could have also been used. Alternatively, the recent work of Wood (2011) advocates the use of generalized linear mixed models (GLMMs) estimated by restricted maximum likelihood for smoothing parameter selection. Our analysis of the DTI dataset did not consider the longitudinal nature of the study. The use of a GLMM to incorporate random effects would allow us to model these extra subject visits in a manner similar to Goldsmith et al. (2010a). Datasets with this type of structure are becoming more and more common; for example, see the analysis in Di et al. (2009) of the Sleep Healthy Heart Study.

There are multiple alternatives to the Bayesian approach we used for obtaining approximate confidence bands for the estimated surface F̂. Ruppert et al. (2003, Chapter 6) provides an overview of some of them. Bootstrap procedures are commonly used and have been developed for functional nonparametric regression (Ferraty et al. 2010). Fahrmeir and Lang (2001) use a Bayesian approach involving Markov random field priors with estimation performed using MCMC. We note that with the approach we use, it is also possible to obtain confidence intervals for nonlinear functions of the model parameters (see Wood (2006a)).

Also of interest for further work would be obtaining formal tests of the additivity and linearity assumptions for our model and the FLM, respectively and convergence rates for F̂. Recent results for P-splines suggest we can obtain theoretical results for the Riemann sum approximation to our model. Li (2011) shows the equivalence of a P-spline estimator to a backfitting projection algorithm and uses this result to obtain asymptotic results for the P-spline estimator for the case of piecewise constant or linear splines with first or second order difference penalties. Care must be taken to deal with the high degree of multicollinearity among the covariates; the assumptions placed on the probabilistic structure of the functional predictors will likely have an important role in obtaining rates of convergence.