A general binomial regression model to estimate standardized risk differences from binary response data

Abstract

Estimates of absolute risks and risk differences are necessary for evaluating the clinical and population impact of biomedical research findings. We have developed a linear-expit regression model (LEXPIT) to incorporate linear and nonlinear risk effects to estimate absolute risk from studies of a binary outcome. The LEXPIT is a generalization of both the binomial linear and logistic regression models. The coefficients of the LEXPIT linear terms estimate adjusted risk differences, while the exponentiated nonlinear terms estimate residual odds ratios. The LEXPIT could be particularly useful for epidemiological studies of risk association, where adjustment for multiple confounding variables is common. We present a constrained maximum likelihood estimation algorithm that ensures the feasibility of risk estimates of the LEXPIT model and describe procedures for defining the feasible region of the parameter space, judging convergence, and evaluating boundary cases. Simulations demonstrate that the methodology is computationally robust and yields feasible, consistent estimators. We applied the LEXPIT model to estimate the absolute five-year risk of cervical precancer or cancer associated with different Pap and human papillomavirus test results in 167,171 women undergoing screening at Kaiser Permanente Northern California. The LEXPIT model found an increased risk due to abnormal Pap test in HPV-negative that was not detected with logistic regression. Our R package blm provides free and easy-to-use software for fitting the LEXPIT model.

1. Introduction

The association between an exposure and a dichotomous disease outcome can be expressed using the odds ratio, risk ratio, or risk difference. Because the odds ratio can be estimated from all study designs and the logit link is the canonical link for binomial regression, logistic regression is the default model for studying disease etiology. Once an exposure-disease association is established, the clinical and population impact of interventions based on the exposure can be considered. This requires an assessment of the absolute risk difference associated with a given exposure [1–5], and the number of individuals who might benefit from an intervention to reduce exposure, which is the reciprocal of the risk difference [6].

A standardized risk is a risk estimate that is adjusted for measurable confounders [7]. Although it is possible to estimate standardized risk differences from logistic regression, in our experience, it is cumbersome and not commonly done. With logistic regression, standardizing the risk difference requires integration over the joint distribution of the confounders [8]. Also, if continuous variables are used, separate risk differences must be calculated for each fixed difference in exposure. Thus, when an exposure is hypothesized to have an additive effect on disease risk or when it is of interest to estimate the absolute effect of an exposure, it would be useful to conduct regression analyses on the probability scale.

In this paper, we introduce a regression model for the analysis of binary response data. Although the model can be applied to randomized and nonrandomized study designs, we will focus on its application to observational studies, where adjustment for multiple confounding variables is common. The model is named the linear-expit (LEXPIT) model because it allows for the incorporation of linear and nonlinear risk effects, where the nonlinear term is the inverse-logit (expit) function. Because of this structure, both the binomial linear model (BLM), with strictly linear effects, and the logistic regression model, with strictly logistic effects, can be considered special cases of the LEXPIT. Like hybrid regression models for time-to-event outcomes [9] and grouped survival data [10], the LEXPIT model has the methodological strength of providing the analyst greater flexibility in the type of risk effects that can be investigated. The LEXPIT could also be a useful tool in studies of disease etiology based on population-based case-control data because it allows an etiological factor's effect to be quantified in terms of individual risk.

The LEXPIT model was developed in response to difficulties we encountered when using standard methods to estimate confounder-adjusted absolute risks of cervical precancer or cancer in a cohort of women treated at Kaiser Permanente Northern California (KPNC). In logistic regression analyses of the cervical cancer risk associated with different combinations of Pap and human papillomavirus (HPV) test results at baseline, we found a strong negative interaction for Pap and HPV positive test screens and no increased risk for HPV-negative women with a positive Pap test. Because these findings were not in agreement with current clinical understanding about cervical cancer etiology, we suspected that this interaction was purely statistical, indicating a departure from additivity on the log-odds scale. We developed the LEXPIT to allow the screening variables to have an additive effect on cervical cancer risk. The LEXPIT significantly improved the model's fit and interpretation, showing a small but measurable elevated risk for HPV-negative women with a positive Pap. This was a substantively important finding because the magnitude of the elevated risk in Pap-positive and HPV-negative women is a critical issue in the current debate on how HPV testing should be used in population screening for cervical cancer [12, 13].

In the past, linear effects in binomial regression have been difficult to compute because of the parameter constraints needed to keep estimated risks within the valid probability range [14–17]. With the advent of constrained optimization algorithms in mainstream software, this challenge can now be largely overcome. In this article, we propose estimation methods for the LEXPIT model based on an augmented Lagrangian method of constrained likelihood maximization [18, 19]. The algorithm requires the specification of inequality constraints, the selection of feasible starting values, and monitoring of boundary cases. We describe how this algorithm can be used for estimation and inference of the LEXPIT model and present guidelines to minimize the operational complexity involved. In simulation studies, we show that the proposed methodology has better convergence properties than unconstrained iteratively reweighted least squares. We demonstrate LEXPIT regression in risk association analyses of five-year cervical cancer and precancer outcomes in the KPNC cohort.

2. Model

2.1. Linear-expit model

Let Y denote the random variable of disease occurrence. Conditional on p covariates X and q covariates Z, Y|(X = x, Z = z) ∼ Bernoulli(π(x, z)). The LEXPIT model for the conditional disease risk is,

$$\pi (x,z)={\beta }^{\prime }x+\text{expit}({\gamma }_0+{\gamma }^{\prime }z),$$ (1)

where expit(x) = exp(x)/(1 + exp(x)) is the inverse-logit (expit) function. The expit function has the property that ∀x ∈ ℛ, expit(x) ∈ (0, 1). Because the expit always contributes a positive probability to x′β, it is the natural place to model the baseline risk, given by expit(γ₀) in Equation (1). A formulation that placed the intercept in the linear term would inappropriately add a positive probability of one-half to x′β when all the z factors were zero.

Let x_−k denote the set of explanatory variables x with the kth variable, x_k, set to zero. Under the LEXPIT, the risk difference between individuals differing only in the kth risk factor is

$$\pi (x,z)-\pi (x_{-k},z)={\beta }_k{x}_k.$$ (2)

Thus, each β_k represents the risk difference associated with a unit increase in the corresponding linear variable x_k, adjusted for all other explanatory variables in the model. For individuals differing in the kth component of the z variables, their comparative risk is most easily expressed on the log-odds scale,

$$logit(\pi (x,z)-{\beta }^{\prime }x)-logit(\pi (x,z_{-k})-{\beta }^{\prime }x)={\gamma }_k{z}_k$$ (3)

where π(x, z) − β′x is a residual risk and can be interpreted as the disease risk in individuals without exposure to the x variables. Equation (3) shows that each exp(γ_k) represents the residual odds ratio associated with a unit increase in the corresponding covariate z_k, adjusted for all other explanatory variables.

When all β are zero, the LEXPIT reduces to a standard logistic model. The binomial linear model (BLM) is a another special case encompassed by the LEXPIT, in which all the z factors of (1) are zero or when z is equal to a single binary factor. In a rare disease setting, where the risk in the reference group, π₀, is small, a Taylor expansion of the LEXPIT model about γ near zero shows that it approximates a BLM

$$\pi (\gamma )={\pi }_0+{\beta }^{\prime }x+{\gamma }^{\prime }z{\pi }_0(1-{\pi }_0)+O({\gamma }^2),$$ (4)

and the γ will be on the order of the residual binomial variance, π₀(1 − π₀), in the reference population.

3. Estimation

The observed data for the ith individual (i = 1, …, n) is (y_i, x_i, z_i). Here y_i is the disease status after follow-up time τ, x_i is a set of explanatory variables with additive effects, and z_i are explanatory variables with multiplicative effects. Estimates for the parameters Θ = (β,γ₀,γ) are the solutions to the following constrained maximization problem,

$$\widehat{\mathrm{\Theta }}={\text{argmax}}_{\mathrm{\Theta }\in ℱ}l(\mathrm{\Theta }|y_1,\dots ,y_n).$$ (5)

In Equation (5), l(Θ|y₁, …, y_n) is the log-likelihood under the LEXPIT model (1),

$$l(\mathrm{\Theta }|y_1,\dots ,y_n)=\sum _{i=1}^n[y_{i}logit(\pi (x_i,z_i))+log(1-\pi (x_i,z_i))],$$

with the parameters Θ subject to the constraints

$$ℱ=\{0\le {\beta }^{\prime }x+\text{expit}({\gamma }_0+{\gamma }^{\prime }z)\le 1,\forall (x,z)\in (\mathcal{X},\mathcal{Z})\},$$

where 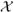and 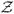are the set of unique covariate patterns for the population from which the sample was drawn. The parameter space defined by ℱ is needed to ensure that any risk for an individual within the target population is a valid measure of probability. The region defined by ℱ is known as the feasible region for Θ. Since the expit function will be within the probability range for any linear combination of γ, the LEXPIT constraint problem can be compared to a BLM with modified probability bounds, (−expit(γ₀ + γ′z), 1 − expit(γ₀ + γ′z)). Thus, for a fixed set of explanatory variables, the LEXPIT will require fewer constraints than BLM to ensureComparing BLM and LEXPIT models with the same number of parameters, the LEXPIT model will generally have a lower probability of crossing the boundary.

We use an augmented Lagrangian method to enforce the feasible region of the LEXPIT model [18, 19]. The method defines the feasible region with the system of constraints c₁(Θ),…, c_m(Θ) where each c_j(Θ) ≥ 0. The procedure satisfies the constraints by introducing linear and quadratic terms of the system of inequalities into the log-likelihood function. The resulting objective function for the maximization is

$$\phi (\mathrm{\Theta },\lambda ,\sigma )=l(\mathrm{\Theta }|y_1,\dots ,y_n)+\sum _{j=1}^m{\lambda }_j{d}_j(\mathrm{\Theta })-\frac{1}{2}\sigma \sum _{j=1}^m{d}_j{(\mathrm{\Theta })}^2$$ (6)

where λ_j are the Lagrangian multipliers, σ is a large fixed constant (the penalty term), and the modified inequality constraints, d_j, are

$$d_j(\mathrm{\Theta })=\{\begin{array}{cc}{c}_j(\mathrm{\Theta })& c_j(\mathrm{\Theta })\le {\sigma }^{-1}{\lambda }_j\\ {\sigma }^{-1}{\lambda }_j& \mathit{\text{Otherwise}}.\end{array}$$

The λ multipliers are non-zero only for active constraints, i.e. when Θ is at the boundary of the feasible region for some d_j(Θ), in which case d_j(Θ) = c_j(Θ). The d_j(Θ) arise from the introduction of slack variables into the objective function so that the c_j(Θ) can be treated as equality constraints without defining a tolerance threshold for c_j(Θ) = 0.

This constrained maximization approach is ‘augmented’ with respect to classical barrier methods that do not incorporate a penalty term [20, 21]. Optimization of the objective function consists of two stages: inner iterations to maximize the unconstrained log-likelihood for fixed σ and λ parameters and outer iterations that update λ and σ. The solution of the inner loop is $\widehat{\mathrm{\Theta }}=\{\mathrm{\Theta }:\frac{\partial \phi (\mathrm{\Theta },\widehat{\lambda },\sigma )}{\partial \mathrm{\Theta }}=0\}$, where λ̂ are the maximizing Lagrangian multipliers at Θ̂. A basic outline of the augmented Lagrangian algorithm for the LEXPIT model is:

1. Initialize Θ = Θ⁽⁰⁾, each ${\lambda }_j^{(0)}=0$, and σ⁽⁰⁾ = σ₀.

   At the rth loop,

2. Set Θ^(r) = argmax_Θφ(Θ,λ^(r−1), σ^(r−1)).

3. Set ${\lambda }^{(r)}={\lambda }^{(r-1)}-{\left[\frac{{\partial }^2\phi ({\mathrm{\Theta }}^{(r)},{\lambda }^{(r-1)},{\sigma }^{(r-1})}{\partial \lambda \partial {\lambda }^{\prime }}\right]}^{-1}\frac{\partial \phi ({\mathrm{\Theta }}^{(r)},{\lambda }^{(r-1)},{\sigma }^{(r-1)})}{\partial \lambda }$.

4. If any λ^(r) > 0, σ^(r) = 10 × σ^(r−1).

5. Repeat Steps 2-4 until convergence.

The quasi-Newton method of Broyden-Fletcher-Goldfarb-Shanno is used for the inner maximization in Step 2 [22]. Convergence to the constrained MLE is declared when each component of the evaluated gradient, $\frac{\partial \phi (\widehat{\mathrm{\Theta }},\widehat{\lambda },\widehat{\sigma })}{\partial \mathrm{\Theta }}$ is small or when the objective function value does not change. When σ is sufficiently large (σ > 100 in our implementation), this algorithm yields an estimate for Θ that is the local maximum of the augmented objective function [18].

3.1. Defining the feasible region

The feasible region ℱ is approximated from the empirical covariate classes of the study sample. Given the observed design matrices X and Z, we define the observed feasible region

$$\stackrel{\sim }{ℱ}=\{0\le {\beta }^{\prime }x+\text{expit}({\gamma }_0+{\gamma }^{\prime }z)\le 1,\forall (x,z)\in (X,Z)\}$$

The region ℱ̃ consists of the system of paired constraints, (β′x_j + expit(γ₀ + γ′z_j), 1 − β′x_j − expit(γ₀ + γ′z_j)), forming the set of m c_j(Θ). ℱ̃ approximates the population ℱ. As a consequence, risk estimates outside of the training sample are not guaranteed to be feasible. However, out-of-sample covariate patterns could be added to the model's system of constraints if they were known to be within the target population.

3.2. Initialization

To construct Θ⁽⁰⁾, we obtain the ordinary least squares solutions to the linear model π_i = π₀ + β′x_i. We then obtain a linear projection of the least-squares solutions, which satisfy the system of linear constraints defined by 0 ≤ π_i ≤ 1 for all x_i. Denote the projected parameters as (π̂₀,β̂₀). The baseline risk is initialized to ${\gamma }_0^{(0)}=logit({\widehat{\pi }}_0)$, the linear effects β to β⁽⁰⁾ = β̂, and all remaining parameters are initialized to zero.

3.3. Gradient and Hessian of the objective function

In what follows, we present the gradient and Hessian components of the augmented log-likelihood function that are needed to implement the optimization procedure. For simplification, γ will be used to refer to the γ₀ and γ parameters collectively. For the inner loop of the maximization algorithm, the gradient, $\frac{\partial \phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial \mathrm{\Theta }}$, is separated into components for β and γ. For β, the gradient is

$$\frac{\partial \phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial \beta }=\sum _{i=1}^n{x}_i[\frac{y_i}{\pi (x_i,z_i)}-\frac{(1-y_i)}{(1-\pi (x_i,z_i))}]+\sum _{j=1}^m({\lambda }_j-2\sigma d_j(\mathrm{\Theta }))J_j(\beta )$$

where the m constraints, d₁(Θ), …, d_m(Θ) are as given in Equation (6), and J_j(β) is the derivative of d_j(Θ) with respect to β. This derivative will be a sign of the linear covariates of the constraint, for active constraints, and zero otherwise. For γ,

$$\frac{\partial \phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial \gamma }=\sum _{i=1}^n\eta ({\gamma }^{\prime }{z}_i)z_i[\frac{y_i}{\pi (x_i,z_i)}-\frac{(1-y_i)}{(1-\pi (x_i,z_i))}]+\sum _{j=1}^m({\lambda }_j-2\sigma d_j(\mathrm{\Theta }))J_j(\gamma )$$

where η(z) = expit(z)(1 − expit(z)), the derivative of the expit function. The element J_j(γ) is the derivative of d_j(Θ) with respect to γ.

The ‘Hessian’ of the augmented log-likelihood will be denoted

$$\mathscr{H}(\mathrm{\Theta })=\left[\begin{array}{cc}\mathscr{H}(\beta )& \mathscr{H}(\beta ,\gamma )\\ \mathscr{H}{(\beta ,\gamma )}^{\prime }& \mathscr{H}(\gamma )\end{array}\right]$$ (7)

The submatrix ℋ(β) is

$$\mathscr{H}(\beta )=\sum _{i=1}^n-x_i^{\prime }{x}_i[\frac{y_i}{\pi {(x_i,z_i)}^2}+\frac{(1-y_i)}{{(1-\pi (x_i,z_i))}^2}]-2\sigma \sum _{j=1}^m{J}_j{(\beta )}^{\prime }{J}_j(\beta )$$

And ℋ(γ) is

$$\mathscr{H}(\gamma )={\sum }_{i=1}^n{z}_i^{\prime }{z}_i(\dot{\eta }({\gamma }^{\prime }{z}_i)[\frac{y_i}{\pi (x_i,z_i)}-\frac{(1-y_i)}{(1-\pi (x_i,z_i))}]-\eta {({\gamma }^{\prime }{z}_i)}^2[\frac{y_i}{\pi {(x_i,z_i)}^2}+\frac{(1-y_i)}{{(1-\pi (x_i,z_i))}^2}\left]\right)+{\sum }_{j=1}^m(({\lambda }_j-2\sigma d_j(\mathrm{\Theta })){\dot{J}}_j(\gamma )-2\sigma J_j{(\gamma )}^{\prime }{J}_j(\gamma ))$$

where η̇(x) = η(x)(1 − 2expit(x)) and J̇_j(γ) is the second derivative of d_j(Θ) with respect to γ. The off-diagonal p by q + 1 submatrix ℋ(β,γ) is

$$\mathscr{H}(\beta ,\gamma )=-\sum _{i=1}^n{x}_i^{\prime }{z}_i\eta ({\gamma }^{\prime }{z}_i)[\frac{y_i}{\pi {(x_i,z_i)}^2}+\frac{(1-y_i)}{{(1-\pi (x_i,z_i))}^2}]-2\sigma \sum _{j=1}^m{J}_j{(\beta )}^{\prime }{J}_j(\gamma )$$

We note that when there are no active constraints, so that all c_i(Θ̂) are zero, the form of the objective function is the log-likelihood. In this case, the covariance-variance for Θ̂ could be estimated with a large-sample approximation based on the unconstrained weighted Hessian, $\widehat{\text{Var}}(\widehat{\mathrm{\Theta }})=-\mathscr{H}{(\widehat{\mathrm{\Theta }})}^{-1}$ [23].

For the updating of λ, order the m λ_i so that the first λ₁, …, λ_s are the active constraints, followed by m − s inactive constraints. The gradient for each λ_j is $\frac{\partial \phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial {\lambda }_j}=d_j(\mathrm{\Theta })$ and the second derivative is

$$\frac{{\partial }^2\phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial \lambda \partial {\lambda }^{\prime }}=-\left[\begin{array}{cc}J(\mathrm{\Theta })\mathscr{H}{(\mathrm{\Theta })}^{-1}J{(\mathrm{\Theta })}^{\prime }& 0\\ 0& {\sigma }^{-1}{I}_{m-s}\end{array}\right]$$

where J(Θ) = [J̃(β) J̃(γ)], with J̃(β) equal to the Jacobian of the active constraints with respect to β and J̃(γ) with respect to γ.

3.4. Extending to case-control study designs

When sampling fractions are available for the cases and controls of a case-control study, the methods we have presented can be applied to a modified objective function. Letting each component of the likelihood in Equation (5) be denoted as l_i(Θ|y_i). For a case-control design, each individual would have a weight w_i, representing the inverse sampling fraction for the ith individual. As an example, for a population-based case-control study with J strata and simple-random-sampling of n_j controls out of N_j eligible controls in each stratum, w_ij for the ith control of the jth stratum is N_j/n_j and for each case is w_ij = 1. Weights are incorporated into the estimation procedure by replacing each l_i(Θ|y_i) with w_il_i(Θ|y_i), making Equation (5) a pseudo-log-likelihood. Because the constraints do not depend on the sampling design, they are unaltered, and, after substitution of the pseudo-log-likelihood, the constrained optimization procedure follows the methodology presented for the cohort design.

3.5. Inference and boundary monitoring

Influence-based methods are used to estimate the variance-covariance matrix for the parameters Θ̂ [24]. Influence methods yield a Taylor-linearized variance estimate from the sum-of-squared deviations of Taylor deviates, the analytic equivalent to leave-one-out jackknife residuals. To derive the Taylor deviates for Θ̂ we first re-write the form of the objective function in (6) terms of the per-subject contributions, φ(Θ, λ, σ) = Σ_i φ_i(Θ, λ, σ), where each component of the sum is

$${\phi }_i(\mathrm{\Theta },\mathrm{\lambda },\mathrm{\sigma })=l(\mathrm{\Theta }|y_i)+\frac{1}{m_{k(i)}}[\sum _{j\in k(i)}({\mathrm{\lambda }}_j{d}_j(\mathrm{\Theta })-\frac{1}{2}\sigma d_j{(\mathrm{\Theta })}^2)],$$

k(i) is an index for the set of constraints imposed on the covariate class (x_i, z_i) and m_k(i) is the number of individuals of the sample with the k(i) covariate class. Letting Δ{.} denote the influence operator, the ith Taylor-deviate for Θ is

$$\mathrm{\Delta }{\{\mathrm{\Theta }\}}_i=-{\left[\frac{{\partial }^2\phi (\mathrm{\Theta },\lambda ,\sigma )}{\partial \mathrm{\Theta }\partial {\mathrm{\Theta }}^{\prime }}\right]}^{-1}\frac{\partial {\phi }_i(\mathrm{\Theta },\lambda ,\sigma )}{\partial \mathrm{\Theta }},$$ (8)

and is evaluated at the estimated values for each model parameter. We note that the deviate of Equation (8) is equal to the component of the sum in the update of a Newton-Raphson algorithm.

From the Taylor deviates, an estimate of the variance-covariance for Θ̂ is

$$\widehat{\text{Var}}[\widehat{\mathrm{\Theta }}]=\sum _{i=1}^n(\mathrm{\Delta }{\{\widehat{\mathrm{\Theta }}\}}_i-\overline{\mathrm{\Delta }}\{\widehat{\mathrm{\Theta }}\}){(\mathrm{\Delta }{\{\widehat{\mathrm{\Theta }}\}}_i-\overline{\mathrm{\Delta }}\{\widehat{\mathrm{\Theta }}\})}^{\prime },$$

where Δ̄{Θ̂} is the mean of the n deviates. Confidence intervals for the regression parameters and related test statistics apply standard large-sample normal theory with the variance estimator $\widehat{\text{Var}}[\widehat{\mathrm{\Theta }}]$.

An advantage of the influence-based methodology is that it can be readily modified to account for weights in the objective function, as would be needed for LEXPIT regression with case-control study designs (Section 3.4). Graubard and Fears describe influence function strategies for deriving Taylor-linearized standard errors of complex statistics with weighted estimating equations, and they provide specific applications for estimates of adjusted attributable risk from survey data [25].

Boundary conditions of the converged LEXPIT estimates are determined from the estimates of λ_j, the augmented Lagrangian parameters in Equation (6). A non-negative λ_j is indicative of an actively constrained fitted risk. The covariate patterns corresponding to bounded estimates should be regarded as potential points of influence. Having more than a few observations at the boundary could be evidence of a poorly fit model. Model fit can be inspected with graphical diagnostics on binned risk estimates, and formally tested with goodness-of-fit statistics, such as the Hosmer-Lemeshow chi-squared statistic.

In the simulation studies in the next section, we examine the properties of these inferential methods under different boundary conditions.

4. Simulation studies

4.1. Methods

Simulation studies were conducted to investigate the bias and precision of LEXPIT using the methodology proposed in this paper. In designing the simulation experiments, we were particularly concerned with the properties of the proposed methods when fitted values of the model were actively constrained, that is, when the LEXPIT estimates were at the bounds of the feasible region. For each simulation condition, the ith outcome was generated from Y_i|(X = x_i, Z = z_i) ∼ Bernoulli(π(x_i, z_i)), with the LEXPIT model for the event probability,

$$\pi (x_i,z_i)=\beta x_i+\text{expit}({\gamma }_0+\gamma z_i).$$ (9)

The expit covariate was a univariate Bernoulli variable, z_i ∼ Bernoulli(1/3), while continuous and binary scenarios for the univariate linear covariate x_i were each considered. For the binary condition, x_i ∼ Bernoulli(1/2), and for the continuous condition x_i ∼ Gamma(1, 5).

The number of covariates was limited to two in order to allow for direct comparison between the LEXPIT and BLM, and, thereby, assess whether the expit formulation was able to reduce the frequency of boundary cases in contrast to a strictly linear model. The use of a univariate binary z_i made direct comparison possible because, in this case, model (9) can be reparameterized as a BLM with coefficients,

$$\pi (x_i,z_i)=\text{expit}({\gamma }_0)+\beta x_i+[\text{expit}({\gamma }_0+\gamma )-\text{expit}({\gamma }_0)]z_i.$$ (10)

We studied eighteen different simulation conditions in which the variable parameters were the baseline risk, study sample size, and the linear covariate data type. Three settings for the baseline risk were considered, {0.005, 0.01, 0.05}, each specifying a low probability for the disease outcome in order to induce boundary cases at the lower risk bound. Cohort studies of sample sizes considered were {500, 1000, 3000}, corresponding to an expected case count of {2.5, 5, 15} at the lowest baseline rate. In all conditions, γ = 3, while β varied depending on whether x_i was continuous or binary. In the binary case, β = 0.05; in the continuous case, β = 0.005. Summaries of the bias, mean-squared error, and coverage interval for the LEXPIT and BLM estimates were based on 1000 simulated dataset for each scenario. As a measure of the extremity of the boundary conditions and the convergence performance of the constrained optimization algorithm, we report the percentage of convergence failures when using iterative reweighted least squares (IRLS) to fit the BLM.

4.2. Results

In fitting a strictly linear model, constrained optimization converged to feasible parameters for all scenarios considered, whereas the convergence failure of IRLS was as frequent as 29% (Table 1). The BLM risk difference estimates were unbiased with generally good coverage and accurate precision. However, the baseline risk estimate and standard error had a positive bias when the expected number events in the reference population was small, conditions in which there was a higher probability of convergence to the boundary. The bias for the point estimates and standard error diminished as the expected number events increased, but, for conditions where the expected number events was ≤ 10, the coverage interval for the baseline risk was still not at the nominal level. When we examined the empirical shape of the baseline risk for these conditions, we found that it was right-skewed. Thus, even though the accuracy of the baseline risk estimands improved with increasing sample size, when there was a non-negligible chance of hitting the boundary, the constrained MLE were not normally distributed.

Table 1.

Summary of BLM simulation studies (1000 iterations per cell; All values are given as %).

Baseline risk	N [Ref E(Y)]*	IRLS Failure**	Active†	Mean Est	ESE	Mean SE	95% Coverage
				[0.50, 5.00, 8.67]‡
0.5	500 [1]	29.2	41.8	(0.51, 5.10, 8.76)	(0.55, 1.74, 2.78)	(0.83, 1.84, 2.74)	(99.8, 96.7, 94.0)
	1000 [2]	23.3	17.2	(0.50, 5.04, 8.72)	(0.37, 1.19, 1.95)	(0.48, 1.26, 1.91)	(100, 95.5, 94.4)
	3000 [5]	10.1	0.5	(0.50, 5.01, 8.62)	(0.23, 0.72, 1.06)	(0.21, 0.70, 1.09)	(88.9, 94.8, 95.4)
				[1.00, 5.00, 15.87]
1	500 [2]	20.3	20.7	(0.96, 4.98, 16.06)	(0.77, 1.93, 3.37)	(0.82, 1.89, 3.34)	(95.2, 94.2, 94.3)
	1000 [4]	10.5	3	(1.00, 4.95, 15.77)	(0.53, 1.34, 2.43)	(0.53, 1.32, 2.35)	(88.4, 93.6, 93.7)
	3000 [10]	1	0	(1.01, 4.99, 15.91)	(0.31, 0.75, 1.39)	(0.30, 0.76, 1.36)	(93.4, 95.4, 94.7)
				[5.00, 5.00, 46.39]
5	500 [9]	0.4	0	(4.86, 5.13, 46.49)	(1.64, 2.65, 4.37)	(1.57, 2.63, 4.29)	(91.5, 94.8, 94.7)
	1000 [18]	0	0	(5.00, 5.04, 46.31)	(1.16, 1.84, 3.07)	(1.14, 1.87, 3.04)	(94.0, 95.5, 94.6)
	3000 [53]	0	0	(4.98, 4.98, 46.45)	(0.66, 1.05, 1.78)	(0.66, 1.08, 1.75)	(94.0, 94.9, 95.1)

ESE, Empirical standard error; MSE, Mean squared error

^*Expected number of events in reference group.

^**Unconstrained iterative reweighted least squares failed to converge.

^†One or more active constraints.

^‡[γ₀, β, γ], Simulation values for model, π = γ₀ + βx + γz.

When the LEXPIT model was applied to the same data for the binary linear exposure, the parameters were less likely to have active constraints than with the strictly linear model (Table 2). This resulted in improved coverage intervals for the covariate effects and the baseline risk—nearly all were within 1% of the nominal 95% level. When the expected number events in the reference population was < 5, there was a positive bias in the nonlinear effects and their standard error. Graphical assessments showed there was less skew in the empirical distribution of these parameters as compared to the baseline risk of the BLM when the baseline risk estimate was near to zero. This suggested that, in these conditions, the LEXPIT model parameters have a faster rate of convergence to a normal density than the BLM, resulting in improved coverage, but have larger bias when the expected number events in the lowest risk group is < 5.

Table 2.

Summary of LEXPIT simulation studies (1000 iterations per cell; Risk differences given as %).

Baseline risk	N [Ref E(Y)]*	Active**	Mean Est	ESE	Mean SE	95% Coverage
			[5.00, -5.29, 3.00]†
0.5	500 [1]	0	(5.05, -7.39, 5.03)	(1.60, 3.26, 3.27)	(1.70, 4.65, 4.72)	(96.0, 94.8, 95.4)
	1000 [2]	0	(5.02, -6.02, 3.71)	(1.16, 1.88, 1.88)	(1.20, 2.58, 2.60)	(95.1, 96.6, 97.1)
	3000 [5]	0	(5.01, -5.41, 3.11)	(0.72, 0.59, 0.60)	(0.70, 0.49, 0.50)	(94.8, 95.6, 95.6)
			[5.00, -4.60, 3.00]
1	500 [2]	0	(4.99, -5.78, 4.17)	(1.86, 2.62, 2.60)	(1.84, 3.86, 3.87)	(94.3, 96.5, 96.5)
	1000 [4]	0	(4.96, -4.84, 3.23)	(1.33, 1.00, 1.00)	(1.31, 0.78, 0.78)	(93.4, 96.5, 96.1)
	3000 [10]	0	(4.99, -4.63, 3.04)	(0.75, 0.32, 0.33)	(0.76, 0.31, 0.32)	(95.4, 96.0, 95.7)
			[5.00, -2.94, 3.00]
5	500 [9]	0	(5.33, -3.05, 3.09)	(2.65, 0.40, 0.41)	(2.64, 0.37, 0.38)	(94.5, 95.0, 95.2)
	1000 [18]	0	(5.44, -3.00, 3.04)	(1.72, 0.26, 0.27)	(1.88, 0.25, 0.26)	(96.3, 95.0, 95.0)
	3000 [53]	0	(5.60, -3.00, 3.03)	(0.86, 0.13, 0.14)	(1.09, 0.14, 0.15)	(95.4, 94.3, 96.1)

ESE, Empirical standard error; MSE, Mean squared error

^*Expected number of events in reference group.

^**One or more active constraints.

^†[γ₀, β, γ], Simulation values for model, π = βx + expit{γ₀ + γz}.

An important finding of the simulation studies was that, even in conditions when the strictly linear model was actively constrained, both the BLM and LEXPIT estimators for the linear term risk differences were unbiased and consistent. The same properties were found for the simulation conditions with a continuous linear exposure variable (Supporting Materials, I).

5. Application: Cervical cancer risk in a screening program

Starting in 2003, KPNC enrolled women in a cervical cancer screening program using concurrent cervical cytology (Pap test) and HPV testing [13]. Among these women, we considered a cohort of 167, 171 30-55 year-olds who had no cervical intraepithelial neoplasm (CIN) at enrollment, no hysterectomy before or during the study observation period, and whose CIN status was known 5 years after the baseline visit. Screening test results were dichotomized. In the study cohort, 375 (0.22%) cases of cervical precancer or cancer (CIN grade 3 or worse (CIN3⁺)) developed over 5 years.

We fit BLM, LEXPIT, and logistic models to estimate differences in the five-year cumulative risk of CIN3⁺ by the HPV and Pap screening result types. We assessed model fit with the Akaike information criterion (AIC), Pearson's chi-squared statistic (χ²) in models with fewer than ten covariate classes, and the Hosmer-Lemeshow chi-squared test in models with ten or more covariate clases. Lower values of both the AIC and chi-square statistic are indicative of an improved fit, and reductions in the goodness-of-fit diagnostics were our method of assessing whether a given covariate's risk associations were better described by linear or multiplicative effects on the absolute risk scale.

We first considered a risk model without adjustment for other covariates. Strong main effects of HPV and Pap screening results were found for the BLM and logistic models (Table 3). A significant interaction was found in the logistic analysis but not in the BLM. When each model was fit without an interaction term, the fit for BLM was unchanged while that of the logistic model was significantly poorer for both the AIC and Pearson's χ²(1) measures (Table 4). This suggested that the screening risk effects were acting additively and the significant interaction of the logistic model, showing a surprising reduced risk associated with a double positive screen on Pap and HPV, was a statistical artifact of the logistic model's poorer fit.

Table 3.

Models of screening results and risk of five-year CIN3⁺ without confounder adjustment (n=167,171).

Factor	RD	BLM t-statistic	Logistic
			OR	t-statistic
HPV	278.0	14.8	52.84	30.8
Pap	21.3	2.9	4.86	5.3
Interaction	-59.2	-1.6	0.18	-5.2

RD, Risk difference (per 10,000); OR, odds ratio

Table 4.

Goodness-of-fit statistics for unadjusted models of screening results and risk of five-year CIN3⁺ (n=167,171).

Subgroup	Obs.	BLM Exp.	Logistic Exp.
HPV−/Pap−	13	12.1	3.2
HPV+/Pap−	84	84.2	93.8
HPV−/Pap+	57	67.4	66.8
HPV+/Pap+	221	211.3	211.2
χ2 (P-value)		2.18 (0.3355)	33.25 (< 0.001)
AIC		4162	4180

Next we included confounders: age at enrollment, history of a previous normal biopsy for cervical cancer, and history of a previous abnormal Pap test. Age (in years) was categorized as [30, 35), [35, 45), [45, 56), and separate age effects for HPV-positive women were included in all models. Previous biopsy and previous abnormal Pap smear were each entered as binary variables. For the BLM, all terms were linear on the probability scale; for the LEXPIT, the screening variables of baseline HPV and Pap were linear terms while all remaining explanatory variables were expit terms; for the logistic model, all variables were linear on the log-odds scale. All models had nine parameters and equivalent degrees of freedom. Using a Pentium(R) 4 3.60 GHz CPU, the elapsed time for fitting the BLM and LEXPIT models with the blm package was approximately one minute; the glm function fit the logistic model in 16 seconds.

In the fully-adjusted analyses, significant additive main effects for HPV and Pap positive screens were found in models on the absolute risk scale. For the BLM, the adjusted main effect for a positive Pap screen at baseline was an increased risk difference of five-year CIN3⁺ of 17.3 per 10,000 women (95% CI = 4.3 to 30.1), while HPV-positivity was associated with an adjusted risk difference of 297.4 per 10,000 women (95% CI = 239.8 to 355.1) (Table 5). When Pap and HPV screening outcomes were additive on the log-odds scale, the adjusted effect of Pap-positivity was not significant, OR = 1.06 (95% CI = 0.80 to 1.39), whereas a positive HPV screen at baseline had an adjusted odds ratio of 33.9 (95% CI = 22.7 to 52.3).

Table 5. Adjusted risk differences of five-year CIN3⁺ per 10,000 women by risk model (n=167,171).

Risk Group	No. cases/ non-cases	BLM		LEXPIT		Logistic*
		Est	95% CI	Est	95% CI	Est	95% CI
HPV−/Pap− (Ref.)	84/152117	9	(6, 12)	9	(6, 12)	9	(6, 13)
HPV+/Pap−	57/2264	298	(240, 355)	298	(240, 355)	294	(234, 353)
HPV−/Pap+	13/4841	17	(4, 30)	18	(5, 31)	1	(-2, 3)
HPV+/Pap+	221/7574	315	(256, 374)	315	(257, 374)	313	(226, 400)

^*standardized by summing over confounders

The logistic model had the poorest fit based on chi-squared and AIC measures. Pearson's chi-squared for the logistic model was χ²(39) = 96.45 (p < 0.0001), BLM χ²(39) = 32.302 (p = 0.7673) and LEXPIT χ²(39) = 33.727 (p = 0.6673). The covariate classes with the greatest discrepancy for the logit model were for the risk group of HPV positive, Pap negative 30-35 year-olds (O – E = 7.49) and for HPV negative, Pap positive 35-45 year-olds (O – E = 5.49). Given the large number of covariate patterns in the expanded model, goodness-of-fit was further assessed with the Hosmer-Lemeshow chi-squared statistic. For the logistic model, this was χ²(8) = 14.6 (p = 0.0671); for BLM, χ²(8) = 11.3 (p = 0.1848); for LEXPIT, χ²(8) = 12.3 (p = 0.1385). The AIC provided further support of linear risk effects for the screening variables as there was a 14-point improvement in the AIC for the BLM and a 17-point improvement for the LEXPIT over the logistic model fit (Logistic AIC = 4139; BLM AIC = 4125; LEXPIT AIC = 4122). When the models were re-fit with age at entry as a continuous variable, the fit of each model generally improved (BLM χ²(8) = 6.8, LEXPIT χ²(8) = 11.1, Logistic χ²(8) = 12.7) but did not change the substantive conclusions for the screening effects.

To better assess the implications of these differences on the interpretation of the risk effects for each HPV/Pap subgroup, we have calculated standardized risk differences from the fully adjusted logistic model and contrast these in Table (5) to the estimates of the BLM and LEXPIT. The estimated risk difference in each subgroup is the change in risk of five-year CIN3⁺ for a 30-35 year-old woman, the reference age group of the model, as compared to an otherwise comparable woman who was negative on both the HPV and Pap tests. In the confounder-adjusted BLM and LEXPIT models, the effects of HPV and Pap were linear, so the risk differences were obtained directly from the fitted linear coefficients. In the logistic model, the risk difference is a function of all the model confounders and, consequently, changes across confounder-matched comparisons. To estimate absolute risks using logistic regression we, therefore, summed over the distribution of the confounders.

As an example of this calculation, consider estimating the risk difference for a 30-35 year-old woman with a positive HPV test and negative Pap. Confounding variables were previous biopsy and previous abnormal Pap, giving J = 4 confounder classes, which were all possible combinations of these confounders. Let p_j be the sample proportion of the jth covariate class z_j among 30-35 year olds. An estimate of the standardized risk difference associated with an HPV positive screen was

$$\widehat{\text{RD}}(\widehat{\beta })=\sum _j{p}_j[\text{expit}\{{\widehat{\gamma }}_0+\widehat{\beta }+{\widehat{\gamma }}^{\prime }{z}_j\}-\text{expit}({\widehat{\gamma }}_0+{\widehat{\gamma }}^{\prime }{z}_j)]$$

where γ̂₀ was the estimated intercept parameter, β̂ the log-odds ratio for an HPV positive versus negative result, and γ̂ the log-odds ratios for confounding factors. The delta method was applied to obtain a large sample 95% confidence interval for the standardized risk difference $\widehat{\text{RD}}(\widehat{\beta })$ (Supporting Materials, II).

The BLM and LEXPIT gave nearly identical risk difference estimates for each screening group within the 30-35 year-old age group (Table 5). The increased risk associated with HPV positivity based on the risk difference for the logistic model was consistent with the linear model estimates. However, the models differed in their assessment of the risk associated with a Pap test result. While the linear and LEXPIT models estimated that a HPV negative 30-35 year old woman with a positive Pap smear had an excess CIN3⁺ risk of 17 to 18 per 10,000 women, the logistic model found no increased risk with an abnormal Pap test (1 per 10,000 women, 95% CI -2 to 3). A finding of no increased risk is scientifically implausible because women with abnormal Pap tests routinely receive a more extensive diagnostic workup [13].

6. Discussion

We introduced the LEXPIT model, a regression model for analysis of binary response data that focuses on the estimation of confounder-adjusted absolute risk and risk differences. The LEXPIT model provides a convenient way to directly estimate risk differences from cohort or population-based case-control studies in a multivariable regression analysis that allows the simultaneous assessment of additive and multiplicative risk effects on the probability scale. We adapted modern optimization algorithms to develop a constrained maximum likelihood procedure that is operationally comparable to the IRLS algorithm of generalized linear models. Our computational methods yield consistent estimates for the BLM and LEXPIT models. Although linear effects on the risk scale have historically been difficult to compute, simulations showed that our methodology provided a robust means of fitting the BLM and LEXPIT, in contrast to unconstrained IRLS. When no member of the generalized linear model family for binomial data provides an adequate fit, the LEXPIT could be useful because it extends both the BLM and logistic models, explicitly modeling standardized risk differences for exposures of interest and reducing the chance of boundary cases by modeling remaining confounders in the expit term. Our methodology for fitting the BLM and LEXPIT models can be implemented with the freely available R package blm [26].

The LEXPIT model adds to the class of partially linear risk models, allowing both additive and non-additive effects, which includes the absolute excess risk Poisson regression models for grouped survival data [10] and the Cox-Aalen model for time-to-event data [9]. Although the Poisson regression model could be adapted to binomial regression under a rare disease assumption, the LEXPIT model requires no rare disease assumption. The LEXPIT model is appropriate for general binomial regression and, to our knowledge, it is the only hybrid risk model that enforces the feasible region of the parameter space as part of the estimation procedure. The constrained maximization method could be readily extended to other smooth likelihoods whose parameters are subject to constraints of the form, ℱ = {l ≤ f(Θ, x) ≤ u, ∀x ∈ 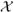}, where f(Θ, X) is the model specifying the distribution for Y. A linear model for a Poisson rate is one possible extension, where λ = f(θ, x) = x′Θ and (l, u) = (0, ∞).

Partially linear models retain properties of the simpler linear model while relaxing the assumptions of the linear model, which might not be satisfied for many practical problems [27]. Smoothed regression splines have been used to combine nonlinear and linear effects in models of disease risk, including models for osteoporosis [28], prostate cancer [29], and spontaneous abortion [30]. A disadvantage with this form of additive model is that the coefficients of spline functions lack a meaningful interpretation. The LEXPIT is an appealing partially linear absolute risk model because it inherits properties of the binomial linear and logistic regression models. As with other partially linear models, the added flexibility of the LEXPIT introduces the challenge of deciding whether a covariate in the model has linear or nonlinear effects. To address the challenge of covariate structural selection, we recommend that analysts consider linear effects for the exposure variables of primary interest and, for remaining confounding variables, narrow the dimension of the model search by graphically assessing the functional form of these covariates on the additive risk scale. Comparisons among the subset of multivariable-adjusted models can then be based on goodness-of-fit diagnostics, such as the Hosmer-Lemeshow chi-squared test presented in the KPNC application.

A more theoretically justificable procedure would simultaneously select the structure of candidate predictors while fitting the regression model. Zhang, Cheung, and Liu presented a method for discovering the structure and effect estimates of covariates in partially linear regression models of a continuous outcome [31]. The procedure they propose, the Linear and Nonlinear Discoverer, can be described as a solution to a regularization problem with a smoothing spline ANOVA. It would be a valuable extension of the present work to determine whether a similar discovery method could be constructed for the LEXPIT.

The introduction of the LEXPIT will allow more routine consideration of multiple risk scales in studies of risk association. Modeling of cervical cancer outcomes in the KPNC cohort provided one example where additive effects on the absolute risk scale for screening covariates improved fit when compared to a standard logistic model. Importantly, this improvement was gained without the requirement of an interaction term. This highlights the importance of considering multiple models on different risk scales in the assessment of effect modification to protect against the overinterpretation of significant interactions that might only indicate a model's statistical departure from additivity [32].

Inference at the boundary of the feasible region remains an important unresolved challenge of maximization problems with linear or nonlinear inequality constraints. Although there have been thorough studies of the asymptotic properties of bounded maximum likelihood estimators [33], the literature on the asymptotics of estimators constrained by a system of inequalities is more limited. In the case of the LEXPIT, since individual risk predictions are bounded rather than the regression coefficients themselves, one might expect that when the number of active constraints are few the asymptotic properties of the model's maximum likelihood estimates would be approximately those under standard conditions. Our simulation studies of rare disease scenarios support this because they showed that the BLM was unbiased and had good coverage for estimated risk differences in the presence of active constraints. However, the coverage interval for the baseline risk was poor when the frequency of a boundary case was high. The use of the expit function in the LEXPIT model provided improvement in coverage by reducing this frequency. Further study is needed to determine under which conditions the application of standard inference procedures for the constrained maximum likelihood estimates of the LEXPIT might not be appropriate.

Models of relative risk or relative odds can be useful for identifying etiological factors but are less useful when there is a need to understand a covariate's impact on individual risk. Given an individual risk profile, the LEXPIT model quantifies the probability of failure, independent of any reference group. For this reason, the LEXPIT model could have utility in clinical settings, where the assessment of an individual's probability of disease is vital to risk counseling. When covariates include modifiable health factors, LEXPIT regression could also be used to assess the impact of public health interventions. Risk predictions for the population of interest could be estimated under differing scenarios of an intervention's effectiveness and the benefit of the intervention could be judged by the estimated absolute risk reduction for the defined population. The potential clinical and epidemiological uses of the LEXPIT model make it an important extension of standard regression models for binary data analysis.