The Free Energy Landscape of Pseudorotation in 3′–5′ and 2′–5′ Linked Nucleic Acids

Abstract

The five-membered furanose ring is a central component of the chemical structure of biological nucleic acids. The conformations of the furanose ring can be analytically described using the concept of pseudorotation, and for RNA and DNA they are dominated by the C_2′-endo and C_3′-endo conformers. While the free energy difference between these two conformers can be inferred from NMR measurements, a free energy landscape of the complete pseudorotation cycle of nucleic acids in solution has remained elusive. Here, we describe a new free energy calculation method for molecular dynamics (MD) simulations using the two pseudorotation parameters directly as the collective variables. To validate our approach, we calculated the free energy surface of ribose pseudorotation in guanosine and 2′-deoxyguanosine. The calculated free energy landscape reveals not only the relative stability of the different pseudorotation conformers, but also the main transition path between the stable conformations. Applying this method to a standard A-form RNA duplex uncovered the expected minimum at the C_3′-endo state. However, at a 2′–5′ linkage, the minimum shifts to the C_2′-endo conformation. The free energy of the C_3′-endo conformation is 3 kcal/mol higher due to a weaker hydrogen bond and a reduced base stacking interaction. Unrestrained MD simulations suggest that the conversion from C_3′-endo to C_2′-endo and vice versa is on the nanosecond and microsecond time scale, respectively. These calculations suggest that 2′–5′ linkages may enable folded RNAs to sample a wider spectrum of their pseudorotation conformations.

Introduction

The furanose ring links phosphate groups into an extended linear backbone and anchors the heterocyclic bases to form the unique chemical structure of RNA, DNA, TNA and related nucleic acids. It has long been recognized from X-ray crystallographic studies that the furanose moiety is not planar but can take many distinct puckered conformations.^1,2 Proton NMR studies of nucleosides and mononucleotides suggested a rapid interconversion of these pucker states.^3,4 In conventional 3′–5′-linked RNA, the optimal pucker state can shift from C_3′-endo in a standard A-form duplex to C_2′-endo in other structural motifs.^5,6 This inherent flexibility of the ribose backbone allows RNA to fold into specific tertiary structures with exquisitely specific molecular recognition and catalytic activities. The catalytic abilities of folded RNA structures lend strong credibility to the hypothesis of an RNA world,⁷ in which RNA served as both the genetic material and the principal catalysts of primitive life.

The emergence of the RNA world from prebiotic chemistry is poorly understood. Experimental efforts to synthesize a self-replicating protocell have been hindered by a series of problems in achieving nonenzymatic RNA replication.⁸ One of these apparent problems is the relatively poor regiospecificity of nonenzymatic RNA copying. However, recent studies in this laboratory revealed that folded RNA structures can tolerate a significant amount of backbone heterogeneity.^9,10 Certain aptamers and ribozymes can retain their functions even when 25% of the original 3′–5′ linkages are substituted by 2′–5′ linkages.¹⁰ This shifts the paradigm from the view that 2′–5′ linkages are deleterious for RNA replication to one in which a certain level of backbone heterogeneity is advantageous because it may facilitate thermal denaturation and therefore RNA replication, while remaining compatible with the biological functions of RNA.^8,10 Subsequent X-ray crystallographic studies and molecular dynamics (MD) simulations showed that in RNA duplexes, the structural perturbations caused by 2′–5′ linkages are largely confined to the two nearest base pairs and have minimal effects upon the rest of the duplex.¹¹ Furthermore, 2′–5′-linked nucleotides can adopt either the C_3′-endo or C_2′-endo conformation, with a preference for the latter.¹¹ This is in sharp contrast with conventional 3′–5′-linked RNAs and prompted us to systematically calculate the free energy landscape of sugar puckering and to investigate how this landscape is modulated by distinct backbone linkages.

Calculating a free energy landscape requires a set of judiciously chosen collective variables (CV) that reduces the high-dimensional phase space to a low-dimensional CV space while still distinguishing all significant conformers. The free energy for each point in the CV space is then calculated by advanced simulation methods such as umbrella sampling^12,13 and metadynamics.^14,15 These free energy calculations have provided critical insights into many fundamental chemical¹⁶ or biophysical problems^17,18 by allowing one to determine not only the population of any given conformer but also the free energy along a transition path that connects two stable conformers.

The ideal CVs for studying the conformational changes of sugar pucker are the two pseudorotation parameters, the phase angle P and the amplitude τ_m, which were first proposed by Altona and Sundaralingam² and subsequently generalized by Cremer and Pople.¹⁹ These two parameters analytically describe the complete spectrum of all possible puckered states. Following the Cremer–Pople definition, early theoretical studies calculated the potential energy surface of the phase angle P for several nucleoside analogues in vacuo and revealed that the conversion between C_2′-endo and C_3′-endo occurs via the O_4′-endo pathway, with an energy barrier of 2–3 kcal/mol.¹⁹⁻²² The alternative O_4′-exo pathway has a much higher barrier and is thus less favorable.²² The high computational cost, however, precluded the possibility of applying such ab initio methods to nucleic acids in explicit solvent. For these larger systems typically with no less than tens of thousands of atoms, MD simulation based on empirical force fields is an attractive approach that balances computational cost and accuracy. Indeed, starting with a minimized conformation, benchmark simulations of various ribo- and deoxyribo-nucleosides as well as DNA, RNA, and DNA/RNA hybrid duplexes reproduced the stable sugar pucker modes observed in experiments.²³⁻²⁵ The sampling from these unrestrained simulations, however, is often insufficient to identify high free energy barriers or other minima that are separated by such barriers. As such, a complete free energy landscape of the entire pseudorotation cycle has not yet been described even for simple nucleosides.

As a step toward elucidating the structural effects of 2′–5′ linkages upon functional RNAs, and to provide a unified description of the various puckered conformations of nucleic acids, we developed a computational method that directly used P and τ_m as the CVs to calculate pseudorotation free energy. Compared to previous work that used root-mean-square-displacement as an indirect CV,²⁶ this new approach overcame the insufficiency of sampling and allowed us to sample the entire two-dimensional pseudorotation cycle. In two nucleoside model systems, the calculation not only accurately predicted the free energy difference between the two main pucker states, C_2′-endo and C_3′-endo, but also determined the free energy of key transition intermediates, the O_4′-endo and O_4′-exo states. Application to a native RNA duplex revealed the C_3′-endo state as the single dominant free energy minimum. For a 2′–5′-linked nucleotide in an otherwise identical RNA duplex, our free energy calculation revealed a flattened free energy landscape, in which the C_2′-endo state is only 3 kcal/mol more stable than the C_3′-endo conformation. The interconversion between these two states is coupled to a switch of hydrogen bonds between O_3′–H and the pro-S_P-oxygen or pro-R_P-oxygen. The free energy barrier corresponds to the C_4′-exo state, with no intramolecular hydrogen bond between 3′-OH and either nonbridging oxygen of the downstream phosphate. This conclusion is supported by 420 unrestrained MD simulation trajectories in which the nucleotide spontaneously migrates to the more stable C_2′-endo state from the initial C_3′-endo conformation. From these simulations, we estimated that the transition from C_3′-endo to C_2′-endo occurs in nanoseconds, whereas the reverse transition requires approximately microseconds. Such a rapid interconversion will allow 2′–5′-linked RNA to swiftly sample various pseudorotation states across the flattened energy landscape, and such an expanded conformational flexibility could allow a single RNA sequence to sample multiple functional conformations.

Materials and Methods

Simulation Systems

Guanosine (rG) and 2′-deoxyguanosine (dG) nucleosides were solvated in 29 × 29 × 34 ų TIP3P water boxes with a total of ∼2.6 × 10³ atoms for each system. The native RNA duplex (5′-CCGGCGCCGG-3′) simulation was based on the reported 1.32 Å resolution X-ray crystal structure (PDB code: 4MS9), and the C5–2′–5′-linked RNA duplex (5′-CCGGC*GCCGG-3′, where the asterisk represents a 2′–5′ phosphodiester bond) was based on the reported 1.55 Å resolution structure (PDB code: 4MSB).¹¹ Both systems were set up as previously described.¹¹ The final systems contained ∼1.2 × 10⁴ atoms including RNA, water, and ions. Simulation setup and molecular visualizations were performed using VMD.²⁷

Unrestrained MD Simulations

A total of 1.4 μs of unrestrained MD simulations (Table S1, Supporting Information) were performed using the program NAMD 2.9²⁸ with the CHARMM36 parameter set.^29,30 All simulations were performed using periodic boundary conditions in the isobaric–isothermal (NPT) ensemble. Langevin dynamics was used to keep the temperature at 298 K with a damping constant of 5 ps^–1, and a Langevin piston³¹ was applied to maintain the pressure at 1 atm. The bonded, nonbonded, and electrostatic interactions were calculated at time steps of 1, 2, and 4 fs, respectively. The switching (cutoff) distance for nonbonded interactions was set at 10 (12) Å. To compute long-range electrostatic interactions, the Particle Mesh Ewald method³² with a grid density of at least 1 Å^–3 was used.

To provide a benchmark for the pseudorotation of nucleosides, 300 ns unrestrained simulations were performed for both rG and dG (Table S1, Supporting Information). Both systems were first subjected to 10 000 steps of minimization using the conjugate gradient method. To enhance the sampling as well as estimate the sampling variability, five replica runs were set up using the same minimized initial structure but different initial velocities. Each replica was equilibrated for 10 ns followed by 50 ns production runs. The coordinates of the simulation trajectories were saved at 0.5 ps intervals and used to calculate p(P,τ_m), the probability of observing a given pseudorotation conformation. The pseudorotation free energy is then calculated by F(P,τ_m) = −k_BT ln p(P,τ_m).

To study the kinetics of the C_3′-endo to C_2′-endo transition of C5 in the C5–2′–5′-linked RNA duplex, 40 distinct configurations sampled at 100 ps intervals were extracted from a 4 ns simulation in which the pucker state of C5 was restrained at the C_3′-endo conformation. Each configuration was used as the initial coordinate for 20 1-ns unrestrained simulations with different initial velocities. The aggregate simulation time used to study this conformational change was 800 ns (Table S1, Supporting Information).

Umbrella Sampling Using Pseudorotation Coordinates

We implemented P and τ_m as the CV for umbrella sampling and metadynamics in a modified version of NAMD 2.9²⁸ using the Cremer–Pople pseudorotation definition,¹⁹ from which the gradient of P and τ_m can be computed analytically. The derivation of these equations, together with a brief introduction to the Cremer–Pople definition, is provided in the Supporting Information. In the Results and Discussion section, the P and τ_m values calculated according to the Cremer–Pople definition are converted to the Altona–Sundaralingam definition that is more widely used in the literature using the following equations:³³

1

2

Figure 1 illustrates the relationship between P and various sugar pucker conformations.

Figure 1.

Pseudorotation cycle of the furanose ring. Phase angles P, based on the Altona–Sundaralingam definition, are given in multiples of 36°. The corresponding structures of the furanose ring are shown on the periphery of the circle.

The umbrella sampling calculation of nucleoside pseudorotation comprises five replicas of simulations at 298 K with a biasing harmonic potential centered on P (varying successively from −180 to 180° every 10° with a force constant of 0.007 kcal mol^–1 deg^–2) and τ_m (varying successively from 0.2 to 0.55 Å every 0.05 Å with a force constant of 280 kcal mol^–1 Å^–2). Each simulation was 400 ps, and the distribution of (P, τ_m) from the last 280 ps trajectory was used as the input to reconstruct the unbiased free energy surface. The weighted histogram analysis method (WHAM)¹³ with Bayesian bootstrapping³⁴ was applied to generate 200 bootstrapped free energy surfaces from 1440 histograms of the five replica runs (Table S1, Supporting Information). A reliable free energy reconstruction requires significant overlap between the histograms from adjacent simulation windows. Indeed, extensive overlap was observed for both rG (Figure S3, Supporting Information) and dG (Figure S4, Supporting Information). The average and standard deviation of the free energy was calculated on the basis of these 200 bootstrapped free energy surfaces. The source code for the analyses was developed on the basis of the one-dimensional WHAM code written by David Minh,³⁵ and has been deposited to simtk.org.

For C5 in the native RNA duplex, the umbrella sampling calculation focused on the “east half” of the pseudorotation space, with biasing potential centered on P (varying successively from −90 to 90° every 10° with a force constant of 0.008 kcal mol^–1 deg^–2) and τ_m (varying successively from 0.15 to 0.50 Å every 0.05 Å with a force constant of 320 kcal mol^–1 Å^–2). For C5 in C5–2′–5′-linked RNA duplex, a similar setup was used except P was sampled at every 7.5° and τ_m was sampled from 0.10 to 0.50 Å with 0.05 Å intervals. Each simulation was performed for 800 ps, and the last 500 ps was used for free energy calculation. As above, the distributions from adjacent simulation windows overlap extensively (Figure S5, Supporting Information, for native RNA duplex; Figure S6, Supporting Information, for C5–2′–5′-linked RNA duplex). For each duplex, five replicas were performed, and the free energy surface was reconstructed using the same protocol as for free nucleosides.

Results and Discussion

Free Energy Landscape of Pseudorotation in Guanosine

We first calculated the free energy surface defined by P and τ_m for guanosine (rG) in solution by directly using P and τ_m as the collective variables in umbrella sampling (see Materials and Methods for computational details). The resulting free energy surface represents the intrinsic properties of guanosine pseudorotation in the absence of other structural constraints imposed by secondary or tertiary structures of RNA, and therefore, it serves as an important reference for understanding nucleic acid pseudorotation. Previous NMR³⁶ and crystallographic³⁷ studies provide critical experimental data for testing the accuracy and validity of our computational method.

The calculated free energy surface of rG pseudorotation is depicted in Figure 2A. The lowest free energy state corresponds to the C_2′-endo conformation with P from 160 to 180° and τ_m between 35 and 42° (Figure 2D). This agrees well with the one conformer observed in the crystal structure of guanosine dihydrate (P = 161.4°, τ_m = 36.2°).^2,37 The other conformer adopts a C_1′-exo conformation (P = 139.2°, τ_m = 44.3°) that is different from many other purine nucleosides or their derivatives.² This unusual C_1′-exo conformation is likely due to crystal packing. Our free energy calculation also located a second minimum around P = 20° that corresponds to the C_3′-endo conformation (Figure 2B). The free energy difference between these two states is 1 kcal/mol, in excellent agreement with 0.8 kcal/mol derived from previous NMR measurements based on ³J_{H1′–H2′}.³⁶ For 5′-guanosine monophosphate, our previous NMR measurements yield a free energy difference of 0.5 kcal/mol,³⁸ suggesting that the equilibrium between these two states is largely unaffected by the C_5′ exocyclic substituents.

Figure 2.

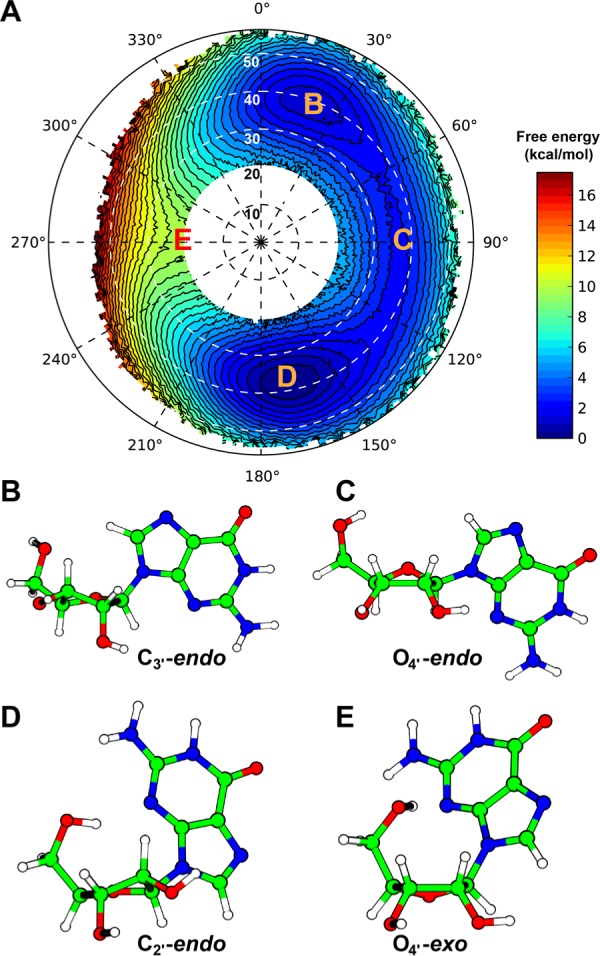
Pseudorotation free energy landscape of guanosine. (A) The pseudorotation free energy of guanosine is plotted in polar coordinates with P, the phase angle, increasing clockwise from a vertical value of P = 0°, and τ_m, the puckering amplitude, increasing radially from the central dot (a completely planar ribose ring). The contour lines are drawn every 0.5 kcal/mol, and the standard deviation (Figure S7, Supporting Information) is in general less than 0.2 kcal/mol. (B–E) Representative structures of key states along the pseudorotation cycle.

The calculated free energy landscape also predicts the free energy barriers of the transitions between the two minima and the corresponding pseudorotation states. The main transition pathway, via an O_4′-endo intermediate, has a barrier of 2 kcal/mol, which can be attributed to the eclipsed O_2′–C_2′–C_3′–O_3′ torsion angle (Figure 2C). The height of this barrier is low enough to be sampled by sufficiently long unrestrained MD simulations and serves as an additional benchmark for our free energy calculations. Five independent unrestrained simulations (60 ns each) were performed. During the 250 ns aggregate production time, 848 transitions between C_2′-endo and C_3′-endo were observed, providing extensive sampling over the “east” half of the pseudorotation cycle. The calculated free energy surface from these unrestrained simulations (Figure S8, Supporting Information) agrees well with the one from umbrella sampling, with an identical 2 kcal/mol free energy barrier. Detailed analyses of these unrestrained simulations regarding the nucleobase orientation and the intramolecular 5′-OH···N3 hydrogen bond^23,39 during the pseudorotation cycle are provided in the Supporting Information. The agreement between umbrella sampling results and independent computational as well as experimental data suggests that our implementation of pseudorotation collective variables allows the accurate calculation of the phase angle, amplitude and the energetics of pseudorotation.

Umbrella sampling can accurately determine the free energies of high free energy conformations, which are otherwise poorly represented or even absent, in unrestrained simulations. Previous ab initio calculations of the conformations of a nucleoside analogue predicted that the O_4′-exo conformer is such an unstable intermediate.²² This state, together with its adjacent C_1′-endo and C_4′-endo states, were not observed in our 300-ns unrestrained simulations (Figure S8, Supporting Information) nor in a previous 50-ns benchmark simulation with a slightly different force field.²³ By employing umbrella sampling with pseudorotation parameters as the collective variables, we could sample these “rare” high energy states and determine their free energies. The O_4′-exo state has the highest free energy of 9.5 kcal/mol, and the origin of this high barrier is illustrated in Figure 2E: in addition to the eclipsed O_2′–C_2′–C_3′–O_3′ torsion angle, the nucleobase and C_5′ exocyclic substituents are also in steric conflict in the O_4′-exo conformation. The calculated two-dimensional free energy surface also revealed that the O_4′-exo state prefers a smaller τ_m (Figure 2A) because a more puckered conformation will reduce the C_1′–C_4′ distance and aggravate the steric conflict.

Free Energy Landscape of Pseudorotation in 2′-Deoxyguanosine

To elucidate how the absence of a 2′-hydroxyl group affects nucleoside pseudorotation, we computed the pseudorotation free energy surface of 2′-deoxyguanosine (dG) in solution. The free energy landscape of dG is generally similar to that of rG but with noticeable alterations (Figure 3A). The absence of the 2′-hydroxyl group releases the constraint imposed by the eclipsed O_2′–C_2′–C_3′–O_3′ torsion angle, stabilizing both the O_4′-exo (Figure 3E) and O_4′-endo states by approximately 2.5 kcal/mol. Consequently, the free energy of the former drops to 7 kcal/mol, whereas the latter merges into a broad basin that includes the C_2′-endo and adjacent C_1′-exo states. The peak of the main transition path shifts to the C_4′-exo state (Figure 3C), with a free energy barrier of 1.5 kcal/mol. This broad basin is 1.0 kcal/mol more stable than the C_3′-endo state (Figure 3B), and the free energy difference again agrees well with previous NMR results³⁶ as well as with our unrestrained MD simulations (Figure S10, Supporting Information).

Figure 3.

Pseudorotation free energy landscape of 2′-deoxyguanosine. (A) The pseudorotation free energy of 2′-deoxyguanosine is plotted in polar coordinates as defined in Figure 2. The contour lines are drawn every 0.5 kcal/mol, and the standard deviation is in general less than 0.2 kcal/mol (Figure S9, Supporting Information). (B–E) Representative structures of key states along the pseudorotation cycle.

Free Energy Landscape of Pseudorotation in a Native RNA Duplex

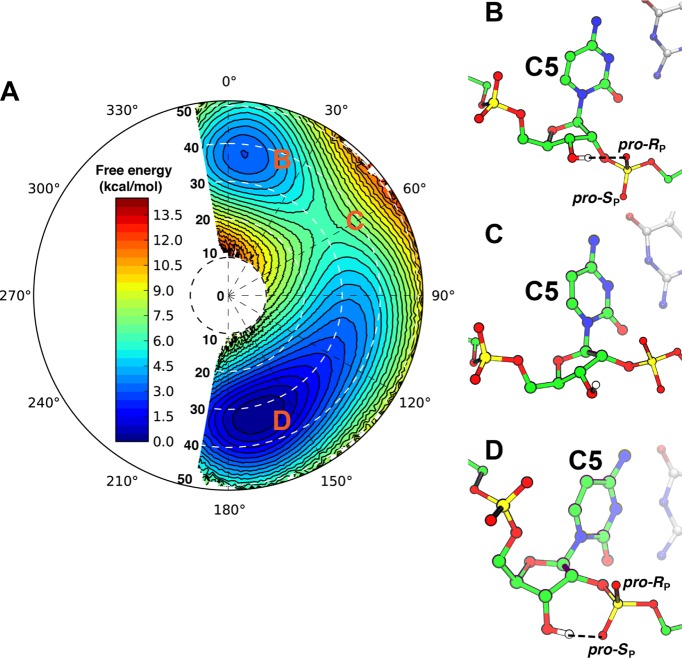
To delineate how distinct backbone connectivities can influence the pseudorotation free energy landscape of RNA, it is critical to compare two regioisomers of a nucleotide at the same position within a duplex to avoid potential interference by positional and sequence effects. Our previous crystallographic studies provided one such opportunity through the high-resolution structures of a native 5′-CCGGCGCCGG-3′ RNA duplex and a regioisomeric 5′-CCGGC*GCCGG-3′ RNA duplex (C5–2′–5′-linked RNA), where the asterisk represents a 2′–5′-phosphodiester bond.¹¹ Here, we first calculated the pseudorotation free energy landscape of C5 within the native RNA duplex using umbrella sampling to cover the “east half” of the pseudorotation cycle, including both C_2′-endo and C_3′-endo states as well as the more preferable O_4′-endo transition pathway. The resulting free energy landscape (Figure 4A) has a deep minimum corresponding to the C_3′-endo conformation, with compact stacking of planar base pairs (Figure 4B). The other minimum matches the C_2′-endo conformation and is significantly less stable by 6 kcal/mol (Figure 4A). Adoption of the C_2′-endo pucker mode destabilizes the A-form duplex because it disrupts the planar base pair structures (Figure 4D), therefore weakening both the stacking and hydrogen-bonding interactions. In some trajectories, the C5 base transiently flipped out of the helix (Figure 4D). The large free energy penalty explains why in all known A-form RNA duplex structures, only the C_3′-endo conformation has been observed.

Figure 4.

Free energy landscape of pseudorotation of a nucleotide in native RNA duplex. (A) The pseudorotation free energy landscape of C5 in an A-form RNA duplex, plotted in polar coordinates as defined in Figure 2. The contour lines are drawn every 1 kcal/mol, and the standard deviation is in general less than 0.4 kcal/mol (Figure S11, Supporting Information). The most stable conformation corresponds to the C_3′-endo state, whose calculated structure is depicted in (B). A second minimum matches the C_2′-endo state, which can adopt two different conformations depending on the orientation of the base (D). The conversion between these two minima occurs via the C_1′-exo state, and (C) shows one representative snapshot of this barrier. Strand A of the RNA duplex is shown in green, and nucleotide C5 is highlighted. The complementary strand is shown in white.

The free energy calculation further revealed that the C_1′-exo state is the least stable puckering state between the C_2′-endo and C_3′-endo conformations; the free energy barrier of this transition is approximately 12 kcal/mol (Figure 4A). Compared to the ribonucleosides, the free energy barrier is significantly higher because of the geometrical constraints imposed by the RNA duplex. The C_1′-exo state is even less stable than the C_2′-endo state because in addition to the nonplanar base pair, it is further destabilized by the heavily eclipsed O_2′–C_2′–C_3′–O_3′ torsion angle (Figure 4C). Experimental measurement of the sugar puckering barrier in an RNA molecule requires site-specifically labeling ribose with ¹³C (ref (40)) and so far has not been performed on an A-form duplex. Therefore, there is no direct experimental data to compare with our calculated barrier. In the GCAA tetraloop, the measured sugar puckering barrier varies from 10 to 18 kcal/mol depending on the local structural context.⁴⁰ Our calculated value falls within the same range and provides a testable prediction that may stimulate further experimental investigations.

Free Energy Landscape of Pseudorotation of Nucleotides with 2′–5′ Linkages

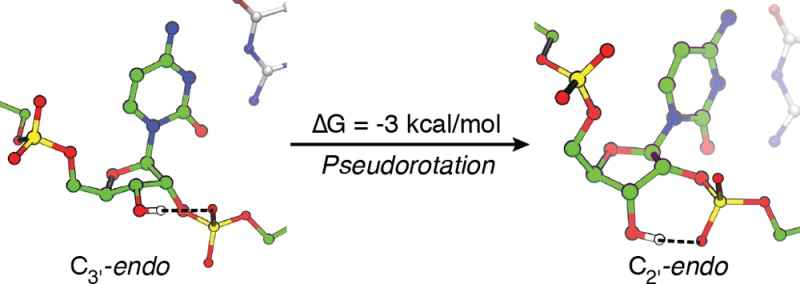
To elucidate the structural effect of 2′–5′ linkages on the pseudorotation of nucleotides in an RNA duplex, we performed a pseudorotation free energy calculation for 2′–5′-linked C5 in an RNA that is regioisomeric to the native RNA duplex described above. As shown in Figure 5A, the most stable conformation of the resulting free energy surface corresponded to the C_2′-endo state (Figure 5D), with P between 150 to 180° and τ_m around 35°, in excellent agreement with the crystallographic result (P = 160 ± 6°, τ_m = 36 ± 2°).¹¹ Previous NMR studies also showed that the C_2′-endo state is preferred in homogeneous 2′–5′-linked RNA duplexes⁴¹ and branched trinucleotides containing 2′–5′-linkages,⁴² suggesting that such a preference may be an intrinsic property of 2′–5′-linked RNAs. The free energy calculation also reveals that the other minimum corresponds to the C_3′-endo conformation (P around 10°, τ_m around 35°, Figure 5B), with a slightly higher free energy of only 3 kcal/mol, which could be overcome with favorable molecular interactions. Indeed, the calculated pseudorotation parameters agree well with a C_3′-endo conformation (P = 16.7°, τ_m = 40.8°) that we serendipitously captured in G3 of an RNA duplex with identical sequence but three 2′–5′-linkages¹¹ (5′-CCG*GC*GC*CGG-3′, where the asterisks represent the 2′–5′ phosphodiester bonds, hereafter referred to as “triple 2′–5′-linked RNA”). Compared to the native duplex, which has a deep free energy minimum at the C_3′-endo state, a 2′–5′ linkage profoundly flattens the pseudorotation free energy landscape and shifts the minimum to the C_2′-endo state.

Figure 5.

Pseudorotation free energy landscape of a 2′–5′-linked nucleotide in an RNA duplex. (A) The pseudorotation free energy landscape of 2′–5′-linked C5 in an RNA duplex, plotted in polar coordinates as defined in Figure 2. The contour lines are drawn every 0.5 kcal/mol, and the standard deviation is in general less than 0.2 kcal/mol (Figure S12, Supporting Information). The most stable conformation corresponds to the C_2′-endo state, whose calculated structure is depicted in (D). The hydrogen bond between the 3′-hydroxyl group and the pro-S_P-oxygen is indicated by black dashed lines. The C_3′-endo conformation forms a second minimum that is 3 kcal/mol less stable (B). In the C_3′-endo state, the hydrogen bond shifts to O_3′–H···pro-R_P-oxygen (indicated by the black dashed lines). The conversion between these two minima occurs via the C_4′-exo state, and (C) shows a representative snapshot of this barrier, in which there is no hydrogen bond between the 3′-hydroxyl group and the downstream phosphate. Strand A of the RNA duplex is shown in green, and nucleotide C5 is highlighted. The complementary strand is shown in white. Hydrogen atoms, except on the 3′-hydroxyl group, are omitted for clarity.

To understand what destabilized the C_3′-endo state, we performed a 50-ns MD simulation in which the ribose of C5 was restrained in the C_3′-endo state (P = 15 ± 5°, Table S2, Supporting Information). A conformational ensemble of the C5–2′–5′-linked RNA duplex with C5 in the C_3′-endo pucker state was generated using 20 000 frames of the last 40-ns trajectory sampled at 2 ps intervals, and was subsequently used to calculate structural parameters including pseudorotation, base pair, and base-pair step parameters. Most of the parameters are indistinguishable from those of the C_2′-endo conformation,¹¹ although the C5 G6:G6 C5 base-pair step in the C_3′-endo state has a smaller overlap area (Tables S2 and S3, Supporting Information). This may weaken the base-stacking and partly explain the instability of the C_3′-endo state.

The MD simulation also confirmed that the conformational shift from C_2′-endo to C_3′-endo concomitantly altered the hydrogen bond between the 3′-OH and the downstream phosphate from O_3′–H···pro-S_P-oxygen to O_3′–H···pro-R_P-oxygen (Figure 5B,D), a result that was initially inferred on the basis of the oxygen–oxygen distance in the crystal structures.¹¹ A close examination of the conformational ensemble from our restrained simulations further revealed that this hydrogen bond in the C_3′-endo state is weaker than its counterpart in the C_2′-endo state (Figure S13, Supporting Information), with a longer average O–O distance (2.94 Å in C_3′-endo versus 2.86 Å in C_2′-endo), and a larger deviation from the desired in-line conformation (O–H–O angle is 136 ± 20° in C_3′-endo versus 152 ± 12° in C_2′-endo). Therefore, the relative instability of the C_3′-endo state can be attributed to both a weaker hydrogen bond and weaker stacking, although we cannot rule out other possibilities.

According to our free energy calculation, the peak of the C_2′-endo to C_3′-endo transition path is at the C_4′-exo state (P is from 40 to 60°, and τ_m is around 30°), and the corresponding free energy barrier is approximately 6 kcal/mol (Figure 5C). In this C_4′-exo state, the intramolecular hydrogen bond between 3′-OH and either nonbridging oxygen of the downstream phosphate is broken (Figure 5C). A similar conformation is observed in C7 of the triple 2′–5′-linked RNA crystal structure, albeit with a slightly larger amplitude (P = 42.8°, τ_m = 42.8°).¹¹ In this case the 3′-OH group forms a hydrogen bond with a nearby water molecule instead of phosphate (Figure S14, Supporting Information). This supports the notion that in the C_4′-exo state there is no intramolecular hydrogen bond between the 3′-OH and the downstream phosphate.

Estimation of Transition Rates

To study the kinetics of the interconversion between the C_2′-endo and C_3′-endo conformations of a 2′–5′-linked nucleotide in an RNA duplex, 800 1-ns unrestrained simulations were carried out from 40 distinct initial coordinate sets with C5 in the C_3′-endo conformation. Among these, 420 trajectories (52.5%) successfully reached the more stable C_2′-endo conformation with 144° < P < 180°. To further extract kinetic details of these spontaneous conformational changes from C_3′-endo to C_2′-endo, we focused on 5 ps trajectories immediately prior to forming a stable C_2′-endo state. Analysis of these trajectories confirmed that during the spontaneous transition from the C_3′-endo to C_2′-endo state, the breaking of the O_3′–H···pro-R_P-oxygen hydrogen bond precedes the formation of the O_3′–H···pro-S_P-oxygen hydrogen bond, and both hydrogen bonds are absent in the C_4′-exo state (Figure 6). We also noticed that in the initial stage of these spontaneous transitions, the heavy atom distance of the O_3′–H···pro-R_P-oxygen hydrogen bond is already significantly elongated to approximately 3.4 Å, even though C5 remains in the C_3′-endo state (Figure 6). This suggests that the transition would first occur among a subpopulation of C_3′-endo states with weakened O_3′–H···pro-R_P-oxygen hydrogen bonds.

Figure 6.

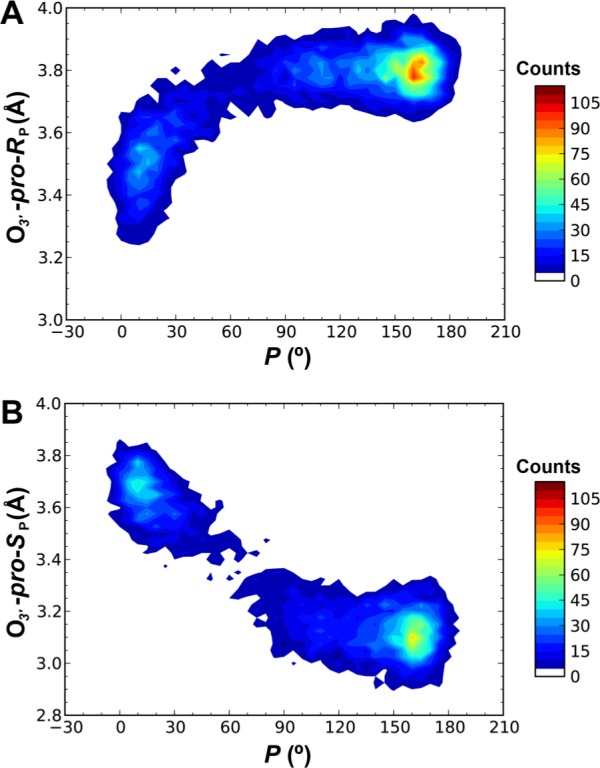
Dynamics of hydrogen-bond switching during the pseudorotation conformational change of a 2′–5′-linked nucleotide. The spontaneous transition from the C_3′-endo to the C_2′-endo state was observed in 420 out of 800 1-ns unrestrained trajectories. A 5-ps trajectory immediately prior to forming a stable C_2′-endo state was extracted for each of the 420 trajectories and used to calculate two-dimensional histograms of P versus O_3′···pro-R_P-oxygen distance (A) and O_3′···pro-S_P-oxygen distance (B). Contour lines are drawn for every five counts.

These unrestrained simulations also suggest that t_1/2 of the transition is approximately 1 ns. Given that the C_2′-endo state is about 3 kcal/mol more stable than the C_3′-endo state, t_1/2 of the reverse transition (C_2′-endo to C_3′-endo) should be approximately 150 ns. It should be noted that estimating transition rates from unrestrained MD simulations is still a great challenge in computational chemistry. Indeed, the error of the calculated binding and unbinding rates of benzamidine to trypsin was about an order of magnitude, even though the extensive sampling accurately predicted the ligand binding mode and the binding free energy.⁴³ Therefore, the rates from these calculations should be interpreted cautiously: they only suggest that the transition rates between these two conformations can occur on roughly the ns and μs time scale, respectively. Nevertheless, these calculations suggest a rapid interconversion between the C_2′-endo and C_3′-endo states of a 2′–5′-linked nucleotide in an RNA duplex.

Conclusion

The reported free energy calculations and unrestrained MD simulations provide important insights into the thermodynamic and kinetic properties of native RNA duplexes and those containing 2′–5′ linkages. Our study highlights a flattened free energy landscape for pseudorotation in 2′–5′-linked nucleotides, which can switch rapidly between the C_2′-endo and C_3′-endo conformations. This is in contrast with a single dominant C_3′-endo minimum found in the native RNA duplex. Therefore, in addition to lowering the melting temperature, the presence of 2′–5′ linkages may expand the conformational space accessible for an RNA duplex. Mechanistically, our calculations demonstrate that hydrogen bonding between the 3′-hydroxyl group and the downstream phosphate serves as a molecular switch for this backbone conformational change.

Our study establishes the feasibility of an atomic-level description of the pseudorotation free energy for free nucleosides, as well as nucleotides in RNA duplexes in solution. Even though some intermediates are too unstable to be sampled efficiently with conventional MD simulation techniques, we were able to gain insights into these structures by implementing a set of collective variables for use in conjunction with advanced free energy calculation methods. The methodology we developed in this study may be further applied to investigate other processes in which pseudorotation plays a significant role, such as nonenzymatic primer extension reactions.³⁸ Furthermore, applications to other synthetic nucleic acid systems (e.g., threose nucleic acids⁴⁴) may lead to a fuller understanding of the chemical etiology of nucleic acid structure.⁴⁵

Supporting Information Available

Supporting text, Figures S1–S16, Tables S1–S5, and the complete reference (29). This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.