Data Dependent Peak Model Based Spectrum Deconvolution for Analysis of High Resolution LC-MS Data

Abstract

A data dependent peak model (DDPM) based spectrum deconvolution method was developed for analysis of high resolution LC-MS data. To construct the selected ion chromatogram (XIC), a clustering method, the density based spatial clustering of applications with noise (DBSCAN), is applied to all m/z values of an LC-MS data set to group the m/z values into each XIC. The DBSCAN constructs XICs without the need for a user defined m/z variation window. After the XIC construction, the peaks of molecular ions in each XIC are detected using both the first and the second derivative tests, followed by an optimized chromatographic peak model selection method for peak deconvolution. A total of six chromatographic peak models are considered, including Gaussian, log-normal, Poisson, gamma, exponentially modified Gaussian, and hybrid of exponential and Gaussian models. The abundant nonoverlapping peaks are chosen to find the optimal peak models that are both data- and retention-time-dependent. Analysis of 18 spiked-in LC-MS data demonstrates that the proposed DDPM spectrum deconvolution method outperforms the traditional method. On average, the DDPM approach not only detected 58 more chromatographic peaks from each of the testing LC-MS data but also improved the retention time and peak area 3% and 6%, respectively.

Liquid chromatography coupled with high resolution mass spectrometry (LC-MS) is widely used in both proteomics and metabolomics. Several software packages have been developed for analysis of the high resolution LC-MS data.¹⁻⁵ The first step of analysis is to reduce the instrument data into a peak list, that is, spectrum deconvolution. There are many analysis steps involved in spectrum deconvolution, including baseline correction, denoising, peak detection, resolving overlapping peaks, etc. Even though every single step can affect the overall accuracy of spectrum deconvolution, selected ion chromatogram (XIC) construction and chromatographic peak integration are the key steps for spectrum deconvolution.

XIC is usually constructed by selecting all signals that have an m/z value matched to the m/z value of an ion of interest, with a user defined variation window. There are two potential challenges in this approach. One is that the user defined m/z variation window may not be optimal, and therefore, it is possible that the true signals are excluded due to a small m/z variation window, or multiple signals from the same scan are selected because of a large m/z variation window. Second, it is always possible that the m/z value of a signal can be assigned to multiple XICs because the m/z ranges of these XICs overlap within the user defined m/z variation window. In this situation, it is a challenge to decide to which XIC a signal in question should be assigned, even though a common approach is to assign the signal to an XIC in which the signal in question has a smaller value of m/z difference with the reference signal of the XIC. The MetSign software resolved the second challenge by constructing the XICs in favor of abundant signals,⁶ where the XICs are constructed in descending order of the signal abundance. That is, all signals in an LC-MS data set are first sorted based on abundance, and the m/z value of the most abundant signal is used as the reference m/z value to construct the first XIC. After the construction of the first XIC, the second XIC is constructed using the most abundant signal of the remaining data. This process is repeated until all data points in the LC-MS data set are used. However, this approach still requires a user defined m/z variation window.

To calculate the area of a chromatographic peak from an XIC, one approach is to sum all signals belonging to the chromatographic peak, while the other approach is to fit the chromatographic peak with a predefined peak model. In the first approach, the challenge is to accurately define the peak boundary, that is, the smallest scan number and the largest scan number of a chromatographic peak, especially in cases of low abundance peaks that usually have a poor peak shape. Another challenge is that the accuracy of resolving the overlapping peaks is very poor. The overlapping signals cannot be accurately partitioned between the overlapping peaks without the peak shape information. In the case of a chromatographic peak model based approach, the peak model is currently predefined by the user and only one peak model is used to deconvolute all chromatographic peaks. It is likely that the predefined peak model may not be the optimal peak model because the chromatographic peak shape can be affected by experimental conditions.⁷

The objective of this study was to develop a spectrum deconvolution method for analysis of LC-MS data acquired on a high resolution mass spectrometer. We first developed a clustering-based machine learning method to construct XICs without the use of a user defined m/z variation window. After removing the background signals and detecting peak position using the second derivative test,⁶ an optimal peak model is selected from a set of predefined peak models, including Gaussian mixture (GMM), log-normal (LN),⁸ Poisson,⁹ gamma,¹⁰ hybrid of exponential and Gaussian (EGH),¹¹ and exponentially modified Gaussian (EMG) models.¹² The optimal peak models are then applied to the entire data set for peak fitting. The developed methods are entitled “data dependent peak model (DDPM)” based spectral deconvolution and have been implemented in MetSign using MATLAB 2010b. The performance of DDPM was evaluated by analyzing a set of spiked-in data acquired on an LC-MS system.

Experimental Section

Spiked-in Samples

A total of 14 mouse liver samples were used to prepare a pooled sample. About 60 mg of liver tissue from each mouse was mixed with deionized water at a ratio of 100 mg/mL. The mixture was then homogenized for 2 min and stored at −80 °C until use. To extract metabolites from liver tissue, 100 μL of each homogenized liver sample was mixed with 20 μL of butylated hydroxytoluene (BHT) mixture (50 mg of BHT into 1 mL methanol) and 800 μL methanol. The mixture was vortexed for 1 min followed by centrifugation at 4 °C for 10 min at 15 000 rpm. A portion (700 μL) of the supernatant was aspirated into a plastic tube and dried by N₂ flow. After dissolving the dried sample with 100 μL of methanol, a stock solution was prepared by diluting the sample 10 times. Twenty microliter aliquots of each of 14 mouse liver exacts were combined to make a pooled sample for this work.

A mixture of 16 compound standards was prepared at a concentration of 100 μg/mL for each compound, including three fatty acid (heptadecanoic acid, heneicosanoic acid, and nonadecanoic acid), five triglycerides (trilauroyl-glycerol, trimyristin, tripalmitin, tricaprylin, and tricaprin), and eight phospholipids (PC(16:0/16:0), PC(16:0/14:0), PC(12:0/12:0), PC(6:0/6:0), LysoPC(16:0/0:0), LysoPC(10:0), PC(18:2(9Z,12Z)/18:2(9Z,12Z)), and PC(24:1(15Z)/24:1(15Z)). To prepare the spiked-in samples 100 μL of the pooled sample was added to each of three sample vials, followed by addition of 20, 50, and 80 μL of the standard mixture to the first, second, and third vial, respectively. Dichloromethane/methanol (v/v = 2:1) was then added to each of the three vials to make the total volume of 200 μL. This resulted in three sample groups with spiked-in compound standards. The concentration of compound standards in each of the spiked-in sample groups was 10, 25, and 40 μg/mL, respectively.

LC-MS Analysis

A Citius LC-HRT high resolution mass spectrometer (LECO Corp., St. Joseph, MI) equipped with an Agilent 1290 Infinity UHPLC with a Waters Acquity UPLC and a BEH hydrophilic interaction chromatography (HILIC) 1.7 μm, 2.1 mm × 150 mm, column was used in this work. The sample was loaded in H₂O + 5 mM NH₄OAc + 0.2% acetic acid (buffer A) and separated using a binary gradient consisting of buffer A and buffer B (90/10 acetonitrile/H₂O + 5 mM NH₄OAc + 0.2% acetic acid). Flow rate was set at 250 μL/min on the column, with 100% B for 4 min, 45% B at 12 min holding to 20 min, 100% B at 21 min and holding to 60 min for the gradient. The Citius LC-HRT was operated with an electrospray ionization source in positive ion mode with spray voltage set at 3.0 kV, nozzle temperature at 125 °C, desolvation heater temperature at 900 °C, desolvation flow at 7.5 L/min and nebulizer pressure at 50 psi. The system was optimized in high resolution mode (R = 50 000 (fwhm)) with folded flight path (FFP) technology and was mass calibrated externally using Agilent ESI tune mixture (G2421A). The mass spectrometry was operated in a full mass mode (low energy) followed by a tandem MS/MS mode (high energy) with a mass range of m/z = 50–1000. The scan frequency for acquiring the full mass spectra and MS/MS spectra is five spectra per second. Each spiked-in sample was analyzed six times via repetitive injection on LC-MS.

Theoretical Basis

Machine Learning-Based XIC Construction

To detect metabolite peaks at the chromatographic dimension, the selected ion chromatogram, XIC, is first constructed for each m/z value of the metabolite ions. To avoid the use of a user defined m/z variation window, the density based spatial clustering of applications with noise (DBSCAN)¹³ was used in this study to cluster the m/z values of the LC-MS data.

DBSCAN generates a number of clusters starting from an estimated density distribution of data points. It requires two input parameters, Eps and MinPts. Eps is a distance constraint for Eps-neighborhood, and MinPts is a minimum number of data points in an Eps-neighborhood. In this study, the Eps-neighborhood refers to all m/z values in an LC-MS data set, and each data point in the Eps-neighborhood is a m/z value. We used the Euclidean distance, E_p,q, as the measure of distance between two m/z values p and q, that is, E_p,q = |(m/z)_p – (m/z)_q|. We further assumed that all m/z values acquired in a LC-MS data set are the true signals, that is, each m/z value can be clustered into a cluster. Therefore, Eps can be estimated as follows:¹⁴

1

where X is the input of all m/z values, X_max is the maximum of m/z values, X_min is the minimum of m/z values, k is a constant coefficient and is set to MinPts, Γ is the gamma function, d is the dimensionality of X vector, and L is the total number of m/z values in X. In this study, MinPts and d were set to 2 and 1, respectively.

In DBSCAN, a cluster C is defined as a nonempty subset of m/z values satisfying two conditions. First, given any two m/z values p and q, if p ∈ C and E_p,q ≤ Eps, then q ∈ C. Second, given any two m/z values p and q in a cluster, E_p,q ≤ Eps, that is, p is density reachable to q. Thus, for all m/z values in a data set, starting from a selected one, if it has not been classified, DBSCAN searches all density reachable points by Euclidean distance measurement within threshold Eps. By iteratively considering each point, all m/z values are grouped into several density-based clusters, of which each contains all signals belonging to one XIC.

To reduce the computation burden, all m/z values acquired in an LC-MS experiment are grouped into multiple subgroups after sorting the m/z values in an ascending order. The initial number of m/z values in a subgroup, N_init, is defined as

2

where n_mz is the total number of m/z values in an LC-MS data set, n_sc is the number of scans with mslevel equal to 1 (i.e., excluding the scans of MS/MS data), and a is the number of initial subgroups with a condition of a ≥ 2. Starting from the minimum m/z value, the first N_initm/z values are selected. Within these selected m/z values, the maximum m/z difference between two adjacent m/z values are detected. Then, the selected N_initm/z values are split into two parts by these two adjacent m/z values. The first part is considered as the first subgroup. The second part is put back to the m/z pool for the selection of the next subgroup. The aforementioned process is repeated to construct the remaining subgroups until all m/z values are used up. In this work, the constant a was set to 5.

The Silhouette score¹⁵ is used to evaluate the clustering performance as follows:

3

where S_i is the Silhouette score of the ith cluster, d_intra is the average pairwise m/z value difference within the ith cluster, d_inter is the minimum average distance between the ith cluster and all other clusters. The range of S_i is from −1 to 1, with a negative value meaning bad clustering result and a value close to 1 referring to better performance achieved by clustering.

Chromatographic Peak Models

After construction of the XICs, the noise in each XIC is estimated using the approaches described by Wei et al. in MetSign software.⁶ Briefly, each XIC is first segmented into several peak groups based on the continuity of scan number, and the noise level is estimated by all XIC signals, except the regions potentially with presence of chromatographic peaks. After removal of noise, the chromatographic peaks in the XIC are detected using both the first and the second derivative tests. To fit each chromatographic peak or peak cluster, six peak models are selected in this work based on a literature study.⁷ Each of the selected chromatographic peak models is described as follows:

The ideal chromatographic peak shape is the Gaussian model (GM) defined as

4

where a is the height of the peak, b is the center of the peak, and c denotes the deviation of the peak.

Log-normal model (LNM) assumes that a chromatographic peak is the logarithm of a normal distribution and is defined as⁸

5

where h is the height of the peak, s and w control the peak variance, and z is the peak center.

Poisson model (PM) is chosen where the mutual correlation of parameters is less than others and is defined as⁹

6

where h is peak height, a is a constant with a > 1, and z is a normalization value to input x.

The gamma model (GaM) is defined as¹⁰

7

where h is the peak height, s describes the peak shape, z is the peak center, and w is the peak deviation, and x ≥ w + z – sw.

The exponentially modified Gaussian model (EMG) is defined as¹²

8

where λ = {y₀,A,x_c,w,t₀}, y₀ is the initial value, A is the amplitude, x_c is the center of the peak, w is the width of the peak, t₀ is the modification factor, and z = (x – x_c)/w – w/t₀; erf is the error function.

The hybrid of exponential and Gaussian (EGH) mixture model¹¹ is a mixture of a hybrid of exponential and Gaussian distributions, which is defined as

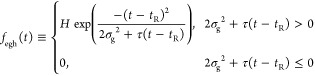9

where H denotes the maximum of peak height, σ_g is the standard deviation of the Gaussian component, t_R is the peak center, and τ is the time constant of the exponential component.

Data Dependent Peak Fitting

The retention time dependent optimal peak models are selected using a training-based approach, where a number of XICs with intense chromatographic peaks are first selected. In each selected XIC, the top 50% of abundant chromatographic peaks that do not overlap with other peaks are collected and fitted with each of the six peak models, respectively. The best fitting model for each peak is then determined based on fitting scores:

10

11

where M_j,t^o is the optimal peak model for the jth peak with fitted peak location at retention time t, R_i,j,t² is fitting score indicating the quality of the ith peak model for fitting the jth peak located at t; x_j(t) is the original intensity value of the jth peak at retention time t, n is the number of peak intensity values in the jth peak, x̂_i,j(t) is the fitted intensity values of the jth peak by peak model i at t, and x̅(t) = (1/n)∑_j=1x_j(t) is the mean intensity value in the jth peak.

The retention times of all fitted chromatographic peaks of the selected XICs are then sorted in ascending order, and each retention time is associated with the best peak model of its corresponding chromatographic peak. The retention time dependent optimal peak models are then determined using a voting mechanism, within a retention time window covered by five fitted chromatographic peaks. If two adjacent chromatographic peaks have different optimal peak models, the middle point of these two peaks is selected as the break point for the application of the two optimal peak models.

Results

About 35–42 m/z subgroups were generated from each of the LC-MS data of the 18 spiked-in samples for DBSCAN clustering, and 14–781 clusters were created from each m/z subgroup by DBSCAN, with one cluster denoting one XIC. In each LC-MS data set, 5164–6033 clusters (XICs) were obtained. In the case of the first spiked-in sample, S₂₅¹, the raw LC-MS data were split into 39 m/z subgroups, and DBSCAN clustered all these data into 5646 m/z clusters (XICs). For instance, one m/z subgroup has 266 m/z clusters (XICs). The mean of the standard deviation of the m/z values in each cluster is STD = 0.0021 ± 0.0011. This magnitude of m/z variation within each cluster agrees with the vendor suggested instrument variation. Figure 1A depicts the cumulative distribution of the number of XICs with respect to the span of m/z values within each XIC. The span of the m/z values within an XIC ranges from 0.49 to 37 ppm. However, as shown in Figure 1B, the number of chromatographic peaks detected in an XIC decreases with the increase of the m/z span in an XIC, meaning that each of the XICs with a large m/z span is a collection of noise. Figure 2 depicts the histogram of Silhouette scores of all clusters obtained by DBSCAN from the entire LC-MS data of sample S₂₅.

Figure 1.

Information of m/z span within the XICs generated by DBCSAN for analysis of LC-MS data acquired from sample S₂₅¹: (A) the cumulative distribution of the Δm/z values of all XICs; (B) the relationship of m/z span in XICs and the number of chromatographic peaks detected in the corresponding XICs.

Figure 2.

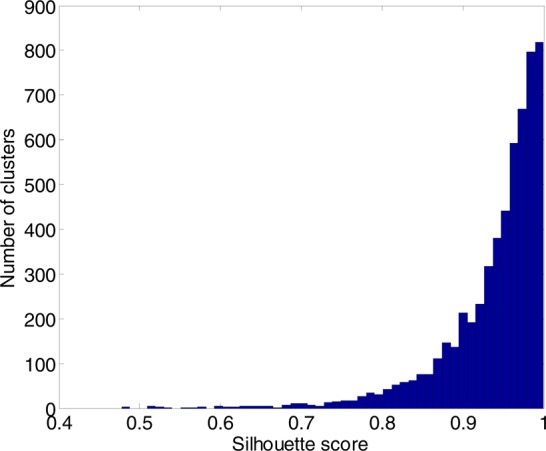
The distribution of Silhouette scores of all clusters obtained by DBSCAN from the entire LC-MS data of sample S₂₅¹.

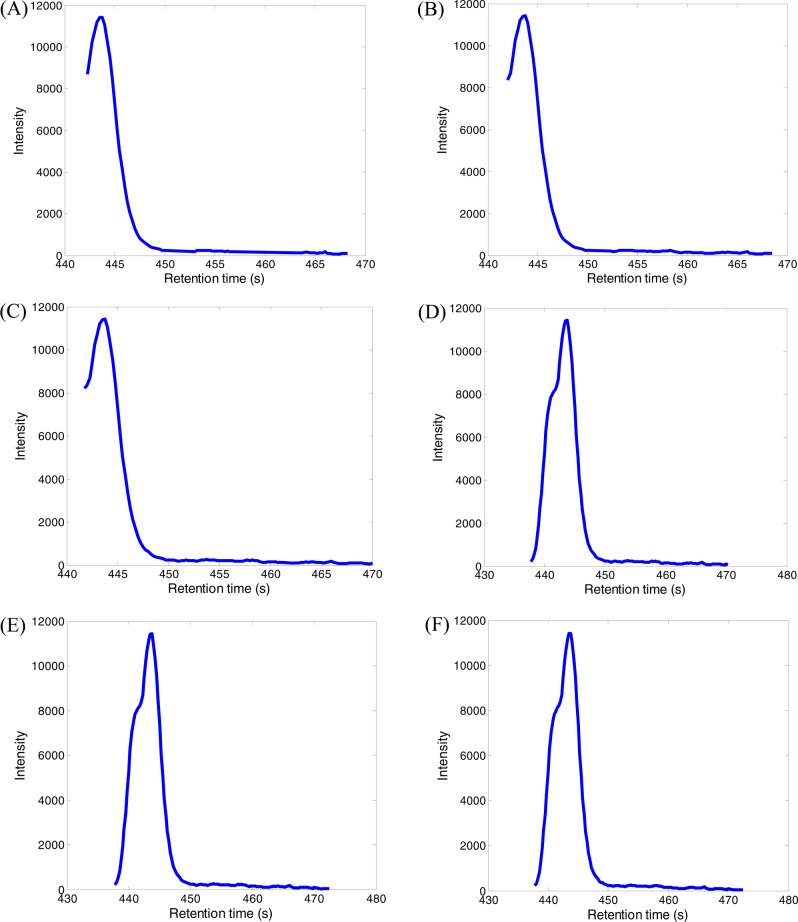
Figure 3 is an example of an XIC generated by using the DBSCAN and a set of user defined m/z variation windows of 4, 5, 6, 7, and 8 ppm. The DBSCAN method detected 140 data points with m/z ranges from 812.6105 to 812.6217 and retention time ranges from 437.75 to 470.50 s. However, the user defined m/z variation window approach generated different XICs for the same data depending on the size of user defined m/z window, Δm/z. For example, a total of 114 data points were found for this XIC with m/z ranges from 812.6123 to 812.6127 and retention time ranges from 441.75 to 470.00 s, when Δm/z was set as ≤6 ppm. The DBSCAN method created a complete XIC, while the m/z variation window approach created partial XIC until Δm/z was increased to ≤8 ppm. Upon increase of the variation window to 9, 10, and 11 ppm, the same XICs were generated as those using Δm/z ≤ 8 ppm. When Δm/z was further increased to ≤12 ppm, multiple data points were selected from the same scan for the construction of XICs.

Figure 3.

An example of XICs generated using different user defined m/z variation windows and DBSCAN approach: (A) Δm/z ≤ 4 ppm; (B) Δm/z ≤ 5 ppm; (C) Δm/z ≤ 6 ppm; (D) Δm/z ≤ 7 ppm; (E) Δm/z ≤ 8 ppm; (F) DBSCAN approach.

Figures S1–S4 in the Supporting Information depict the other example XICs constructed by the m/z variation window approach with different Δm/z values. These XICs were selected based on the height of their chromatographic peaks, ranging from low to high. It can be seen that DBSCAN constructed a complete XIC for each of these chromatographic peaks of interest. However, the optimal size of m/z variation window is data dependent in the m/z variation window approach. The m/z variation windows for the construction of a complete XIC for these randomly selected chromatographic peaks are ≤15, ≤9, ≤7, and ≤11 ppm for the data displayed in Figures S1, S2, S3, and S4, respectively.

Table 1 summarizes the analysis results of all 18 spiked-in LC-MS data sets using the user defined m/z variation window (Δm/z ≤ 7 ppm) and the DBSCAN approach, respectively. N_XIC is the average of XICs constructed in all 18 spiked-in samples, and N_peak is the average of the chromatographic peaks detected. In order to investigate the accuracy of the detected chromatographic peaks in terms of peak area and retention time, all 18 peak lists generated from the spiked-in data were aligned using algorithm reported previously,^2,6 where the chromatographic peaks generated by the same metabolite in different samples are recognized based on the similarity of retention time and mass of parent ions. After alignment, the relative standard deviation (RSD) of retention time and peak area of each aligned peak were respectively calculated for sample groups 10 μg/mL, 25 μg/mL and 40 μg/mL. The mean of RSDs of peak area and retention time of the aligned peaks were further calculated for each sample group. μ_{rt_10}, μ_{rt_25} and μ_{rt_40} are respectively the mean of the RSDs of the retention times of the aligned peaks in sample group 10 μg/mL, 25 μg/mL and 40 μg/mL. μ_{area_10}, μ_{area_25} and μ_{area_40} are respectively the means of the RSDs of the peak areas of the aligned peaks in sample group 10 μg/mL, 25 μg/mL and 40 μg/mL.

Table 1. The Analysis Results of All Spiked-in LC-MS Data Set Using the User Defined m/z Variation Window (Δm/z ≤ 7 ppm) and the DBSCAN Approach.

	NXIC	Npeak	μrt_10 (%)	μarea_10 (%)	μrt_25 (%)	μarea_25 (%)	μrt_40 (%)	μarea_40 (%)
Δm/z ≤ 7 ppm	5141	1827	0.41	14.3	0.41	14.5	0.38	14.2
DBSCAN	5557	1885	0.39	14.3	0.34	13.7	0.33	13.7

Discussion

DBSCAN Clustering

The k-means clustering and hierarchical clustering are the two popular clustering methods. However, these two methods face challenges in the convergence condition and determining the number of clusters for the XIC construction. The DBSCAN clustering can find any shape of the clusters without requiring one to specify the number of clusters in the data a priori.¹³ Theoretically, the DBSCAN assigns data points into clusters based on density reachability, wherein the data points within a cluster contain high density while the noise points have less density than any clusters. Even though DBSCAN was designed to solve the class identification problem in a two-dimensional space data, it can be applied to different dimensional data. We adopted it to construct XICs (one-dimensional data in terms of m/z values) from an LC-MS data set and use the Euclidean distance to measure the distance reachability between two m/z values.

As discussed in the original paper,¹³ DBSCAN requires two input parameters, Eps (a distance constraint for Eps-neighborhood) and MinPts (a minimum number of points in Eps-neighborhood). For the LC-MS data, we assume no noise point in the data in order to assign every m/z value to a closest cluster. Thus, MinPts is simply set to 2. Eps is estimated through the statistics of the data calculated by eq 1. For each m/z value that is not yet classified, the DBSCAN algorithm searches all of its density reachable or density connected points by Euclidean distance within threshold Eps. A data point is entered into a cluster if its distance to a member in that cluster is less than Eps. By iteratively considering each data point, all m/z values would be grouped into several density-based clusters. Each cluster contains all m/z values belonging to one XIC.

Preprocessing of LC-MS Data

A high resolution LC-MS data set contains a large number of m/z values. For instance, over 2 500 000 data points are present in the data set acquired in each of the LC-MS experiments in this work. To cluster these data points by iteratively estimating and evaluating the number of clusters is a great challenge for any of the existing clustering algorithms, including the DBSCAN method. This is because the estimation of cluster numbers is not accurate enough on the large number of data points. Furthermore, the convergence cannot be achieved in a limited time. To make the clustering methods practically feasible, we designed a preprocessing method to automatically split the data points in an LC-MS data set into multiple subgroups according to the m/z differences among all m/z values sorted in ascending order.

The constant a in eq 2 determines the number of initial subgroups N_init into which the user wants to split the entire set of LC-MS data points. A large a value enables a fast DBSCAN performance. However, an extreme large value of a can cause each of the initial subgroups containing only partial data points for an XIC. In case of analyzing the LC-MS data of sample S₂₅¹, all m/z values in the LC-MS data were first sorted in ascending order. By setting a = 5, all LC-MS data points were separated into five segments. The first segment containing 20% of the data points with small m/z values was selected initially for XIC construction. Within the selected m/z values, the maximum m/z difference between two adjacent m/z values was between data points 106.1145 and 107.0482. Therefore, the selected m/z values were split into two parts by these two adjacent m/z values. The first part was considered as the first subgroup m/z ∈ [100.0212, 106.1145], while the second part was put back to the m/z pool for the selection of the next subgroup. This process was repeated to construct the remaining subgroups until all m/z values were used up, generating a total of 39 subgroups.

The Eps values for these 39 subgroups range from 5.1412 × 10^–4 to 0.0154. The minimum Eps was calculated from subgroup m/z ∈ [132.0431, 143.1264] and the maximum Eps from subgroup m/z ∈ [1360.7580, 1606.0836], corresponding to about 3.89 and 11.3 ppm, respectively. Equation 1 indicates that the threshold Eps is data distribution dependent with a trend that Eps value increases with the increase of m/z values. Such data distribution dependent nature of the Eps value significantly increases the accuracy of constructing the m/z clusters. During DBSCAN clustering, the m/z value with the highest abundance is first selected as the reference data point to search all other candidate data points with condition m/z ∈ [p_r – Eps, p_r + Eps], where p_r is the m/z value of the reference data point. Each of the selected data points are further used as the reference data points again to find the data points that are not yet clustered and have Euclidean distance of m/z less than Eps, respectively. This process is repeated until all data points in the current subgroup are evaluated. After this process, a complete cluster of the most abundant data point in the subgroup is constructed. Then, the most abundant data point in the remaining data points of the current subgroup is selected as the reference data point to search for all other cluster members from the remaining data points to construct the second cluster. This process is repeated until all data points in the current subgroup are selected into a cluster. The clusters constructed in this manner are in favor of ions with abundant signals, where the XICs are constructed in descending order of the signal abundance.

It should be noted that DBSCAN automatically determines the threshold Eps and the number of clusters (i.e., the number of XICs) based on the data distribution. Such a process eliminates the use of a user defined m/z value variation window (bin size). Currently, the m/z variation window is either determined by a trial-and-error approach or by analysis of a set of calibration chemicals. An improperly determined variation window could significantly affect the XIC construction, as depicted in Figure 3 and Figures S1–S4, Supporting Information. The DBSCAN approach constructs better XICs than the m/z variation window based method.

Figure 1A shows that more than 97% of the XICs constructed by DBSCAN have a m/z span of less than 15 ppm, with a maximum m/z span of 37 ppm. The Silhouette score ranges from 0.48 to 1.0 with a majority of the XICs having large scores as depicted in Figure 2. A small value of the Silhouette score indicates the clustering resulting in a large m/z variation within the corresponding XIC. During DBSCAN clustering, we assumed that every signal in a LC-MS data set should be assigned to a cluster. For this reason, a large number of XICs were constructed by the DBSCAN (Table 1). The XICs with large m/z variations and small Silhouette scores most likely contain a set of noise, and therefore, the number of chromatographic peaks detected in each of these XICs decreases with the increase of m/z span (Figure 1B). Figure 4 depicts the XIC with the largest m/z variation, Δm/z = 37 ppm. This XIC is composed of a set of noise without any chromatographic peak and, therefore, is eliminated during the step of chromatographic peak fitting. In general, an abundant chromatographic peak has a small value of m/z difference among the signals collected for that chromatographic peak.

Figure 4.

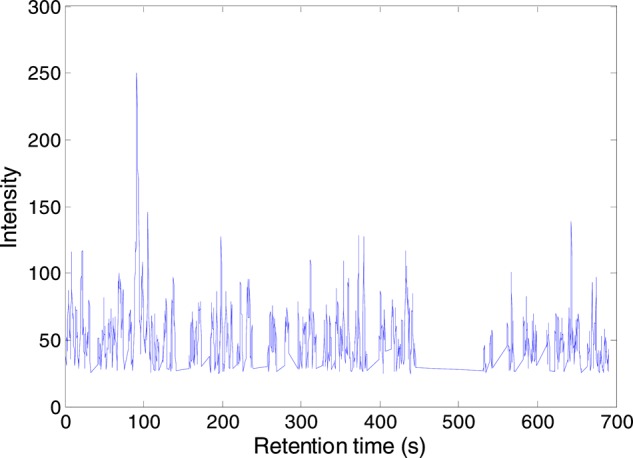
A sample XIC constructed by DBSCAN approach with m/z variation of 37 ppm.

Peak Model Selection

Chromatographic peak shape can be affected by many experimental conditions during LC separation. Based on literature study,⁷ a total of six peak models including PMM, EGHM, GMM, GaMM, LNMM, and EMGM were selected in this work, assuming that at least one of the six models can describe the true chromatographic peak shape at a given retention time. Each of PMM, EGHM, GMM, GaMM, LNMM, and EMGM models has, respectively, (S·2 + 1), (S·3 + 1), (S·2 + 1), (S·2 + 1), (S·2 + 1), and (S·3 + 1) parameters to estimate, where S is the number of mixture components (i.e., the number of overlapping chromatographic peaks). In this study, the peak boundary is fixed by the starting and ending scan number of a given peak region. Chromatographic peak fitting is performed only when the number of data points for a given peak region is greater than or equal to the required number of parameters for a selected probability model.

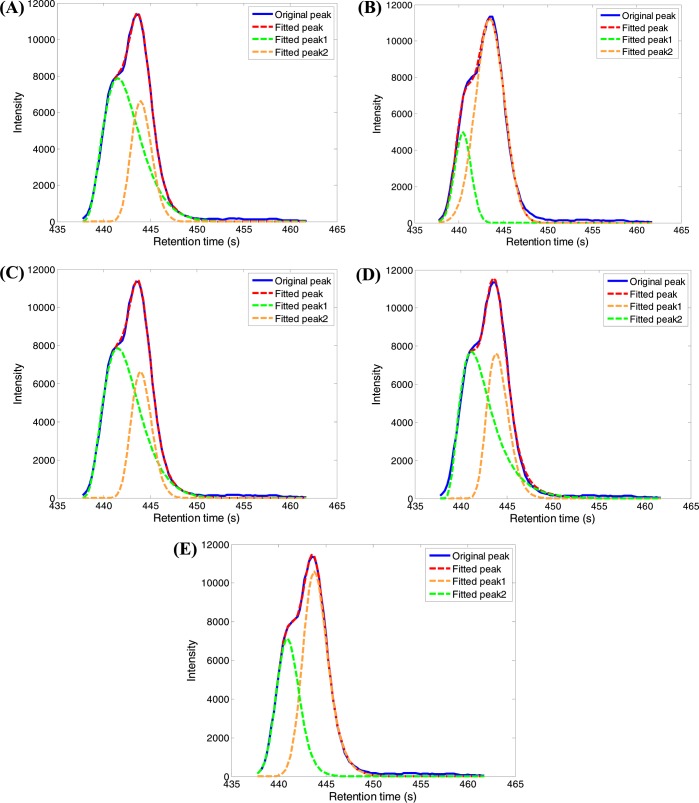
Figure 5 shows the results of using five peak models analyzing the same data. EGHM model failed to fit the experimental data in this case. The fitting scores of the other five peak models in ascending order are LNMM (R² = 0.9977) < GMM (R² = 0.9978) < PMM (R² = 0.9990) = GaMM (R² = 0.9990) < EMGM (R² = 0.9992). Even though the EMGM model performed the best, the difference among the fitting scores of these five models is quite small. However, different peak models generate completely different peak areas for the deconvoluted peaks. Such dramatic differences in the peak area of the deconvoluted peaks can significantly affect the results of compound quantification. Therefore, it is critical to find the right chromatographic peak model for spectral deconvolution, especially in analysis of complex samples.

Figure 5.

Effect of five chromatographic peak models in fitting a region of an XIC containing overlapped chromatographic peaks: (A) PMM model; (B) GMM model; (C) GaMM model; (D) LNMM model; (E) EMGM model.

In order to choose a proper peak model, we developed a training-based method to automatically select the best peak model from a set of predefined peak models. The training data are a set of chromatographic peaks with high quality, selected from multiple XICs. We first selected 50 XICs that are evenly distributed in the retention time domain. Each of the selected XICs has the most abundant chromatographic peak compared with its neighbor XICs in the segment of its retention time. In each selected XIC, the top 50% of abundant chromatographic peaks that do not overlap with other peaks are then collected and fitted with each of the six peak models, respectively. The best fitting model for each peak is then determined based on fitting scores, that is, the maximum R² value. The retention times of all fitted chromatographic peaks of the selected XICs are then sorted in ascending order, and each retention time is associated with the best peak model fitted for its corresponding chromatographic peak. The retention time dependent optimal peak models are then determined using a voting mechanism, within a retention time window covered by five fitted chromatographic peaks. In the case that two adjacent chromatographic peaks have different optimal peak models, the middle point of these two peaks is selected as the break point for the application of the two optimal peak models. In this study, the EMGM model was selected as the optimal peak model across the entire retention time range. Figures S5–S7, Supporting Information, depict the effectiveness of the EMGM model for abundant peaks, less abundant peaks, and low abundance peaks, respectively.

Determining the number of overlapped peaks is critical for accurately deconvoluting overlapped peaks in an XIC. In case the second derivative test is used to detect small peaks overlapping with other peaks, the number of overlapped peaks is usually achieved by predefining a minimum number of data points on the two sides of a data point x_rc, where the second-derivative crosses the zero position.⁶ A large number of predefined data points will generate a small number of overlapped peaks for peak fitting. A wrong selection of the number of overlapped peaks will introduce a significant variation in both the retention time and peak area of the fitted peaks. In order to find the optimal number of overlapped peaks, a trial-and-error approach was used in this study by testing the data number on each side of data point x_rc as 3, 5, 7, 9, and 11. The optimal number of overlapped peaks is then determined by the data number that generates the maximum R² score. Even though such a trial-and-error approach significantly increases the computation time, we believe the accuracy of spectral deconvolution is much more important.

Overall Performance

The performance of the proposed DDPM method was evaluated by analyzing a set of spiked-in data. Table 1 summarizes the results of spectrum deconvolution using DBSCAN and m/z variation window approaches, respectively. The DBSCAN approach obtained about 5557 XICs per LC-MS data set, from which 1885 chromatographic peaks were detected. However, the m/z variation window approach only detected 1827 chromatographic peaks from 5141 XICs. On average, the DBSCAN approach detected 58 more chromatographic peaks in each of the spiked-in samples. Table 2 lists the numbers of aligned peaks detected using DBSCAN and the variation window approaches. Compared with the variation window approach, the DBSCAN method detected three more peaks that are present in all samples and 18 more peaks in more than 90% of samples. Among these 21 peaks, the peak area ranges from 7624 to 203 146, indicating that the variation window approach missed detecting not only small peaks but also the abundant peaks. The chromatographic peak fitting score R² of the 21 missed peaks ranges from 0.9187 to 0.9978, showing that the missed peaks also have very good chromatographic peak shape.

Table 2. The Number of Aligned Chromatographic Peaks Detected in All 18 Spiked-in Samples Using the XICs Constructed by m/z Variation Window Approach and DBSCAN Approach.

frequencya (%)	number of samples	Δm/z ≤ 7 ppm	DBSCAN
100	18	295	298
80–99	15, 16, 17	255	270
60–79	11, 12, 13, 14	206	223

^aFrequency refers to the ratio of the number of samples from which a chromatographic peak was aligned divided by the total number of samples.

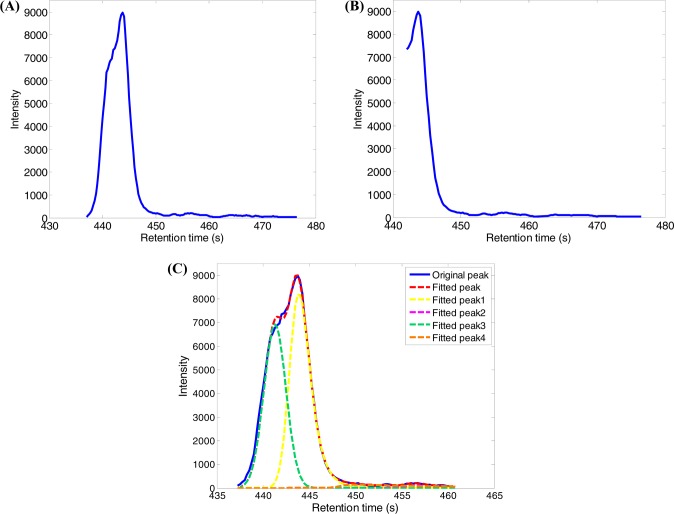
The main reason for the variation window approach not detecting these peaks is that it failed to correctly construct the XICs for these peaks. Figure 6A,B depicts two XICs of a peak with m/z value of 812.6157 constructed from sample S₄₀³ by DBSCAN and m/z variation window approaches, respectively. The best chromatographic peak model for fitting the XIC constructed by DBSCAN is EMGM with a fitting score R² of 0.9937 (Figure 6C), while the XIC constructed by the variation window approach does not have a complete peak shape and therefore can only detecte three peaks and misses the far left hidden peak at retention time of 441 s (the fitted peak 3 in Figure 6C). Figure S8A, Supporting Information, depicts another sample XIC, from which two peaks were detected by the DBSCAN approach with a fitting score of R² = 0.9978 (Figure S8B). Figure S8C shows the XIC of the same ion constructed by the m/z variation window approach. Due to the poor quality of the XIC, the fitting error is very big, resulting in no peak detected for this ion.

Figure 6.

Comparison of XIC construction using DBSCAN and m/z variation window approaches: (A) XIC of a peak with m/z value of 812.6157 constructed from sample S₄₀³ by DBSCAN; (B) XIC of the same peak constructed using a m/z variation window of 7 ppm; (C) four fitted peaks by EMGM model using the XIC data presented in part A.

In terms of the accuracy of retention time and peak area, both the mean of retention time variation and the mean of relative standard deviation of peak area of the aligned peaks are smaller than the corresponding values obtained by the variation window approach in all three sample groups (Table 1). Overall, the proposed spectrum deconvolution method improves the retention time and peak area of fully aligned peaks up to 3% and 6%, respectively. These results demonstrate that the DBSCAN-based XIC construction approach outperforms the m/z variation window approach for accurate deconvolution of the LC-MS data, in terms of detecting more chromatographic peaks and generating high accuracy of retention time and peak area for the deconvoluted chromatographic peaks.

The effectiveness of modern “omics” studies is greatly hampered by the limited peak capacity of analytical platforms. For this reason, a multidimensional separation system was developed to increase molecular coverage in both proteomics and metabolomics.¹⁶⁻¹⁸ However, it may be even more important that we need to maximize our capability of accurately uncovering all molecular information from the experimental data. A key step in this effort is to ensure that the mass spectra acquired in a LC-MS can be accurately deconvoluted. Compared with the conventional m/z variation window approach, the proposed DDPM method significantly outperforms the current spectrum deconvolution method by detecting more molecular peaks and providing modest gain in accuracy of determining peak area and retention time. Such improvement will not only result in identifying an increased number of low signal species or overlapping species but also improve the accuracy of molecular quantification, such as identifying disease biomarkers.

Even though the optimal peak models selected by the proposed DDPM method are data- and retention-time-dependent, the DDPM approach has some potential limitations. One is that it can only select the optimal peak model from a list of user predefined peak models. We expect that the use of multiple chromatographic peak models could, at least, increase the chance that the true peak model is selected. It is critical to make sure the true peak model is actually present in the list of predefined peak models. The other limitation is that extensive computation is involved due to the large number of peak models and the trial-and-error approach in determining the number of peaks in an overlapping region. Therefore, parallel computation is required and implemented in this study.

Conclusions

A data dependent peak model based spectrum deconvolution method entitled DDPM was developed for analysis of high resolution LC-MS data. For spectrum deconvolution, peak picking is achieved at selected ion chromatogram (XIC) level. To construct the XICs, a density-based clustering method, the density based spatial clustering of applications with noise (DBSCAN), is applied in all m/z values of an LC-MS data set to cluster the m/z values into each XIC. Using DBSCAN clustering to construct XICs eliminates the need for a user defined m/z variation window. After the XIC construction, the peaks of molecular ions in each XIC are detected using both the first and the second derivative tests. To accurately determine the number of overlapping peaks, a trial-and-error approach is used by testing the different numbers of data on each side of the data point where the second-derivative crosses the zero position. The optimal number of overlapping peaks is determined by the data number that generates the maximum fitting score.

A total of six chromatographic peak models are considered, including Gaussian, log-normal, Poisson, gamma, exponentially modified Gaussian, and hybrid of exponential and Gaussian models. A set of abundant nonoverlapping peaks evenly distributed across the retention time are chosen to find the optimal peak models that are both data- and retention-time-dependent. Analysis of a set of spiked-in data demonstrates that the density-based clustering method for XIC construction has quick convergence and outperforms the traditional m/z threshold-based method. Moreover, the data dependent peak model based peak fitting provides accurate deconvolution of the LC-MS data in terms of retention time and peak area. Overall, the proposed DDPM method improves the retention time and peak area of the detected chromatographic peaks 3% and 6%, respectively. It also can detect more chromatographic peaks that are not detected by the conventional m/z variation window approach. On average, about 58 more chromatographic peaks were detected from each of the testing data sets by the DDPM approach.

Supporting Information Available

Additional information as noted in text. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States