Collective Variable Approaches for Single Molecule Flexible Fitting and Enhanced Sampling

1. Introduction

It is now well established that proteins and nucleic acids undergo local and global conformational fluctuations to perform a variety of cellular functions such as signal transduction, transport, and catalysis.¹ Many experimental techniques such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, small-angle X-ray scattering (SAXS), and single-particle electron microscopy (EM) have indeed provided structural evidence at different resolutions to support the view of multiple functional states of biomolecules. Yet it remains difficult to characterize the vast conformational repertoire of biomolecules via experimental methods alone. Therefore, biophysical theory, modeling, and simulation techniques rooted in statistical mechanics are often useful for a detailed molecular understanding of biomolecular structures.²⁻⁵ Despite the limitations of molecular mechanics interaction potentials, computational methods can now be combined with low-resolution structural data to generate experimentally consistent conformational ensembles as well as to probe underlying mechanistic questions.

Analyses of structural data for different functional states of biomolecules have revealed large-scale conformational rearrangements on the scales of entire domains. This means that a large group of atoms collectively move in a concerted way to facilitate functional movements. Traditionally, one relatively less expensive computational method to analyze collective motions in proteins has been to carry out normal-mode analysis (NMA) of equilibrium structures, because low-frequency modes are typically indicative of high-amplitude/large-scale motions.⁶⁻⁸ Such global and collective modes are robust, independent of sequence detail, and are intrinsically accessible to each biomolecule because they are encoded in their global shape.⁹⁻¹³ Given that the total number of degrees-of-freedom (DOF) in biomolecules is very large, NMA provides an efficient way to describe biomolecular dynamics in a reduced number of variables. As was originally pointed out by Hayward and Go,⁶ this reduction in dimensionality has led to the concept of an important subspace of variables, “collective variables (CVs)”, that are well-suited to characterize the dynamics of biomolecules. Interestingly, the concept of CVs as reaction coordinates has been recently extended to atomistic molecular dynamics (MD) simulations,¹⁴ which has significantly increased their capability in capturing long time-scale motions. This is chiefly possible because sampling in these CVs can be carried out more extensively in comparison to all possible DOF. Such methods are typically referred to as enhanced sampling techniques because they increase the likelihood of observation of a rare biomolecular event.

The range of studies in which NMA and MD simulations have played a central role is immense, and it is not possible to do justice to all such studies in this focused Review. However, we refer the reader to pertinent comprehensive literature on those subjects along the way. Therefore, we have limited the scope of this Review to some specific applications of NMA, and enhanced sampling via temperature-acceleration in the context of flexible fitting to low-resolution EM data on macromolecular complexes. Particularly, we concentrate on two methods in this Review: (a) normal mode flexible fitting (NMFF)^15,16 for structural refinement into EM maps; and (b) temperature-accelerated molecular dynamics (TAMD)^17,18 for conformational exploration and flexible fitting. We first discuss theoretical underpinnings of all-atom and coarse-grained NMA of protein structures, which is followed by highlights of various successful applications. The theory and applications of NMA for flexible fitting of protein structures into EM maps are described thereafter. This is immediately followed by a discussion of the importance of enhanced sampling in biomolecular simulations, and how dynamics in these systems can be explored by evolving CVs via temperature acceleration, for example. Specifically, we discuss in detail various aspects of TAMD. During these discussions, we further highlight a few of the many cases where NMA and TAMD have alleviated difficulties faced by other methods in understanding large-scale functional excursions in biomolecules. This Review concludes with a brief overview and future outlook for these methods.

2. Normal Mode Analysis

2.1. Theory

Normal mode analysis is a well-established technique to understand physical phenomena, and has a long history of applications to biomolecular systems.^6,19−24 It is based upon a harmonic approximation of the underlying potential energy landscape, which suggests that systems at equilibrium fluctuate in a single well-defined minimum in the potential energy surface. Therefore, we can model the dynamics of biomolecules by considering a collection of independent harmonic oscillators through the solution to the eigenvalue problem for these oscillators. Central to such analysis is the diagonalization of a 3N × 3N (where N is the total number of atoms) matrix of the second derivatives of the potential energy with respect to the atomic Cartesian coordinates, also known as the Hessian. Solving the Hessian leads to a set of normal modes, each with a direction eigenvector and its related eigenvalue (frequency). A positive or a negative eigenvalue represents a local minimum or maximum on the potential energy surface. In a nutshell, NMA is comprised of three steps: (a) energy minimization; (b) calculation of the Hessian; and (3) the solving of the eigenvalue problem.⁶

In the computed mode spectrum, low-frequency modes represent large-amplitude and collective structural deformations, while high-frequency modes are related to local structural perturbations such as in the residue side-chains. From a physical standpoint, global low-frequency modes are most easily accessible, and deformations along these require the least amount of energy (the energy of a mode is directly proportional to the square of its frequency), thereby making these softer modes. Such modes have been observed to correlate remarkably well with large-scale movements inferred from experimental structures, which is why they bear functional significance. It is important to note here that large-scale excursions along a specific low-frequency mode tend to violate the harmonic approximation, and a re-evaluation of normal modes at a different minimum may be needed in such cases. Additionally, normal modes represent displacements that are tangent to the direction of motion at equilibrium, due to which violations of internal constraints such as bond lengths/angles may occur unless appropriate preventive measures are taken.

As was pointed out above, a key step in NMA is the diagonalization of the Hessian, which is a computationally expensive procedure for large biomolecules. Therefore, an approach is needed to decrease the number of DOF during this step. Although early workers attempted to address this problem by using the lower dimensional dihedral angle space as opposed to Cartesian space,²⁵ more useful methodologies such as diagonalization in mixed basis (DIMB) were later proposed by Perahia and colleagues.^26,27 In this method, an iterative diagonalization utilizing partial solutions to the entire problem is performed to calculate the normal modes of proteins up to 300 amino acids. To deal with much larger systems, the rotation translation block (RTB) method was proposed by Sanejouand and co-workers.^28,29 In this method, approximate low-frequency normal modes are computed by dividing the biomolecular system into a number of rigid blocks (a group of residues). The blocking scheme reduces the 3N DOF to 6n_b (where n_b is the number of blocks). The RTB method led to successful applications in studies of large biomolecular machines such as the ribosome, RNA polymerase, and ATPases.³⁰⁻³² Some workers have also combined the RTB method with a dihedral angle basis to perform normal mode calculations of massively sized icosahedral viruses.^33,34

A conventional approach to carry out NMA is to consider atoms in a biomolecule as classical point masses, where interaction energy terms between all atoms are given by a molecular mechanics (MM)-based potential energy function, “force-field”. In such models, it is quite difficult to ensure an adequate energy minimization of equilibrium structures, and the quality of modes is dependent on finding the true minimum on the potential energy surface. Despite these limitations, if carried out carefully, all-atom NMA based on atomistic force-field can provide useful information on natural frequencies of slow modes. In a seminal paper,³⁵ Tirion introduced a simplified single-parameter representation of the potential energy function by considering biological systems as three-dimensional elastic networks of atoms connected by harmonic springs. Such elastic network model (ENM) representation can be readily extended to any level (typically C_a-atoms in proteins and P-atoms in nucleic acids) of coarse-graining by proposing different cutoff distances between individual nodes, and spring constants connecting the nodes in this network can be treated uniformly or nonuniformly. Popular models in this category are the anisotropic network model (ANM)³⁶⁻³⁹ and the Gaussian network model (GNM).^40,41 These ANM/GNM-based elastic network models have been extensively developed and applied on various proteins by Bahar, Jernigan, and co-workers.^10,42−46

2.2. Applications

As was pointed out in the Introduction, there are numerous successful applications of NMA to a variety of biological systems, and a review of all such applications is beyond the scope of this work. Hence, we recommend the reader to follow earlier research and review papers that describe methodological advances and their applications.^{6,7,9,12,22,38,47−61} To highlight a few examples, Jernigan and colleagues applied a coarse-grained elastic network NMA to study dynamics in the GroEL–GroES complex.⁶² This work revealed complex details on cooperative cross-correlations between subunits: slowest modes were suggested to uniquely characterize opposing torsional rotations of the two GroEL rings by alternating compression/expansion of the GroES cap binding region. NMA has also been applied to study maturation transitions in icosahedral virus capsids and their mechanical properties.^34,63−69 Specifically, comprehensive studies by Brooks and co-workers^64,65,68,70 on viruses of different sizes and symmetries such as Hong Kong 97 (HK97), cowpea chlorotic mottle virus (CCMV), cucumber mosaic virus (CMV), rice yellow mottle virus (RYMV), southern bean mosaic virus (SBMV), and nudaurelia capensis virus (NωV) have suggested that the structural transitions are largely dominated by a few icosahedrally symmetric low-frequency normal modes. Other systems that have been successfully studied via NMA include RNA/DNA polymerases, adenylate kinase, hexameric helicases, and motor proteins.^31,53,71,72 For a comprehensive review of NMA of biomolecular structures, we direct the reader to a recent work by Bahar and co-workers.¹³ However, relevant to our work are also applications of normal mode theory in the interpretation of low-resolution EM data, which we discuss below.

Single-particle EM is a powerful methodology to probe both the architecture as well as the underlying conformational dynamics of biomolecules.⁷³⁻⁸² This technique is very useful for the structural exploration of large complexes or in general for biomolecules that are challenging to study by X-ray crystallography or NMR. Primarily due to imaging limitations as well as the inherent flexibility of macromolecules, 3D EM maps of macromolecules are often obtained at a resolution lower than 15 Å, and therefore require interpretation with the help of available high resolution structures of subregions that are fit manually or computationally in the EM envelope. Many computational algorithms that use all-atom or coarse-grained models of biomolecules to carry out rigid-body or flexible fitting into EM maps have been proposed and compared.^{15,16,83−97} To highlight a few, the molecular dynamics flexible fitting (MDFF) method was developed and applied to generate density-guided structural models by Schulten and co-workers,⁸⁵⁻⁸⁷ MultiFit and Flex-EM were developed by Sali and co-workers for iterative comparative modeling and fitting multiple components into EM envelopes,^91,98−100 MDfit was developed and applied by Sanbonmatsu and co-workers,⁸⁸⁻⁹⁰ and EM-Fold was proposed and applied by Meiler and colleagues.^101−104 Structural refinement methods based upon EM density have also been implemented in other software programs. For example, Rosetta is a popular ab initio protein structure modeling, prediction, and refinement software suite that has been applied for the improvement of NMR and X-ray crystal structures.^105−108 Dimaio et al.¹⁰⁹ recently described a Rosetta-based rebuilding-and-refinement protocol for fitting protein structures into density maps. Many of these methods were put to test during the “2010 Cryo-EM Modeling Challenge”,⁹⁶ and have been reviewed in detail recently.¹¹⁰ Among all methods in the flexible fitting domain, the normal mode flexible fitting (NMFF)^15,16 technique of Brooks and co-workers was one of the first methods with successful applications in large macromolecular complexes such as the ribosome. In the following, we highlight some of the achievements of this method.

2.3. Normal Mode Flexible Fitting

2.3.1. Theory

The need for a flexible fitting technique arises from the fact that in many cases simple rigid-body orientations of biomolecular structures are not sufficient to explain the conformation of a biomolecule in solution, as represented by a single particle EM map, regardless of resolution. Although one could alleviate this difficulty by dividing the system in independent parts, the problem is that the partitioning scheme for a multidomain assembly is not known a priori, and such partitioning often leads to disjoint conformations of the biopolymer chain. There are three main ingredients of a structural fitting protocol: (a) availability of a set of initial coordinates of the biomolecule; (b) existence of an experimental map of the biomolecule at some resolution; and (c) a flexible fitting methodology. NMFF^15,16 is one such flexible fitting computational method based upon elastic network NMA in which coarse-grained representations of biomolecules are typically fitted into low-resolution EM data. Given that the target data for flexible fitting are of low-resolution, all-atom representations may lead to overfitting of structural elements unless preventative measures are applied.^111,112 Therefore, methods such as NMFF that use only a few DOF to carry out fitting process are ideally suited for structural refinement applications. NMFF takes advantage of the fact that low-frequency normal modes of a system collectively represent most facile deformations, and due to this interesting property, they can be used as search directions in a refinement protocol.²³ The fitting is performed by iteratively deforming the initial structure along a set of low-frequency normal modes, which increases the cross-correlation coefficient (CCC) between the calculated electron density from the atomic model and the observed density from the EM map. Gradient-following techniques in the space of collective normal modes can then be used to maximize CCC. The aim of the entire procedure this way is to conform the initial structure to the target EM map. The simulated electron density for computing CCC with the target map is generated as:^15,16

1

where ρ^sim(i, j, k) is the density of voxel (i, j, k), (xⁿ, yⁿ, zⁿ) are the Cartesian coordinates of atom n, N represents the total number of atoms, the volume of the voxel is V_ijk, and g(x, y, z; xⁿ, yⁿ, zⁿ) represents the density of each non-hydrogen atom by a Gaussian kernel. Therefore, the displacements along the collective low-frequency normal modes that increase the correlation coefficient gradually lead to conformations that better fit the target EM map. Although a set of only a few (∼10–20) low-frequency normal modes is sufficient in most cases for structural refinement, one can also use rotational/translational modes to further improve the rigid-body fit into the density map.

2.3.2. Applications

Although NMFF was formally proposed in 2004,^15,16 an NMA-based strategy was used earlier to study the mechanism and pathway of pH-induced swelling in CCMV.⁶⁴ CCMV is a plant virus, whose genome consists of three single-stranded RNA molecules. The viral capsid in CCMV is composed of 180 protein subunits, thereby making it a virus with T-number (T) of 3 (total subunits in the capsid are given by 60T). Native CCMV is stable around pH 5.0, but at pH 7.0, it undergoes a massive structural transition to a swollen form during which the average size of the particle increases by ∼10%.¹¹³ In this study, the native form of CCMV was displaced along the direction of a single low-frequency mode, and many candidate structures of swollen virus particles were generated and a putative pathway for virus expansion was proposed. The proposed models were in good agreement with the EM data on swollen particles at 28 Å resolution. The analysis of structures along the expansion pathway further revealed that significant loss of interactions occurs in the initial stages of the maturation transition. NMFF was also applied successfully to refine the structure of Red clover necrotic mosaic virus (RCNMV) in an 8.5 Å-resolution EM map.¹¹⁴ The results from this study indicated that the divalent cations play a significant role in the capsid dynamics, and at low ionic concentrations, it may lead to the release of viral RNA.

Tama et al.³² used NMA to understand ratchet-like rearrangement of the 70S ribosome observed in EM maps. The ribosome is a ribonucleoprotein structure that is responsible for protein synthesis in all cells by translating mRNA into a specific sequence of amino acids. Frank and Agrawal observed a ratchet-like relative rotation of the two ribosomal subunits.¹¹⁵ The coincidence of experimentally observed dynamic transitions with a few low-frequency modes suggested that the shape of macromolecular assemblies may be a robust parameter that dictates their underlying dynamics. A structure of the E. coli protein-conducting channel was further solved with the help of NMFF and imaging via EM.¹¹⁶ NMFF-based structural refinement suggested that the channel formation takes place by opening of two linked SecY halves during polypeptide translocation, and a model for cotranslational protein translocation was also proposed.

In 2005, two other landmark applications of NMFF were reported.^117,118 The first application¹¹⁸ was for Myosin II, which is an ATP-dependent molecular motor in smooth muscle cells. A combination of EM data, homology modeling, and NMA was used to obtain structural models of putative activated and inhibited states, and mechanistic details of coupling between Head and S2 domains were explored. In the second application,¹¹⁷ a structure of chaperonin GroEL-GroES complex was determined at 13 Å resolution. The GroEL chaperonin is an essential protein that assists in the folding of other polypeptides in an ATP-dependent manner. NMFF analysis of this chaperonin bound to a protein substrate revealed that the observed conformational changes induced by protein binding are variable, and may depend on the properties of a specific substrate. NMFF was also applied to a toxic complex of anthrax to understand conformational changes in the lethal factor and the protective antigen heptamer.¹¹⁹ The concerted structural arrangements in the lethal factor and heptamer were suggested to facilitate the ingress of the ligand into the lumen of the heptamer. NMFF application was also demonstrated on the experimental maps of Elongation Factor G (EF-G) bound to the ribosome and on the E. coli RNA polymerase.¹⁶ The correlation coefficients for the final NMFF-generated models of each system were 0.81 and 0.88, respectively. NMFF fitting of other proteins such as lactoferrin and Ca²⁺-ATPase into 10 Å resolution EM maps also resulted in relatively high (greater than 0.9) final correlation coefficients.¹⁵ We briefly note that NMFF-based strategies have also been applied to small-angle X-ray scattering (SAXS) data.^120,121

The methodologies that we have described so far are based upon the analyses of static structures that can been deformed in the CV-space without invoking the dynamical aspects of the system evolution in this reduced coordinate set. Interestingly, it is possible via MD simulations to carry out dynamics in the multidimensional CV-space¹⁴ for conformational exploration of biomolecules. There are many such rapidly evolving enhanced sampling techniques, and therefore we highlight in the following only a few of these methods that have been applied to biomolecular systems.

3. Enhanced Sampling Methods

Extensive equilibrium sampling of biomolecules remains a challenging goal.¹²² Sampling of phase space at equilibrium requires access to all possible regions of configuration space, information on which, for a system at constant temperature and fixed volume, is encoded in the equilibrium probability distribution function:

2

where p is the probability density function, X is the complete 3N-dimensional atomic coordinate set, U is the potential energy function, k_B is Boltzmann’s constant, and T is the absolute temperature. Although exhaustive conformational exploration in all possible DOF for biomolecules may not be feasible, many useful techniques with similar/overlapping theoretical basis that use dimensionality reduction as a tool to explore conformational landscape in a few CVs have been proposed. In these methods, the 3N-dimensional atomic configuration of the system is mapped to an M-dimensional CV space (where M is typically significantly smaller than 3N), and the dynamics restricted to the M-dimensional CV space are explored. Many such enhanced sampling methods for equilibrium and nonequilibrium systems are periodically reviewed, and we refer the reader to consult excellent existing literature on such topics.^14,122−135 However, we briefly point out the following: (a) the adaptive biasing force (ABF) method of Darve et al.^134,135 has found applications in biomolecular conformational sampling;^136−138 and (b) the metadynamics method (and its variants) by Parrinello and co-workers^{123,124,139−142} is another popular approach that has been extensively applied to a variety of problems in biophysics.^143−147 There also exist “tempering” protocols that use high temperature as a way to overcome barriers.^148−150 These protocols are often employed in Replica Exchange MD (REMD) simulations (and its variants) and have been applied for understanding folding of proteins.^151−153 Various tempering methods have also been recently reviewed and compared.^154,155 Among all of these methods, we only focus on the theory and recent applications of enhanced sampling in the CV-space via temperature acceleration. Particularly, TAMD^17,18 is discussed as a promising method to study rare events in biomolecular systems.¹³²

3.1. Temperature-Accelerated Molecular Dynamics: Theory

TAMD was originally introduced by Maragliano and Vanden-Eijnden^17,18 as a method to explore the physical free-energy landscape in a large but finite set of CVs, which are functions of the atomic Cartesian coordinates. In TAMD, additional dynamical variables z = (z₁, z₂,...z_m) are introduced along with physical DOF, and an extended Lagrangian is proposed. These auxiliary variables are harmonically coupled (with spring constant κ) to CVs θ = (θ₁(x), θ₂(x),...θ_m(x)), and the potential energy of the system V(x) is augmented with an additional term, thereby describing the coupled motion of the [x, z] set over the following extended potential:

3

The auxiliary variables are assigned a fictitious mass as well as temperature different from that of the physical system. There are no restrictions, in principle, on the dynamics of the auxiliary variables that can be described via Langevin, Nosé–Hoover, and other related schemes. Adiabatic separation of the motion of the physical and fictitious variables is achieved by simply increasing the mass of the fictitious variables and assigning appropriate values to the thermostat parameters such as the friction coefficient. By guaranteeing in this way that z moves slower than x, one can generate a trajectory z(t), which moves at an artificial temperature β̅^–1 on the free energy landscape computed at the physical temperature β^–1. Sufficiently high temperature for the fictitious variables leads to accelerated sampling of the free-energy surface restricted to the CVs. The following coupled system of equations thus describes the motion of physical and auxiliary variables:

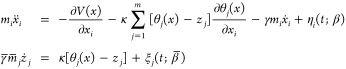4

where m_i are the masses of x_i, V(x) is the interatomic MD potential, κ is the “coupling spring-constant”, γ is the Langevin friction coefficient, η is a white noise source satisfying the fluctuation–dissipation theorem at physical temperature β^–1, γ̅ and m_j, respectively, are fictitious friction and masses of the variables z_j, and ξ is the thermal noise at artificial temperature β̅^–1.

In TAMD simulations, equilibrium distributions may deviate from the canonical Boltzmann distribution, and ways to correct such deviations by reweighting have been proposed.¹⁵⁶ We note that there are some similarities between TAMD and well-tempered metadynamics. For example, similar to the fictitious temperature in TAMD, a parameter ΔT is used in the well-tempered ensemble to control the extent of exploration near free-energy minima. A key difference is the adiabatic separation, which is perfectly achieved in TAMD only when CVs never move. Given that CVs are dynamic, TAMD never achieves perfect adiabatic separation. However, in metadynamics, errors due to poor adiabatic separation gradually decrease with the progress of metadynamics trajectory. Because metadynamics also aims to reconstruct free-energy surfaces, it must exhaustively sample space around a specific point for accurate free-energy estimation. TAMD, on the other hand, is only aimed at fast exploration of the CV-space. A major consequence of this fact is that TAMD can handle a significantly large CV-space for conformational exploration, while metadynamics may be somewhat limited.

3.1.1. Free-Energy Reconstruction

It is often informative and insightful to compute via simulations relative free-energy differences¹²⁵ between metastable/stable states of biophysical processes such as conformational transitions. However, as was pointed out above, TAMD is a method to explore fast the free-energy landscape restricted to the chosen CV-space without actually reconstructing it. In principle, one can accumulate the histograms of auxiliary variables to reconstruct the free energy surface explored via TAMD, yet it remains rather difficult primarily because it would require that the trajectories of CVs visit relevant regions of phase space several times to allow statistics to be gathered.¹³² Notwithstanding these challenges, a method for on-the-fly parametric calculation of free energy functions (TAMD/OTFP) in arbitrary collective variables was recently proposed and applied to simple test cases.¹⁵⁷ In this approach, forces from a running TAMD simulation are used to progressively optimize the best set of some parameters λ on which a free energy of known functional form depends. There are two other methods that can be used in combination with TAMD to compute free energies in a large CV-space: (1) the single-sweep method;¹⁸ and (2) the string method in CVs.¹⁵⁸ In the single-sweep method,¹⁸ TAMD forces are first used to quickly sweep through the underlying free-energy landscape and identify important regions in the landscape where one can compute mean forces. In a follow-up step, free energy is reconstructed from mean forces by representing the free energy using radial basis functions, and minimizing/optimizing certain parameters. The method is useful to compute free energies in several yet a low number of collective variables. However, the finite-temperature string method is an approach to compute the minimum free energy path (MFEP) in a large but finite set of CVs. The string method algorithm requires iterative refinement of an initial string, that is, a collection of discrete system configurations also known as “images”. TAMD is ideally suited for generating such initial paths/strings because it allows exploration of the physical free-energy landscape. At each iteration, application of the string method algorithm requires the calculation of the mean force at each image along the string. This mean force is generally obtained from restrained MD simulations by keeping the CVs relatively fixed in phase space. The images in the string are updated by measuring the negative gradient of the free energy for each CV. The convergence of the string calculation can be monitored by computing the root-mean-squared deviation of the string in CV-space as well as by computing the average string deviation over different iterations. A variant of the string method called on-the-fly string method has also been proposed¹⁵⁹ and applied successfully.¹²⁶ Many successful applications of TAMD and associated free-energy methods in various contexts are emerging, which we discuss in the following section.

3.2. Temperature-Accelerated Molecular Dynamics: Applications

Although classical MD simulations in principle can provide atomistically resolved details on conformational ensembles of proteins, observing collective large-scale structural transitions on reasonable time scales remains a challenging goal. Using special hardware and improved algorithms, it is now possible to carry out long MD simulations to capture rare biomolecular events in some cases.^160−165 Similar long time-scale biophysical processes have also been studied via relatively short TAMD simulations, as described below.

3.2.1. Protein Conformational Sampling

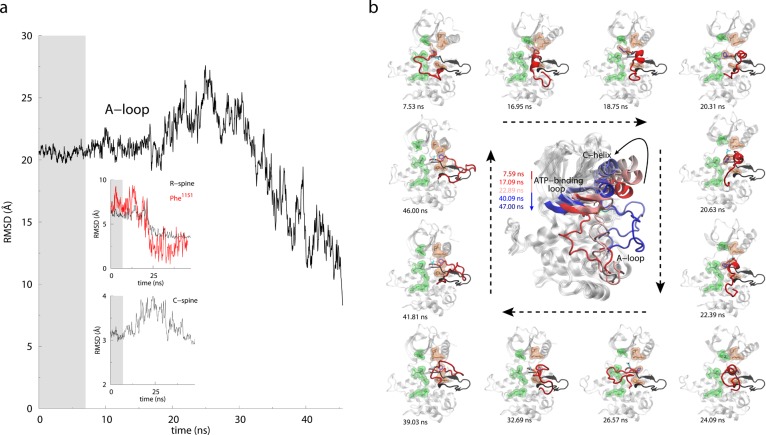
Based upon the TAMD equations described above, Abrams and Vanden-Eijnden developed a conformational sampling algorithm for proteins.¹⁶⁶ Specifically, they demonstrated that by using a fairly general partitioning scheme to define subdomains (spatially contiguous groups of residues) in a protein and defining centers-of-mass (COMs) of these subdomains as CVs, one can carry out enhanced conformational sampling at the physical temperature of the simulation. They applied this algorithm to study large-scale conformational changes in the three-domain GroEL subunit and HIV-1 gp120 without a priori knowledge of their target states. Relatively modest temperature accelerations between 6 and 10 kcal/mol were sufficient to trigger conformational changes in each case. Specifically, the apical domain in the GroEL subunit is displaced by 30 Å and 90° relative to the equatorial domain leading to prediction of a final structure within 5 Å RMSD from the known target structure. In gp120, counter-rotations of inner and outer domain as well as disruption of the bridging sheet were observed, the underlying mechanisms of which may be useful in the development of inhibitors and immunogens. This conformational sampling algorithm was later applied to several other proteins such as the insulin receptor, maltose-transporter, and regulators of G-protein coupled receptor proteins.^167−170 Insulin receptor (IR) is a homodimeric transmembrane glycoprotein of the receptor tyrosine kinase (RTK) superfamily. Insulin binding to the extracellular domain triggers activation in the intracellular kinase modules.¹⁷¹ Vashisth et al.¹⁶⁷ studied the activation mechanism of the IR kinase domain (IRKD) using TAMD. In this work, TAMD simulations consistently showed a folding/unfolding transition in the activation loop (A-loop) of IRK. A key structural feature of this transition is a helical conformation of the A-loop (Figure 1) that drives flip of the phenylalanine residue located in the conserved “Asp-Phe-Gly (DFG)” motif. Further free-energy calculations using the string method in collective variables¹⁵⁸ revealed that the helical intermediate predicted by TAMD alone is robust. The findings of this study broaden our understanding of the kinase activation and suggest conformations that can be potential therapeutic targets. Vashisth and Abrams also applied TAMD to study conformational change in the C-terminus of the B-chain of insulin (Figure 2) in the insulin/IR complexes.¹⁶⁹ This conformational change exposed residues buried in the core of hormone for it to achieve a tighter registry and higher affinity for IR. Similar to the kinase work, TAMD-generated conformations in this study were also further validated with the help of string method in CVs. TAMD was further applied to study the allosteric mechanism of inhibition of the regulator of G-protein signaling protein 4 (RGS4) by an inhibitor molecule.¹⁷⁰ Conformational exploration of RGS4 structures consistently reveals that a pair of helices in RGS4 can spontaneously span open-like conformations, allowing binding of the inhibitor to the buried side-chain of Cys95 (Figure 3). Remarkably, NMR experiments on RGS4 suggested chemical shift perturbations consistent with TAMD predictions. By adding an additional angle-dependent harmonic potential to the TAMD equations, Vashisth and Brooks showed that robust conformational transitions can be observed in components of the maltose-transporter,¹⁶⁸ a membrane protein responsible for transport of small nutrients. Moreover, they demonstrated that every functional displacement in the TAMD-generated pathways of each protein could be characterized by a few low-frequency normal modes. These results suggested, for the first time, that conformational sampling in Cartesian CVs is governed by low-frequency soft modes.

Figure 1.

TAMD-generated conformational change in the activation loop of the insulin receptor kinase domain. (a) RMSD versus simulation time (ns) for the activation-loop (the A-loop), R-spine, C-spine, and Phe¹¹⁵¹ with respect to the active crystal structure. Gray background in the plots indicates first ∼7 ns of MD equilibration, which is followed by ∼40 ns of TAMD. (b) Representative snapshots of IRKD from TAMD simulation are shown at various time-points with the A-loop in red, side-chains of Asp¹¹⁵⁰ and Phe¹¹⁵¹ in cyan and blue, respectively. The conformation of the A-loop in the active crystal structure is shown as a black cartoon. The large panel in the center shows the conformations of IRKD with highlighted structural motifs: αC-helix, nucleotide-binding loop, and the activation loop from TAMD simulation at t = 7.59 (red), 17.09, 22.89, 40.09, and 47.00 ns (blue). Arrow directions guide along the increasing simulation time. Adapted with permission from ref (167). Copyright 2012 Elsevier.

Figure 2.

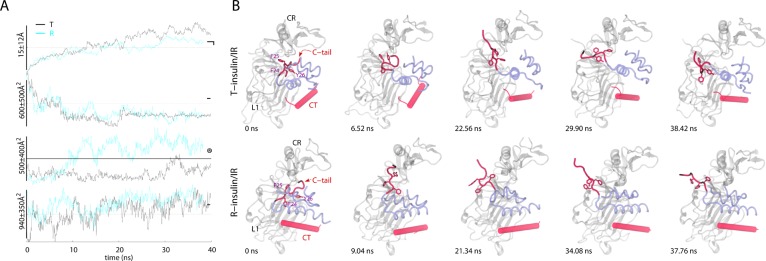
TAMD-generated conformational change in the C-terminus of the B-chain of each insulin. (A) Traces (T-insulin, black; R-insulin, cyan) of the root-mean-squared deviation (RMSD) and buried surface area (BSA) versus simulation time (ns) are shown for each insulin/IRΔβ complex. Circled digits indicate the following: (①) RMSD of the C-terminus (residue B21–B30) of the B-chain of each insulin. For RMSD computation, the insulin molecules were aligned based upon the residues of each A- and B-chain (A1–A21 and B1–B20; C_α); (②) BSA between the C-terminus of the B-chain (residues B21–B30) of each insulin and rest of the insulin molecules; (③) BSA between each insulin molecule (except the B-chain residues B21–B30) and the L1 domain; and (④) BSA between CT and the L1 domain. Horizontal lines indicate the values measured in the IRΔβ crystal structure (PDB code 3LOH) except the dotted horizontal lines that are arbitrarily drawn for guidance. (B) Conformational change in the C-terminus of the B-chain of each insulin is highlighted. Representative snapshots of each insulin (transparent blue), CT (transparent red), and the L1 and CR domains of IRΔβ (transparent white) are shown at various time-points of respective TAMD simulations. The residues F^B24, F^B25, and Y^B26 are shown in sticks and labeled in the first snapshot for each insulin/IRΔβ complex. Initial positions of CT are different (from the crystal structure) for each insulin/IRΔβ complex because TAMD trajectories were started based upon the Monte Carlo (MC) docked and MD-equilibrated structural models of each insulin/IRΔβ complex. Some of the terminal residues of CT spontaneously fold/unfold during TAMD trajectories. Adapted with permission from ref (169). Copyright 2013 John Wiley & Sons, Inc.

Figure 3.

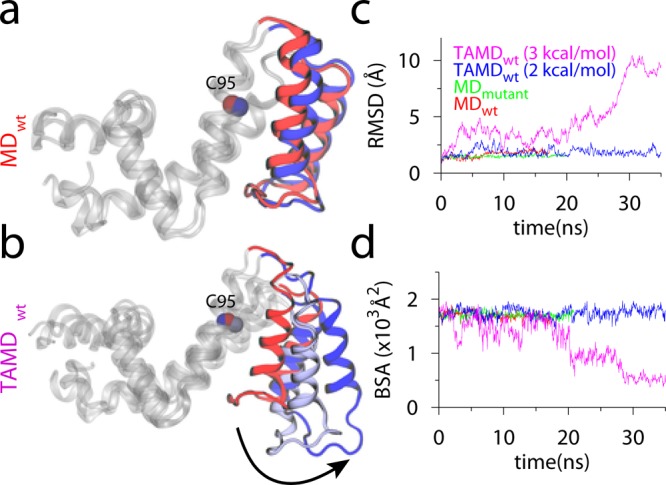
MD and TAMD simulation data for RGS4 runs with initial coordinates from PDB code 1AGR. (a and b) Overlay of cartoon representations of apo-RGS4 (red, beginning; blue, end of simulations). All helices of RGS4, except the α₅–α₆ pair, are shown in white cartoons. (c) The C_α-RMSD traces with reference to starting conformations. (d) Buried surface area (BSA) between the α₅–α₆ helix pair and the rest of RGS4. Adapted with permission from ref (170). Copyright 2013 American Chemical Society.

3.2.2. Ligand Diffusion

Given that proteins are therapeutic drug targets, novel small molecules are designed typically to block the activity of a specific protein. Diffusion processes of small molecules inside the proteins are therefore essential to understand. Specifically, free-energy barriers associated with ligand diffusion in proteins remain difficult to quantify, but their knowledge is necessary for a structure-based rational drug-design approach. Many simulation techniques have been applied to understand CO diffusion in myoglobin (Mb), and TAMD was also used to study diffusion of either CO or CO/water in Mb.^172,173 Maragliano et al.¹⁷² first showed the existence of a complicated network of pathways for the exit of CO in which a histidine gate is the closest exit from the binding site of the ligand. Lapelosa and Abrams further showed that the histidine gate is also the preferred entry/exit portal for water molecules in addition to CO. A key implication of these results is that the models of gas transport in proteins should also explicitly consider the transport of water molecules. In each of these studies, single-sweep method¹⁸ for free-energy calculation in a finite CV-space was combined with TAMD for free-energy reconstruction.

3.2.3. Structural Refinement via Flexible Fitting

MDFF is a popular method to carry out flexible fitting of atomic structures into EM maps. Structural fitting of a number of large biological complexes has been carried out using via MDFF.^{82,85,86,174,175} Vashisth et al.^111,112 showed that the capabilities of MDFF can be extended by combining it with TAMD for faster structural fitting. The first application of TAMD-assisted MDFF (TAMDFF) was demonstrated on a well-known enzyme, adenylate kinase (AdK), as a test system. The final structures of AdK generated by MDFF and TAMDFF were in good agreement with each other (Figure 4), thereby suggesting that enhanced structural fitting can be achieved in EM maps. Interestingly, TAMD can also be used to generate better starting configurations for MDFF fitting. As an example, conformational exploration of the G_α-subunit of the β₂-adrenergic receptor led to better starting configurations for MDFF fitting, while rigid-body docked conformations of same protein could not be correctly placed in EM maps via MDFF (Figure 5).¹¹¹ TAMDFF was further applied to nucleic acid systems and a small ribonucleoprotein complex.¹¹² In each case, TAMDFF generated final structural modes similar to or better than MDFF alone. In case of the ribosomal helix 44 (H44) fitting into experimental EM maps, TAMDFF could fit the structure in 1 ns, which takes MDFF ∼4 ns (Figure 6). This means that computational gain for large macromolecular complexes can be significant if simulations are carried out in explicit solvent.

Figure 4.

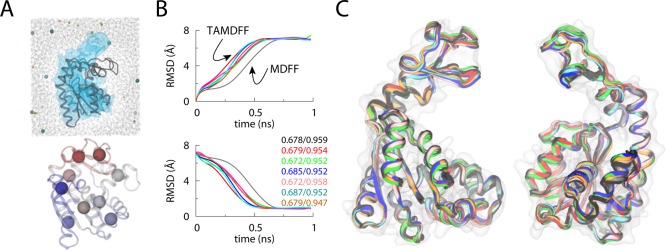
MDFF versus TAMD-assisted MDFF (TAMDFF) fitting of adenylate kinase in explicit solvent. (A; top panel) Schematic representation of the simulation domain (29416 atoms) of the adenylate kinase (ADK) as viewed along the z-axis: starting docked closed-conformation of ADK (black cartoon), 5 Å resolution target map (blue surface), water molecules (wireframe), and ions (spheres). (A; bottom panel) Subdomain partitions of ADK are shown for the TAMD simulation. Each sphere represents the center-of-mass (COM) of a mutually exclusive subdomain. Entire ADK structure was divided into 9 subdomains. (B) Top and bottom panels, respectively, show the C_α-RMSD traces from the known initial and final crystal conformations of ADK. The black trace is from an MDFF simulation, while the traces of other color are from six independent TAMD-assisted MDFF (TAMDFF) simulations. Initial/final correlation coefficients for all seven simulations are shown in the bottom panel. (C) Cartoon representations of two different views of the overlay of final conformations generated via MDFF and TAMDFF simulations are shown. Cartoon colors are the same as the RMSD traces in panel B. Adapted with permission from ref (111). Copyright 2012 Elsevier.

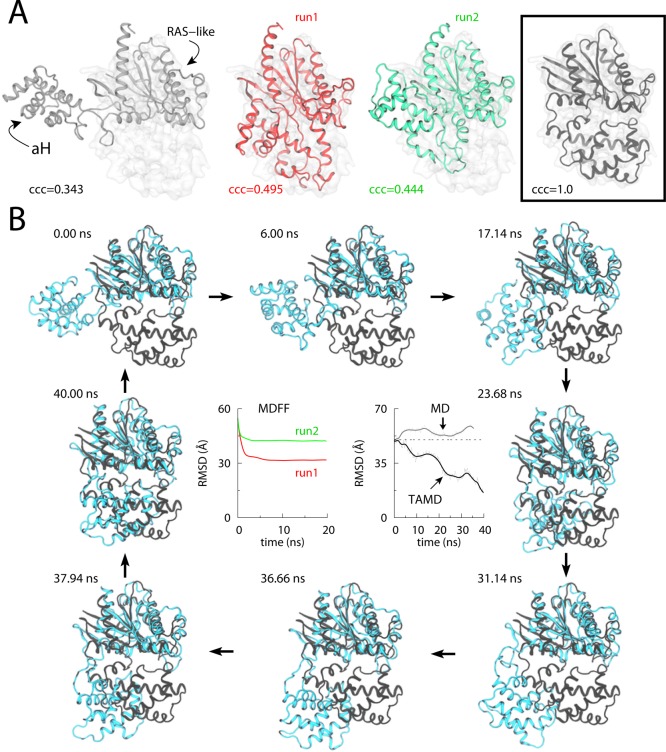
Figure 5.

Conformational change in the G_α-subunit of a GTP-binding protein (G-protein) studied via MDFF and TAMD simulations. (A) Cartoon representations for MDFF fitting of G_α at 5 Å target-map resolution: initial docked open-state crystal conformation (white cartoon; left panel), final conformations generated via two independent 20-ns MDFF simulations (red and green cartoons; middle panels), and the known target closed-state crystal conformation with perfect correlation coefficient of 1.0 (black cartoon; boxed right-most panel). The C_α-RMSD (with respect to the final crystal structure) traces for each 20-ns MDFF run are shown in panel B. (B) Representative snapshots from a 40-ns TAMD simulation of G_α are shown at various time-points during the simulation. TAMD-generated conformation is shown in cyan, and the known closed-state crystal structure conformation is in black. The C_α-RMSD (with respect to the final crystal structure) trace from the ∼40-ns TAMD simulation is shown in the central right-panel along with the RMSD trace from an unbiased ∼36-ns explicit-solvent MD simulation of G_α. Adapted with permission from ref (111). Copyright 2012 Elsevier.

Figure 6.

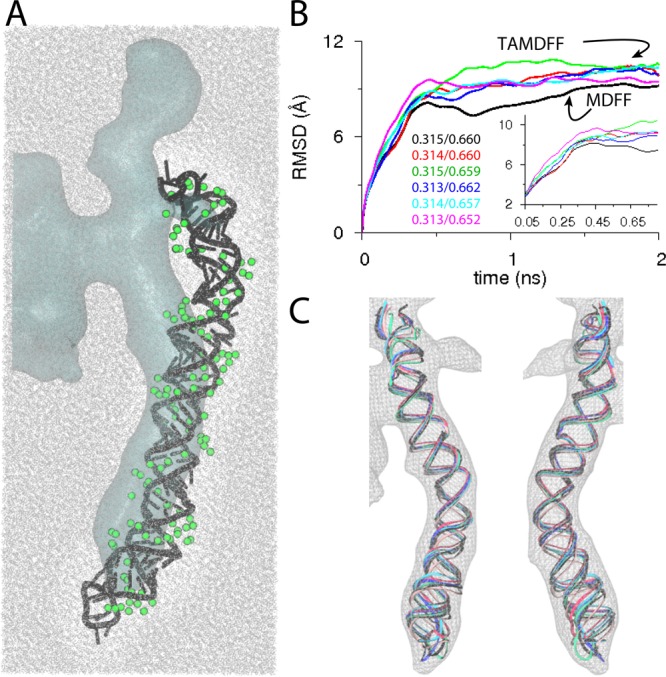
Explicit-solvent MDFF versus TAMDFF fitting of helix-44 (H44) from the mature small (40S) eukaryotic ribosomal subunit¹⁷⁹ into an experimental map of a pre-40S maturation intermediate.⁸² (A) Schematic representation of the simulation domain (208390 atoms) of solvated H44 as viewed along the z-axis: starting docked conformation of H44 (black cartoon), ∼18 Å resolution target map (cyan surface), water molecules (wireframe), and Mg²⁺ ions (green spheres). The additional globular blobs of density near H44 are from some accessory factor proteins (not modeled here). (B) The backbone (P-atoms) RMSD traces from the known initial crystal conformation of H44 (PDB code 3U5F). The black trace is from an MDFF simulation, while the traces of other color are from five independent TAMDFF simulations. Initial/final correlation-coefficients for all six simulations are also shown. Inset highlights the RMSD traces in early parts of MDFF and TAMDFF simulations. (C) Map-docked cartoon representations are shown for two different views of the overlay of final conformations generated via MDFF and TAMDFF simulations. Adapted with permission from ref (112). Copyright 2013 American Chemical Society.

3.2.4. Other Applications

TAMD was briefly applied to study the dynamic process of β₂-adrenergic receptor activation,¹⁷⁶ and was also part of a study that extends capabilities of Anton, a special-purpose machine for MD simulations, to include more diverse set of methods.¹⁷⁷ An interesting nonbiological application of TAMD was to study structures of hydrated nafion polymer in different morphologies.¹⁷⁸ In this study, TAMD allowed observation of the trans–gauche transition (a rare event) in the backbone of nafion strands.

4. Outlook

In this work, we have discussed some established as well as emerging computational techniques that exploit dimensionality reduction as a tool to understand large-scale conformational changes in biomolecules. Particularly, methods solely based upon analysis of static structures such as NMA and methods based upon MD simulations such as TAMD were highlighted. Theoretical considerations and recent key applications to complex biomolecular systems are discussed. In many cases, conformations generated by enhanced sampling methods such as TAMD were in good agreement with crystallographic,¹⁶⁷ NMR,¹⁷⁰ and low-resolution EM data.^111,112 These successful applications provide encouragement to practitioners of molecular simulations for testing the validity of these methods further on a diverse set of proteins, nucleic acids, and their complexes. Although Cartesian CVs have been remarkably successful for protein conformational sampling,^166−170 other CVs for conformational sampling of biomolecules need to be explored. Furthermore, there is a need for future studies on TAMD that systematically investigate the effects of different variables on dynamics such as the size of subdomains, fictitious temperature, coupling spring constant, friction coefficient associated with thermostat on auxiliary variables, presence of solvent, and different schemes for dynamic evolution of auxiliary variables. The hope is that a better understanding of the limitations of these methods will be helpful in choosing the right technique (amidst a vast array of available methods) for appropriate application.

Glossary

Abbreviations

NMA

normal-mode analysis

TAMD

temperature-accelerated molecular dynamics

CV

collective variable

ENM

elastic network model

Biographies

Harish Vashisth is an Assistant Professor in the Department of Chemical Engineering at the University of New Hampshire, Durham, NH. He was born in Haryana (India) where he obtained his early education. He obtained his Bachelor of Technology (B. Tech.) degree in Chemical Engineering from the National Institute of Technology, Warangal (India), in 2005, and immediately joined the doctoral program in Chemical and Biological Engineering at Drexel University under the guidance of Professor Cameron F. Abrams. In 2010, he received his Ph.D. in Chemical and Biological Engineering for his thesis work on the molecular simulation studies of the hormones and receptors of the insulin family. From 2010 to 2013, he pursued postgraduate work with Professor Charles L. Brooks III in the Department of Chemistry and Biophysics Program at the University of Michigan, Ann Arbor. During this period, he worked on the development and application of enhanced sampling molecular simulation methods to understand large-scale conformational changes in proteins and nucleic acids, and for the interpretation of low-resolution electron-microscopy data.

Georgios Skiniotis is a faculty member at the University of Michigan Life Sciences Institute, an Associate Professor of Biological Chemistry at the University of Michigan Medical School, and a Pew Scholar of Biomedical Sciences. Skiniotis obtained his B.Sc. in Biochemistry at the University of Leeds in UK and his Ph.D. in Structural Biology at the European Molecular Biology Laboratory in Heidelberg, Germany. After postdoctoral studies at Harvard Medical School, he joined the University of Michigan in 2008.

Charles L. Brooks III was born in Detroit (Michigan) and took his early education in chemistry, physics, and mathematics in rural Michigan elementary, middle, and high schools. He received a Bachelor of Sciences degree from Alma College in these disciplines in 1978. He pursued graduate studies at Purdue University under the direction of Professor Stephen A. Adelman. His graduate work focused on the development of nonequilibrium statistical mechanical theories for reactions on surfaces, in solids, and in liquids using molecular time scale generalized Langevin (MTGLE) theory. In 1982 he received his Ph.D. in Physical Chemistry from Purdue University. He pursued postgraduate work at Harvard University with Professor Martin Karplus between the years of 1982 and 1985, where he was the recipient of an NIH Postdoctoral Fellowship between 1983 and 1985. His work at Harvard set the stage for his career in theoretical and computational biophysics. In 1985 Professor Brooks joined the Chemistry Faculty of Carnegie Mellon University, where he remained until 1994. Between 1992–1993 he spent a sabbatical year working at the Karolinska Institute in Stockholm, Sweden, and The Scripps Research Institute in La Jolla, California. Professor Brooks moved his research group to The Scripps Research Institute in 1994. In 2008, Professor Brooks moved to the University of Michigan, where he holds the positions of Warner-Lambert/Parke-Davis Professor of Chemistry and Professor of Biophysics. Professor Brooks has received a number of honors and awards. He received an Alfred P. Sloan Research Fellowship in 1992. In 1997 he was recognized for his pioneering work in computational biophysics with a Computerworld Smithsonian Award. In 2002 he was elected as a Fellow of the American Association for the Advancement of the Sciences. Dr. Brooks was recognized for his impact on the field of Chemistry, being noted as one of the “top 100 chemists of the decade, 2000–2010” by Thomson Reuters. His work in protein simulations and modeling was recognized by the Protein Society with presentation of the Hans Neurath Award in 2012. Professor Brooks’ service to the scientific community includes stints on review panels for the NIH and NSF, reviewing for all of the major scientific journals, as well as founding and serving on the Steering and Oversight Committees of the La Jolla Interfaces in Sciences Interdisciplinary Training Program, the Center for Theoretical Biological Physics, and the direction of an NIH funded research resource center for Multiscale Modeling Tools in Structural Biology (MMTSB). He is an Editorial Board Member for the journals Proteins and Molecular Simulation. Since January 2004 he has been the North American Editor for the Journal of Computational Chemistry. Professor Brooks and his research group have pioneered many methods and applications of biomolecular simulation to important biological problems. These include the λ-dynamics free energy approach to receptor–ligand interaction free energies, constant pH molecular dynamics, novel approaches to generalized Born implicit solvent/implicit membrane theories, protein folding free energy landscapes and mechanisms, coarse grained and multiscale approaches to the mechanics of macromolecular machines and motors, and virus capsid structure, energetics, assembly, and design principles. He has published more than 300 peer-reviewed papers, and currently his H-index is 77.

The authors declare no competing financial interest.

We note that a review article¹⁸⁰ discussing various enhanced sampling methods and their applications, including those of TAMD, appeared in print shortly before acceptance of our article.

Funding Statement

National Institutes of Health, United States