Coupled Enzyme Reactions Performed in Heterogeneous Reaction Media: Experiments and Modeling for Glucose Oxidase and Horseradish Peroxidase in a PEG/Citrate Aqueous Two-Phase System

Abstract

The intracellular environment in which biological reactions occur is crowded with macromolecules and subdivided into microenvironments that differ in both physical properties and chemical composition. The work described here combines experimental and computational model systems to help understand the consequences of this heterogeneous reaction media on the outcome of coupled enzyme reactions. Our experimental model system for solution heterogeneity is a biphasic polyethylene glycol (PEG)/sodium citrate aqueous mixture that provides coexisting PEG-rich and citrate-rich phases. Reaction kinetics for the coupled enzyme reaction between glucose oxidase (GOX) and horseradish peroxidase (HRP) were measured in the PEG/citrate aqueous two-phase system (ATPS). Enzyme kinetics differed between the two phases, particularly for the HRP. Both enzymes, as well as the substrates glucose and H₂O₂, partitioned to the citrate-rich phase; however, the Amplex Red substrate necessary to complete the sequential reaction partitioned strongly to the PEG-rich phase. Reactions in ATPS were quantitatively described by a mathematical model that incorporated measured partitioning and kinetic parameters. The model was then extended to new reaction conditions, i.e., higher enzyme concentration. Both experimental and computational results suggest mass transfer across the interface is vital to maintain the observed rate of product formation, which may be a means of metabolic regulation in vivo. Although outcomes for a specific system will depend on the particulars of the enzyme reactions and the microenvironments, this work demonstrates how coupled enzymatic reactions in complex, heterogeneous media can be understood in terms of a mathematical model.

Introduction

Important differences between the dilute buffers typically used for biochemical studies and the intracellular environments in which biomolecules such as enzymes actually operate are increasingly realized.¹⁻⁷ These can include the following: (1) excluded volume effects due to high concentrations of other background molecules, (2) attractive and repulsive interactions between molecules of interest and other solutes or solvent molecules, and (3) physical and chemical heterogeneity in the reaction medium. The first two differences can be approximated by including macromolecular crowding agents either alone or in concert with small molecules that interact with biomacromolecules of interest.^3,8−11 In this manuscript, we focus on heterogeneity, which has received considerably less attention compared to crowding and chemical effects. The existence of microenvironments within the cell could impact local and overall reaction kinetics due to variations in local reactant, enzyme, or inhibitor concentrations, chemical interactions, excluded volume, and/or local viscosities.^6,7,12,13 Here, we achieve chemical and physical heterogeneity by using a polyethylene glycol (PEG)/citrate aqueous two-phase system (ATPS).¹⁴⁻¹⁶ This ATPS has PEG-rich and citrate-rich phases that differ substantially in viscosity, macromolecular crowding, and salt concentration. Thus, although its components are not those of the intracellular environment, it offers a test system for evaluating the impact of heterogeneous media on a coupled biochemical reaction.

Experimental and modeling studies have demonstrated the impact of macromolecular crowding agents such as polyethylene glycol (PEG), dextran, or Ficoll on the structure, association, and activity of various biomacromolecules.^3,9,17−21 A major aspect of the macromolecular crowding effect is due to excluded volume from intracellular polymers (proteins, nucleic acids, polysaccharides) that combined can make up ∼30% weight percent in cytoplasm.¹ Additionally, chemical effects due to attractive and repulsive interactions between molecules (solutes and/or solvent molecules) can alter outcomes as compared to dilute solution.^4,10,22−24 These chemical effects are observed even for small molecule cosolutes that do not exclude appreciable volume (e.g., ethylene glycol, trimethylamine N-oxide (TMAO)). For example, Record and co-workers found that DNA duplexes and hairpins were destabilized by small molecular weight PEG due to favorable interactions with the PEG monomers.⁹ Such efforts to better mimic the crowded environments in which biomacromolecules function are very important to our understanding of macromolecular crowding in vivo, but because they are performed in homogeneous media, they do not capture all aspects of the intracellular environment.

The intracellular milieu is heterogeneous in addition to being crowded. Different concentrations of various small molecules, ions, proteins, and nucleic acids are found in different regions within the cell and its compartments.²⁵ The concentration of biomolecules into subcellular compartments could offer a means of increasing reaction rates and controlling the site of a reaction,¹³ or regulating a pathway based on the formation and dissolution of a compartment.^6,26 Reaction compartmentalization is thought to be crucial for a variety of cellular functions including metabolism, transcription and translation, and cell division. For example, the citric acid cycle is confined to the mitochondrial membrane,²⁷ and lysosomes perform their catabolic functions separate from the rest of the cell.²⁸ In addition to the membrane-bounded organelles, numerous other subcellular and subnuclear compartments have been identified that lack membranous boundaries. Some structures are transient, such as the purinosome, with formation/dissolution thought to correspond to biological activity.²⁶ Two nonmembrane bounded compartments, the nucleolus and P-granules, have recently been demonstrated to behave as liquids, suggesting that these subcellular structures are the result of aqueous phase separation.^29,30

Single enzymatic reactions have been performed in polymer/salt ATPS and aqueous/organic biphasic media; these systems are attractive for bioconversion reactions for which the substrate and enzyme partition to the same phase (generally the bottom, salt-rich, or aqueous phase), while the product partitions to the other phase (generally the top, polymer-rich, or organic phase), where it is prevented from inhibiting the reaction and can be continuously removed if desired.³¹⁻³³ These reactions are often performed with bulk phases (macroenvironments) that have a well-defined interfacial area rather than with media in which one phase exists as droplets dispersed in the other (microenvironments); this facilitates continuous product removal. A sequential reaction of lipase and lipoxygenase has been performed in a macroheterogeneous octane/aqueous buffer system of carefully controlled interfacial area, where the substrates partitioned to the octane phase and the enzymes to the aqueous phase. Experiments and simulations showed that the rate of the second reaction was determined by the first reaction and also by mass transfer in this system.³⁴

Few studies have attempted to mathematically model enzymatic reactions occurring within heterogeneous media.³⁴ Instead, most have focused on predicting partitioning coefficients in the equilibrium state^35,36 or the phase behavior of the ATPS.^14,37 To accomplish this goal, they employed thermodynamic models based on Gibbs excess (G^E-models). On the other hand, a few papers have exploited models describing the behavior of heterogeneous liquid–liquid (organic/aqueous) systems to find the concentration profile in time.^38,39 Quadros et al. used linear regression to derive a statistical model to estimate the product concentration,³⁸ while van Woezik and Westerterp used conservation equations to derive a mechanistic model to study the reaction rates in a semi batch reactor.³⁹ Additionally, a continuous flow of ATPS in which there is no chemical reaction has been modeled to understand the steady state and transient behavior of the system.⁴⁰ However, to the knowledge of the authors, there is no mathematical model presented in the open literature to predict the dynamic behavior of partitioned species in an ATPS, in which both mass transfer and chemical reactions have to be accounted for simultaneously. Moreover, previous modeling efforts did not consider the microscale geometry of the model and as a result investigated only changes of average concentrations of the species with time. In this work, we take a mechanistic modeling approach and develop a complex model that also includes an interesting interface geometry.

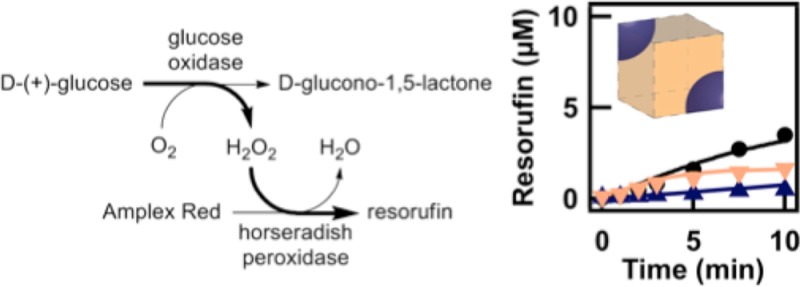
Here, the well-studied enzymes glucose oxidase (GOX) and horseradish peroxidase (HRP) were used to perform a sequential reaction in a PEG/citrate ATPS that was mixed to generate droplets during the reaction (Scheme 1). The PEG/citrate ATPS was selected for this study because its two aqueous phases differ greatly in composition: the top, polymer-rich phase is crowded and viscous, while the bottom, citrate-rich phase is quite salty. The phases impact enzyme kinetics differently, more so than would be expected from typical polymer/polymer ATPS such as the PEG/dextran system where both phases are more similar in crowding and salt concentration.⁴¹ Additionally, partitioning leads to differences in local concentrations for the enzymes and some of the small molecules. A computational model that takes into account measured enzyme kinetics for each phase as well as enzyme and substrate partitioning was then derived and informed on the basis of experimental results for the two-phase system. Through formulating the governing mass transfer equations for this system, we obtained a system of coupled PDEs. Solving these equations simultaneously using finite element methods in COMSOL provided us with temporal as well as spatial concentration distributions of the species in both phases. The kinetics for the sequential reaction were well-described by this model, which was then used to predict reaction kinetics at higher enzyme concentrations.

Scheme 1. (A) The Sequential Enzyme System of Glucose Oxidase (GOX) and Horseradish Peroxidase (HRP) with the Substrates, Intermediates, and Products of Interest Shown; (B) Illustration Depicting How the Enzymes, Substrates, and Products Partition within a PEG:Citrate ATPS.

The reaction was monitored by the fluorescent product resorufin.

This work demonstrates how, despite substantial and nontrivial media effects for the different phases, by experimentally determining key parameters (partitioning coefficients, K_M, k_cat in each phase), a sequential reaction within a heterogeneous reaction medium can be understood in terms of simple kinetic and partitioning experiments with the aid of mathematical modeling.

Results and Discussion

To understand the sequential enzyme reaction of Scheme 1 in the ATPS, and to generate an accurate mathematical model for this reaction, it was first necessary to characterize the content and kinetic effects of the individual phases. Enzymatic reactions in the full ATPS were then performed and a mathematical model derived to describe the kinetics in this system. The model was then used to predict the enzyme activity at a higher concentration of HRP.

Phase Composition and Properties

The PEG:citrate ATPS had an overall composition of 13.3 w/w % PEG 8 kDa and 10.0 w/w % citrate prepared in a 50 mM sodium phosphate buffer pH 7.4 with 1 mM EDTA. This ATPS has roughly equal volumes of a PEG-rich top phase and a citrate-rich bottom phase, which have very different chemical and physical properties that impact the enzymatic reactions (Supporting Table 1, Supporting Information). The PEG-rich phase contained most of the polymer, making it much more macromolecularly crowded (24 vs <1 w/w % PEG) and ∼17× more viscous than the citrate-rich phase, while the citrate-rich phase was considerably saltier (1.1 M citrate vs ∼100 mM). A phase diagram for the PEG 8 kDa/citrate system, with the location of the composition highlighted, is included as Supporting Figure 1 (Supporting Information).

Enzyme Kinetics in the Individual Phases

On the basis of their different compositions, we anticipated that enzyme kinetics would be different in the two phases of the ATPS. Results from Michaelis–Menten assays performed in each of the individual phases are shown in Figure 1 and Table 1. GOX kinetics were similar, but not identical, between the two phases, while differences in HRP kinetics were substantial. The K_M value for H₂O₂ was ∼30× lower in the PEG-rich phase than in the citrate-rich phase, and k_cat was nearly 2 orders of magnitude lower in the PEG-rich phase. K_M for the other substrate of HRP, Amplex Red, could not even be measured in the PEG-rich phase as the rate continued to increase with increasing Amplex Red concentration even at high concentrations (up to 1 mM). Possible explanations for these large effects on the HRP reaction in the PEG-rich phase include changes in enzyme conformation or the increased solubility of the hydrophobic substrate Amplex Red in the PEG-rich phase. PEG has been reported to interact with hydrophobic amino acids in proteins³ and to increase the solubility of hydrophobic solutes in aqueous solution;⁴²⁻⁴⁴ we reason it may be competing with the enzyme for Amplex Red.

Figure 1.

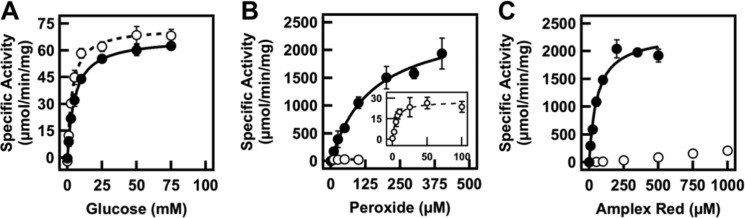
Michaelis–Menten assays for GOX and HRP in the PEG-rich phase (open circles) and citrate-rich phase (closed circles). (A) Effect of glucose concentration on GOX rate, measured at 0.05 U/mL GOX (2.1 nM). Effect of substrate concentration on HRP rate for (B) peroxide and (C) Amplex Red. HRP concentrations were 0.005 U/mL (0.45 nM) for PEG-rich phase experiments and 0.0005 U/mL (0.045 nM) for the citrate-rich phase.

Table 1. Michaelis–Menten Constants of GOX and HRP within PEG:Citrate ATPS.

	KM (μM)	Vmax (μmol/min/mg)	kcat (s–1)
GOX (Glucose)
PEG-rich	3400 ± 400	73 ± 2a	194 ± 5
citrate-rich	5400 ± 200	66.9 ± 0.6a	178 ± 2
HRP (H2O2)
PEG-rich	5 ± 1	28 ± 2b	20 ± 1
citrate-rich	150 ± 20	2600 ± 200c	1900 ± 100
HRP (Amplex Red)
PEG-rich	n.a.d	n.a.b	n.a.
citrate-rich	60 ± 10	2300 ± 100c	1700 ± 100

^aV_max for enzyme concentrations of 0.05 U/mL.

^bV_max for enzyme concentrations of 0.005 U/mL.

^cV_max for enzyme concentrations of 0.0005 U/mL.

^dNot applicable. Rate increased linearly to the limit of substrate solubility.

We also performed the sequential reaction in the individual phases. Reactions contained 0.05 U/mL GOX, 0.005 U/mL HRP, 1 mM glucose, and 50 μM Amplex Red. An initial lag period was observed for the first ∼3 min in the citrate-rich phase as the concentration of peroxide generated by GOX increased (Figure 2). After 10 min, 15.4 ± 1.6 μM resorufin had been formed in the citrate-rich phase as compared with only 0.69 ± 0.05 μM in the PEG-rich phase, an approximately 22-fold difference. These results, along with the individual assays described above, suggested that PEG had a detrimental effect on HRP activity, particularly with respect to Amplex Red. This in turn made the sequential reaction much slower in the PEG-rich phase than the citrate-rich phase.

Figure 2.

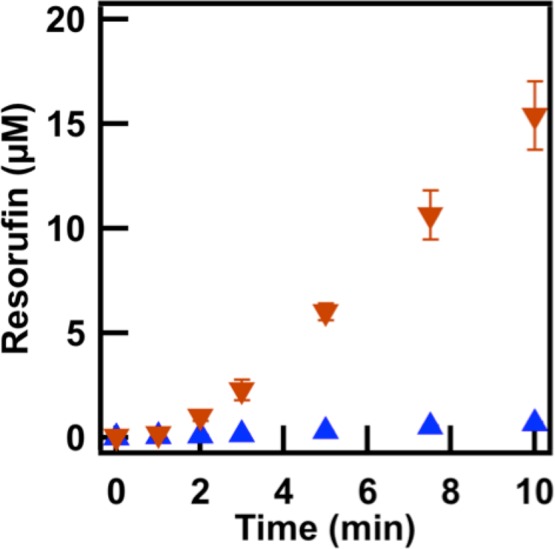
Product formation of the sequential GOX and HRP reaction in the citrate-rich phase (inverted orange triangles) and the PEG-rich phase (blue triangles).

Partitioning

All of the reactions described above were performed in single phases. When both phases of the ATPS are present, the enzyme and substrate concentrations may differ between the phases; this partitioning can impact the sequential kinetics. Solute partitioning is quantified as the partitioning coefficient, K = C_P/C_C, where C_P and C_C are the solute’s concentration in the PEG-rich and citrate-rich phases, respectively. Except where noted, a 1:1 volume ratio of PEG-rich to citrate-rich phases was used for these measurements. Table 2 reports partitioning values for enzymes and small molecules of interest in the sequential reaction. Enzymes were fluorescently labeled with different dyes for these measurements and were tested simultaneously, since any potential protein–protein interactions would affect their partitioning coefficient.⁴¹ Both enzymes were more concentrated in the citrate-rich phase. K_GOX = 0.036 and K_HRP = 0.63, indicating a 28-fold and 1.6-fold concentration excess for GOX and HRP, respectively, in this phase. Glucose and peroxide also partitioned somewhat to the citrate-rich phase (K_g = 0.53 and K_p = 0.6, respectively), while the hydrophobic substrate and product strongly partitioned to the PEG-rich phase with K_a = 60 for Amplex Red and K_r = 23 for resorufin.

Table 2. Partitioning Coefficients in the Experimental ATPS at Various Volume Ratios.

	partitioning coefficient
sample	4:1	1:1	1:4
GOXa	0.023 ± 0.006	0.036 ± 0.004	0.074 ± 0.004
HRPb	0.35 ± 0.04	0.63 ± 0.09	1.4 ± 0.2
glucose	n.a.c	0.53 ± 0.04	n.a.
hydrogen peroxide	n.a.	0.6 ± 0.1	n.a.
Amplex Red	n.a.	60 ± 5	n.a.
resorufin	n.a.	23 ± 2	n.a.

^aGOX partitioning was determined at the concentration used in the enzyme assays (2.1 nM).

^bHRP was measured at 4.5 nM HRP because at 0.45 nM, which was used in the sequential assays, the fluorescence was too low to quantify.

^cNot applicable. Partitioning coefficients of small molecules were only measured at a 1:1 PEG:citrate volume ratio.

The partitioning coefficient is a thermodynamic constant and should not normally change with volume ratio or solute concentration; however, exceptions are well-known for proteins in PEG:salt ATPS because the salt-rich phase may “salt out” the protein into the PEG-rich phase or it may precipitate to the interface.⁴⁵⁻⁴⁷ The increased apparent hydrophobicity of proteins in high salt solutions can lead to changes in partitioning, in particular an increased preference for the more hydrophobic PEG-rich phase, and/or multimerization or aggregation of the protein. Additionally, at distances far from the critical point of the phase diagram, small deviations from the tie line, caused by minor dilution from adding the enzymes/substrates to the ATPS, can change partitioning even in the absence of salting out effects.⁴⁵ Therefore, we measured the partitioning coefficients of GOX and HRP at all the volume ratios and diluted the samples by the same amount, as will be done with the assays below. We did not see evidence of protein precipitation in our system (see below); however, differences in partitioning with volume ratio were observed for both proteins (Supporting Scheme 1, Supporting Information, Table 2). These differences in enzyme partitioning with volume ratio, while underscoring the importance of careful analysis of the experimental system, also enabled us to examine the effect of such changes on the overall reaction kinetics. As the volume of the citrate-rich phase increased, both enzymes partitioned less strongly. GOX remained partitioned in the citrate-rich phase; however, for HRP, which partitioned only slightly to the citrate-rich phase at a volume ratio of 1:1, a switch in partitioning preference to the PEG-rich phase was observed at a 1:4 PEG-rich to citrate-rich volume ratio. We also measured the effect of enzyme concentration on partitioning at the three volume ratios (Supporting Figure 2, Supporting Information). K_GOX was sensitive to both concentration and volume ratio. K_HRP however was insensitive to the concentration of HRP over the range tested (4.5–45 nM). We assume K_HRP measured at 4.5 nM HRP is valid at 0.45 nM, the concentration used in Figure 2, which was below our quantification limits for K_HRP determination.

Due to the known salting out behavior in these systems as discussed above, confocal microscopy was used to determine if any aggregation of protein at the interface could be observed. Fluorescently labeled enzymes were added at 21 and 45 nM of GOX and HRP, respectively (10× GOX, and 10× or 100× used for HRP as compared to the assays). The sample was vortexed and quickly placed on a coverslip for imaging (Supporting Figure 3, Supporting Information). The observed partitioning of the enzymes was consistent with the bulk partitioning measurements and no obvious aggregation or precipitation to the interface was observed, although any multimeric complexes that remained in suspension may be too small to be seen. Ideally, we would have measured resorufin production via confocal microscopy as well; however, laser illumination has been shown to induce resorufin production in the presence of HRP, even without the peroxide substrate.⁴⁸ Unfortunately, the rate of this undesirable reaction was too rapid to be ignored in our system (Supporting Figure 4, Supporting Information); hence, we were unable to experimentally observe the spatial distribution of resorufin production at the microscale.

Enzyme Assays in the ATPS

We used the same conditions as the individual phases; continuously mixing the system induced the formation of phase droplets, increasing the surface area for exchange of enzymes and substrates between the phases. The rate of formation of resorufin was significantly different among the volume ratios with the trend (PEG-rich:citrate-rich) 4:1 < 1:1 < 1:4 (Figure 3). Interpretation of these data is nontrivial due to the differences in reaction rates in the two media, the partitioning of small molecules and enzymes, and the variation in enzyme partitioning with volume ratio. In an effort to better understand the reactions in ATPS, we also conducted assays in which the enzymes and substrates were partitioned, but there was no interface available. This was achieved by adding all of the reaction components and physically separating the two phases, thereby allowing the reactions to proceed with mixing in separate containers. We observed that, for all of the prepartitioned phase controls, resorufin was produced quickly in the citrate-rich phase and leveled off at the prepartitioned amount of Amplex Red that was in that phase. The PEG-rich phase controls proceeded linearly throughout at each ratio at a much slower rate (Figure 3).

Figure 3.

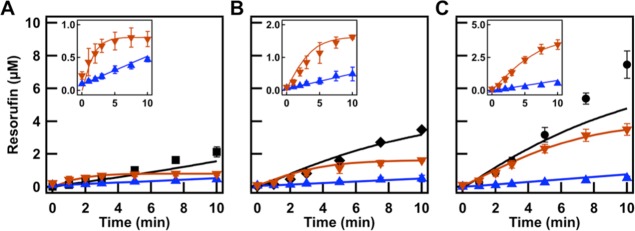
PEG:citrate volume ratios (A) 4:1, (B) 1:1, and (C) 1:4. The assay conditions were 2.1 nM GOX, 0.45 nM HRP, 1 mM glucose, and 50 μM Amplex Red. The points represent the experimental data. Black traces represent the model predictions to experimental ATPS volume ratios. Model parameters are obtained from prepartitioned assays in separated PEG-rich phase (blue triangles) and citrate-rich phase (inverted orange triangles) and single phase control assays (Figure 1). Insets highlight the phase-separated controls.

Mathematical Modeling

To describe the reaction within the two-phase system, we developed a mathematical model to describe the species concentration as a function of space and time that took into account the partitioning coefficients of the species as well as the reaction rates in each phase.

Computational Domain

We assumed the ATPS consisted of droplets of the first phase (the one in the least amount) in a second phase medium. Thus, on the basis of the PEG:citrate volume ratio, the droplets created contained either a PEG-rich phase or a citrate-rich phase surrounded by the opposite media. In the case of 1:1 ratio, we performed simulations for both PEG and citrate droplets; there was no significant difference in the simulation predictions. Assuming that the droplets are distributed uniformly within the solution, we limited our attention to the interactions between one droplet and its immediate surroundings, including other droplets (shown in Figure 4A). Taking advantage of the symmetry of the problem to further reduce the computational demands, one-eighth of the domain was simulated in COMSOL shown in Figure 4B. The droplets were approximated as spheres of radius R = 50 μm, based on the approximate droplet sizes imaged right after mixing, before extensive coalescence. The edge length of the cube, d, was calculated on the basis of the volume ratio of the phases.

Figure 4.

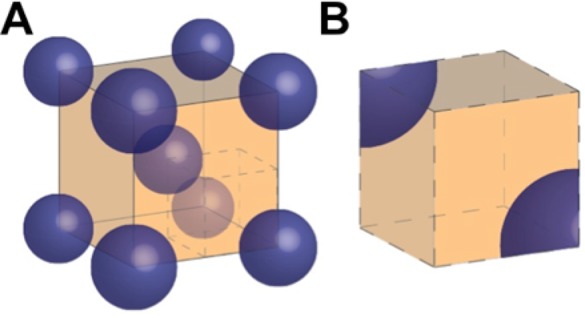
Illustration of the geometry used in modeling. (A) For a 1:4 PEG:citrate volume ratio, PEG-rich phase droplets (blue) are within the continuous citrate-rich phase (orange). (B) The computational domain of the mathematical model is a subsection of part A.

Mass Conservation Equations

Modeling the mentioned two-phase system involved the coupling of two phenomena, i.e., mass diffusion and chemical reaction. Under the assumption that the diffusion coefficients are constant and that convective phenomena can be neglected for the considered simulation volume (i.e., the velocity variation of the fluid within the computational domain is negligible), the material conservation equations obtain the following partial differential equation (PDE) expression:

1

Here, i denotes the species, i.e., i = {g, p, a, r} which represents glucose, peroxide, Amplex Red, and resorufin, respectively; j = {P, C} denotes the corresponding PEG-rich or citrate-rich phase, respectively; and c_i,j and D_i,j are the corresponding concentration and diffusion coefficient of species i in phase j, respectively. The diffusion coefficients were calculated from the Stokes–Einstein equation, using the viscosities of the phases listed in Supporting Table 1 (Supporting Information). The net rate of the reactions that involve species i in phase j are represented by r_i,j. To derive expressions that are consistent with the geometry and the boundary conditions of the problem, we employed spherical coordinates within the droplet domain and Cartesian coordinates within the surrounding cubic domain. The Laplace operator (of appropriate form depending on the coordinate system) is denoted by ∇². For each species i, at the interface between the two phases of the droplet, the fluxes are continuous (interfacial mass conservation), and concentrations are related by the partitioning coefficient, K_i (interfacial chemical potential equilibrium), presenting us with the boundary conditions:

2

where ∇ denotes the gradient operator of appropriate form depending on the coordinate system. In case one species is consumed or produced in one phase, these boundary conditions by transporting mass from one phase to the other guarantee that the partitioning condition is still satisfied and the species is always in a thermodynamic equilibrium at the interface.

Also, due to the symmetric nature of the model, periodic boundary conditions are applied at opposite faces of the cube.

3

where a and b denote two opposite faces of the cube and F_i,j|_l = −D_i,j∇c_i,j|_l represents the inward flux to the phase j of the i component at face l. To solve the presented system, the reaction expressions need be identified.

Reaction Rate Expressions

We assume oxygen is in excess in the considered experiments; therefore, the GOX reaction can be modeled by the Michaelis–Menten equation. However, in the second reaction, two substrates both influence the reaction rate. Consequently, the describing reaction rate requires a more complex expression. In this work, the Dalziel expression was utilized to model this enzymatic reaction rate.^49,50 Note that the species are sufficiently dilute that we may assume the product inhibitory effect is insignificant⁵¹ and we experimentally observed no rate decrease throughout the reaction.

The rate of glucose consumption is equal to the peroxide production rate, and it is dependent only on glucose and GOX concentrations. On the other hand, peroxide and Amplex Red are consumed in the second reaction and produce resorufin at the same rate. As a result, the net production rate of the various species for both phases can be expressed in the following form:

4

5

6

7

The parameters k_cat,2,j, k_12,j, k_2,j, k_1,j, and k_0,j in Dalziel’s expression were unknown. Therefore, the experimental data of the prepartitioned phase controls and the nonpartitioned controls in the PEG-rich phase and the citrate-rich phase, described earlier, were used to calculate the Dalziel parameters for HRP (Supporting Table 2, Supporting Information).

To identify the unknown parameters, a least-squares problem was formulated. To simplify the problem at hand, we assumed that the enzyme activities are constant during the experiment. Moreover, since during the control experiments the samples were being mixed, we assumed the concentration of all species in each phase is uniform (well mixed system assumption). Therefore, the original governing material conservation equations of eq 1 simplified to a system of ordinary differential equations (ODEs) for the control experiments

8

where c_n,j represents a vector of all the species concentrations at phase j, respectively. Note that the ordinary differential equation system was employed only to calculate the reaction rate constants for the control experiments.

PDE Model

As expressed in eqs 1–3, the species concentrations versus time are obtained through the solution of a system of partial differential equations. To aid the stability of the simulation, it is convenient to nondimensionalize the equations:

9

10

11

12

13

The dimensionless parameters are defined in Table 3. Furthermore, c_g,0 is the initial glucose concentration, and is equal to 1 mM in all experiments. The time length of the experiments is denoted by τ and is 10 min. The partial differential equation model was used to obtain species concentrations for the ATPS and draw conclusions.

Table 3. Definitions of the Dimensionless Parameters Used in eqs 9–13.

dimensionless parameter	definition
Ci	ci/cg,0
T	t/τ
αi	Diτ/d2
β	kcat,1cGOXτ
γ	km/cg,0
ϕ0	kcat,2cHRPτ/k0
ϕ12	k12/cg,02k0
ϕ2	k2/cg,0k0
ϕ1	k1/cg,0k0

Simulation Results

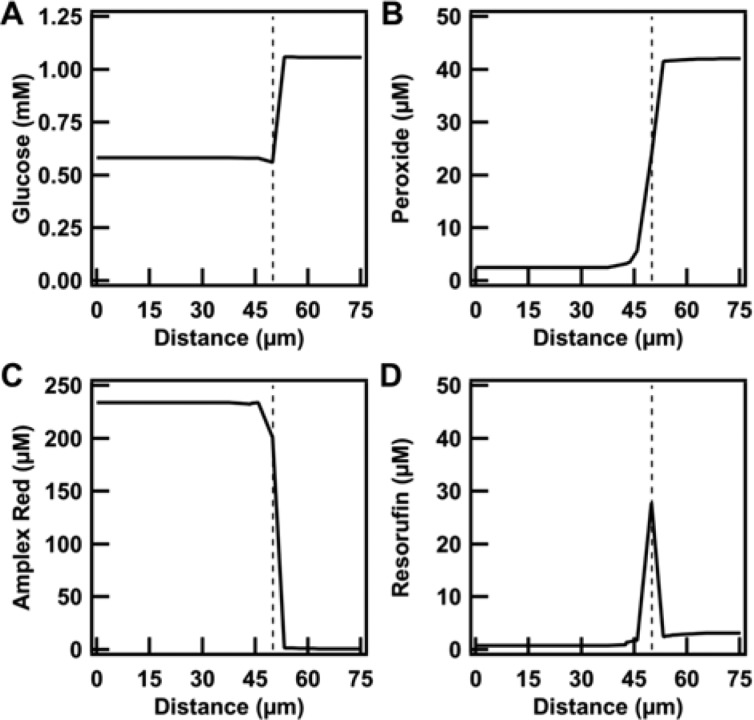
Upon computing the reaction parameters, we employed the PDE model of eqs 9–13 to simulate the system (using COMSOL). In Figure 5, we present the spatial distribution of the reactant and product species at a time of 10 min for the 1:4 volume ratio case. We observe that the three reactant concentrations are relatively uniform in each phase. That would allow us to consider a well-mixed system assumption for each phase, simplifying the model description to the ODE form of eq S.1 (see Supporting Discussion 1, Supporting Information). Mathematically, a possible explanation is that the α_i parameters in eq 9 are large enough compared to the other terms’ coefficients and hence the concentration gradients are approximately zero. Note that the resorufin concentration varies significantly as a function of space; however, as it does not enter the reaction rate expressions and we only employ the total amount of resorufin produced when calculating the reaction rate constants, it does not affect the least-squares solution accuracy. This observation remained valid for the other investigated cases also (i.e., different volume ratios, drop sizes, and diffusivity) (Supporting Figures 5–8, Supporting Information). That simplification would however cause some minor errors in prediction, which would become pronounced when the reactions become faster at higher enzyme concentrations (Supporting Figure 9, Supporting Information). To prevent the onset of such prediction errors, we proceeded with the PDE model predictions.

Figure 5.

Concentration profiles of all species in a 1:4 PEG:citrate volume ratio, depicted from the center of a phase droplet outward at the end of the assay. (A) Glucose, (B) peroxide, (C) Amplex Red, and (D) resorufin show that there is a uniform distribution within each phase. The dotted line represents the 50 μm radius of the phase droplet.

Looking back at Figure 3, we can compare the experimental data points with the solid lines from the performed simulations in the ATPS at three different volume ratios that represent the model of eqs 9–13 prediction using optimized parameters. The reaction dynamics were obtained on the basis of Figure 2 and the individual phases of Figure 3. Despite the complexity of the experimental system due to partitioning and different media effects in the PEG-rich and citrate-rich phases, we observed good agreement between the predictions and the experiment in ATPS for volume ratios 4:1 and 1:1. At a volume ratio of 1:4, where the citrate-rich phase is largest, the model somewhat underpredicts the experimental data. The nonpartitioned citrate-rich phase control is not as well fit by the model as the nonpartitioned PEG-rich phase (Supporting Figure 10, Supporting Information). This suggests additional effects in the citrate-rich phase that differ between the citrate-rich phase control and the prepartitioned citrate-rich controls, and may also be responsible for the underprediction of resorufin production in the 1:4 ATPS (Figure 3). Changes in enzyme specific activity with enzyme concentration due to the high salt of this phase is a possible explanation;⁴⁶ any salting-out effects (e.g., changes in hydration leading to possible conformational changes or multimerization) are expected to be less apparent at lower protein concentrations. The citrate-rich phase control had a lower enzyme concentration than the corresponding phase of the ATPS samples or prepartitioned controls. Nonetheless, the PDE model predicts the ATPS reaction well, especially for systems in which the citrate-rich phase is of equal or smaller volume as compared to the PEG-rich phase.

Model Predictions at Different Enzyme Concentration

Initially, we optimized the kinetic reaction parameters from single-phase assay control experiments in which, since they were uniform, diffusion phenomena could be neglected. We then employed the governing mass conservation equations of eqs 9–13 to describe the ATPS. In order to ensure the mathematical model properly captured the importance of enzyme and substrate spatial localization, we conducted the assay under the same conditions as previously described except that a 10× higher concentration of HRP was used (0.05 U/mL).

Initially, predictions for each of the prepartitioned individual phases at the three volume ratios were carried out employing the ODE model of eq 8 (Figure 6; insets). Additionally, the nonpartitioned controls were conducted (Supporting Figure 11, Supporting Information) and compared to the ODE model predictions. We found that, for the nonpartitioned controls, the ODE mathematical model of eq 8 overpredicts the resorufin formation in the citrate-rich phase. This is a larger effect than that seen at the lower enzyme concentrations (Supporting Figure 10, Supporting Information), and as discussed above may have been the result of some enzyme activity loss due to salting-out effects described by Huddleston et al. and others.^45,46,52 For the prepartitioned PEG-rich phase separated reactions, the ODE model of eq 8 showed good agreement, except for the 1:1 PEG-rich phase which we attribute to experimental error; this particular set of samples had greater variability than the others, most likely caused by errors in separating the two phases from each other.

Figure 6.

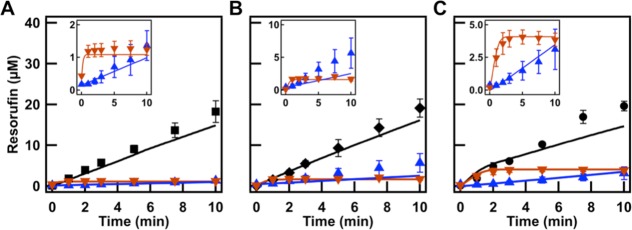
PEG:citrate volume ratios (A) 4:1, (B) 1:1, and (C) 1:4 with 10× more HRP. Model predictions were applied to experimental ATPS volume ratios (black traces) and prepartitioned assays in separated PEG-rich phase (blue triangles) and citrate-rich phase (orange triangles). Insets highlight the phase-separated controls.

For the ATPS reactions, we see good agreement at the 4:1 and 1:1 volume ratios and a small underprediction by the PDE model of eq 9 for the 1:4 case. The significance of diffusion can be illustrated here, since if we employ the ODE model of eq S.1 predictions (assuming well-mixed individual phases and instantaneous interfacial transport; Supporting Discussion 1, Supporting Information), we see good agreement at the 4:1 volume ratio, a small overprediction by the model at 1:1, and a large overprediction for the 1:4 case (Supporting Figure 9, Supporting Information). The PDE model of eq 9 can thus be reasonably expected to predict the activity if the enzyme concentration changes, but if the partitioning coefficient or enzyme activity were to change unexpectedly, then the model would not be able to predict the reaction kinetics without further information (i.e., the new K_enzymes and activities). The behavior of the system at other volume ratios may also be directly predicted, but the accuracy of the predictions will similarly depend on the accuracy of the enzyme partitioning coefficients and activities, which for these complex systems cannot always be extended to new conditions without experimental verification.

The Role of Diffusion and Interface

To further understand the role of the interface and the diffusion in the system, we assayed the enzymes in a cuvette in the bulk where the reaction was unmixed (Figure 7). We observed resorufin formation in the citrate-rich phase as early as 1.5 min. After 10 min, we saw the pink product resorufin was being formed at the interface. Over the next several minutes, the interface remained bright pink as the resorufin diffused throughout the PEG-rich phase. At 180 min, the PEG-rich phase was nearly uniformly pink. These results showed that, because the substrate was strongly partitioned to the PEG-rich phase, diffusion across the interface was critical for product formation. These observations were consistent with the concentration profile data in Figure 5, where the resorufin concentration shows significant variations in space, especially at the interface. The accumulation of resorufin in the PEG-rich phase was due to partitioning, although it was preferentially produced in the citrate phase due to the higher concentration of the enzymes there, and hence initial resorufin concentrations were highest in the interfacial region.

Figure 7.

A 1:1 PEG:citrate volume ratio assay was conducted in a cuvette without mixing. The production of resorufin is clearly visible at the interface of the phases. Eventually, resorufin was homogeneously distributed in the PEG-rich phase.

Additionally, we ran the volume ratio assays without mixing and quantified the amount of resorufin formed. The enzymes and substrates were added to an ATPS and briefly vortexed to make a homogeneously mixed sample, and the reaction was immediately aliquoted into individual containers and centrifuged to reform the distinct phase-separated system. Interfacial area was therefore substantially decreased in this assay as compared to the mixed sample that produced small phase droplets. We found there was a significant decrease in the concentration of resorufin formed at 10 min for all of the volume ratios at 0.05 U/mL of both enzymes (Supporting Figure 12, Supporting Information). The largest difference was for the 4:1 ratio, where only 2.9 ± 0.5 μM resorufin was made at 10 min compared to 18.2 ± 2.6 μM for the mixed assays. During the volume ratio assays that were continuously mixed, there was sufficient interfacial area for the substrate to diffuse across the interface to permit product formation and we observed increased resorufin production. This suggested that the interfacial area and ability of the substrates, particularly Amplex Red, to diffuse into the citrate-rich phase where the majority of the enzymes were localized was necessary for maximal resorufin production.

The effect of diffusivity and partitioning coefficient in the behavior of the system would be even more pronounced if resorufin was a reaction intermediate due to its predicted and observed formation primarily at the interface. In the present work, we employed a mathematical model to observe the spatiotemporal profile of species (Figure 5, Supporting Figures 5–8, Supporting Information). It is important to consider interfacial phenomena especially when the production of a species happens at a compartment where the species has low solubility and much higher solubility in a different compartment in contact with it. This phenomenon becomes especially important when this happens to a reaction intermediate. For the rest of the species, the effect of interfacial diffusion is significantly less pronounced than that for resorufin.

Conclusion

We described a sequential reaction within heterogeneous biphasic media consisting of two distinct phases with very different chemical and physical properties. A well-studied sequential enzyme pair was used to investigate complex cellular metabolism where local concentrations of metabolites are ever-changing due to partitioning within the biphasic system. Even with the complex behavior of the system, a mathematical model was developed that could reasonably approximate the sequential reaction at a different enzyme concentration using enzyme and substrate partitioning coefficients in addition to the rates in individual phases. To design this mathematical model, we needed to know the corresponding reaction rate parameters. The GOX reaction parameters were obtained experimentally using Michaelis–Menten expressions; however, the HRP rate reaction did not follow Michaelis–Menten kinetics. As a result, we first optimized the unknown Dalziel parameters using the least-squares method to find the best fitting curve which describes the total average resorufin concentration in time. We then validated the model by predicting produced resorufin in an ATPS in different volume ratios. Finally, we showed the obtained parameters could even be employed to predict the product concentration in a higher level of HRP concentration.

This general combined experimental and computational approach should be applicable to other synthetic or biological phase separated media, where local environments differ in enzyme concentrations or activities, physical properties such as viscosity, ionic strength, or crowding effects, and partitioning of reaction substrates, intermediates, and products. Although the rate behavior will vary with the specific system under evaluation, by knowing the reaction parameters in each phase, product formation in the complex media can be predicted. This work complements studies in the literature that have focused on the effects of macromolecular crowding in terms of excluded volume and chemical attractive/repulsive effects. The findings are also relevant for biotechnological applications, where PEG/salt ATPS are used primarily to increase an enzymatic product yield. Careful understanding of enzyme rates in addition to enzyme and substrate partitioning coefficients in those cases may lead to a more efficient output.

Experimental Section

Materials

Poly(ethylene glycol) 8 kDa, sodium citrate tribasic dihydrate, d-(+)-glucose, 30% hydrogen peroxide solution, o-dianisidine hydrochloride tablets, glucose oxidase from Aspergillus niger type X-S, sodium phosphate dibasic dihydrate, sodium phosphate monobasic dihydrate, and Amicon 0.5 mL filters (MWCO 3000) were purchased from Sigma-Aldrich (St. Louis, MO). Horseradish peroxidase EIA grade, Amplex Red reagent, Amplex Red/Amplex Ultra Red Stop Reagent, Alexa Fluor 488, Alexa Fluor 546, and Alexa Fluor 647 labeling kits, and 13 mm SecureSeal Spacers were purchased from Life Technologies (Carlsbad, CA). mPEG-NH2 MW 5000 was purchased from Shearwater Polymers. Dimethylsulfoxide was purchased from Alfa Aesar. Ethelynediaminetetraacetic acid (EDTA) was purchased from IBI Scientific (Peosta, IA). Deionized water with a resistivity of 18.2 MΩ·cm from a Barnstead NANOpure Diamond water purification system (Van Nuys, CA) was used for all experiments. Buffers were filtered using 0.45 μm pore size Nalgene filter units. All reagents were used as received without further purification.

Instrumentation

Fluorescently labeled enzyme concentrations and resorufin concentrations were measured using a Horiba Jobin Yvon Fluorolog 3-21 fluorimeter with FluorEssence software. The citrate composition of the ATPS and glucose partitioning within the ATPS were determined using an Agilent 1260 HPLC system with a 1260 Infinity Quaternary Pump, 1260 Infinity Thermostatted Column Compartment, 1260 Infinity Diode Array Detector, a 1260 Infinity Manual Injector, and Agilent ChemStation software. The GOX activity and degree of enzyme labeling were determined using an Agilent 8453 diode-array UV–visible spectrometer with Agilent ChemStation Software. Confocal images were acquired using a Leica TCS SP5 laser scanning confocal inverted microscope (LSCM) with a 20× air objective. Refractive index measurements of the aqueous two-phase system were made using a Leica Abbe Auto Refractometer. Viscosity measurements were made using an Ostwald viscometer.

ATPS Preparation

A phase diagram was created to determine which weight percents of PEG and citrate would form an ATPS. Several citrate weight percents were chosen, and the weight percent of PEG was varied close to the expected weight percents that would cause phase separation. Samples were vortexed, and phase separation was observed when a turbid solution formed, indicating phase separation. A 50.00 g ATPS was prepared by addition of 6.67 g of PEG 8 kDa and 5.00 g of sodium citrate tribasic dihydrate in 38.33 g of 50 mM sodium phosphate buffer pH 7.4 with 1 mM EDTA. EDTA was added to complex any trace metal ions present from the sodium citrate. After the PEG and citrate had dissolved, it was added to a separatory funnel and allowed to phase separate overnight. At these weight percents, the ATPS as prepared was approximately a 1:1 PEG-rich phase:citrate-rich phase. After separation, each phase was collected in separate containers so that they could be recombined at the desired volume ratios (PEG-rich:citrate-rich, 1:4, 1:1, 4:1).

Phase Composition Determination

The composition of each phase was determined using a combination of refractometry and HPLC. The weight percent of citrate in each phase was determined by HPLC using standards of known weight percents of citrate. The citrate was isocratically separated at 0.3 mL/min with 0.013 N H₂SO₄ as a mobile phase on an Aminex HPX 87H cation exchange column (300 × 7.8 mm i.d.) with a Micro-Guard IG Cation H precolumn from Bio-Rad at 25 °C for 35 min, using an analysis wavelength of 210 nm.⁵³ The weight percent of PEG 8 kDa was determined through refractometry. The refractive index of each phase was measured. Calibration curves of known weight percents of PEG 8 kDa and citrate were created. Due to the additive nature of refractive indices, the known contribution of citrate was subtracted from the refractive index of each phase. The remaining refractive index contribution was attributed to PEG.

Protein Labeling

Glucose oxidase and horseradish peroxidase were labeled according to the manufacturer’s instructions with Alexa Fluor 488 and Alexa Fluor 546, respectively. mPEG-NH2 MW 5000 was labeled with Alexa Fluor 647. Free dye was removed from the labeled polymer using an Amicon 3000 MWCO filter.

Partitioning

Fluorescently labeled GOX and HRP were measured by fluorimetry. The enzymes were added at a final concentration of 0.05, 0.25, or 0.5 U/mL each in a total volume of 1050 μL (1000 μL of each volume ratio and 50 μL of enzymes in buffer.) The enzymes were briefly vortexed and settled for 1 h and centrifuged to reform the distinct phases. An aliquot from each phase was taken, and the fluorescence was measured. The concentration of enzyme in each phase was determined using calibration curves of a known amount of enzyme in each phase. Resorufin partitioning was measured by fluorimetry. Resorufin was added to a 1:1 ATPS (500 μL of PEG-rich phase, 500 μL of citrate-rich phase, 50 μL of buffer/sample), and after mixing, the samples were centrifuged to form distinct phases. Amplex Red partitioning was determined by addition of Amplex Red to a 1:1 ATPS at a final concentration of 50 μM. The solution was vortexed and phase separated by centrifugation. An aliquot from each phase was taken and placed in separate centrifuge tubes. A small excess of hydrogen peroxide was added with 0.5 U/mL of HRP in order to convert all of the Amplex Red to resorufin. The reaction proceeded to completion, and the resorufin fluorescence was measured in each phase. A similar approach was used to measure the hydrogen peroxide concentration in each phase using excess Amplex Red. Glucose partitioning was measured by HPLC. Glucose was partitioned in a 1:1 ATPS, and samples were mixed by inversion for 10 min and phase separated by centrifugation. An aliquot from each phase was diluted 10× before injection on the HPLC. The phase samples were isocratically separated at 0.2 mL/min with a mobile phase of 0.005 N H₃PO₄ on an Aminex HPX 87H cation exchange column (300 × 7.8 mm i.d.) with a Micro-Guard IG Cation H precolumn from Bio-Rad at 80 °C for 35 min at an analysis wavelength of 190 nm.^54,55

Enzyme Assays. Michaelis–Menten Parameters in Individual Phases

All enzyme assays were repeated three times. GOX was assayed using a modified procedure provided by Sigma-Aldrich.⁵⁶ The enzyme activity was measured in each phase individually at a final concentration of 0.05 U/mL of glucose oxidase, 0.160 mM o-dianiside dihydrochloride, and 6 U/mL of HRP while varying the glucose concentration from 0 to 75 mM. The activity was measured for 3 min, and an extinction coefficient of oxidized o-dianisidine (7.5 mM^–1 cm^–1) at 500 nm was used to calculate the product formation. The standard Michaelis–Menten equation (eq 14) was used to fit the data in order to determine K_M and V_max using Igor CarbonPro nonlinear regression analysis. For HRP in the citrate-rich phase, a concentration of 0.0005 U/mL was used. To determine the V_max and K_M of HRP with respect to peroxide, the peroxide concentration was varied from 0 to 300 μM, while the Amplex Red concentration was fixed at 400 μM. Exposure to light was avoided for all Amplex Red assays due to the known photo-oxidation of Amplex Red to resorufin.⁴⁸ The K_M with respect to Amplex Red was determined by varying the Amplex Red concentration from 0 to 500 μM, while hydrogen peroxide was fixed at 1 mM. For HRP in the PEG-rich phase, a concentration of 0.005 U/mL was used. Hydrogen peroxide was varied from 0 to 400 μM with a fixed concentration of Amplex Red at 400 μM. All reactions proceeded for 5 min. Time points were taken by removing an aliquot during the assay. The reaction was stopped with Amplex Red Stop Reagent, and the concentration of resorufin was measured at each point. The activity was calculated by the slope of the resulting linear plot of concentration vs time.

14

Enzyme Assays. Single-Phase Controls

The single-phase controls consisted of 0.05 U/mL GOX and 0.05 or 0.005 U/mL HRP. The final concentrations of substrates were 1 mM glucose and 50 μM Amplex Red using 1 mL of either PEG-rich or citrate-rich phase in addition to the 50 μL of enzymes, substrates, and buffer. For comparison, the assay was conducted in buffer and a control was done in buffer without the addition of glucose to ensure Amplex Red was not being converted to resorufin due to its known oxidation by light.⁴⁸

Mixed Volume Ratios

The ATPS samples were prepared by addition of the appropriate amounts of each phase to reach a final concentration of 1 mL (e.g., a 1:4 PEG:citrate volume ratio would contain 200 μL of PEG-rich phase and 800 μL of citrate-rich phase). The final concentrations were 0.05 U/mL GOX, 0.05 or 0.005 U/mL HRP, 1 mM glucose, and 50 μM Amplex Red. The volume of added enzymes, substrates, and excess buffer was maintained at 50 μL throughout all assays to ensure only minor dilution of the ATPS. The enzymes and the Amplex Red were vortexed to uniformly mix the sample. A 100 μL aliquot was taken to serve as the zero time point and added to 200 μL of Amplex Red Stop Reagent. The reaction was then initiated with addition of glucose, vortexed again, and placed on a rotisserie that mixed at ∼18 rpm. For each time point (1, 2, 3, 5, 7.5, 10 min), a homogeneous 100 μL aliquot was removed from the reaction and immediately added to 200 μL of stop reagent. This not only stopped the HRP reaction but also diluted the sample to one phase so the resorufin concentration could be measured by fluorimetry.

Physically Separated Phases

Prepartitioned phase separated control samples were prepared by adding enzymes and Amplex Red to the experimental volume ratios. After vortexing, the sample was centrifuged and the distinct phases were reformed. The phases were physically separated and transferred to separate reaction containers. To initiate the reaction, the calculated partitioned amount of glucose was added to each phase. Aliquots were taken at the necessary time points and were diluted with Stop Reagent.

Unmixed Volume Ratios

Samples were prepared in the same manner as the volume ratio assays by addition of the enzymes and Amplex Red to each volume ratio. Glucose was added, but after vortexing, the samples were promptly aliquoted into individual containers and centrifuged to reform the two phases. Each aliquot was then stopped at the desired time point with 200 μL of Stop Reagent, and the resorufin concentration was measured. To visualize this further, a 1:1 volume ratio assay was transferred to a quartz cuvette. After initial sample preparation, the sample was vortexed and subsequently centrifuged to induce phase separation. The phases were separated and carefully reconstituted in the cuvette. Photographs were taken with a Kodak EasyShare camera to monitor product formation.

Confocal Microscopy

To visualize enzyme partitioning, images were collected on a Leica TCS SP5 confocal microscope with excitation at 488, 543, and 647 nm for Alexa Fluor 488, Alexa Fluor 546, and Alexa Fluor 647, respectively. GOX and HRP were added to the experimental volume ratios at a final concentration of 0.5 U/mL. Samples were thoroughly vortexed prior to imaging.

Simulation Method

To simulate the developed model with partial differential equations as governing equations, we used COMSOL 4.3a. The maximum element size of the created mesh in the simulation was 0.05. Additionally, the dimensionless time element during the study was set to 10^–2. In order to address the concentration discontinuity present at the interface, we employed a change of variables to have continuous values in the equations. Then, we related the corresponding local concentrations of each phase through using eq 2.

The rest of the computations that are discussed in the Results and Discussion section were performed using MATLAB R2009. To find the unknown Dalziel’s parameters, the resorufin concentration was predicted in time in single-phase control consisting of 0.05 U/mL GOX and 0.005 U/mL HRP for both PEG and citrate. Then, using a genetic algorithm in MATLAB, the relative prediction error of the mathematical model for each phase using a least-squares error formulation was minimized.

Supporting Information Available

Physical properties of the ATPS, phase diagram of the PEG 8 kDa sodium citrate system, volume ratio scheme, partitioning coefficient as a function of enzyme concentration and volume ratio, confocal microscopy of fluorescently labeled enzymes, resorufin photooxdidation by confocal microscopy, definition of parameters used, optimized parameters for the prepartitioned and phase controls, concentration profiles of the substrates and products at a volume ratio of 1:1, at a volume ratio of 1:4 with 100× less diffusivity, and a volume ratio of 1:4 with 25 and 75 μm radius drop sizes, model fit to the PEG-rich and citrate-rich individual phase controls for 0.005 and 0.05 U/mL HRP, ODE and PDE predictions of ATPS volume ratio assays, and unmixed volume ratios. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^§ These authors contributed equally.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States