Coarse Grained Models Reveal Essential Contributions of Topological Constraints to the Conformational Free Energy of RNA Bulges

Abstract

Recent studies have shown that simple stereochemical constraints encoded at the RNA secondary structure level significantly restrict the orientation of RNA helices across two-way junctions and yield physically reasonable distributions of RNA 3D conformations. Here we develop a new coarse-grain model, TOPRNA, that is optimized for exploring detailed aspects of these topological constraints in complex RNA systems. Unlike prior models, TOPRNA effectively treats RNAs as collections of semirigid helices linked by freely rotatable single strands, allowing us to isolate the effects of secondary structure connectivity and sterics on 3D structure. Simulations of bulge junctions show that TOPRNA captures new aspects of topological constraints, including variations arising from deviations in local A-form structure, translational displacements of the helices, and stereochemical constraints imposed by bulge-linker nucleotides. Notably, these aspects of topological constraints define free energy landscapes that coincide with the distribution of bulge conformations in the PDB. Our simulations also quantitatively reproduce NMR RDC measurements made on HIV-1 TAR at low salt concentrations, although not for different TAR mutants or at high salt concentrations. Our results confirm that topological constraints are an important determinant of bulge conformation and dynamics and demonstrate the utility of TOPRNA for studying the topological constraints of complex RNAs.

Introduction

The function of many RNA molecules is predicated on an ability to robustly fold into precise 3D structures and undergo specific structural dynamics.^1,2 Understanding the behavior of RNA requires insights into the forces that shape its free energy landscape. Decades of research have revealed that the RNA free energy landscape is largely hierarchical, with the forces that determine secondary structure being much stronger than those stabilizing 3D structure, and with folding of secondary structure typically preceding tertiary folding.^3,4 While not all RNAs strictly follow this hierarchical model,⁵⁻⁷ its general validity indicates that much of 3D folding and dynamics is dictated by the forces that govern the conformation of prefolded helices.

Interhelical junctions are central to understanding helical conformation.⁸⁻¹⁰ These motifs, which are defined as regions of single-stranded or noncanonical base pairs that link two or more Watson–Crick (WC) paired helices, govern the orientations of their flanking helices. Given that the local structure of WC-paired helices has nearly uniform A-form structure,¹¹ junctions serve as the primary point of variability in global 3D structure.^2,12 Functional transitions also often involve specific changes in the orientations of helices about junctions.² Bioinformatics and knowledge-based computational studies have made advances in predicting junction conformation and by extension RNA 3D structure,¹³⁻¹⁷ and both computational and experimental approaches have demonstrated the existence of functional relationships between secondary and 3D structure.¹⁸⁻²² However, despite these findings, a comprehensive understanding of the forces driving junction conformation and dynamics has remained elusive.

Junctions are governed by a complex interplay of forces, including attractive interactions such as stacking between helices and pairing and stacking of the junction-comprising nucleotides, and repulsive forces such as electrostatics.^{18,21,23−27} Long-range tertiary interactions and proteins can also play an important role in stabilizing specific junction conformations.¹⁰ In addition to these forces, basic polymer physics dictates that the simple steric and connectivity properties of polymer chains should also give rise to forces that affect molecular conformation.²⁸ It follows that RNA junctions should be similarly influenced by their connectivity and excluded volume properties. However, in part because these forces are difficult to isolate experimentally, this aspect of the RNA free energy landscape has been much less explored.

Recently, work by us^12,29 and Herschlag and colleagues³⁰ has provided new insights into the significance of connectivity and sterics in RNA junctions. Using simple heuristic models, we demonstrated that the relative orientation of helices connected by two-way junctions is strongly limited by basic chemical connectivity and steric constraints (together termed topological constraints) to <5–40% of the theoretical possiblities.^12,29 Here, small changes in the number of single-stranded nucleotides in the junction significantly alter the number of accessible conformations. Similarly, in their studies of helices linked by polyethylene glycol tethers, Herschlag and colleagues³⁰ demonstrated that the global conformation of two-way junction mimics is strongly modulated by the topology of the tethering. Together, these studies suggest that topological constraints account for the distribution of two-way junction conformations observed in the PDB,^12,29 explain aspects of junction dynamics,^12,29 and potentially influence the stability of RNA tertiary interactions.³⁰

While these studies highlight the importance of topological constraints in defining RNA structure, their role in more complex and biologically relevant RNAs has yet to be investigated. Many computational tools have been developed that can be potentially used for such studies. All-atom molecular dynamics methods,^31,32 and hybrid methods thereof,^33,34 offer the highest degree of physical accuracy but are difficult to scale to large systems due to computational expense. By contrast, our previous heuristic models are highly efficient but rely on approximations that make it impractical to extend them to systems containing higher-order junctions.^12,29 Specifically, we assumed that interhelical motions were limited to pivoted rigid-body rotations and modeled junction-linking single-stranded nucleotides using a simple distance constraint that ignores sterics and stereochemistry. Coarse-grained (CG) molecular dynamics methods represent a good compromise between these two extremes.³⁵ Existing CG approaches include the NAST³³ and YUP³⁶ models, which use one pseudoatom to represent each nucleotide; the three pseudoatom models of Thirumalai and co-workers,^37,38 Dokhoylan and co-workers,^39,40 and Chen and co-workers;¹⁷ the five pseudoatom models of Levitt and co-workers⁴¹ and Ren and co-workers;⁴² and the six to seven pseudoatom HiRE-RNA⁴³ model. However, none of these CG models are ideally suited to study topological constraints. Notably, one pseudoatom models cannot fully capture the stereochemical constraints of the RNA backbone. Higher resolution CG models generally allow breaking of secondary structure pairs and include the full suite of RNA forces; while more realistic, these complexities can make it difficult to isolate effects of topological constraints which are dependent only on secondary structure. Moreover, many of these CG models are implemented as specialty codes, which presents development challenges.

In this work, we introduce a new CG model, TOPRNA (TOPological modeling of RNA), that is implemented in CHARMM.⁴⁴ TOPRNA uses a three pseudoatom per nucleotide representation similar to that used in preexisting CG models^17,37,39,45 but otherwise differs in that its sole design purpose is to isolate the effects of topological constraints on RNA structure. Nucleotides participating in canonical base pairs are permanently bonded together and parametrized to maintain helical structures, but all other nucleotides are treated as freely rotatable chains. In addition, attractive interactions involving single-stranded nucleotides and all electrostatics are ignored. Thus, biases from non-topological-constraint energy terms are minimized and only negligible energy barriers separate alternative conformations. This approach is similar to that employed by the NAST³³ and YUP³⁶ models, though these models use one pseudoatom per nucleotide representations and are primarily optimized for structure prediction applications.

As a first application, we use TOPRNA to reevaluate the role of topological constraints in two-way junction bulge motifs. Through extensive simulations, we corroborate our prior findings while demonstrating that the greater physical accuracy of TOPRNA captures new aspects of the topological constraints on bulges. Significantly, we find that the topological constraints encode complex free energy landscapes that appear to play a central role in dictating the 3D conformation and dynamics of bulges. The methods we develop here are easily transferrable to other RNA systems and should facilitate future studies into the broader impact of topological constraints on RNA structure.

Materials and Methods

Model Development

TOPRNA uses three pseudoatoms to represent the phosphate (P), sugar (S), and base (B) moieties of each nucleotide (Figure 1).^17,37,39,45 The B pseudoatom was taken as a positional average of a base’s cyclic nitrogen and carbon atoms; the S pseudoatom as an average over the C1′, C2′, C3′, C4′, C5′, and O4′ atoms; and the P pseudoatom as the phosphorus atom. Given a user-input secondary structure, base-paired nucleotides are permanently bonded together and contiguously paired regions are parametrized to adopt A-form helical structure. By contrast, all nucleotides not in AU, GC, or GU pairs are left without backbone dihedral potentials and are freely rotatable (Figure 1B). Backbone dihedrals that link distinct helices are also freely rotatable (Figure 1B). All electrostatic interactions are ignored, and aside from a small attractive interaction only experienced between base-paired B pseudoatoms (see below), all attractive interactions such as stacking or hydrogen bonding of single-stranded nucleotides are ignored.

Figure 1.

Outline of the TOPRNA model. (A, B, C) A secondary structure element is shown according to its ladder cartoon, and in 2D and 3D TOPRNA representations. In part B, circular arrows denote freely rotatable bonds, thick solid lines with small open circles denote permanent base pair bonds with an accompanying “M” filler pseudoatom, and dashed lines denote improper dihedral angles used to maintain helical twist. (D) The adenine P_i–S_i bond potential is shown as a representative harmonic potential. Black and gray lines indicate the different potentials used for base-paired and single-stranded nucleotides, respectively, following the observation that these bonds exhibited strong and weak harmonic potential behavior at short and large deviations. Two different potentials were also used for angles involving this bond, but other bonds and angles were assigned the same K regardless of base-pairing status. (E) The S_i–P_i+1–S_i+1–P_i+2 dihedral potential placed between sequentially paired residues i and i + 1 is shown as a representative example. The dashed line indicates the original cosine series fit to the statistical potential, with the solid line indicating the final TOPRNA potential after the K’s obtained from the original fit were uniformly doubled. Statistical potentials were calculated by binning every 0.01 Å and 3.6° for bonds and dihedrals, respectively, with unpopulated bins excluded, and are shown using open circles in parts D and E.

We implemented TOPRNA in CHARMM⁴⁴ using the standard CHARMM potential

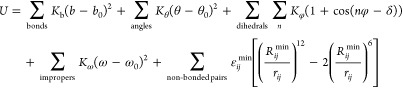1

Nucleic-acid-like geometry between pseudoatoms is maintained through the application of bond, angle, and S pseudoatom chiral center improper torsion potentials to each nucleotide. The helical conformation of base-paired nucleotides is maintained by dihedral potentials placed along the backbone and across the base-pair bond (Figure 1). Potential parameters were derived from fits to statistical potentials constructed through Boltzmann conversions at 300 K

2

where P_v(x) is the probability of a structural parameter v having a value of x (Figure 1). Basic connectivity and geometry parameters, as well as backbone dihedrals for base-paired nucleotides, were derived from fits to the RNA05 structural database.⁴⁶ Base-pairing specific parameters were derived from fits to a database comprising the 6677 four-base-pair continuous helices returned by an RNA FRABASE⁴⁷ search performed on May 28, 2010.

Backbone bond and angle potentials, b₀ and θ₀, were set as the RNA05 database mean values and K_b and K_θ were manually chosen to allow a range of motions consistent with that exhibited by the statistical potentials (Figure 1D). The P_i–S_i bond and angles involving this bond exhibited stiffer and weaker harmonic potential behavior at small and large deviations (Figure 1D). Given that the minimum of these potentials corresponded to helical conformations, we assigned the stiff potential to base-paired nucleotides postulating that they should be confined to values near the helical minimum. Conversely, we assigned the weaker harmonic to single-stranded nucleotides, allowing them to adopt the full range of conformations observed in the database. All other K of a given bond or angle type are invariant with respect to nucleotide-identity or base-pairing status. While b₀ and θ₀ were set on a nucleotide-specific basis, they vary by only < ∼0.6 Å and < ∼10°, respectively. The improper potential applied to the S pseudoatom chiral center was given parameters of ω₀ = 30° and K_ω = 3.5 kcal/mol/rad² for all nucleotide types.

Base pairs (AU, GC, and GU) were implemented by placing bond, angle, and dihedral potentials directly between paired B pseudoatoms. Bond and angle parameters were determined as above using our helix database. Dihedrals across the base-pair bond, of type S_i–B_i–B_j–S_j, were treated as n = 1 cosines, with K_φ and δ determined through fits to the statistical potentials using the Algorithm::CurveFit module of Perl; K_φ of all pairs were later increased to 5 kcal/mol to increase helical rigidity (see below). Dihedrals of type P_i–S_i–B_i–B_j were found to be harmonic, and parametrized as weak impropers (ω₀ set to the helical database means and K_ω = 0.5 kcal/mol/radian²).

The helical conformation of contiguous base pairs was enforced through backbone dihedral potentials of type B_i–S_i–P_i+1–S_i+1 and S_i–P_i+1–S_i+1–P_i+2 that were placed between base-paired nucleotides i and i + 1. An improper dihedral, indicated by the dashed lines in Figure 1B, is also placed between consecutive base pairs. As emphasized above, none of these potentials are applied to single-stranded nucleotides or to regions that serve as pivots between distinct helices (Figure 1). The ω₀ and K_ω of the impropers were derived from our helical database consistent with the procedure used for other harmonic potentials. The two backbone dihedrals were parametrized as four-term cosine series fit to RNA05-derived statistical potentials as above. S_i–P_i+1–S_i+1–P_i+2 potentials were treated as residue-type-independent and were derived from statistics combined from all RNA05 trinucleotide sequences (Figure 1E). K_φ was later uniformly doubled for all backbone potentials to increase helical rigidity (Figure 1E). The need for these increases, along with those of the K_φ of the base-pair bond dihedrals mentioned above, is likely due to two factors: cosine series cannot capture the full steepness of the A-form helix energy well, and for the backbone dihedrals, the statistical potentials were derived from a mix of both helical and nonhelical conformations, causing them to overestimate helical flexibility.

Electrostatics were eliminated by setting all charges to 0, and nonbonded van der Waals (VDW) interactions were only considered between pseudoatoms separated by four or more bonds. These interactions were truncated at 8 Å using a switching function turned on at 6 Å. VDW parameters were uniformly assigned with ε_ij^min = 0.01 kcal/mol, which effectively eliminates attractive VDW energies but also reduces the repulsive component of these potentials. Thus, R_i^min/2 (R_ij^min = R_i^min/2 + R_j^min/2) were obtained as the values that produced a repulsive energy of U_vdw ≈ 0.6 kcal/mol at radial distances approximating the shortest radial dimension of the chemical moiety being represented. For example, R_i^min/2 was set to 4.0 Å for P pseudoatoms, which produces a repulsive energy of U_vdw ≈ 0.6 kcal/mol at a radius of 2.7 Å. While this parametrization fairly approximates sugar and phosphate moieties, it does a poorer job of capturing the oblong steric profile of bases. For single-stranded nucleotides, this simply means that TOPRNA provides a lower bound approximation of the steric constraints on RNA. However, for paired nucleotides, this decreased steric profile results in an ∼2 Å steric gap between the paired B pseudoatoms that in rare cases allowed helices to interpenetrate one another. To prevent such behavior, we placed a fourth filler pseudoatom (termed M) in parallel to the base-pair bond of paired bases. M pseudoatoms were parametrized to be collinear with and at the midpoint of their respective B–B bonds, with K_b and K_θ set to values ∼10% of those used for the B–B bonds and angles, and with VDW radii approximating 1 Å. This parametrization ensures that M pseudoatoms minimally affect the dynamics of the base-pair bond, serving only to fill the steric gap.

As an exception to default nonbonded parameters, attractive VDW interactions were placed between the B pseudoatoms of base-paired nucleotides to simulate intrahelix stacking using the CHARMM NBFIX functionality. We reiterate that these interactions are not experienced by single-stranded nucleotides. For two helical B pseudoatoms of nucleotide types X and Y, ε_ij^min was set to the most negative of the ΔG₃₇° measured for either an unpaired X stacking 3′ to a paired Y or an unpaired Y stacking 3′ to a paired X.(48) These ε_ij^min ranged in value from −0.1 to −1.7 kcal/mol. R_ij^min was determined by computing the average 5′ → 3′ and 3′ → 5′ distances between the B pseudoatoms of stacked X and Y nucleotides from our helical database, choosing the minimum of these two values, and subtracting 0.15 Å (which was found to produce more A-form consistent helices). While these attractive interactions minimally affect interhelical stacking across a junction, on some rare occasions, two helices would form nonphysical interactions between their major grooves, mediated by extensive favorable B–B pseudoatom interactions. Selective increases in the R_ij^min of interactions between M atoms and the S and P pseudoatoms of base-paired nucleotides to effective radii of ∼5 and ∼6.5 Å, respectively, and increases of the R_ij^min between two M pseudoatoms to ∼3 Å, successfully prevented the formation of these conformations.

Dynamics simulations were performed by assigning pseudoatom masses as the sum of the represented moiety’s heavy atom masses and using the Langevin equation integrated with a 20 fs time step and 5 ps^–1 friction coefficient.

Benchmarking Simulations of TOPRNA Helical Parametrization

12-Nucleotide (nt) random sequence hairpins were constructed such that stem base pairs had a 20 and 80% probability of being a GU or WC pair, respectively. Initial coordinates were obtained by first initializing the sequences as linear single-stranded chains containing both 5′ and 3′ P pseudoatoms. A short simulation was then run in the presence of backbone dihedral and distance restraints that forced the stem nucleotides to adopt a helix-like conformation. This was followed by a removal of the restraints, addition of the base-pair bonds, M pseudoatoms, and other associated pairing potentials, and then minimization of the system. Simulations of HIV-1 and HIV-2 TAR molecules were initialized from coordinates built from the first member of the NMR-MD ensembles.⁴⁹ The A22·U40 base pair at the top of TAR helix 1, which is unstable in the NMR-MD ensemble, was excluded from later analyses. Both hairpin and TAR dynamics simulations were performed for 100 ns at 300 K, recording conformations every 200 ps.

The RMSD of the generated helices from idealized A-form structure was computed by aligning base-paired S and P pseudoatoms to a TOPRNA representation of an idealized A-form helix,⁵⁰ excluding the 5′-most P pseudoatom of each stem strand. The helical twist of TOPRNA base-pair steps was determined by adapting a previously developed all-atom procedure:⁵¹ for two sequential base pairs, i and i + 1, the rotation transform that brings the B and S pseudoatom coordinates of i into concordance with the B and S pseudoatoms of i + 1 was computed and related to the base-pair steps’ local parameters of twist (ω), bending (Γ), and bending phase-angle (ϕ) through

3

The local parameters were then used to determine the helical twist Ω_h through

4

R_z and R_y are rotations about the x and y axes, respectively.

Bulge Simulations

Bulge motifs were constructed from the random sequences specified in Supporting Information Table S1 and initialized as single linear chains with a 3-nt linker connecting the two strands. Similar to the hairpins above, temporary restraints were used to fold the chains into helical structures, after which appropriate base-pair bonds, M pseudoatoms, and other associated potentials were added and the linker nucleotides deleted, leaving trailing 3′ and 5′ P pseudoatoms on both strands for symmetry. Initial coordinates for the no-connectivity systems were obtained by deleting the B, S, and P pseudoatoms of the bulged nucleotide of the 1-nt systems. Two independent temperature replica exchange (TREX) simulations, each comprising 100 000 exchanges, were run using three replicas spanning 300–400 K with 1000 steps of dynamics separating exchange attempts. The low temperature conformations of each simulation were combined to achieve a total of 200 000 exchanges of sampling for each sequence and 2 000 000 exchanges for each bulge. TREX simulations were performed through the MMTSB replica exchange server,⁵² with 100 000 cycles of TREX requiring ∼10 wall and ∼30 CPU hours.

Previously described protocols were used to measure Euler angles, (α_h, β_h, γ_h), that describe the interhelical angle of each bulge conformation.⁵⁰ Alignments were done to a TOPRNA representation of an idealized helix⁵⁰ using the P and S pseudoatoms of the bulge-helices’ three base pairs, excluding the 5′-most P pseudoatoms of each strand; these 5′ P pseudoatoms lack dihedral potentials and are not confined to A-form-consistent conformations. Measured angles were rounded to their nearest 10° grid increment, and the fraction of total angles that were sampled was computed as previously described.⁵⁰ Comparisons to our prior models were done by only considering the rigid-body predicted angles that were increments of 10°.²⁹

Free energies (ΔA^Topo) of different interhelical conformations were computed from our simulations using the equation

5

P_i is the probability of the interhelical angle i being sampled by a given bulge type, and was computed by counting the number of times the angle was sampled over 2 000 000 REX cycles at 300 K and then dividing by 2 000 000. P_max is the maximum over all P_i of a given bulge and T is the temperature, set to 300 K.

Comparisons to PDB Bulges

The set of interhelical angles observed in the PDB was obtained by querying the RNA FRABASE⁴⁷ for all X-ray and NMR RNA structures containing two helices of at least 3-bp connected by 1- to 6-nt bulges. The searches were performed on September 20, 2012 and done in accordance with our earlier procedures.²⁹ Each bulge was converted to a TOPRNA representation and its interhelical orientation measured as described above. Conformations were counted as “sampled” if they were ≤10° from the nearest TOPRNA sampled grid point.⁵⁰

ΔA^Topo estimates for PDB interhelical conformations were obtained by averaging the TOPRNA sampling probabilities (P_i in eq 5) of all grid points within a 10° radius of the PDB-measured angle. Grid points not sampled by TOPRNA were included in the average by setting their P_i = 0. This average, ⟨P_i⟩, was then substituted for P_i in eq 5. This averaging was done to account for the ∼10° errors associated with measuring interhelical angles,⁵⁰ and for the steep changes in ΔA^Topo across grid points. Analysis of the 525 PDB bulges with ΔA^Topo > 2.5 kcal/mol was done by clustering the bulges according to sequence and similar interhelical angles and then manually examining several representatives from each cluster for RNA tertiary, protein, or crystal contacts. Contacts were defined as a heavy atom distance ≤3.5 Å.

Measuring TOPRNA-Predicted RDCs

Residual dipolar couplings (RDCs) report on the average orientation of individual RNA bond vectors with respect to the NMR external magnetic field.^53,54 Given an ensemble of structures {X}, the average RDC ⟨D_nm⟩ of the internuclear bond vector between atoms n and m can be calculated as

6

where γ_n is the gyromagnetic ratio of nucleus n, r_nm is the internuclear distance, S_kl are the order tensor elements describing the global alignment of the molecule, and α_k is the angle of the bond vector with respect to the kth axis of the molecular frame.⁵⁵S_kl were set equal to the experimental values obtained for either the HI or HII elongated helices of domain-elongated TAR and assumed to be independent of molecular conformation.^56,57 {X} was obtained by performing the necessary interhelical rotations²⁹ to two idealized all-atom helices of the same sequence as TAR for all interhelical angles sampled by TOPRNA. The subsequent ensemble averages were weighted according to the TOPRNA populations of each angle.

Results and Discussion

TOPRNA Accurately Models A-Form Helical Structure and Dynamics

To verify that the TOPRNA force field generates helices possessing correct A-form structure, we performed simulations of 400 different 4-base-pair (bp) helices capped by 4-nucleotide (nt) hairpin loops and compared the structural characteristics of these helices to that observed in the PDB (Figure 2A,B). Both the RMSDs of the helices from idealized A-form structure and helical twists fall within the range of values observed in the PDB (Figure 2A,B). The few helices possessing mean RMSDs greater than one standard deviation above the PDB mean contained at least one GU base pair, consistent with these pairs’ ability to induce helical distortions.^58,59

Figure 2.

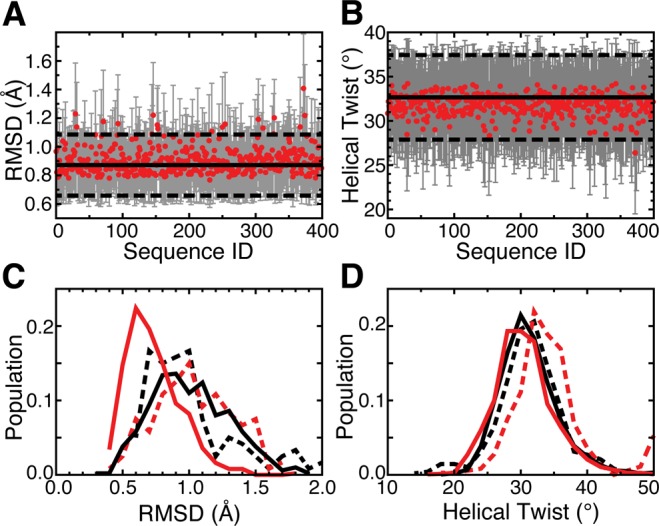
Simulations of different RNA helices confirm TOPRNA’s ability to reproduce A-form helical behavior. (A, B) The means and standard deviations of helical parameters measured for simulations of 400 random-sequence 4-bp hairpins are shown as red points and gray bars. Solid and dashed horizontal lines indicate the means and standard deviations of these parameters measured from our database of PDB helices. The helical twist values in part B have been averaged over the three hairpin base-pair steps. (C, D) The distribution of helical parameters measured from TOPRNA simulations (solid lines) and the NMR-MD dynamic ensemble of HIV-1 TAR (dashed lines).⁴⁹ Parameters were measured for the first five base pairs of the lower helix (black) and the four base pairs of the upper helix (red), and the populations of the helical twist parameters represent distributions over both different conformations and base-pair steps.

We also examined the ability of TOPRNA to reproduce the dynamic behavior of helices in solution by comparing TOPRNA simulations of HIV-1 and HIV-2 TAR RNAs to previously constructed NMR-MD dynamic ensembles of these molecules.⁴⁹ Built by using residual dipolar coupling (RDC) NMR measurements to select high-confidence structures from all-atom molecular dynamics (MD) simulations, these ensembles provide the most accurate available picture of the thermodynamic ensemble of states populated by RNA helices.⁴⁹ Shown in Figure 2C,D and Figures S1 (Supporting Information), TOPRNA helices are slightly more idealized over those observed in the NMR-MD ensembles but overall exhibit close agreement in helical twist and idealized A-form RMSD distributions. Combined, these results demonstrate that TOPRNA accurately captures both the structure and dynamics of RNA helices.

TOPRNA Analysis of Topological Constraints in Bulge Junctions

As the first application of TOPRNA, we set out to further characterize the topological constraints that govern two-way junction bulge motifs. In previous work using our idealized rigid-body rotation models, we demonstrated that these motifs are strongly topologically confined to a small subset of interhelical conformations.^12,29 However, necessary approximations made by these models, such as neglecting the volume-excluding properties of single-stranded bulge nucleotides, have obscured a complete understanding of the role that topological constraints play in dictating bulge conformation.

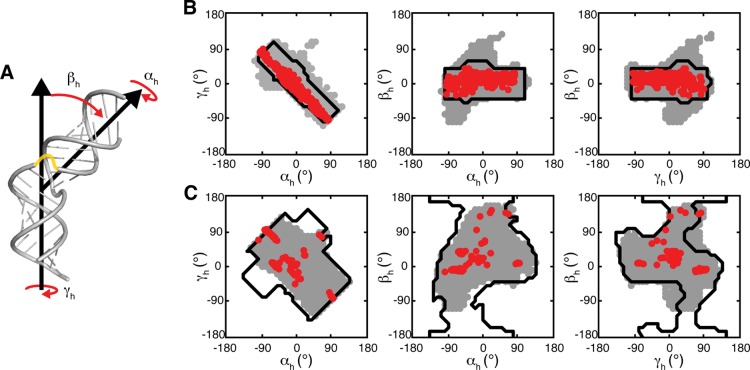
Through extensive simulations of model junctions comprising two, 3-bp helices connected by bulges of 1 to 4 nt’s in length, we utilized TOPRNA to achieve unprecedented sampling of the set of interhelical conformations accessible to different bulge motifs (Figure 1). For completeness, each of the different bulge types was simulated using 10 different randomized sequences for 200 000 cycles of temperature replica exchange, generating a total of 2 000 000 different conformations per bulge. Then, employing the (α_h, β_h, γ_h) Euler angle convention (Figure 3A), where α_h and γ_h represent the twists of the two helices and β_h the interhelical bend,⁵⁰ we quantified the sampled interhelical conformations and compared them to our prior results.

Figure 3.

TOPRNA simulations of two-way junction bulge motifs reproduce the topologically allowed space. (A) Cartoon of the (α_h, β_h, γ_h) convention used to quantify interhelical conformations, shown using an artificial junction between two idealized helices. A possible path of the single-stranded bulge is drawn in yellow. (B, C) 2D projections of the (α_h, β_h, γ_h) sampled by TOPRNA (gray), observed in the PDB (red), and predicted to be allowed in ref (29) (black outlines), are shown for 1-nt and 3-nt bulges, respectively.

As shown in Figures 3 and S2 (Supporting Information), these simulations reveal strong agreement with our prior rigid-body models. Not only do the sampled regions largely overlap (Table 1), but also the finer contours of these regions, such as the linear correlation among α_h and γ_h,^12,29 are duplicated in both models (Figure 3 and S2, Supporting Information). Both models also sample similar magnitudes of the interhelical conformational space (Table 1). Thus, TOPRNA provides an independent corroboration of the significance of topological constraints in RNA structure.

Table 1. Comparison between the (α_h, β_h, γ_h) Sampled by TOPRNA Bulge Simulations, the (α_h, β_h, γ_h) Conformations Observed in the PDB, and Conformations Predicted by the Rigid-Body Model²⁹.

bulge	fraction of total (αh, βh, γh) sampled by TOPRNA (rigid-body)a	fraction of TOPRNA (αh, βh, γh) overlap with rigid-bodyb	fraction of rigid-body (αh, βh, γh) overlap with TOPRNAc	fraction of PDB conformations sampled by TOPRNA (rigid-body)d
1-nt	0.075 (0.053)	0.61	1.0	1.0 (1.0)
2-nt	0.11 (0.097)	0.72	0.95	0.99 (0.79)
3-nt	0.15 (0.20)	0.81	0.80	1.0 (0.99)
4-nt	0.20 (0.38)	0.81	0.53	1.0 (0.93)

^aDue to rounding (α_h, β_h, γ_h) to a 10° vs 5° grid, the rigid-body fractions differ slightly from that reported in ref (29).

^bThe fraction of TOPRNA sampled conformations that are found within the ref (29) idealized-helix topologically allowed space.

^cThe fraction of ref (29) idealized-helix topologically allowed conformations sampled by TOPRNA, excluding ref (29) conformations that were added to the rigid-body-rotation-derived allowable conformations as estimates of error padding or “intrinsic helical degrees of freedom”.

^dComparisons were done to a total of 1853, 705, 347, and 30 PDB structures of 1-, 2-, 3-, and 4-nt bulge systems, respectively.

Nonidealized Helical Behavior Allows Sampling of New Interhelical Conformations

Despite the overlap between the two models, important differences do exist. 19–39% of the TOPRNA sampled conformations correspond to “new” states that were not predicted by our rigid-body models, with the 1- and 2-nt TOPRNA bulges sampling 40 and 10% more of the (α_h, β_h, γ_h) conformational space, respectively (Figure 3, Table 1, and Supporting Information Figure S2). In contrast, the 3- and 4-nt simulations sample 25 and 50% fewer conformations. To resolve the physical significance of these differences, we examined the ability of the models to capture the distribution of (α_h, β_h, γ_h) observed among the bulge junctions in the PDB. Strikingly, TOPRNA samples 99.9% of the PDB (α_h, β_h, γ_h) compared to 94.8% achieved by the rigid-body models (Figure 3, Table 1, and Supporting Information Figure S2). Furthermore, the single PDB conformation not sampled by TOPRNA, the 2-nt bulge of PDB 4ERD,⁶⁰ is only 11° from the nearest TOPRNA sampled angle (distances of ≤10° count as “sampled”), whereas it is 31° outside of the rigid-body topologically allowed space.

The increased sampling of PDB-observed conformations indicates that the new conformations sampled by TOPRNA are physically relevant. We had previously found that deviations in helical structure, particularly those associated with bulges possessing GU closing base pairs, could modify the steric interactions of a junction and thus make new interhelical conformations accessible.²⁹ Indeed, the 5.2% of PDB junctions not captured by the rigid-body models either possess GU closing pairs or correspond to the 4ERD or four earlier identified NMR outliers.²⁹ Hypothesizing that TOPRNA is capturing such deviations in helical structure, we compared the newly TOPRNA sampled (α_h, β_h, γ_h) to topologically allowed spaces built previously²⁹ from nonidealized helices; ∼70% corresponded to conformations also found in these “nonideal” allowed spaces. Analysis of the variances in sampling exhibited by the different TOPRNA simulated sequences further demonstrates that these arise from sequence-dependent variations in helical structure; each TOPRNA sequence samples 100% of the PDB conformations that share its same junction-closing base pairs (excluding the 4ERD outlier) but only 88–100% of the PDB conformations possessing different closing pairs. Therefore, even though the composition of the (α_h, β_h, γ_h) sampled by different sequences differs by only ∼14% on average, with the varying angles typically no more than 12° outside of the set of (α_h, β_h, γ_h) sampled by other sequences, these differences can be important in shaping a bulge’s topologically allowed space.

We also previously noted that translational motions between the helices of a junction, which are not captured by the rigid-body model, had the possibility of dramatically increasing the number of conformations accessible to bulge motifs.²⁹ Comparison between these previously predicted translation-mediated conformations and the newly TOPRNA-sampled (α_h, β_h, γ_h) revealed that translations explain an additional 7% of the new sampling, with these conformations typically no more than ∼20° outside of the allowed spaces predicted by the rigid-body model. Thus, while TOPRNA does capture such motions, they appear to be relatively insignificant.

Together, helix nonideality and translational motions explain ∼80% of the new conformations sampled by TOPRNA, demonstrating that the model captures these degrees of conformational freedom. On average, the other 20% are within ∼24° of the rigid-body predictions. Determining the physicality of these unexplained conformations requires a fully atomistic model and is outside the scope of this work. We note that, even if all are nonphysical, the small number of these conformations (<10% of the total sampled by TOPRNA) makes it unlikely that they will introduce significant errors to our analysis.

Topological Constraints on Bulges Exceed Prior Estimates

As mentioned above, the 3- and 4-nt TOPRNA bulge simulations sample significantly fewer overall interhelical conformations than predicted by the rigid-body models yet still capture 100% of the conformations found in the PDB. This indicates that the constraints on these systems are much greater than previously estimated. As TOPRNA explicitly models the geometry and sterics of bulge-comprising single-stranded nucleotides whereas the rigid-body models ignored these constraints,^12,29 this result is not unexpected. Determination of the TOPRNA energies of the rigid-body-predicted but “TOPRNA-unsampled” (α_h, β_h, γ_h) conformations confirmed that these states are precluded due to elevated energies that primarily arise from bulge nucleotides (see text and Figure S3 in the Supporting Information).

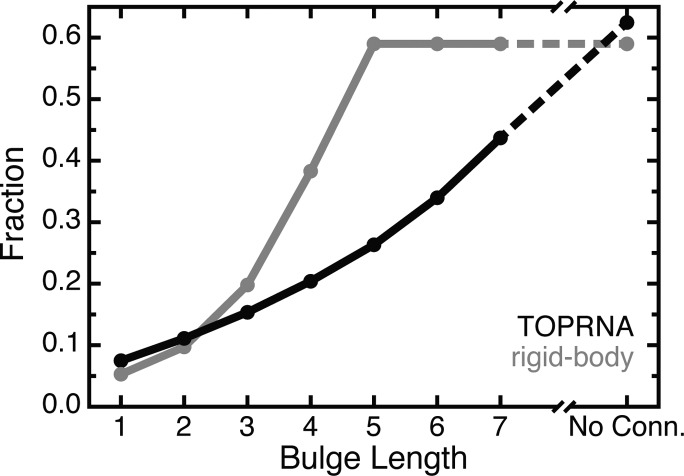
An important consequence of these greater constraints is that a bulge’s topologically allowed space continues to increase in size across a broad range of bulge lengths. Previously, we had predicted that a 5-nt bulge had sufficient length to enable sampling of all sterically possible (α_h, β_h, γ_h) conformations.²⁹ However, TOPRNA simulations of 5-, 6-, and 7-nt bulges using the same procedures as described above revealed this prediction to be incorrect. The additional steric and stereochemical constraints of the bulge nucleotides in TOPRNA limit even 7-nt bulges to ∼2/3 of the (α_h, β_h, γ_h) space that is accessible to junctions that do not have “bulge”-strand connectivity (see Methods, Figure 4). Thus, though few if any RNAs in the PDB possess junctions containing bulges of length >6 nt,⁴⁷ in theory such longer bulges could be important in allowing RNAs to access conformations that would be forbidden to shorter bulges.

Figure 4.

The fraction of (α_h, β_h, γ_h) space sampled by TOPRNA (black) and predicted by the rigid-body models (gray) for different bulge motifs.²⁹ “No conn.” denotes a bulge-like junction that lacks bulge-strand connectivity.

Topological Constraints Explain the Distribution of Conformations Sampled by Polypyrimidine Bulges at Low Salt Concentrations

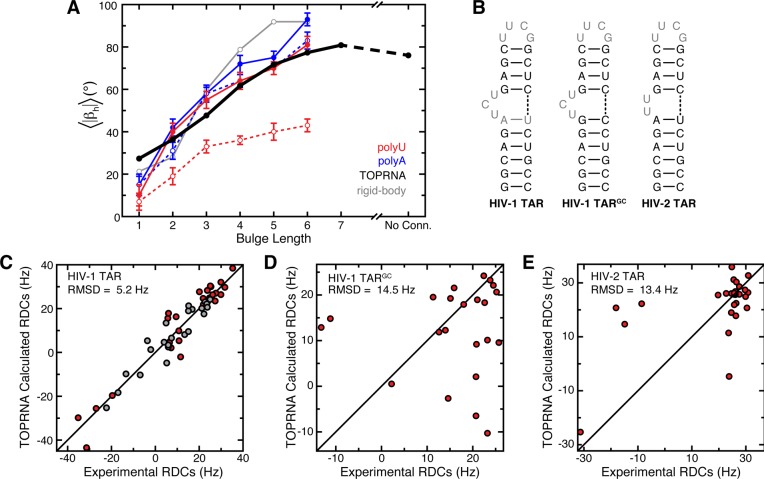
We previously showed that ensemble averages over the topologically allowed space reproduce both the experimentally measured magnitude and directionality of bulge-induced bends,²⁹ suggesting that topological constraints may be responsible for the behavior of these systems. Evidenced by the similar anisotropies of the TOPRNA and rigid-body topologically allowed spaces (Figures 3 and S2, Supporting Information), TOPRNA also captures the directionality of bulge-induced bends. Ensemble averages over the length of our simulations also reproduce the experimentally measured magnitude of these bends, matching, to approximately within experimental error, the mean bend measured for flexible polyU bulge systems in the absence of Mg²⁺ (Figure 5A).⁶¹ Furthermore, our simulations reproduce the experimental observation that the magnitude of bulge-induced bends plateaus and then decreases as the bulge increases past 6 nt’s in size (Figure 5A).⁶² However, this agreement does not hold for 1-nt bulges or for polyU bulges in the presence of Mg²⁺ (Figure 5A). PolyA bulges also exhibit larger bends than polyU and TOPRNA bulges, and have different Mg²⁺-dependent behavior than polyU bulges.⁶¹

Figure 5.

Ensemble averages over TOPRNA bulge simulations reproduce experimentally measured properties of bulge motifs. (A) |β_h| averaged over TOPRNA simulations (black) and over the ref (29) predicted allowed spaces (gray) for different bulge motifs is plotted next to the bend angles measured by transient electronic birefringence for polyU (red) and polyA (blue) bulges in the absence (solid line, filled circles) and presence (dashed line, open circles) of Mg²⁺.⁶¹ Error bars denote experimental error.⁶¹ “No conn.” denotes a bulge-like junction that lacks connectivity in its bulge strand. (B) HIV-1 TAR, HIV-1 TAR^GC, and HIV-2 TAR secondary structures. RDCs from nucleotides shown in gray were excluded from the RDC analysis. (C, D, E) HIV-1 TAR, HIV-1 TAR^GC, and HIV-2 TAR experimental RDCs versus values computed from either 3-nt or 2-nt TOPRNA bulge simulations.^56,57 In part C, red and gray points correspond to RDCs from helix I and helix II TAR elongations, respectively.⁵⁶ N–H bond vectors were excluded from all RDC analysis.

We suggest that the above observations can be explained through the following model. At low salt concentrations, electrostatic repulsion between helices cancels out otherwise favorable interhelical stacking interactions. For polyU bulges, which lack strong intrabulge stacking, this results in a highly dynamic state that is largely governed by topological constraints and approximated by TOPRNA. Higher salt concentrations screen this repulsion and thus promote interhelical stacking that is ignored by our simulations. The lower conformational entropy of the unstacked state of 1-nt bulges also stabilizes stacking at low salt. By contrast, the alternative behavior of polyA bulges arises because stronger stacking interactions between the bulged adenines stabilize highly bent conformations at all salt concentrations.⁶¹

Significantly, the above model is also consistent with the behavior of HIV-1 TAR, a biologically important 3-nt polypyrimidine bulge that has been extensively characterized by NMR and other methods (Figure 5B).^{49,56,63−66} These studies have shown that TAR exists in an equilibrium between a dynamic unstacked state that populates a broad range of interhelical conformations and a coaxially stacked state. At low Na⁺ and Mg²⁺ concentrations, TAR is predominantly unstacked, with increases in salt progressively stabilizing the stacked state but not altering the nature of the unstacked ensemble.⁶⁵ Small molecule binding or selective mutations to the closing base pairs of the junction can also stabilize stacking.^56,57 To further test our hypothesis that TOPRNA approximates the behavior of polypyrimidine bulges at low salt, we thus assessed the ability of our simulations to reproduce atomic-level NMR RDC measurements made on TAR at such conditions.⁵⁶ We note that RDCs are ideal for such a test, as they depend strongly on the entire distribution of populated (α_h, β_h, γ_h) conformations.^56,67 Remarkably, ensemble averages over the (α_h, β_h, γ_h) sampled by our 3-nt bulge simulations yield RDCs that match the experimental values to a root-mean-square difference (RMSD) of 5.2 Hz (Figure 5C; see Methods). This value is comparable both to the uncertainty associated with the experimental RDCs (∼4 Hz) and to that of the all-atom NMR-MD ensemble mentioned earlier that was specifically optimized for its agreement with a superset of these RDCs (RMSD = 4.8 Hz).⁴⁹ It is also substantially better than the ∼15 Hz RMSD obtained when averaging over the nonoptimized 80 ns MD-simulation source of the NMR-MD ensemble.⁴⁹ By contrast, TOPRNA does a poor job of approximating the RDCs measured on TAR^GC, a mutant with strengthened interhelical stacking interactions that stacks even at low salt (RMSD = 14.5 Hz; Figure 5B,D).⁵⁷

We also tested the ability of TOPRNA simulations to reproduce the RDCs of HIV-2 TAR, which contains a 2-nt polyU bulge (Figure 5B).⁵⁶ Here, we also found poor agreement due to interhelical stacking effects neglected by TOPRNA (RMSD = 13.4 Hz; Figure 5E). For example, the NMR-MD ensemble constructed for HIV-2 TAR is dominated by coaxially stacked (|β_h| < 15°) conformations and has no conformations possessing |β_h| > 30°.⁴⁹ This stacked conformation closely resembles the low-bend Mg²⁺-present state of polyU bulges observed by Zacharias and Hagerman (Figure 5A),⁶¹ and can be explained by the higher Na⁺ concentrations used in the NMR experiments.⁵⁶

Taken together, these results support a model where the distribution of interhelical conformations populated by polypyrimidine bulges is governed by an interplay of interhelical stacking, electrostatic repulsion, and topological constraints. Whereas stacking predominates for short bulges and at high salt conditions, topological constraints govern the behavior of long polypyrimidine bulges at low salt. While the extent to which this holds true for non-polypyrimidine bulges is unclear, this finding nevertheless indicates topological constraints to be a highly significant driver of bulge conformation. It is worth emphasizing that it would be difficult to draw our conclusions regarding the role of topological constraints from models that include all RNA forces. We also note that, while our simulations highlight the importance of interhelical stacking to bulge conformation, increasing the strength of these interactions beyond the minor attraction already present between paired B pseudoatoms is counter to the topological constraint focus of the model.

Topological Constraints Encode Conformational Free Energies

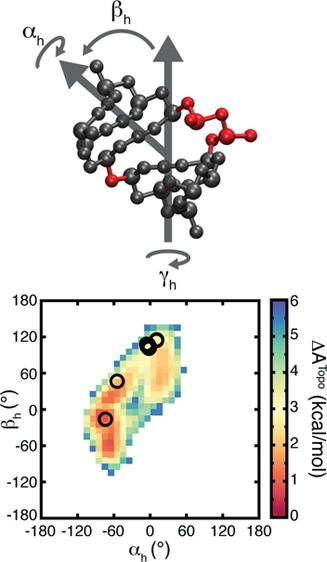
The agreement between ensemble averages over our simulations and experiments on polypyrimidine bulges at low salt implies that the free energy landscape explored by TOPRNA mirrors that of real RNAs. We directly computed these energy landscapes from our simulations by converting the sampling probability of each (α_h, β_h, γ_h) angle into a free energy cost, ΔA^Topo, relative to a given bulge’s highest probability (α_h, β_h, γ_h) conformation (see Methods, eq 5). ΔA^Topo reflects both the entropic and internal energy costs imposed by topological constraints. It captures, for example, whether an interhelical orientation requires its bulge nucleotides to adopt a strained conformation, or alternatively if an orientation is entropically favored because it preserves the conformational freedom of its bulge nucleotides. Note that the small attractive interaction experienced between paired B pseudoatoms also provides a slight favorable contribution to the ΔA^Topo of coaxially stacked conformations. Interestingly, these calculations reveal that the ΔA^Topo of different (α_h, β_h, γ_h) conformations is on average ∼3 kcal/mol and can be as large 6 kcal/mol (Figure 6), indicating that topological constraints strongly favor some bulge conformations over others.

Figure 6.

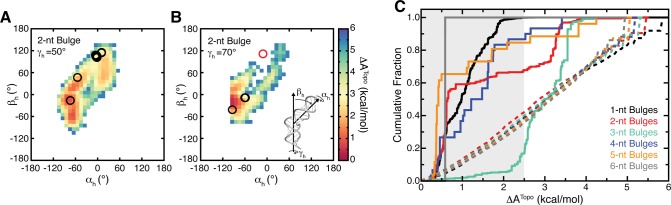
Bulge conformations found in the PDB are consistent with the TOPRNA free-energy landscape. (A, B) Representative 2D slices of the 2-nt bulge free energy landscape (T = 300 K) are shown for constant γ_h = 50° (A) and γ_h = 70° (B). Open circles denote conformations observed in the PDB, with the red circle in part B highlighting the 4ERD outlier. The inset in part B is a cartoon illustrating the physical meaning of the (α_h, β_h, γ_h) angles. (C) Cumulative distribution functions showing the fraction of (α_h, β_h, γ_h) conformations with ΔA^Topo less than a given cutoff value. The distributions for (α_h, β_h, γ_h) conformations observed in the PDB are shown as solid lines. The distributions for (α_h, β_h, γ_h) in the TOPRNA topologically allowed spaces are shown as dashed lines. The gray background highlights ΔA^Topo values <2.5 kcal/mol. 1853, 705, 347, 30, 26, and 1 structures are represented by the PDB curves of 1-nt, 2-nt, 3-nt, 4-nt, 5-nt, and 6-nt bulges, respectively.

To further evaluate the significance of these energy landscapes, we again utilized comparisons to the set of (α_h, β_h, γ_h) observed among bulges in the PDB. As the conformations captured by crystallography or NMR primarily reflect “folded” states that are stabilized by attractive interactions ignored by TOPRNA, we do not expect exact correspondence between ΔA^Topo and the distribution of (α_h, β_h, γ_h) in the PDB. However, given that intrajunction attractive interactions are typically ≤2.5 kcal/mol,^25,68 if ΔA^Topo is significant, then we should observe few if any PDB bulges with ΔA^Topo greater than this threshold. Remarkably, we find that this is indeed the case, with 82% of bulges possessing ΔA^Topo ≤ 2.5 kcal/mol (Figure 6C). Moreover, analysis of the bulges possessing ΔA^Topo ≥ 2.5 kcal/mol revealed that 98% either participate in protein or RNA tertiary interactions, possess such interactions directly up/downstream of the bulge, or possess crystal packing interactions. For example, the apparently different behavior of 3-nt bulges in Figure 6C arises because two motifs, helix 12 of the 16S rRNA and helix 96 of the 23S rRNA, collectively comprise ∼80% of the 3-nt bulges in our database; both of these motifs participate in either RNA–RNA or protein–RNA tertiary interactions.

The above observations suggest that bulges with high ΔA^Topo are only observed because they are stabilized by auxiliary interactions. For several bulges, this claim is directly supported by the existence of alternative lower-energy structures. Notably, in two different crystals,^69,70 the 5-nt bulge of the HCV IRES IIa domain adopts conformations possessing ΔA^Topo = 3.8–4.3 kcal/mol. However, in an alternative ligand-bound crystal structure⁷¹ and in solution NMR structures,^72,73 this bulge is limited to conformations having ΔA^Topo = 1.1–2.1 kcal/mol. Similarly, of nine structures of HIV-1 TAR in our database,⁷⁴⁻⁸¹ eight possess ΔA^Topo < 1.7 kcal/mol, with only the crystal-contact stabilized 397D(75) structure exhibiting a high-energy conformation (ΔA^Topo = 3.1 kcal/mol). The protein-bound 2-nt bulge of the 4ERD(60) outlier mentioned earlier (ΔA^Topo > 5.5 kcal/mol) and the 2-nt bulge of helix III of the 5S rRNA (ΔA^Topo = 1.5–2.6 kcal/mol in various ribosome structures; see, for example, refs (82 and 83)) have also been shown by NMR^84,85 to adopt lower-energy apo conformations possessing ΔA^Topo = 2.0 and ΔA^Topo = 0.6 kcal/mol, respectively.

The 2% of ΔA^Topo ≥ 2.5 kcal/mol bulges that are not explained by auxiliary stabilizing interactions correspond to NMR structures. Of the 10 total, 7 were solved without RDC restraints,⁸⁶⁻⁸⁹ suggesting that their global structures may be unreliable,⁹⁰ and 1 is an averaged structure of the HCV IRES derived from an ensemble whose best representative conformation has ΔA^Topo = 1.7 kcal/mol.⁷² The final two are from the unpublished NMR structure 1U3K, for which refinement details were unavailable.

Together, these results strongly indicate that topological constraints play an important role in defining the RNA free energy landscape. In the absence of external stabilizing interactions, bulges are largely limited to low ΔA^Topo conformations that are encoded by secondary structure. In addition, as evidenced by the experimental agreement above, these topological-constraint-encoded energy landscapes provide a reasonable estimate of the ensemble of structures sampled by dynamic polypyrimidine bulges at low salt. We note that electrostatics, preferred backbone rotameric states, and attractive interactions involving single-stranded nucleotides, all of which are ignored by the TOPRNA force field, are also key drivers of final RNA 3D structure. Indeed, detailed models that include these forces should be expected (and have been shown)^{14,15,17,37,39,91} to achieve superior experimental agreement given sufficient sampling. However, the success of TOPRNA indicates that, for a bulge with stable secondary structure, these other energetic terms serve to fine-tune the energy landscape predefined by topological constraints. This finding emphasizes the continuing need for a more holistic understanding of the forces that dictate RNA 3D structure. We suggest that, while not suitable by itself for high-resolution structure prediction, this finding may help guide further improvements in dedicated structure prediction and design methods. NMR structure refinement protocols may also benefit by considering the energetic contributions of topological constraints.

We also note the striking parallels between this finding and that obtained by Herschlag and co-workers³⁰ from their studies on simplified junction mimics. In these systems, topological constraints were shown to destabilize certain junction conformations by as much as ∼5 kcal/mol and were hypothesized to play a potential role in encoding specificity of RNA 3D structure. By establishing that such topological-constraint-defined energies also exist in biologically relevant junctions, our analysis provides a tantalizing clue that secondary structure, independent of exact sequence, may indeed be encoding the 3D structure of many RNAs. Exploration of this hypothesis as well as complete characterization of the importance of these energies and their interplay with other RNA structural forces in folding should be an exciting topic for future study.

Conclusions

We have developed the coarse-grained molecular dynamics model TOPRNA that is optimized to explore the contributions of topological constraints to the folding and dynamics of complex RNA systems. TOPRNA simulations of two-way bulge junctions recapitulate our prior findings that topological constraints are significant determinants of bulge 3D structure. In particular, these basic constraints limit the set of interhelical conformations accessible to 1- to 4-nt bulges to 7–20% of the total theoretical space. With the greater physical accuracy afforded by TOPRNA, we show that deviations in idealized A-form helix structure and stereochemical constraints posed by bulge-linking nucleotides play a critical role in defining the set of allowed conformations. However, interhelical translations play a relatively insignificant role.

Strikingly, in addition to defining a limited range of allowed conformations, our simulations demonstrate that topological constraints contribute as much as 6 kcal/mol to the free energy of different bulge conformations. The majority of bulges in the PDB adopt conformations with low ΔA^Topo, and the few bulges with high ΔA^Topo appear to be stabilized by interactions with external partners such as proteins. The surprising ability of our simulations to reproduce experimental measurements made on polypyrimidine bulges at low salt concentrations suggests that in some cases bulge conformational free energy is primarily determined by ΔA^Topo alone. However, for sequences that more strongly stack, or at higher salt concentrations, other energetic terms such as electrostatics and attractive interactions are needed to explain RNA behavior.

Understanding the relationship between RNA secondary structure and 3D structure remains an important goal. The generality of both the TOPRNA force field and the methods we used should make it possible to explore the role of topological constraints in a wide variety of RNAs. For example, we have used TOPRNA to study the pseudoknot of the preQ₁ riboswitch,⁹² and in studies that are to be published elsewhere, we have used TOPRNA to study the topological constraints of the four-way junction of tRNA. The force field and related software is available for download at http://brooks.chem.lsa.umich.edu/.

Supporting Information Available

Description and results of the energy analysis of the rigid-body predicted conformations that were not sampled by TOPRNA; description of the sequences used for bulge simulations; comparisons between TOPRNA helices and the HIV-2 TAR NMR-MD ensemble; topologically allowed (α_h, β_h, γ_h) maps for 1-nt, 2-nt, 3-nt, and 4-nt bulges. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare the following competing financial interest(s): H.M.A. is an advisor to and holds an ownership interest in Nymirum, an RNA-based drug-discovery company.

Author Present Address

^§ Department of Biochemistry, Duke University Medical Center, Durham, NC 27710.

Funding Statement

National Institutes of Health, United States