Accounting for Misclassified Outcomes in Binary Regression Models Using Multiple Imputation With Internal Validation Data

Abstract

Outcome misclassification is widespread in epidemiology, but methods to account for it are rarely used. We describe the use of multiple imputation to reduce bias when validation data are available for a subgroup of study participants. This approach is illustrated using data from 308 participants in the multicenter Herpetic Eye Disease Study between 1992 and 1998 (48% female; 85% white; median age, 49 years). The odds ratio comparing the acyclovir group with the placebo group on the gold-standard outcome (physician-diagnosed herpes simplex virus recurrence) was 0.62 (95% confidence interval (CI): 0.35, 1.09). We masked ourselves to physician diagnosis except for a 30% validation subgroup used to compare methods. Multiple imputation (odds ratio (OR) = 0.60; 95% CI: 0.24, 1.51) was compared with naive analysis using self-reported outcomes (OR = 0.90; 95% CI: 0.47, 1.73), analysis restricted to the validation subgroup (OR = 0.57; 95% CI: 0.20, 1.59), and direct maximum likelihood (OR = 0.62; 95% CI: 0.26, 1.53). In simulations, multiple imputation and direct maximum likelihood had greater statistical power than did analysis restricted to the validation subgroup, yet all 3 provided unbiased estimates of the odds ratio. The multiple-imputation approach was extended to estimate risk ratios using log-binomial regression. Multiple imputation has advantages regarding flexibility and ease of implementation for epidemiologists familiar with missing data methods.

Misclassification of outcome variables is common in epidemiology and threatens the validity of inferences from epidemiologic studies (1, 2). However, standard approaches to epidemiologic data analysis typically assume outcome misclassification is absent. Although approaches to account for bias in crude effect estimates due to use of a misclassified binary outcome have existed for more than half a century (2), these methods are rarely used because epidemiologists commonly wish to present results that have been adjusted for several confounding variables. More recently, investigators have developed maximum likelihood approaches (2, 3) to produce odds ratio estimates that account for outcome misclassification while adjusting for relevant confounders using logistic regression, but these methods have not been widely applied in the epidemiologic literature. Here we describe an alternative approach to account for outcome misclassification using missing data methods that are familiar to epidemiologists.

Methods to account for misclassification rely on information relating the observed outcome to the gold-standard outcome measure. This relationship can be estimated by comparing the observed outcome to the gold-standard outcome in a validation subgroup that is a random subset of the main study or in external data. In the present study, we focused on the former case, in which internal validation data are available for a subgroup of the population under study. We treated outcome misclassification as a missing data problem in which the true outcome status is known only for participants in the validation subgroup and is missing for all other participants (4). This perspective allowed misclassification bias to be addressed by applying well-established methods for handling missing data (5–7). In the sections that follow, we described an approach to account for outcome misclassification using multiple imputation to estimate odds ratios and risk ratios, provided examples using cohort data (8), and explored some finite sample properties of the proposed method by Monte Carlo simulation.

MATERIALS AND METHODS

Study population

We illustrate the use of multiple imputation to account for outcome misclassification using data from the Herpetic Eye Disease Study, a randomized trial of acyclovir for the prevention of ocular herpes simplex virus (HSV) recurrence at 58 university and community-based sites in the United States (9). Participants were 12 years of age or older and had an episode of ocular HSV in the 12 months before the study, but their disease had been inactive during the 30 days preceding the study. During the study, the 703 participants received either oral acyclovir or placebo for 12 months. The goal of the study was to compare the 12-month incidence of ocular HSV recurrence between the group randomized to receive acyclovir and the group randomized to receive the placebo. Information was also collected on age, race, sex, and number of ocular recurrences before randomization. Here, we restricted analyses to the 308 of 703 participants who co-enrolled in a study that collected weekly diaries about ocular HSV symptoms and possible triggers between 1992 and 1998 (10).

Outcome ascertainment and validation

The outcome of interest was a binary indicator of HSV recurrence over the 12-month study period (any recurrence versus none) assessed in 2 ways. Study-certified ophthalmologists examined participants using microscopy when symptoms were apparent or at planned study visits in months 1, 3, 6, 9, and 12. In addition, participant-reported HSV recurrence was obtained from a weekly diary. We consider participant-reported HSV recurrence to be the observed, and possibly mismeasured, version of the outcome variable (W = 1 if the participant reported any recurrence, W = 0 otherwise), and physician-diagnosed HSV recurrence to be the gold standard (D = 1 if the ophthalmologist diagnosed a recurrence, D = 0 otherwise). We randomly sampled 30% (n = 91) of the 308 participants to treat as a validation subgroup. In the present analysis, we assumed that W was available for all participants and D was observed only for those selected to be in this hypothetical validation subgroup.

Statistical methods

We used logistic regression to estimate the odds ratio comparing ocular HSV recurrence between participants randomly assigned to acyclovir and those assigned to placebo. We compared the results of an ideal analysis on the full cohort of 308 participants using the physician diagnosis as the outcome variable with results from 4 methods for handling outcome misclassification: 1) the naive analysis, in which W represented the outcome status for all 308 participants; 2) the validation subgroup, in which the physician-diagnosed outcomes (D) were compared between those receiving acyclovir and those receiving placebo in the validation subgroup of 91 participants; 3) a direct maximum likelihood approach (3) to account for outcome misclassification and; 4) multiple imputation to account for outcome misclassification. Direct maximum likelihood and multiple-imputation approaches were evaluated under the assumptions of both differential and nondifferential misclassification of the outcome with respect to treatment group. We further extended the direct maximum likelihood and multiple-imputation approaches to estimate risk ratios using log-binomial regression.

The direct maximum likelihood approach accounted for outcome misclassification using the method described by Lyles et al. (3). This approach included data from all participants, with those in the validation subgroup providing data on the correctly classified outcome and those not in the validation subgroup providing data on the misclassified outcome. In contrast, the naive analysis included data from all participants but used only the misclassified outcome, and the validation analysis included data from participants in the validation subgroup only but used the correctly classified outcome. To account for nondifferential misclassification in the direct maximum likelihood approach, we estimated the sensitivity and specificity from the records in the validation subgroup. These values were used to compute the likelihood to be maximized, which was a product of the main study likelihood and the validation sample likelihood, as detailed in Web Appendix 1 (available at http://aje.oxfordjournals.org/). To relax the assumption of nondifferential misclassification, we added treatment group to the model for sensitivity and specificity.

Multiple imputation is a standard technique for handling missing data (7, 11). We use multiple imputation to account for outcome misclassification by exploiting the relationships between D, W, treatment group (X), and other covariates (Z) among participants in the validation subgroup to impute values for D for all other participants.

The first step is to model the relationship between physician-diagnosed HSV recurrence and participant-reported HSV recurrence in the validation subgroup. In this example, we use the logistic regression method for monotone missing data (7). To do this, we regress physician-diagnosed HSV recurrence (D) on participant-reported HSV recurrence (W), treatment group (X), and other covariates (Z) using a logistic regression model:

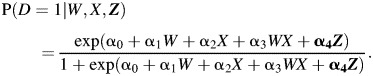(1)

We then draw a set of regression coefficients for each of K imputations from the posterior predictive distribution of the parameters. We set K = 40 in this analysis. We assume parameters follow a multivariate Gaussian distribution with mean vector 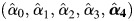and covariance matrix 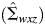estimated from the logistic regression model above. Drawing regression coefficients for each imputation allows uncertainty about the relationship between W, X, and D to propagate through the analysis (7).

A new variable, 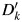, is created to represent the imputed outcome. For participants in the validation subgroup, 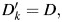where k indexes the number of imputations. For participants not in the validation study, values for 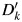are imputed based on the regression coefficients drawn for that imputation. For each imputation, 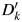is assigned by a random draw from a Bernoulli distribution with probability p_k, where

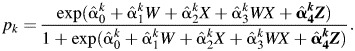(2)

The analysis model is then used to compare imputed outcomes between treatment and placebo groups conditional on other covariates. In the example, we first use a logistic regression model to estimate the odds ratio comparing imputed HSV recurrence for participants assigned to acyclovir and those assigned to placebo in each imputation and combine results using standard multiple-imputation techniques (11). The logistic models for the imputed outcome given treatment group and relevant covariates for k = 1 to 40 are

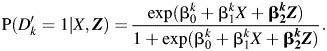(3)

The estimated odds ratio is

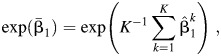(4)

where 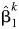is the natural log of the estimated odds ratio from the kth imputed dataset. The variance for 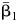is given by

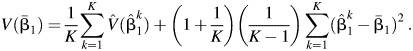(5)

In a closed cohort, it may be preferable to estimate the risk ratio instead of the odds ratio (12–14). To illustrate the ability of the proposed multiple-imputation approach to estimate different parameters of interest, we also use a log-binomial regression model to estimate the risk ratio comparing imputed HSV recurrence for participants assigned to acyclovir and those assigned to placebo in each imputation. To estimate a risk ratio, the binomial model for the imputed outcome given the treatment group and relevant covariates for k = 1 to 40 is used in place of the logistic model shown in equation 3:

(6)

Multiple imputation can be used to account for misclassification of the outcome that is differential or nondifferential with respect to the treatment group. The assumption of nondifferential misclassification implies that α₃ = 0 in the imputation model (equation 2). In models in which α₃ was allowed to be different from 0 because the validation subgroup was relatively small, we used Firth's correction (15) to prevent separation of data points (16). Firth's correction uses a modified score function to obtain maximum likelihood estimates when response variables can be perfectly predicted by a linear combination of risk factors (16), a situation known as separation (17) or monotone likelihood (18). Firth's correction may be viewed as a multivariable extension of a continuity correction. Web Appendix 2 provides the SAS code for multiple imputation to account for outcome misclassification. Alternatively, one could use standard programs for multiple imputation that are included in many statistical software packages, such as SAS's PROC MI (SAS Institute, Inc., Cary, North Carolina) or IVEware (University of Michigan, Ann Arbor, Michigan).

Although the cohort originated as part of a randomized trial, selection into the cohort for analysis was dependent on the participant keeping a weekly diary, which could have been influenced by several covariates. To estimate measures of association that were not biased by this selection, we adjusted for age, sex, and number of previous HSV occurrences by including these covariates in the Z vector in all analyses.

Simulation study

The bias, 95% confidence interval coverage, mean squared error, and statistical power for each method were evaluated under 15 simulation scenarios (Web Appendix 3). Each scenario represented different values of key parameters: sensitivity, specificity, size of the validation subgroup, and total sample size. One set of simulations was designed to mimic the example; that is, for each trial, 300 participants were generated with values for treatment group, true disease status, reported disease status, and whether that individual was in the validation subgroup.

Another set of scenarios used the same parameter values but simulated a study of 1,000 participants. For each simulation, we randomly selected either 10% or 30% of participants for the validation subgroup. In each scenario, the odds ratio for the effect of acyclovir on ocular HSV recurrence was estimated using each of the 4 methods described above and summarized over 10,000 simulations. In a separate scenario assuming no exposure effect in 10,000 cohorts of 1,000 participants with 30% validation subgroups, we assessed the type-1 error rates of the maximum likelihood and multiple imputation approaches. For both approaches, the type-1 error rate was 0.051.

RESULTS

Study participants had a median age of 49 years; 48% were female and 85% were white. Table 1 presents the data on self-reported recurrence (W) and physician-diagnosed ocular HSV recurrence (D) from the Herpetic Eye Disease Study. Of the 308 study participants for whom both outcome measures were available, 91 were randomly selected for the hypothetical validation subgroup. Of the 14 participants in the validation subgroup who reported HSV recurrences, 8 were diagnosed with HSV recurrence by a physician; of the 77 participants who did not report HSV recurrence, 65 had no physician-diagnosed recurrence. Specificity of self-reported HSV recurrence was 0.9 (95% confidence interval (CI): 0.8, 1.0) and did not differ by treatment group. Sensitivity appeared to be higher for participants assigned to acyclovir (sensitivity = 0.5; 95% CI: 0.3, 0.6) than for participants assigned to placebo (sensitivity = 0.3; 95% CI: 0.2, 0.5), though the difference was imprecise (P = 0.2). The sensitivity and specificity of self-reported HSV recurrence in the validation subgroup were similar to the sensitivity and specificity in the full cohort.

Table 1.

Characteristics of Full Cohort and Validation Subgroup^a (n = 308), Multicenter Herpetic Eye Disease Study, 1992–1998

	Full Cohort (n = 308)		Validation Subgroup (n = 91)
	No. on Placebo	No. on Acyclovir	No. on Placebo	No. on Acyclovir
No self-reported recurrenceb
No diagnosed recurrence	104	119	30	35
Diagnosed recurrence	26	14	8	4
Self-reported recurrenceb
No diagnosed recurrence	11	10	3	3
Diagnosed recurrence	12	12	4	4
Sensitivityc	0.32	0.46	0.33	0.50
Specificityd	0.90	0.92	0.91	0.92

^a Self-reported outcomes and physician records were available for all 308 participants. We sampled a synthetic validation subgroup of 91 participants for the purposes of illustration.

^b Participants reported ocular HSV recurrences through a weekly diary and were seen by an ophthalmologist every 3 months. Self-reported recurrences were determined from data obtained from patient diaries, and physician-diagnosed recurrences were determined via examination by the study ophthalmologist.

^c Sensitivity was the proportion of patients with a physician-diagnosed recurrence who also self-reported a recurrence.

^d Specificity was the proportion of participants without a physician-diagnosed recurrence who did not self-report a recurrence.

Table 2 presents estimates of the odds ratio from each method to account for outcome misclassification. In the complete data, the odds ratio comparing the gold-standard outcome measure, physician-diagnosed HSV recurrence, between treatment groups was 0.62 (95% CI: 0.35, 1.09; standard error (SE), 0.29). The odds ratio comparing self-reported HSV recurrence between participants assigned to acyclovir and those assigned to placebo was 0.90 (95% CI: 0.47, 1.73; SE, 0.33). Restricting the analysis to the 91 participants in the validation subgroup yielded an odds ratio estimate of 0.57 (95% CI: 0.20, 1.59; SE, 0.52). Although this result was similar to the estimate from the complete data, it was less precise, as was expected based on the smaller sample size. Assuming outcome misclassification was nondifferential with respect to treatment group, the direct maximum likelihood approach estimated an odds ratio of 0.62 (95% CI: 0.26, 1.53; SE, 0.46). Assuming differential misclassification, the estimated odds ratio from the direct maximum likelihood approach was 0.59 (95% CI: 0.22, 1.55; SE, 0.49). Accounting for outcome misclassification through multiple imputation produced estimated odds ratios of 0.60 (95% CI: 0.24, 1.51; SE, 0.47) and 0.62 (95% CI: 0.24, 1.61; SE = 0.49) assuming nondifferential and differential misclassification, respectively. Estimates from the direct maximum likelihood and multiple imputation approaches were similar in magnitude to estimates from the validation subgroup alone and marginally more precise. Table 3 presents results from several analyses of the risk ratio. Direct maximum likelihood and multiple imputation produced estimates of the risk ratio that were similar to the estimate of the risk ratio from the complete data using physician-diagnosed recurrence as the outcome measure (risk ratio = 0.68; 95% CI: 0.44, 1.07; SE, 0.23). Accounting for outcome misclassification using direct maximum likelihood produced an estimated risk ratio of 0.68 (95% CI: 0.34, 1.38; SE, 0.36) assuming nondifferential misclassification and 0.65 (95% CI: 0.31, 1.40; SE, 0.39) assuming differential misclassification. The estimated risk ratios from the multiple imputation approach were 0.69 (95% CI: 0.35, 1.36; SE, 0.35) and 0.69 (95% CI: 0.34, 1.41; SE, 0.36) assuming nondifferential and differential misclassification, respectively. Estimates of the risk ratio from both direct maximum likelihood and multiple imputation were similar in magnitude to estimates from analysis limited to the validation subgroup (risk ratio = 0.61; 95% CI: 0.27, 1.35, SE, 0.41) and were slightly more precise.

Table 2.

Estimates of the Odds Ratio Comparing Recurrence of Ocular Herpes Simplex Virus Between Participants Randomized to Acyclovir or Placebo From Various Models (n = 308), Multicenter Herpetic Eye Disease Study, 1992–1998

Model	No. of Outcomes	No. at Risk	Adjusted ORa	95% CI	SE for ln(OR)
Complete data, physician- diagnosed recurrence
Acyclovir group	26	155	0.62	0.35, 1.09	0.29
Placebo group	38	153	1
Total	64	308
Naive analysis
Acyclovir group	22	155	0.90	0.47, 1.73	0.33
Placebo group	23	153	1
Total	45	308
Validation subgroupb
Acyclovir group	8	46	0.57	0.20, 1.59	0.52
Placebo group	12	45	1
Total	20	91
Direct maximum likelihood (nondifferential)			0.62	0.26, 1.53	0.46
Direct maximum likelihood (differential)			0.59	0.22, 1.55	0.49
Multiple imputation (nondifferential)			0.60	0.24, 1.51	0.47
Multiple imputation (differential)			0.62	0.24, 1.61	0.49

Abbreviations: CI, confidence interval; ln(OR), natural log of the odds ratio; OR, odds ratio; SE, standard error.

^a All models were adjusted for race, sex, age, and number of previous recurrences.

^b Validation subgroup included 91 participants.

Table 3.

Estimates of the Risk Ratio Comparing Recurrence of Ocular Herpes Simplex Virus Between Participants Randomized to Acyclovir or Placebo From Various Models (n = 308), Multicenter Herpetic Eye Disease Study, 1992–1998

Model	No. of Outcomes	No. at Risk	Adjusted RRa	95% CI	SE for ln(RR)
Complete data, physician- diagnosed recurrence
Acyclovir group	26	155	0.68	0.44, 1.07	0.23
Placebo group	38	153	1
Total	64	308
Naive analysis
Acyclovir group	22	155	0.93	0.55, 1.59	0.27
Placebo group	23	153	1
Total	45	308
Validation subgroupb
Acyclovir group	8	46	0.61	0.27, 1.35	0.41
Placebo group	12	45	1
Total	20	91
Direct maximum likelihood (nondifferential)			0.68	0.34, 1.38	0.36
Direct maximum likelihood (differential)			0.65	0.31, 1.40	0.39
Multiple imputation (nondifferential)			0.69	0.35, 1.36	0.35
Multiple imputation (differential)			0.69	0.34, 1.41	0.36

Abbreviations: CI, confidence interval; ln(RR), natural log of the risk ratio; RR, risk ratio; SE, standard error.

^a All models were adjusted for race, sex, age, and number of previous recurrences.

^b Validation subgroup included 91 participants.

Simulation results

Results from the simulations indicated that multiple imputation removed bias due to outcome misclassification under all combinations of sensitivity, specificity, and validation subgroup sizes explored. Naive estimates were biased dramatically towards the null in scenarios with both nondifferential and differential misclassification, with bias increasing as sensitivity decreased (Tables 4 and 5). In contrast, the multiple-imputation approach yielded estimates of the odds ratio with less bias than the naive analysis in all scenarios examined. Bias in odds ratios estimated by multiple imputation was similar in magnitude to bias in estimates from analyses limited to the validation subgroup and bias in estimates obtained using direct maximum likelihood. Bias decreased as the proportion of participants in the validation subgroup increased, but all 3 correction methods succumbed to finite sample bias when the total number of subjects in the validation subgroup was small.

Table 4.

Bias, 95% Confidence Interval Coverage, and Mean Squared Error for Simulation Studies^a Under 9 Scenarios for Nondifferential Misclassification

Sensitivity	Specificity	Sample Size	Validation Percentb	Naive			Validation			Direct Maximum Likelihood			Multiple Imputation
				Biasc	Coverd	MSEe	Bias	Cover	MSE	Bias	Cover	MSE	Bias	Cover	MSE
0.9	0.9	1,000	10	24	62	8	−5	96	47	−4	96	33	2	97	27
		1,000	30	24	62	8	−1	95	10	−1	95	6	−1	95	6
		300	30	24	85	13	−5	96	47	−4	96	42	2	97	27
0.6	0.9	1,000	10	35	40	15	−5	96	47	−5	96	48	−3	96	29
		1,000	30	35	40	15	−1	95	10	−1	95	8	−1	95	8
		300	30	35	76	21	−5	96	47	−4	96	48	−3	96	33
0.3	0.9	1,000	10	51	20	30	−5	96	47	−5	96	54	−4	95	35
		1,000	30	51	20	30	−1	95	10	−1	95	9	−1	95	9
		300	30	51	66	38	−5	96	47	−5	96	58	−3	96	37

Abbreviation: MSE, mean squared error.

^a Results are summarized over 10,000 simulations.

^b Percent of all participants included in the validation subgroup.

^c Bias was defined as 100 times the difference between the average estimated log odds ratio and the true log odds ratio.

^d Confidence interval coverage was calculated as the percentage of simulations in which the estimated 95% Wald-type confidence limits included the true value.

^e MSE was calculated as the sum of the bias squared and the variance.

Table 5.

Bias, 95% Confidence Interval Coverage, and Mean Squared Error for Simulation Studies^a Under 6 Scenarios for Differential Misclassification

Sensitivityb	Specificity	Sample Size	Validation Percentc	Naive			Validation			Direct Maximum Likelihood			Multiple Imputation
				Biasd	Covere	MSEf	Bias	Cover	MSE	Bias	Cover	MSE	Bias	Cover	MSE
(0.95, 0.85)	0.9	1,000	10	34	36	14	−5	96	47	−5	96	41	4	100	12
		1,000	30	34	36	14	−1	95	10	−1	95	6	1	97	6
		300	30	34	75	19	−5	96	47	−4	96	42	3	99	17
(0.70, 0.50)	0.9	1,000	10	60	4	39	−5	96	47	−5	96	46	3	98	17
		1,000	30	60	4	39	−1	95	10	−1	95	8	0	96	7
		300	30	60	47	45	−5	96	47	−5	96	49	2	98	23

Abbreviation: MSE, mean squared error.

^a Results are summarized over 10,000 simulations.

^b Sensitivity differs by exposure group; presented as (sensitivity for X = 1, sensitivity for X = 0).

^c Percent of all participants included in the validation subgroup.

^d Bias was defined as 100 times the difference between the average estimated log odds ratio and the true log odds ratio.

^e Confidence interval coverage was calculated as the percentage of simulations in which the estimated 95% Wald-type confidence limits included the true value.

^f MSE was calculated as the sum of the bias squared and the variance.

Confidence intervals from the naive analysis showed poor coverage that varied as a function of sensitivity and sample size. Confidence intervals from multiple imputation maintained appropriate coverage, as did those from the validation subgroup and direct maximum likelihood.

Multiple imputation and direct maximum likelihood generally had smaller mean squared errors than did analysis limited to the validation subgroup. However, all 3 methods used to account for outcome misclassification typically had larger mean squared errors than did the naive analysis because the added imprecision of the correction methods offset the corresponding reduction in bias.

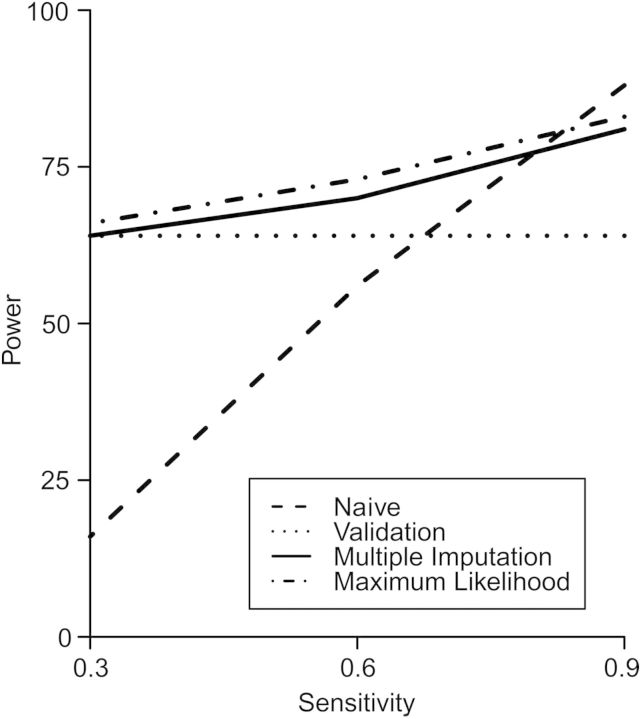
Results from simulations indicated that both direct maximum likelihood and multiple imputation had higher statistical power than did limiting the analysis to the validation subgroup at levels of sensitivity commonly seen in the literature (0.9 and 0.6), but that all 3 nonnaive methods had similar statistical power at low values of sensitivity (0.3), as seen in the example (Figure 1). Analyses that accounted for misclassification using multiple imputation were slightly less powerful than those that used direct maximum likelihood. As expected, statistical power for the methods to account for outcome misclassification increased as the sensitivity of the observed outcome measure increased. Despite a pronounced null bias, the naive analysis had high statistical power when sensitivity was large due to its high precision. However, when sensitivity decreased, bias in the naive analysis caused power to fall well below that of the other methods.

Figure 1.

Relationship between statistical power and sensitivity of the observed outcome measure in simulations with a 30% validation subgroup and a total sample size of 1,000 for the naive analysis, analysis limited to the validation subgroup, analysis using the direct maximum likelihood method, and analysis using the multiple-imputation method to account for outcome misclassification.

DISCUSSION

Multiple imputation performed well to account for bias due to outcome misclassification in the Herpetic Eye Disease Study example and the scenarios explored through simulation. Estimates from multiple imputation were similar in magnitude to estimates from the complete data using the gold-standard outcome and were marginally more precise than estimates from the analysis limited to the validation subgroup. Multiple imputation produced estimates that were similar in magnitude and precision to estimates obtained using direct maximum likelihood to account for outcome misclassification. These results were supported in Monte Carlo simulations, in which multiple imputation yielded estimates with little bias in all scenarios and was sometimes more statistically powerful than analyses limited to the validation subgroup.

Both multiple imputation and direct maximum likelihood have been used to handle traditional missing data situations (7, 19, 20) and exposure measurement error (4, 21). Both approaches have been shown to provide consistent and asymptotically normal estimates. The direct maximum likelihood approach produces estimates that are asymptotically efficient, whereas multiple imputation produces estimates that approach asymptotic efficiency as the number of imputations increases (22). Although multiple imputation uses a 2-stage estimation procedure, it can be implemented with standard missing data methods. In contrast, though direct maximum likelihood methods perform estimation in a single step, these methods must be programmed explicitly using a procedure that is able to obtain maximum likelihood estimates given a general likelihood expression, such as the SAS procedure NLMIXED. We could have addressed outcome misclassification with other techniques to handle missing data, such as inverse probability weights or the expectation maximization algorithm. We chose to use multiple imputation because the standard inverse probability–weighted estimator is inefficient (23) and the expectation maximization algorithm is more difficult to implement in standard software.

In the example, we demonstrated that the multiple imputation approach can be easily adapted to estimate risk ratios using log-binomial regression. Had the binomial model not converged, we could have applied the multiple-imputation approach with any standard method to estimate the risk ratio, including the “copy method” applied in the binomial model (24, 25), modified Poisson regression (26), or Bayesian techniques (27). More importantly, flexibility in the choice of analysis models enables the multiple-imputation techniques illustrated here to be further extended to account for misclassification of nonbinary outcomes by altering the imputation and analysis models. For continuous outcomes measured with error, the observed outcome measure and covariates could be regressed on the gold-standard outcome measure in the validation subgroup using linear regression. Coefficients from this model could be used to impute outcomes for study participants not in the validation subgroup, and the complete data set could then be analyzed using the appropriate analysis model.

Another advantage of the multiple-imputation approach is that it easily allows researchers to include different sets of variables in the imputation model and the analysis model. Performing the imputation and analysis using different models avoids the problem of conditioning on variables influencing only the relationship between the observed and gold-standard outcome in the final analysis model. Likewise, the imputation model could be altered to use more flexible prediction functions in place of the linear-logistic model used to impute outcomes in this example (28).

Although the present work focuses on estimation of effect measures in a closed cohort, flexibility in the choice of analysis model allows the multiple-imputation approach to be extended to account for outcome misclassification in analysis of time-to-event outcomes in situations in which the event type is subject to error but the event date is assumed to be known. In this scenario, the event indicator could be imputed using the monotone logistic method, and the hazard ratio or rate ratio would be estimated in each imputation and summarized using equation 4.

Measurement error methods typically assume that the relationship between the true outcome and the observed outcome variable is monotonic, which implies that the observed outcome measure increases, plateaus, or decreases with increasing levels of the gold-standard measure but does not decrease after an increase or vice versa (29). Monotonicity is ensured for binary outcome variables (as in the example) but must be considered for nonbinary outcomes.

In the example, accounting for misclassification with multiple imputation and direct maximum likelihood offered only slight gains in precision over analysis limited to the validation subgroup. We expect estimates from multiple imputation and direct maximum likelihood to be more precise than estimates from the validation subgroup because these methods use information from all participants in the study to estimate the effect size, whereas analysis limited to the validation subgroup discards all information on participants missing the gold-standard outcome measure. Because in our example the observed outcome was a poor proxy for the gold-standard outcome, the imputation model contained a high degree of uncertainty that propagated through to the variance of the final effect estimate. Larger gains in precision would be expected if sensitivity in the example data were higher or the proportion of participants in the validation substudy were smaller. However, in the example, when the proportion of participants in the validation substudy was further reduced, the absolute numbers in the validation substudy became so small that results became unstable.

In simulations, we used mean squared error to assess the tradeoff between bias and precision. Despite its large bias, the naive analysis had a smaller mean squared error than did methods to account for outcome misclassification in most of the scenarios explored through simulation. Because mean squared error places equal weight on bias and variance, the precision of the naive analysis offset its bias. In large sample sizes, where mean squared error is dominated by bias instead of random error, the nonnaive methods will be superior to the naive analysis. The simulation results can be interpreted only under the assumption that the underlying data-generating mechanism matches the parametric models used to simulate the data. It is unclear how multiple imputation and direct maximum likelihood would have performed under a misspecified analysis model.

We have shown that multiple imputation works well to account for both nondifferential and differential outcome misclassification. When the degree of misclassification varied across levels of exposure, we often saw separation of data points in the imputation model. Separation is likely to occur when the positive predictive value of the observed outcome is high. In this analysis, we applied Firth's correction to obtain point estimates in these models. Alternatively, Bayesian methods could be used to address the problem of separation by incorporating prior information to stabilize regression coefficients.

A limitation of the both multiple-imputation and direct maximum likelihood approaches is that they depend on correct specification of the model relating the observed outcome to the gold-standard outcome measure. Estimates of the association between exposure and outcome could be biased if the relationship between the observed and gold-standard measurements is not transportable, implying that it is not consistent between the validation subgroup and the complete data. Obtaining a representative validation subgroup is vital to any method using a validation study to account for misclassification, as these methods typically assume that information on the gold-standard outcome measure is missing at random. Because inclusion in the validation subgroup determines if the gold-standard outcome is missing for a participant, the probability of being included in the validation study must be independent of that participant's gold-standard outcome given the observed outcome and the covariates. When information on the gold-standard outcome measure is not missing at random, the transportability assumption may not be met.

We must also consider the possibility that the gold-standard measurement is itself misclassified. A fundamental limitation of all validation studies is that they assume that the gold-standard outcome measure represents the true outcome. In the example, physician diagnosis may have been misclassified if a participant experienced a recurrence of HSV that resolved before the opportunity for physician diagnosis or if errors occurred during chart abstraction. In situations in which the gold-standard measurement is itself subject to nonnegligible error, using methods that rely on validation data to account for outcome misclassification may yield biased and falsely precise estimates (30).

Under the assumptions mentioned above, applying multiple imputation to account for outcome misclassification removes bias in effect estimates from logistic and log-binomial regression. This technique uses well-established missing data methods that can be implemented using standard statistical software and provides an opportunity for data analysts to account for outcome misclassification in wide range of statistical models.