Abstract
Modern case–control studies typically involve the collection of data on a large number of outcomes, often at considerable logistical and monetary expense. These data are of potentially great value to subsequent researchers, who, although not necessarily concerned with the disease that defined the case series in the original study, may want to use the available information for a regression analysis involving a secondary outcome. Because cases and controls are selected with unequal probability, regression analysis involving a secondary outcome generally must acknowledge the sampling design. In this paper, the author presents a new framework for the analysis of secondary outcomes in case–control studies. The approach is based on a careful re-parameterization of the conditional model for the secondary outcome given the case–control outcome and regression covariates, in terms of (a) the population regression of interest of the secondary outcome given covariates and (b) the population regression of the case–control outcome on covariates. The error distribution for the secondary outcome given covariates and case–control status is otherwise unrestricted. For a continuous outcome, the approach sometimes reduces to extending model (a) by including a residual of (b) as a covariate. However, the framework is general in the sense that models (a) and (b) can take any functional form, and the methodology allows for an identity, log or logit link function for model (a).
Keywords: Case–control studies, Generalized linear models, Statistical genetics, Secondary outcomes
1. Introduction
Case–control studies typically collect information on a large number of outcomes, often at considerable cost. These data are of potentially great value for studying associations, involving a secondary outcome other than the disease outcome defining case–control status. For instance, secondary outcomes analyses are now routine in genetic epidemiology, with several recent papers on genetic variants influencing human quantitative traits such as height, body mass index, and lipid levels, using data mostly from case–control studies of complex diseases (diabetes, cancer, and hypertension) (Lettre and others, 2008; Loos and others, 2008; Sanna and others, 2008; Weedon and others, 2007). Other examples have emerged in environmental epidemiology, such as the recent study of Weuve and others (2009), which uses data taken, in part, from a case–control study nested within the Nurses’ Health Study (NHS). In the NHS Lead Study, Boston-area NHS participants had extensive lead exposure assessment (bone and blood measures). Associations of lead measures with hypertension, bone mineral density/metabolism, and cognition were then assessed. However, the Lead Study selected women on the basis of their blood pressure status. Therefore, analyses that aim to evaluate risk factors of osteoporosis (a binary outcome) and cognitive function decline (a continuous outcome), may be affected by the case–control sampling design. In fact, Monsees and others (2009) and Lin and Zeng (2009) established that the non-random ascertainment from the study base, when ignored, can sometimes lead to inflated Type I error rate for tests of associations of a secondary outcome in re-purposed case–control samples. They further showed that commonly used analytic techniques, such as least-squares regression for quantitative traits, can sometimes give biased estimates, and that such bias can be present when covariates in the regression model in view, are associated with the case–control outcome, which itself is independently associated with the secondary outcome.
A number of analytic strategies have been proposed to eliminate selection bias associated with oversampling of cases in analyses of secondary outcomes; see, for instance, Nagelkerke and others (1995), Lee and others (1997), Jiang and others (2006), Reilly and others (2005), Richardson and others (2007), Lin and Zeng (2009), Monsees and others (2009), Li and others (2010), Wang and Shete (2011), and Wei and others (2013). Suggested strategies include: (i) weighting the standard analysis by the inverse of sampling probabilities (IPW); (ii) performing the analysis only in controls; (iii) analyzing cases and controls separately, i.e. stratifying the analysis by case–control status; (iv) including case–control status as a covariate in the regression model of the secondary outcome.
The first strategy (i) gives a viable simple solution as it recovers correct inferences about association measures, without the burden of additional modeling that would be required had data been sampled independently of case–control status. However, simply weighting by sampling rates will often be inefficient (Robins and others, 1994; Tchetgen Tchetgen, 2012). The second method is appropriate only when the disease status is rare in the population but does not use data on cases which might render it relatively inefficient. Methods that adjust for the primary disease status by either (iii) or (iv) may yield flawed conclusions because the associations between a secondary outcome and an exposure of interest in the case and control groups can be quite different from the association in the underlying target population. More formal likelihood methods have also appeared in the literature. For instance, (v) Jiang and others (2006) considered various likelihood methods for categorical secondary outcomes that can be more efficient than (i). (vi) Recently, Lin and Zeng (2009) further generalized the likelihood framework for a continuous secondary outcome by assuming the latter follows a specific parametric distribution, with special emphasis given to a normal model.
They also establish that the likelihood approach is well approximated by strategy (iv) under the following specific conditions: (LZ.1) a rare disease assumption about the disease outcome defining case–control status, (LZ.2) no interaction between the secondary outcome and covariates in a regression model for the case–control outcome, and (LZ.3) the secondary outcome is normally distributed.
Thus, Lin and Zeng (2009) justify formally via a maximum likelihood argument, the conditional approach (iv) under conditions (LZ.1)–(LZ.3). More recently, (vii) Wei and others (2013) develop an estimating equations approach for a continuous secondary outcome which relaxes the distributional assumption made in (v) somewhat, and instead requires that the secondary outcome regression is “strongly homoscedastic” in the following sense. They assume that residuals from the secondary outcome regression are independent of covariates, but their density is otherwise unrestricted. In other words, they suppose that any association between the vector of covariates and the secondary outcome is completely captured by a location shift model. Their inferential framework relies crucially on this assumption, and may be biased if the assumption does not hold exactly.
An additional approach is proposed by Chen and others (2013) who uses a bias correction formula for an odds ratio parameter, while Ghosh and others (2013) adopt a retrospective likelihood framework, further extending the likelihood framework of Lin and Zeng (2009).
In this paper, the author generalizes the conditional approach (iv) to allow for possible violation of any or all of assumptions (LZ.1)–(LZ.3), without assuming the location shift model of Wei and others (2013). The new approach is based on a careful non-parametric re-parameterization of the conditional model for the secondary outcome given the case–control outcome and regression covariates, in terms of: (a) the population regression of interest for the secondary outcome given covariates and (b) the population regression of the case–control outcome on covariates.
Because non-parametric inference may not be practical for regression analysis with numerous covariates, parametric, and semiparametric models will invariably be used in practice for (a) for (b). Crucially, the re-parameterization ensures models for (a) and (b) are variation independent, in the sense that, whether parametric or semiparametric, a choice of model for (a) places no restriction on a corresponding choice of model for (b) and vice-versa. An important feature of the proposed strategy is that the error distribution for the secondary outcome conditional on covariates and case–control status is unrestricted. For a continuous outcome, the approach sometimes simplifies to extending model (a) by including the residual of (b) as an additional regression covariate producing a regression model for the secondary outcome conditional on case–control status, that is directly parameterized in terms of model (a). We show such a re-parameterization can appropriately account for selection bias without compromising inference about the population regression parameter. The framework is general in the sense that models (a) and (b) can take any functional form, and the methodology is developed to allow the use of the identity, log (described in supplementary material available at Biostatistics online) or logit link function in model (a). For inference, a simple estimating equation framework is first developed, and a strategy for obtaining a semiparametric locally efficient estimator is subsequently described. Simulations and an empirical example are used to illustrate the approach.
2. Regression with an identity link function
2.1. Re-parameterization of conditional regression function
Consider an unmatched case–control sample of i.i.d data consisting of the case–control status D, a continuous secondary outcome Y, and covariates X. Unless otherwise stated, we will assume that the sampling fraction is known for cases and controls, respectively. This is often a reasonable assumption, that is, fairly standard in the literature on secondary outcomes (e.g. Jiang and others, 2006; Lin and Zeng, 2009; Wei and others, 2013), and the assumption is usually satisfied by design in nested case–control studies. An equivalent assumption is that the disease prevalence is known to be 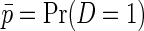 in the target population, and
in the target population, and 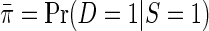 in the case–control sample, where S indicates selection into the case–control sample. Formally,
in the case–control sample, where S indicates selection into the case–control sample. Formally, 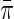 may be taken as the limiting proportion of cases in the case–control study with increasing sample size. As we will see below, the assumption that
may be taken as the limiting proportion of cases in the case–control study with increasing sample size. As we will see below, the assumption that  is known will usually not be needed when the disease is rare for all levels of X in the population
is known will usually not be needed when the disease is rare for all levels of X in the population The main target of inference is the population mean model for Y given X which we denote for the identity link,
The main target of inference is the population mean model for Y given X which we denote for the identity link, 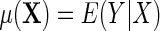 . A familiar example of such a model is
. A familiar example of such a model is
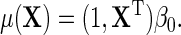 |
(2.1) |
We will also consider the conditional mean of Y given 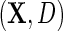 , which we denote
, which we denote 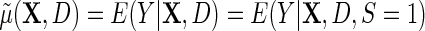 , where the second equality holds by design, because selection into the unmatched case–control sample is independent of
, where the second equality holds by design, because selection into the unmatched case–control sample is independent of 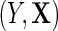 given D. Then, the following relation between
given D. Then, the following relation between 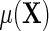 and
and 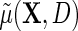 also holds,
also holds,
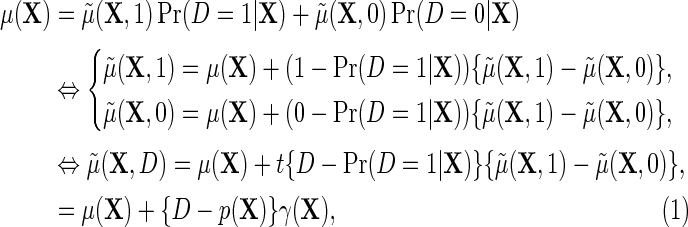 |
(2.2) |
where 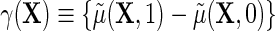 describes the association between Y and D on the mean difference scale, within levels of X, and
describes the association between Y and D on the mean difference scale, within levels of X, and 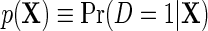 is the population risk of D within levels of X. From the alternative representation of
is the population risk of D within levels of X. From the alternative representation of 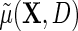 given in the display above, one learns that the conditional mean function
given in the display above, one learns that the conditional mean function 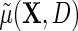 can be directly parameterized in terms of the population regression function of interest
can be directly parameterized in terms of the population regression function of interest 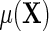 , and the additional functions
, and the additional functions 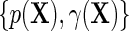 . Note that the proposed re-parameterization is non-parametric, in the sense that it is not restricted to a particular choice of models for
. Note that the proposed re-parameterization is non-parametric, in the sense that it is not restricted to a particular choice of models for 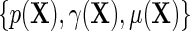 and therefore in principle, parametric, semiparametric, and non-parametric models can be used for each of these functions. Crucially, these functions are also variation independent, so that the choice of parameterization does not a priori rule out any possible data-generating mechanism. The function
and therefore in principle, parametric, semiparametric, and non-parametric models can be used for each of these functions. Crucially, these functions are also variation independent, so that the choice of parameterization does not a priori rule out any possible data-generating mechanism. The function 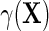 may be viewed as a selection bias function induced by an association between D and Y within levels of X. Thus, the re-parameterization confirms what we might naturally expect, that the marginal and conditional regressions of Y on X coincide exactly when selection bias is absent on the additive scale, i.e.
may be viewed as a selection bias function induced by an association between D and Y within levels of X. Thus, the re-parameterization confirms what we might naturally expect, that the marginal and conditional regressions of Y on X coincide exactly when selection bias is absent on the additive scale, i.e. 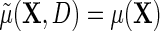 if
if 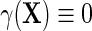 . Furthermore, the re-parameterization ensures that even when
. Furthermore, the re-parameterization ensures that even when 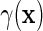 is not zero for at least one level of
is not zero for at least one level of 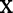 , as one would hope, upon averaging over D in the underlying population,
, as one would hope, upon averaging over D in the underlying population, 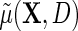 reduces to
reduces to 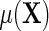 exactly. Additionally, one learns from the re-parameterization that when, (ETT.1)
exactly. Additionally, one learns from the re-parameterization that when, (ETT.1)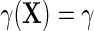 does not vary with X, and, (ETT.2) the disease is rare in the population, so that
does not vary with X, and, (ETT.2) the disease is rare in the population, so that 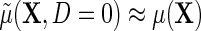 and
and 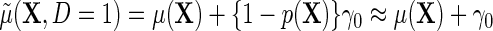 , then
, then 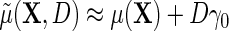 , which in the special case of model (2.1) takes the standard linear form
, which in the special case of model (2.1) takes the standard linear form 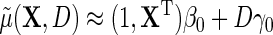 . This implies that, under conditions (ETT.1) and (ETT.2), the simple strategy of extending the population model of interest
. This implies that, under conditions (ETT.1) and (ETT.2), the simple strategy of extending the population model of interest 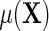 by adding a main effect for D to the regression to adjust for case–control sampling, is approximately correct. Although the ensuing approximation to the regression
by adding a main effect for D to the regression to adjust for case–control sampling, is approximately correct. Although the ensuing approximation to the regression 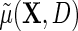 is equal to that of Lin and Zeng (2009), we note that their required assumptions (LZ.1)–(LZ.3) imply assumptions (ETT.1) and (ETT.2), while the converse is not generally true. Specifically, it is straightforward to verify that assumptions (LZ.2) and (LZ.3) imply the no-heterogeneity assumption (ETT.1). However, without the normality assumption, (LZ.2) and (ETT.2) are not necessarily equivalent. The appeal of (ETT.2) is that it does not require distributional assumptions for the secondary outcome. Finally, one should note that (LZ.2) and (ETT.1) are empirically testable, and can be relaxed to account for possible effect heterogeneity. Specifically, as we will see in the next section, (ETT.1) may be relaxed by modeling
is equal to that of Lin and Zeng (2009), we note that their required assumptions (LZ.1)–(LZ.3) imply assumptions (ETT.1) and (ETT.2), while the converse is not generally true. Specifically, it is straightforward to verify that assumptions (LZ.2) and (LZ.3) imply the no-heterogeneity assumption (ETT.1). However, without the normality assumption, (LZ.2) and (ETT.2) are not necessarily equivalent. The appeal of (ETT.2) is that it does not require distributional assumptions for the secondary outcome. Finally, one should note that (LZ.2) and (ETT.1) are empirically testable, and can be relaxed to account for possible effect heterogeneity. Specifically, as we will see in the next section, (ETT.1) may be relaxed by modeling 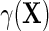 , which leads to the modified approximation
, which leads to the modified approximation 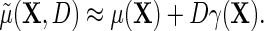 For instance, taking
For instance, taking 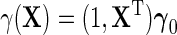 gives under model (2.1), the standard linear form
gives under model (2.1), the standard linear form 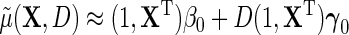 . Crucially, one may note that while the modified approximation now incorporates possible interactions between D and X, i.e.
. Crucially, one may note that while the modified approximation now incorporates possible interactions between D and X, i.e. 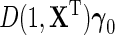 , both the main effect of D and its interactions with X are not interpretable as part of the marginal association between X and Y for the population, only the first term of the approximate expression for
, both the main effect of D and its interactions with X are not interpretable as part of the marginal association between X and Y for the population, only the first term of the approximate expression for 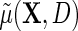 , i.e.
, i.e. 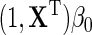 encodes the marginal association of interest.
encodes the marginal association of interest.
We should also note that, while we have assumed, and we will continue to do so unless otherwise noted, that the data arise from an unmatched case–control study, the above parameterization would continue to hold in the presence of matching, provided that the factors defining the matched set were also included in X. This is illustrated in the matched case–control ovarian cancer study reported in Section 6.
2.2. Inference via simple estimating equations
Next, let 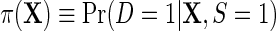 denote the risk function of D within levels of X in an unmatched case–control sample.
denote the risk function of D within levels of X in an unmatched case–control sample. 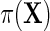 and
and 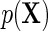 are well known to satisfy the following relation:
are well known to satisfy the following relation:
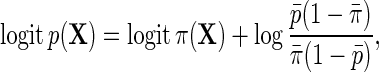 |
so that population and the case–control risks of D agree on the logit scale, up to a constant shift in the intercept. Suppose that 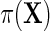 follows a logistic model
follows a logistic model
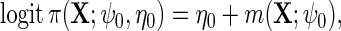 |
(2.3) |
where 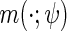 is a known function indexed by a parameter
is a known function indexed by a parameter 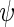 satisfying
satisfying 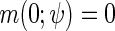 , with unknown intercept
, with unknown intercept 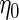 and slope
and slope 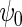 . In the following, we will assume for simplicity that
. In the following, we will assume for simplicity that 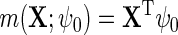 , although more elaborate models can also be used. Thus,
, although more elaborate models can also be used. Thus, 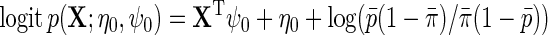 . For simplicity, we will also assume without loss of generality that
. For simplicity, we will also assume without loss of generality that 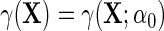 , where
, where 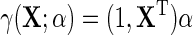 . Together, these various parametric assumptions produce a corresponding model for
. Together, these various parametric assumptions produce a corresponding model for 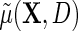 :
:
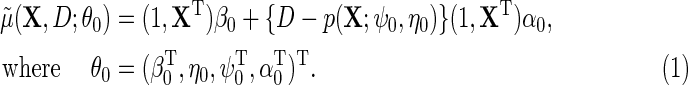 |
(2.4) |
We propose to estimate 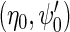 by standard logistic maximum likelihood of (2.3) using data on
by standard logistic maximum likelihood of (2.3) using data on 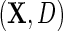 , i.e. by maximizing the partial log-likelihood
, i.e. by maximizing the partial log-likelihood 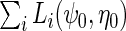 w.r.t.
w.r.t. 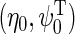 where
where 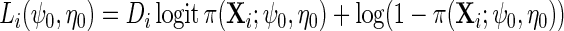 . For any
. For any 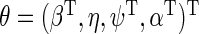 , let
, let 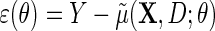 and define the estimating function
and define the estimating function
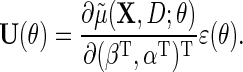 |
(2.5) |
This corresponds for the simple parametric models considered above to, 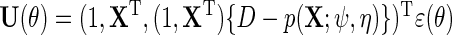 , where
, where 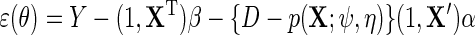 . We propose to estimate
. We propose to estimate 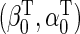 , with
, with 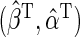 which solves
which solves 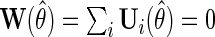 . In principle, one may specify any vector
. In principle, one may specify any vector 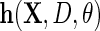 of dimension
of dimension 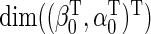 in place of
in place of 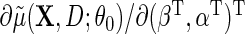 in (2.5), to obtain
in (2.5), to obtain 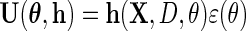 provided the derivative of the resulting estimating equation, more precisely its expectation, is not singular, and the variance–covariance matrix of
provided the derivative of the resulting estimating equation, more precisely its expectation, is not singular, and the variance–covariance matrix of 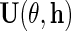 is finite. Interestingly, IPW estimation is recovered upon setting
is finite. Interestingly, IPW estimation is recovered upon setting 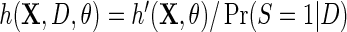 and
and 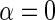 , so that D only appears in the inverse-probability weight for selection into the sample, and no longer in the outcome regression. From this observation, we also have that one can expect IPW to be suboptimal compared with the proposed approach, in the absence of model mis-specification, since by the proposition given in Section 4, setting
, so that D only appears in the inverse-probability weight for selection into the sample, and no longer in the outcome regression. From this observation, we also have that one can expect IPW to be suboptimal compared with the proposed approach, in the absence of model mis-specification, since by the proposition given in Section 4, setting 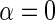 and
and 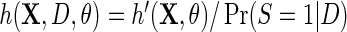 is inefficient. One may also verify using the proposition given in Section 4, that assuming
is inefficient. One may also verify using the proposition given in Section 4, that assuming 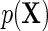 is known, the optimal choice of
is known, the optimal choice of 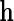 is
is 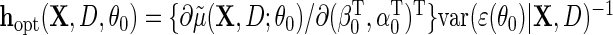 , and therefore
, and therefore 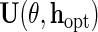 is optimal, in the sense of producing an estimator with minimal asymptotic variance among regular and asymptotically linear estimators (RAL), when
is optimal, in the sense of producing an estimator with minimal asymptotic variance among regular and asymptotically linear estimators (RAL), when 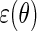 is homoscedastic and
is homoscedastic and 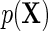 is known. A standard argument shows that under standard regularity conditions, the resulting estimator
is known. A standard argument shows that under standard regularity conditions, the resulting estimator 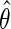 is in large sample approximately:
is in large sample approximately:
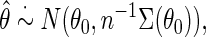 |
(2.6) |
where 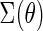 is the variance–covariance matrix of
is the variance–covariance matrix of 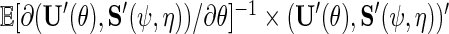 with
with 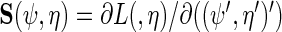 .
.
3. Regression with a logit link function
Next, suppose that Y is binary. We introduce a similar re-parameterization of 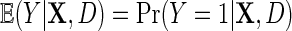 on the logit scale, in terms of
on the logit scale, in terms of 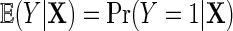 . To proceed, let
. To proceed, let 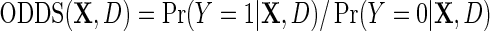 denote the odds of
denote the odds of 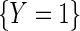 within levels of
within levels of 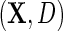 . Likewise, let
. Likewise, let 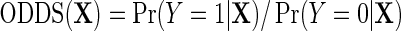 denote the odds of
denote the odds of 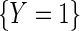 within levels of X. Then, note that
within levels of X. Then, note that
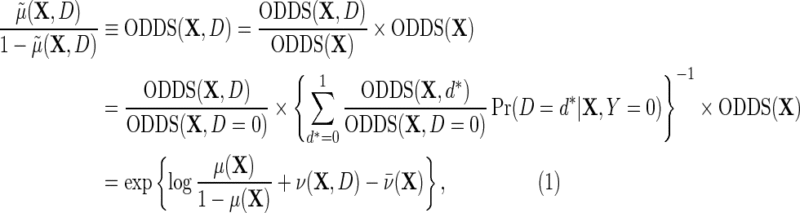 |
(3.1) |
where 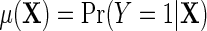 is the outcome risk function in the population, the function
is the outcome risk function in the population, the function 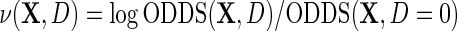 measures the log-odds ratio association between D and Y within levels of X, and accounts for selection bias due to the sampling design. As shown in supplementary material available at Biostatistics online, the parameter
measures the log-odds ratio association between D and Y within levels of X, and accounts for selection bias due to the sampling design. As shown in supplementary material available at Biostatistics online, the parameter 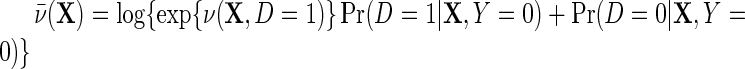 is not a free parameter, and is introduced to ensure that upon marginalization over D in the target population, as one would hope to be the case, the conditional risk function
is not a free parameter, and is introduced to ensure that upon marginalization over D in the target population, as one would hope to be the case, the conditional risk function  marginalizes to
marginalizes to 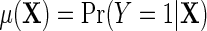 exactly. Interestingly, note that the population density of D used in the above re-parameterization conditions on
exactly. Interestingly, note that the population density of D used in the above re-parameterization conditions on 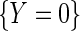 and hence differs from the density function of D involved in previous re-parameterizations for the identity or log-link functions. This choice of parameterization is tied to a property of probability odds functions which is key to our developments. We have that, while
and hence differs from the density function of D involved in previous re-parameterizations for the identity or log-link functions. This choice of parameterization is tied to a property of probability odds functions which is key to our developments. We have that, while 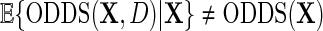 , it is, however, the case that
, it is, however, the case that 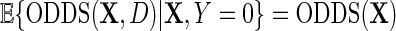 , in other words, marginalization of the conditional odds with respect to disease status in the underlying population free of the secondary outcome recovers the marginal odds function of primary interest. Equation (3.1) is equivalently written as a conditional logistic regression,
, in other words, marginalization of the conditional odds with respect to disease status in the underlying population free of the secondary outcome recovers the marginal odds function of primary interest. Equation (3.1) is equivalently written as a conditional logistic regression, 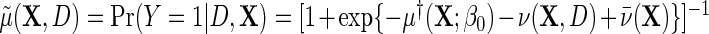 , where
, where 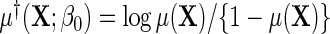 . Suppose that the log-odds function
. Suppose that the log-odds function 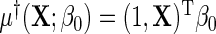 , and the log-odds ratio function
, and the log-odds ratio function 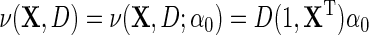 . We redefine
. We redefine
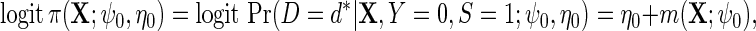 |
(3.2) |
using as before the convenient choice 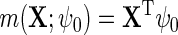 . Again, more elaborate models could be used to incorporate interactions and non-linearities. Let
. Again, more elaborate models could be used to incorporate interactions and non-linearities. Let 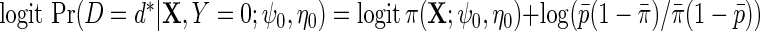 denote the corresponding model in the population, accounting for retrospective ascertainment. The resulting parametric model for
denote the corresponding model in the population, accounting for retrospective ascertainment. The resulting parametric model for 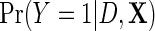 is given by
is given by
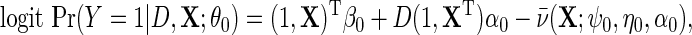 |
(3.3) |
where 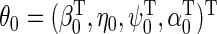 . Estimation and inference about
. Estimation and inference about 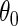 can then proceed as in the identity or log link settings, by solving the estimating equation
can then proceed as in the identity or log link settings, by solving the estimating equation 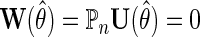 given by (2.5), upon substituting in (3.3) for the conditional mean model
given by (2.5), upon substituting in (3.3) for the conditional mean model 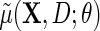 , but with
, but with 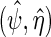 the maximum likelihood estimator obtained using the log-likelihood function
the maximum likelihood estimator obtained using the log-likelihood function 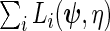 where
where 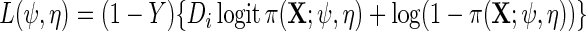 . The asymptotic distribution of
. The asymptotic distribution of 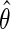 is then given by (2.6) once the above substitution is made. Finally, we briefly note that when D is rare, the logit link is well approximated by the log link and
is then given by (2.6) once the above substitution is made. Finally, we briefly note that when D is rare, the logit link is well approximated by the log link and 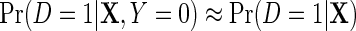 and therefore the approximate approach developed for the log link also applies here, see supplementary material available at Biostatistics online.
and therefore the approximate approach developed for the log link also applies here, see supplementary material available at Biostatistics online.
4. Semiparametric locally efficient estimation
In this section, we present an alternative, potentially more efficient strategy for estimating 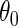 , based on semiparametric efficiency theory. To proceed, first note that as argued by Breslow and others (2000), the law of the observed data is formally given by the conditional density
, based on semiparametric efficiency theory. To proceed, first note that as argued by Breslow and others (2000), the law of the observed data is formally given by the conditional density 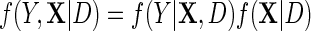 which is up to a proportionality constant equivalent to the density of an experiment in which D is itself randomly sampled from a Bernoulli density with known event probability equal to
which is up to a proportionality constant equivalent to the density of an experiment in which D is itself randomly sampled from a Bernoulli density with known event probability equal to 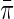 . Thus, we derive the efficient score for i.i.d data (Y, X, D) sampled from the joint density
. Thus, we derive the efficient score for i.i.d data (Y, X, D) sampled from the joint density
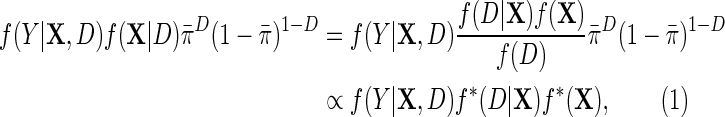 |
(4.1) |
where 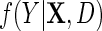 is the population density of Y given (X, D), f(D) is the known marginal density of D in the target population;
is the population density of Y given (X, D), f(D) is the known marginal density of D in the target population; 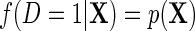 is the population probability that
is the population probability that 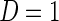 given X;
given X; 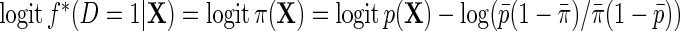 is the probability that
is the probability that 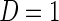 given X in the case–control sample;
given X in the case–control sample; 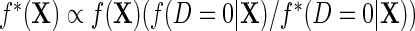 is the case–control density of X. Define the semiparametric model
is the case–control density of X. Define the semiparametric model 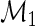 , with sole restrictions given by the restricted mean model
, with sole restrictions given by the restricted mean model 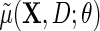 for Y given
for Y given 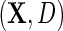 , with identity link (2.4) or log link (see supplementary material available at Biostatistics online); and the parametric model (2.3) for D given X. The model is otherwise non-parametric in the density of
, with identity link (2.4) or log link (see supplementary material available at Biostatistics online); and the parametric model (2.3) for D given X. The model is otherwise non-parametric in the density of 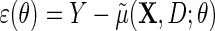 given
given 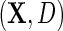 , as well as in the population density f(X) and thus in
, as well as in the population density f(X) and thus in 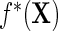 .
.
The following theorem gives the efficient score for 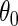 in model
in model 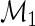 , a similar result for the logit link is relegated to supplementary material available at Biostatistics online.
, a similar result for the logit link is relegated to supplementary material available at Biostatistics online.
Proposition 1 —
The efficient score of
in model
is given by
with
and
, where
.
Next, suppose that 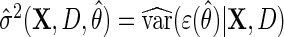 is a consistent estimate of the conditional variance
is a consistent estimate of the conditional variance 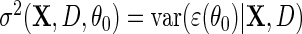 , then, upon defining
, then, upon defining 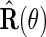 as
as 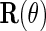 by replacing
by replacing 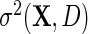 with
with 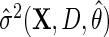 , the estimator
, the estimator 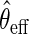 that solves
that solves 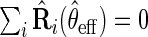 is regular and asymptotically linear, with large sample variance the semiparametric efficiency bound in
is regular and asymptotically linear, with large sample variance the semiparametric efficiency bound in 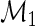 which is given by
which is given by 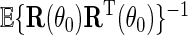 . In practice,
. In practice, 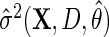 may be based on a parametric/semiparametric model, and therefore, may be inconsistent if mis-specified. Then,
may be based on a parametric/semiparametric model, and therefore, may be inconsistent if mis-specified. Then, 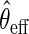 would still be RAL, although not necessarily asymptotically efficient. For this reason,
would still be RAL, although not necessarily asymptotically efficient. For this reason, 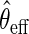 is known as a semiparametric locally efficient estimator that is consistent and asymptotically normal regardless of whether
is known as a semiparametric locally efficient estimator that is consistent and asymptotically normal regardless of whether 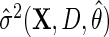 is consistent or not, and that is asymptotically efficient at the submodel where
is consistent or not, and that is asymptotically efficient at the submodel where 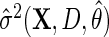 is consistent. Interestingly, upon close inspection of the efficient score
is consistent. Interestingly, upon close inspection of the efficient score 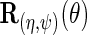 one notes that information about
one notes that information about 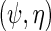 the parameter indexing the density of D given X, naturally comes from the score of the corresponding factor of the likelihood function, i.e.
the parameter indexing the density of D given X, naturally comes from the score of the corresponding factor of the likelihood function, i.e. 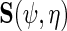 ; however, additional information is obtained from the factor corresponding to the conditional density of Y given
; however, additional information is obtained from the factor corresponding to the conditional density of Y given 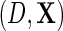 . Although unusual, this is not entirely surprising given that this density was carefully re-parameterized to depend on
. Although unusual, this is not entirely surprising given that this density was carefully re-parameterized to depend on 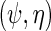 . This further reveals that the simple estimating equations approach that gave
. This further reveals that the simple estimating equations approach that gave 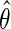 in previous sections, do not generally exploit this additional information since
in previous sections, do not generally exploit this additional information since 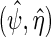 solve the score equation
solve the score equation 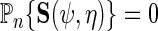 instead of the efficient score equation
instead of the efficient score equation 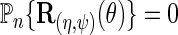 , and is therefore generally inefficient, except perhaps when the disease is rare.
, and is therefore generally inefficient, except perhaps when the disease is rare.
5. A simulation study
We performed a simulation study to compare in the context of simple linear regression, the performance of the locally efficient estimator to that of two common strategies used in practice. The first approach involves inverse-probability weighting by the selection probability given case–control status, while the second approach involves including case–control status as a covariate in the regression for the secondary outcome. We also compared these methods to ordinary linear regression based on the entire data set, which one expects to be significantly biased. We generated X from a mixture of normals with density N(0, 4) with probability 0.88 and density N(2, 4) otherwise. The logistic model is 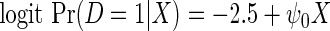 , where
, where 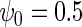 . The model for Y given X is the linear regression model,
. The model for Y given X is the linear regression model, 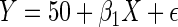 , where
, where 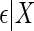 is a mean zero residual error, that is, generated such that model (2.4) holds with
is a mean zero residual error, that is, generated such that model (2.4) holds with 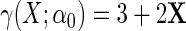 , and
, and 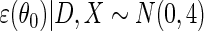 . The simulation study explores both null (
. The simulation study explores both null (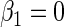 ) and non-null (
) and non-null (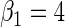 ) conditions. The rate of disease is approximately 0.12 in the target population and therefore, the rare disease approximation does not hold. The case–control study has 500 cases and 500 controls, we generated 1000 simulated data sets.
) conditions. The rate of disease is approximately 0.12 in the target population and therefore, the rare disease approximation does not hold. The case–control study has 500 cases and 500 controls, we generated 1000 simulated data sets.
For the simulation study, the locally efficient approach is implemented by maximizing the log-likelihood 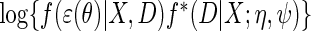 which corresponds exactly to solving the efficient score of Proposition 1, under homoscedastic normal error, i.e. assuming
which corresponds exactly to solving the efficient score of Proposition 1, under homoscedastic normal error, i.e. assuming 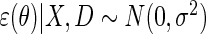 . This specific choice of likelihood model facilitates the implementation of the locally efficient approach using standard off-the shelf software, we used Proc NLMIXED in SAS to implement the approach.
. This specific choice of likelihood model facilitates the implementation of the locally efficient approach using standard off-the shelf software, we used Proc NLMIXED in SAS to implement the approach.
The simulation results given in Table 1 confirm that IPW and the locally efficient approach both have small bias and produce 95% confidence intervals with appropriate coverage under either the null or the alternative hypothesis. In contrast, as expected, ordinary linear regression using the entire sample and ignoring the sampling design is noticeably biased with disastrous coverage (=0%) in all scenarios. Simply adding a main effect for disease status corrects some of the bias but still produces 95% confidence intervals with poor coverage. In terms of efficiency, as expected, locally efficient estimation clearly outperforms IPW in both scenarios with relative efficiency sometimes >200%. Although remarkable, this efficiency gain is not entirely surprising from a semiparametric perspective, since by altogether avoiding to model 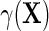 and
and 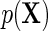 , IPW essentially allows these two models to remain unrestricted in estimating
, IPW essentially allows these two models to remain unrestricted in estimating 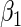 , i.e. non-parametric, whereas the proposed approach relies crucially on parametric models for these functions to estimate
, i.e. non-parametric, whereas the proposed approach relies crucially on parametric models for these functions to estimate 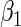 . These additional restrictions for the most part explain the efficiency gain.
. These additional restrictions for the most part explain the efficiency gain.
Table 1.
Simulation results
| Absolute bias | Variance | Coverage | |
|---|---|---|---|
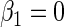 | |||
| Standard OLS | 0.734 | 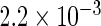 |
0.000 |
| Conditional OLS | 0.227 | 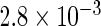 |
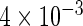 |
| IPW | 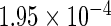 |
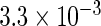 |
0.970 |
| Locally efficient | 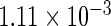 |
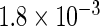 |
0.960 |
| Simple estimating equation | 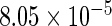 |
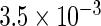 |
0.978 |
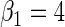 | |||
| Standard OLS | 0.730 | 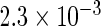 |
0.000 |
| Conditional OLS | 0.231 | 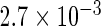 |
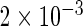 |
| IPW | 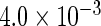 |
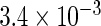 |
0.957 |
| Locally efficient | 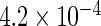 |
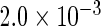 |
0.956 |
| Simple estimating equation | 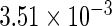 |
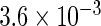 |
0.985 |
We also implemented the inefficient estimating equations of Section 2.2, together with standard logistic maximum likelihood estimation of  . Although both approaches show little bias (Table 1), as projected by Proposition 1, the locally efficient estimator outperforms this alternative strategy in terms of efficiency and demonstrates remarkable efficiency gain not only for the parameter of primary interest
. Although both approaches show little bias (Table 1), as projected by Proposition 1, the locally efficient estimator outperforms this alternative strategy in terms of efficiency and demonstrates remarkable efficiency gain not only for the parameter of primary interest 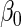 (
(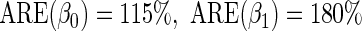 ), where
), where 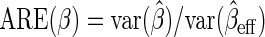 but also for the logistic regression parameter
but also for the logistic regression parameter 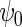 (
(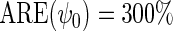 ). This result confirms that as projected by Proposition 1, the locally efficient approach can, when the disease is not rare, recover information about
). This result confirms that as projected by Proposition 1, the locally efficient approach can, when the disease is not rare, recover information about 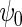 that standard logistic regression cannot exploit.
that standard logistic regression cannot exploit.
6. An empirical application
This section illustrates the locally efficient approach in an analysis of data from a population-based case–control study of ovarian cancer Modan and others, 2001. Two controls per case were selected from a central population registry in Israel, matching on age within 2 years, area of birth and place, and length of residence. Blood samples were collected on both cases and controls and were tested for the presence of mutation in two major breast and ovarian cancer susceptibility genes BRCA1 and BRCA2. Additional data were collected on reproductive and gynecologic history, such as parity, number of years of oral contraceptive use, and gynecologic surgery. The main objective of the study was to examine the interplay of the BRCA1/2 genes and known reproductive/gynecologic risk factors for ovarian cancer. In reanalyses of these data, a number of authors have exploited a gene-environment independence assumption to obtain more efficient estimates of interactions between BRCA1/2, and parity and oral contraceptive use, respectively (Chatterjee and Carroll, 2005; Tchetgen Tchetgen and Robins, 2010; Tchetgen Tchetgen, 2011). Specifically, they assumed that in the target population BRCA1/2 is jointly independent of parity and oral contraceptive within levels of covariates. As a secondary analysis, we evaluate this hypothesis empirically and estimate the mean association in the target population, between BRCA1/2 status and years of oral contraceptive use 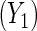 and parity
and parity 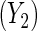 , respectively, adjusting for covariates. Thus, let
, respectively, adjusting for covariates. Thus, let 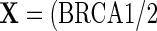 , age (categorical defined by decades), ethnic background (Ashkenazi or non-Ashkenazi), the presence of personal history of breast cancer, a history of gynecologic surgery, and family history of breast or ovarian cancer (no cancer vs. one breast cancer in the family vs. one ovarian cancer or two or more breast cancer cases in the family)). The analysis uses data on 832 cases and 747 controls who did not have bilateral oophorectomy and who were interviewed for risk factor information and successfully tested for BRCA1/2 mutations. To illustrate the method with both identity and log link functions,
, age (categorical defined by decades), ethnic background (Ashkenazi or non-Ashkenazi), the presence of personal history of breast cancer, a history of gynecologic surgery, and family history of breast or ovarian cancer (no cancer vs. one breast cancer in the family vs. one ovarian cancer or two or more breast cancer cases in the family)). The analysis uses data on 832 cases and 747 controls who did not have bilateral oophorectomy and who were interviewed for risk factor information and successfully tested for BRCA1/2 mutations. To illustrate the method with both identity and log link functions, 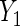 is coded as number of years of oral contraceptive use and a linear regression of
is coded as number of years of oral contraceptive use and a linear regression of 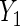 on X is evaluated, while
on X is evaluated, while 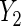 is a count of live births, and a log-linear model is assumed for the regression of
is a count of live births, and a log-linear model is assumed for the regression of 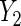 on
on 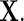 As suggested by Chatterjee and Carroll (2005), we set the population rate of ovarian cancer to
As suggested by Chatterjee and Carroll (2005), we set the population rate of ovarian cancer to 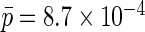 which implies the rare disease approximation is appropriate, and thus an estimate of the risk of ovarian cancer as a function of X is not strictly needed. Nonetheless, we performed both analyses, with and without the rare disease approximation, and obtained identical results.
which implies the rare disease approximation is appropriate, and thus an estimate of the risk of ovarian cancer as a function of X is not strictly needed. Nonetheless, we performed both analyses, with and without the rare disease approximation, and obtained identical results.
For each outcome, we compare inferences based on standard OLS ignoring case–control status, IPW and the locally efficient approach with and without possible effect heterogeneity by BRCA1/2 in the case–control adjustment, i.e. 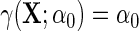 vs.
vs. 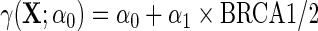 .
.
Table 2 summarizes the results for BRCA1/2 associations with 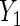 and
and 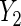 . In both sets of analyses, standard OLS gives the largest point estimates for the effect of BRCA1/2 on the average years of oral contraceptive use and parity, respectively. For both outcomes, IPW and the locally efficient approach incorporating a
. In both sets of analyses, standard OLS gives the largest point estimates for the effect of BRCA1/2 on the average years of oral contraceptive use and parity, respectively. For both outcomes, IPW and the locally efficient approach incorporating a 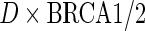 interaction correct the OLS estimate, nonetheless the three methods agree in their conclusion and none rejects the null hypothesis of no gene-environment association at the
interaction correct the OLS estimate, nonetheless the three methods agree in their conclusion and none rejects the null hypothesis of no gene-environment association at the 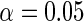 level. Interestingly, not including the interaction in the locally efficient approach has different effects in the two analyses. For
level. Interestingly, not including the interaction in the locally efficient approach has different effects in the two analyses. For 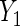 , not including the interaction leads to a wider Wald 95% confidence interval that rejects the null hypothesis of no BRCA1/2 association, which suggests the need to account for the interaction. In contrast, removing the interaction in the
, not including the interaction leads to a wider Wald 95% confidence interval that rejects the null hypothesis of no BRCA1/2 association, which suggests the need to account for the interaction. In contrast, removing the interaction in the 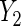 regression leads to a shorter confidence interval without altering the overall conclusion, suggesting that perhaps the interaction is not necessary.
regression leads to a shorter confidence interval without altering the overall conclusion, suggesting that perhaps the interaction is not necessary.
Table 2.
Parameter estimates (standard errors) of mean effect of BRCA1/2 on oral contraceptive use and Parity
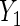 |
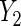 |
|
|---|---|---|
| BRCA1/2 (se) | BRCA1/2 (se) | |
| Standard OLS | 0.212 (0.144) |
 0.053 (0.047) 0.053 (0.047) |
| IPW | 0.327 (0.570) |
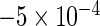 (0.142) (0.142) |
| Locally efficient without interaction | 0.332 (0.152) |
 0.020 (0.033) 0.020 (0.033) |
| Locally efficient with interaction | 0.287 (0.109) | 0.094 (0.175) |
7. Conclusion
In this paper, we have described a general, yet simple framework for performing regression analysis for a secondary outcome in the context of case–control sampling. The current results focused on the three most common link functions used in practice, the identity link typically used for a continuous outcome, the log link typically used with counts, and the logit link typically used for binary data. A simple set of estimating equations is described for inference, and a potentially more efficient approach is also given. A particular appeal of the approach is that it is readily implemented with off-the-shelf statistical software. The framework also gives a formal justification for including the case–control status as a covariate in the regression model in view to account for study design when the case–control disease is rare, without requiring the distributional assumptions that have previously appeared in the literature. It is also straightforward to extend our basic argument to justify this type of conditional approach for other link functions, such as the complementary log-log link, or the probit link, under rare disease. When the disease is not rare, the approach requires that sampling fractions are known for cases and non-case–controls, which may be a challenge in certain settings, but is usually feasible when the case–control sample is nested within a well-defined cohort study. As we also describe, it is straightforward to use the proposed methods for matched case–control studies, simply by including matching factors in X. Also note that as was done in the simulation study, the locally efficient estimator can sometimes be implemented using simple maximum likelihood, in which case, standard likelihood-based methods, such as Akaike's information criterion or the Bayesian information criterion can also be used to assess goodness-of-fit. Due to space restrictions, specific methods for goodness-of-fit methods will be explored in detail elsewhere.
Finally, an interesting and important direction for future work is to further develop the framework to handle settings where the secondary outcome is a vector of correlated variables, arising either from a longitudinal process, or due to spatial or other potential sources of clustering.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Acknowledgements
Conflict of Interest: None declared.
References
- Breslow N. E., Robins J. M., Wellner J. A. On the semiparametric efficiency of logistic regression under case-control sampling. Bernoulli. 2000;6(3):447–455. [Google Scholar]
- Chatterjee N., Carroll R. J. Semiparametric maximum likelihood estimation exploiting gene-environment independence in case-control studies. Biometrika. 2005;92:399–418. [Google Scholar]
- Chen H. Y., Kittles R., Zhang W. Bias correction to secondary trait analysis with case-control design. Statistics in Medicine. 2013;32:1494–1508. doi: 10.1002/sim.5613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A., Wright F., Zou F. Unified analysis of secondary traits in case-control association studies. Journal of the American Statistical Association. 2013 doi: 10.1080/01621459.2013.793121. ( doi:10.1080/01621459.2013.793121.) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y., Scott A. J., Wild C. J. Secondary analysis of case-control data. Statistics in Medicine. 2006;25:1323–1339. doi: 10.1002/sim.2283. [DOI] [PubMed] [Google Scholar]
- Lee A. J., McMurchy L., Scott A. J. Re-using data from case-control studies. Statistics in Medicine. 1997;16:1377–1389. doi: 10.1002/(sici)1097-0258(19970630)16:12<1377::aid-sim557>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- Lettre G., Jackson A., Gieger C., Schumacher F. R., Berndt S., Hirschhorn J. Identification of ten loci associated with height and previously unknown biological pathways in human growth. Nature Genetics. 2008;40(5):584–591. doi: 10.1038/ng.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Gail M. H., Berndt S., Chatterjee N. Using cases to strengthen inference on the association between single nucleotide polymorphisms and a secondary phenotype in genome-wide association studies. Genetic Epidemiology. 2010;34:427–433. doi: 10.1002/gepi.20495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D. Y., Zeng D. Proper analysis of secondary phenotype data in case-control association studies. Genetic Epidemiology. 2009;33:256–265. doi: 10.1002/gepi.20377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loos R., Lindgren C. M., Li S., Wheeler E., Zhao J. Association studies involving over 90,000 samples demonstrate that common variants near MC4R influence fat mass, weight and risk of obesity. Nature Genetics. 2008;40(6):768–775. doi: 10.1038/ng.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modan M. D., Hartge P., Hirsh-Yechezkel G., Chetrit A., Lubin F., Beller U., Ben-Baruch G., Fishman A., Menczer J., Struewing J. P. Parity, oral contraceptives and the risk of ovarian cancer among carriers and noncarriers of a BRCA1 or BRCA2 mutation. New England Journal of Medicine. 2001;345:235–40. doi: 10.1056/NEJM200107263450401. and others. [DOI] [PubMed] [Google Scholar]
- Monsees G., Tamimi R., Kraft P. Genomewide association scans for secondary traits using case-control samples. Genetic Epidemiology. 2009;33:717–728. doi: 10.1002/gepi.20424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerke N. J. D., Moses S., Plummer F. A., Brunham R. C., Fish D. Logistic regression in case–control studies: the effect of using independent as dependent variables. Statistics in Medicine. 1995;14:769–755. doi: 10.1002/sim.4780140806. [DOI] [PubMed] [Google Scholar]
- Reilly M., Torrang A., Klint A. Reuse of case–control data for analysis of new outcome variables. Statistics in Medicine. 2005;24:4009–4019. doi: 10.1002/sim.2398. [DOI] [PubMed] [Google Scholar]
- Richardson D. B., Rzehak P., Klenk J., Weiland S. K. Analysis of case–control data for additional outcomes. Epidemiology. 2007;18:441–445. doi: 10.1097/EDE.0b013e318060d25c. [DOI] [PubMed] [Google Scholar]
- Robins J. M., Rotnitzky A., Zhao L. P. Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association. 1994;89:846–866. Reproduced courtesy of the American Statistical Association. [Google Scholar]
- Sanna S., Jackson A. U., Nagaraja R., Willer C. J., Chen W. M., Bonnycastle L. L., Shen H., Timpson N., Lettre G., Usala G. Common variants in the GDF5-UQCC region are associated with variation in human height. Nature Genetics. 2008;40(2):198–203. doi: 10.1038/ng.74. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen E. Robust discovery of genetic associations incorporating gene-environment interaction and independence. Epidemiology. 2011;22(2):262–272. doi: 10.1097/EDE.0b013e318207ffc3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen E. J. Leveraging auxiliary information to enhance power in the analysis of nested case-control GWAS. Technical Report. 2012 Harvard University. [Google Scholar]
- Tchetgen Tchetgen E. J., Robins J. The semi-parametric case-only estimator. Biometrics. 2010;66(4):1138–1144. doi: 10.1111/j.1541-0420.2010.01401.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen E. J., Rotnitzky A. Double-robust estimation of an exposure-outcome odds ratio adjusting for confounding in cohort and case-control studies. Statistics in Medicine. 2011;30(4):335–347. doi: 10.1002/sim.4103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Shete S. Estimation of odds ratios of genetic variants for the secondary phenotypes associated with primary diseases. Genetic Epidemiology. 2011;35:190–200. doi: 10.1002/gepi.20568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weedon M. N., Lettre G., Freathy R. M., Lindgren C. M., Voight B. F., Perry J. R., Elliott K. S., Hackett R., Guiducci C., Shields B. A common variant of HMGA2 is associated with adult and childhood height in the general population. Nature Genetics. 2007;39(10):1245–1250. doi: 10.1038/ng2121. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J., Carroll R. J., Muller U., Van Keilegom I., Chatterjee N. Locally efficient estimation for homoscedastic regression in the secondary analysis of case-control data. Journal of the Royal Statistical Society, Series B. 2013;75:186–206. doi: 10.1111/j.1467-9868.2012.01052.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weuve J., Korrick S., Weisskopf M., Ryan L., Schwartz J., Nie H., Grodstein F., Hu H. Cumulative exposure to lead in relation to cognitive function in older women. Environmental Health Perspectives. 2009;117:574–580. doi: 10.1289/ehp.11846. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.