Abstract
It is well known that our perceptual system integrates local information to generate global percepts. Although events in the real world occur over time, it is still unclear how we integrate temporally dispersed information. Here, I systematically explore the relation between the intensity of local signals and the resultant of temporal-integration. Presented sequentially with two directions of variably coherent random dot patterns (40 degrees apart), participants were instructed to report a perceived motion direction by using a mouse driven cursor. As the strength of the motion signal was varied, the behavioral results and qualitative analyses indicate existence of two aspects of temporal-integration, subthreshold integration and suprathreshold integration. In subthreshold integration (when the local signals are subthreshold), stronger signals enhance integration. On the other hand, in suprathreshold integration (when the signals are above threshold), stronger signals decrease integration. As a result, relatively weaker, subthreshold or near threshold signals produce more precise temporal-integration than suprathreshold signals.
Previous studies have shown that our visual system spatially and temporally integrates local images into a global image1,2,3,4. For instance, two brief static-images that are presented separately in time can be perceived as a temporally integrated unitary configuration2. In the same manner, dynamic images are perceived as a global representation of moving objects. For example, when a dynamic random-dot (DRD) display with coherently moving dots (signal) and randomly moving dots (noise) is presented, we perceive the direction of coherently moving dots as a coherent motion3,4. Increase in the ratio of signal dots to the total number of dots (coherence ratio) enhances correct detection of the direction of coherent motion. Furthermore, our visual system integrates multiple directions of coherent motions into a global motion direction. For instance, when two local-motions are shown at 10 and 30 degrees, we can perceive the central direction between them, that is, 20 degrees motion direction as the global motion direction.
Not only behavioral but also physiological studies have shown that our brain has cortical regions that process such motion signals. All visual information from our eyes proceed to the primary visual cortex of the occipital lobe (V1) and then to a variety of visual areas of higher processing such as motion processing5. Monkey middle temporal (MT)3,4,5,6,7 and human middle temporal (MT+) regions8 are the visual areas that are specialized for motion signals. It is suggested that area MT+ takes the central role in processing of global motion as well as local motion9,10. Also, increase in the ratio of signal dots to the total number of dots (coherence ratio) more strongly activates MT+ regions.
These results would lead to the prediction that stimuli with higher motion coherence will produce more precise motion integration over time. In other words, increased motion coherence should provide higher probability that judgements of the direction of two motion patches will be to the central, or global motion direction. However, this prediction has not been directly tested.
Results
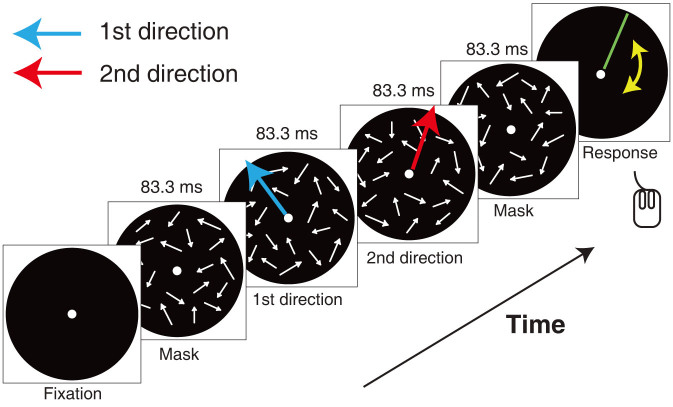
To examine the relationship between the strength of local-motion signals and the resultant of temporal-integration, a series of psychophysical experiments was conducted. Newsome and Pare's paradigm3 was used because it allows the duration and the strength of the stimulus (coherence) to be systematically varied. In the main experiment, participants viewed a DRD display consisted of dots that moved in different fashion, some coherently (signal) and randomly (noise)3. The signal was manipulated by changing the percentage (0–100) of coherently moving dots/the total number of dots.Two different directional motions with the same coherent ratio were sequentially presented (Figure 1). The participants were instructed to report a perceived motion direction by using a mouse driven cursor (See Methods). The angle between two motion directions was fixed at 40 degrees but the global motion direction was randomly assigned on each trial. On each trial the coherence ratio was selected randomly to be 10, 22, 34, 46, or 70% (See Methods).
Figure 1. Design of motion integration experiment.
Arrows represent motion vectors. Between the mask stimuli (0% coherent motions display), two different motions with the same coherence ratio (blue and red arrows) were sequentially presented. The angle between two motion directions was 40 degrees. The coherence ratios varied across trials. Participants reported a perceived motion direction after display offset by rotating a green line whose orientation corresponded to the angular position of the mouse cursor relative to fixation.
In order to measure how participants integrate the motion patches, I investigated the proportion of participants' responses. As a result, the probability of a response to the central direction (Figure 2a; pink bar) increased from 10% to 34% coherency but decreased as coherency increased beyond 34% (Figure 2b). This reversal in the proportion of responses to the central direction (Figure 2b) suggests that at high coherence ratios the participants are less likely to integrate the two motion directions into the global motion direction. In a separate session, I measured the participant's thresholds for local-motion coherence ratio (See Methods and Supplementary Information). The results showed that the 34% coherence ratio was below psychophysical threshold of local motion (42.0 ± 4.9%, Figure 2b; purple line, See Supplementary Information) while 70% was above the threshold. Taken together, these results suggest that weak motion signals can produce more precise motion integration, particularly if the signals are below threshold.
Figure 2. Probability Distribution of response.
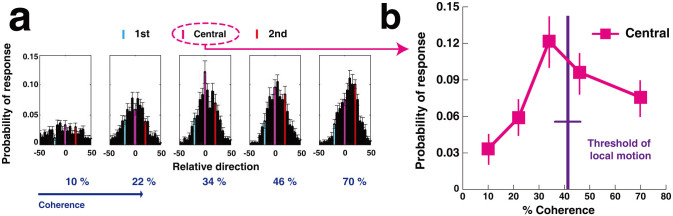
a, Mean probability distribution of responses for each coherence ratio (n = 13, only between −50° to +50°). The bin size of 5 degree was determined based on mean motor error measured in a separate experiment (See Supplementary Information). ‘0’ in the scale of relative direction indicates the global motion direction. The blue and red bars correspond to the relative direction of the 1st (−20°) and 2nd (+20°) motion directions, respectively. Vertical error bars, ±1 SEM. b, Mean probability of response at the central direction as a function of the coherence ratio (n = 13). Vertical error bars, ±1 SEM. A vertical purple bar represents the mean psychophysical threshold of local-motion with a horizontal purple bar, ±1 SEM (from the results of the motion threshold test: See Methods and Supplementary Information). The probability of response at 34% coherence ratio was significantly higher than that at 10, 22, and 70% coherence ratios (n = 13, p < 0.01 for each t test with Bonferroni correction).
To qualitatively examine the change in the probability distributions across coherence ratios, I compared the behavioral results (Figure 2a) with the computational modeling using two types of models: a motion integration model and a non-integration model (See Supplementary Information). The motion integration model assumed that the visual system integrates motion directions by calculating a weighted sum of the directions. This model estimated the best fitting probability distribution that corresponds to a single distribution. The non-integration model assumed that participants did not integrate and reported either the 1st or the 2nd motion direction, predicting that probability distribution of responses is described by a weighted mixture of two distinct distributions. Akaike's information criterion (AIC)11, which takes the number of free parameters of a model into account, and a bootstrap resampling method12 were used to determine which model is more likely to describe the behavioral results (See Supplementary Information). A comparison of the AIC values for the non-integration and motion integration models indicated that only the probability distributions at lower coherence ratios were better described a model including only a single distribution (Figure 3a). I repeated the bootstrap analysis 100 times and calculated percentage of win for the motion integration model for each coherence ratio. The result showed that the percentage of win for the motion integration model (a single distribution) decreased as coherence ratio increased (Figure 3b). Taken together, both analyses suggest that the motion integration model better describes the data at lower coherence ratios. On the other hand, the non-integration model better describes the data at higher coherence ratios such as 46% and 70% coherences.
Figure 3. Results of model comparison between integration and non-integration models.
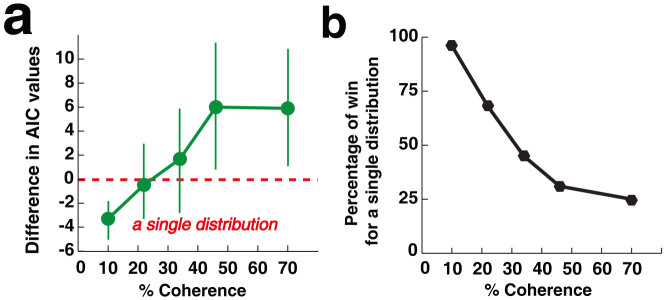
a, Mean difference in AIC values between the motion-integration and non-integration models (negative values indicate a better fit with the motion integration model (a single distribution)). Error bars are population standard deviations calculated from 100 resamples. b, Percentage of win for the motion integration model (a single distribution) calculated from the bootstrap resampling analysis.
I also investigated the probability of responses to the 1st (−20°) and 2nd (+20°) direction (blue and red bars, Figure 2a). The probability of responses to the 2nd direction was significantly higher than for the 1st direction when motion coherence was higher such as 46% and 70% (n = 13, p < 0.01 for each t test with Bonferroni correction), but not when motion coherence was at lower. This finding also suggests that the decrease in precise motion integration when signals are above threshold reflects a propensity to respond to the second motion patch, and the participants more likely reported the feature of the stimulus presented in later. One might think that this bias towards the 2nd motion direction was caused by a motion after effect (MAE)13,14,15 from the 1st motion stimulus. However, in a control experiment, I found no significant MAE induced by our displays (See Methods and Supplementary Information). Thus, MAE does not significantly appear to contribute to the present results.
Discussion
The results of the present study demonstrate two distinctive types of temporal-integration, subthreshold and suprathreshold integration. In subthreshold integration, stronger signals increase the precision of integration when local signals are subthreshold (Figure 4, red line). In fact, the sigma values of the distribution assuming the motion integration model (a single distribution) are decreased from 10% to 34% coherences (41.4, 20.1, and 18.2 respectively; 68.3% for the estimates of standard deviation). On the other hand, in suprathreshold integration, the precision of integration is inversely proportional to signal intensity of the local signals (Figure 4, green line), because participants seem more likely to report the direction of the first or second motion direction (the non-integration model) rather than the averaged direction (the motion integration model), especially that of the second motion at higher coherence (Figure 4). Based on the computational analyses, it is assumed that motion integration eventually disappears at the strongest signals, which might produce ‘center missing’ (Figure. 4). However, the actual data in this study does not provide the absolute ‘center missing’(See “70%” panel in Figure 2a), further studies are needed to clarify it.
Figure 4. Schematic illustration of the hypothesized relationship between temporal-integration and intensity of local signal.
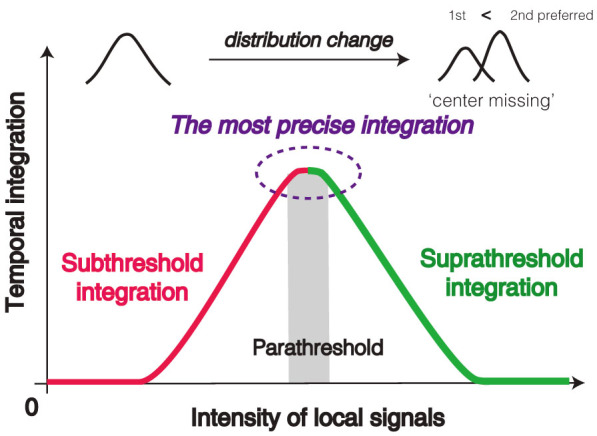
Subthreshold integration (red) and suprathreshold integration (green). The most precise temporal-integration (purple dotted circle) occurs when the local signals are subthreshold or parathreshold, because perception of suprathreshold signals that are presented more recently is too strong to allow integration, which also might make the probability distribution consist of a combination of two distributions, ‘center missing’.
One of other possible explanations for the decrease of motion integration at stronger signals (Figure 4) is because of motion transparency16,17,18,19,20. Motion transparency is one of motion perceptions in which we perceive more than one direction when multiple motions are presented within the same visual field. Although motion transparency is generally observed when multiple motions are simultaneously shown in the same spatial field, it might be occurred even when the two directions of coherent motion are presented sequentially19. If this is the case, an alternative interpretation of the current results is that subthreshold and suprathreshold integration are qualitatively similar, but the modal directions become more salient at higher coherence levels, with the mean direction being still available if the participants are encouraged to report it17. In the suprathreshold case, the participants reported one of the three directions or guess. One would expect that the proportion of responses in the mean direction would relatively drop in suprathreshold integration. To test this possibility, it might be useful to investigate how area MT activities are involved in this phenomenon, because some recent physiological studies have shown that we can distinguish the neural activities in area MT for global-motion processing from the ones for local-motion processing10,21. It is also necessary to physiologically examine the motion pathway (from the primary visual cortex to area MT.) for understanding the neural mechanism of the current results.
Although it is still unclear whether the participants reported one of the three perceived motion directions or one perceived direction, as a result of the decrease of probability of response at the central direction at stronger signals, relatively weaker signals, that is, subthreshold or parathreshold signals22 could more precisely trigger perceptual temporal-integration (Figure 4). This perceptual phenomenon is different from the style of perceptual simultaneous-integration, that is to say, relatively stronger signals induce integration more effectively1,3,4,5,6. In addition, the part of suprathreshold integration in the hypothetical framework is also consistent with some types of non-liner neural response activities such as winner-take-all manner23,24, because only one of signals' features (2nd motion direction in this case) dominantly affects perception. Furthermore, the part of subthreshold integration in this framework may provide one of insights on why some too weak perceptual experiences to be detected lead to relatively robust effects on our behavior and brain, such as distractor and perceptual learning effects25,26,27,28.
Methods
Participants
19 participants (11 females and 8 males), aged from 19 to 35, with normal or corrected vision, participated in the experiments. All participants gave written informed consent prior to the experiments. The experiments were performed in accordance with the Federal Regulations and Harvard policies. The study was approved by the Harvard University Institutional Review Board.
Stimuli
Random dot motion was presented as a visual stimulus within an annulus subtending 1.5–10 deg diameter on a black background. The luminance-contrast of the dot and fixation are 66.3 and 14.4 cd/m2 respectively. Dot density was 1.78 dots per deg square. The number of dots in a frame is 140. The dots were wrapped around when they moved out of the circular stimulus (See Psychtoolbox3 (http://psychtoolbox.org) if need more detail.). The motion display consisted of coherently and randomly moving dots. The coherently moving dots are called signal dots, and the randomly moving dots are called noise dots. Each white dot (0.3 deg square) was randomly classified into either signal or noise dots in each frame of 16.7 ms. Signal dots moved to a predetermined direction at the speed of 12 deg/sec, and noise dots were placed in random positions. For instance, at 10% coherence ratio, 10% of the dots moved in the predetermined direction from one frame to the next frame, and then a different set of dots moved in that direction in the next frame transition3.
Apparatus
A LCD display (1680 × 1050 resolution, 60 Hz refresh rate) was used for all psychophysical experiments. Visual stimuli were presented by using Psychtoolbox 3 (http://psychtoolbox.org) on Mac OSX.
Procedure
Before starting the actual experiments, the experimenter told the participants the character of ‘coherent motion’ with showing DRD display containing only one directional motion.
In the main experiment (Figure 1), two directional coherent motions were presented successively for 83.3 ms each. In order to avoid the possible effects of the mechanism difference between first- and second-order motion perception on the task29,30,31, the mask displays (0% coherent motions display) were presented for 83.3 ms right before and after the coherent motion displays. The coherence ratio was varied from trial to trial, 10, 22, 34, 46, and 70%. The angle between directions of the two coherent motions was 40 degrees at all trial. The set of two motion directions was randomly selected within 360 degrees. The participants were asked to report the perceived motion direction by rotating a line with a mouse. In a complete experiment, each coherence condition was repeated 60 times, so that a total number of trials consisted of 5 coherence ratios X 60 repetitions = 300 trials. The order of presentation of these conditions was randomly determined for each participant. No accuracy feedback was given to the participants.
To measure participants' local-motion thresholds, I employed two-interval forced choice design. Two DRD displays were presented in a trial (See Supplementary Information). One of two DRD displays included coherent motion, and the other display consisted of noise motion. The coherence ratio was varied from trial to trial, 10, 22, 34, 46, and 70%. The participants were engaged in reporting which DRD display included coherent motions. In a complete experiment, each coherence condition was repeated 80 times, so that a total number of trials was 400. The order of presentation of these conditions was randomly determined for each participant. No accuracy feedback was given to the participants.
In the MAE test, one directional coherent motion was presented for 83.3 ms after the mask stimulus in the half of trials (See Supplementary Information). The coherence ratio was varied from trial to trial, 10, 22, 34, 46, and 70%. The participants were asked to report the perceived direction at the time when the fixation was green. In a complete experiment, each coherence condition was repeated 60 times, so that a total number of trials consisted of 5 coherence ratios X 60 repetitions = 300 trials. The order of presentation of these conditions was randomly determined for each participant. No accuracy feedback was given to the participants.
Supplementary Material
Supplementary Information
Acknowledgments
I thank Ken Nakayama, Daryl Fougnie, Kazuhisa Shibata, and Yasuhito Sawahata for their valuable comments and supports.
References
- Williams D. W. & Sekuler R. Coherent global motion percepts from stochastic local motions. Vision Res. 24, 55–62 (1984). [DOI] [PubMed] [Google Scholar]
- Dixon P. & Di Lollo V. Beyond visual persistence: An alternative Account for temporal integration and segmentation in visual processing. Cognitive Psychol. 26, 33–63 (1994). [DOI] [PubMed] [Google Scholar]
- Newsome W. T. & Pare E. B. A selective impairment of motion perception following lesions of the middle temporal visual area (MT). J. Neurosci. 8, 2201–2211 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon J. A. & Newsome W. T. Visual response properties of striate corrtical neurons projecting to area MT in macaque monkeys. J. Neurosci.16, 7733–7741 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maunsell J. H. R. & Newsome W. T. Visual processing in monkey extrastriate cortex. Annu. Neuro. Neurosci. 10, 363–401 (1987) [DOI] [PubMed] [Google Scholar]
- Mikami A., Newsome W. T. & Wurtz R. H. Motion selectivity in macaque visual cortex. II. Spatiotemporal range of directional interactions in MT and V1. J. Neurophysiol. 55, 1328–1339 (1986). [DOI] [PubMed] [Google Scholar]
- Smith M. A., Majaj N. J. & Movshon J. A. Dynamics of motion signaling by neurons in macaque area MT. Nat. Neurosci. 8, 220–228 (2005). [DOI] [PubMed] [Google Scholar]
- Rees G., Friston K. & Koch C. A direct quantitative relationship between the functional properties of human and macaque V5. Nat. Neurosci. 3, 716–723 (2000). [DOI] [PubMed] [Google Scholar]
- Adelson E. H. & Movshon J. A. Phenomenal coherence of moving visual patterns. Nature 300, 523–525 (1982). [DOI] [PubMed] [Google Scholar]
- Hedges J. H. et al. Dissociation of neuronal and psychophysical responses to local and global motion. Curr. Biol. 21, 2023–8 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19, 716–723 (1974). [Google Scholar]
- Efron B. “The jackknife, the bootstrap, and other resampling plans”. Society of Industrial and Applied Mathematics CBMS-NSF Monographs, 38, 1–92 (1982). [Google Scholar]
- Anstis S. M. & Moulden B. P. After effect of seen movement: evidence for peripheral and central components. Q. J. Exp. Psychol. 22, 222–229 (1970). [DOI] [PubMed] [Google Scholar]
- Derrington A. & Suero M. Motion of complex patterns is computed from the perceived motions of their components. Vision Res. 31, 139–150 (1991). [DOI] [PubMed] [Google Scholar]
- van de Grind W. A., Verstraten F. A. J. & van der Smagt M. J. Storage for free: A surprising property of a simple gain-control model of motion aftereffects. Vision Res. 44, 2269–2284 (2004). [DOI] [PubMed] [Google Scholar]
- Hiris E. & Blake R. Direction repulsion in motion transparency. Visual Neurosci. 13, 187–197 (1996) [DOI] [PubMed] [Google Scholar]
- Zohary E., Scase M. O. & Braddick O. J. Integration across directions in dynamic random dot displays: Vector summation of winner take all? Vision Re. 36, 2321–2331 (1996) [DOI] [PubMed] [Google Scholar]
- Braddick O. J., Wishart K. A. & Curran W. Directional performance in motion transparency. Vision Res. 42, 1237–1248 (2002) [DOI] [PubMed] [Google Scholar]
- Watamaniuk S. N. J., Flinn J. & Stohr R. E. Segregation from direction differences in dynamic random-dot stimuli. Vision Res. 43, 171–180 (2003) [DOI] [PubMed] [Google Scholar]
- Edwards M. & Greenwood J. A. The perception of motion transparency: A signal-to-noise limit. Vision Res. 45, 1877–1884 (2005) [DOI] [PubMed] [Google Scholar]
- Majaj N. J., Carandini M. & Movshon J. A. Motion integration by neurons in Macaque MT is local, not global. J. Neurosci. 8, 366–370 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsushima Y., Seitz A. R. & Watanabe T. Task-irrelevant learning occurs only when the irrelevant feature is weak. Curr. Biol. 18, R516–R517 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salzman C. D. & Newsome W. T. Neural mechanisms for forming a perceptual decision. Science. 264, 231–237 (1994). [DOI] [PubMed] [Google Scholar]
- Busse L., Wade A. R. & Carandini M. Representation of concurrent stimuli by population activity in visual cortex. Neuron. 64, 931–42 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsushima Y., Sasaki Y. & Watanabe T. Greater disruption due to failure of inhibitory control on an ambiguous distractor. Science 314, 1786–1788 (2006). [DOI] [PubMed] [Google Scholar]
- Watanabe T., Náñez J. E. & Sasaki Y. Perceptual learning without perception. Nature 413, 844–848 (2001). [DOI] [PubMed] [Google Scholar]
- Tsushima & Watanabe T. Roles of attention in perceptual learning from perspectives of pscyhophysics and animal leaning. Learning and Behavior 37, 126–32 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meteyard L., Zoklaei N., Bahrami B. & Vigliocco G. Visual motion interferes with lexical decision on motion words. Curr. Biol. 18, R732–R733 (2008). [DOI] [PubMed] [Google Scholar]
- Cavanagh P. & Mather G. Motion: The long and short of it. Spatial Vision 4, 103–129 (1989) [DOI] [PubMed] [Google Scholar]
- Vaina L. M., Cowey A. & Kennedy D. Perception of first-and second-order motion: Separable Neurological Mechanism. Hum. Brain Mapp. 7, 67–77 (1999) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishida S., Ledfeway T. & Edwards M. Dual multiple-scale processing for motion in the human visual system. Vision Res. 31, 139–150 (1991). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information