Temporal Analysis of Reference Frames in Parietal Cortex Area 5d during Reach Planning

Abstract

The neural encoding of spatial and postural reference frames in posterior parietal cortex has traditionally been studied during fixed epochs, but the temporal evolution of these representations (or lack thereof) can provide insight into the underlying computations and functions of this region. Here we present single-unit data recorded from two rhesus macaques during a reach planning task. We found that area 5d coded the position of the hand relative to gaze before presentation of the reach target, but switched to coding the target location relative to hand position soon after target presentation. In the pretarget period the most relevant information for success in the task is the position of the hand relative to gaze; however, after target onset, the most task-relevant spatial relationship is the location of the target relative to the hand. The switch in coding suggests that population activity in area 5d may represent postural and spatial information in the reference frame that is most pertinent at each stage of the task. Moreover, although target−hand coding was dominant from soon after the reach target onset, this representation was not static but built in strength as movement onset approached, which we speculate could reflect a role for this region in building an accurate state estimate for the limb. We conclude that representations in area 5d are more flexible and dynamic than previously reported.

Introduction

During movement planning, the brain uses incoming sensory information about the location of a target to compute the appropriate motor commands for action. For visually guided reaching, the coding of the target is transformed from a retinotopic, or gaze-centered, reference frame to a hand or body-centered reference frame, with reciprocal circuits between multimodal parietal cortex and frontal regions thought to be critical for this sensorimotor transformation (Caminiti et al., 1998; Andersen and Cui, 2009). The temporal stability of reference frames within identified subregions of posterior parietal cortex is currently an open question that has implications for the computation underlying sensorimotor transformations. If a particular reference frame within a subregion is maintained consistently throughout a trial, this would suggest that the transformation occurs via simultaneous recruitment and readout of separate, dedicated, subregions (Buneo et al., 2008). Alternatively, if the encoding within a subregion evolves over the course of a trial, this would indicate a sequential transformation process that can occur within a single area, as well as demonstrate flexibility of representations within an area.

Despite some heterogeneity among individual cells (Avillac et al., 2005; Chang and Snyder, 2010; McGuire and Sabes, 2011), identified subregions in posterior parietal cortex appear to code in distinct and systematic reference frames. For example, in the parietal reach region (PRR) the target is represented predominantly in a gaze-centered reference frame (Andersen et al., 1998; Batista et al., 1999; Buneo et al., 2002; Cohen and Andersen, 2002; Pesaran et al., 2006), whereas the dorsal aspect of area 5 (area 5d) shows positional tuning during stationary posture (Georgopoulos et al., 1984; Lacquaniti et al., 1995) and codes upcoming targets mainly in a hand-centered reference frame (Bremner and Andersen, 2012). However, few studies have addressed the question of temporal stability; most previous work examined only a single, relatively short, epoch during reach planning. One study reported that reference frames in both area 5d and PRR are invariant with respect to time following target onset (Buneo et al., 2008), whereas another group reported trends for shifts toward gaze-centered encoding in both these areas as the task progressed (McGuire and Sabes, 2011). However, neither experiment used sufficient variables to be able to test thoroughly for all combinations of gaze-centered (T−G), hand-centered (T−H), and hand–gaze (H−G) coding. A sufficient number of variables are required to distinguish reference frames from eye and limb position gain effects (Bremner and Andersen, 2012).

To assess the temporal stability of reference frames during reach planning, we used a range of target, hand, and gaze positions and analyzed firing rates in area 5d with a sliding window and across multiple epochs. We found that population activity in area 5d was more dynamic than previously reported: the position of the hand relative to gaze was encoded in the fixation period, but this representation declined after target presentation. Furthermore, coding of the target position relative to the hand emerged early in the task but increased in strength during the reach planning period, suggesting that this area may be involved in aspects of movement planning downstream from the actual sensorimotor transformation.

Materials and Methods

Two adult male rhesus monkeys (Macaca mulatta, G and T) participated in this study. All surgical and animal care procedures were conducted in accordance with National Institutes of Health guidelines and were approved by the California Institute of Technology Animal Care and Use Committee.

Behavioral task

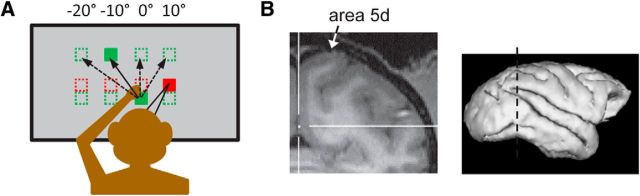
The behavioral paradigm was a delayed reaching task under visual fixation, as illustrated in Figure 1A and described previously (Pesaran et al., 2006; Bremner and Andersen, 2012). Each animal was trained to fixate his gaze (G) on a red square at one of four possible horizontal starting locations (−20°, −10°, 0°, or 10° in screen-centered coordinates) and touch a green square at one of the same four positions with his left hand (H). After successfully maintaining the H and G fixation positions for 1 s, a second green square (the target, T) was illuminated. The target position was also located −20°, −10°, 0°, or 10° horizontally and 16° either above or below the fixation positions, depending on which vertical position best activated the recorded cell. The monkey continued to hold the ocular and manual fixations for a variable delay period (1.2–1.5 s) until the initial manual fixation point was extinguished, at which point he made a reach to the target location without breaking visual fixation. If the monkey successfully acquired the target within 0.7 s and then held his hand on it for 0.25 s without moving his gaze, he was rewarded with a drop of juice. Eye position was monitored with an infrared eye-tracking camera (ISCAN; Arrington Research). Reaches were made within the frontal plane formed by the touchscreen (Elo TouchSystems), which was at a distance of 30 cm (monkey G) or 26 cm (monkey T) from the eyes. Behavioral tolerance windows had radii of 4° (eye fixation) and 5° (initial hand position and target). The G, H, and T positions were varied independently across trials, giving a total of 4 × 4 × 4 = 64 different trial types.

Figure 1.

A, The reference frame reaching task. Gaze fixation (red squares), starting hand position (lower green squares), and targets (upper green squares) were located at −20°, −10°, 0°, or 10° horizontally. B, Coronal fMRI section from monkey G showing the area 5d recording site.

Data collection

Single-unit recordings were made with ∼1–2 MΩ Pt/Ir microelectrodes in a single-channel microdrive (FHC) from the posterior portion of dorsal area 5 (area 5d), in the surface cortex adjacent to the medial bank of the intraparietal sulcus (IPS; Fig. 1B). The center of the cluster of recordings for monkey T was ∼1.25 mm lateral and 1 mm anterior to the center of recordings in monkey G. Recordings from both animals spanned ∼3 mm rostral to the IPS and were between 0.14 and 3.5 mm in depth from the estimated cortical surface, with a median depth of 0.93 mm. Cells in the recorded area are distinct from those in the nearby PRR both anatomically and functionally. PRR is located deeper in the IPS, and PRR cells generally show a clear response to cue onset and have higher peak firing rates than cells in area 5d. The dataset of cells reported here is the same as that collected for Bremner and Andersen (2012). Recorded neural activity was passed through a headstage, then filtered (154 Hz–8.8 kHz), amplified, and digitized (Plexon) and saved for off-line sorting (Plexon Offline Sorter) and analysis (MATLAB 7.8; MathWorks). The main reference frame task was run only when a well isolated, spatially tuned cell had been identified. Spatial tuning was assessed in a standard center-out reaching task. In some sessions, additional well isolated neurons were recorded on the same electrode: these were included in the dataset regardless of spatial tuning.

Data analysis

Only single units with a minimum of three trials per condition were included in the dataset. Data were aligned to reach target onset for the fixation (−450 to −50 ms) and early delay (200–600 ms) epochs, and to movement onset for the late delay epoch (−500 to −100 ms). To identify underlying reference frames as distinct from gain field effects (Andersen and Mountcastle, 1983), we analyzed firing rate matrices for individual cells as follows:

Firing rate matrices.

For each pair of variables (TH, TG, HG), we constructed four 4-by-4 matrices of mean firing rates, with each element in a matrix corresponding to a unique combination of hand position, gaze position, and target location. For example, an individual hand–gaze (HG) matrix represents the firing rates for all 16 different arrangements of starting hand and gaze positions, but with target position constant at, say, −20° in all trials. The remaining three HG matrices have the same hand and gaze structure, but are composed of trials in which the target was located at −10°, 0°, or 10°, respectively. Epoch analyses were conducted on only one matrix per variable pair at the peak response for the third variable, to maximize the signal-to-noise ratio. For example, in Figure 2B, late delay epoch, H, was constant at 10° for the TG matrix, G was constant at −10° for the TH matrix, and T was constant at −20° for the HG matrix. The temporal analysis was conducted on the full set of 12 matrices for each cell.

Figure 2.

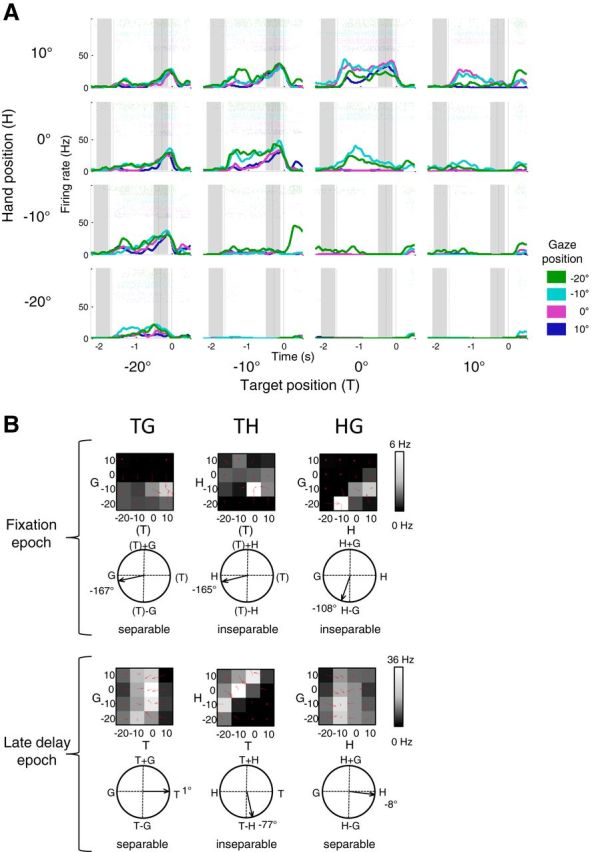
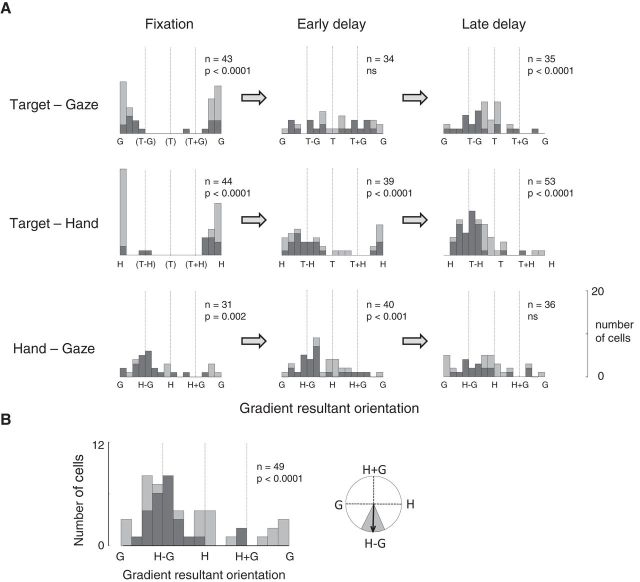
Example area 5d cell with hand–gaze encoding in the fixation epoch and target–hand coding in the late delay epoch. A, Peristimulus time histograms and raster plots for all 64 conditions. Each subplot shows the response of the neuron to a particular combination of target position and hand position, for all four possible gaze fixation positions. Trials are aligned to movement onset with the dashed lines indicating the mean target onset and go signal, respectively. The shaded regions designate the fixation and late delay epochs. B, Matrices and gradient resultant orientations for the cell shown in A during the fixation (top) and late delay (bottom) epochs.

Gradient analysis.

We used a combination of gradient analysis and singular value decomposition (SVD) of the matrices to assess how each variable affects the firing rate of individual cells at different stages of the task (Peña and Konishi, 2001; Buneo et al., 2002; Pesaran et al., 2006, 2010). The gradient of a matrix was estimated with the MATLAB gradient function and plotted as red arrows on the matrix elements. The directions and lengths of the set of red arrows indicate the relative importance of each variable on the firing rate of the cell. For example, in Figure 2B, late delay epoch, HG matrix, the arrows predominantly point left and right, reflecting the dominance that changes in H have over changes in G on the firing rate for this cell in this epoch. The circular plots beneath each matrix essentially summarize this information into a single resultant. However, the coordinate framework matrices often show a symmetrical pattern (as in the HG matrix example described above), so gradient elements would cancel each other out during calculation of the resultant. To avoid this, we doubled the angle for each gradient element before computing the resultant. We visualized this resultant angle on circular plots from 0° to ±180° with 0° representing a left–right pattern of red arrows, ±180° representing an up–down pattern of red arrows, and −90° representing arrows pointing to the diagonal (Fig. 2B). Each circular plot is notated with the appropriate variable or combination of variables to aid with interpretation (for example, H at 0°, G at ±180°, H−G at −90°, and H+G at +90° in an HG matrix). The angle of the gradient resultant therefore indicates the overall orientation of the coordinate bias and hence the relative influence of each variable within a pair on the firing rate.

Each coordinate framework matrix was classed as tuned if the resultant length was significantly greater than the resultant length calculated after randomization of the matrix elements (randomization test). Rayleigh's test was used to assess the uniformity of circular histograms for tuned resultant angles (p < 0.05, with Bonferroni correction for multiple comparisons). Previous studies have referred to the individual coordinate frame matrices as response fields for a cell (Pesaran et al., 2006, 2010; Bremner and Andersen, 2012). To minimize confusion with spatial response fields, we have avoided this usage here. In place of terms such as “response field orientation,” we refer more explicitly to “orientation of the gradient resultant.”

Singular value decomposition.

Although the gradient analysis can tell us whether there is significant tuning within a matrix and to which variable(s) a cell responds the most, it cannot distinguish between important patterns of coding. For example, the relationship between firing rate and a pair of variables for a given cell may be best described as a gain relationship:

where the response to one variable is scaled by the value of the second variable. In this example, the effects of each variable on firing rate are by definition multiplicatively separable. For a different cell, the relationship may take a vector form:

where the two variables T and H form part of the same function and cannot be multiplicatively separated from each other (inseparable). In such a case, the peak of the tuning curve for one variable is inextricably linked to the position of the second variable, creating a distinctive bottom-left to upper-right diagonal pattern in the response matrix (Fig. 2B, fixation epoch, HG matrix and late delay epoch, TH matrix). For the T−H example, the vector relationship can also be referred to as coding the target in a hand-centered reference frame, or coding the target relative to the hand position. A gradient resultant pointing to T+H (or T+G or H+G) would indicate that the underlying matrix had a peak response pattern aligned with the opposite diagonal (upper left to bottom right). A separable T+H relationship would be produced if T and H were independent factors with opposite monotonic spatial tuning: this would create a peak in the upper left or lower right corner of the matrix. An inseparable T+H (or T+G or H+G) relationship has no intuitive explanation and, in fact, is rarely observed (Fig. 6A).

Figure 6.

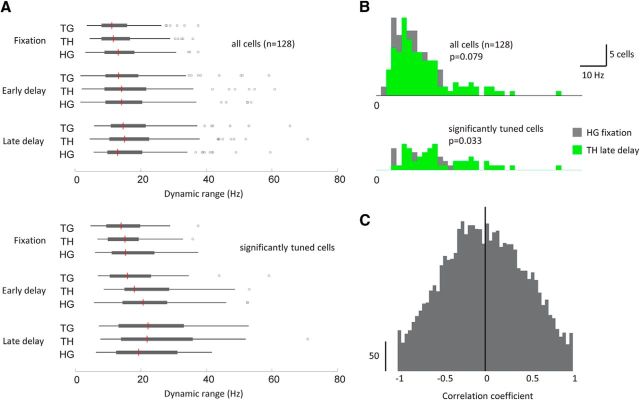
Area 5d codes the hand position relative to gaze before target presentation, but codes the reach vector as movement onset approaches. A, Histograms show the distribution of orientations of the matrix gradient resultants and SVD analysis for the population of tuned cells at three epochs during the task (fixation, early delay, and late delay). Each stacked bar represents 22.5° of the circular orientation plot; pale gray indicates separable responses and dark gray indicates inseparable responses. p values show the results of the Rayleigh test for uniformity, corrected for multiple comparisons. B, Histogram for the HG variable pair as described in A, but showing results when trials were collapsed across upcoming target positions (left). Mean gradient resultant orientation when trials were collapsed was −91°; the shaded area represents 95% confidence limits (right).

SVD was used to determine whether the relationship between pairs of variables was separable (in other words, a multiplicative, gain relationship) or inseparable (vector relationship). For the example TH matrix, SVD reduces the matrix to a weighted sum where the weights (s₁, s₂, etc.) are known as the singular values:

If the first singular value is very large such that the second and further terms are insignificant, then the matrix can be adequately described by the first term alone:

which is a gain relationship identical to Equation 1. If two or more singular values are necessary to capture the response matrix, then T and H are inseparable and their relationship cannot be modeled as a gain effect of one variable on the other. Matrices were mean-subtracted before performing the SVD. A matrix was classified as separable if the first singular value was significantly large (p < 0.05) when compared with the first singular value obtained after randomization of the matrix elements. Otherwise, the matrix was deemed inseparable. It has been shown previously using simulated data from idealized neuronal responses that this method is sufficiently sensitive to detect gain fields with as few as three trials per condition (Pesaran et al., 2010).

Time-step analysis: For each cell, we calculated the resultant length and angle of the coordinate framework gradient in 200 ms windows positioned at 100 ms intervals. Firing rates were aligned to the target onset from 1000 ms before to 800 ms after reach target onset, and to movement onset from 800 ms before to 1000 ms after the start of the reach. The length of the resultant at each time step is an indication of the strength of the tuning or coordinate bias at that point in time. For the population sliding analysis, we calculated the mean resultant from the entire population of 128 recorded cells at each time step for each variable pair. Arrow lengths for the population analysis are therefore normalized within a variable pair. An arrow length equal to one would indicate that the gradient resultant had the same orientation in all cells for that variable pair at that time step.

Firing rate–reaction time correlation.

For each cell–trial-type combination, we calculated the correlation between firing rate and reaction time on a trial-by-trial basis. As a comparison, we broke any correlation between firing rate and reaction time by randomizing the reaction times with respect to the firing rate within each cell–trial-type combination and repeating the analysis on the shuffled data. We compared the mean correlation coefficient of the actual dataset with the mean correlation coefficients from 1000 shuffled datasets to assess significance.

Results

We recorded extracellular spiking activity in parietal area 5d while monkeys performed a visually guided delayed reaching task. We isolated activity from 292 cells in total; 67% (196/292) of these had spatially tuned, reach-related activity as assessed in a center-out screening task (see Materials and Methods). The main task was designed to have a large number of independent combinations of hand, gaze, and target positions so that we could assess the contributions of each of these variables on cell firing rate. Specifically, we used four hand positions, four gaze positions, and four target locations (Fig. 1A). This large number of trial types (4 × 4 × 4 = 64) resulted in some cells losing isolation before enough trial repetitions had been completed: these cells were excluded from the database. Two monkeys were trained in the task before recordings began until their success rates plateaued. Typical success rates were 78–84% trials correct for monkey G and 70–78% trials correct for monkey T. Reaction times were comparable for both animals with means (and SDs) of 314 (132) ms for monkey G and 289 (120) ms for monkey T. Our eventual database consisted of 128 well isolated cells in total,79 cells from monkey G and 49 cells from monkey T, with data pooled across animals in all analyses.

Changes in reference frame coding within a single cell

Figure 2A illustrates the responses of a sample cell, with firing aligned to the movement onset. During the delay period, this cell showed particularly robust firing whenever the horizontal displacement of the target was 10° to the left of the starting hand position [i.e., target (T) at 0° and hand (H) at 10°, T at −10° and H at 0°, T at −20° and H at −10°]. In other words, this cell codes the target location in a hand-centered reference frame, also referred to as the extrinsic reach vector T−H, as previously reported for the population of area 5d cells (Bremner and Andersen, 2012). This result can be seen more clearly in the three firing-rate matrices of spiking during the late delay epoch (500–100 ms before movement onset; Fig. 2B, bottom). Each 4-by-4 matrix represents the mean firing rates for 16 trial types in which one of the three variables was held constant at the location, which elicited the peak response while the remaining two variables were each allowed to vary from −20 to 10°. The TH matrix for this cell has a gradient resultant angle of −77° (referred to in previous studies as a response field orientation of −77°; Pesaran et al., 2006, 2010; Bremner and Andersen, 2012). This shows that changes in target and hand position both influence the firing rate to a similar degree. The inseparable nature of this matrix indicates the relationship between the two variables has a vector form (T−H; equivalent to H−T) rather than being a simple gain effect of hand position [f(H)*f(T); see Materials and Methods]. Furthermore, the TG and HG late delay period matrices for this cell encoded T (1°) and H (−8°), respectively, confirming that gaze location had little influence on the firing rate of the cell during this epoch. Figure 2B, top, however, shows the firing rate matrices for the same cell during the fixation epoch, before presentation of the target. Despite the low firing rate and subsequent noisiness of the mean responses at this point, the cell is clearly influenced by gaze location as well as hand position and the HG matrix shows a diagonal pattern indicative of coding the hand position relative to the direction of gaze (−108° and inseparable; H−G vector encoding, equivalent to G−H).

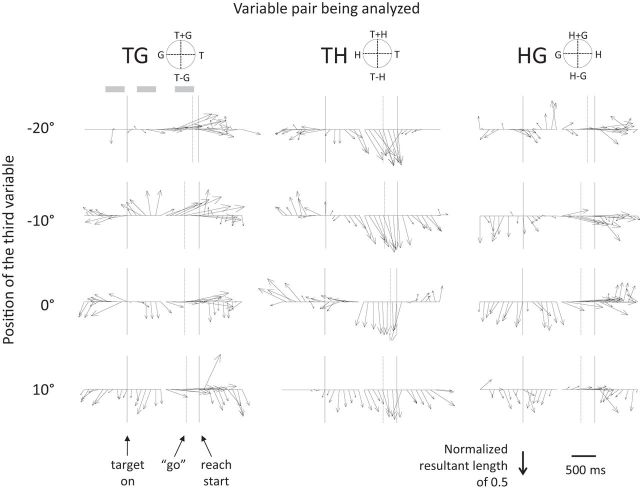
To investigate this change in reference frame coding in more detail, we conducted a sliding window time-step analysis of gradient resultants during the task, starting after the animal acquired the initial hand and gaze fixation points and ending after acquisition of the reach target. Figure 3 illustrates the results of this analysis for the sample cell described above. The direction of the arrows at each time step indicates which of the variables in each pair influences the firing rate the most, and the length of each arrow indicates the strength of the tuning at that moment in time. The center column shows that the reach vector T−H is instantiated in the firing rate within ∼600 ms of the target appearance, but that it increases in strength as the delay period progresses, peaking just before the reach onset. The right column confirms weaker but generally consistent H−G coding in the pretarget period that either decays or shifts to encoding only the hand position as the movement approaches. T−G encoding for this cell is somewhat sporadic and inconsistent through the early part of the delay period, with target position eventually becoming the dominant influence on firing in the late part of the delay period.

Figure 3.

Time-step analysis for the example cell shown in Figure 2. Each column shows the response of the cell to a pair of variables (e.g., TG) at each of the four positions for the third variable (e.g., H). In each subplot, the arrows represent the orientation of the matrix gradient resultant calculated for a 200 ms window centered at 100 ms intervals through the trial. Circular plots at the top of each column indicate the appropriate interpretation of arrow direction for each variable pair. Arrow length indicates tuning strength. Data were aligned to target onset (first solid vertical line) for the first 17 time steps and to movement onset (second solid vertical line) for the second 17 time steps, with a short gap indicating the break in alignment. The vertical dashed line indicates the mean go signal and the three shaded boxes at top left show the fixation, early delay, and late delay epochs.

Evolution of population responses

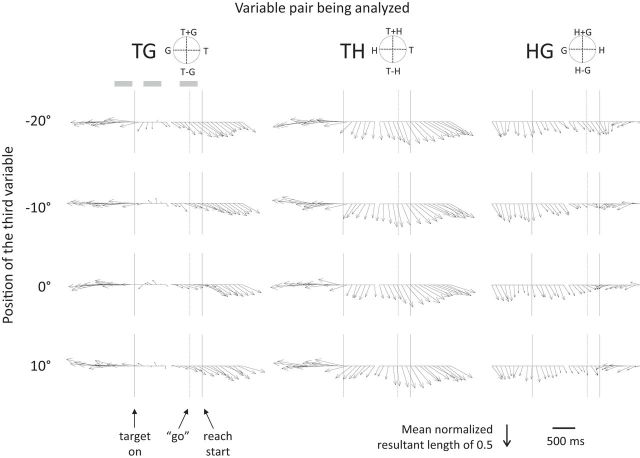
We applied the sliding window analysis to all 128 cells recorded from area 5d and pooled the results to assess how the population response evolves during the task (Fig. 4). In this figure the population resultants are normalized within each variable pair. The population resultants for TH demonstrate that the predominantly hand-centered reference frame previously reported for this region is present shortly after the target appears, consistent with previous reports (Fig. 4, center; Buneo et al., 2008). The analysis reveals a shift and strengthening of the reach vector as the task progresses, but it is noteworthy how clear and consistent the population T−H coding is even as early as 300 ms after target onset.

Figure 4.

Time-step analysis for the population of 128 cells showing evolution of reference frames during the task. Columns show the population response to a pair of variables (e.g., TG) at each of the four positions for the third variable (e.g., H). In each subplot, the arrows represent the mean resultant for the population of cells at 100 ms time steps (200 ms window). Circular plots at the top of each column indicate the appropriate interpretation of arrow direction for each variable pair. Arrow length indicates the circular concentration of the matrix gradient orientations and is therefore normalized within each variable pair. Data were aligned to target onset (first solid vertical line) for the first 17 time steps and to movement onset (second solid vertical line) for the second 17 time steps, with a short gap indicating the break in alignment. The vertical dashed line indicates the mean go signal and the three shaded boxes at top left show the fixation, early delay, and late delay epochs.

The progressive increase in T−H coding through the delay period could reflect a role for area 5d in preparation for movement initiation. In primary motor cortex (M1) and dorsal premotor cortex (PMd), faster reaction times are observed on trials with higher firing rates (Riehle and Requin, 1993; Afshar et al., 2011). We analyzed the correlation between firing rates and reaction time on a trial-by-trial basis for each cell–trial-type combination and found only a slight trend toward a negative correlation (Fig. 5C, mean correlation coefficient = −0.009, p = 0.068), indicating that area 5d does not have a strong role in movement initiation. In marked contrast to the strong hand-centered coding, gaze-centered coding of target position is absent throughout most of the delay period, only becoming weakly represented in the population during the final 400 ms before the reach (Fig. 4, left). This suggests that a transformation of target information from gaze centered to hand centered does not take place as a sequential process within area 5d. Also noticeable is the presence of hand–gaze encoding during the fixation epoch, and the gradual decay of this coding after target onset (Fig. 4, right). Our previous study examined the premovement epoch when H−G coding is not significant in the population; the evolution of this signal is only revealed by examining the time course across the entire trial.

Figure 5.

Dynamic range distributions by variable pair and epoch. A, Box-and-whisker plots for the full set of dynamic ranges for all cells (top) and only those cells with significant tuning to the variable pair (bottom). In each case, the red line denotes the median, the solid box denotes the 25th and 75th percentiles, and the whiskers extend to the last data point not considered an outlier (open circles). B, Histograms show in more detail the distribution of dynamic ranges for the two main effects reported: HG during the fixation epoch (gray) and TH during the late delay epoch (green). C, Distribution of correlation coefficients from trial-by-trial calculations of the correlation between firing rate and reaction time for individual cell–trial-type combinations.

The normalization of population resultants within each variable pair masks the strengths of the underlying discharge modulations during the different stages of the task. For the cell shown in Figure 2, for example, the dynamic range for HG during the fixation epoch (450–50 ms before target onset) is much lower than the dynamic range for TH during the late delay epoch. However, as shown in Figure 5B, top, this was not reflected in the population as a whole. The distributions of dynamic ranges for these effects overlapped substantially, indicating that the H−G coding during fixation is of comparable strength to the T−H coding during the late delay period. However, the two distributions were significantly different when only cells with significant tuning to a variable pair were included with TH late delay having more activity than HG fixation (Kolmogorov–Smirnov test, p = 0.033; Fig. 5B, bottom). Figure 5A illustrates the full set of dynamic ranges, broken down by epoch and variable pair.

The very short population resultants for TG in the early part of the delay period (Fig. 4, left) could be due to a real lack of gaze-centered coding or could instead be caused by, for example, a population of cells with a bimodal distribution, the peaks of which would cancel during circular averaging. Moreover, the 200 ms window used in the sliding time course analysis is too short to produce reliable results in the SVD analysis for separability, leaving open the question of whether the variables have a gain field or vector type of encoding at different stages of the task. To address these issues, we conducted a number of additional epoch analyses (Fig. 6).

In the fixation epoch 31/128 (24%) cells had an HG matrix with a significantly long gradient resultant and were therefore classed as significantly tuned to the HG variable pair. The distribution of gradient resultant orientations for these 31 cells, together with their associated separability or inseparability, is plotted in the lower left histogram of Figure 6A. The majority of these cells were inseparable (22/31; 71%), and the distribution of resultant angles was nonuniform (p = 0.002) with a mean orientation of −100° (95% CI [−66°, −133°]), confirming the finding of hand–gaze encoding at this stage in the task. Despite the results reaching significance, low firing rates and resulting noisy matrices limited the number of cells that were significantly tuned during this epoch. To counter this, we collapsed the data across upcoming “targets” to increase the number of trials per condition and improve the signal-to-noise ratio, strengthening the result [Figure 6B; 49/128 (38%) cells significantly tuned; 26/49 (53%) inseparable, mean gradient resultant orientation of −91° (95% CI [−66°, −117°]), significantly nonuniform distribution (p < 0.0001)]. As apparent in the sliding-window analysis, hand–gaze encoding is maintained through the early delay epoch (200–600 ms after target onset): 40/128 (31%) cells are tuned to the HG variable pair, 25/40 (63%) of these have inseparable response matrices, and the distribution is nonuniform (p < 0.001). The mean gradient resultant orientation, however, is −54° (95% CI [−25°, −83°]) in this epoch versus −100° in the fixation epoch. Although the two distributions are not significantly different (Kuiper test) and there is overlap between the 95% CIs for the mean in the two epochs, the trend suggests that hand position is beginning to have an increased influence over gaze position on cell firing by this point in the task. As previously published, the hand position is no longer encoded relative to gaze position in the late delay epoch [500–100 ms before movement onset; 36/128 (28%) cells significantly tuned to the HG pair; 18/36 (50%) inseparable; distribution not significantly different from uniform].

For TG encoding, analysis of the early delay epoch showed that the distribution of resultant angles was not significantly different from uniform. Twenty-seven percent (34/128) of cells had significantly tuned firing rate matrices, of which 20/34 (59%) were classed as inseparable. The target position and/or gaze direction influenced the firing rate in these cells, but the flat distribution demonstrates that the population did not encode the target in gaze-centered coordinates (the T−G vector) even at this early stage in the task. The short population resultants in the sliding window analysis are therefore due to a uniform rather than bimodal distribution of individual coordinate frame resultant angles.

The epoch analysis also confirms the emergence of the reach vector in the population early after target presentation: 39/128 cells had significantly tuned TH matrices during the early delay epoch, of which 23/39 (59%) were inseparable, and the distribution was significantly nonuniform (p < 0.0001). However, the distributions for TH differ significantly between the early and late delay periods (p < 0.005, Kuiper test), reflecting both a shift in mean gradient orientation [from −134° (95% CI [−110°, −157°]) to −73° (95% CI [−57°, −89°])] and the strengthening of the T−H representation in the population (from n = 39 to n = 53 cells with significant tuning) as the movement onset approaches.

Recruitment of neuronal subpopulations at different time points

The time-dependent increase in the number of cells significantly tuned for the TH matrix raises an important issue: Are the observed changes in the population response a result of the dynamic nature of representations within individual neurons during the task, or is there instead differential recruitment of neuronal subpopulations, with each subpopulation coding in a static reference frame? The example cell in Figures 2 and 3 has both decaying H−G encoding and increasing T−H encoding, so reference frames are not necessarily unitary or static within a single cell. Thirteen percent (16/128) of cells were similarly tuned for HG during the fixation epoch followed by TH during the late delay epoch. However, this does not preclude additional changes in subpopulation recruitment.

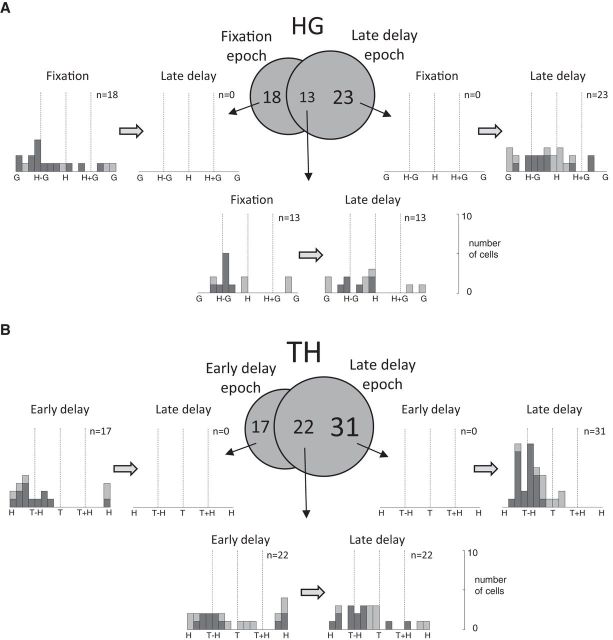
The Venn diagram in Figure 7A illustrates that 13 cells were significantly tuned to the HG variable pair in both fixation and late delay epochs, but a majority of tuned cells (18 + 23 = 41) was significantly tuned to HG in only one of these epochs. A similar breakdown can be seen when looking at the TH tuning in the early and late delay epochs: 22 cells are tuned in both epochs, whereas 48 cells are tuned in only one of the epochs, with a substantially larger proportion of these tuned in the late delay (n = 31) versus the early delay (n = 17) epoch (Fig. 7B). This suggests that independent subsets of neurons contribute differentially to the population resultant at different time points in the task.

Figure 7.

Differential recruitment of subpopulations across epochs. Venn diagrams show the numbers of cells significantly tuned to the HG variable pair during the fixation and late delay epochs (A) and to the TH variable pair during the early delay and late delay epochs (B). Some cells were tuned only within a single epoch, whereas others were tuned during both epochs. Histograms show the orientations of the matrix gradient resultants and SVD analysis for each subgroup of cells in the Venn diagram across the specified epochs. Stacked bars represent separable (pale gray) or inseparable (dark gray) responses.

Discussion

In this study, we investigated how sensorimotor reference frames develop over time in parietal area 5d during the course of a delayed reaching task. The experimental design included a large number of different combinations of hand, gaze, and target positions that allowed us to examine this question in detail. Our study reveals the existence of temporal changes in the neural representations in area 5d both across different epochs of the task and as the reach movement approaches.

In particular, we show that the reference frame used during the pretarget, fixation period appears to be different from that used in later stages of the task. Previous studies have shown a general dominance in this region for signals involving the hand, arm, and shoulder rather than the gaze, and also a specific lack of hand–gaze encoding during the late delay period (Georgopoulos and Massey, 1985; Ferraina and Bianchi, 1994; Scott et al., 1997; Bremner and Andersen, 2012). We therefore anticipated that cells would encode the position of the hand in body-centered or extrinsic space during the fixation epoch, similar to that reported by Lacquaniti et al. (1995). Instead we found that hand position is in fact coded relative to gaze location at this point in the task, possibly reflecting the immediate behavioral goal of maintaining hand and gaze fixation. The source of this signal could be the PRR or PMd, both of which have similar H−G encoding during the fixation period (Chang et al., 2009; Pesaran et al., 2010, their supplemental material). The H−G signal is not maintained throughout the task, but becomes progressively weaker in the population once the reach target is present and the behavioral goal is shifted toward planning the upcoming reach.

Psychophysical studies have shown that sensorimotor integration can be context dependent (Vetter and Wolpert, 2000; Kording and Wolpert, 2004; Sober and Sabes, 2005). Recent fMRI experiments further demonstrated that the reference frame in which a motor goal is encoded in human posterior parietal cortex depends on the sensory modality through which the target is presented, with flexible switching occurring between the different representations (Bernier and Grafton, 2010). Similarly, our results suggest that neural responses in area 5d may represent postural information in the reference frame that is most appropriate at each stage in the task.

An alternative explanation that we cannot rule out is that the animals may be covertly forming a default reach plan during the fixation period. Before the presence of an explicit target, the most naturalistic behavior is to reach toward the location of gaze, in which case the planned “reach” vector would be H−G. This default plan would be replaced by the actual reach plan after target onset, and the activity in area 5d would at all times be representing the reach vector in the current plan, either default (during the fixation period) or actual (during the delay period). This hypothesis could also explain why hand and gaze are encoded in a vector form during the fixation period despite being independently manipulated. Cells in area 5d do not typically respond in the delay period during planning of saccades. It would therefore be interesting to record from neurons during interleaved reach and saccade planning trials to see whether the H−G activity we observed in the fixation epoch is also present when the default movement plan would be for a saccade rather than a reach.

Second, we show that the pooled population response in area 5d is not static even after the onset of the reach target. During the delay period, the reach vector T−H is the dominant representation in the population, compared with T−G and H−G, and remains so until movement execution, consistent with previous reports of time-invariant reference frames in posterior parietal cortex (Buneo et al., 2008; Lehmann and Scherberger, 2013). However, both the sliding window and epoch analyses show for the first time that the population T−H representation is not static during this time but builds in strength from target onset to movement onset, in part due to recruitment of additional tuned cells. The timing of this increase corresponds with an increase in firing rate commonly observed in the later stages of the delay period in area 5d cells and may reflect anticipatory activity, although trial-by-trial analysis of the correlation between firing rate and reaction time did not reveal a prominent role for area 5d in initiating the reach. The previous study by Buneo et al. (2008) reported invariance of reference frames over time in a sliding window analysis. However, they used variability in firing rate to assess the best-fitting reference frame and it is likely that this different outcome measure explains the difference between their results and those reported here. In addition, our study used a comprehensive set of trial types enabling us to take a more detailed approach to the question.

Our results also show a striking lack of gaze-centered coding for target position (T−G) during the early delay period. This is when the visual target first appears, and it might be expected that there would be at least a brief gaze-centered response at the onset of the visual stimulus. There is some influence of gaze position on firing rate for a subset of cells, but the combined SVD and gradient analysis demonstrates that this is limited to nonsystematic effects (Fig. 6A). The example cell in Figure 2A shows a small visual-related response but, in general, cells in area 5d have little increase in firing with the onset of a visual cue and instead ramp up their activity as the time of movement onset approaches. This is in contrast to neighboring PRR where cells usually show a clear cue-related peak, followed by sustained firing during the delay period (see Cui and Andersen, 2011, Figure 3, for examples of population responses for PRR and area 5d). PRR has been found to code reach targets in a predominantly gaze-centered reference frame (Andersen et al., 1998; Batista et al., 1999; Buneo et al., 2002; Cohen and Andersen, 2002; Pesaran et al., 2006, but see Mullette-Gillman et al., 2005, 2009; Chang and Snyder, 2010; McGuire and Sabes, 2011). There is no a priori reason why cells that code an upcoming reach movement relative to the direction of gaze should also have visually evoked responses. However, in terms of the overall flow of information in the brain–from retinotopic inputs to motor output–earlier processing stages would seem to be more likely to respond directly to a visual stimulus, with this response diminishing in later stages.

While we cannot rule out the possibility of an extremely rapid gaze-centered response that was too transient to be captured in the 200 ms sliding window, our temporal analysis strongly suggests that there is no progression from sensory to motor reference frames within area 5d. Instead, it is likely that area 5d is downstream of the transformation, reading out the results of a computation taking place in other regions or circuits, such as the reciprocal circuit between the PRR and PMd. Our results are consistent with computational models in which the input layer (e.g., gaze-centered spatial information) is mapped to the output layer (e.g., hand or body-centered spatial information) via an intermediate or hidden layer (Zipser and Andersen, 1988; Pouget and Snyder, 2000; Xing and Andersen, 2000). Once such circuits are established, the sensorimotor transformation can occur almost immediately, in only the time it takes for signals to propagate through the network. The gain modulated properties of cells in PRR (Andersen et al., 1998; Chang et al., 2009) and the relative coding scheme in PMd (Pesaran et al., 2006, 2010) suggest that these nodes in the frontoparietal reaching circuit may be candidates for the hidden layer, with area 5d serving as an output layer.

The function of this output layer may be to combine plans for future movement with sensory feedback and efference copy of motor commands to form an accurate estimate of the current and upcoming limb dynamics. The brain is thought to generate such an internal forward model of the arm to reduce the instability in movements that would occur if the system relied solely on the relatively slow visual and proprioceptive signals from the periphery for feedback (Wolpert and Miall, 1996; Desmurget and Grafton, 2000). Evidence from lesion studies and transcranial magnetic stimulation in humans, as well as neurophysiological studies in monkeys, has long pointed to the superior parietal lobe as a critical node in the network responsible for on-line control of limb movement through state estimation (Georgopoulos et al., 1984; Lacquaniti et al., 1995; Wolpert et al., 1998; Desmurget et al., 1999; Pisella et al., 2000; Gréa et al., 2002; Galletti et al., 2003; Della-Maggiore et al., 2004; Battaglia-Mayer et al., 2013). The observed strengthening of the reach vector (T−H) described above suggests that area 5d is not merely reading out the pending motor plan, which would require no change in strength of tuning as the delay period progresses, but may instead be involved in building the state estimate for the limb. Previous studies of area 5d during reaches and joystick movements have found neurons that reflect the arm or cursor trajectory with timing slower than required for the outgoing motor command yet more rapid than would be expected for incoming sensory feedback (Mulliken et al., 2008; Archambault et al., 2009, 2011). Such intermediate timing is suggestive of area 5d as the locus for a forward model of the arm within the superior parietal lobe. In the delayed reaching task used in the current study the arm was stationary during all measured epochs so that we could accurately assess the reference frame(s); we therefore cannot make inferences about area 5d as a potential forward model. However, it is worth noting that the population gradient resultant orientations for TH in the time after the start of the reach shift increasingly from T−H toward T (Fig. 4, center column). At this point in the task, the hand (H) is not fixed but is moving toward and ultimately converges on the target position (T): in other words T = H at the moment of target acquisition. The shift in matrix gradient orientation after movement onset indicates that area 5d is reflecting the convergence of the hand onto the target. We did not formally analyze the movement epoch because we did not track hand motion once the hand had left the touch screen, but this pattern is consistent with first planning and then on-line coding of the reaching trajectory. Interestingly, similar conclusions were drawn from the results of an earlier reaching study in which the activity of subsets of area 5 neurons was observed to be related to the initial or upcoming position of the limb (Lacquaniti et al., 1995), though eye position was not controlled or monitored in that study.

There are several caveats to our results. Neurons in area 5d are heterogeneous in their responses: 23% of all our recorded neurons did not respond in a spatially tuned way to the reaching task. This suggests that, in common with other high-level cortical regions, area 5d almost certainly serves multiple functions, of which a possible role in state estimation is only one. Second, it was not experimentally feasible to test for all potential representations or transformations, such as head centered, body centered, or shoulder centered, and reaches were confined to the range −20 to 10°. However, had it been practical to track more representations across a wider spatial range, we would not expect this to alter our finding that reference frames in area 5d are modulated during reach planning. Simultaneous recording from a population of cells would shed further light on the temporal dynamics of reference frame encoding, but was beyond the scope of the current study.