Abstract
A fundamental feature of pennate muscles is that muscle fibers are oriented at an angle to the line of action and rotate as they shorten, becoming more oblique throughout a contraction. This change in fiber orientation (pennation angle) can amplify the shortening velocity of a fiber and increase output velocity of the muscle. The velocity advantage resulting from dynamic changes in pennation angle can be characterized as a gear ratio (muscle velocity/fiber velocity). A recent study has shown that a pennate muscle’s gear ratio varies automatically depending on the load such that a muscle operates with a high gear during rapid contractions and low gear during forceful contractions. We examined whether this variable gearing behavior can be replicated in a pennate array of artificial muscles. We used McKibben type pneumatic actuators, which shorten in tension when filled with compressed gas. Similar to muscle fibers, the actuators expand radially during shortening, a feature thought to be a critical part of the variable gearing mechanism in pennate muscles. We arranged McKibben actuators in an array oriented to mimic a pennate muscle, and quantified the system’s gear ratio during contraction against a range of loads. Video was used to measure the gear ratio during each contraction. We find that similar to pennate muscles, the gear ratio decreases significantly with increasing load and that variable gearing results from load-dependent variation in the amount of actuator rotation. These results support the idea that variable gearing in pennate muscles is mediated by difference is fiber rotation and the direction of muscle bulging. The behavior of our artificial muscle array also highlights the potential benefits of bio-inspired architectures in artificial muscle arrays, including the ability to vary force and speed automatically in response to variable loading conditions.
1. INTRODUCTION
The architectural properties of muscles can affect function by altering the capacity for generating force and displacement (Gans, 1982; Otten, 1988). The relationships between force, length and shortening velocity in a single muscle fiber in isolation can be characterized by the interactions of actin and myosin and the dynamics of cross-bridge formation. However, the orientation of that fiber within the muscle can determine how the forces and displacements generated by the muscle fiber are transmitted to the skeletal system and ultimately act against an external load. The functional variation in architectural properties is often simplified to a comparison of pennate and parallel fibered muscles. Pennate muscles have fibers that are oriented at an angle relative to the line of muscle action, while parallel muscles have fibers oriented parallel to muscle action. In pennate muscles the oblique fiber orientation allows more fibers to be packed into a given volume of muscle. Packing more fibers in parallel allows pennate muscles to generate relatively higher force (Alexander, 1968). In contrast, parallel fibered muscles have longer fibers with more sarcomeres in series, allowing for greater muscle shortening and velocity during a contraction (Lieber and Friden, 2000).
An important difference between pennate and parallel fibered muscles is that the fibers of pennate muscles change orientation (pennation angle) during a contraction. The rotation of fibers during a contraction increases the amount of muscle shortening for a given fiber shortening, because the displacement at the level of the whole muscle results from a combination of translation and rotation at the level of the fiber (Brainerd and Azizi, 2005). The amplification of fiber shortening in pennate muscles can be characterized by a muscle’s architectural gear ratio (AGR), defined as the ratio of whole muscle shortening (or velocity) to muscle fiber shortening (or velocity) (Brainerd and Azizi, 2005). In pennate muscles, the effect of fiber rotation during a contraction results in a gear ratio greater than one.
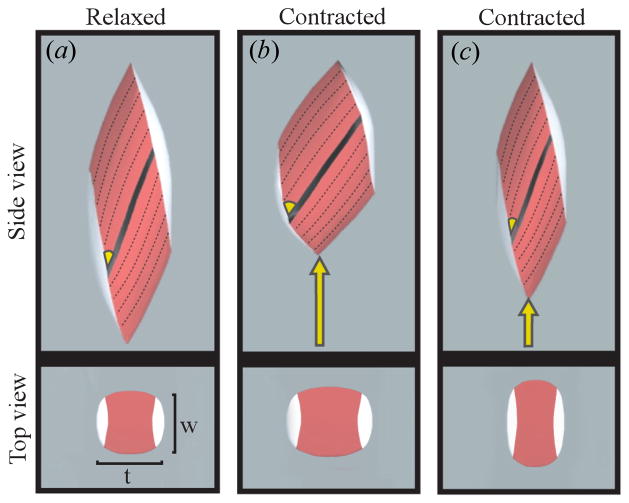
A recent study has shown that pennate muscles operate with a range of gear ratios depending on the load experienced during contraction (Azizi et al. 2008). Variable gearing results from load-dependent variation in fiber rotation during contractions. When contracting against light loads, muscle fibers undergo significant changes in pennation angle, and the muscle increases in thickness and produces a large amount of muscle displacement (Fig. 1b). Conversely, when contracting against heavy loads, muscle fibers rotate less, the muscle decreases in thickness and produces a smaller amount of muscle displacement (Fig. 1c). This variable gearing mechanism suggests that pennate muscles have the capacity to operate with an “automatic transmission system” to better match force and velocity outputs to the specific demands of the contraction.
Figure 1.
Simulations of contractions in an isovolumetric, three-dimensional, virtual pennate muscle. (a) The muscle belly and aponeurosis shown at rest. Note the specified muscle thickness (t) and muscle width (w), both measured in planes orthogonal to the line of muscle action. (b) A simulation of a contraction in which muscle fibers shorten by 13% of resting length with an increase in thickness and pennation angle. This contraction produces a large amount of muscle shortening (arrow) and a high gear ratio, favoring velocity. (c) A simulation of a contraction in which muscle fibers shorten by 13% of resting length with a decrease in thickness and a small amount of fiber rotation. This contraction results in a small amount of muscle shortening (arrow) and a low gear ratio. The decreased fiber rotation also favors force production because a higher component of fiber force remains aligned with the muscle’s line of action. Adapted from Azizi et al. 2008.
The ability to automatically alter the gear ratio or the mechanical advantage with which actuators act against loads may be a broadly advantageous mechanism for use in robotics, powered prostheses and orthoses. The design of many modern actuators used in such applications now includes a number of mechanical features inspired by muscle (Bar-Cohen, 2006). For example, many pneumatic actuators and electroactive polymers possess compliance, shape, weight and force properties similar to those of natural muscles (Meijer et al. 2003). Most often actuators used in robotics, powered prostheses and orthoses are oriented directly along a given line of action in order to create motion at a joint (e.g. Hosoda et al. 2006, Sawicki et al. 2002, Tondu et al. 2005). The recent advances in our understanding of the architectural features of skeletal muscle may provide new design inspiration for artificial actuator systems. Specifically, the utilization of a variable gearing mechanisms may allow some ability to respond to changes in mechanical conditions independently of central controllers.
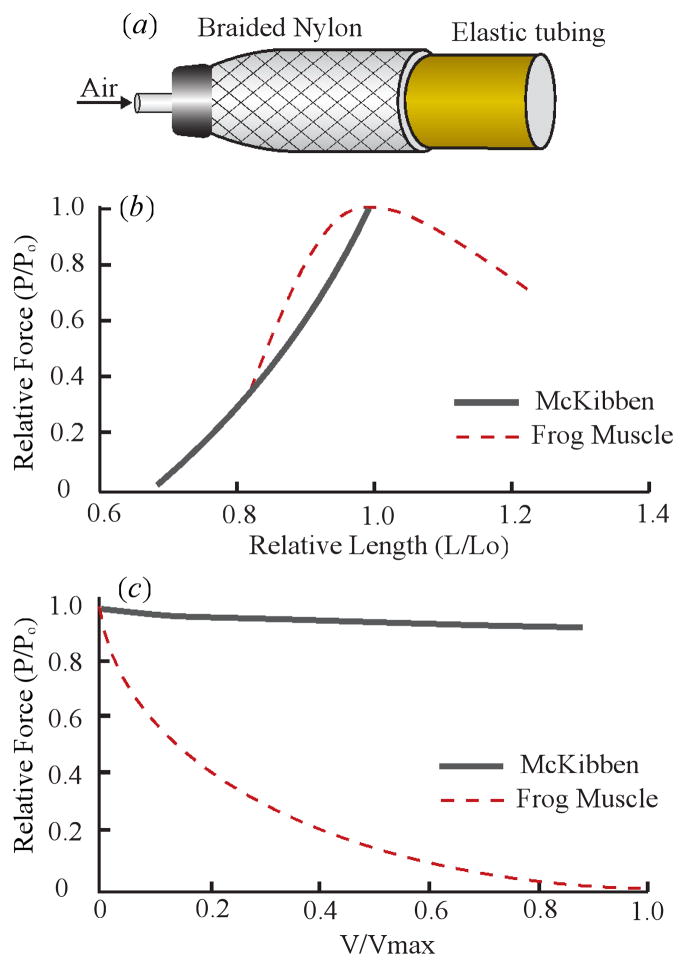
In this study, we constructed a mechanical actuator array inspired by the architecture of a pennate muscle and consisting of five McKibben type pneumatic actuators. We chose to use McKibben pneumatic actuators for several reasons. First, McKibbens have high power to weight ratio making them a commonly used biomimetic actuator (Daerden and Lefeber, 2002). In addition, McKibben pneumatic actuators are appropriate linear models for natural muscle fibers due to their similar force-length relationships (Klute et a. 2002; Fig. 2b). Most importantly, similar to skeletal muscle fibers, McKibben actuators expand radially when they shorten. This shape change is thought to be a critical feature of the variable gearing mechanism in pennate muscles. Finally, unlike skeletal muscle where force and velocity are inversely coupled, velocity has little effect on force in McKibbens (Klute, 2002; Fig. 2c). This feature allowed us to decouple the effect of load from actuator velocity in ways that are not practical in skeletal muscle.
Figure 2.
Summary of key mechanical properties of McKibben actuators. (a) The McKibben type pneumatic actuator consisting of an internal elastic tube, surrounded by braided polyester. Inflation of the inner tubing causes shortening of the actuator along its long axis as well as the radial expansion of the actuator (b) The force-length relationship of a McKibben muscle (Klute et al. 2002) shown with the curve for a frog plantaris muscle (Azizi and Roberts, 2010). The McKibben actuator relationship shows an increase in force as length increases until it reaches its maximum length. (c) The Force-velocity relationship of the McKibben muscle (Klute et al. 2002) alongside the curve for the frog plantaris muscle (Azizi and Roberts, 2010). Unlike skeletal muscle, McKibben actuator shows little decrease in force as velocity increases.
We used a pennate array of McKibben actuators to test the hypothesis that the gear ratio of an actuator array varies in a load-dependent manner. Specifically, we tested the prediction that similar to pennate muscles, gear ratio will decrease with increasing load such that the array favors force production at high loads and favor velocity at low loads. Although the physical model is inspired by pennate muscles, the system is greatly simplified in order to isolate the few mechanical features likely responsible for the variable gearing mechanism. We aimed to both mimic the biological system in order to highlight a potentially more effective design for actuator arrays and to use a simple physical model to better understand the mechanical behavior of pennate muscles.
2. MATERIALS AND METHODS
2.1 Construction and Assembly
We constructed the McKibben pneumatic actuators according to methods used by Ferris and coworkers (Ferris et al. 2005). McKibben actuators are constructed from an inner tube that expands under air pressure, and an outer sleeve with helically wound fibers that translate increases in diameter of the inner tube to shortening of the entire unit. In our actuators, the inner latex tubing for each actuator had an inner diameter of 1.7 cm, thickness of 1.7 mm, and length of 26 cm. We capped the distal end of the tubing with a hex plug, and the proximal end with a hex plug with a 90° elbow valve connected via tygon tubing to a supply of compressed air. We inserted the tubing into a braided polyester sleeve (Techflex Inc., NJ, USA) and folded over the spare ends of the polyester through two D-rings on each side, in order to secure the actuators in the array. (Fig. 2a) We sealed each end of the sleeve with rubber latex and tightly pressed an ear clamp on each end. The final length of each actuator is approximately 31.5 cm with a resting diameter of 2 cm and maximum active diameter of 4 cm.
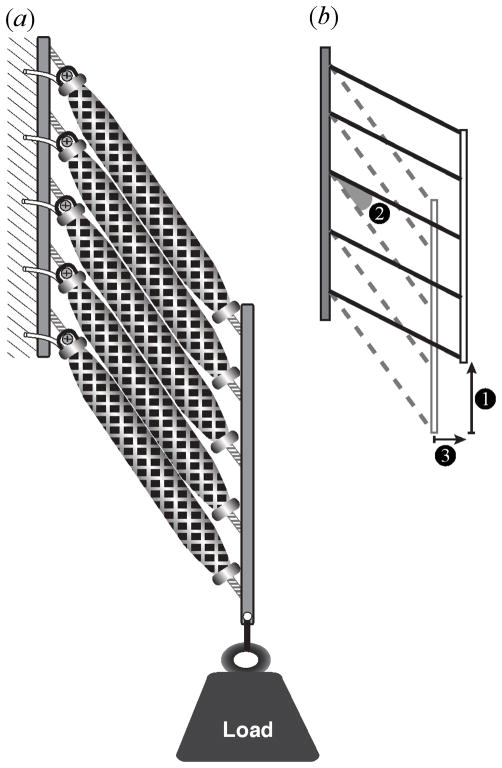
We assembled our array using a vertical frame constructed from extruded aluminum (80/20 Inc., IN, USA). On the proximal end of the array, we screwed five eye-bolts to the vertical supported piece of 80/20, each 3.6 cm apart, and attached one actuator to each with a bolt loosely connecting the D-rings to the eye bolt in order to allow for free rotation of the actuator relative to the vertical frame at the proximal attachment point of the actuator (Fig. 3a). On the distal end, a piece of acrylic (21.5 cm × 3 cm), with five tapped holes each 3.6 cm apart was used to tightly attach the actuators using eye-bolts. A hole at the end of the distal piece of acrylic was used to attach various weights to the array using Kevlar rope. All five actuators were inflated simultaneously with compressed air at 50 psi. In preparation for recording and digitizing, the proximal and distal ends of the all actuators as well as the attachment point of the load were marked for easy visualization. In all cases the initial orientation of the actuators was about 30° relative to the vertical.
Figure 3.
Schematic of the pennate actuator array. (a) The array consisted of five McKibben actuators oriented at an angle relative to the line action (vertical). Actuators were rigidly fixed to acrylic plates at each end but were able to rotate freely during contractions. A load was lifted vertically in each trial, and a series of trials was conducted over a range of loads. (b) A schematic depicting the variables measured during each trial. In addition to the length of each actuator, the vertical displacement of the load (1), the change in the orientation of the actuator (2) and the change in the thickness of the array were measured for each trial (3).
2.2 Data Collection
A digital video camera (JVC 9800) was used to record the kinematics of the McKibben array at 30 frames per second during each contraction. To begin the contraction of the McKibben array, a valve was opened which allowed inflation of all actuators simultaneously. The array contracted and lifted the load until the actuator shortened maximally, at which point the air was released from all of the actuators. The array acted against 11 different loads ranging from 0 to 10 kg, increasing in 1kg increments. Five contractions were recorded at each load.
2.3 Data Analysis and Statistics
Videos were uploaded to a PC and the position of several landmarks was digitized in each frame throughout each contraction using Matlab software (MathWorks Inc.) and a direct linear transformation tracking algorithm (Hedrick, 2008). The digitized points included 1) the proximal end of each actuator, 2) the distal end of each actuator, and 3) the bottom of the distal acrylic sheet. X-Y positions of digitized points were used to calculate instantaneous distances. All distances were then calibrated using a grid placed in the field of view.
The four variables calculated for each trial included: actuator shortening, array shortening, array thickness and actuator rotation (Fig. 3b). All variables were analyzed for 1s, beginning from the time the load was lifted off the ground. Unlike muscles, actuator velocity is independent of load, meaning that all of the contractions in the current study shortened at a fixed velocity. Thus a constant contraction time of 1s resulted in the same amount of actuator shortening across loading conditions. This was validated independently is a subset of contractions. Although the lengths of all actuators in the array were measured, little difference was observed between actuators and therefore only the middle actuator was used in our formal analyses. Actuator shortening is the change in length of the middle actuator. Array shortening was measured as the vertical (Y) displacement of the point on the bottom of the array (Fig. 3b). The change in array thickness was the horizontal displacement of the point on the bottom of the array (Fig. 3b). Actuator rotation was the change in the pennation angle (acute angle relative to vertical) of the middle actuator (Fig. 3b). The AGR of each contraction was calculated as the ratio of the vertical velocity of the array and the actuator shortening velocity. All variables were calculated using Igor Pro V.6 (Wavemetrics Inc., OR, USA). Each of the measured variables was regressed against load to determine how the behavior of the array changed with increasing load. Linear regressions were performed using JMP software (SAS Inc., NC, USA).
3. RESULTS
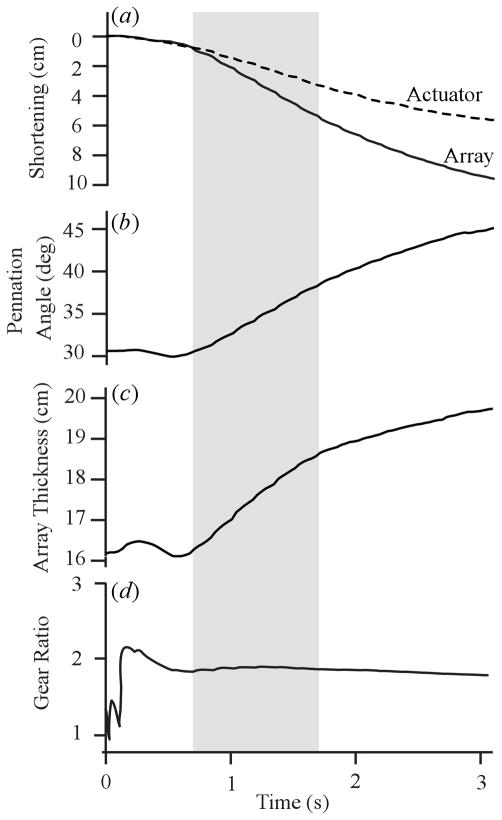
During all contractions of the McKibben pennate array, the shortening velocity of the array (in the vertical direction) exceeded the shortening velocity of the actuators (Fig. 4a). This confirmed that similar to pennate muscles, the array operated with a gear ratio greater than one. The amplification of actuator velocity resulted from changes in the orientation of the actuators, as indicated by the measured increase in pennation angle throughout each contraction (Fig. 4b). The thickness of the array also increased in each contraction, highlighting the dynamic shape changes of the muscle array associated with actuators shortening and radial expansion (Fig. 4c).
Figure 4.
Representative data from the McKibben actuator array contracting against a 20 N load. For each trial, we analyzed measurements from when the load left the ground until one second afterwards (gray bar). (a) The relative shortening of the actuator (dashed) and array (solid) during the contraction. In all trials the amount of array excursion measured in the vertical direction exceeded the shortening of individual actuators. For this trial the initial length of the actuator is 30.2 cm. (b) Changes in pennation angle during the contractions. In all trials shortening of the actuator along its length was accompanied by changes in its orientation relative to the vertical (pennation angle). (c) Increase in array thickness during the contraction. (d) A plot of instantaneous gear ratio during the trial.
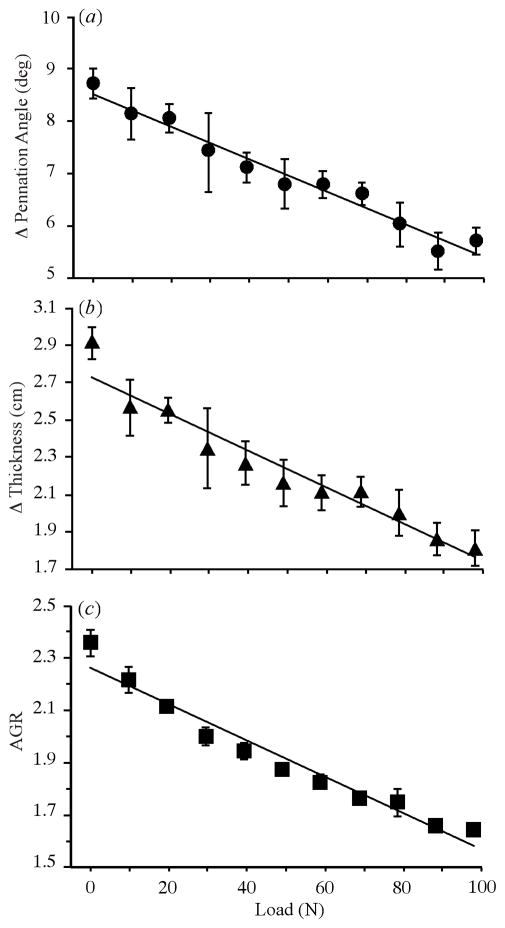
The pattern of change in array thickness and actuator rotation was consistent with the proposed mechanism for load-dependent variable gearing (Azizi et al., 2008). The amount of actuator rotation decreased significantly with increasing load (p<0.0001; Fig. 5a). Similarly, change in array thickness decreased significantly with increasing load (p<0.0001; Fig. 5b). These results were consistent with predictions from muscle simulations, which show that the increases in thickness and fascicle/actuator rotation should be coupled (Azizi et al. 2008). Load-dependent variation in actuator rotation and changes in thickness resulted in a load-dependent pattern in architectural gear ratio (AGR) similar to that observed in biological muscle. AGR decreased significantly with increasing load (p<0.0001; Fig 5c). For example, when the array lifted 0kg, it operated at a gear ratio of 2.36, indicating that the array shortening velocity is amplified 136% relative to the actuator velocity. Conversely, when lifting 10kg, it operated at a gear ratio of 1.64, corresponding to a 64% amplification in velocity. Reduced actuator rotation at higher loads is potentially beneficial to the overall force production of the array since a larger component of the actuator force remains oriented along the array line of action (vertical).
Figure 5.
Changes in architectural gear ratio, fiber rotation and thickness at different loads. (a) The architectural gear ratio (array velocity/actuator velocity) decreases significantly with increasing load (p<0.0001). (b) Rotation of the McKibben actuators decreases significantly with increasing load (p<0.0001). This decrease in fiber rotation corresponds with a decrease in array shortening at high loads. (c) The increase in array thickness during a contraction decreases significantly with increasing load (p<0.0001). Note that the architectural gear ratio of an actuator array oriented parallel to the line of action would be 1 and would be invariant as a function of load. Values are mean ± SD; n = 5 trials.
In this study, we varied the load that the McKibben array lifted during each contraction, but were not able to control the shortening velocity of the actuators. Though there were significant load-dependent changes in fiber rotation, array thickness and AGR, there was no significant effect of load on actuator shortening velocity (p=0.17). This result confirmed that for the range of loads studied, there is negligible effect of load on McKibben actuator velocity. In addition, this result suggests that variations in AGR, actuator rotation and array thickness are independent of actuator shortening velocity and depend solely on the architecture of the array and the varying loads against which the array contracts.
4. DISCUSSION
In this study, a pennate McKibben actuator array displays a variable gearing mechanism similar to natural muscles. In our McKibben array, AGR, actuator rotation and array thickness varied inversely with load, similar to the pattern that has been observed in pennate muscles (Azizi et al. 2008). Both systems operate with a high AGR during contractions against light loads (Fig. 6). This suggests that the architectural features present in both biological muscles and our artificial muscle array operate with a velocity advantage when high forces are not required. However, when operating against a high load, actuators and muscle fascicles undergo less rotation and therefore maintain a higher proportion of force oriented along the line of action (Fig.6). This allows the system to operate with a better mechanical advantage for force when subject to high loads.
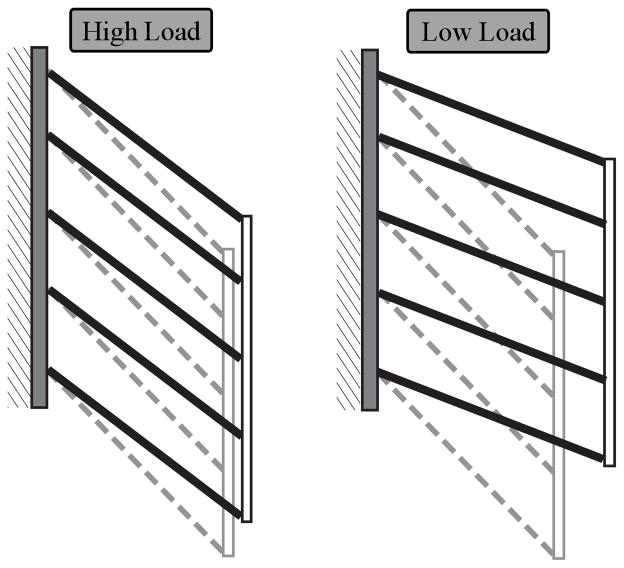
Figure 6.
A schematic depicting the behavior of the actuator array under different loads. The images are based on representative trials and show two contractions with the same actuator shortenings but significant differences in the array’s output displacement. At low loads the array has significantly greater actuator rotation, which causes greater vertical array displacement and greater array thickness between its two vertical constraints. At high loads the array has less actuator rotation, which causes significantly less vertical array displacement and lower array thickness. The decreased change in actuator orientation allows a larger component of actuator force to remain parallel to the line of action when contracting against a high load.
The mechanism of variable gearing described here is automatic, resulting not from any control mechanism but from the intrinsic mechanical behavior that emerges from the actuator architecture. Such a variable gearing mechanism may be beneficial in the design of bio-actuator systems as it allows the system to respond to changes in mechanical loading conditions rapidly and without sensory information or feedback control. The variable gearing behavior of a pennate-like array could provide robust response to external perturbations, expand the greater range of mechanical performance compared with a single actuator, and under some conditions reduce the level of feedback control needed in response to changes in load.
Our results show that obliquely oriented McKibben actuators follow different trajectories when shortening against different external loads. It has been previously proposed that such dynamic changes in the muscle behavior result from the intramuscular forces and pressures on connective tissue elements (Azizi et al. 2008). Muscles maintain a constant volume during contraction (Baskins and Paolini, 1967) and therefore need to expand in directions orthogonal to their line of action as they shorten. Tissues that resist such expansion may therefore mediate how the muscle changes shape and ultimately determine the gear ratio with which the muscle operates. It is clear that the McKibben array used in this study lacks many of the complex architectural features hypothesized to govern variable gearing in muscles. However, only a few key features of the Mckibben actuator array appear to be sufficient to reproduce the essentials of a variable gearing mechanism. Specifically, the actuators expand radially upon shortening (Daerden and Lefeber, 2002). In the array tested here, the radial expansion of the actuators was limited by the expansion of neighboring actuators during the contraction. As a result, the packing of McKibbens in a tight space likely functions to constrain the shape changes of the array in a manner that is load-dependent. Lower gearing at high loads resulted from reduced actuator rotation, likely due to load-dependent resistance to radial expansion in the vertical direction. Therefore, similar to pennate muscles the variable gearing mechanism observed in this study is likely mediated by directional resistances to shape changes, which ultimately alter gearing.
In a simplified condition where the shape changes in the actuator are not resisted and they expand radially in all directions we can express changes in muscle/array thickness (ΔMt) as function of the initial radius of the actuator (r), the longitudinal strain of the actuators (εl), and the pennation angle (θ),
| (1) |
Here we assume that actuators retain a constant volume and that the component of radial expansion oriented along the thickness of the array causes an increase in thickness. The expansion in muscle thickness is then summed based on the number of actuators (n) in the array. This relationship provides a first approximation of the effect of initial angle, strain, and actuator dimensions on the potential change in thickness, but it is simplified in that it does not account for changes in pennation angle during the shortening event. It is also based solely on kinematic and geometric considerations, and does not include the complex shape changes (e.g., non-symmetrical radial expansion of actuators) that underlie the variable response of the array to load. Although this simplified relationship doesn’t examine how changes in loads acting on the array can alter changes in muscle thickness it can accurately predict changes in muscle thickness at low loads, therefore suggesting that higher loads force the actuators to deviate from the assumption of uniform radial expansion.
Our results also suggest that variable changes in muscle thickness can result in variation in architectural gear ratio. A simple model based on array geometry can also be used to define the relationship between architectural gear ratio (AGR) and changes in muscle thickness (ΔMt), initial actuator length (L), initial pennation angle (θ) and actuator strain (εl).
| (2) |
This equation is derived by solving the geometric relationship between the architecture of the array before the contraction and architecture of the array at the end of the contraction. We simplify the system to two right triangles one representing the initial and one representing the final geometry of the array. Using the initial pennation angle, and strain of the actuator, all other dimensions can be calculated. This relationship predicts that an increase in muscle thickness will increase the array’s gear ratio. Inputting the geometry and dimensions of our physical model into equations 1 and 2 and assuming an actuator strain of 20%, we calculate that the array would operate with a gear ratio of 1.69. While this predicted value is reasonable, it underestimates some of the higher gear ratios we recorded during trials at low loads suggesting that these trials deviated from some of our simplifying assumptions. The relationships derived above are based solely on geometric considerations and are therefore insufficient to describe the intricate relationship between load and AGR. Nonetheless such simplified relationships may serve as useful first approximation for comparing the behavior of different actuator systems and varying array designs.
A pennate actuator array may be effectively tuned for different tasks by adjusting a few design parameters. One such parameter is the initial orientation of the array. In this study actuators were oriented at 30° relative to the line of action. Increasing this angle would likely increase the range of gear ratios with which the system operates (Brainerd and Azizi, 2005). The variable gearing mechanism could potentially be refined through the addition of structures that constrain array shape. Specifically, encasing the array in a material with directionally heterogeneous mechanical properties may allow for tuning of the system by varying the range of available gears.
The utility of the architectural design highlighted in this study likely extends beyond McKibben actuators. For many applications, pneumatic actuators like McKibbens are not ideal. Despite having a high power to weight ratio and length-tension properties that resemble natural muscles, McKibbens can be impractical for use in prostheses and orthoses because 1) a heavy canister of compressed air must accompany the actuators for inflation and 2) expulsion of air after each contraction is loud and conspicuous (Chou and Hannaford 1996). In contrast, artificial muscles constructed from electroactive polymers (EAP) only require a small power source and are silent during activation (Kaal and Herold, 2011). In addition, EAPs have similar strain, shape and performance as natural skeletal muscle when formed into cylindrical units (Herr et al. 2004). EAPs also share a critical feature with McKibbens as both actuators expand radially upon activation. In particular, electric EAPs use electricity to cause a polymer to change thickness and length using Coulomb’s attraction/repulsion forces (Meijer et al. 2003). As discussed above, the radial expansion of the actuator is thought to be critical in driving the shape changes in the array and therefore thought to be a necessary part of a variable gearing mechanism. Given that EAPs, like KcKibben actuators shorten under isovolumetric conditions, we believe the mechanism of variable gearing described in this paper can be expanded to EAP based actuator arrays.
One key difference between the properties of Mckibben actuators and natural muscle fibers is the intrinsic relationship between force and velocity. In skeletal muscle, the relationship between force and velocity is well-described by a hyperbolic function, which highlights that the force muscle fibers generate decreases with increasing speed of contraction (Hill, 1953; Fig. 2d). Due to this intrinsic relationship, it can be difficult to decouple the effect of force and velocity on the variable gearing mechanism. Previous experimental results are mixed with some showing that changes in a muscle’s gear ratio result from changes in the load associated with the contraction (Azizi et al. 2008), while others suggest that variable gearing results from changes in contraction speed (Wakeling et al. 2011; Randhawa et al. 2012). The fundamental trade-off between force and speed is not present in McKibben actuators, which can maintain a constant shortening velocity despite increases in force (Klute, 2002; Fig. 2c). Taken together, the independence of force and velocity in the McKibben array and presence of variable gearing mechanism provide support for the hypothesis that variation in mechanical load is a critical determinant of variation in a muscle’s gear ratio.
Here we show that a pennate-like actuator array can mimic the variable gearing mechanism previously described for pennate muscles. This mechanism is a purely architectural feature and allows an actuator array to operate with a range of gears depending on the mechanical load. As a result the array is automatically tuned to a specific task without reliance on sensors and controllers. This design feature may be useful in robotics applications as well the design of powered orthoses and prostheses. More generally, the design of muscle-like actuators may benefit from a consideration of the mechanical behavior not just of single force-producing units, but of the potential advantages of assembling actuators in arrays inspired by the architecture of natural muscles.
Acknowledgments
The authors thank Brian Fisher and Greg Sawicki for guidance in McKibben construction. We thank Gavin Crynes for experimental assistance. This work was funded by NIH grant AR055295.
References
- Alexander R, McN . Animal Mechanics. London: Sidgwick and Jackson; 1968. [Google Scholar]
- Azizi E, Roberts TJ. Muscle performance during frog jumping: influence of elasticity on muscle operating lengths. Proceedings of the Royal Society B-Biological Sciences. 2010;277:1523–1530. doi: 10.1098/rspb.2009.2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E, Brainerd E, Roberts T. Variable Gearing in Pennate Muscles. Proceedings of National Academy of Sciences. 2008;105:1745–1750. doi: 10.1073/pnas.0709212105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Cohen Y. Biomimetics using electroactive polymers (EAP) as artificial muscles - A review. Journal of Advanced Materials. 2006;38:3–9. [Google Scholar]
- Baskin RJ, Paolini PJ. Volume change and pressure development in muscle during contraction. Am J Physiol. 1967;213:1025–1030. doi: 10.1152/ajplegacy.1967.213.4.1025. [DOI] [PubMed] [Google Scholar]
- Brainerd EL, Azizi E. Muscle fiber angle, segment bulging and architectural gear ratio in segmented musculature. Journal of Experimental Biology. 2005;208:3249–3261. doi: 10.1242/jeb.01770. [DOI] [PubMed] [Google Scholar]
- Caldwell DG, Tsagarakis Biomimetic Actuators in Prosthetic and Rehabilitation Applications. Technology and Health Care. 2002;10:107–120. [PubMed] [Google Scholar]
- Chou C-P, Hannaford B. Measurement and Modeling of McKibben Pneumatic Artificial Muscles. IEEE Transactions on Robotics and Automation. 1996;12:90–102. [Google Scholar]
- Daerden F, Lefeber D. Pneumatic Artificial Muscles: actuators for robotics and automation. European Journal of Mechanical and Environmental Engineering. 2002;47:11–21. [Google Scholar]
- Ferris DP, Czerniecki JM, Hannaford B. An ankle-foot orthosis powered by artificial pneumatic muscles. Journal of Applied Biomechanics. 2005;21:189–197. doi: 10.1123/jab.21.2.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gans C. Fiber architecture and muscle function. Exercise and Sports Sciences Reviews. 1982;10:160–207. [PubMed] [Google Scholar]
- Hedrick TL. Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspiration & Biomimetics. 2008;3:1–6. doi: 10.1088/1748-3182/3/3/034001. [DOI] [PubMed] [Google Scholar]
- Herr H, Kornbluh R. New Horizons for Orthotic and Prosthetic Technology: Artificial Muscle for Ambulation. Proceedings of SPIEs Smart Structures and Material. 2004;5385:1–9. [Google Scholar]
- Hosoda K, Takuma T, Nakamoto A. Design and control of 2D biped that can walk and runwith pneumatic artificial muscles. Proc. IEEE–RAS Int. Conf. on Humanoid Robots; Genova. 2006. pp. 284–289. [Google Scholar]
- Hill AV. The mechanics of active muscle. Proceedings of the Royal Society B-Biological Sciences. 1953;141:104–17. doi: 10.1098/rspb.1953.0027. [DOI] [PubMed] [Google Scholar]
- Kaal W, Herold S. Electroactive Polymer Actuators in Dynamic Applications. Ieee-Asme Transactions on Mechatronics. 2011;16:24–32. [Google Scholar]
- Klute GK, Czerniecki JM, Hannaford B. McKibben Artificial Muscles: Actuators with Biomechanical Intelligence. International Conference on Advanced Intelligent Mechantronics; Atlanta, GA. 1999. pp. 221–226. [Google Scholar]
- Klute GK, Czerniecki JM, Hannaford B. Artificial Muscles: Actuators for Biorobotic Systems. International Journal of Robotics Research. 2002;21:295–309. [Google Scholar]
- Lieber RL, Friden J. Functional and clinical significance of skeletal muscle architecture. Muscle & Nerve. 2000;23:1647–1666. doi: 10.1002/1097-4598(200011)23:11<1647::aid-mus1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Meijer K, Bar-Cohen Y, Full RJ. Biologically Inspired Intelligent Robots. SPIE Press; 2003. Biological Inspiration for Muscle Like Actuators in Robots; pp. 25–4. [Google Scholar]
- Randhawa A, Jackman M, Wakeling J. Muscle gearing during isotonic and isokinetic movements in the ankle plantarflexors. European Journal of Applied Physiology. 2012 doi: 10.1007/s00421-012-2448-z. [DOI] [PubMed] [Google Scholar]
- Sawicki GS, Gordon KE, Ferris DP. Powered lower limb orthoses: applications in motor adaptation and rehabilitation. Paper presented at: IEEE 9th International Conference on Rehabilitation Robotics; Chicago, IL. 2005. [Google Scholar]
- Tondu B, Ippolito S, Guiochet J, Daidie A. A Seven-degrees-of-freedom Robot-arm Driven by Pneumatic Artificial Muscles for Humanoid Robots. International Journal of Robotics Research. 2005;24:257–274. [Google Scholar]
- Wakeling JM, Blake OM, Wong I, Rana M, Lee SSM. Movement mechanics as a determinate of muscle structure, recruitment and coordination. Philosophical Transactions of the Royal Society B-Biological Sciences. 2011;366:1554–1564. doi: 10.1098/rstb.2010.0294. [DOI] [PMC free article] [PubMed] [Google Scholar]